Computational Modeling of Extracellular Mechanotransduction

Abstract

Mechanotransduction may occur through numerous mechanisms, including potentially through autocrine signaling in a dynamically changing extracellular space. We developed a computational model to analyze how alterations in the geometry of an epithelial lateral intercellular space (LIS) affect the concentrations of constitutively shed ligands inside and below the LIS. The model employs the finite element method to solve for the concentration of ligands based on the governing ligand diffusion-convection equations inside and outside of the LIS, and assumes idealized parallel plate geometry and an impermeable tight junction at the apical surface. Using the model, we examined the temporal relationship between geometric changes and ligand concentration, and the dependence of this relationship on system characteristics such as ligand diffusivity, shedding rate, and rate of deformation. Our results reveal how the kinetics of mechanical deformation can be translated into varying rates of ligand accumulation, a potentially important mechanism for cellular discrimination of varying rate-mechanical processes. Furthermore, our results demonstrate that rapid changes in LIS geometry can transiently increase ligand concentrations in underlying media or tissues, suggesting a mechanism for communication of mechanical state between epithelial and subepithelial cells. These results underscore both the plausibility and complexity of the proposed extracellular mechanotransduction mechanism.

INTRODUCTION

Cells often communicate through the exchange of extracellular autocrine and/or paracrine signals. Changes in the local levels of these molecules, derived from alterations in production, metabolism or transport, are dynamically sensed, allowing cells to respond appropriately to their microenvironment (1). We have proposed a mode of mechanotransduction whereby cells respond to changes in the local extracellular concentration of autocrine ligands that are caused solely by deformation of the extracellular space (2). In support of this hypothesis, we demonstrated that the extracellular space in cultured human bronchial epithelial cells deforms under transcellular compressive stress, and that an autocrine ligand-receptor signaling loop is activated by the same mechanical stimulus (2). The essential components of autocrine ligand-receptor circuits are frequently found to be constitutively expressed and colocalized in the basolateral compartment of epithelial cells (3). In our previous work, a simple analytical relationship was derived to predict the steady-state ligand concentration in the local extracellular space before and after mechanical loading (2). While this steady-state analysis was essential in establishing the plausibility of the extracellular mechanotransduction mechanism, it could not address the kinetics of the process, and omitted potentially important effects of convection.

Here we develop a generalized finite-element solution of the one-dimensional diffusion-convection equation to evaluate the temporal changes in ligand concentration occurring in a dynamically collapsing interstitial space between epithelial cells. We introduce a new geometry for the model that accommodates the diffusion and convection of ligands shed into the lateral intercellular space, which is continuous with an underlying media reservoir. Employing the model, we explore the parameter space of the governing equations, examining the effect of ligand diffusivity, shedding rate, and rate of extracellular space change on the kinetics of ligand accumulation. The new model geometry reveals the transient effect of convection on ligand concentration changes in the underlying space (e.g., media for the in vitro case or tissues in vivo), suggesting a potential mechanism for communication of a change in the mechanical state of the epithelium to underlying tissues. Moreover, the model offers a novel explanation for how cells could discriminate between mechanical processes occurring over a range of rates in different physiological scenarios. We use insights gained from the model to propose two explanations for a selective contribution of the EGF family-ligand heparin-binding EGF (HB-EGF) to the transduction of mechanical stress via autocrine signaling in a collapsing extracellular space.

METHODS

We modeled the lateral intercellular space (LIS) separating neighboring cells as idealized parallel plates and assumed free diffusion of ligand into the media reservoir below the LIS. Boundary conditions to represent the special case of an epithelial layer were imposed: impermeable tight junction at the apical surface; open to a large reservoir (e.g., the underlying media), such that sufficiently far below the basal surface the ligand concentration is assumed to be zero (see Fig. 1). Previously we solved the one-dimensional diffusion equation (Fick's law) analytically, with a source term included to account for the constitutive shedding of ligand into the LIS, to obtain the steady-state ligand concentration profile within the LIS:

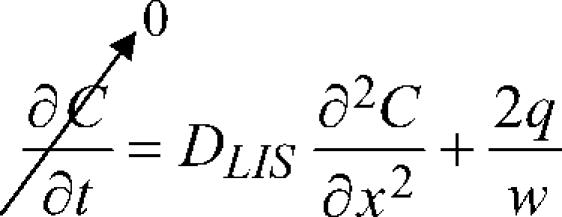(1)

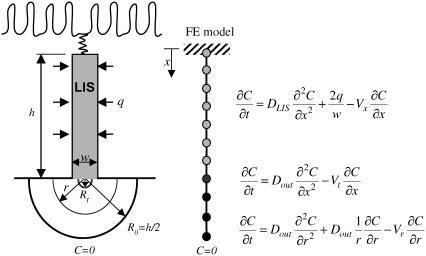
FIGURE 1.

Schematic of LIS finite element (FE) model. Neighboring cells are separated by the LIS. Ligands are constitutively shed into LIS from the cell surface at a rate q. In the space below the LIS, it is assumed that at a radial distance R₀ = h/2 (where h is the LIS height), the ligand concentration is zero. The second boundary condition is an impermeable wall at the top due to the tight junctions (no flux at x = 0). Using one-dimensional isoparametric finite elements we discretize the space into three domains: LIS (for 0 < x < h), transitional (for h < x <h + R_t), and radial (for R_t < r < R₀). Note that the finite elements are not to scale. Each of the domains has its own governing diffusion-convection equation. In the three domains the corresponding bulk fluid velocities are V_x in the LIS, V_t in the transitional, and V_r in the radial domain. The diffusivities D_LIS and D_out (inside and outside the LIS, respectively) may be different. The transitional domain extends R_t = w/π below the LIS.

Here the ligand shedding rate q (distributed along the lateral cell boundary) and ligand diffusion coefficient in the LIS D_LIS are assumed to be constants, and w is the LIS width. Solving for the steady-state ligand concentration C(x) yields

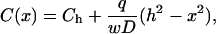(2)

where C_h is the ligand concentration at the LIS boundary x = h.

To account for convective effects, as well as to determine how the concentration at and below the LIS boundary changes during a collapse, we now introduce an extended model geometry with three domains: LIS, transitional, and radial (see Fig. 1). The LIS domain includes the LIS space, from the tight junction to the basal boundary. The transitional domain corresponds to the space between LIS and radial domains, where we numerically switch from a Cartesian to a cylindrical coordinate system. The radial domain represents the outside space (i.e., underlying media or tissues) and allows for radial diffusion of ligand once it leaves the LIS. The governing transport equations for each domain are

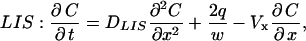(3a)

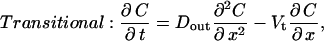(3b)

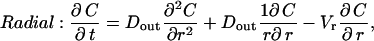(3c)

where D_LIS and D_out are the ligand diffusivities in the LIS and outside space, respectively, V_x is the bulk fluid velocity in the LIS caused by changes in LIS dimensions, V_t is the fluid velocity in the transitional domain (assumed to be uniform), and V_r is the radial fluid velocity at a radius r measured from the LIS boundary. Notice that in Eqs. 3b and 3c there is no q (ligand shedding) term because shedding is assumed to occur only from the lateral surfaces of the LIS.

By conservation of mass and fluid incompressibility, it can be shown that, in the LIS,

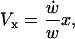(4a)

where 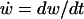is the rate of change of LIS width, and that, in the radial domain,

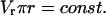(4b)

The transitional regime extends to a distance R_t = w/π from the LIS boundary. This distance was determined by matching the fluxes corresponding to Cartesian (w) and radial (πR_t) lengths, through which the flux passes. We further approximate the velocity field in this domain as uniform, being equal to the bulk velocity at the LIS exit V_t = V_x(x = h). The transitional regime was included to avoid numerical difficulties that can occur when switching coordinate systems. The approximations made in this domain have little impact on the overall concentration profile inside and outside of the LIS (data not shown).

The radial domain encompasses the region between R_t (end of the transitional domain) and R₀ = h/2 (where we assume the ligand concentration to be zero). Mathematically, the zero-concentration boundary would be infinitely far away from the LIS (i.e., R₀ → ∞), but for efficient numerical simulations we determined that for a LIS height h = 15 μm (2), R₀ = 7.5 μm is sufficiently far away from the LIS boundary such that further increasing R₀ had little effect on the overall concentration profile (data not shown). Hence, for all of the simulations we fixed the value of R₀ = 7.5 μm to be half of the previously measured LIS height h = 15 μm (2).

The diffusion-convection equations, along with the boundary conditions of no-flux at the most apical point (impermeable tight junction) and zero concentration at R₀, were solved using the PAK finite element method software package (4). The LIS and outside space were discretized by one-dimensional isoparametric finite elements (see Fig. 1). The governing differential equations, Eqs. 3a–3c, were first converted to the appropriate finite element system of first-order nonlinear differential equations, which were further linearized and integrated in time using a time-step Δt. A Newton-Raphson iterative scheme was employed for each time-step Δt (5) . The final system of incremental-iterative equilibrium equations for a time step is

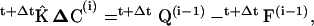(5)

where ΔC is the vector of concentration increments at the finite element nodal points, 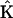is the system matrix, Q is the convection and shedding vector, F is the out-of-balance vector, the left superscript t + Δt shows that matrices and vectors were evaluated at the end of the time step, and the right superscript indicates the equilibrium iteration counter.

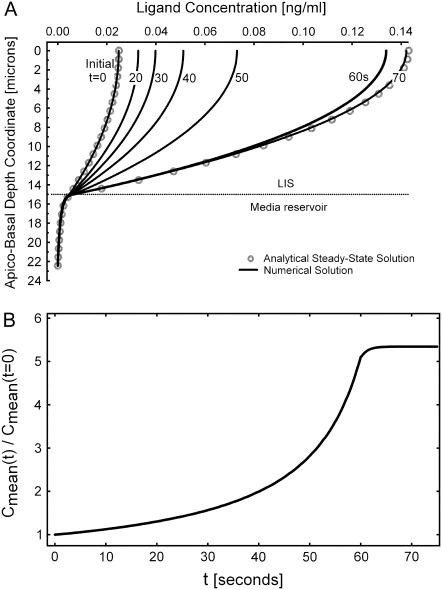
A time-series of the concentration profiles C(x,t) during a linear decrease in w by 85%, from 1.5 to 0.225 μm (based on previous experimental results (2)) over a 60-s duration is shown in Fig. 2 A. The open circles correspond to the analytical, pre- and postcollapse steady-state solutions based on Eq. 2. Each of the solid-line curves represents a solution of Eqs. 3a–3c at different time points. The height of the LIS was chosen to be 15 μm and the LIS width w to be initially 1.5 μm (2) (thus the outside space extended to R₀ = h/2 = 5w₀ = 7.5 μm below the LIS). For this example, the ligand diffusivity and shedding rate were arbitrarily selected (D_LIS = D_out = 75 μm²/s and q = 10 molecules/cell/minute). Another way to represent the same time-series of ligand concentration profiles is to calculate the fold change in the mean ligand concentration: C_mean(t)/C_mean(t = 0) (Fig. 2 B). Here, 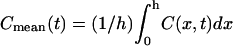and C_mean(t = 0) is the mean LIS ligand concentration just before the change in LIS width.

FIGURE 2.

Solutions obtained by solving for the ligand concentration from the governing diffusion-convection equations. (A) Evolution of the time-dependent concentration profile during a LIS collapse to 15% of its original width (from 1.5 to 0.225 μm) over 60 s. Concentration is plotted versus the apico-basal depth coordinate, where x = 0 at the apical tight junction, x = 15 at the LIS boundary, and at a depth of 22.5 μm the concentration is zero. The corresponding finite element model is shown in Fig. 1. For comparison, the open circles represent the analytical steady-state solution before LIS collapse and upon reaching the new, after-collapse steady state. The numbers next to the curves indicate seconds after onset of collapse. (B) Concentration profiles from panel A are plotted as fold-mean concentrations: C_mean(t)/C_mean(t = 0). Here, 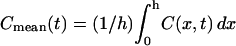, h is the LIS depth equal to 15 μm, and C_mean(t = 0) is the mean LIS ligand concentration just before the change in LIS width.

RESULTS

Exploring the parameter space of the governing equations

Cells express a variety of autocrine mediators with a range of diffusivities dependent on molecular size and charge characteristics (6,7). These mediators are likely released at various rates, further influencing their kinetics within the LIS. We therefore explored the parameter space of the governing equations to characterize the relative importance of ligand properties by varying the diffusion coefficient D and the shedding rate q over several orders of magnitude. In all these simulations, the LIS width was decreased to 15% of its initial, precollapse value (from 1.5 to 0.225 μm) linearly over 60 s. The magnitude of this change was selected to correspond to our previous experimental results in bronchial epithelial cells compressed by an apical to basal pressure gradient of 30 cm H₂O (2). The rate of LIS width change was arbitrarily selected; we address the importance of this parameter later.

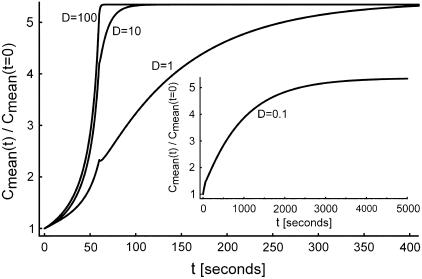
The diffusion-convection equations, Eqs. 3a–3c, were first solved for a constant q of 10 molecules per cell per minute (8) (evenly distributed along the cell boundary), with diffusion coefficients of 100, 10, 1, and 0.1 μm²/s (Fig. 3). Diffusivities on the order of 100 μm²/s characterize free diffusion of smaller molecules whose molecular weight ranges from ∼0.1–10 kDa, whereas D on the order of 10 μm²/s corresponds to free diffusion of larger molecules 10–1000 kDa. The cases of D = 0.1 and 1 μm²/s represent hindered diffusion of large molecules (6). We further assumed equal diffusivities inside and outside of the LIS, D_LIS = D_out (this assumption will be addressed later). The results of these simulations are plotted alongside each other in Fig. 3. The case of D = 0.1 μm²/s is shown in the inset due to the difference in the timescale. In general, the smaller the ligand diffusivity (or conversely the larger the ligand), the slower the increase in the normalized mean concentration during LIS width change.

FIGURE 3.

Effect of diffusion coefficient on concentration. A 60-s collapse was examined for cases of D = 0.1, 1, 10, and 100 μm²/s, where the LIS width decreases linearly to 15% of its original value (from 1.5 to 0.225 μm) over a 60-s interval. Diffusion coefficient units are μm²/s. Inset is for the case of D = 0.1 μm²/s (timescale goes to 5000 s). All cases assume a constant shedding rate of q = 10 molecules/cell/min.

A similar order-of-magnitude analysis was performed for shedding rates from 0.1 to 1000 molecules/cell/min (8) (data not shown). Although the shedding rate affected the absolute value of ligand concentration, it did not alter the normalized fold change in concentration induced by LIS collapse; this was true both at steady state and during the dynamic changes in LIS dimensions. Hence, the influence of shedding rate was limited to effects on the absolute ligand concentrations in our system.

Estimating HB-EGF diffusion coefficient in the LIS

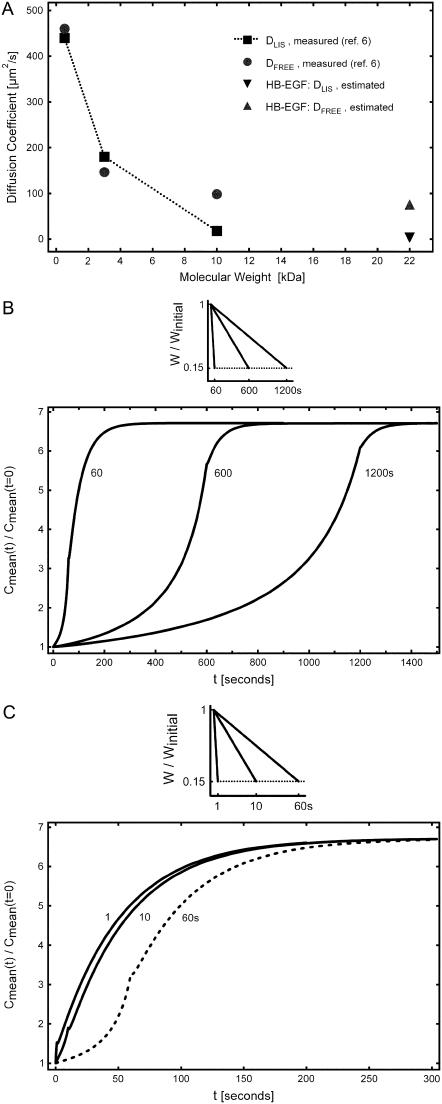
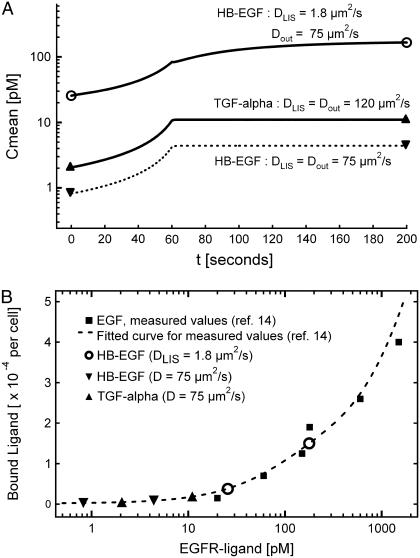
In the LIS of MDCK epithelial cells, which share a similar architecture with human bronchial epithelial cells, large molecules experience hindered diffusion due to the protrusion of a glycocalyx into the LIS (6). Specifically, while a 3-kDa molecule diffuses in the LIS of MDCK cells as if in free solution, a significant decrease in diffusion coefficient is observed for a 10-kDa molecule relative to that for free diffusion (Fig. 4 A). Because our previous work in human bronchial epithelial cells suggested a key role for HB-EGF in mechanotransduction (2,9), we used these existing diffusion data to estimate the diffusivity of HB-EGF in a typical LIS. HB-EGF that is proteolytically processed and shed into the LIS has a molecular mass of ∼22 kDa (3,10) and is also heavily charged (10). Previous studies have shown that interactions between a charged molecule and the glycocalyx can hinder diffusion beyond the expected size effect (11). Therefore, we assumed that HB-EGF diffusion in the LIS would be significantly hindered due both to its size relative to smaller molecules (6) (Fig. 4 A), and due to charge interactions with the glycocalyx. Based on these data we approximated the HB-EGF diffusion coefficient in the LIS as D_LIS = 1.8 μm²/s, while outside the LIS it was assumed to be an unhindered (free solution) value of D_out = 75 μm²/s. The choice of the hindered LIS diffusion coefficient is only an order-of-magnitude estimate based on hindered diffusion of large molecules in the LIS. The actual value, once experimentally determined, can be easily incorporated into the numerical model.

FIGURE 4.

(A) Diffusion coefficients for 524-Da HPTS, and for 3- and 10-kDa dextran molecules measured by Kovbasnjuk et al. (6) in the LIS of MDCK cells (squares connected by dotted line), and in free solution (circles). For a 10-kDa dextran with D_out = D_FREE = 98 μm²/s, hindered diffusion in the LIS was observed (D_LIS = 18 μm²/s) (6). For HB-EGF of size 22 kDa, we estimated a LIS diffusion coefficient of D_LIS = 1.8 μm²/s (down-triangle), an order-of-magnitude less than that measured for a 10-kDa dextran; outside the LIS the HB-EGF free solution value was estimated as D_out = D_FREE = 75 μm²/s (up-triangle), based on extrapolation of the measured free solution values, assuming D_FREE ∝ (mol. wt.)^−1/3. (B) Incorporating the estimated HB-EGF diffusion coefficients, we examined three cases of LIS collapse when the LIS width decreased linearly to 15% of its initial, precollapse value (from 1.5 to 0.225 μm) over t_collapse = 60, 600, and 1200 s. (C) Additional cases, where the same LIS collapse (to 15% of the initial width) occurred in t_collapse = 1 and 10 s (solid lines). The 60-s collapse case from panel B (dashed line) is shown for comparison. For all cases we assumed that the shedding rate is constant and equal to q = 10 molecules/cell/min.

Rate sensitivity of extracellular mechanotransduction

Biomechanical forces develop on a range of timescales, from milliseconds for traumatic injury, to hours or days for cellular proliferation and tissue morphogenesis. We have previously shown that the relevant timescale for compression of the LIS of airway epithelial cells and subsequent cellular signaling is on the order of seconds to minutes (2). Specifically, we know that at 20 min after the onset of 30 cm H₂O of transcellular compressive stress, a new steady state in LIS geometry is established, whereby the LIS width shrinks to 15% of its original value (2). However, due to imaging system limitations we do not know the temporal behavior of the LIS width during this 20-min span. While the temporal behavior of LIS deformation is likely to be complex, we chose as a first approximation linear changes in LIS dimensions, and modeled a range of different rates of collapse of the LIS width occurring linearly over durations from 1 to 1200 s (Fig. 4, B and C). We incorporated our estimates for hindered diffusion of HB-EGF inside the LIS, and free diffusion outside of the LIS. For clarity, the 60-s case is illustrated in both panels. As the figures indicate, the rate of change in LIS dimension plays a dominant role in defining both the rate of ligand accumulation, and the shape of relationship between ligand concentration and time.

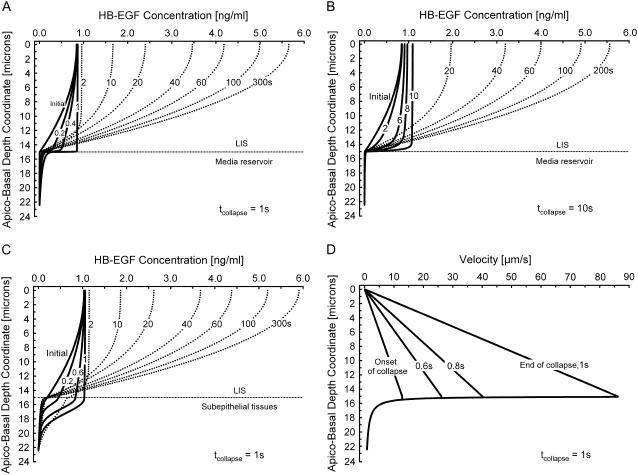
To illustrate the localized variation in concentration induced by dynamic changes in LIS geometry, we calculated the HB-EGF concentration profiles in the LIS at several times during (solid lines) and after (dotted lines) LIS collapse for the 1- and 10-s cases (Fig. 5, A and B). These two cases are identical to those shown in Fig. 4 C, but now represent concentration profiles as functions of depth and time.

FIGURE 5.

(A) Evolution of concentration profiles (each curve is labeled with its corresponding time) for a 1-s linear collapse (see Fig. 4 C) for the in vitro case where D_LIS = 1.8 μm²/s and D_out = 75 μm²/s, LIS height h = 15 μm (boundary between LIS and underlying media), and concentration is assumed zero at 7.5 μm below the LIS boundary. Solid lines indicate times when the LIS width is changing (number next to curve represents the time in seconds corresponding to the profile), and dotted lines represent times after the LIS has reached its new steady-state geometry. (B) Concentration profiles for a 10-s linear collapse (see Fig. 4 C) for the in vitro case with the same parameters as in panel A. (C) Evolution of concentration profiles for a one-second linear collapse for the in vivo case where D_LIS = D_out = 1.8 μm²/s. The geometry is the same as that described in panel A. (D) Velocity profiles corresponding to panel A.

Considering first the case where the LIS collapse occurs over 1 s, we see that due to the rapid decrease in LIS width the concentration within the LIS becomes uniform, reaching a level equal to the most apical concentration (Fig. 5 A). In the space immediately below the LIS, the concentration tends to increase during the collapse due to convection, since velocities increase with width decrease (Eq. 4a). This increase in extra-LIS concentration (equaling approximately one-quarter of the most apical LIS concentration at the end of the collapse) permeates several microns into the underlying media. After the collapse has ended, convection stops and diffusion alone becomes the governing process. This transition from a diffusive-convective to a purely diffusive regime results in a change in slope (at the end of the collapse) of the normalized mean concentration curve (Fig. 4 C). After the conclusion of the LIS collapse, the concentration profile transitions to a parabolic shape (Fig. 5 A). Soon thereafter, the effect of shedding ligand into a now much smaller space causes the concentration to increase until the new steady state is reached after 300 s (Fig. 5 A).

In the case of a 10-s collapse (Fig. 5 B) the concentration at the end of the collapse also tends to be uniform throughout the LIS and equal to the concentration at position x = 0; however, the x = 0 concentration is greater at 10 s than at the start of collapse. Another difference between the 1- and 10-s cases is that much less increase in concentration below the LIS boundary is observed for the 10-s collapse (diminished convective effects for the 10-s case). The new steady state is reached some 200 s after the onset of collapse (Fig. 5 B).

The previous two cases were intended to approximate the in vitro situation, where airway epithelial cells were grown on a porous substrate below which lies an essentially infinite reservoir of media. The HB-EGF diffusion coefficients inside and outside the LIS were assumed to be different based on the hindered diffusion in the LIS and free diffusion outside of the LIS. We modified these assumptions to simulate a scenario potentially encountered in vivo: instead of media below the cells, we assumed that sub-LIS tissues would hinder diffusion by the same amount as seen in the LIS (D_LIS = D_out = 1.8 μm²/s). For a very rapid 1-s collapse, where again the LIS width decreases linearly to 15% of its initial, precollapse value, we determined the evolution of the concentration profiles (Fig. 5 C). As in the one-second in vitro case, there is a tendency toward uniform x = 0 concentration throughout the LIS during the collapse. Here, though, the concentration changes permeate much deeper below the cells. For instance, just before the end of collapse the ligand concentration 3 μm below the LIS reaches 40% of the LIS value, representing a 10-fold increase from an initial precollapse value of 0.04 to 0.4 ng/ml in 1 s. These results highlight the fact that a rapid in vivo LIS collapse could transiently signal to underlying cells via a convective increase in ligand concentration that permeates into the surrounding tissues. This suggests a potential mechanism for communicating events that affect the epithelium to subepithelial tissues.

To see how the LIS collapse affects bulk velocity profiles inside and outside of the LIS, we examined the one-second in vitro case from above (see Fig. 5, A and D). The bulk velocity profile inside the LIS is linear (starting from zero at the impermeable tight junction x = 0), whereas outside the LIS the velocity decreases proportionally to the inverse of the radius (Fig. 5 D and Fig. 1). Both the linear and 1/r dependence follow from conservation of mass (Eqs. 4a and 4b). For the one-second in vitro case, the corresponding local Peclet numbers along the depth of the LIS (Pe = V_xh/D_LIS) can be calculated to range from 0 at x = 0 to >700 at the LIS boundary. Thus, since Pe ≫ 1 for most of the LIS, convection dominates during rapid collapse. Furthermore, a Peclet number can be obtained across the LIS width w, ranging from 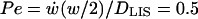at the LIS wall to 0 at a distance w/2 from the wall. Here, 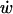represents the rate of change of the width w, i.e., the velocity of the LIS wall. The small values of the Peclet number over the LIS width, combined with the large height/width ratio of the LIS geometry, justify our use of a one-dimensional model in which we assume uniform concentrations across the LIS width.

Determining maximum rate of ligand concentration change during LIS collapse

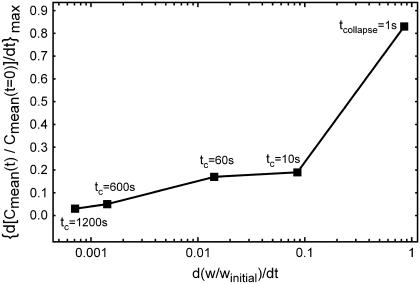
Computational and experimental studies have demonstrated that receptor activation and downstream signaling are influenced not only by the magnitude, but also by the rate of ligand concentration change in the cellular microenvironment (12). To explore this facet of transduction in our model, we first differentiated the normalized C_mean curves shown in Fig. 4, B and C, with respect to time and then found the maximum rate of concentration change. In Fig. 6, the maximum rate of concentration change (i.e., the maximum slope of the fold-mean curves of Fig. 4, B and C) is plotted versus the time-derivative of the corresponding collapse of LIS width (see Fig. 4, B and C, w/w_initial linear relationships). In our simulations the LIS width decreased linearly over time and the resulting time derivatives (i.e., rate of collapse) were constant for each case. The largest rate of concentration change was for the fastest collapsing LIS, i.e., the one-second collapse. A fourfold decrease in the maximum rate of ligand accumulation was observed when comparing the 10-s case to the 1-s case, with a small further decrement of 10% occurring between the 10- and 60-s cases. The slower collapsing LIS cases (such as 600 and 1200 s) exhibited maximum rates of ligand concentration change that were lower by more than an order of magnitude when compared to the 1-s case. Thus, the rate of LIS geometry change profoundly affects the peak rate of LIS ligand concentration change.

FIGURE 6.

Maximum rate of change of the fold-mean-concentration as a function of the corresponding rate of LIS collapse for five cases from Fig. 4, B and C. Individual squares represent the maximum rate of concentration change for a given rate of collapse. For example, in the case of t_collapse = 10 s, the LIS collapses by 85% linearly over 10 s, and thus the rate of collapse is constant and equal to 0.085 s⁻¹. For this 10-second collapse, the maximum rate of change of concentration was obtained by finding the largest slope of the C_mean(t)/C_mean(t = 0) curve (see 10-s curve in Fig. 4 C).

The results of our analysis demonstrate that while the magnitude of ligand concentration change depends on the change in w, the kinetics of ligand accumulation depend predominately on 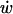and D. Strikingly, these results suggest that all other parameters being equal, the fastest change in ligand concentration will occur for the highest diffusivity (and hence, smallest) molecules. How then can we explain the selective role for HB-EGF in transducing mechanical stress in human airway epithelial cells exposed to compressive stress (2,9,13) when it is known that these cells make other ligands that bind to the same receptor (e.g., TGF-α) and exhibit higher diffusivities?

HB-EGF versus TGF-α concentration dynamics

While proteolytically processed and shed HB-EGF is ∼22 kDa in size, shed TGF-α (and EGF) is approximately four-times smaller, being ∼5.5 kDa (3,10). If we were to assume free diffusion of each ligand, the difference in ligand size would predict a ∼35% difference in the expected free diffusion coefficient for these two ligands (Fig. 4 A). However, upon returning to the diffusivity measurements made in the LIS of MDCK cells, it was found that these two ligands straddle the molecular size-range over which diffusion becomes significantly hindered in the LIS (6). Thus, the diffusivity in the LIS can be approximated as D_LIS = 1.8 μm²/s for HB-EGF (22 kDa), while for TGF-α (5.5 kDa) the D_LIS = 120 μm²/s is the same as for free diffusion (see Fig. 4 A). If we further assume both ligands are shed at the same rate of q = 10 molecules/cell/min, the solution of the governing diffusion-convection equations during a 60-s collapse yield the absolute mean concentration curves (not normalized) for HB-EGF and TGF-α shown in Fig. 7 A. For comparison, the case assuming free-diffusion for HB-EGF both inside and outside the LIS (D_LIS = D_out = 75 μm²/s) is also shown (dashed line in Fig. 7 A). Note that the units here are picomolar; thus, whereas the mass concentration of free-diffusing HB-EGF is higher than for TGF-α, its molar concentration is lower due to its larger molecular weight.

FIGURE 7.

(A) Mean molar LIS concentration for HB-EGF (top solid and bottom dashed curves) and TGF-α (solid middle curve) for a 60-s LIS collapse when the LIS width decreases to 15% of its initial, precollapse value (from 1.5 to 0.225 μm). For HB-EGF, we examined two cases: free solution inside and outside of LIS with D_LIS = D_out = 75 μm²/s (bottom dashed curve), and hindered diffusion in the LIS with D_LIS = 1.8 μm²/s and free diffusion outside of the LIS with D_out = 75 μm²/s (top solid curve). For TGF-α, free diffusion was assumed both inside and outside of LIS with D_LIS = D_out =120 μm²/s (middle solid curve). In all cases, shedding rate was constant and equal to q = 10 molecules/cell/min. The open circles represent hindered HB-EGF mean concentration at the start and after collapse, while up and down triangles represent free diffusing TGF-α and HB-EGF mean concentrations, respectively, pre- and after-collapse. (B) EGFR-ligand biding curve (dashed line) as a function of concentration, fitted from experimental measurements (solid squares) made by Lauffenburger et al. (14). Only the portion of the curve relevant to the model results is shown here (14). The mean concentrations for HB-EGF and TGF-α for pre- and after-collapse are represented by the symbols shown in panel A. TGF-α concentration increases due to the collapse, but (like free-diffusion HB-EGF) remains on the flat part of the curve, whereas hindered HB-EGF concentration moves up the receptor occupancy curve, rendering it more effective for receptor activation.

We observe that for hindered HB-EGF in the LIS, the mean absolute concentrations are an order-of-magnitude higher those of TGF-α (Fig. 7 A). A corollary to this result is that, to have a similar LIS concentration for both ligands, with the assumption of hindered diffusion in the LIS for HB-EGF, the cell must shed TGF-α at a rate ∼10 times higher than that of HB-EGF. Furthermore, this result reveals two potential explanations for a selective role for HB-EGF in extracellular mechanotransduction. In the first case, the different mean concentrations that arise in the LIS as a consequence of different ligand diffusivities could place HB-EGF and TGF-α on different parts of an EGFR-ligand binding curve (14) (see Fig. 7 B). Assuming a constant and equivalent shedding rate for each ligand, and equivalent ligand-receptor affinities (15) and signaling properties, the absolute concentrations of each of the ligands at the start and end of collapse correspond to the values of Fig. 7 A. Therefore, the differences in HB-EGF and TGF-α concentrations could result in HB-EGF shifting up the EGFR-ligand binding curve. On the other hand, the low concentration of TGF-α (as well as free-diffusing HB-EGF) could place it on the flat portion of the curve, rendering it an ineffective activator of the EGFR in response to mechanical deformation (Fig. 7 B).

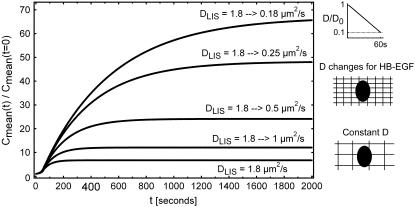
A second potential explanation is that the molecular sieving properties of the LIS might become amplified by the geometric decrease in LIS space (Fig. 8). While we have thus far assumed that during the LIS collapse the shrinking of the intercellular space does not affect ligand diffusivity, the decrease in LIS width could form a more tightly packed space and a greater barrier to diffusion, especially for large, highly charged molecules like HB-EGF, while leaving smaller ligands like TGF-α relatively unaffected. We modeled this putative effect by assuming that the size/charge interactions (6,11) would decrease the HB-EGF diffusion coefficient during the course of a LIS collapse. In Fig. 8, we illustrate several scenarios in which the HB-EGF diffusivity decreases linearly along with the linear LIS width decrease over 60 s (see Figs. 4 B and 8). A decrease in D_LIS during collapse could amplify the increase in HB-EGF concentration, potentially mediating or magnifying cellular mechanotransduction.

FIGURE 8.

Fold change in mean concentrations for various geometry-dependent changes in diffusion coefficients during LIS collapse. All cases are for a 60-s LIS collapse where the LIS width decreases to 15% of its initial, precollapse value (from 1.5 to 0.225 μm, Fig. 4 C). The case of constant HB-EGF diffusion coefficient D_LIS = 1.8 μm²/s is shown as the bottom curve. In the other four cases, we assume that the collapsing LIS causes a linear decrease (after LIS geometry) in HB-EGF diffusion coefficient during the 60-s collapse. For example, the top curve D_LIS = 1.8 → 0.18 μm²/s indicates the case where the diffusion coefficient changes linearly over 60 s from the initial value of 1.8 μm²/s to the final value of 0.18 μm²/s (see side panel). In the other three cases of decreasing D_LIS, the diffusion coefficient linearly decreases over 60 s from 1.8 to 0.25, 0.5, and 1 μm²/s. The side schematics illustrate how the shrinking volume of the LIS could considerably amplify the effect of hindered diffusion caused by size and charge interactions of ligands with the glycocalyx.

DISCUSSION

How cells transduce changes in their mechanical environment is an area of intense study (16). Both recent and classic studies demonstrate that the interstitial spaces separating confluent epithelial cells are deformed by mechanical stress (2,17). These spaces are the site of localized autocrine loops (3), raising the possibility that mechanical stress-induced changes in the extracellular space may lead to changes in the concentration of constitutively shed autocrine ligands and subsequent intracellular signaling (2). In this study, we developed a computational framework to help us understand how the concentration of constitutively shed ligands changes as a result of simple geometric changes in the spaces separating cells. Our computational model includes both diffusive and convective effects, allowing us to study the temporal relationship between deformation and ligand accumulation, and the dependence of this relationship on system characteristics such as ligand diffusivity, shedding rate, and rate of deformation. The model geometry is expanded over previous efforts (2) to include both the LIS and the underlying space, thereby also providing an assessment of the effect of convection and diffusion on ligand concentration in the basal space underlying the LIS.

The modeling results reveal several key facets of extracellular mechanotransduction. How fast the local ligand concentration changes depends primarily on the rate of change of the extracellular geometry (Fig. 4, B and C); on the other hand, the magnitude of the change in concentration (at steady state) is entirely determined by the magnitude of the geometry change. Although the fold-change in ligand concentration that occurs with LIS collapse is independent of the ligand shedding rate, the absolute concentration of ligand is not (Fig. 7 A). Thus, ligands with different shedding rates could occupy different regimes on a receptor dose-response curve (Fig. 7 B). Similarly, the absolute concentration of a ligand depends on its diffusivity; low diffusivity molecules accumulate at higher baseline concentrations when shed into the LIS, and vice versa (Eq. 2 and Fig. 7 A). We used these system properties to propose two explanations for the selective role of HB-EGF as a key mechanotransduction ligand in bronchial epithelial cells (2,9); both mechanisms are based on the large size of HB-EGF relative to other EGF-family ligands (3), and the assumption that HB-EGF diffusion will be hindered in the LIS (6). Clearly, additional experimental measurements will be needed to shed light on these proposed mechanisms. The shedding rate of each EGF-family ligand into the LIS will need to be experimentally defined (7). Similarly, the diffusivity of each ligand in the LIS, both before and during collapse, will need to be measured (6,7). Once available, both measurements could easily be incorporated into the computational model, and the diffusion-convection equations for various ligands could be solved simultaneously to predict the concentration dynamics for each ligand.

By including convection and expanding the model geometry, we were able to examine how dynamic changes in LIS geometry alter the ligand concentration in the underlying space (which we chose to be either a media reservoir or subepithelial tissues; see Fig. 5, A–C). We showed that for low diffusivity molecules and fast geometric changes, convection leads to large but transient increases in ligand concentration that permeate several microns below the cellular layer. This convective effect could allow nearly immediate communication of the mechanical state of epithelial cells to underlying cells, which frequently share responsibility for management of tissue architecture (18).

The modeling results demonstrate how the varying kinetics of geometric changes in the extracellular space are translated into varying rates of change of ligand concentration (Fig. 6). Recent experimental and computational studies have clearly demonstrated that the rate of ligand concentration change encodes important signaling information (12,19). Together these observations raise the possibility that cellular mechanotransduction through the proposed extracellular mechanism could discriminate between different rate processes, based on the velocity of ligand accumulation and subsequent receptor activation.

Fully understanding the physiological relevance of the proposed mechanism for mechanotransduction will require a comprehensive analysis of the relationship between mechanical loading and the rate and magnitude of geometric changes induced in the interstitial spaces separating cells. For instance, what are the effects of varying the magnitude or rate of loading on geometric changes, and how do these loading conditions relate to various physiological scenarios? Although not currently available, dynamic measures of the geometric response of the interstitium to loading, both in vitro and eventually in vivo, could be coupled to the model described here to predict the overall relationship between mechanical loading and local autocrine ligand concentration. The validity of the proposed mechanotransduction mechanism could then be assayed by comparing model predictions to experimental observations of changes in local ligand concentrations, or as a proxy receptor phosphorylation, under a range of loading conditions.

Computational modeling of the EGFR system, from autocrine activity (20–24) to receptor trafficking (25–27) and downstream signal pathways (12,19,27,28), has been essential to our understanding of this important biological pathway. The model described here offers an estimate of changes in the concentration of shed ligands in an extracellular compartment, based solely on geometric changes; this model could be easily coupled to previously developed cell membrane and intracellular compartmental models. When linked together, these models of ligand kinetics, receptor trafficking, and intracellular signaling will provide a comprehensive framework for understanding how mechanical or architectural changes in cells and tissues that modulate extracellular geometry are converted into biological signaling responses.