Effect of Hydrophobic Mismatch on Phase Behavior of Lipid Membranes

Abstract

We investigate the competing effects of hydrophobic mismatch and chain stretching on the morphology and evolution of domains in lipid membranes via Monte Carlo techniques. We model the membrane as a binary mixture of particles that differ in their preferred lengths, with the shorter particles mimicking unsaturated nonraft lipids and the longer particles mimicking saturated raft lipids. We find that phase separation can be induced upon increasing either the ratio of the hydrophobic surface tension J to the compressibility modulus . J/ determines the decay length for thickness changes. When this decay length is larger than the system size the membrane remains mixed. Furthermore, increasing the thickness relaxation time can induce transient phase separation.

INTRODUCTION

Strong evidence has been obtained that suggests the presence of heterogeneities in the plasma membrane of many cells (1–5). One type of membrane heterogeneity, termed rafts, is enriched in cholesterol, sphingomyelin (SM), and certain membrane proteins (6,7). Rafts have putative roles in many physiological processes, such as signal transduction, endocytosis, apoptosis, protein trafficking, and lipid regulation (7–11).

Raft lipids typically have saturated hydrocarbon chains. For example, SM comprises a sphingoid base that has a saturated hydrocarbon chain plus a very long amide-linked saturated acyl chain that is, on average, 20–24 carbons in length (12). Glycerol-based phosphatidylcholine, on the other hand, which is the major class of nonraft lipids that have, on average, 18 carbons per acyl chain (13), is less saturated than naturally occurring sphingomyelins, which generally contain one saturated and one unsaturated acyl chain (14). These unsaturated bonds produce kinks in the lipid chains, increasing the area per molecule. Therefore, this leads to a reduction in lipid thickness due to volumetric considerations. Cholesterol, a molecule that is enriched in lipid rafts, has a shorter hydrophobic length of 17.5 Å (15). However, it does not change the length of SM. With or without cholesterol, C18:0 SM has been found to form bilayers with a thickness of 46–47 Å (16). Hence, because of the differences in lipid thickness between raft and nonraft lipids, and since energetically it can be expected that the lengths of the hydrophobic moieties of neighboring membrane components will be approximately equal to avoid unfavorable exposure of hydrophobic surfaces to a hydrophilic environment, it is reasonable to assume that nonraft lipids should coalesce and predominantly give rise to smaller bilayer thicknesses compared to raft lipids (17,18). Indeed, in studies of model membranes comprising dioleoylphosphatidylcholine (DOPC), SM, and cholesterol, phase separation is observed giving rise to SM- and cholesterol-rich raft domains (19–21). Atomic force microscopy studies reveals that these domains are typically of order 1-nm thicker that the surrounding DOPC-rich region (19).

However, it has been shown that proteins are able to integrate into a membrane while tolerating a length variation of ∼10 amino acids, depending on the amino acid composition (22,23). This therefore raises the questions: How important is hydrophobic mismatch for membrane structure and organization, and how do membranes relieve hydrophobic mismatch between proteins and lipid bilayers? Possible adaptations for the relief of hydrophobic mismatch in membranes include phase separation of lipids of different thicknesses, ordering and disordering of the acyl chains, peptide backbone deformation, peptide aggregation, peptide tilt, no transmembrane association of the peptide with the membrane, or nonlamellar phase formation. Little is known about which will be favored under certain conditions (24,25).

The goal of this article is to investigate how hydrophobic mismatch in a simple model membrane comprising two species of particle influences the membrane phase behavior. Specifically, we model adaptations to hydrophobic mismatch by stretching or compressing the particles, hence ordering or disordering the lipid acyl chains.

Theories that address acyl-chain stretching or compression due to the incorporation of a peptide of a different hydrophobic thickness include the phenomenological approaches by Owicki et al. (26,27) and Jähnig et al. (28–30). In these theories, they assume the location of the proteins to be fixed and so they do not induce thermodynamic phase separation. The phenomenological mattress model by Mouritsen and Bloom (31) is a two-component real solution theory and hence allows for phase separation. In their model, they relate the energy stored in the undulations of the membrane surface caused by the mismatch to the elastic properties of the lipids and proteins. They do not include microscopic detail of the lipids, but use as input the known thermodynamic properties of the pure lipid system. They also include indirect lipid-protein interactions induced by the mismatch as well as direct lipid-protein van der Waals-like interactions between the hydrophobic parts of the lipid bilayer and the proteins. The mattress model has been replicated in a Monte Carlo simulation scheme by Sperotto and Mouritsen (32). They allowed for different microstates of the lipids, classified according to Pink's 10-state model (33), hence enabling a pure lipid bilayer phase transition. A major theoretical advance was the work of Fattal and Ben-Shaul (34), who provided a molecular theory for the behavior of the lipid chains. This molecular modeling was combined with phenomenological free energy contributions accounting for the opposing effects of headgroup repulsions and hydrocarbon-water surface tension. Duque et al. (35) described the effects of an embedded protein in a bilayer via molecular theory, which yielded the free energy of the entire system. All these theories predict a significant stretch of the acyl chains of lipids that are adjacent to a long peptide. These perturbations in lipid thickness decrease for the lipids that are at a greater distance from the peptide.

Many experimental studies of model membranes support these theories. Deuterium (²H) NMR measurements on lipids with perdeuterated acyl chains show that a reduction in both acyl-chain order and bilayer thickness occurs when an embedded peptide has a smaller hydrophobic thickness than that of the lipid bilayer (36,37). Additionally, electron cryomicroscopy measurements showed a reduction in bilayer thickness when a short peptide was incorporated into a DOPC liposome (38). For the opposite case when a peptide has a hydrophobic thickness that is greater than that of the bilayer, it has been found via (²H) NMR experiments that the bilayer increases its acyl-chain order and thickness. Interestingly, upon increasing the peptide hydrophobic length, the membrane thickness does not match this increment, although its thickness does always increase (36,37,39). Hence, it appears that complementary mechanisms of adaptation to hydrophobic mismatch occur concomitantly with changes in lipid acyl-chain order and thickness.

Issues that have not been addressed previously relating to acyl-chain stretching or compressing to relieve hydrophobic mismatch include the initial instability of a membrane that could, for example, be induced biologically after delivery of lipids having a different hydrophobic thickness to a membrane, and also the potential induced large-scale structure. In this article, we study how the hydrophobic mismatch between two species of particle in a bilayer influences the membrane phase behavior and the kinetics of phase separation. In particular, a large hydrophobic mismatch between particles that are stiff can induce phase separation since the particles are unable to stretch or compress to relieve the mismatch. The two species of particle, U and S, represent unsaturated and saturated lipids, respectively, with the U particles having a shorter preferred hydrophobic length than the S particles. The mechanism of adaptation to hydrophobic mismatch is modeled by stretching and compression of the particles, analogous to stretching and compression of lipid acyl chains. To implicitly treat a bilayer, a particle is assumed to be the same lipid on opposite sides of the bilayer. Hence, a change in particle hydrophobic thickness will stretch (or compress) both lipids in opposite directions. We investigate the effects of hydrophobic mismatch on membrane phase behavior in two ways. Firstly, we present a mesoscopic calculation that probes the intermediate to late stages of composition and bilayer thickness growth. These regimes are explored via Monte Carlo computer simulation. Secondly, we present an analytic treatment describing the early stages of growth.

MESOSCOPIC MODEL

Free energies

Initially we study the effects of hydrophobic mismatch on domain morphology for a mesoscopic model. We model the bilayer as a two-dimensional square lattice with sides of length L. Each lattice site, having an area a², is occupied by either a U or S particle. The particles have two degrees of freedom. They can laterally exchange positions with a neighboring particle or they can change their thickness. A particle is assumed to be the same lipid on opposite sides of the bilayer and so a change in particle thickness will stretch (or compress) both lipids in opposite directions. All energies are measured in units of k_BT and all lengths are measured in units of the lattice spacing a.

The free energy G of the membrane comprises three terms: the lipid-lipid interaction energy G_int, the lipid stretching energy G_stretch, and the hydrophobic mismatch energy G_mismatch.

The lipid-lipid interaction energy is given by

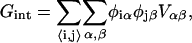(1)

where φ_iα is equal to 1 if species α is at lattice site i or equal to 0 if species α is not at lattice site i. The value α can be U or S. The value V_αβ is the contact energy of neighboring species α and β. The physical contribution to V_αβ is from electrostatic and van der Waals interactions between the lipids. However, these interactions are not modeled explicitly. This term can lead to phase separation in a two-component system if the strength of the energetic interaction between U and S particles (V_US) relative to their self-interactions (V_UU, V_SS), χ, given by

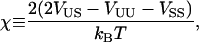(2)

satisfies χ > χ_MF = 2 within mean-field theory (40), or χ > χ_c = 3.526 in a physical system incorporating critical fluctuations (Ising model) (41). Hence, for V_UU = V_SS = 1, phase separation occurs if V_US > 1.88.

The lipid stretching energy is given by

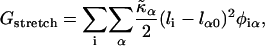(3)

where l_i is the actual thickness at site i, and l_α0 is the preferred thickness of species α at site i. The preferred length of a particle is constant throughout a simulation. Hence, phase transitions between liquid-ordered and gel states are not modeled since they are usually accompanied by changes in lipid length. The value 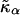is the compressibility modulus of particle α. The stretching energy arises due to a lipid not having its preferred thickness. For simplicity 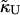and 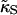are assumed to be equal in this study, hence we will refer to 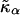as 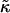. However, in a physical system, 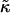will be larger for lipids that are more saturated, therefore having straighter and less flexible hydrocarbon chains.

The hydrophobic mismatch energy is proportional to the exposed hydrophobic area and is given by

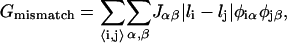(4)

where the exposed hydrophobic area is linear in the particle thickness difference. We have not included an explicit bending penalty in the mesoscopic model because bending, a long wavelength phenomenon, will arise from coarse-graining Eqs. 3 and 4 up to longer length scales. The value J_αβ is the hydrophobic surface tension between nearest and next-nearest species α and β. The value G_mismatch will be minimized when the particles are of equal thickness. Physically, this means that the lipid headgroups will be directly adjacent, hence avoiding contact between the aqueous environment and the lipid hydrocarbon chains, and/or avoiding contact between the water molecules around the lipid headgroup of one lipid and the hydrocarbon chains of the other lipid. In this study, we do not model lipid headgroups. Hence, we assume that the hydrophobic surface tension between a lipid headgroup and hydrocarbon chains, and the hydrophobic surface tension between the aqueous environment and the hydrocarbon chains, are equal. Additionally, for simplicity we assume J_αβ ≡ J independent of particle type. However, in a physical system the hydrophobic surface tension will be higher for unsaturated lipids due to the acyl chains being kinked. This leads to a larger available contact area between the lipid chains and water around neighboring lipid headgroups or the aqueous environment.

Model approximations

Our model assumes that the two monolayers are symmetric. Hence, a concentration of a short component in one leaflet implies a similar concentration in the opposite leaflet (Case I), and thus local membrane thinning. Alternatively, an excess of short components in one leaflet could be compensated by an excess of longer components in the opposite leaflet (Case II), thereby reducing the hydrophobic mismatch. There are two main contributions to the difference in free energies ΔG = G_I – G_II between phase-separated morphologies in these two cases. The first contribution is due to the hydrophobic mismatch between domains. This incurs a free energy penalty ΔG_line ∼ λL_d, where L_d is the domain interface length and λ is the line tension. The second contribution is due to differences in the free energy of bilayer assembly 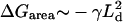, since we expect the symmetric bilayer to have the lower energy state. The competition between these two free energy differences leads to a length scale, 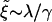. At early times, 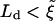, suggesting that Case II will be the preferred configuration. However, at later times L_d will exceed 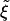, which should favor Case I. Our model is appropriate for the limit of 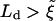. We leave the very interesting physics of the interplay between these two configurations to future work.

We also assume negligible frame tension, which prevents the area per particle from decreasing. The work done against a frame tension 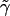is given by

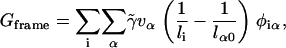(5)

where v_α is the volume of species α. This would therefore shift the phase boundaries slightly; i.e., a deeper quench will be needed to effect phase separation that would lead to an overall smaller area per particle.

Simulation details

The simulations are initialized by distributing the particles randomly, with each species assigned its preferred thickness. We only consider the symmetric case of equal compositions φ_U = φ_S = 1/2 here. The thicknesses then undergo a preliminary relaxation period, where each particle is allowed to relax a possible 1000 times. A thickness move consists of randomly selecting a particle and choosing a thickness change randomly between ±δl_max; this change is accepted or rejected according to the Metropolis criterion (42). The choice δl_max = 1 allowed thermal fluctuations to be sampled efficiently. After the initial thickness relaxation, composition moves are made in conjunction with thickness relaxation. Lateral exchanges are chosen that preserve the thicknesses of the individual particles: e.g., a U particle of thickness l at site i and an S particle of thickness l′ at site j are swapped so that site i now contains an S particle of thickness l′. These exchanges are implemented by the usual Kawasaki dynamics (43) and accepted according to the Metropolis criterion. After each possible composition exchange, the thicknesses on sites i, j, and those of the particles in the surrounding shell of lattice sites, are allowed to relax a possible n_r times per particle. The thickness relaxation is performed regardless of whether the particle lateral exchange was accepted or rejected, to allow continual thickness relaxation. We define one Monte Carlo (MC) cycle as the number of steps required for each lattice site to have the opportunity to have a particle lateral exchange. The ratio of characteristic times for thickness relaxation and diffusion can be adjusted by changing n_r, with a decrease in n_r leading to slower thickness relaxation.

MORPHOLOGY AND EVOLUTION OF DOMAINS USING THE MESOSCOPIC MODEL

Domain morphologies

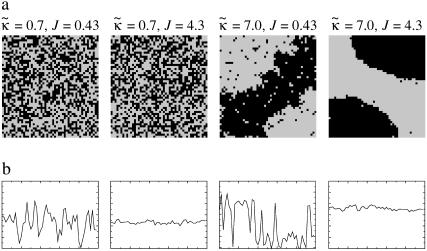
Simulations were performed to investigate the effects of hydrophobicity on domain morphology. Firstly, however, we will demonstrate the effects of χ in the absence of coupling to thickness for comparison purposes. Fig. 1 a shows the domain morphologies obtained after 131,072 MC cycles in the absence of coupling composition with thickness (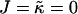) and increasing χ from 0 to 8. For χ = 0 the membrane remains mixed since there is no driving force for phase separation. As χ is increased, the system moves toward the critical point between the one-phase and two-phase regimes. Hence, larger scale fluctuations occur. As the system crosses the critical point (χ_c = 3.526), phase separation occurs. Upon further increasing χ, purer phase-separated domains are observed that coarsen more slowly since the energy cost of a U–S contact becomes higher.

FIGURE 1.

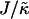Intermediate-time domain morphologies in the absence of coupling to thickness (a), and when coupling to thickness for l_u0 = 36, l_s0 = 54, δl_max = 1.0, n_r = 1, L = 50, and time t = 131,072 MC cycles (b–d). Varying for χ = 0 and (b). Varying for 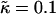and χ = 0 (c) and χ = 5 (d). Note that the value of 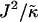is not constant for panels c and d. U (solid); S (shaded); φ_u = φ_s. Below the domain morphologies are the respective thickness profiles taken at L/2 (b–d). The x and y axes range from position x = 0…50 (b–d) and thickness l = 9…65 (b), while in panels c and d the y axes range from thickness l = 25…65 for each graph.

When considering hydrophobicity we find two ratios of interest, 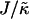and 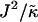, with 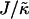having units of length while 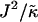has units of energy. To compare the effects of hydrophobicity with the effects due to χ (Fig. 1 a), we use the ratio 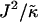since this has units of energy, similarly to V_αβ (recall that 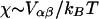). We anticipate similar trends to those observed in Fig. 1 a, provided the particles U and S have different preferred thicknesses. For small 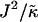, the membrane should remain mixed since the energetic cost of a difference in thickness between neighboring particles will be low and hence there will be no driving force for phase separation. Increasing 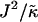should drive the system into the phase coexistence regime to minimize the energy of the system by placing particles with similar thicknesses together.

As can be observed in Fig. 1 b, the effects of hydrophobicity probed by increasing 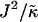are indeed similar to the effects of increasing χ. Domains are not observed for 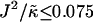, since there is no impetus for phase separation. As 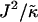is increased to 0.0875, critical fluctuations are observed. For 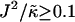, phase separation occurs, where domains coarsen more slowly upon increasing 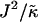, due to higher incompatibilities between the unlike species.

We next investigate the effects of increasing the length 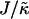for χ = 0 and 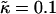for a system of size L = 50 (Fig. 1, c and d). As can be observed, the phase behavior differs significantly at high 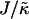to that observed at high 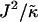. Domain formation does not occur for 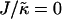and χ = 0, since there is no incentive for phase separation. As 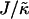is increased to 0.2, critical fluctuations are observed. Upon increasing 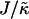from 0.4 to 2, phase separation occurs. A similar trend is observed to increasing either χ (Fig. 1 a) or 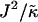(Fig. 1 b) in that as the system moves further from the critical point, domains coarsen more slowly due to higher incompatibilities between the unlike species. However, as 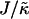is increased from 2 to 53, domains become larger and less pure after the same number of MC cycles. Hence, there is a reversal in behavior. In the next subsection, we will discuss the relative rates of growth in composition and thickness, and their dependence on the relative relaxation times for composition and thickness. 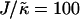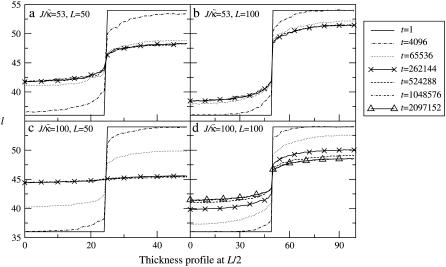Interestingly, for , the membrane mixes for all initial configurations. To understand this behavior, simulations were performed for phase-separated membranes where only the particle thicknesses were allowed to relax (Fig. 2), therefore probing whether phase separation will be obtained for a given value of 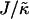at late times. For 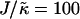and L = 50 (Fig. 2 c), the thickness profile is approximately flat after equilibration, implying that the composition will decouple from the thickness for these simulation parameters, which for χ = 0 would imply a mixed state. Indeed, as 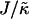is increased to 100 in Fig. 1, c and d, the particle thicknesses become equal and, hence, there is no impetus for phase separation from hydrophobicity. However, upon increasing the system size L to 100 for 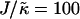(Fig. 2 d), there is a clear gradient in the thickness profile at the domain interface after equilibration. The difference in thickness profiles for different system sizes suggests that there is a decay length 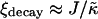, due to the competition between hydrophobic mismatch and particle stretching, which controls phase separation. For ξ_decay > L, hydrophobic mismatch dominates, resulting in particle thicknesses becoming equal and therefore decoupling from the composition. However, for ξ_decay < L, particle stretching dominates, which can result in phase separation depending on the value of 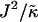. For 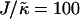and L = 50, ξ_decay > L and therefore phase separation is not observed. Note that starting the simulation from a phase-separated and flat state for this set of parameters results in remixing. Hence, the lack of phase separation at high 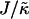is not thought to be a kinetic effect, but a finite size effect.

FIGURE 2.

Thickness profiles taken at L/2 for simulations that had a fixed phase-separated composition allowing the particle thicknesses to fully equilibrate. Each phase-separated domain was composed of either all U or all S, and had sides of length L and L/2. 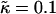, l_u0 = 36, l_s0 = 54, δl_max = 1.0, φ_u = φ_s, and χ = 0. (a) 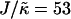and L = 50, (b) 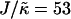and L = 100, (c) 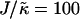and L = 50, and (d) 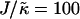and L = 100. Time t is in MC cycles, where in this figure an MC cycle is defined as the number of steps required for each lattice site to have the opportunity to have a particle-thickness change.

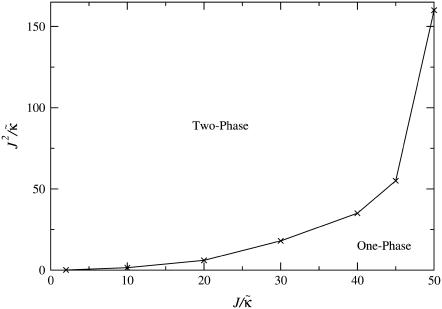
We next determine the 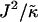versus 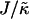phase diagram (Fig. 3) for χ = 0 and system size L = 50. As can be seen, as 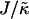approaches the system size L, finite size effects lead to a significant increase in the magnitude of 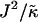required to induce phase separation.

FIGURE 3.

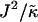versus 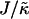phase diagram for χ = 0, L = 50, l_u0 = 36, l_s0 = 54, δl_max = 1.0, n_r = 1, φ_u = φ_s, and time t = 131,072 MC cycles. The crosses (×) mark simulation data points.

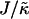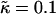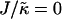Fig. 1 d shows the membrane morphologies obtained when increasing for χ = 5 and . For the membrane has phase-separated due to χ. Upon increasing 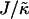to 0.4, domains decrease rather than increase in size. This is due to the membrane already being below the critical point at 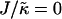. Above 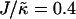, similar trends are observed to those shown in Fig. 1 c, with the composition decoupling from thickness at 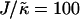since ξ_decay > L.

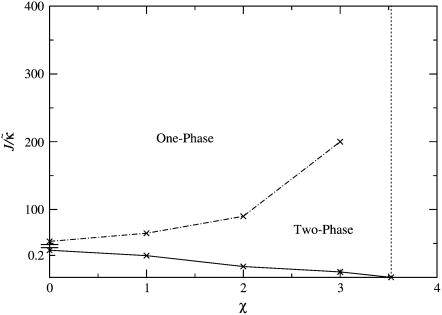
Fig. 4 shows the 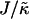versus χ phase diagram for symmetric quenches (i.e., φ_u = φ_s) into the phase coexistence regime for L = 50 and for 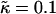(note that, as with Fig. 1, c and d, the value of 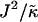is not constant). Above χ_c = 3.526, the membrane will demix regardless of the value of 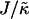. However, below χ_c, the membrane will mix for either small or large values of 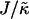. The lower limit of 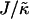that leads to phase separation decreases upon increasing χ, and the upper limit of 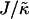that leads to phase separation increases upon increasing χ. As discussed above, this upper phase boundary between mixing and phase separation for χ < χ_c is a finite size effect due to ξ_decay > L. For χ = 0, increasing 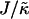at fixed 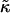in Fig. 4 traces a parabola in Fig. 3, which intersects the phase boundary in Fig. 3 at two points. This leads to the progression of states from one-phase to two-phase to one-phase.

FIGURE 4.

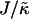versus χ phase diagram for 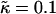, l_u0 = 36, l_s0 = 54, δl_max = 1.0, n_r = 1, L = 50, φ_u = φ_s, and simulation time t = 131,072 MC cycles. The crosses (×) are simulation data marking the approximate boundaries of the two-phase regime. The dashed-dotted line marks the upper phase boundary between the one- and two-phase regimes, where the position of this line depends on the system size. The dotted line is predicted behavior and is only schematic. For χ > χ_c = 3.526 (dashed line), phase separation will occur regardless of the value of J. For comparison purposes between the phase diagram shown here and the phase diagram in Fig. 3, the lower phase boundary for χ = 0 occurs at 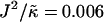, while the upper phase boundary occurs at .

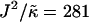The results presented thus far illustrate trends in behavior upon changing χ and the hydrophobicity parameters J and 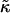. We will now investigate membrane phase behavior for biologically relevant parameters. X-ray diffraction measurements of lipid bilayers have determined that at 30°C, fluid phase DOPC has a cross-sectional area of 73 Ų and a bilayer thickness of 37 Å (44). At 22°C, gel phase SM (C18:0) has been found to have a cross-sectional area of 45 Ų and a bilayer thickness of 50.5 Å (45). Assuming no area change upon mixing, 1:1 SM/DOPC bilayer has an average cross-sectional area of 59 Ų, giving rise to an average distance between neighboring lipids of 8.6 Å. Lengths in the simulations are measured in units of the lattice spacing a. Therefore, reasonable estimates for the preferred thickness of the U species of particle l_u0 that mimics DOPC and the preferred thickness of the S species of particle l_s0 that mimics SM are 4.3 a and 5.9 a, respectively.

Measured values for the area compressibility modulus κ_A on fluid lipid bilayers and free biological cell membranes range from (100–230) mJm⁻² = (0.242–0.556) k_BT Å⁻² at 300 K (46–48). The elastic energy per molecule can be expressed as a difference between the actual area A and the preferred area A₀ per molecule by (49)

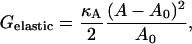(6)

and in the mesoscopic model studied here, the elastic stretching energy per molecule is expressed as a difference in thicknesses by

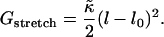(7)

If the change in volume v = Al of the lipid as it stretches is negligible, then

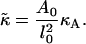(8)

Therefore, an average value of 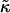for DOPC and SM is 0.01 k_BT Å⁻² = 0.7 k_BT a⁻².

The hydrophobic surface tension J, due to tail-water or tail-headgroup interactions, provides the dominant contribution to the energy cost due to a mismatch in thicknesses of neighboring lipids. The interfacial tension γ_WC of hydrocarbons with bulk water lies in the range (40–50) mJm⁻² = (0.097 – 0.121) k_BT Å⁻² at 300 K (49). This tension will mainly be due to the hydrophobic effect. When the headgroup is in contact with the lipid tails, γ_WC needs to be scaled by the amount of water present in the heads, which, for a DPPC bilayer, is approximately one-third of the total headgroup volume (44). Hence, a rough estimate for the interfacial tension between a lipid headgroup and lipid acyl chains γ_HC is 0.04 k_BT Å⁻². However, entropy that is associated with the hydrogen-bond network of water contributes on the order of 85% to the hydrophobic interaction (49). Since the hydrogen-bond network of water will be significantly perturbed in the lipid head environment, the interfacial tension should be even lower, of the order of 85%. This leads to γ_HC ∼ 0.006 k_BT Å⁻². In the simulations, J is given by

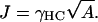(9)

Therefore, for an average cross-sectional area of DOPC and SM, J = 0.05 k_BT Å⁻¹ = 0.43 k_BT a⁻¹, assuming that hydrophobic mismatch only occurs between lipid heads and neighboring lipid tails.

Fig. 5 illustrates the effects observed when simulating a membrane comprising two species of particle mimicking SM and DOPC, with the rough estimates for J and 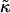. As can be seen, phase separation does not occur during the timescale of the simulation; however, increasing 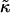by a factor of 10 results in domain formation.

FIGURE 5.

Domain morphologies (a) and thickness profiles (b) taken at L/2 for simulations having approximate biologically relevant parameters with l_u0 = 4.3, l_s0 = 5.9, δl_max = 1.0, n_r = 1, L = 50, φ_u = φ_s, t = 131,072 MC cycles, and χ = 0 (rough estimates for biologically relevant 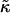and J calculated in Morphology and Evolution of Domains Using the Mesoscopic Model are 0.7 and 0.43, respectively). U (solid); S (shaded). The x and y axes range from position x = 0…50 and thickness l = 4…7, respectively, for each graph.

Domain growth and effect of changing relative relaxation times between thickness and composition

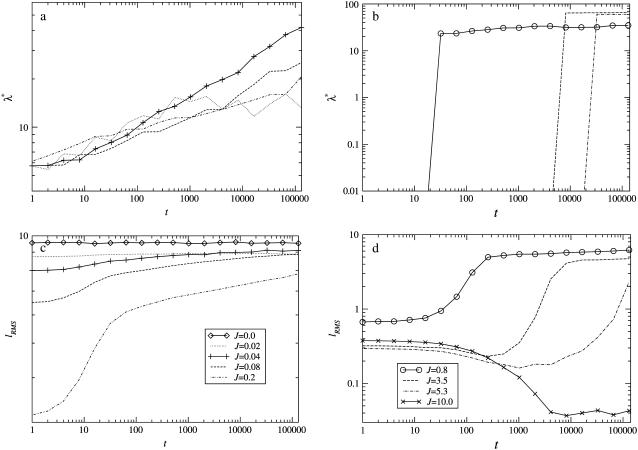
We will next examine the growth in composition and thickness. Fig. 6 shows both the length scale of compositional growth λ* (determined from the peak in the structure factor) and the growth in the root mean-square thickness fluctuations l_RMS for various values of J for n_r = 1, φ_u = φ_s, and 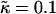. Increasing J from 0.04 to 0.2 leads to slower coarsening with a change in power law, indicative of a change in the mechanism of growth. Interestingly, initial domain growth is not observed for J equal to 0.8, 3.5, and 5.3, with the delay in growth increasing for larger values of J. This is due to increasingly slower relaxation of the particle thicknesses. Note that since all quenches performed were symmetric, spinodal decomposition will have been the mechanism of domain growth. Growth during the early stages of such domain coarsening is expected to be due to diffusion, while coarsening at the late stages is expected to be due to interface-driven hydrodynamics (50). In this study, only the diffusion is simulated. Therefore, our model data will most accurately reproduce domain growth in atomic force microscopy experiments on supported lipid bilayers, in which growth by hydrodynamics is expected to be significantly damped. This is because the thin hydration layer between the support and the lower leaflet of the bilayer will exert strong hydrodynamic stress.

FIGURE 6.

Characteristic length scale of growth in composition λ* (a,b) and growth in RMS thickness fluctuations l_RMS (c,d) for J from 0 to 10 (for J from 0.0 to 0.2, each trace is an average of 10 data sets; and for J from 0.8 to 10.0, each trace is an average of five data sets) for 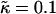, l_u0 = 36, l_s0 = 54, δl_max = 1.0, n_r = 1, L = 50, φ_u = φ_s, and χ = 0. There is no compositional growth for J = 0 and 10.

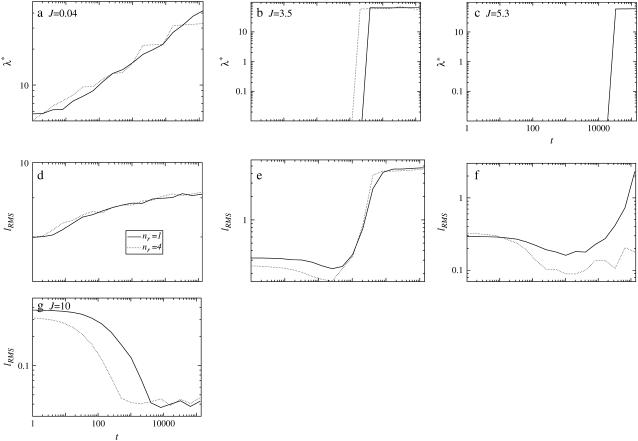
The dependence of the delay of compositional growth on thickness relaxation for J = 0.8, 3.5, and 5.3 can be demonstrated by changing the relative relaxation times between composition and thickness. This can be done by changing n_r. For example, an increase in n_r leads to a faster thickness response, or alternatively a relative decrease in particle lateral mobility. Fig. 7 illustrates the effects of changing n_r on both the growth in composition and thickness, where each growth trace is averaged from five simulations. For small values of J (J = 0.04), increasing n_r from 1 to 4 has little effect on growth in composition and thickness since the impetus for equilibrating the particle thicknesses is also small. Increasing J to 3.5 leads to faster thickness relaxation for n_r = 4 than for n_r = 1. This increase in thickness relaxation enables the growth in composition to also hasten. Again, for J = 5.3 the thickness response is faster for n_r = 4 than for n_r = 1. However, in this case, there is no overall compositional growth observed for n_r = 4 during the timescale of the simulations.

FIGURE 7.

Effects of changing the relative thickness relaxation time on the characteristic length scale of composition growth λ* (a–c) and RMS thickness fluctuation growth l_RMS (d–g) for J equal to 0.04, 3.5, 5.3, and 10.0 (each trace is an average of five data sets). 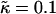, l_u0 = 36, l_s0 = 54, δl_max = 1.0, L = 50, φ_u = φ_s, and χ = 0. There was no compositional growth for J = 5.3 and n_r = 4, and J = 10.0, n_r = 1, and n_r = 4.

The magnitude of 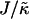determines whether or not an increase in n_r enhances compositional growth. For smaller 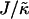, the stretching free energy G_stretch will dominate the free energy penalty, which will encourage particles to have their preferred thicknesses. This occurs faster for larger n_r. Therefore, within a concentration fluctuation that enhances a given species, the particle thicknesses will quickly relax toward their preferred thicknesses for large n_r, minimizing both the stretching free energy (in the bulk) and also the hydrophobic mismatch free energy (which only occurs at the interface). Hence, an increase in n_r will lead to faster compositional growth for small 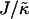. However, for large 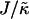the hydrophobic mismatch free energy G_mismatch dominates the free energy penalty. G_mismatch will encourage the particle thicknesses to become equal regardless of composition, with this occurring faster for larger n_r. Hence, because the thickness gradient will be smaller for larger n_r, thermal fluctuations will be able to break up concentration fluctuations that lead to clustering of like species more easily. Indeed, in Fig. 8 (J = 5.3 and n_r = 4), the composition profile taken at t = 65,536 MC cycles clearly shows the early stages of phase separation, while at a later time (t = 131,072 MC cycles) the membrane has remixed. It should be noted that both the growth in composition λ* and the growth in thickness fluctuations l_RMS shown in Fig. 7 are averaged from five data sets. Therefore, the compositional growth for J = 5.3 (Fig. 7) does not show this transient domain growth. It is anticipated that for smaller n_r, these transient domains will have a longer lifetime since the thickness gradient at the domain interface will take longer to relax. In a physical system it is expected that the thickness relaxation will be fast, implying short-lived transient domains.

FIGURE 8.

Composition profiles for J = 5.3, n_r = 4, 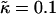, l_u0 = 36, l_s0 = 54, δl_max = 1.0, L = 50, and χ = 0. Time t is in MC cycles.

Thus far we have demonstrated via Monte Carlo simulation that hydrophobic mismatch between neighboring particles can lead to phase separation. Two ratios of interest have been identified; the ratio 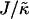of the hydrophobic surface tension J to the compressibility modulus 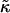, which has units of length, and the ratio 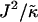, which has units of energy. Increasing either of these ratios leads to phase separation, with the phase-separated domains coarsening more slowly upon increasing the ratios above zero. However, upon further increasing 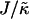, domain sizes become larger after the same number of MC cycles. Interestingly, for high enough 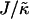the membrane remains mixed; this is a finite size effect, due to a decay length 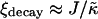that becomes greater than the system size L at high 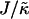. Physically this is because the gradient in the particle thicknesses at the domain interface is too small to maintain phase separation after a concentration fluctuation. It has also been shown that faster thickness relaxation affects the speed of compositional growth.

CONTINUUM MODEL

In the previous section we examined coarsening and the late stages of phase separation due to hydrophobic mismatch. We will now use a continuum model to probe the initial instability of a membrane due to hydrophobic mismatch and the resultant initial domain growth.

The continuum model describing the evolution of composition φ and lipid thickness l can be written, to fourth order in the gradients of composition and thickness, as

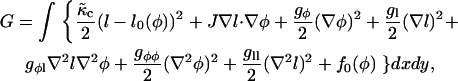(10)

where the term containing 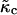is the coarse-grained version of Eq. 3. The value 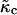is related to the compressibility modulus in the mesoscopic model by 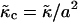. The value l₀(φ) is the preferred local lipid thickness. We expect coarse-graining to lead to a l₀(φ) that depends on 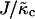. For large 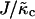, l₀(φ) is expected to be a very weak function of φ. The value f₀(φ) is the free energy per area of mixing, given by

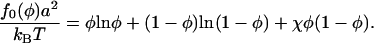(11)

The terms involving gradients in Eq. 10 are coarse-grained versions of Eqs. 3 and 4. Specifically, the terms comprising g_l, g_φl, and g_ll are coarse-grained versions of the hydrophobic mismatch (Eq. 4), with the terms containing g_ll and g_φl describing the bending penalty (51). The values g_φ and g_l are the second-order gradient coefficients in composition and thickness, respectively, and g_φl, g_φφ, and g_ll are the next terms in the gradient expansions for composition and thickness, respectively. The higher order g_φφ and g_ll gradient terms are required to stabilize the growth rate at small length scales.

Phase separation

The local composition variable φ (typically area fraction) obeys the continuity equation (mass conservation),

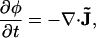(12)

where the flux 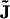of material is given by Fick's law (40),

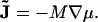(13)

M is the particle lateral mobility and μ ≡ δG/δφ is the chemical potential. Upon combining Eqs. 12 and 13 we can expand the composition dynamics to linear order in deviations of composition and thickness. We use a Fourier expansion,

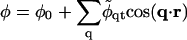(14)

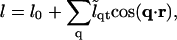(15)

and we assume an initial configuration of uniform composition φ₀ and a corresponding average thickness l₀.

To linear order in the q ≠ 0 modes, we find

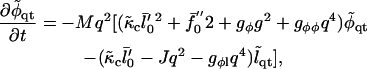(16)

where 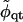is a small perturbation in composition, 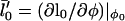, and .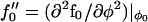

Thickness growth

The thickness evolves by relaxational kinetics,

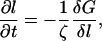(17)

where the friction coefficient ζ is due to dissipation within the membrane. Using Eqs. 10 and 17, we find

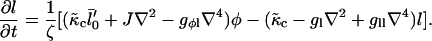(18)

In Fourier space this is given by

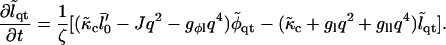(19)

Coupled composition and thickness growth

Finally, we consider simultaneous composition and thickness evolution after a quench. Equations 16 and 19 can be written as

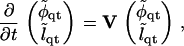(20)

where

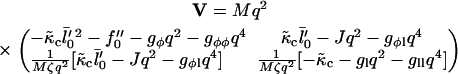(21)

The value 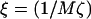controls the dynamic coupling. For ξ < 1, the diffusive coarsening is faster than thickness growth, while for ξ > 1 the thickness evolves faster than diffusive coarsening. Note that ξ > 1 is likely to be the more physical regime since the frictional forces incurred upon lipid stretching or compressing will be less than those incurred upon lipids exchanging lateral positions. ξ > 1 is indeed found in the following simple calculation: For lipids in a bilayer the diffusion coefficient, D ∼ 5 × 10⁻⁸ cm² s⁻¹ (52), is roughly estimated as D ≈ a²/2τ_d, where a is a molecular diameter and τ_d is the hopping time. Hence, for a ∼ 9 Å we estimate τ_d ∼ 80 ns. The relaxation time τ_l for the slowest peristaltic mode of a lipid bilayer, which corresponds to the relaxation of thickness fluctuations, calculated via molecular dynamics simulation is ∼4 ns (53). Hence, the ratio of these times τ_d/τ_l is ξ ∼ 20.

Assuming the solutions

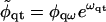(22)

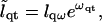(23)

we have

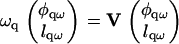(24)

The eigenvalues (Λ₁, Λ₂) of the matrix V yield the rates ω_q, which govern the growth of composition and thickness fluctuations. Because the second eigenvalue Λ₂ was stable in the entire q-range for the parameters we consider, we will focus on the effect of Λ₁ on domain growth.

Parameters are chosen as follows. All lengths, including the thickness variable l, are scaled by the lattice size a, and all energies are scaled by 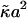. The gradient terms g_φφ, g_φl, and g_ll can be, in principle, derived as higher-order expansions of terms 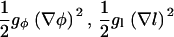, etc. Hence we write these as

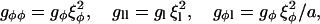(25)

where ξ_φ and ξ_l are the ranges of the interactions in the gradient expansion. Since all gradient expansions will be governed by the lattice size a, which is of the order of a lipid diameter, we choose ξ_φ = ξ_l = a ∼ 9 Å. Note that the gradient expansion in thickness may also involve the thickness l₀, but the largest effect should be due to splay near the surface, so we take as an estimate ξ_l = a (an upper bound on this may be 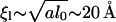). This leads to the following dimensionless parameters:

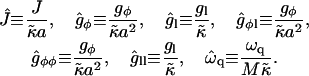(26)

The bending modulus, 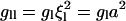(51) is of order 24 k_BT (at 300 K), and we estimate a = 9 Å, J = 0.4 k_BT a⁻¹, 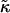= 0.7 k_BT a⁻², and g₁ = 24 k_BT a⁻² (See near eqs. 6–9 for the estimates of a, J, and 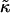). This leads to the following estimates:

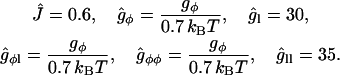(27)

We assume g_φ ∼ 1 k_BT, which is of the order of the result from the Random Phase Approximation applied to a mixture of monomers (54). This leads to the estimates

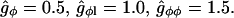(28)

We control the quench depth by 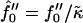, where, within mean-field theory, 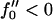leads to growth. Finally, the thickness l_DOPC of a DOPC bilayer is 37 Å and that of SM is l_SM = 51 Å, leading to 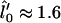, assuming ideal mixing l(φ) = φ l_DOPC + (1 – φ) l_SM.

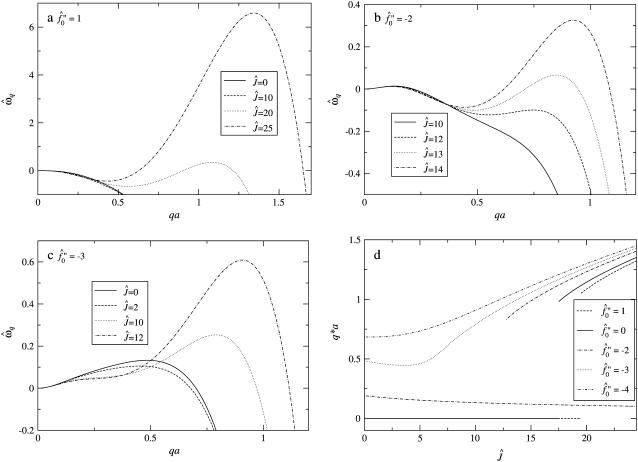
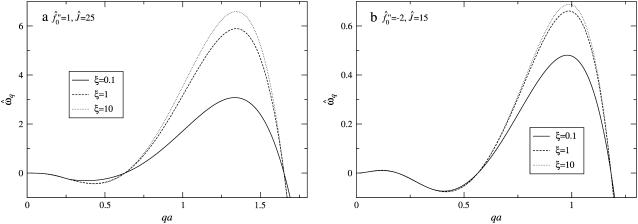
Fig. 9 a shows the growth rate 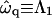as a function of qa for a shallow quench depth 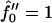and for the dimensionless measure of the hydrophobic surface tension Ĵ from 0 to 25. For small Ĵ, the membrane is stable. However, hydrophobic mismatch starts to drive phase separation upon increasing Ĵ, with the dominant growing wavelength 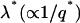decreasing. Upon increasing the quench depth 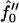to −2 (Fig. 9 b), the membrane becomes unstable at Ĵ = 0, and hence is below the critical point. There are two dominant growing wavelengths for this quench depth, one that increases and one that decreases upon increasing Ĵ . The large wavelength instability is a perturbation of the ordinary spinodal instability after a quench in a two-phase mixture. The small wavelength instability is due to the coupling of concentration and thickness gradients; this coupling renders the theory unstable in the absence of higher order thickness and composition gradient terms, which stabilize the instability at a higher wavenumber. Upon further increasing the quench depth to 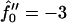(Fig. 9 c), there is only one dominant growing wavevector. The dominant growing wavenumber q*a versus Ĵ for 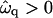and increasing quench depths is shown in Fig. 9 d. The decrease in q*a (increase in λ*) upon increasing Ĵ for 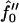equal to −2 and −3 is due to the fast thickness relaxation coupling to the composition, so that hydrophobicity perturbs the ordinary phase separation. The increase in q*a (decrease in λ*) upon further increasing Ĵ for all quench depths shown is due to the competition between hydrophobicity and bending effects. The hydrophobic coupling induces a short wavelength instability (see Eq. 10), stabilized by the bending energy which is higher-order in wavenumber.

FIGURE 9.

Growth rate 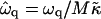versus qa for different Ĵ with increasing quench depth 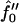from 1 (a) to −2 (b), and −3 (c). (d) q*a versus Ĵ for 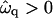with increasing quench depth 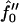from 1 to −4. .

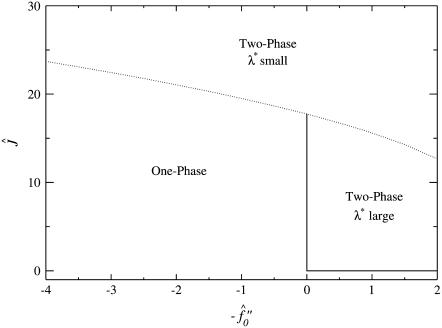
Next we will ensure that our mesoscopic and continuum models produce consistent results. Obviously these models address different time regimes and so a comparison between, for example, Figs. 1 and 9 is not possible. However, both models should accurately predict the existence of mixed and demixed membrane morphologies. To investigate this, we have determined the Ĵ versus −f″₀ phase diagram (Fig. 10) from the continuum model, where increasing −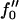 corresponds to increasing the quench depth and therefore χ. As can be observed in Fig. 10, an increase in quench depth leads to a decrease in the value of Ĵ required to induce phase separation. The same qualitative behavior is displayed by the lower phase boundary in the phase diagram determined numerically (Fig. 4). Note that the lower phase boundary in Fig. 4 corresponds to the case where finite size effects are unimportant. Obviously, this is the relevant phase boundary for comparison with Fig. 10 since finite size effects are also unimportant here. For quenches where 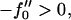phase coexistence occurs regardless of the hydrophobicity (Fig. 10). The discontinuity observed is due to the mean-field nature of our continuum model. We expect that fluctuations will smooth out the discontinuity because growing modes will become coupled.

FIGURE 10.

Ĵ versus 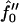phase diagram where 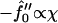, 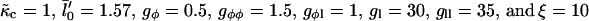. The solid line locates the onset of domain growth at large length scales due to perturbation of the ordinary spinodal instability after a quench in a two-phase mixture. The dotted line locates the onset of growth at small length scales due to the coupling of concentration and thickness gradients.

Next we investigate the effect of decreasing the thickness relaxation time via increasing ξ for 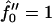and Ĵ = 25 (Fig. 11 a) and 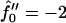and Ĵ = 15 (Fig. 11 b). Changing ξ, i.e., the system kinetics, does not effect the range of unstable modes or appreciably effect the dominant growing wavelength λ*. However, λ* does become more unstable upon increasing ξ. Hence, a faster thickness response reduces the resistance to coarsening, allowing faster coarsening.

FIGURE 11.

Growth rate 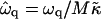versus qa for different degrees of dynamic coupling 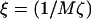. (a) 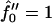and Ĵ = 25. (b) 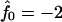and Ĵ = 15. .

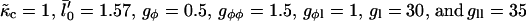In summary, we have used a continuum model to investigate both the instability and the resultant initial domain growth of a membrane due to hydrophobic mismatch. We have found that the characteristic size for domain formation is a nonmonotonic function of the dimensionless measure of hydrophobic surface tension Ĵ for the quench depths 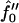equal to −2 and −3. Firstly, domains increase in size upon increasing Ĵ. Upon further increasing Ĵ, domain sizes decrease for all quench depths investigated. Next, we investigated the effects of decreasing the thickness relaxation time via increasing ξ. We found that upon an increase in ξ, there was no appreciable change in the dominant growing wavevector. However, an increase in ξ did allow faster coarsening.

CONCLUSIONS

In this article, we have studied how the stretching and compression of acyl chains due to hydrophobic mismatch between lipids in a bilayer influences the phase behavior. We initially studied a mesoscopic description of a bilayer, comprising a binary mixture of particles, via Monte Carlo computer simulation, hence allowing fluctuation effects. The particles, U and S, differ in their preferred lengths, with the shorter U particles mimicking the shorter and unsaturated, nonraft lipids, and the longer S particles mimicking the saturated rafts lipids. An increase in either the ratio 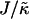of the hydrophobic surface tension J to the particle compressibility modulus 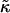, which has units of length, or 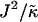that has units of energy, can induce phase separation, with the phase-separated domains coarsening more slowly upon increasing either of these ratios above zero (Fig. 1). This trend is similar to the trend observed upon increasing χ. However, upon further increasing 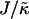there is a reversal in behavior, with domain sizes becoming larger after the same simulation time. Most surprisingly, if 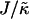is high enough the membrane remains mixed. The absence of phase separation at high 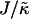is due to finite size effects. This suggests that there is a decay length 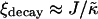, due to the competition between hydrophobic mismatch and particle stretching, which controls phase separation. If ξ_decay > L, then the membrane will mix. This is because it is energetically favorable for the particle thicknesses to become equal to minimize the hydrophobic mismatch energy. Hence, the composition decouples from the thickness. However, transient domains can be induced upon increasing the particle thickness relaxation time, since the thicknesses do not equilibrate before subsequent compositional change. In a physical system, it is expected that the thickness relaxation will be fast, therefore implying that any transient domains will be short-lived.

We next determined the 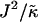versus 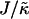phase diagram (Fig. 3) for χ = 0 and system size L = 50. We found that as 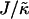approaches the system size L, finite size effects lead to a significant increase in the magnitude of 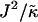required to induce phase separation.

When simulating a membrane with rough estimates for biologically relevant parameters, coarsening was not observed (Fig. 5). However, an increase in 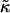and J by a factor of 10 leads to phase separation. Hence, in a biological membrane with embedded proteins having larger values of 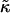and J, it is reasonable to assume that hydrophobic mismatch between the proteins and the surrounding lipids could induce phase separation.

Next, we studied, analytically, the initial growth in composition and thickness, as a function of the dimensionless measure of the hydrophobic surface tension Ĵ and the ratio of the characteristic times for thickness relaxation and diffusion ξ. For ξ < 1, the diffusive coarsening is faster than thickness growth; whereas for ξ > 1, the thickness evolves faster than diffusive coarsening. The value ξ > 1 is expected to be the more physically relevant regime since the frictional forces incurred upon lipid stretching or compressing will be less than those incurred upon lipids exchanging lateral positions.

We have found that for fixed ξ, the characteristic size for domain formation is a nonmonotonic function of Ĵ for the quench depths 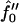equal to −2 and −3 (Fig. 9). Firstly, domains increase in size upon increasing Ĵ . This is due to the fast thickness relaxation coupling to the composition, so that hydrophobicity perturbs the ordinary phase separation. Upon further increasing Ĵ, domain sizes decrease for all quench depths investigated. This is due to the competition between hydrophobicity and bending effects. The hydrophobic coupling induces a short wavelength instability (see Eq. 10), stabilized by the bending energy which is higher-order in wavenumber. Upon increasing ξ, the dominant growing wavelength λ* does not change appreciably (Fig. 11). However, λ* does become more unstable. Hence, a faster thickness response reduces the resistance to coarsening, allowing faster coarsening. We have shown consistency between our mesoscopic and analytical models by determining the Ĵ versus – 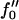phase diagram (Fig. 10) from the analytical model. This phase diagram qualitatively agrees with the phase diagram determined via our mesoscopic model (Fig. 4).

In this article, we have developed a simple model to describe how the competition between hydrophobic mismatch and acyl-chain stretching can lead to phase separation in a lipid bilayer. Estimates for the model parameters for our simple model can be obtained from microscopic and mesoscopic theories (see (55) for a review). The advantage of our approach is that it enables the prediction of large-scale structures. This model can be extended to include proteins embedded in a mixed lipid bilayer. Hence, the influence of the protein on both phase separation and also on the perturbation of the hydrophobic thickness of the bilayer, and alternatively the influence of the bilayer on protein organization, can be investigated. To investigate the validity of this model, an ideal experiment would be to cool a mixed planar membrane comprising two species of lipid that only differ in their acyl-chain lengths, and simple α-helical transmembrane peptides of variable hydrophobic length (55). A convenient method to observe the membrane thickness profile would be atomic force microscopy (19).