Stimulus Equivalence: Testing Sidman's (2000) Theory

Abstract

Sidman's (2000) theory regarding the origin of equivalence relations predicts that a reinforcing stimulus common to distinct equivalence classes must drop out of the equivalence relations. This prediction was tested in the present study by arranging class-specific reinforcers, R1 and R2, following correct responding on the prerequisite conditional discriminations (Ax–Bx, Cx–Bx) for two stimulus classes, A1B1C1 and A2B2C2. A class-common reinforcer, R3, was presented following correct responding on the prerequisite conditional discriminations for a further two stimulus classes, A3B3C3 and A4B4C4. Sidman's theory predicts reinforcer inclusion within Classes 1 and 2 only, given this training arrangement. Experiment 1 tested for the emergence of four equivalence classes and of stimulus–reinforcer and reinforcer–stimulus relations in each class. Four of the 6 subjects demonstrated the reinforcer-based relations in all four equivalence classes, rather than in only those classes with a class-specific reinforcer, as Sidman's theory predicts. One of the remaining 2 subjects showed the reinforcer-based relations in three of the four classes. Experiment 2 extended these findings to document the emergence of interclass matching relations based on the common reinforcer R3, in 5 of 6 subjects, such that a Class 3 sample occasioned the selection of a Class 4 sample when the Class 3 comparison was absent, and similarly, a Class 4 sample occasioned the selection of a Class 3 comparison when the Class 4 comparison was absent. These interclass relations emerged despite the simultaneous maintenance of Class 3 and 4 baseline conditional discriminations, so that the Class 3 and 4 stimuli and reinforcer simultaneously were, and were not, part of a single larger equivalence class. These data are irreconcilable with Sidman's theory, and question the utility of the application of the equivalence relation in describing derived stimulus relations.

Stimulus classes with the defining properties of equivalence are typically established using conditional discrimination procedures. In these procedures, at least two different sample stimuli are presented alone and successively across trials. At least two comparison stimuli are presented either concurrently with, or following the presentation of a sample stimulus. Responses to one comparison are reinforced only in the presence of a particular sample, and responses to the second comparison are reinforced only in the presence of the second sample. The comparison stimulus designated as correct is thus conditional on the sample presented (Cumming & Berryman, 1965).

Sidman and Tailby (1982) formalized the properties necessary to assert that a set of stimuli are equivalent by applying mathematical set theory to conditional discrimination performances. Stimuli are said to be members of an equivalence class when conditional discrimination performance shows the properties of reflexivity, symmetry, and transitivity. A reflexive relation demands that a stimulus be matched to itself (if A1 then A1). A symmetrical relation requires the reversal of the learned relation (if A1–B1 then B1–A1). To satisfy the property of transitivity, a subject must match the sample of one trained conditional discrimination (e.g., A1 from A1–B1) to the comparison of another trained conditional discrimination (e.g., C1 from B1–C1) where the comparison of the first, and sample of the second, discriminations are the same stimulus (if A1–B1 and B1–C1, then A1–C1). When these stimulus relations are demonstrated by the subject without explicit training, the relations are described as emergent, and the stimuli are said to be members of an equivalence class.

The following notation will be used to describe Sidman's (2000) theory and throughout the remainder of the present paper: stimuli will be referred to by an alphanumeric term so that, for example, A1 refers to the member, A, of Class 1. The hyphenation of two stimulus terms (e.g., A1–B1) indicates the selection of the class-consistent second term (the comparison) given the first term (the sample) from a set of stimuli that typically includes all numeric forms of the second term (i.e., B1, B2, B3, etc.). The response and reinforcer terms of Sidman's analytic units are abbreviated as “resp” and “R”, respectively, and in cases of multiple response and reinforcer elements, each is given a numeric descriptor (e.g., resp1, resp2, R1, R2). Note that for response and reinforcer elements, the numeric descriptor does not necessarily correspond to stimulus class membership as it does for stimuli. Hyphenation of stimulus, response, and reinforcer elements (e.g., A1–B1–resp1–R1) indicates the consistent selection (or emission) of those elements given the initial element. Terms grouped together (e.g., A1B1C1) indicate that those terms are members of a stimulus class defined by the properties of equivalence. For ease of exposition, X is used to denote all members of the class defined by the numeric descriptor. X4, for example, refers to all members of Class 4. Where x is used as the numeric descriptor, x is used to denote all possible classes. For example, Ax–Bx refers to all possible A–B relations (e.g., A1–B1, A2–B2, A3–B3) given the specified training arrangement.

Sidman (1994, 2000) proposed that “a reinforcement contingency produces at least two types of outcome: analytic units and equivalence relations” (2000, p. 128). The analytic units referred to here are those of an earlier exposition (Sidman, 1986). In that exposition, reinforcement of an operant gives rise to a two-term, response–reinforcer unit of analysis (cf. Donahoe, 1994; Moxley, 1996). Two-term units can come under the control of discriminative stimuli if the response is reinforced only in the presence of a defined stimulus. Alternative responses in the presence of the defined stimulus, or the emission of the defined response in the presence of alternative stimuli, do not result in reinforcement. Control of a two-term unit by antecedent stimuli requires a simple discrimination, and constitutes a three-term unit of analysis: discriminative stimulus–response–reinforcer. The four-term analytic unit arises from the conditional discrimination in which the three-term unit itself comes under the control of a conditional stimulus: conditional stimulus–discriminative stimulus–response–reinforcer. The conditional stimulus is said to function as a “selector of discriminations”, strengthening the discriminative function of the stimulus to which a response will be reinforced (Cumming & Berryman, 1965).

Sidman (2000) argued that reinforcement contingencies produce not only the units of analysis predicted by the experimenter, but also equivalence relations. Equivalence relations, he proposed, can consist of pairs of all positive terms participating in particular reinforcement contingencies, including responses and reinforcers. Suppose we arranged conditional discrimination contingencies to establish the baseline analytic units: A1–B1–resp1–R1; B1–C1–resp1–R1; A2–B2–resp1–R1; and B2–C2–resp1–R1. The stimulus members of these analytic units will form two three-member equivalence classes (A1B1C1 and A2B2C2). If the resulting equivalence relations also included the common response and reinforcer elements as members, then all stimuli would be equivalent via the common reinforcer and response members (see also Dube, McIlvane, Mackay, & Stoddard, 1987). For example, A1 would become equivalent to B2 through the common elements resp1 and R1, so that a subject could not learn even the baseline conditional discriminations. Yet training arrangements such as this are commonplace, and are sufficient to produce both the outcomes that Sidman argues result from reinforcement contingencies—namely, the baseline analytic units and the stimulus–stimulus equivalence relations.

In order to resolve the dilemma of contingencies that on the one hand specify class distinction, and on the other hand promote class union through equivalence relations, Sidman (2000) made an assumption to maintain the logical consistency of his theory:

Our theory requires us to assume that when the two outcomes of the reinforcement contingency come into conflict, the analytic unit takes precedence over the equivalence relation… In order for the common response and reinforcer elements to retain their membership in the analytic unit, they must selectively drop out of the equivalence relation… making it possible for the smaller classes, A1B1C1 and A2B2C2, to form. (p. 132).

This suggestion is crucial to Sidman's theory which sees the reinforcement contingency as producing two outcomes, for without the analytic units, which are instantiated as the baseline conditional relations, the equivalence relations are not possible. According to this theory, then, demonstrating the inclusion of all the possible members in the equivalence class requires arranging a set of contingencies in which there is no conflict between the units of analysis and the equivalence pairs that may arise from experience with those contingencies. For example, we may train a subject to perform: A1–B1–resp1–R1; B1–C1–resp1–R1; and A2–B2–resp2–R2; B2–C2–resp2–R2. Here, Classes 1 and 2 have specific response and reinforcer elements which may then participate in the equivalence relations resulting from those reinforcement contingencies.

Sidman's (1994, 2000) notion that responses and reinforcers can become members of equivalence classes involving samples and their corresponding comparisons has some empirical support. Class expansion via stimulus-reinforcer relations has been reported in a number of studies (Dube et al., 1987; Dube, McIlvane, Maguire, Mackay, & Stoddard, 1989; Goyos, 2000; Schenk, 1994). In these experiments, arbitrary matching-to-sample training established two equivalence classes, A1B1C1, and A2B2C2. Correct responses on Class 1 trials were always followed by R1, and correct responses on Class 2 trials were always followed by R2. In addition, subjects received identity matching trials for all A, B, and C stimuli, and also for D1 and D2 stimuli. Again, correct selection of D1 on identity matching trials produced R1, whereas correct responding on D2 trials produced R2. On test trials subjects matched D1 to A1, B1, and C1, and matched D2 to A2, B2, and C2, even though D stimuli never featured on arbitrary matching trials. This demonstrates class expansion via common reinforcers to include D stimuli. The inclusion of D1 and D2 into their respective classes can only have resulted from their relations with class-specific reinforcers, demonstrating that reinforcer stimuli can participate in equivalence relations.

Class establishment via stimulus–reinforcer relations alone was demonstrated by Schenk (1994, Experiment 2). Subjects received identity matching trials only, where correct selections of A1, B1, C1, and D1 produced R1, and correct selections of A2, B2, C2, and D2 produced R2. On arbitrary matching probes for equivalence-class formation, 6 of 8 subjects were able to match A1, B1, C1, and D1 to one another at levels of accuracy that were significantly greater than chance, and similarly for Class 2 stimuli. The 6 subjects who demonstrated the emergence of two four-member equivalence classes also correctly matched R1 to Class 1 stimuli, and R2 to Class 2 stimuli. As subjects in Experiment 2 of Schenk's study never received arbitrary matching-to-sample training, the equivalence classes shown by 6 subjects could only have been possible if the training procedures resulted in equivalence classes A1B1C1D1R1, and A2B2C2D2R2, showing that class-specific reinforcers can become members of the stimulus classes they are used to establish, and that stimulus–reinforcer relations are sufficient to produce equivalence class formation.

Sidman (1994, 2000) outlined various testable predictions arising from his theory regarding the formation of equivalence classes through class-specific reinforcement or class-specific responses. As stimulus–reinforcer relations are the focus of the present study, only his test for class formation via reinforcer relations will be described here. In this test, four conditional discriminations (A1–B1, D1–C1, A2–B2, and D2–C2) are established with class-specific reinforcers, R1 and R2. Correct selections of B1 and C1 in the presence of A1 and D1 respectively are reinforced with R1, whereas correct selections of B2 and C2 in the presence of A2 and D2 respectively are reinforced with R2. Each individual conditional discrimination has no common conditional- or discriminative-stimulus members with any other conditional discrimination. There are, however, common reinforcing stimuli to draw stimuli into two potential equivalence classes. A1, B1, C1, and D1 should form an equivalence class due to the common reinforcer R1. Similarly, A2, B2, C2, and D2 should form another class due to the common R2 element. Tests for the emergence of these equivalence classes include all between-discrimination pairs for each class (i.e., Ax–Dx, Ax–Cx, Bx–Dx, Bx–Cx, and the reverse of each).

Maki, Overmier, Delos, and Gutmann (1995, Experiment 3) carried out this proposed experiment and reported results consistent with Sidman's predictions, though they did not test all possible emergent relations. In their differential-outcomes group, 2 normal children were trained to choose B1 conditionally upon A1 in order to receive R1, a bead of a particular color (either blue or red, where blue beads were exchangeable for toys and red beads were exchangeable for food). R1 also served as the outcome following correct selections of C1 after D1 had served as a sample. Another set of stimuli were trained with R2, a bead of a different color from R1 (red or blue). R2 was used to reinforce selections of B2 following A2, and of C2 following D2 (i.e., Ax–Bx–Rx, and Dx–Cx–Rx training). Maki et al. carried out two blocks of test trials after training. The first test block arranged Ax–Cx trials for 1 subject and Dx–Bx trials for the second subject. The mean accuracy score in Test Block 1 was 72% correct. The second test block presented the first subject with Dx–Bx trials, and the second subject with Ax–Cx trials. The mean accuracy in Test 2 was 90.5% correct. That these test block accuracies were significantly greater than 50% correct can only have been possible through the common reinforcing stimulus used to train the baseline relations, and indicates that Rx was substitutable for each Class X stimulus.

The experiments described above support Sidman's (2000) prediction that class-specific reinforcers can become members of an equivalence class and, therefore, form the basis for the emergence of new stimulus–stimulus relations. However, his prediction that a reinforcer common to more than one stimulus class must drop out of all equivalence relations to allow the preservation of the analytic units remains to be tested. This was the goal of the present study.

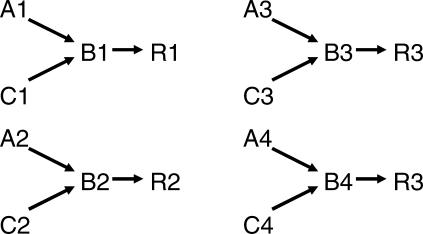
Subjects were exposed to many-to-one training (Ax–Bx, Cx–Bx; x ranges from 1 to 4) where correct Class 1 responses were reinforced with R1, correct Class 2 responses were reinforced with R2, and both correct Class 3 and 4 responses were reinforced with a common reinforcer, R3 (see Figure 1). This training arrangement should result in the emergence of four classes (AxBxCx). With regard to inclusion of Rx stimuli, Sidman's (2000) theory predicts the following results: subjects should include R1 as a member of Class 1 and R2 as a member of Class 2. If, for example, we present R1 as a sample, subjects should consistently choose A1 when A1 to A4 are presented as comparisons, B1 when B1 to B4 are presented as comparisons, and C1 when C1 to C4 are presented as comparisons. Similarly, the theory predicts the emergence of the relations Ax–Rx, Bx–Rx, and Cx–Rx when stimulus members of Classes 1 and 2 are presented as samples and the three reinforcers R1, R2, and R3 are presented as comparisons.

Fig 1. Schematic diagram of trained baseline relations.

Class 1 and 2 relations are reinforced with class-specific reinforcers whereas Class 3 and 4 relations are reinforced with a common reinforcer.

However, Classes 3 and 4 share a common reinforcer, R3. According to Sidman's (2000) theory, this should create conflict between the units of analysis and the equivalence relations so that the reinforcer element R3 drops out of the equivalence relations. This means that if we present R3 as a sample, subjects should not consistently choose A3, B3, C3, or A4, B4, or C4, when available as a choice stimulus. Also, the reverse relations (e.g., A3–R3) should not emerge when the three reinforcers are presented as comparison stimuli.

These relations were trained using a modified version of a computer-controlled conditional discrimination training procedure with differential outcomes for adult subjects reported by Miller, Waugh, and Chambers (2002). In the present study, adult subjects were trained on conditional discriminations involving Japanese kanji characters as both samples and comparisons. Reinforcing stimuli were pictures representing entries into a draw to win specific prizes. The prizes were indicated by presenting pictures of cash, chocolates, or movie tickets following correct choices. Incorrect choices were followed only by feedback informing the subject of his or her error. Stimulus relations were trained and tested as outlined above to evaluate the prediction arising from Sidman's (2000) theory that reinforcing stimuli common to at least two stimulus classes must drop out of those classes in order to maintain the integrity of the baseline analytic units.

Experiment 1

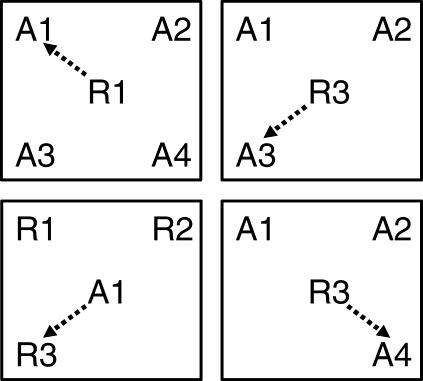
Reinforcer test trials presented R stimuli in sample or comparison positions as shown in Figure 2. The top left panel shows a test trial for a Class 1 reinforcer–stimulus relation (Class 2 reinforcer–stimulus trials were similar) with all category A stimuli presented as comparisons. Here, Sidman's theory would predict the selection of A1 given the described baseline training. The bottom left panel shows an A3–R3 test trial (stimulus–reinforcer test trials for all other classes were similar). As only three R stimuli were used during training, the number of comparisons to be presented on stimulus–reinforcer test trials is, unavoidably, only three. The top and bottom right panels illustrate reinforcer–stimulus test trials for Classes 3 and 4, respectively. On a Class 3 reinforcer–stimulus test trial the Class 4 comparison was not presented in the comparison array, and on a Class 4 reinforcer–stimulus test trial the Class 3 comparison was not presented as a comparison1.

Fig 2. Schematic diagram of trials testing for stimulus–reinforcer and reinforcer–stimulus relations.

The top left panel shows a test trial for a Class 1 reinforcer–stimulus relation (Class 2 reinforcer–stimulus test trials were similar). The bottom left panel shows a Class 3 stimulus–reinforcer test trial (stimulus–reinforcer test trials for all other classes were similar). The top right panel shows a Class 3 reinforcer–stimulus test trial in which the Class 4 exemplar is absent from the comparison array. The bottom right panel shows a Class 4 reinforcer–stimulus test trial in which the Class 3 exemplar is absent from the comparison array.

Method

Subjects

Six undergraduate psychology students, 3 men and 3 women, served as subjects and were numbered S1 to S6. Subjects were not familiar with stimulus equivalence research, had never participated in experiments involving conditional discriminations, and had no prior experience with Japanese kanji characters.

Apparatus

Subjects sat at a table that supported a standard computer mouse and a computer monitor measuring 228 mm high and 306 mm wide, on which all stimuli were displayed. All responses were made via the left button of the computer mouse. Stimulus presentation and data collection were controlled by an IBM-PC^©-compatible personal computer running customized software programmed in Delphi5^©. The computer recorded the identity and position of all stimuli and the choice response emitted on each trial, together with the times of all experimental events.

Stimuli

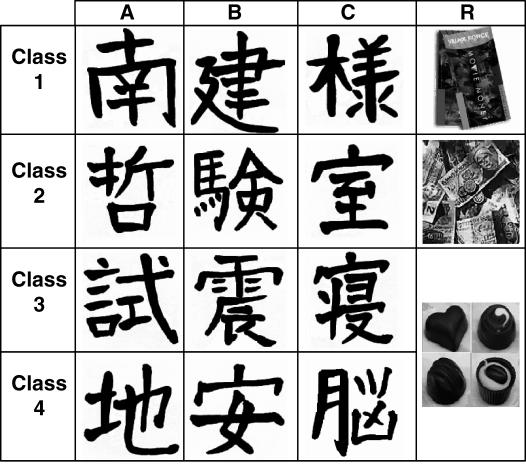
Figure 3 shows the stimuli used as samples, comparisons, and reinforcers. Each stimulus was contained within an area 160 pixels high and 150 pixels wide. The samples and comparisons were black Japanese kanji characters on a white background. Class-specific reinforcer stimuli were pictures of movie tickets (R1), cash (R2) and chocolates (R3). The incorrect feedback stimulus comprised the words “That was incorrect” written in black on a red background and was accompanied by the words “Click for the next trial” written above the incorrect feedback stimulus. Sample stimuli and reinforcer stimuli appeared at the center of the screen and comparison stimuli were presented at the corners of the screen, 63 mm from the side of the screen and 25 mm from the top or bottom of the screen. During training and equivalence testing (symmetry; and combined symmetry and transitivity, hereafter referred to as combined tests), all four corner positions were used for comparison presentation. On stimulus–reinforcer tests, only three of the four corner positions, pseudorandomly selected for each trial, displayed a comparison stimulus. On Class 1 and 2 reinforcer–stimulus tests, all four corner positions displayed a comparison, whereas on Class 3 and 4 reinforcer–stimulus tests, only three corner positions displayed a comparison.

Fig 3. Training and reinforcing stimuli for all potential stimulus classes.

The reinforcing stimuli were colored pictures of movie tickets, cash, and chocolates.

Procedure

All trials involved a zero-delay matching-to-sample task. A trial began with the presentation of the sample stimulus at the center position on the computer screen. A mouse click within the stimulus area resulted in the removal of the sample stimulus and the immediate presentation of comparison stimuli in the corners. A response to any comparison resulted in the immediate removal of all comparison stimuli, and the presentation of feedback at the center of the screen. Correct responses resulted in the presentation of the reinforcer stimulus corresponding to the stimulus class being trained on that trial (see Figure 1). Incorrect responses resulted in the presentation of feedback informing the subject that his or her response was incorrect. A response to either the reinforcer stimulus or the incorrect feedback stimulus resulted in its removal after 1 s, followed by a 1-s intertrial interval, after which the next trial began.

Part 1: Instructions and Baseline Training

Before an experimental session began, subjects were presented with the following instructions on the screen:

Welcome. In this experiment you will be shown a number of kanji characters. Your task is to learn which kanji go together. In a single trial, a kanji will appear in the centre of the screen. Click the kanji to make another four kanji appear. Choose the kanji you think goes with the first one. You will be given feedback about your choice. A correct choice will give you an entry into one of three different prize draws: movie tickets, cash, or chocolates. To begin with, you will have to guess, so you will get about 1 in 4 correct. As you progress through the experiment though, you will learn which kanji go together, and you will get more entries into the prize draws. The computer will tally these for you and tell you at the end how many of each you received.

At some point in the experiment different trials will appear.

Answer these as correctly as possible.

More instructions will appear later in the experiment.

A many-to-one (Ax–Bx, Cx–Bx) training structure was used such that four three-member classes (excluding reinforcer stimuli) could emerge from baseline training. Class-specific reinforcers were arranged for Classes 1 and 2, so that correct responding on Class 1 trials always resulted in the presentation of R1 (cash picture) and correct responding on Class 2 trials always resulted in the presentation of R2 (movie tickets picture) (see Figures 1 and 3). A common reinforcer was arranged for Classes 3 and 4 where correct responding on trials for both classes always resulted in the presentation of R3 (chocolates picture). Feedback was presented on every trial in Part 1. Every presentation of a reinforcing stimulus advanced a counter for the number of entries into the corresponding prize draw. This counter was not visible to the subject during the experiment.

Training was conducted in blocks of 64 trials. For each block, trials were sampled without replacement from all possible sample-comparison combinations. One block contained eight trials of each relation to be trained (e.g., A1-B1) with the correct comparison being presented in each of the four comparison locations twice. Part 1 was continued until responding was at least 85% correct, averaged across all baseline trials in each of two successive training blocks.2 When this criterion was reached subjects were given the following instructions:

The experiment will continue but you will now receive no feedback.

Feedback may appear later. Take a break and click to continue.

A response to the instruction text advanced training to Part 2.

Part 2: Removal of Feedback and Baseline Maintenance

All feedback was removed in Part 2. Selection of a comparison stimulus was, therefore, immediately followed by the 1-s intertrial interval. The block structure in Part 2 was as in Part 1. In order to progress to testing, responding had to be maintained at 85% correct, averaged across all classes in one block of trials. No new instructions were given prior to testing. However, if the performance criterion for baseline maintenance was not satisfied, the subject was presented with the following instructions:

The experiment will continue but you will now receive feedback.

Take a break and click to continue.

A response to the instruction text was followed by a repetition of Part 1. The criteria for advancement of training remained the same. All subjects maintained 85% correct during Part 2 so that a return to Part 1 was never required.

Part 3: Testing

Tests for symmetrical stimulus relations (Bx–Ax, Bx–Cx), combined symmetrical and transitive stimulus relations (combined trials: Ax–Cx, Cx–Ax), stimulus–reinforcer and reinforcer–stimulus matching relations (Ax–Rx, Bx–Rx, Cx–Rx, Rx–Ax, Rx–Bx, and Rx–Cx) were conducted. The test block contained 224 trials and comprised 64 baseline trials, 32 symmetry trials, 32 combined trials, 48 stimulus–reinforcer, and 48 reinforcer–stimulus trials. Baseline trials were sampled as for Part 1. Four trials of each symmetry and combined relation were randomly sampled without replacement from all possible sample-comparison combinations. Four trials of each stimulus–reinforcer and reinforcer–stimulus relation were sampled in the same manner. Trials testing symmetrical, combined, stimulus–reinforcer, and reinforcer–stimulus matching relations were mixed with baseline trials and presented in a random order. No feedback was programmed for any of these trials.

On all baseline, symmetry, and combined trials, four comparison stimuli were presented. For example, when an A1–C1 trial was arranged, C1 to C4 were presented as comparisons. On all stimulus–reinforcer test trials, only three comparisons (R1 to R3) were presented (see bottom left panel of Figure 2). Reinforcer–stimulus trials were different: Class 1 and 2 reinforcer–stimulus trials always had four comparison stimuli. For example, on an R2–A2 trial, R2 was the sample and A1 to A4 were comparisons. Class 3 and 4 reinforcer–stimulus trials always had three comparison stimuli. On R3–X3 test trials the Class 4 comparison was not presented (see top right panel of Figure 2). Similarly, the Class 3 comparison was not presented on R3–X4 test trials (see bottom right panel of Figure 2).

The criterion for maintenance of baseline relations was set at 85% correct, averaged over all baseline trials during Part 3 testing, and was assessed upon completion of an entire test block. If this criterion was not met, instructions that feedback was to be implemented again (see Part 2) were presented, and Part 1 procedures were reintroduced. As in Part 2, this retraining procedure was never needed because all subjects maintained the baseline relations at greater than 85% correct.

All parts were conducted within one experimental session with a duration of about 1 hr. Upon completion of the entire experiment, recipients of the cash, chocolate, and movie tickets prizes were randomly selected and provided with their prize.

Results

Baseline Training

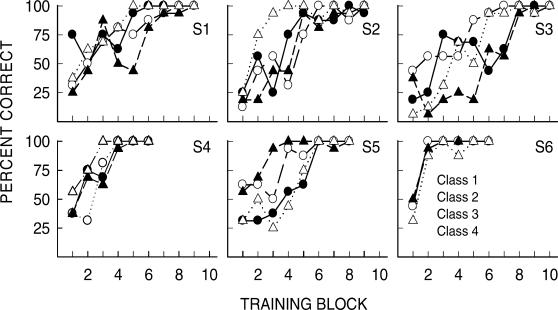
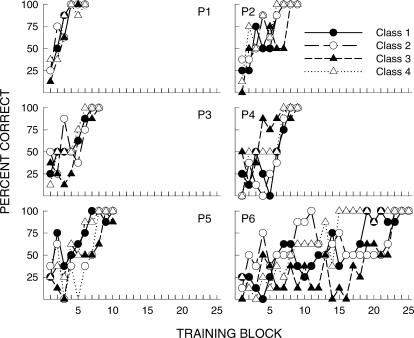
Figure 4 shows acquisition of Class 1 to 4 baseline relations for each subject where percent correct is plotted as a function of the number of training blocks for each class separately. All subjects except S2 attained 100% correct on baseline trials with all four classes by the end of baseline training. The number of training blocks required for a subject to meet the criterion for progressing to testing ranged from 6 to10. Figure 4 shows no systematic differences among the acquisition functions for the four classes. In particular, there is no evidence of a differential-outcomes effect (Trapold, 1970) in acquisition of class relations with class-specific reinforcers (Classes 1 and 2) compared with the acquisition of class relations reinforced with shared outcomes (Classes 3 and 4). A differential-outcomes effect would have been expressed in Figure 4 by steeper functions for Class 1 and 2 relations, reaching asymptotic values earlier than the corresponding functions for Classes 3 and 4. However, idiosyncratic patterns of acquisition are shown by subjects in Figure 4. All subjects maintained baseline relations with an accuracy of at least 85% correct when feedback was removed in Part 2.

Fig 4. Percent correct obtained for each subject on Class 1 to 4 stimulus relations for all Part 1 and 2 training blocks.

The rightmost data point for each subject and class denotes accuracy in Part 2 (removal of feedback).

Testing

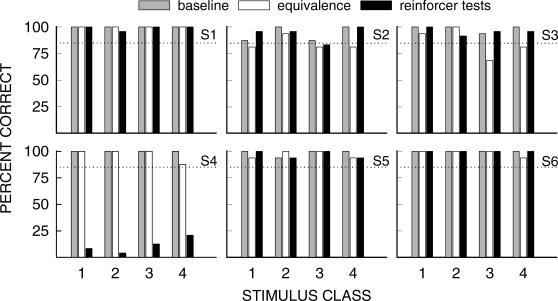
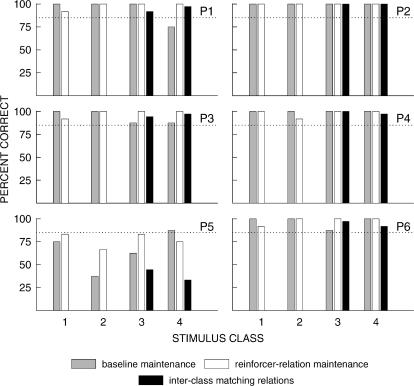
Figure 5 shows percent correct during Part 3 trials for all subjects. Data from symmetry and combined trials are pooled together and presented as equivalence tests. Data from stimulus–reinforcer and reinforcer–stimulus trials are pooled together and presented as reinforcer tests. All subjects maintained accuracies of at least 85% correct for overall conditional discrimination accuracy on baseline trials, and also for each individual stimulus class. The criterion for documenting the emergence of equivalence, stimulus–reinforcer, and reinforcer–stimulus relations was 85% correct, averaged over all trials of a particular test. Figure 5 shows that all subjects met the criterion for the emergence of four equivalence classes (open bars) with the exception of Subjects 2 and 3. S2 met the accuracy criterion for equivalence relations with Class 2 stimuli only, whereas S3 did so for only Classes 1 and 2. Figure 5 shows that all subjects met the criterion for reversible stimulus–reinforcer relations (dark bars) in all classes with the exception of S2 and S4. S2 failed to meet this criterion with the Class 3 stimuli and reinforcer. S4 failed to meet this criterion with stimuli from all classes.

Fig 5. Percent correct responses for each subject on baseline trials, equivalence (symmetry, and combined symmetry and transitivity), and reinforcer tests for all stimulus classes.

The 85% criterion for baseline maintenance, equivalence class formation, and reinforcer inclusion is indicated by the dotted line on each graph.

Discussion

Sidman's (2000) theory states that a reinforcement contingency gives rise to two outcomes: the unit of analysis and equivalence relations between all members of that unit, including reinforcer elements. If these outcomes conflict, any member of the equivalence relation involved in such conflict must drop out of the equivalence relation in order that the analytic units remain intact. As discussed earlier, Sidman's theory predicts the inclusion of the class-unique reinforcers R1 and R2 in Classes 1 and 2, respectively, so that A1B1C1R1 and A2B2C2R2 emerge. However, the class-common reinforcer R3 should not be included in Class 3 or 4, so that only A3B3C3 and A4B4C4 should emerge.

Behavior on reinforcer test trials in the present experiment did not support this prediction. Five subjects (except S4) met the criterion for stimulus–reinforcer and reinforcer–stimulus relations with Class 1 and 2 stimuli. However, 4 of these subjects (except S2) also met this criterion with Class 3 and 4 stimuli, whereas the fifth (S2) did so with Class 4 stimuli. The remaining subject (S4) failed to meet the criterion for stimulus–reinforcer and reinforcer–stimulus relations in all classes. In summary, R3 usually, though not always, remained a member of Classes 3 and 4 simultaneously, inconsistent with Sidman's (2000) theory.

The observation of stimulus–reinforcer relations in Classes 3 and 4 could perhaps be accounted for by appealing to exclusion (Type R control; e.g., Carrigan & Sidman, 1992) in the following way. Suppose Sidman's (2000) theory is correct in that a reinforcing stimulus can only ever be included in an equivalence class if that reinforcing stimulus is specific to one class. In the present experiment, we should only have observed symmetric X1–R1 and X2–R2 relations emerging from baseline training. It could be argued that subjects who demonstrated stimulus-reinforcer relations in all classes may have done so with only these X1–R1 and X2–R2 relations and without any relations involving R3. Recall that stimulus–reinforcer test trials presented R1, R2, and R3 as comparisons. On X3–R3 trials then, choosing R3 may be a result of responding controlled by exclusion, with both R1 and R2 being rejected due to their equivalence with X1 and X2, respectively, and the nonequivalence of X1 and X2 with X3, thus leaving the choice of R3 as the only remaining option. In this way, high levels of accuracy on Class 3 and 4 stimulus–reinforcer test trials may not reflect the emergence of Class 3 and 4 stimulus-reinforcer relations.

However, the case for exclusion on R3–X3 reinforcer–stimulus trials is not so clear. Recall that on an R3–X3 trial, X1, X2, and X3 were comparisons in the presence of an R3 sample. If R3 was not a member of any stimulus class, then we might expect responding on these trials to be equally distributed among X1, X2, and X3. Progression through the testing block may have resulted in the gradual emergence of R3–X3 relations due to responding by exclusion on X3–R3 trials, but then we would not expect accuracies of 100% correct on Class 3 and 4 reinforcer test trials, as some subjects showed. Nevertheless, responding controlled by exclusion may have played some part in Experiment 1.

To eliminate the possibility of an account based on exclusion, Experiment 2 included trials testing for interclass matching relations between Class 3 and 4 stimuli. Trials testing for X3–X4 matching relations were arranged with Class 3 samples (i.e., X3) presented with comparisons from Classes 1, 2, and 4 only. Similarly, by arranging trials with Class 4 samples and Class 1, 2, and 3 comparisons, we tested for X4–X3 matching relations. X3–X4 matching relations cannot be accounted for by exclusion given these trial arrangements as X1, X2, and X4 are equally unrelated to X3, just as X1, X2, and X3 are equally unrelated to X4 on X4–X3 test trials. Observation of these interclass matching relations would therefore support the suggestion of Experiment 1 that R3 had not “dropped out” of equivalence relations with X3 and X4 stimuli, contrary to the predictions of Sidman's theory.

Experiment 2

A pilot experiment to test for X3–X4 and X4–X3 interclass matching relations was conducted with 1 subject. This pilot experiment was identical to Experiment 1, with the addition of X3–X4 and X4–X3 test trials in Part 3. Part 3 therefore contained baseline trials to assess maintenance of baseline, symmetry and combined tests, reinforcer test trials for all classes, and the additional X3–X4 and X4–X3 interclass matching test trials. The pilot subject showed the emergence of four three-member stimulus classes defined by equivalence, but reinforcer relations with Classes 2 and 4 only, scoring 67% and 88% correct respectively. Because the addition of another type of test trial to the only testing block seemed to have a detrimental effect compared to Experiment 1 procedures, with regard to observing all stimulus–reinforcer relations necessary for the interclass matching relations, tests in Experiment 2 were introduced sequentially and after a return to baseline.

Method

Subjects

Six undergraduate psychology students, 2 men and 4 women, served as subjects and were numbered P1 to P6. Subjects were not familiar with stimulus equivalence research, had never participated in experiments involving conditional discriminations, and had no prior experience with Japanese kanji characters.

Apparatus

As for Experiment 1.

Procedure

The trial structure was as in Experiment 1. Three comparison stimuli were presented on all stimulus–reinforcer and reinforcer–stimulus trials, and on all X3–X4 and X4–X3 interclass matching trials.

A sequential training protocol was implemented. Subjects first received baseline training, followed by the removal of all feedback during baseline maintenance. Maintenance blocks were always followed by a block of test trials, provided subjects met the set criterion during the baseline maintenance block. Completion of a test block (with the exception of the final test block) was always followed by a return to baseline training and maintenance. Progression to new test blocks was dependent on accuracies obtained in the most recently completed test block.

The first test block tested for the emergence of stimulus relations defined by equivalence. Following equivalence testing, subjects were returned to baseline training and maintenance. If the criterion for the emergence of equivalence relations was not met during the first exposure to equivalence testing, this repetition of baseline training and maintenance was again followed by equivalence testing. If a subject did meet the criterion for equivalence relations, the repetition of baseline training and maintenance was followed by tests for stimulus–reinforcer and reinforcer–stimulus matching relations. Following reinforcer testing, subjects were again returned to baseline training and maintenance.

If the criterion for reinforcer relations was not met during the first exposure to reinforcer testing, the completion of baseline training and maintenance was followed by reinforcer testing again. If a subject did meet the criterion for reinforcer relations, the return to baseline and maintenance was followed by tests for X3–X4 and X4–X3 interclass matching relations. No criteria were set for the interclass relations test block, and the experiment ended after the completion of this block.

Part 1: Instructions and Baseline Training

Before the experiment, subjects were presented with the same instructions as in Experiment 1. Part 1 procedures, including the accuracy criterion that needed to be met before maintenance, were as for Experiment 1 except that training was conducted in blocks of 32 trials. For each block, trials were sampled without replacement from all possible sample-comparison combinations. One block contained four trials of each relation (e.g., A1B1) with the correct comparison being presented in each comparison position once.

Part 2: Removal of Feedback and Baseline Maintenance

As for Experiment 1.

Parts 3, 4, and 5: Testing

No explicit introduction to test procedures was given. Upon completion of Part 2 and satisfaction of the criterion, the last intertrial interval of Part 2 was followed by the first trial arranged for the given test block. No feedback was given during testing. The criterion for maintenance of baseline relations was set at 85% correct, averaged across all baseline trials during all testing blocks. The criterion for the emergence of equivalence relations in Part 3, and for reinforcer relations in Part 4, was set at 85% correct, averaged across all equivalence trials, and reinforcer test trials, respectively. Following Parts 3 and 4, subjects were returned to Part 1. If the criterion for emergent relations in Parts 3 or 4 was not met, the completion of baseline Parts 1 and 2 was followed by a repetition of the part for which the criterion was not met.

Part 3: Equivalence testing

Symmetrical and combined stimulus relations were tested. The Part 3 test block contained 96 trials, comprising 32 baseline trials, 32 symmetry trials, and 32 combined trials. Baseline trials were sampled as in one block of Part 1 trials. Four trials per class of each symmetrical and combined relation were sampled randomly without replacement from all possible sample-comparison combinations. All trials sampled for the test block were mixed and presented in a random order.

Part 4: Reinforcer-relation testing

The Part 4 test block contained 104 trials consisting of 32 baseline trials, 36 stimulus–reinforcer test trials, and 36 reinforcer–stimulus test trials. Baseline trials were sampled as for one block of Part 1 trials. Three trials of each stimulus–reinforcer and reinforcer–stimulus relation were sampled for each class from all possible sample-comparison combinations. All trials sampled for the test block were mixed and presented in a random order.

Part 5: Interclass matching relations testing

Part 5 contained 152 trials. Maintenance trials included 32 baseline trials (eight each for Classes 1 to 4), 24 stimulus–reinforcer trials (six per class), and 24 reinforcer–stimulus trials (six per class). All possible interclass matching relations were tested. Subjects received four of each of the following Class 3–Class 4 trial types: A3–A4, A3–B4, A3–C4; B3–A4, B3–B4, B3–C4; C3–A4, C3–B4, C3–C4; and four each of the symmetric Class 4–Class 3 relations: A4–A3, A4–B3, A4–C3; B4–A3, B4–B3, B4–C3; C4–A3, C4–B3, and C4–C3, making a total of 72 interclass matching relation test trials. On X3–X4 test trials only X1, X2, and X4 comparisons were presented. X4–X3 test trials presented X1, X2, and X3 comparisons only. No performance criteria were set for any of the relations tested in Part 5, and the experiment ended after completion of Part 5.

All parts were conducted within one experimental session lasting approximately 1.5 to 2 hr. Upon completion of the entire experiment, recipients of the cash, chocolate, and movie tickets prizes were selected randomly and provided with their prize.

Results

Baseline Training

Figure 6 shows percent correct on Class 1 to 4 trials in each successive training block during initial Part 1 and 2 baseline training for P1 to P6. All subjects except P5 attained 100% correct on baseline trials over all four classes by the end of baseline training. The number of training blocks required for a subject to meet the criterion for progression to equivalence testing ranged from 6 to 25 blocks. Figure 6 shows no systematic differences among the four acquisition functions across subjects, indicating no evidence of a differential, outcomes effect in acquisition of class relations with class-specific reinforcers (Classes 1 and 2) compared with the acquisition of class relations reinforced with shared outcomes (Classes 3 and 4). Idiosyncratic patterns of acquisition were shown by the subjects in Figure 6.

Fig 6. Percent correct obtained for each Experiment 2 subject on Class 1 to 4 stimulus relations for all Part 1 and 2 training blocks.

The rightmost data point for each subject and class denotes accuracy in Part 2 (removal of feedback).

Testing

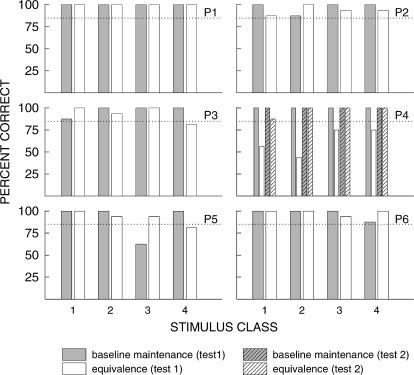
Figure 7 shows percent correct on Part 3 (Equivalence testing) trials for each stimulus class, for subjects P1 to P6. Data from symmetry and combined trials are pooled together and presented as equivalence tests. All subjects maintained accuracies of at least 85% correct for overall conditional discrimination accuracy on baseline trials, and also for each individual stimulus class, except P5 on Class 3 baseline trials. All subjects except P4 met the set criterion (85% correct over all baseline maintenance trials, and 85% correct over all equivalence test trials) for progression to Part 4 testing, following the return to Part 1 and 2 procedures. A Part 3 retest for P4 showed the emergence of all four equivalence classes to a level that satisfied the criterion for progression to Part 4 testing (following a return to baseline).

Fig 7. Percent correct responses for each Experiment 2 subject on Part 3 baseline trials and equivalence (symmetry, and combined symmetry and transitivity) tests for all stimulus classes.

The 85% criterion for baseline maintenance and equivalence class formation is indicated by the dotted line on each graph.

Figure 8 shows percent correct for each subject on baseline maintenance trials and reinforcer test trials in Part 4 (Reinforcer relation) testing. P1 and P6 were the only subjects to satisfy the criterion (85% correct over all baseline maintenance trials, and 85% correct over all reinforcer test trials) for progression to Part 5 testing (following a return to baseline) during their first exposure to Part 4 testing. P2 to P5 satisfied the criterion for progression to Part 5 testing on their second exposure to Part 4 testing.

Fig 8. Percent correct responses for each Experiment 2 subject on Part 4 baseline trials and tests for reinforcer relations.

The 85% criterion for baseline maintenance and reinforcer inclusion is indicated by the dotted line on each graph.

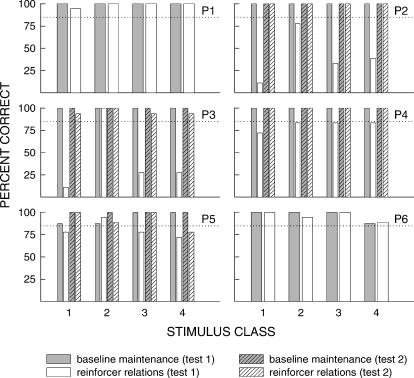
Figure 9 shows percent correct for each subject on Part 5 baseline and reinforcer–relations maintenance trials, and interclass matching relations test trials across each stimulus class. Interclass matching relations test trials beginning with a Class 3 sample are presented as stimulus Class 3, and those beginning with a Class 4 sample are presented as stimulus Class 4. Subjects P1 to P4, and P6, maintained accuracies of at least 85% correct on baseline trials for each individual stimulus class, except P1 on Class 4 baseline maintenance trials. These subjects also maintained accuracies of at least 85% correct on reinforcer–relation trials across all classes. On interclass matching relations test trials these subjects responded with accuracies of at least 85% correct on both X3–X4 and X4–X3 test trials.

Fig 9. Percent correct responses for each Experiment 2 subject on Part 5 baseline maintenance, stimulus–reinforcer and reinforcer–stimulus relations maintenance trials, and interclass matching relations test trials.

The 85% criterion for baseline and reinforcer–relation maintenance, and for interclass matching relations, is indicated by the dotted line on each graph.

P5 showed a marked deterioration of baseline relations in Part 5 testing, with accuracies of less than 85% correct on all but Class 4 baseline maintenance trials, and a minimum of 37.5% correct on Class 2 baseline maintenance trials. A similar pattern was observed in the reinforcer–relation accuracies for P5. P5 scored below 50%, and below 40% correct on interclass matching relations test trials beginning with Class 3 and Class 4 samples, respectively.

Discussion

The data from Experiment 1 suggested that a reinforcing stimulus common to two distinct equivalence classes can become a member of those two distinct equivalence classes, but the procedures of Experiment 1 allowed for the possibility of responding, at least on stimulus–reinforcer trials, to be controlled by exclusion. To eliminate an explanation based on exclusion, Experiment 2 presented trials testing for interclass X3–X4 and X4–X3 matching relations.

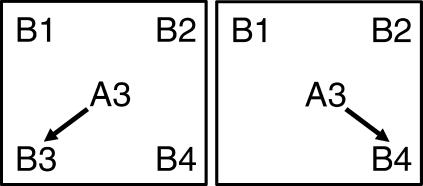
Recall that the baseline Ax–Bx and Cx–Bx relations for Classes 3 and 4 were trained with the same reinforcing stimulus, R3. This training was sufficient for subjects to perform the novel equivalence relations such that A3, B3, and C3 samples occasioned the selection of one another when comparisons from Classes 3 and 4 were present (left panel of Figure 10). Similarly A4, B4 and C4 occasioned the selection of one another when comparisons from Classes 4 and 3 were present, therefore documenting the emergence of two distinct nonoverlapping equivalence classes, Class 3 (A3B3C3) and Class 4 (A4B4C4). In Part 5 interclass matching-relations tests, however, a Class 3 sample consistently occasioned the selection of a Class 4 comparison when the Class 3 comparison was absent (right panel of Figure 10). Similarly, a Class 4 sample occasioned the selection of the Class 3 comparison when the Class 4 comparison was absent. The consistent performance of these interclass matching relations could only have been possible through the combination of two relations involving the same reinforcing stimulus (e.g., A3–R3 and C4–R3 to give A3–C4), confirming the suggestion of Experiment 1 and Part 4 of Experiment 2, that a reinforcing stimulus common to two distinct equivalence classes can participate in equivalence relations with stimuli from those classes.

Fig 10. Schematic diagram outlining the stimulus relations shown on an A3–B3 baseline trial (left panel), and an interclass A3–B4 test trial in Part 5 (right panel).

General Discussion

There are two methodological flaws in our design that need some comment. First, we did not counterbalance the stimuli across subjects. That is, the experimenter-defined classes contained the same kanji characters for all subjects. It is therefore possible that the stimulus–stimulus relations that emerged owed at least something to simple stimulus generalization due to unintended physical similarities between the kanji within a class. Although this may have had some impact, we suggest that it is unlikely to have been major. The results were in general consistent across subjects, test trial types, and stimulus classes. The probability that our classes corresponded in all four cases to groups of stimuli sharing common features, that were identified by almost all subjects, seems low. It is even more unlikely that the Class 3 and 4 stimuli were so chosen as to show enough distinction between classes for baseline maintenance and at the same time enough similarity between classes to produce interclass matching independent of the training procedure (Part 5, Experiment 2).

Second, the design arranged multiple cycles of training and testing within subjects. It is possible that repeated transitions between reinforced training and unreinforced testing blocks could have served as a cue to the subjects to change their pattern of responses, perhaps by responding randomly in test blocks. Again, the strikingly consistent results argue that this was not an important influence. The expected equivalence outcomes were shown in the first block of test trials for all subjects in Experiment 1 and in either the first or second block in Experiment 2. Importantly, the critical finding of interclass matching relations in Part 5 of Experiment 2 was clear in the behavior of all subjects in the first block of test trials. We therefore suggest that neither the lack of stimulus counterbalancing nor the arrangement of repeated cycles of training and testing endangers the validity of these results.

Sidman (2000), in describing the outcomes that we should observe following A1–B1–resp1–R1, B1–C1–resp1–R1, A2–B2–resp1–R1, and B2–C2–resp1-R1 training, wrote:

In the four-term units … Reinforcer 1 and Response 1 are common to all of the units. If pairs of events that included those elements were to remain in the equivalence relation, the contingencies themselves could not work. They could not work because all conditional and discriminative stimuli in all units that the reinforcement contingencies create would be related to the same defined reinforcer and response. These common elements would bring all stimuli into one large equivalence class. With Stimuli A1, A2, B1, B2, C1, and C2 all becoming equivalent to each other, subjects would fail to demonstrate the conditional or even the simple discriminations… With all of the stimuli being members of a single class, subjects would, for example, treat the A1B1 and A2B2 pairs as equivalent; would react to B2 and B1 in the same way; and so on. (pp. 131–132; emphasis added).

The present data, however, have shown that the same reinforcing stimulus can participate in equivalence relations with stimuli from two distinct equivalence classes. In particular, 5 of the 6 subjects in Experiment 2 showed consistent interclass matching relations between Class 3 and 4 stimuli, indicating that those two classes had become one, while at the same time maintained baseline conditional discriminations between Class 3 and 4 stimuli, indicating that they had remained as distinct classes. This result overturns Sidman's (2000) predictions as exemplified by the passage quoted above, and incompatible class membership must cause problems for any class-based account. We are left with two possible approaches. The first is to consider Sidman's own attempt to maintain a class- and equivalence-based account of conflicting class membership. The second is to consider alternative accounts of multiple stimulus relations, including relations between stimuli and reinforcers, and relations between stimuli apparently in different classes, that deemphasize the importance of the equivalence class as an organizing concept and as the cause of emergent stimulus relations. Each will be considered in turn.

Contextual Control

Sidman (1994) also noted the complicating factor that stimuli sometimes are members of multiple classes, as in the present data. The mechanism he proposed to account for this is that class membership may itself come under contextual control. This mechanism has been investigated by several studies that explicitly arranged different contingencies of reinforcement in the presence of different contextual, or higher-order conditional, stimuli. In such procedures, the composition of the resulting stimulus classes can indeed change as a function of the contextual stimuli (e.g., Bush, Sidman, & DeRose, 1989; Gatch & Osborne, 1989; Meehan & Fields, 1995; Wulfert, Greenway, & Dougher, 1994). However, no such differential reinforcement of conditional discriminations in different contexts was arranged in the present experiments. That is, any contextual control would have to have emerged, rather than have been explicitly trained. All that was necessary to produce changes in the elements composing a stimulus class was the removal of the opportunity for the subject to respond in accordance with an already established stimulus–stimulus matching relation. To set the occasion for responding to occur in accordance with stimulus–reinforcer relations, and for changes in class composition to result, the Class 3 comparison was removed from Class 3 baseline trials, and the Class 4 comparison was removed from Class 4 trials (Part 5, Experiment 2). Might these changes in the array of comparison stimuli be usefully conceptualized as contextual changes?

There is some precedent for this idea: Sidman's (1986, 1994, 2000) analyses specifically incorporate the contextual control into his analytic units in the form of increasing orders of conditional control, but he also notes that contextual control may operate in other forms: “The options we have available will also help determine which class a particular thing or event belongs to…” (1994, p. 476); and in an earlier paper: “A subject may reject a comparison in one context and select it in another, even with the same sample. Uncontrolled physical or functional similarities, arising from the current experimental environment or from the subject's history, may transform a first-order conditional discrimination into a second- or higher-order relation” (Sidman, Kirk, & Willson-Morris, 1985, p. 40; emphasis added). In our Experiment 2, it might be that on a Class 4 A4–B4 baseline trial, for example, in the context of the baseline comparison array [B1, B2, B3, and B4], A4 and B4 join the same class. On an X3–X4 interclass matching-relations trial, such as A4–B3, in the context of the comparison array [B1, B2, B3, but not B4], A4 and B3 join the same class. That is, the entire comparison array serves as a contextual stimulus and controls the composition of the resulting equivalence class.

This notion, however, seems an unsatisfactory elaboration of Sidman's (2000) theory, which these experiments were designed to test. This is because the suggested mechanism for contextual control of equivalence classes based on stimulus–reinforcer relations can only operate if the reinforcer common to Class 3 and Class 4 conditional discriminations does not drop out of the equivalence relations, which is irreconcilable with Sidman's theory. Secondly, Sidman's incorporation of contextual control in his analyses embodies an explicitly hierarchical view of stimulus control, because contextual stimuli control a cascade of higher-order conditional discriminations. If a functional similarity like a common reinforcer transforms a first-order conditional discrimination into a second- or higher-order conditional discrimination, it is difficult to maintain this hierarchical position.

Because the context for stimulus classes based on stimulus–stimulus or stimulus–reinforcer relations is either the presence of the original comparison array with exemplars from all four classes, or the absence of the originally class-consistent comparison, a hierarchical view of contextual control must see the function of the sample stimulus as being undefined until the comparisons were presented. Most unusual, however, would be the control operating on an originally class-consistent trial (e.g., baseline trial), where the class-consistent comparison (contextual stimulus) would alter the conditional function of the sample, which would then alter the discriminative function of that same comparison stimulus. In short, a hierarchical notion of stimulus and contextual control does not give a parsimonious account of the multiple class membership seen in the present study. This means that our data cannot easily be reconciled with Sidman's (2000) theory even if the possibility of contextual control is admitted. The inadequacy of a hierarchical view of stimulus control also has been noted by researchers investigating equivalence relations with complex, multielement stimuli (e.g., Markham & Dougher, 1993; Stromer, McIlvane, & Serna, 1993), where putative contextual stimuli were shown to participate in equivalence relations.

Even disregarding the problems with a hierarchical view of stimulus control, appealing to contextual control in the absence of any reinforcement contingencies for such control to emerge ultimately means that “contextual control” might be used to explain the emergence of any consistent matching relations in a novel environment. The danger with a “contextual control” account is that those two words obscure the search for the underlying variables that result in the emergence of consistent matching relations in the first place. Of course, presenting subjects with a novel stimulus array where they are forced to make novel matching relations is a change in stimulus context, but this does not explain why, in Experiment 2, that context change should have resulted in 5 of the 6 subjects consistently relating X3 to X4 on Part 5 interclass matching relations tests. These data do not seem to be predictable without concluding that R3 did not drop out of the equivalence relation.

Alternative Accounts

Based solely on operant processes, Sidman's (2000) theory argues that all elements of a reinforcement contingency become equivalent simply by participation in that contingency on multiple occasions. The theory therefore predicts the inclusion of reinforcing stimuli in equivalence classes at a time comparable to that at which the stimulus–stimulus equivalence relations are observed. The present experiment, however, has documented a number of cases where stimulus–stimulus equivalence relations emerged without stimulus–reinforcer relations, although there was no conflict between these relations and therefore no need for the reinforcer to drop out of the equivalence class. Subjects S4 in Experiment 1 and P2 and P3 in Experiment 2 failed to respond in a class-consistent manner on Class 1 and 2 reinforcer tests, despite showing the emergence of stimulus–stimulus equivalence relations. These data question Sidman's suggestion that “three- and four-term simple and conditional discrimination procedures generate at first a large equivalence class that contains pairs of all contingency components, and that eventually, the common reinforcer and response elements drop out of the class” (p. 132; emphasis added), as all subjects who demonstrated Class 1 and 2 equivalence relations also should have demonstrated the stimulus–reinforcer relations according to Sidman's analysis. Inconsistent with Sidman's prediction that reinforcing stimuli initially become part of a large equivalence class from which they then drop out, these data instead suggest that reinforcing stimuli become functionally equivalent to contingency-related stimuli after the stimulus–stimulus relations have been established through the reinforcement contingencies, and through some process other than that described by Sidman.

If stimulus–reinforcer matching relations emerge only after stimulus–stimulus matching relations are established, then stimulus–stimulus relations have a longer history in the subject's repertoire. We might therefore expect that subjects, if presented with a choice between the two, will be more likely to respond in accordance with stimulus–stimulus relations. For example, on an A3–Bx trial where the choice of B3 is consistent with the stimulus–stimulus relation, and the choice of B4 is consistent with the stimulus–reinforcer relations (i.e., the common association with R3), the longer and explicitly reinforced history of responding in accordance with stimulus–stimulus (i.e., kanji–kanji) relations, compared to no history of reinforced responding in accordance with kanji–reinforcer relations, can account for our data: If B3 is available (a baseline maintenance trial) it will be chosen, but if it is not (an interclass matching trial) then B4 will be chosen. This was the pattern of responding shown by most subjects in these experiments.

A likely alternative process for the emergence of stimulus-reinforcer relations is the systematic pairing of reinforcing stimuli with sample and comparison stimuli. Stimulus class formation through nonoperant procedures has been well documented in cases described as respondent-type conditioning (e.g., Leader, Barnes & Smeets, 1996; Leader, Barnes-Holmes, & Smeets, 2000; Smeets, Leader, & Barnes, 1997) and others emphasizing the role of stimulus correlations in function transfer (Tonneau, 2001; Tonneau & González, 2004). In these respondent-type training procedures, subjects were consistently presented with certain stimulus pairs in the absence of explicit responding and the absence of any experimentally arranged reinforcers. Subjects were later able to respond in accordance with the stimulus pairs and their subsequent classes during matching-to-sample tests. Stimulus pairings in the form of complex stimuli are sufficient to establish function transfer (e.g., Schenk, 1993, 1995; Smeets & Striefel, 1994), and consistent pairings of sample and comparison stimuli, achieved by varying the incorrect comparison/s across trials (and without explicit reinforcement) also are sufficient to produce function transfer indicative of class formation (e.g., Harrison & Green, 1990). Given the difficulties (noted above) that a strictly class-based and strictly operant account has with the present data, our tentative conclusion is that respondent-type pairings between reinforcers and stimuli also were responsible for the emergent relations seen here.

An account in terms of Relational Frame Theory (RFT; Hayes, 1991; Hayes, Barnes-Holmes, & Roche, 2001) also may be possible, although we would argue that it is ultimately unconvincing. A controversial but influential theory (see Burgos, 2003; Palmer, 2004a, 2004b), one of RFT's central tenets is the notion that a relational response (here, responding controlled by stimulus-stimulus relations) is itself treated as an operant. RF (relational frame) theorists view derived relational responding as learned behavior, and instances of derived relational responding seen in equivalence and RF experiments are conceptualized as generalized operants (see Barnes-Holmes & Barnes-Holmes, 2000). In this manner, RF theorists argue that relational responding can be viewed as a higher-order, or purely functional response class (Healy, Barnes-Holmes, & Smeets, 2000), thereby maintaining Skinner's class-based analysis of an operant (cf. Palmer, 2004b). A relational frame is a “specific class of arbitrarily applicable relational responding that shows the contextually controlled qualities of mutual entailment, combinatorial entailment, and transformation of functions” (Hayes, Fox, et al., 2001 p. 33), and is “conceptualized as a three-term contingency… the contextual cue is the third term, the relational response (e.g., responding to stimulus B in terms of stimulus A and responding to A in terms of B) is the second term, and the history of differential reinforcement correlated with the contextual cue is the first term in the contingency” (Barnes & Roche, 1996, p. 490). The relational frame relevant to equivalence relations has been termed one of “coordination”, referring to a relation of identity or sameness between those stimuli held in the frame, and equivalence relations are a result of mutual and combinatorial entailment of at least two frames of coordination (Hayes, 1991), which gives rise to the transformation of function observed on the equivalence tests.

In an RFT analysis, the frame of coordination was observed on equivalence tests in Experiment 2 where (a) the context of a comparison array containing exemplars from all classes cued (b) the stimulus–stimulus relational response (e.g., A3–C3 because of their common relation to B3), because of (c) the history of differential reinforcement for making stimulus–stimulus relations correlated with the context of comparison exemplars from all classes. Perhaps the frame of coordination was also observed on interclass matching relation tests where (a) the context of a comparison array containing only three exemplars cued (b) the stimulus–reinforcer relational response (e.g., A3–B4 because of their common relation to R3). The last link in this chain, corresponding to (c) above, requires a conceptual leap. The third term of the relational frame unit refers to a history of differential reinforcement for emitting a given relational response in the presence of a contextual cue. There is never differential reinforcement for making stimulus–reinforcer relations, however, so a RF theorist could only say that the frame of coordination has generalized, and transforms stimulus functions in a predictable manner given the type of frame, and in terms of the underlying stimulus–reinforcer relation.

We have described an account of our data in terms of RFT, but this only shows that such an account was possible a posteriori, and does not imply that it was predictable a priori. For example, if we had not observed reinforcer-mediated relations in Part 5 of Experiment 2, we could have supposed that the frame of coordination had not generalized in the manner described above. We emphasize that these experiments were designed to test the more explicit and stringent predictions of Sidman's (2000) account. RFT's predictions about the results of our testing procedures are far from explicit, and the fact that an RFT-flavored interpretation is possible should not be taken as unique support for that theory. Although we consider that we have refuted Sidman's account, RFT does not seem to be refutable in our procedure.

Conclusion

Sidman (2000) pointed out that his descriptive system of equivalence relations “does involve one theoretical assumption, namely, the hypothesis that our behavioral data represent real-world instances of the mathematical abstraction that is termed equivalence relation. If that simple assumption is correct—if our observations are real examples of the mathematical abstraction—then mathematical set theory gives what I have argued is a consistent, coherent, productive, and parsimonious way to describe our data” (pp. 128–129). In our tests, reinforcers simultaneously were (interclass matching relations in Part 5 of Experiment 2) and were not (maintenance of all class-specific conditional discriminations in the interspersed baseline trials) part of the same equivalence relation. This finding constitutes a violation of the integrity of the equivalence relation to a degree that makes Sidman's theory implausible, and provides evidence that data cannot always be consistently and parsimoniously described in terms of the mathematical equivalence relation. Sidman's assumption cited above has been of great value in generating testable predictions, but it seems that there is more to emergent stimulus relations than Sidman's account, and probably any class-based account of equivalence, can explain. We suggest that the role of respondent-type pairings needs greater emphasis in further theoretical development. In that tradition (e.g., Tonneau, 2001), the contribution made by our data is to add to the evidence that respondent-type pairings between reinforcers and stimuli can be responsible for the emergence of multiple stimulus–stimulus relations.

The procedures of the present study provide new methods for investigating multiple stimulus relations where these methods do not rely on substituting symbols for existing relations in a subject's repertoire (e.g., greater than, less than, opposite, same) to establish multiple stimulus relations, as is typically done in RFT experiments. This approach has the advantage of allowing the environmental and behavioral histories of these relations to be thoroughly controlled. Furthermore, the present methods produced multiple, context-dependent, stimulus relations of differing probabilities. Manipulation of the present procedures, therefore, may enable behavior analysts to investigate, for example, the possible transfer and transformation of stimulus functions across different-probability stimulus relations.