Are there better ways to determine wait times?

Recently, the Western Canada Waiting List Project (WCWLP) and the Wait Time Alliance (WTA) independently released benchmark wait times for various medical procedures. Both groups used a panel of experts who reviewed survey data from clinicians, patients and the general public as well as literature on how waiting affects patients and the success of the procedure. The proposed benchmarks were reached by consensus of the respective expert panels.

This survey-and-consensus method for setting benchmark wait times captured much information and many points of view. Ultimately, however, the benchmarks reflect expert opinion and are not the outcome of a transparent, reproducible methodology. There is no assurance that a different panel of experts weighing the same information would recommend the same benchmarks. In the absence of an algorithm, it is unclear what the panels were striving to optimize when they set their benchmarks. Without an optimization principle it is uncertain whether all the factors that might be relevant were included in the analysis. This article proposes a method for computing optimal wait times (once the decision to treat has been made) that is based on the principle of cost minimization.

Waiting periods for treatment impose costs on patients and the health care system. These costs, and their magnitude, are specific to the medical condition of the patient, and may include increased probability of death; risk of a poorer treatment outcome, and thus a lower health-related quality of life after treatment; higher posttreatment health care costs; home care and personal care costs; lost income, lower productivity, or costs related to symptom management to minimize such losses; and unameliorated pain or other suffering.^1,2 The longer the queue for treatment (i.e., the longer the wait time), the higher the cost of waiting, as captured by the upward-sloping curve in Fig. 1. Wait times of zero minimize this cost, which prompts the question: Once the decision to treat has been made, why should there be any waiting (or wait list) at all?

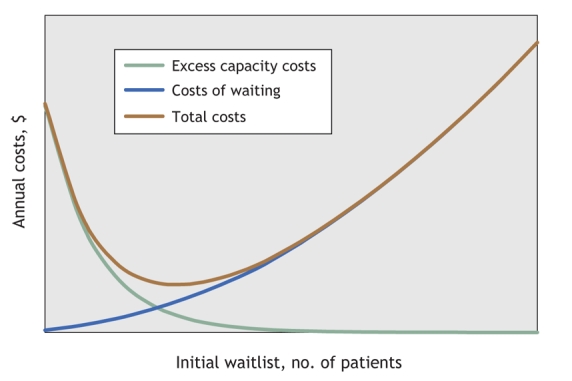
Fig. 1: Typical curves for expected annual costs.

The case for nonzero wait times is based on the more efficient use of treatment capacity when the number of patients referred for treatment is random.³ A hospital configured to perform a specific treatment at the rate of the average weekly number of referrals for this treatment (i.e., the steady-state rate) will find that from time to time, in the absence of a queue, treatment capacity exceeds referrals. Unless this excess treatment capacity (including associated pre-and posttreatment activities) can be redirected immediately and without cost to another treatment of equal benefit, an inefficiency cost is incurred when resources go unused, are temporarily redirected to a less valuable application, or are switched to a similarly valued application but at some cost.

The unit cost of excess capacity is specific to the treatment being considered and the hospital where it is performed. A hospital that provides a wide range of treatments probably has more opportunities for resource reallocation in response to fluctuations in the numbers of patients referred to receive various therapies.

The unit cost of excess capacity (i.e., the dollars per treatment slot not used for the designated purpose) can, in principle, be estimated. The longer the queue for a specific treatment at the beginning of the week, the lower the probability of excess capacity during that week, and thus the lower the expected cost of excess capacity (the downward-sloping curve in Fig. 1).

From the societal perspective, the health care planner has 2 objectives. First, in order to avoid a rising or declining trend in the waiting list, the facility's weekly capacity to treat a specific condition must be set equal to the average weekly number of referrals for this treatment. Second, the planner must select a queue for the start of the planning period that minimizes the sum of the expected cost of waiting and the expected cost of excess capacity over the planning period (assumed to be 1 yr). This is the optimal waitlist around which the actual weekly waitlist will fluctuate in response to the random arrival of patients. The optimal waitlist occurs where the U-shaped curve in Fig. 1, which depicts the sum of the expected annual costs of excess capacity and of waiting, reaches a minimum. A cost-minimizing waitlist must exist because, as the waitlist increases, the expected cost of excess capacity approaches zero; the expected cost of waiting, however, continues to rise indefinitely.

To implement the proposed method, unit costs of excess capacity and of the components of waiting costs are needed. As well, the probability distribution underlying the weekly random referral of patients for a specific treatment must be specified. This probability distribution, in conjunction with any initial waitlist, can be used iteratively to calculate the weekly probability distribution for both the number of patients waiting for treatment and unused treatment slots. These distributions can then be used, along with the unit costs of excess capacity and of waiting, to compute the weekly expected costs of waiting and of excess capacity. Summing these weekly expected costs over the 52-week planning period yields the annual expected costs.

These annual costs are calculated for a range of initial waitlist values. The optimal waitlist is the initial waitlist that minimizes the expected annual costs.

Use of this method for determining optimal queues (wait times) differs from the consensus method in 3 ways. First, it is based on an explicit optimization principle: cost minimization. Second, it includes not only the paramount medical issues but also the cost of excess surgical capacity and the nonmedical costs associated with waiting for treatment. Third, it is transparent and thus reproducible, a fundamental property of any scientific method.

The proposed method identifies 2 factors ignored by the consensus method that are nonetheless clearly relevant for determining optimal wait times. First, how variable is the number of patients referred for treatment each week? The greater the variance, the longer the optimal wait time will be; wait times can be minimal if the number of patients referred each week is constant.

Second, how easily can the capacity to treat be reallocated to a different procedure? This depends not only on the treatment procedure but also on the range of procedures done in the hospital. The law of large numbers dictates that the variance in a hospital's total weekly workload declines as the range of procedures increases. If substitutability of treatment capacity across procedures increases with hospital size because of the broader range of treatments performed and a steadier total workload, large hospitals will have lower unit costs for excess capacity and should have shorter wait times. One would thus expect optimal wait times to be shortest in large urban areas. Regionalizing waitlists should also shorten them, by reducing variability in the number of patients referred each week.

Although this method for computing optimal wait times for medical procedures is an improvement over the consensus method, it does have some limitations in its current format. First, it does not allow for patient attrition while waiting. Second, the mean probability distribution underlying treatment referrals is assumed to be constant (when it probably changes over time) and independent of the length of the waitlist (when weekly referrals may vary inversely with the length of the waiting list).⁴ These 2 limitations result from assumptions made to simplify, and these assumptions can be relaxed without changing the essence of the proposed method. The third limitation, and one that cannot be avoided, is the need to specify the length of the planning period. The longer this period is, the greater the scope for encountering excess capacity as well as long queues. Whether optimum wait times increase or decrease with longer planning periods will depend on specific unit-cost scenarios.

In conclusion, consider how the optimal wait times indicated by the proposed method may compare with those produced with the consensus method. For example, the WCWLP and WTA recommend maximum wait times of 5–6 months for the least urgent surgeries for hip replacement. For most urban areas, this implies a substantial queue of patients and an expected excess capacity cost that is virtually zero. Reducing this wait time to 5–6 weeks likely leaves a sufficiently large queue that the increase in the probability of incurring excess capacity costs is negligible. However, a reduction in such a long wait would lower the expected cost of waiting substantially. Thus, at least for hip replacement surgery, it is likely that the proposed method will indicate optimal wait times that are considerably shorter than the wait times currently recommended by consensus.

Joseph Schaafsma Department of Economics University of Victoria Victoria, BC