Stepwise unfolding of titin under force-clamp atomic force microscopy

Abstract

Here we demonstrate the implementation of a single-molecule force clamp adapted for use with an atomic force microscope. We show that under force-clamp conditions, an engineered titin protein elongates in steps because of the unfolding of its modules and that the waiting times to unfold are exponentially distributed. Force-clamp measurements directly measure the force dependence of the unfolding probability and readily captures the different mechanical stability of the I27 and I28 modules of human cardiac titin. Force-clamp spectroscopy promises to be a direct way to probe the mechanical stability of elastic proteins such as those found in muscle, the extracellular matrix, and cell adhesion.

Recently developed single-molecule atomic force microscope (AFM) techniques have allowed a detailed analysis of the mechanical unfolding pathway of several protein domains found in muscle and the extracellular matrix (1–7). In these experiments, a single protein is pulled away from the tip of a cantilever force probe by a piezoelectric positioner, pulling the protein from its ends. Under these conditions the individual domains of the protein unfold, generating a force-extension curve with a characteristic sawtooth pattern (1). However, during this process the force applies changes constantly over a wide range (0–300 pN), creating a complex time series of unfolding events and resulting in the sawtooth pattern.

Mechanical unfolding, similarly to bond rupture, is a force-dependent process (8, 9). Then, because force is the intensive variable of mechanical unfolding, it is desirable to do force spectroscopy experiments under force-clamp conditions. Here we demonstrate the implementation of an AFM method that can record the unfolding of a modular protein under force-clamp conditions and permits a direct measurement of the force dependency of the unfolding probability. These measurements allow for a more direct way of probing the forced unfolding of a protein under conditions of either constant force or force increasing at a constant rate.

Single protein force-clamp recordings, as demonstrated here, directly measure the kinetics of mechanical unfolding, allowing for the use of simple models to quantitatively analyze the data. This method can be readily extended to study the complex elasticity of other modular proteins engaged in the mechanical functions of muscle, the extracellular matrix, and cell adhesion.

Materials and Methods

Force-Clamp AFM.

Our AFM was constructed by using a Digital Instruments (Santa Barbara, CA) AFM detector head (AFM-689) mounted on top of a Physik Instrumente (Waldbronn, Germany) single-axis piezoelectric positioner (P841.1) with a strain gauge position sensor. Data sampling and control of the piezoelectric positioner were done by means of a PCI-MIO-16XE-10 data acquisition board driven by labview software (National Instruments, Austin, TX). To control the pulling force, we constructed an analog feedback system that compared the deflection of the cantilever with a computer-controlled set point, generating an error signal that was amplified through a proportional, integrative, and differential amplifier (PID in Fig. 1). The error signal then was fed back to the piezoelectric positioner. The feedback system then adjusted the length of the molecule such that the deflection of the cantilever remains at the set point. In the open loop configuration this system permits standard force-extension experiments (Figs. 1 and 2A), whereas in the closed loop configuration it functions as a force-clamp (Figs. 1 and 2 B and C). The step time response of our force-clamp system was ≈20 ms (see the constant force recordings of Figs. 3 and 5 where the lower traces show the force applied as a function of time). Every time there was an elongation of the molecule caused by unfolding the force trace shows a transient deflection with a time constant of ≈20 ms, which is the time it took the feedback to reestablish the set point. Hence, unfolding events that occur within ≈20 ms of each other cannot be resolved by our method. The spring constant of each individual AFM cantilever (Si₃N₄ tip, TwinTips, Digital Instruments, or microlevers from Thermomicroscopes, Sunnyvale, CA) was calibrated in solution, before each experiment. The spring constant was measured by using the equipartition theorem as described by Florin et al. (10). The proteins were suspended in PBS buffer at a concentration of 10–100 μg⋅ml⁻¹ and allowed to adsorb onto freshly evaporated gold coverslips.

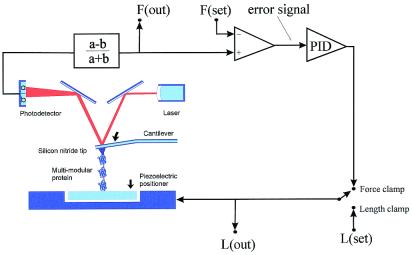
Figure 1.

Schematic diagram of the AFM apparatus and associated control electronics. When pressed against a layer of protein attached to a substrate, the silicon nitride tip of the AFM cantilever may adsorb a single protein molecule. Extension of the molecule by retraction of the piezoelectric positioner results in deflection of the cantilever. We can stretch a single molecule by using either a length-clamp mode or a force-clamp mode. In the standard length-clamp mode we set the desired position (L) and measure the resulting force (F) calculated from the laser deflection (a − b)/(a + b). In the force-clamp mode, the measured force is compared with a set value generating an error signal that is fed to a proportional, integral and differential amplifier (PID) whose output is connected directly to the piezoelectric positioner.

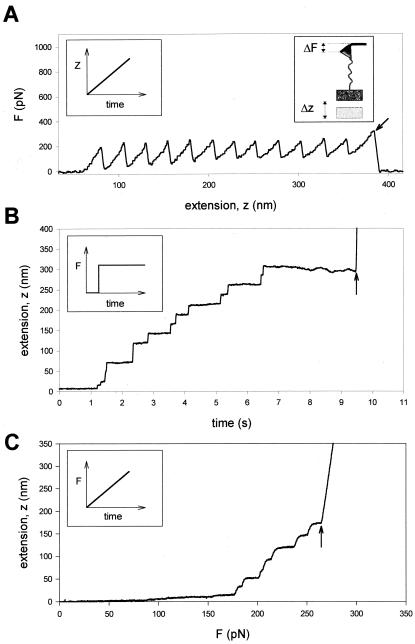
Figure 2.

Comparison of single protein unfolding events captured with an AFM in length-clamp mode (A) and a force-clamp mode (B and C). (A) In standard mode AFM, the positioner is moved linearly as a function of time (Left Inset) and the pulling force is measured from the degree of deflection of the cantilever (Right Inset). When a modular protein is stretched between the cantilever tip and a coverslip attached to a piezo-electric positioner, the resulting force-extension curve shows a sawtooth pattern with equally spaced force peaks, where each force peak represents the unfolding of single protein domains. The recording corresponds to the stretching and unfolding of a polyprotein containing 12 identical repeats of titin Ig domain I27. The last peak corresponds to the detachment of the protein from the cantilever and the measured force drops to zero (arrow). (B and C) In constant force AFM, the force applied on the protein is kept at a set value by using a force-clamp system that continuously changes the position of the piezoelectric device. (B) When a step increase in force is applied to a single I27 polyprotein, the extension-time curve shows step increases in the length of the protein, where each step is about 22 nm in size. This trace was obtained by stepping the force from −400 to 180 pN. (C) Under force-clamp conditions the force applied to a single I27₁₂ polyprotein is increased linearly with time. The figure shows the resulting length versus force trace. As shown, stepwise unfolding events occur over a narrow range of forces (in this case ≈170–250 pN) and a much shorter time (≈2 s) than those observed under constant force. In these experiments the steps are slightly rounded because of the limited frequency response of the feedback system. In both cases (B and C), the last step increase in length marks the detachment of the protein from the cantilever, where the position of the piezoelectric actuator increases rapidly to saturation (arrows).

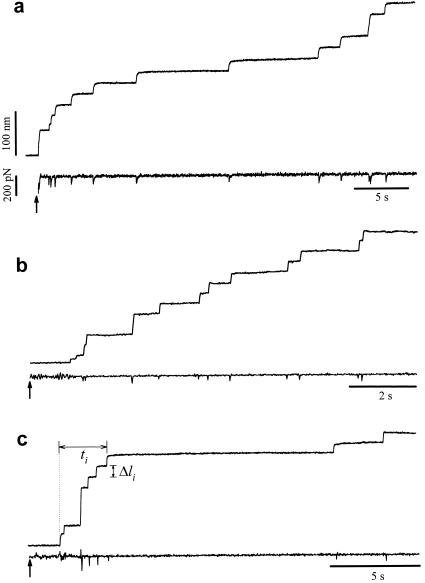
Figure 3.

Different examples of protein unfolding events captured with constant-force AFM. In these examples, the set point was stepped from −500 pN (cantilever pressing on the protein sample) to 200 pN (a), 182 pN (b), and 52 pN (c) at the times marked by the arrows. These recordings contain between nine (c) and 12 (a and b) unfolding events that occur in a time interval of 9 (b) and 32 s (a and c). Notice that some steps are two or three times the unitary size of 22 nm. The force trace shows brief spikes that mark the sudden unfolding of domains. These spikes have a duration of ≈20 ms and correspond to the time response of the force clamp.

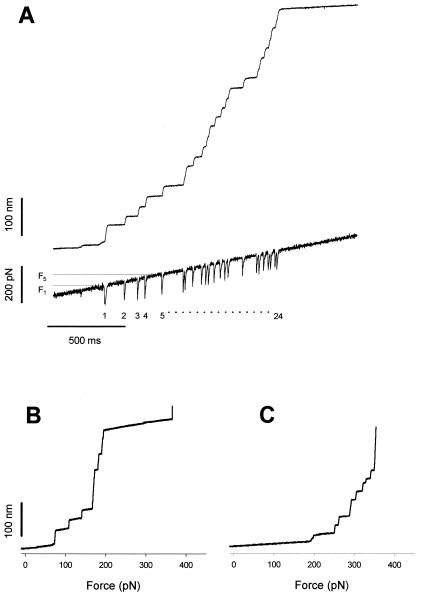
Figure 5.

Measurements of the force dependence of the unfolding probability using a force ramp. Force-ramp experiments apply a linearly increasing force to a folded protein causing the full unfolding of its modules under well-defined conditions and over a relatively short period. (A) Stepwise unfolding of a native cardiac titin molecule using the force-ramp method. The upper trace shows that the molecule elongates in 24 steps over a ≈200 pN range. The lower trace shows the time course of the force. The downward transients are caused by the feedback lag and serve as useful markers of unfolding. (B) Stepwise unfolding events for the I27₁₂ polyprotein recorded under conditions similar to those shown in A. The step increases in length are plotted as a function of the applied force. (C) A similar experiment done with the I28₈ polyprotein shows that this polyprotein unfolds in a higher force range than the I27₁₂ polyprotein.

Single Protein Recordings.

Single proteins were picked up by pressing the cantilever down onto the sample at several nN of force for a few seconds. Upon retraction of the sample away from the cantilever, single proteins occasionally stuck to the cantilever tip and were be stretched by the retracting sample as described (1–7). The probability of picking up a protein was typically kept low (less than one in 50 attempts) by controlling the amount of protein used to prepare the coverslips (see above). If the frequency of pickups is high, it is possible to pick up two or more proteins and stretch them simultaneously. In a length-clamp recording, these events would show up as overlapping sawtooth patterns that are readily distinguished from the characteristic regularly spaced sawtooth pattern that identifies a single molecule. In the force-clamp mode, parallel domain unfolding in two or more proteins would have to be simultaneous to allow for the observed stepwise extension during unfolding. Furthermore, because the applied force is divided by the number of molecules that were picked up, the force at which unfolding is observed would vary by a factor of 2 or more. These variations were not observed. Hence, although we cannot rule them out, such events have a very low probability of occurrence.

Protein Engineering.

We used a custom-made recombinant DNA method to synthesize and express direct tandem repeats of I27 and I28 monomers (4, 6). Full-length native bovine cardiac titin was a kind gift from Mathias Gautel (Max-Planck Institute for Molecular Physiology, Dortmund, Germany).

Cantilever Errors.

The force feedback clamp locks the deflection of the cantilever to the set point. In theory this sets the pulling force, however, this assumes that the resting position of the cantilever remains the same (zero force position). Cantilever drift typically results in a shift of the zero force position, which cannot be tracked during the measurements. Hence, we can only state that recordings were done under approximately constant force conditions and that the results are an average over certain force range. Our signal noise with the force feedback on was ≈50 pN. It is reasonable to assume that there will be fluctuations of this magnitude during the recordings. Because the rate of unfolding is thought to depend exponentially on the applied force (2, 3) an error of ≈50 pN in the set point will significantly alter the kinetics of unfolding observed. Indeed, as shown in Fig. 3, fixing the set point to a high force (e.g., 200 pN; Fig. 3a) did not always result in a faster unfolding rate when compared with another experiment where the set point was set at a lower force (e.g., 50 pN; Fig. 3c). To decrease the impact of cantilever drift we implemented another mode of stretching the proteins. This method consists of exposing a protein to a force ramp that rapidly covers the range of forces where all of the unfolding events are expected. Fig. 2C shows stretching of an I27₁₂ polyprotein under conditions where the force is swept, linearly from 0 to 350 pN. Because the force increases linearly with time, we expected to unfold all of the domains within this force range (Fig. 2C). Because the unfolding events occur in a relatively short time (≈2 s), the impact of cantilever drift is minimized and an accurate measurement of the force dependency of unfolding is now possible.

Results and Discussion

In a typical single-molecule AFM experiment, force was measured by monitoring the deflection of a calibrated cantilever, as it pulled on the molecule. To control the pulling force, we constructed an analog feedback system that compared the deflection of the cantilever with a computer-controlled set point, generating an error signal that was amplified through a proportional, integrative, and differential amplifier (Fig. 1 and Materials and Methods). The amplified error signal then was fed back to the piezoelectric positioner that controls the distance between the protein sample and the cantilever. The feedback system then adjusted the length of the molecule such that the deflection of the cantilever remained at the set point. A sudden increase in the contour length of the protein, caused by module unfolding, will trigger a readjustment of the piezoelectric actuator such that the protein is abruptly extended to an increased length, to keep the pulling force constant. In contrast to the sawtooth pattern recordings of sequential unfolding of a modular protein (Fig. 2A), under force clamp we observed a series of step increases in length, marking the module unfolding events (Fig. 2 B and C). These AFM force-clamp experiments provide exceptionally clear recordings that measure the kinetics of unfolding of a single modular protein.

In our experiments we used engineered polyproteins composed of 12 identical repeats of the I27 (Labeit and Kolmerer nomenclature, ref. 11) Ig module of human cardiac titin (I27₁₂), eight repeats of the I28 module (I28₈), and a full-length native titin purified from bovine cardiac muscle (see Materials and Methods). Fig. 2B shows the pattern of elongation of a single I27₁₂ polyprotein, extended under force-clamp conditions. We readily observed that the protein extends in steps. In this recording we counted eight steps of equal size (≈22 nm), two steps with a size that is double that of the singles (≈44 nm), and two smaller steps that are observed at the beginning of the recording. It is likely that the steps of 22 nm correspond to individual unfolding events of single I27 modules. Fig. 2C shows a different mode of the force clamp where we increased the force linearly with time and also observed a stepwise extension with steps of ≈22 nm.

Fig. 3 shows three detailed examples of force-clamp recording of I27₁₂ unfolding under isotonic conditions. The lower trace in these recordings shows the time course of the applied force, during the stepwise elongation of the protein. The downward glitches are caused by the limited time response of the servo mechanism.

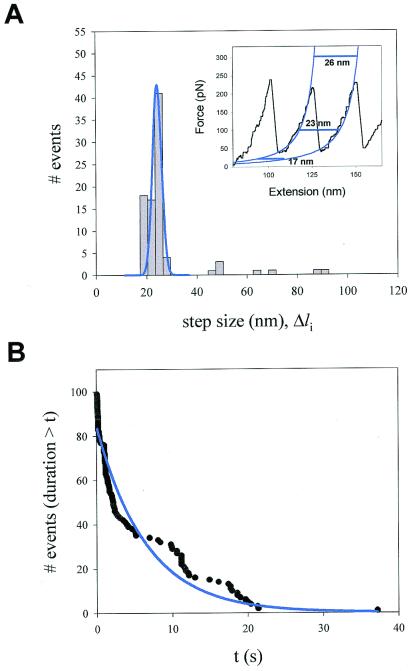
Fig. 4A shows a histogram of the size of the steps measured during experiments of the type shown in Figs. 2B and 3. The distribution shows a principal peak centered at 22.5 nm and three minor peaks that are integer multiples. These larger steps are likely caused by coincidental unfolding events that could not be time-resolved.

Figure 4.

Analysis of the step sizes and dwell times of unfolding events recorded at constant force. (A) Frequency histogram of step sizes for the I27₁₂ polyprotein (n = 99) shows a principal peak centered at 22.4 nm and three additional minor peaks that average 48.1, 67.3, and 89.1 nm. The data were obtained from 16 different experiments at an average force of 147 pN. (Inset) Fits (blue lines) of the worm-like chain (Eq. 1) to a sawtooth pattern of an I27₁₂ polyprotein. The horizontal lines illustrate the expected length increase caused by domain unfolding at various forces. (B) Probability distribution function showing the probability that after applying force, a module remains folded for a time equal or less than t. The distribution was fit by a single exponential function with a time constant τ = 6.7 s (solid line).

Although it is now well established that the unfolding of an I27 module increases its contour length by 28.1 nm (3, 4), such an increase would be observed only at very high forces. If we consider the worm-like chain model of polymer elasticity (12), the restoring force resulting from extending a polymer chain is given by:

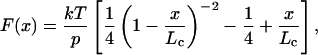1

where F is the force, p is the persistence length, k is the Boltzmann constant, T is the temperature in Kelvin, and L_c is the contour length of the polymer. By fitting the worm-like chain model to sawtooth pattern data (see Inset of Fig. 4A), we measured the increase in L_c that results from the unfolding of the I27 module, ΔL_c = 28.1 nm (6). However, at any given force (F) the observed increase in length was less than the calculated ΔL_c because of the spontaneous tendency of the polymer to coil. For example, using values of p = 0.38 nm and ΔL_c = 28.1 nm we predicted that at 100 pN an unfolding event would elongate the polymer by 23.3 nm (Fig. 4A Inset), which is close to the main peak in Fig. 4A.

The constant force recordings shown in Figs. 2B and 3 were made at an average force of 147 ± 95 pN, n = 16. It is likely that the actual force was lower because of our force signal error and the drift of the cantilever during the recordings (see Materials and Methods).

The mechanical unfolding of a protein module has been likened to a Markovian process where modules unfold in a probabilistic manner (2, 3, 7, 13, 14). A unique characteristic of Markovian processes is that their probability of occurrence is independent of the previous history (no memory) and that the dwell times of the elementary transitions are exponentially distributed (15). By using the force-clamp method, we can readily measure the dwell time distribution of module unfolding. Fig. 3c shows how the measurement is done. For each unfolding event, we measure the elapsed time, Δt_i, between the origin and the unfolding event. Because all I27 modules are exposed to the same force at all times, Δt_i, measures the dwell time of the module in the folded state, before it unfolds. The probability distribution function shown in Fig. 4B (96 events recorded from 16 experiments) was fit by an exponential function returning a time constant of τ = 6.7 s (correlation coefficient = 0.96), corresponding to an unfolding rate of 0.15 s⁻¹. Our data suggest that the dwell time distribution for titin unfolding under force is exponential, although significant deviations are evident. It is possible that the kinetics of unfolding are more complex and that the distribution will be better described by multiple exponentials. These observations suggest that the mechanical unfolding events of a tandem modular protein are independent of the unfolding history, implying that there is no mechanical coupling between unfolding modules. This is important because it is possible that unfolding modules would generate torsional strain (16), altering the unfolding probability of the remaining modules. Surprisingly, this is not the case. Hence, module unfolding must occur in a manner where any torsional strain is quickly relieved by free rotation of the peptide backbone.

An important benefit of a force-clamp measurement is that the force can be set to any arbitrary waveform. The simplest waveform is a step to a constant force (Figs. 2B and 3). However, because the rate of unfolding is thought to depend exponentially on the applied force, measurements done at forces either lower or higher than 100–150 pN produce unfolding events that either take too long (> 10 s) and are seriously affected by drift or are too fast to be resolved. Improvements in the stability of the AFM cantilevers and the speed of the servo mechanism are required before we can obtain a full set of measurements of step changes to different forces within the 10- to 300-pN range. However, a more direct measurement of force dependency of the unfolding probability, P_u, can be made by applying a force ramp that rapidly sweeps over a wide force range (Figs. 2C and 5). In contrast to a constant force experiment where we wait for the modules to unfold, the ramp method exposes the protein to increasingly higher forces, causing all of the modules to unfold within a short time (1–2 s). Fig. 5A shows a staircase of unfolding events obtained from native cardiac titin, using the ramp method. The top trace shows the length increases caused by the consecutive unfolding of the native titin modules. Up to 24 events were observed in this recording [because the AFM tip picks up proteins at random points along their length (6), typically recordings show less than the total number of modules of the protein]. The bottom trace shows the time course followed by the stretching force, which changes linearly with time over a range of ≈300 pN. The downward transients observed in the force recording correspond to the temporary imbalance of the feedback mechanisms and in this case are useful markers of the unfolding events (see Materials and Methods). Fig. 5 B and C shows force-ramp experiments with the I27₁₂ and I28₈ polyproteins, respectively.

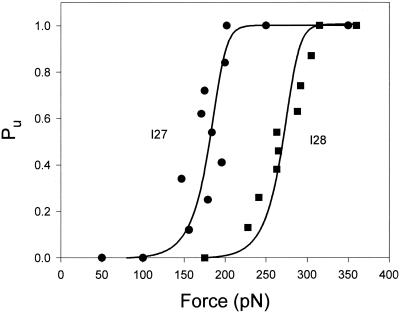
Using the force-ramp method we directly measured the probability distribution function of observing unfolding events at or less than a given force (F). The force dependency of the unfolding probability distribution, P_u, is shown in Fig. 6. Stretching I27₁₂ polyproteins with a force ramp shows an unfolding probability that changes from P_u = 0.1–0.9 over a small force range between 156 and 200 pN (Fig. 6, circles). Similar experiments with the I28₈ polyprotein showed that this protein unfolds in a higher force range (Fig. 6, squares). This result agrees with the higher mechanical stability measured for the I28 module of titin (6).

Figure 6.

Unfolding probability (P_u) as a function of the applied force for the I27₁₂ polyprotein (●) and the I28₈ polyprotein (■). P_u is calculated by counting the number of unfolding events that have occurred up to a given force. For example, there are 24 unfolding events observed in Fig. 5A. The occurrence of event 12 marks the force at which P_u = 0.5. ● correspond to data obtained from the engineered I27₁₂ polyprotein (49 steps from six experiments). ■ correspond to data obtained from the engineered I28₈ polyprotein (31 steps from four experiments). Both sets of data were fitted with a simple two-state model of unfolding that considers that the applied force increases linearly with time (solid lines; see text).

To analyze the data of Fig. 6 quantitatively, we formulated a simple two-state kinetic model for mechanical unfolding (4, 13, 14). In this model, a protein module is exposed to a force that increases linearly with time, simulating the conditions of our force-ramp experiment. We define a simple first-order unfolding reaction as:

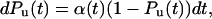2

where, P_u(t) is the probability of observing an unfolding event. We assume that during a force ramp experiment the applied force follows F(t) = a⋅t, where a is the slope of the force ramp in pN/s. Integrating Eq. 2 and changing variables from time (t) to force (F) yields an expression for the probability of observing an unfolding event at a given force, P_u(F),

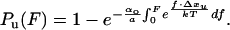3

We fit (Marquardt-Levenberg algorithm implemented by Sigma Plot) Eq. 3 to the data of Fig. 6, returning values of α₀ = 4.6 × 10⁻⁴ s⁻¹ (I27₁₂) and α₀ = 1.9 × 10⁻⁶ s⁻¹ (I28₈). These fits (Fig. 6, solid lines) were done with fixed values for a = 180 pN/s and Δx = 0.25 nm. Using sawtooth pattern recordings of the mechanical unfolding of the I27₁₂ polyprotein we obtained α₀ = 3.3 × 10⁻⁴ s⁻¹ (Δx = 0.25 nm) (4). Hence, for the I27₁₂ polyprotein, there is close agreement between the length-clamp and force-clamp experiments. The rate of unfolding measured for I28₈ using force clamp (α₀ = 1.9 × 10⁻⁶ s⁻¹) is smaller than that measured from sawtooth pattern recordings (2.8 × 10⁻⁵ s⁻¹) but very close to the more stable I28 module found in the chimeric (I27-I28)₄ polyprotein (2.5 × 10⁻⁶ s⁻¹) (6).

Single molecule force-clamp experiments with optical tweezers have been useful in characterizing the function of molecular motors (17, 18). Here we demonstrate that force-clamp AFM measurements can be used to study protein unfolding under a stretching force. The force-ramp technique directly measures the force dependence of the unfolding probability of titin modules. These measurements readily observe the difference between a protein made of identical repeats of the I27 module and one made of repeats of the I28 module. Furthermore, the step size and rates of unfolding observed by using the force-clamp technique are in good agreement with the values obtained from length-clamp experiments (sawtooth patterns). The force-clamp experiments shown here confirm and extend the view that a modular protein can be mechanically unfolded by a stretching force. These experiments also demonstrate a useful addition to the experimental approaches used to study the mechanical stability of single molecules.

Abbreviation

AFM

atomic force microscope