Salt screening and specific ion adsorption determine neutral-lipid membrane interactions

Abstract

The simplest, single-component biological membrane challenges accepted models of macromolecular interactions: lipid lamellar phases swell when immersed in monovalent salt solutions. Moreover, typical of a Hofmeister series, Br salts swell multilayers more than Cl salts, offering an excellent opportunity to investigate long-standing questions of ionic specificity. In accord with earlier measurements of liposome mobilities in electric fields, we find an added electrostatic repulsion of membranes due to anion binding, with a much stronger Br binding compared with Cl. However, contrary to the expectation that electrostatic repulsion should vanish in high salinity, swelling of lipid multilayers is monotonic with increasing salt concentration for both Br and Cl salts. The apparent contradiction is resolved by recognizing that although the electrostatic repulsion is progressively screened by increasing salt concentration, so is the van der Waals (vdW) attraction. Negligible in low salt, weakening of vdW forces becomes significant by the time electrostatic forces vanish. The result is a smooth monotonic swelling curve with no apparent distinction between low and high salt concentration regimes. Furthermore, when compared with theoretical predictions, measured vdW forces decay much too slowly with added salt. However, by accounting for the recently measured salt deficit near lipid bilayers, the expected scaling with Debye screening length is recovered. The combination of ion-specific binding and nonspecific ionic screening of low-frequency fluctuations explains salt effects on lipid membrane interactions and, by extension, explains specific (Hofmeister) effects at macromolecular interfaces between low and high dielectric.

Liposomes of neutral lipids dispersed in salt solutions move under applied electric fields. This measured electrophoretic mobility of liposomes indicates accumulation of electrostatic charge, most likely due to adsorption of salt ions on initially neutral (zwitterionic) bilayers (1, 2). As in many other experiments with salt solutions and buffers, this effect follows the Hofmeister series (3–5): the larger an ion, the larger the measured electrostatic (ζ) potential. Although specific ionic effects have become ubiquitous in both chemical and biological literature (6), a comprehensive theoretical description of the physical interactions responsible for these effects is still elusive. One important class of Hofmeister phenomena involves ions at interfaces between high and low dielectric, e.g., water–air or water–hydrocarbon.

By binding salt ions, lipid membranes are expected to repel each other electrostatically. This expectation naturally suggests that ion binding and specificity can be measured by modification of interbilayer interactions caused by salt. Practically, this measurement can be made because common phospholipids in water spontaneously form colloidal, multilamellar vesicles (MLVs) with the interlamellar spacing set by the balance of attractive and repulsive interactions (7–9). This interlamellar spacing is measurable by x-ray scattering.

The attractive part of membrane interactions is the van der Waals (vdW) force caused by mutually induced charge fluctuations propagating across membrane and solvent slabs with different dielectric properties. The vdW attraction is generally balanced by entropic repulsive forces generated by molecular confinement. Note that these forces are manifested not only within artificially formed MLVs but also within multilamellar biological structures such as myelin sheets surrounding nerve axons.

Intermembrane forces, and therefore spacings, can be altered by modification of solvent dielectric properties, for example by added solutes such as carbohydrates (sugar) (10–12) and glycerol (11). The balance of forces also can be tipped by externally applied osmotic stress (13). Such manipulations of intermembrane spacings therefore can be used to obtain an equation of state for lipid multilayers from which interaction parameters can be derived (7, 9).

By measuring the shift of interbilayer spacings caused by salt and by external osmotic pressure (14), we obtain an equation of state for lipid multilayers in salt solutions. This method has been successful in other instances, for example to measure membrane bending elasticity (9, 15, 16). Because lipid membranes thermally undulate, they repel each other (17). Measuring this added fluctuation repulsion gives us a measure of bending energies. Similarly, here we let membranes report on their accumulation of charge.

One important aspect is that the equation of state obtained by osmotic stress measurements of multilamellar stacks is equivalent to a precise surface force apparatus or colloidal-probe atomic force microscope. At the maximum swelling distance, attractive forces exactly balance the repulsive. It is this internal equilibrium point that has been used to determine the weakening of vdW (dispersion) attraction by soluble carbohydrates (10–12). Just like these solutes, salt also weakens the attractive vdW forces between membranes (18), however, with the added complication of electrostatic forces. Treatment of the forces competing under saline conditions is no trivial exercise. As verified experimentally, salts can quickly equilibrate between external solution and the interlamellar space (18). However, because of competition between salt ions and lipid headgroups for interfacial water, incorporation of salt is only partial. This competition generates a strong salt exclusion, recently measured by neutral buoyancy (19). To resolve the modification of lipid interactions by salt, we therefore need to consider three interconnected aspects: (i) weakening of vdW attraction, (ii) electrostatic charging, and (iii) salt exclusion.

In this work, we use the 12-carbon-chain lipid, 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), to take advantage of its disordered (fluid) state for short equilibration times at room temperatures (19). As measured by small-angle x-ray scattering, multilamellar DLPC vesicles swell progressively with added salt. However, the swelling is highly ion-specific: significantly more swelling is measured for Br salts compared with Cl (18, 20, 21). To distinguish between concurrent modification of vdW and electrostatic forces, we employ a charge-regulation model that calculates self-consistently the partitioning of salt-ions between membrane binding sites and the diffuse double layer (22, 23). We show that binding (and the electrostatic force) is negligible for Cl but not for Br. Electrostatic forces acting at low (physiological) salt concentrations then explain the observed ion specificity. Once electrostatic forces are properly accounted for, we find that screening of vdW forces is essentially nonspecific. Cl and Br data coincide, validating the long-predicted exponential decay of vdW attraction with the Debye screening length of salt (24, 25). Importantly, quantitative agreement between theory and measurement is obtained only by taking into account the recently measured salt exclusion from the interlamellar water (19). The nonspecific vdW screening and the highly specific ion binding presented here for the simple case of DLPC in salt water are expected to act generally in all physiological salt-buffer formulations.

Results

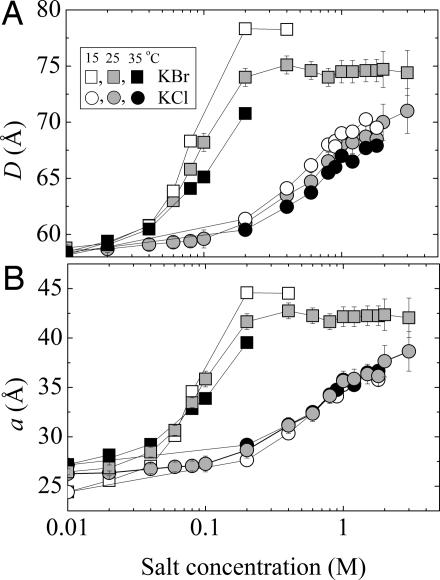
Immersed in salt solutions, multilamellar lipid vesicles swell (21). Repeat spacings, D, for DLPC multilayers formed in KCl and KBr salt solutions are shown in Fig. 1 at three different temperatures. Lipid multilayers swell progressively with increasing salt concentration, with dramatically more swelling in the presence of Br than in the case of Cl. For both salts, swelling is enhanced as the temperature is lowered from 35°C to 15°C. D-spacing variations, in principle, can be due to both interlamellar water as well as membrane thickness. Membrane thickness in particular decreases by a universal coefficient with increasing temperature (26). By subtracting the temperature-dependent membrane thickness from the repeat D-spacings, we obtain the interlamellar water spacings (denoted by the letter a) shown in Fig. 1B. Although for KCl the temperature variations of D-spacing and bilayer thickness are comparable in magnitude, a stronger temperature dependence of D-spacings exists for KBr.

Fig. 1.

Swelling of DLPC multilayers in the presence of KCl (circles) and KBr (squares) salts. (A) Interlamellar repeat spacing, D. (B) Water thickness, a(after subtraction of temperature variable membrane thicknesses from D). Measurements were at 15°C (open symbols), 25°C (gray), and 15°C (black).

The different behavior in Br salts (as the water retention by proteins in brine discovered by Hofmeister) has its origin in the association of Br⁻ ions with the lipid membrane. Indeed, electrophoretic measurements from Tatulian (2) indicate an accumulation of net electrostatic charge on neutral-lipid liposomes in salt solutions, as shown in Fig. 2. Typical of ionic adsorption, the ζ potential initially increases with increasing salt concentration, reaches a maximum, and then decreases because of screening in high salt. Binding is strong for I⁻ and Br⁻ ions, and it is negligible for Cl⁻. The electrostatic charging due to Br⁻ binding could explain the enhanced swelling seen in Fig. 1. To show this phenomenon, we determine electrostatic contributions to interbilayer interactions by measuring the pressure–distance curves for DLPC with and without salt as shown in Fig. 3.

Fig. 2.

Electrophoretic measurement of ξ potential of DLPC liposomes in 100 mM KCl (filled circle) and KBr (filled square) compared with reference data for various salts from Tatulian (1).

Fig. 3.

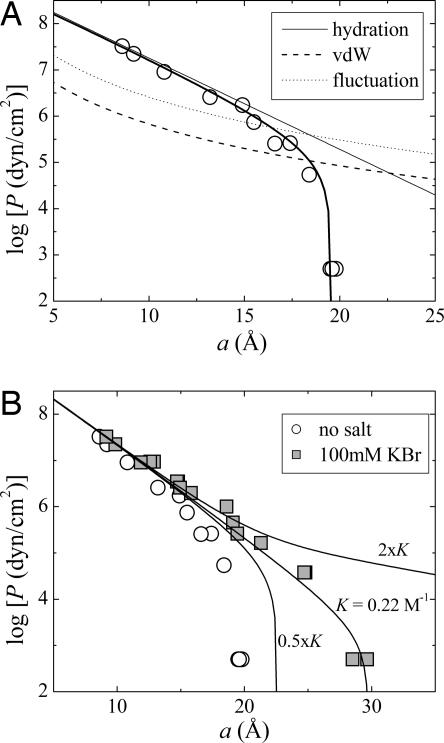
Pressure vs. separation. (A) Decomposition of interbilayer forces (Eq. 5) for DLPC multilayers in pure water at 25°C. (B) Determination of Br binding constant (K) by fitting to DLPC swelling in 100 mM KBr solutions (squares).

In Fig. 3A, we show the equation of state (osmotic pressure P vs. membrane separation, a) for DLPC multilayers in pure water and its decomposition into attractive vdW and repulsive hydration and undulation interactions (see Methods). When DLPC multilayers are equilibrated in 100 mM KBr, an additional, electrostatic term is needed to fit the data (Fig. 3A). The measured swelling determines the apparent Br⁻ binding constant, K, and the salt-dependent Hamaker parameter. The fit gives K = 0.22 M⁻¹. Doubling K would predict an unobserved unbinding of MLVs, whereas half the value significantly underestimates the full swelling.

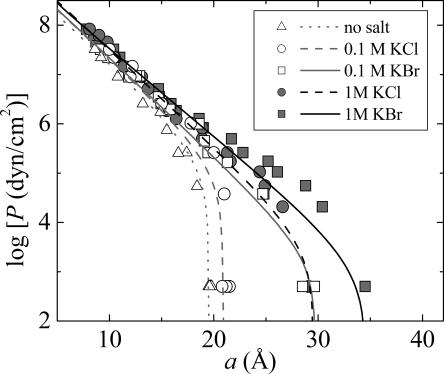
Fits to DLPC in 0.1 and 1 M salt solutions are shown in Fig. 4. Although the functional form at intermediate pressures (<1 atm) is not perfect (due to approximated fluctuation pressure) the data, especially the full swelling data points are reproduced very well. The functional form for the fluctuation pressure acting in the low-pressure regime is discussed in detail in ref. 18.

Fig. 4.

Equation of state (osmotic pressure P vs. interlamellar spacing a) of DLPC multilayers in water (triangles), 100 mM KCl (open circles), 100 mM KBr (open squares), 1 M KCl (gray circles), and 1 M KBr (gray squares) at 25°C.

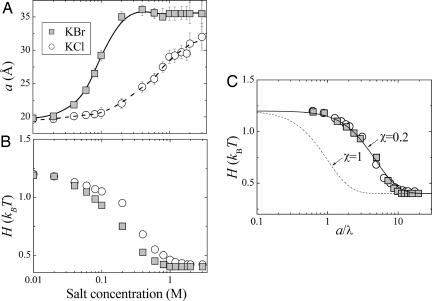
Fitting to full swelling data points (Fig. 5A) gives the salt-dependence of vdW Hamaker parameter (Fig. 5B). The measured weakening of vdW attraction validates the long-predicted ionic screening of the vdW force. Expecting that the screening efficiency is proportional to the ratio of water separation a and the Debye screening length λ, we plot H vs. the ratio p = a/λ in Fig. 5C. Now data for KCl and KBr coincide, indicating that weakening of vdW forces is largely nonspecific (independent of ionic type). However, Fig. 5 also shows that the measured variation of H with salt is much slower than expected theoretically, indicating that interlamellar salt has a reduced screening efficiency when compared with the bath. Introducing an empirical parameter χ < 1 to account for this screening reduction, the data are well fit by the expression

The two-term decomposition in Eq. 1 distinguishes between static (low frequency) and optical (high frequency) dielectric responses of lipid-salt multilayers (27). Static values are modified (screened) by a spatial redistribution of ions, whereas optical values are modified by ionic polarization in response to spontaneous charge fluctuations. Here, H₀ represents the low-frequency contribution to the Hamaker parameter which is progressively screened by salt, and H′ measures high-frequency contribution, practically the only contribution left in high-salt concentrations.

Fig. 5.

Salt-screening of vdW attraction. (A) Charge regulation fit (lines) to swelling data (symbols). (B) Variation of Hamaker parameter with salt concentration. (C) Screening effect of salt: universal variation with a/λ. Solid line shows theoretical functional form with an empirical screening reduction factor χ = 0.2.

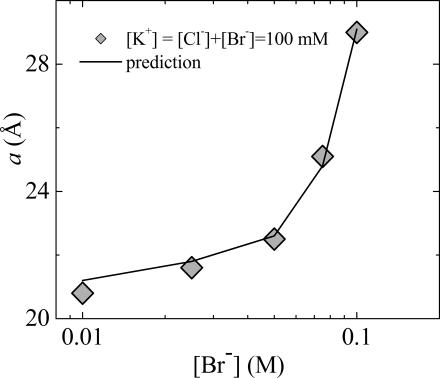
Having determined the nonspecific variation of vdW Hamaker parameter as well as the Br⁻ binding constant, the description of interbilayer interactions in salt is now complete. As a test, we show that competition measurements using mixed KCl/KBr can be fit without any additional parameter. Fig. 6 shows the preferential binding of Br⁻ vs. Cl⁻. At 100 mM total salt, swelling is dominated by the effect of adsorbing Br⁻ ions. Indeed, only a small fraction of bound Br⁻ ions is sufficient to create membrane charges dominating the effect of Cl⁻, far from regular solution behavior. Considering two independent populations of ions, each with a specific binding constant, predicts the strongly nonlinear behavior shown in Fig. 6. Note that the theoretical line in Fig. 6 is not a fit to the data, but the prediction based on the charge-regulation model for two types of anions competing for the same membrane binding sites.

Fig. 6.

Br/Cl competition with constant [K⁺] = 100 mM concentration and varying Br/Cl ratio at 25°C. Line is prediction using separately measured binding constant K = 0.22 M⁻¹ for Br and no Cl binding.

Discussion

Given the many ways that even the simplest ions perturb even the simplest lipids, can we explain or at least rationalize these results in terms of known interactions? The nub of the matter seems to be the ability of some ions to associate with neutral lipids. Br ion association that was previously inferred from electrophoresis of neutral lipid in salt water is quantitatively consistent with the strength of binding sufficient here to charge DLPC bilayers and to drive their extra swelling in multilayers. In both cases, attraction between anion and the bilayer/water interface can be reduced to one apparent binding “constant.” The added electrostatic repulsion created by this one binding constant tips the balance of hydration, vdW, and steric undulatory forces.

Despite the risk of oversimplification, we codify the salt-induced swelling of neutral bilayers in terms of action on three energies.

• By screening “zero-frequency” vdW attraction, initially responsible for about half the attraction that creates multilayers, salt causes multilayer expansion even at low salt concentrations.

• By increasing the high-frequency polarizability of the solution to bring it closer to that of bilayer hydrocarbon, ions also weaken finite-frequency vdW charge-fluctuation attraction (most pronounced in high salt concentrations).

• By binding to the interface between hydrocarbon and water, Br ions, more polarizable than Cl ions, charge the bilayers and add electrostatic double-layer repulsion to the balance of forces.

These three factors dramatically shift the interplay of hydration, vdW, and steric-undulatory repulsion of flexible bilayers that describe salt-free preparations. What is particularly satisfying here is that the binding of Br ions inferred from multilayer swelling is in accord with independent measurements by electrophoresis (1, 2) and density gradients (19).

Salt Screening (Low vs. High Frequencies).

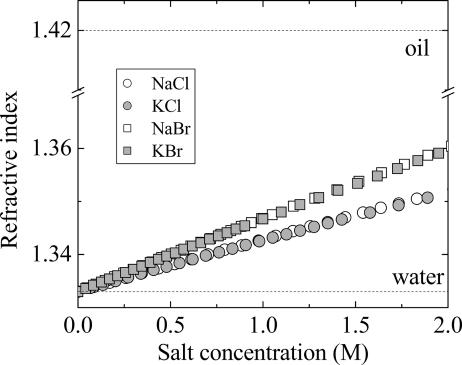
The greater polarizability of Br vs. Cl (Fig. 7) allows it to affect vdW forces at two levels. At the first, there is the possibility of adsorption to the higher-index-of-refraction bilayer, as eloquently argued in many places by Ninham and coworkers (28). The effect here is to charge bilayers whose electrostatic repulsion drives swelling at the lowest salt concentrations where electrostatic screening is negligible. At the second level, the higher index of refraction of the Br solutions (Fig. 7) more closely matches that of the bilayers, diminishing the difference in finite-frequency polarizabilities that are the source of vdW attraction. However, at any salt concentration of sodium bromide, the bilayer refractive index of ≈1.4 cannot be closely matched.

Fig. 7.

Variation of optical refractive index with salt concentration. The index of refraction of KBr is larger than that of KCl, but both are smaller than the bilayer (oil) index of refraction.

At the lowest salt concentrations, charging of bilayers combined with weakening of zero-frequency contributions creates a sudden swelling of Br-immersed bilayers compared with those in Cl. The Br/Cl difference persists as the greater index of refraction of Br solutions weakens finite-frequency fluctuation forces more for Br than for Cl. At [Br⁻] > 0.3 M concentrations, zero-frequency attraction as well as electrostatic repulsion are essentially screened. The constant spacing in this region suggests unchanging contributions from hydration and, more important, steric-undulatory repulsion balanced by severely weakened vdW attraction, a weakening that is only progressively experienced in Cl solutions (Fig. 5A).

The fact that the variation of vdW Hamaker parameter with salt is dominated by nonspecific, zero-frequency screening is demonstrated in Fig. 5, where the plots of H vs. p = a/λ for KCl and KBr are practically indistinguishable. The slightly lower H values for KBr than for KCl at high concentrations are sufficient to explain the larger swelling in the case of KBr.

Binding (Charge-Regulation Mechanism).

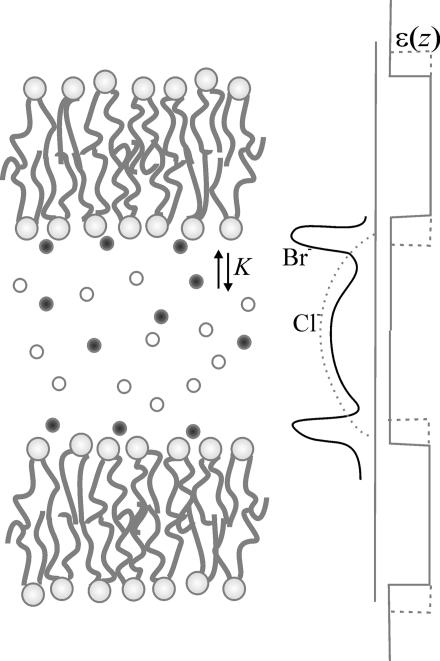
The measured modification of interbilayer forces by KBr gave us a Br⁻ binding constant K = [Lipid Br⁻]/([Lipid][Br⁻]) ∼ 0.22 M⁻¹, where [Lipid Br⁻] and [Lipid] represent the fraction of Br⁻ complexed lipids and of free lipids. To demonstrate the sensitivity of maximum swelling to the strength of ion binding, we calculated swelling limits for various values of the binding constant K (Fig. 3B). Doubling K predicts unbinding, whereas halving K has an effect little different from zero salt. Within experimental uncertainty, our calculated K ∼ 0.22 M⁻¹ pleasingly agrees with Tatulian’s electrophoretic mobility measurements (1, 2). In 100 mM salt, there is one Br⁻ ion bound to ≈60 lipids. The remaining, nonbound Br⁻ ions contribute to the extended double layer, as schematically depicted by the solid line in Fig. 8. With the assumption of being far from saturation, we convert from the measured binding constant K to a binding energy U, related by K = Sδ exp(−U/kT), where the product Sδ decomposes the binding volume into an area S and a layer thickness δ. From previous measurements (19), Br⁻ ions bind within a water layer of thickness δ ∼ 4.5 Å (corresponding to approximately nine waters per lipid). In 100 mM salt, there is one bound Br⁻ for each 60 lipids, corresponding to an area S = 60 × 63 Ų. This ratio gives U ∼ −2kT, i.e., one-fifth of a hydrogen bond.

Fig. 8.

Conceptual drawing showing the interfacial accumulation of Br ions (solid line) regulated by the binding constant K compared with nonbinding Cl (dashed line).

Adsorbed ions are indicated as sharp peaks in Fig. 8. Specific adsorption from salt has been predicted theoretically (29, 30) and modeled by computer simulations (31, 32). However, it escapes direct observation by even high-resolution small-angle x-ray scattering except in special preparations such as catanionic bilayer samples in the presence of structure-breaking ions (33). The weak binding of Br⁻ inferred here makes it unlikely to be seen directly by x-ray scattering, except perhaps by x-ray reflectivity in molar salt concentrations (34). However, Br⁻ does bind stronger than Cl⁻, as shown directly by the competition measurement (Fig. 6). Replacing Cl with Br at constant 100 mM salt demonstrates that Br already asserts itself by 40 mM to create significantly larger spacings. The Br⁻dominated swelling in mixed Cl/Br salts can be quantitatively explained based solely on the predetermined binding constant K ∼ 0.22 M⁻¹.

A binding mechanism also could explain the temperature behavior of multilamellar swelling in the presence of KBr (Fig. 1). As temperature increases, the fraction of bound Br⁻ ions decreases, leading to reduced electrostatic repulsion. However, a quantitative estimate of this effect should include modifications of bilayer structure, bending energy, and vdW forces. The binding mechanism itself is not yet understood. A first quantitative analytical attempt (28, 35, 36) is still under experimental testing using basic observables such as surface tension and ion pair formation (28, 37, 38).

Salt Exclusion.

Salt deficits in macromolecular aggregates have been reported for other systems as well, from single-chain charged surfactants (39) to neutral polymers (40). Here, the distribution of salt in the interlamellar space is determined by the competition between salt and lipid headgroups for interfacial water. Salt exclusion therefore can be thought of as competitive dehydration of headgroups and salt ions. Indeed, our recently reported exclusion measurements (19) correlate with structural measurements by x-ray diffraction and by ²H NMR spectroscopy. Phosphatidylcholine membranes that are dehydrated to <15 water molecules per lipid (vs. 25 at full hydration) undergo strong structural modifications (15). Measurements of samples with various histories: from preequilibration in water to formation in salt solutions, addition of ionophores, and temperature cycling eliminate the possibility that salt exclusion is an equilibration artifact. As explained in detail in ref. 18, results were robust and reproducible.

To see that MLV swelling and salt exclusion can be reconciled, consider the free energy variation with water and salt chemical potential

where N_W and N_S represent the number of water and solutes per lipid, respectively. Using the bath equilibrium condition n_Wdμ_W + n_Sdμ_S = 0, Eq. 2 becomes a function of the excess number of solutes

Because swelling with salt occurs by reduction of favorable intermembrane interactions, the change of the free energy with salt is positive, i.e., dG/dμ_S > 0. It implies that the factor in parentheses (Eq. 3) is negative, giving

Consistent with direct measurements, there is more water per ion in the interlamellar space than in the bath. Salt exclusion explains why Hamaker parameter decreases slower than expected from theory. The screening reduction factor χ, obtained empirically in Fig. 5, corrects for the interlamellar salt deficit.

Separability of Interbilayer Forces.

Under the assumption that electrostatic, membrane undulation, and hydration terms can be simply added to compensate vdW attraction, we have shown that the swelling in monovalent salt can be explained by vdW reduction and added electrostatics. Hydration and fluctuation repulsion need not change with added salt. In addition to separability, the exact functional form of these forces, especially for hydration and fluctuation, is still under debate. Although the exact values of interaction parameters obviously will depend on the choice of functional forms, the observed modification by salt is robust: weakening of vdW by monovalent salt is computed at ≈50% either using Helfrich power-law form for the fluctuation force (this work) or using an empirically determined exponential form (18).

Once nonspecific vdW screening by salt is taken into account, specific ion adsorption, modeled at the level of additive molecular forces between bilayers, can be reconciled by assuming an effective weak binding of polarizable ions as described in the Hofmeister series. Established here in the presence of model salts, this observation is naturally applicable to commonly used buffers. An underappreciated charging effect of initially neutral surfaces occurs due to binding of large polarizable ions, with binding energies on the order of 1–2 k_BT per ion, with a general consequence of induced negative surface potentials of the order of −10 mV in the presence of polarizable anions in the Hofmeister classification. This charging process is expected to affect ionic recognition and selectivity in biological processes.

Methods

X-Ray Measurements.

Highly purified (>99%) synthetic phospholipids (Avanti Polar Lipids) were suspended in salt solutions, cycled between 0°C and 50°C, and stored at 4°C. Osmotically stressed samples also contained known concentrations of polyethylene glycol (PEG) with molecular weight 20,000. Samples were thermally equilibrated at room temperature before being x-rayed for 0.5–1 h with a fine-focus fixed Cu anode x-ray source. X-ray exposures were typically taken at 25°C, 15°C, 35°C, and again at 25°C with variations in equilibration times (18). Sharp, uniform scattering rings were obtained indicative of sample homogeneity upon equilibration. Lattice spacings were recorded as a function of salt concentration and applied osmotic pressure from the position of the first two Bragg peaks.

Electrophoretic Mobility Measurements.

Multilamellar samples prepared as above were sonicated at low power for 1 min to generate liposomes of mean diameter ≈50 nm. Measurements were performed at Saclay (France) using a Coulter Desla 440.

Multilayer Equation of State.

By equilibrating MLVs in high-molecular-weight PEG solutions of known concentrations and osmotic pressure P, we controlled the interlamellar water spacing a. In this way, we measured the curve P vs. a of Eq. 5 below and found the interaction parameters that fit the measured curves.

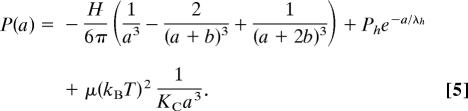The first term in Eq. 5 represents the vdW attraction, with an interaction strength given by the Hamaker parameter (H). The second term represents the hydration force accounting for the energetic cost of water ordering in the vicinity of lipid headgroups. This force is exponential, with a decay length λ_h ∼ 2 Å (8). The third term in Eq. 5 is the shape-fluctuation or undulation term, acting at larger intermembrane separation and accounting for the entropic penalty due to confinement of undulating membranes (17). As initially shown by Helfrich, this entropic force is inversely proportional to the bilayer bending rigidity, K_C, with Helfrich’s proportionality constant μ = 0.115. More recently, alternative functional forms have been derived (41, 42) and empirically determined from analysis of membrane correlation functions measured by x-ray scattering (9, 43). The exact values of interaction parameters have been shown to depend on the choice of fluctuation functional form. For simplicity, and because it does not affect our conclusions, here we use Helfrich’s power-law form, because it has no independent parameters except the bending rigidity K_C. For the full treatment of interactions, synchrotron x-ray measurements are needed for analysis of the stacking compression parameter (43).

Poisson–Boltzmann Model with Ionic Adsorption (Charge Regulation Boundary Condition).

The standard Poisson–Boltzmann equation that governs the electrostatic potential ϕ(x) (expressed in kT/e units) between two parallel charged plates separated by a water region of thickness a reads

where x represents the perpendicular distance to one of the two plates, κ′ = (8πL_Bρ′_s)^1/2 is the screening constant in the reservoir of 1:1 salinity ρ′_s, and L_B = (e²)/(4πε₀εkT) is the Bjerrum length. By symmetry, ϕ′(a/2) = 0. The second boundary condition at the charged plates of surface charge density Σ is given by the Gauss theorem

In our case, each plane is made of neutral surfactant sites of lateral surface A. An anion may adsorb on a site according to the chemical reaction: site⁰ + anion⁻ ↔ site⁻.

The degree of adsorption (fraction of charged sites) will be noted α. Thus, the surface charge density becomes Σ = −α/A < 0. The law of mass action reads

with K being the equilibrium binding constant and ϕ_s = ϕ(0) the surface potential. Eqs. 7 and 8 connecting surface potential and surface charge constitute the so-called charge regulation boundary condition (22, 44, 45).

Abbreviations

DLPC

1,2-dilauroyl-sn-glycero-3-phosphocholine

MLV

multilamellar vesicle

vdW

van der Waals.