Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2006 May;173(1):497–509. doi: 10.1534/genetics.105.046847

Joint Evolution of Dispersal and Inbreeding Load

Frédéric Guillaume 1,1, Nicolas Perrin 1,2
PMCID: PMC1461421  PMID: 16510793

Abstract

Inbreeding avoidance is often invoked to explain observed patterns of dispersal, and theoretical models indeed point to a possibly important role. However, while inbreeding load is usually assumed constant in these models, it is actually bound to vary dynamically under the combined influences of mutation, drift, and selection and thus to evolve jointly with dispersal. Here we report the results of individual-based stochastic simulations allowing such a joint evolution. We show that strongly deleterious mutations should play no significant role, owing to the low genomic mutation rate for such mutations. Mildly deleterious mutations, by contrast, may create enough heterosis to affect the evolution of dispersal as an inbreeding-avoidance mechanism, but only provided that they are also strongly recessive. If slightly recessive, they will spread among demes and accumulate at the metapopulation level, thus contributing to mutational load, but not to heterosis. The resulting loss of viability may then combine with demographic stochasticity to promote population fluctuations, which foster indirect incentives for dispersal. Our simulations suggest that, under biologically realistic parameter values, deleterious mutations have a limited impact on the evolution of dispersal, which on average exceeds by only one-third the values expected from kin-competition avoidance.

THREE distinct ultimate causes are currently recognized to explain the evolution of dispersal, a widespread feature in natural populations of many organisms. Environmental and demographic stochasticity plays a major role by inducing spatio-temporal fluctuations in habitat quality or in population sizes, extinction and recolonization dynamics representing the most extreme case (Van Valen 1971; Olivieri et al. 1995; Gandon and Michalakis 1999; Ronce et al. 2000). Kin-competition and inbreeding avoidance (Hamilton and May 1977; Taylor 1988; Motro 1991; Clobert et al. 2001) provide two other potential incentives, which could drive the evolution of dispersal in equilibrium populations.

Inbreeding is often invoked to account for the large amount of dispersal in natural populations (see Perrin and Goudet 2001, and references therein). However, although clear-cut empirical evidence exists that inbreeding may sometimes play a significant role in dispersal (Packer 1979, 1985; Wolff 1992; Packer and Pusey 1993), alternative explanations exist in many circumstances (reviewed in Blouin and Blouin 1988; Pusey and Wolf 1996). Even features that strongly suggest inbreeding avoidance, including sex biases in dispersal and negative among-species correlations between male and female dispersal rates (Pusey and Packer 1987; Pusey and Wolf 1996), may also arise from kin-competition avoidance (Perrin and Goudet 2001). The empirical problem is further worsened by the fact that population structures that induce close inbreeding (small groups of highly related individuals) are precisely those most likely to promote kin competition as well. As a result, the exact role of inbreeding avoidance in driving dispersal is difficult to determine and has been widely debated. While some authors see it as a major force (e.g., Wolff 1994), others consider it largely irrelevant (e.g., Moore and Ali 1984).

Theoretical studies suggest that inbreeding avoidance might indeed play a significant role of its own (Bengtsson 1978; Waser et al. 1986; Perrin and Mazalov 1999; Morgan 2002), as well as in interaction with kin competition (Motro 1991; Gandon 1999; Perrin and Mazalov 2000; Perrin and Goudet 2001) on the evolution of dispersal. In the absence of inbreeding load (and in stable populations), evolutionary stable strategy (ESS) models predict a balanced solution: both sexes disperse to limit competition with kin. Directional sex biases may then arise from sex asymmetries in dispersal costs, resource competition, or mate competition. When a weak inbreeding load is added, the models still predict sex-balanced ESS solutions, with dispersal values that only slightly exceed those expected under kin-competition avoidance alone (Perrin and Goudet 2001). Moderate inbreeding load is expected to somewhat destabilize the equilibrium, as even slight sex asymmetries (e.g., in local competition) can induce strong sex biases in dispersal. Finally, high inbreeding load may overcome the stabilizing influence of kin competition avoidance and induce boundary solutions: one sex (male or female) remains entirely philopatric, while members of the other sex disperse (Motro 1991; Gandon 1999; Perrin and Mazalov 2000).

One potential problem with these theoretical expectations, however, is that the inbreeding load from which the costs of inbreeding arise is assumed to be constant. In reality, this load results from the dynamic interplay between mutation, drift, selection, and dispersal. Selection coefficients and dominance effects of the deleterious mutants play crucial roles (Wang et al. 1999; Bataillon and Kirkpatrick 2000; Whitlock 2002; Glémin et al. 2003; Roze and Rousset 2004). On the one hand, if the effect of deleterious mutations is large enough that selection is more important than drift, inbreeding load will be rapidly purged (Glémin 2003); however, mutations might still segregate locally at low frequency and induce significant loss in the fecundity of within-deme matings relative to among-deme matings (heterosis, see Whitlock et al. 2000; Glémin et al. 2003; Roze and Rousset 2004), so that selection for dispersal might remain high. On the other hand, if deleterious effects are small enough that drift dominates, mutations are hidden from selection and might become fixed, strongly affecting offspring viability; however, whether these mutations contribute to heterosis and thus to the evolution of dispersal will depend on whether they become locally fixed at the level of demes or in the whole metapopulation.

The boundary between the two domains of accumulation and purging of deleterious mutations depends on the population structure, rate of inbreeding, and level of gene flow (Glémin 2003; Glémin et al. 2003) and hence on dispersal. Furthermore, the accumulation of mildly deleterious mutations may induce demographic effects, affecting both the inbreeding load and the evolution of dispersal. Given its complexity, the problem is currently not analytically tractable without major simplifying assumptions (e.g., low migration, strong selection, infinite population models, no interaction with population demography, etc.; see Bataillon and Kirkpatrick 2000, Glémin et al. 2003, and Roze and Rousset 2004 for one-locus models of deleterious mutation dynamics and their simplifications). A simulation approach appears to be a good way of overcoming these limitations.

Here we present the results of individual-based simulations aimed at investigating the joint evolution of inbreeding load and dispersal in a structured population. Our approach differs from previous inroads in this area in that dispersal is an evolving trait (vs. Lynch et al. 1995b; Wang et al. 1999; Higgins and Lynch 2001), and competitive interactions with kin are taken into account (see Morgan 2002).

METHODS

We built an individual-based, genetically explicit model, with diploid individuals with specified gender, dispersal genotype, and deleterious loci, living in an island model of population with nd demes of carrying capacities N. We used the following life cycle:

  1. Viability selection: newborns survive with a probability derived from their deleterious mutation genotype to give the new offspring generation.

  2. Dispersal: offspring randomly disperse in the metapopulation with a probability given by their dispersal genotype and die during dispersal events with probability c. A disperser cannot return to its natal deme.

  3. Regulation: random regulation of the population occurs, reducing the demic pool of competing individuals of each sex to half of the carrying capacity of the demes, thus leading to equilibrated sex ratio whenever enough offspring of both sexes are present, without between-sex competition.

  4. Reproduction: each individual, male or female, is assigned a fecundity value drawn from a Poisson distribution with constant mean f. They mate randomly in their deme as many times as indicated by their fecundity and produce one newborn per mating. This ensures similar reproductive variances between males and females. Newborn gender is set randomly with an equal probability of being male or female, and their alleles for deleterious and dispersal genes are randomly inherited from their parents' copies and then mutated. Once reproduction has occurred, all adults are removed and the cycle starts again.

This life cycle generates different amounts of demographic stochasticity. The stochastic nature of fecundity, dispersal, and survival could lead to a large interdemic variance in deme sizes and sex ratios at the onset of the regulation episode. The variance is stronger with low fecundity values, small population sizes, and low viability. Stochasticity in this model sometimes reached values high enough to induce demic extinctions or even crashes of the entire metapopulation, even without the presence of deleterious mutations.

Dispersal genes consisted of two independent diploid loci, one controlling the female and the other the male dispersal rate, with allelic values continuously distributed between 0 and 1. Mutation steps (forward or backward) were drawn from an exponential distribution with kurtosis λ = 5 (i.e., mean step = 0.2) and probability = 10−4. Mutated dispersal alleles were truncated at the limits (0 or 1). An individual's dispersal phenotype was determined as the mean of the two alleles present at the corresponding sex-specific locus.

The genetic load was controlled by a set of 1024 (M) independent loci carrying deleterious alleles, all having homozygous effect s and dominance h. The number of new mutations occurring in one genome was drawn from a Poisson distribution with mean equal to the diploid genomic mutation rate: U = 2Mu. Mutations thus occurred at rate u and affected only nondeleterious alleles, turning them into the deleterious form (thus reverse mutation was neglected). When a randomly chosen allele was already of the deleterious form, another was redrawn to replace it, thus ensuring a constant genomic mutation rate. Mutations were assumed to act independently on fitness so that the offspring viability, v, was computed as the product of the fitness effects of each locus: Inline graphic, where n1 is the number of homozygous loci and n2 the number of heterozygous loci.

The parameters of the deleterious mutations (U, h, and s) were set according to empirical estimations from Drosophila melanogaster mainly (reviewed in Charlesworth and Charlesworth 1987, 1999; Lynch et al. 1999). Inbreeding load in natural populations appears to be due to a combination of a few almost fully recessive lethal mutations (modeled here with U = 0.03, s = 1, and h = 0.02; Simmons and Crow 1977; Crow 1993) and many partially recessive, mildly deleterious ones (modeled here with U = 1, 0.01 ≤ s ≤ 0.05, and h = 0.3, as used in stochastic simulations in Wang et al. 1999 and Higgins and Lynch 2001). Accordingly, we designed our simulations to contrast the effects of the two kinds of mutations: large s- and small h-values vs. small s- and large h-values. For small s-values (0.01 and 0.05) we also ran a few simulations with h varying from 0.01 to 0.4 to investigate the role of dominance on inbreeding load. We also investigated the effect of a large genomic mutation rate (U = 1) for both types of mutations to assess the effects of contrasted levels of heterosis in small populations.

At the start of the simulations, individuals were initialized with dispersal gene values drawn from a uniform distribution ranging from 0 to 1 (ensuring a large initial variance and an initial mean of 0.5) and potentially deleterious gene values all set to those of the wild-type allele. Note, however, that the way allelic values are initiated does not affect the ESS values, but only the time courses to equilibrium.

Simulations were first run without deleterious mutations, to isolate the effects of kin competition and compare equilibrium dispersal rates with theoretical expectations (model derived from Gandon and Rousset 1999, with finite population size and sex-specific dispersal) and thereby validate our model. Deleterious effects were then added to estimate the additional dispersal that would evolve in the presence of an inbreeding load. Parameters were set as follows: dispersal costs c = 20 and 70%, mean fecundity f = 20, with a few runs with lower fecundities (f = 8 and 3) to further investigate the importance of demographic stochasticity in the absence of inbreeding load. Heterosis was measured for each female as 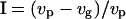Inline graphic (Perrin and Mazalov 1999, 2000), where vg is the average offspring effective viability when the male is from the same deme and vp is that when it comes from a different deme. The extent of purging of the deleterious mutations was measured by the ratio 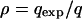Inline graphic of the expected frequency qexp in an infinite and panmictic population at mutation–selection equilibrium relative to the mean observed frequency q (see also Glémin 2003, for definitions of the purging process). ρ is then greater than unity when mutations are purged (i.e., q < qexp) and lower in the case of mutation accumulation (i.e., q > qexp). qexp is given by solutions of the equation 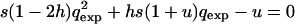Inline graphic (Crow and Kimura 1970, p. 260).

Other statistics measured include the mean overall dispersal rate, the mean male and female dispersal rates (to evaluate any sex bias in dispersal), the mean allele frequency, homozygosity and heterozygosity of deleterious loci, and the number of fixed mutations in the whole population, as well as the mean overall offspring viability and the mean number of lethal equivalents per individual (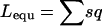Inline graphic, Morton et al. 1956). All parameters were estimated among offspring before dispersal.

Unless otherwise stated, simulations were replicated 100 times over 3000 generations for each set of parameters, and the metapopulation state was recorded every 10 generations for later analysis. To ensure stability, statistics were computed over the 100 last records.

RESULTS

Kin competition avoidance and demographic stochasticity:

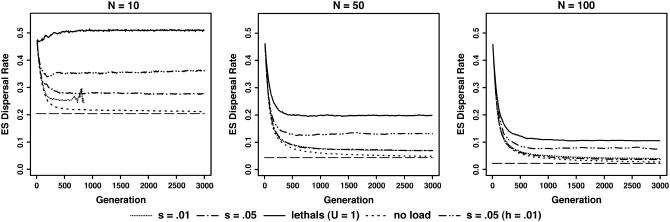
In the absence of inbreeding load, the evolution of dispersal was governed mostly by the effects of kin competition within demes. Equilibrium dispersal values matched the theoretical ESS expectations (Hamilton and May 1977; Comins et al. 1980; Gandon and Rousset 1999), decreasing with increased deme sizes (Figure 1) and dispersal costs (from 20 to 70%, see Table 1). The match was excellent at large population size (100 demes × 100 individuals, results not shown), but theoretical expectations were slightly exceeded at low population numbers, owing to demographic stochasticity.

Figure 1.

Figure 1.

Open in a new tab

Time course of the evolution of dispersal in populations of 10 demes with and without inbreeding load for three demic sizes N = 10, 50, and 100. The long-dashed horizontal line is the theoretically expected dispersal rate under kin competition avoidance (see Table 1). The short-dashed curve corresponds to the simulations performed without genetic load. The others are for the three different mutant effects: dotted line for s = 0.01, dashed-single-dotted line for s = 0.05, and plain line for lethal mutants (s = 1 and h = 0.02). The first two have dominance coefficient of h = 0.3. The dashed-double-dotted line is for very recessive mutations with s = 0.05 and h = 0.01. The other parameters are: genomic mutation rate U = 1 for all types of mutations, nd = 10 demes, M = 1024 deleterious loci, mean fecundity f = 20, and cost of dispersal c = 0.2. Plotted values are the averages over 100 replicates. Note that in the first graph (N = 10), simulations crashed before 1000 generations for s = 0.01.

TABLE 1.

ES dispersal rates

c = 0.2
c = 0.7
N DESS Ds=0 DESS Ds=0
10 0.204 0.22 (0.08) 0.064 0.074 (0.029)
50 0.044 0.05 (0.02) 0.013 0.017 (0.007)
100 0.022 0.03 (0.01) 0.006 0.009 (0.003)
c = 0.2: c = 0.7:
N
s
h
Ds≠0
Ds≠0
10 0.01 0.01 — —
0.3 — —
0.05 0.01 0.34 (0.11) —
0.3 0.28 (0.11) —
50 0.01 0.01 0.09 (0.02) 0.020 (0.005)
0.3 0.07 (0.03) 0.025 (0.006)
0.05 0.01 0.14 (0.03) 0.025 (0.005)
0.3 0.07 (0.03) 0.016 (0.006)
100 0.01 0.01 0.05 (0.01) 0.010 (0.002)
0.3 0.04 (0.01) 0.010 (0.004)
0.05 0.01 0.08 (0.01) 0.010 (0.005)
0.3 0.04 (0.01) 0.010 (0.004)
Lethals
c = 0.2: c = 0.7:
N
s
U
Ds≠0
Ds≠0
10 1 1 0.51 (0.09) 0.094 (0.037)
0.03 0.22 (0.05) 0.073 (0.028)
50 1 1 0.20 (0.04) 0.021 (0.009)
0.03 0.05 (0.02) 0.016 (0.006)
100 1 1 0.11 (0.02) 0.011 (0.004)
0.03 0.03 (0.02) 0.009 (0.004)
Open in a new tab

Results of simulations for the two costs of dispersal c = 0.2 and 0.7 in populations with nd = 10 demes are shown. In the top, ES rates without genetic load (Ds=0) are compared with the theoretical expectations (DESS). The middle and bottom show the ES dispersal rates with genetic load (Ds≠0) for the mild mutations (s = 0.01 and 0.05) as a function of deme size (N) and dominance coefficient (h) and for the lethal mutations (s = 1 and h = 0.02) as a function of the genomic mutation rate (U). Values in parentheses are standard deviations over 100 replicates. Dashes (—) represent populations that crashed before 2000 generations.

In the few runs with a low average fecundity (3 offspring), demographic stochasticity took a larger role: the rate of demic extinction reached 4.8%, and >40% of the replicates went extinct before 2000 generations. This resulted in an increased equilibrium dispersal rate up to 29% for the case of 10 demes with N = 10 (as opposed to 22% with a fecundity of 8). This value, however, was lower than the 37% expected from patch-occupancy models (from Gandon and Michalakis 1999) because occupied demes were not necessarily saturated under our settings (average saturation level of occupied demes 88%), which is known to release competition and thereby counterselect dispersal (Ronce et al. 2000; Parvinen et al. 2003).

Mild mutations:

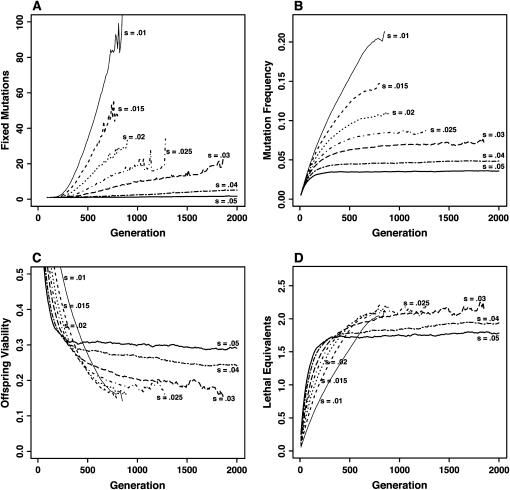
The dynamics of weak and partially recessive mutations (s = 0.01 and h = 0.3) were dominated by drift, which led to their progressive fixation at the metapopulation level (Figure 2A). Accumulation was most rapid for small deme sizes (N = 10), low intrinsic fecundity (results not shown), and high dispersal cost (c = 0.7, see Table 2). These combined conditions led to population crashes before 3000 generations. Increasing deme sizes somewhat reduced the strength of drift, allowing for higher population persistence, but mutations still accumulated (ρ < 1 and qexp = 0.134 for s = 0.01 and h = 0.3, see Table 2).

Figure 2.

Figure 2.

Open in a new tab

Deleterious mutation dynamics for mildly deleterious (s = 0.01–0.05) and partially recessive (h = 0.3) mutations. (A) Number of fixed deleterious mutations in the whole population. (B) Frequency of the mutations in the population. (C) Mean offspring viability. (D) Mean number of lethal equivalents. Parameters are: nd = 10 demes, N = 10, c = 0.2, mean fecundity f = 20, and U = 1. Mutations with effect s < 0.04 caused the mutational meltdown of the populations before 2000 generations, as shown by the interrupted lines.

TABLE 2.

Dynamics of the mildly deleterious mutations

N s h Mfix q Hmz Htz I V Lequ ρ
c = 0.2
10 0.01 0.01/0.3 — — — — — — —
0.05 0.01 2.9 (0.9) 0.065 (0.001) 0.018 (0.001) 0.093 (0.002) 0.16 (0.04) 0.39 (0.02) 3.30 (0.06) 1.47
0.3 1.6 (1.3) 0.035 (0.006) 0.009 (0.002) 0.053 (0.008) 0.04 (0.02) 0.28 (0.05) 1.94 (0.08) 0.89
50 0.01 0.01 17.1 (3.1) 0.258 (0.004) 0.108 (0.004) 0.299 (0.003) 0.07 (0.01) 0.32 (0.01) 2.64 (0.04) 0.84
0.3 8.3 (3.3) 0.194 (0.009) 0.075 (0.009) 0.238 (0.006) 0.02 (0.02) 0.23 (0.02) 1.94 (0.08) 0.71
0.05 0.01 0 (0) 0.080 (0.001) 0.011 (1E-4) 0.138 (0.002) 0.10 (0.02) 0.53 (0.003) 4.10 (0.06) 1.18
0.3 0 (0) 0.032 (0.001) 0.003 (0.001) 0.058 (0.002) 0.03 (0.01) 0.35 (0.01) 1.62 (0.05) 0.96
100 0.01 0.01 0 (0) 0.242 (0.001) 0.078 (0.001) 0.328 (0.002) 0.07 (0.01) 0.44 (0.01) 2.48 (0.01) 0.90
0.3 0.02 (0.14) 0.173 (0.005) 0.048 (0.005) 0.249 (0.005) 0.02 (0.01) 0.29 (0.01) 1.73 (0.05) 0.79
0.05 0.01 0 (0) 0.086 (0.001) 0.011 (1E-4) 0.151 (0.002) 0.10 (0.01) 0.54 (0.003) 4.39 (0.04) 1.11
0.3 0 (0) 0.032 (0.001) 0.003 (4E-4) 0.059 (0.002) 0.02 (0.01) 0.36 (0.01) 1.62 (0.04) 0.96
c = 0.7
10 0.01 0.01/0.3 — — — — — — —
0.05 0.01/0.3 — — — — — — —
50 0.01 0.01 27.4 (5.7) 0.290 (0.005) 0.165 (0.007) 0.250 (0.006) 0.25 (0.03) 0.18 (0.01) 2.97 (0.05) 0.75
0.3 23.2 (30.8) 0.232 (0.008) 0.132 (0.018) 0.200 (0.023) −0.04 (0.13) 0.14 (0.02) 2.37 (0.08) 0.59
0.05 0.01 0 (0) 0.064 (0.001) 0.014 (0.0004) 0.101 (0.003) 0.34 (0.01) 0.47 (0.01) 3.30 (0.06) 1.48
0.3 0 (0) 0.034 (0.001) 0.008 (0.001) 0.054 (0.001) 0.03 (0.04) 0.30 (0.01) 1.75 (0.04) 0.91
100 0.01 0.01 0.3 (0.6) 0.250 (0.004) 0.111 (0.006) 0.277 (0.004) 0.27 (0.05) 0.31 (0.02) 2.56 (0.04) 0.87
0.3 2.1 (13.9) 0.206 (0.002) 0.097 (0.02) 0.220 (0.01) 0.005 (0.10) 0.19 (0.03) 2.10 (0.20) 0.67
0.05 0.01 0 (0) 0.068 (0.002) 0.012 (3E-4) 0.111 (0.004) 0.28 (0.02) 0.50 (0.007) 3.48 (0.9) 1.39
0.3 0 (0) 0.032 (3E-4) 0.005 (3E-4) 0.055 (5E-4) −0.004 (0.046) 0.34 (0.005) 1.64 (0.01) 0.97
Open in a new tab

Results are given for simulations with nd = 10 demes and a genomic mutation rate of U = 1 over 1024 loci. Mfix is the number of loci fixed for the deleterious mutant over the whole population. q, Hmz, and Htz are the mean allelic frequency, homozygosity, and heterozygosity, respectively. I is the heterosis, V the mean offspring viability, Lequ the number of lethal equivalents, and ρ the amount of purge (qexp/q). Values in parentheses are standard deviations over 100 replicates. Dashes (—) represent populations that crashed before 2000 generations.

Because accumulation occurred at the metapopulation level, selection for dispersal due to the advantage of heterosis was low (I 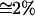Inline graphic, see Table 2). Indirect selection, however, arose from the large population fluctuations and frequent demic extinctions stemming from the high genetic load (mean offspring viability ranged 14–30%, see Table 2). In the case of N = 50 and c = 0.7, for instance, heterosis did not differ significantly from zero, but, owing to a high extinction rate (23%), the mean dispersal rate (Ds≠0 = 0.025) exceeded significantly the value obtained under kin-competition avoidance alone (Ds=0 = 0.017, Table 1). Note, however, that this value was still lower than that expected from patch occupancy models (DESS = 0.31, Gandon and Michalakis 1999) for the aforementioned reason.

Drift lost its importance for the other cases of larger deme sizes or lower costs of dispersal (c = 0.2 or N ≥ 50). Genetic load was then insufficient to generate strong population fluctuations (extinction rate <3%) so that selection for dispersal remained low, and evolutionary stable (ES) values only slightly exceeded those under kin competition alone (average increase of one-third, see Table 1). Drift also progressively lost importance as the selection coefficient was increased from s = 0.01 to s = 0.05 (see Figure 2). In small populations, the genetic load was still large (mean viability ∼30%, Table 2) but a fecundity of f = 20 was sufficient to limit population fluctuations, so that dispersal was only slightly affected (e.g., Ds=0.05 = 0.07 vs. Ds=0 = 0.05 for N = 50 and c = 0.2). In large populations, a selection coefficient of s = 0.05 was enough to prevent accumulation at the metapopulation level, at least over the timescale considered (3000 generations, see Mfix in Table 2). Mutations segregated close to their deterministic expectation (0.89 < ρ < 0.97 with qexp = 0.031, see Table 2), inducing some heterosis (Imax = 4%).

When strongly recessive (h = 0.01), mutations segregated at higher frequencies, being hidden in heterozygotes. However, their lower effect at the heterozygous state more than compensated for their higher frequency (see Table 2), so that offspring displayed higher mean viability (Figure 3D). Compared with their deterministic expectations these frequencies shifted from accumulation to purging (ρ > 1). The value of h at which the shift occurred increased with population size, from hlim ≅ 0.2 for N = 10 to hlim ≅ 0.3 for N ≥ 50 (and s = 0.05). These values agree well with theoretical thresholds for the purging of mildly deleterious mutations (i.e., h < ∼Inline graphic as in Whitlock 2002; Roze and Rousset 2004). However, for very mildly deleterious mutations (s = 0.01) and small population sizes (N = 10), the domain of purging was not reached even for h = 0.01, so that populations still crashed before 2000 generations (see Table 2). Strongly recessive mutations also induced more heterosis, owing to their higher equilibrium frequencies and number of lethal equivalents (Figure 3C). The costs of inbreeding were thus high enough in this case to induce significant incentives for dispersal (Figure 3, A and B). These costs seemed to weakly depend on population size at equilibrium (compare I-values for N = 50 and N = 100 with c = 0.2 in Table 2), as the effective number of migrants was approximately constant at the ES dispersal rate (Table 1).

Figure 3.

Figure 3.

Open in a new tab

Effect of the dominance coefficient of the deleterious mutations when s = 0.05 and N = 10 (solid line) and 50 individuals (dashed line) on the equilibrium dispersal rate (A), the mean heterosis (B), the mean number of lethal equivalents (C), and the mean offspring viability (D). Other parameters are as in Figure 2. Values are the averages over generations 2000–3000 over 100 replicates.

Lethal mutations:

Lethal mutations (s = 1) were largely purged with all deme sizes and dispersal costs, since equilibrium frequencies were much lower than expected in an infinite panmictic population. Purging was enhanced by population structure, in accordance with previous analytical treatments (i.e., purging by drift sensu Glémin 2003). Assuming a biologically realistic genomic mutation rate of U = 0.03 and highly structured populations (c = 0.7), ρ reached values up to 5 (for a qexp = 0.0007), allowing viabilities in excess of 98% (Table 3). Owing to this limited genomic mutation rate, heterosis could never build up (Table 3), and, because high viability values also limited demographic stochasticity, ES dispersal rates did not exceed those under kin-competition avoidance alone (Table 1). Note that under a biologically unrealistic genomic mutation rate of U = 1, heterosis reached high enough values (10–30%; Table 3) to contribute significantly to the evolution of dispersal, even though lethal alleles were also purged (ρ > 1.2) compared to their deterministic equilibrium (qexp = 0.0144; Table 3).

TABLE 3.

Dynamics of the lethal mutations

N U q Htz I V Lequ ρ
c = 0.2
10 1 0.0093 (7E-4) 0.019 (0.001) 0.28 (0.02) 0.69 (0.02) 9.2 (0.6) 1.55
0.03 0.0002 (3E-5) 0.0004 (6E-5) 0.014 (0.001) 0.992 (0.001) 0.21 (0.03) 3.5
50 1 0.0113 (5E-4) 0.023 (0.001) 0.15 (0.02) 0.64 (0.01) 11.3 (0.5) 1.27
0.03 0.0003 (2E-5) 0.0006 (4E-5) 0.009 (0.001) 0.988 (0.001) 0.29 (0.02) 2.3
100 1 0.0117 (4E-4) 0.023 (0.001) 0.13 (0.01) 0.63 (0.01) 11.7 (0.4) 1.23
0.03 0.0004 (2E-5) 0.0007 (4E-5) 0.012 (0.001) 0.986 (0.001) 0.36 (0.02) 2.0
c = 0.7
10 1 0.005 (3E-4) 0.010 (5E-4) 0.31 (0.10) 0.81 (0.01) 5.1 (0.3) 2.87
0.03 0.00015 (8E-6) 0.0003 (2E-5) 0.012 (0.003) 0.994 (3E-4) 0.15 (0.01) 4.7
50 1 0.008 (1E-4) 0.016 (2E-4) 0.22 (0.03) 0.72 (0.004) 8.1 (0.1) 1.83
0.03 0.00025 (8E-6) 0.0005 (1E-5) 0.009 (0.002) 0.990 (2E-4) 0.25 (0.01) 2.8
100 1 0.009 (8E-5) 0.018 (2E-4) 0.16 (0.03) 0.68 (0.002) 9.5 (0.1) 1.55
0.03 0.0003 (7E-6) 0.0006 (1E-5) 0.010 (0.004) 0.987 (3E-4) 0.32 (0.01) 2.3
Open in a new tab

The same simulation parameters as for Table 2 are shown.

Sex-biased dispersal:

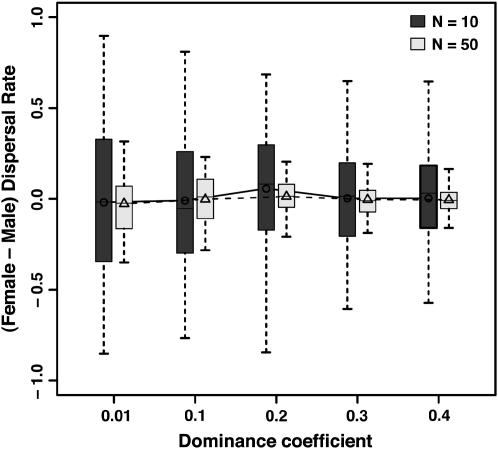
A final important point is that male and female dispersal rates never differed significantly under realistic parameter values. Owing to the purging and accumulation processes, levels of heterosis were not high enough to induce a sex-biased dispersal strategy (bistable equilibrium expected from game-theoretical models, see Perrin and Mazalov 1999, 2000). Although the distribution of the difference between male and female dispersal rates displayed more variance with more recessive mutations and smaller populations (Figure 4), it did not differ from normality and was always centered on zero. Boundary solutions (one sex dispersing while the other is entirely philopatric) did, however, occur under biologically less realistic parameter values (s = 0.3, h = 0.01, U = 1), fostering high levels of mutational load (results not shown).

Figure 4.

Figure 4.

Open in a new tab

Differences in dispersal rates between females and males when s = 0.05 as a function of dominance. Open symbols and solid and dashed horizontal lines plot the mean of the differences over the 100 replicates. The box plots represent the distribution of the differences. The boxes with dark shading and the solid line with open circles are for N = 10 and the boxes with light shading and the dashed line with open triangles are for N = 50. Simulations were performed over 10,000 generations. Other parameters are as in Figure 2.

DISCUSSION

Before addressing the main issue that motivated our study (namely, the evolution of dispersal), a few comments on the dynamics of load and heterosis under our settings will help in delineating the context in which this evolution takes place.

Heterosis and mutation load:

Several analytical treatments of the dynamics of deleterious mutations (Whitlock et al. 2000; Glémin et al. 2003; Roze and Rousset 2004) concur to suggest that mild mutations should contribute more to heterosis than highly deleterious ones, because the former accumulate locally while the latter are mostly purged. Our study confirms these results and also allows further specification of the relative role of mutation parameters and dispersal rate in the building and maintenance of heterosis and mutation load. We show in particular that weakly recessive mutations contribute more to mutation load, while strongly recessive mutations contribute more to heterosis, because their higher equilibrium frequency results in a higher number of lethal equivalents (see also Whitlock et al. 2000; Theodorou and Couvet 2002). Hence, heterosis and load are not favored by the same mutational parameter values, opposing conclusions commonly derived from analytical treatments (Whitlock et al. 2000; Glémin et al. 2003).

Mild mutations contribute very little to heterosis at small population sizes and weak dispersal costs. Under these parameter values, kin competition is strong enough to foster high dispersal, which often reaches values large enough (Nm > 1) that mild mutations spread rapidly among demes. Owing to a low number of demes, mildly deleterious mutations are thus fixed at the metapopulation level, thereby contributing to overall load, but not to heterosis. This effect, however, disappears when overall metapopulation size reaches or exceeds 1000 individuals (10 demes of 100 individuals or 50 demes of 50 individuals; Table 4). Mildly deleterious mutations that previously get fixed at the global scale now cause more localized drift load, so that heterosis reaches values comparable to those gathered from empirical data (Madsen et al. 1996; Richards 2000; Haag et al. 2002; Marr et al. 2002) or predicted from analytical treatments (Whitlock et al. 2000).

TABLE 4.

Dynamics of the mildly deleterious for 50 demes

N s h Dobs Mfix q I V Lequ ρ
c = 0.2
10 0.01 0.01 0.345 (0.036) 17.5 (4.7) 0.264 (0.005) 0.117 (0.008) 0.31 (0.01) 2.71 (0.05) 0.83
0.3 0.231 (0.049) 12.5 (8.7) 0.195 (0.008) 0.039 (0.078) 0.22 (0.02) 2.00 (0.09) 0.70
0.05 0.01 0.467 (0.044) 0 (0) 0.083 (0.002) 0.192 (0.010) 0.53 (0.005) 4.27 (0.10) 1.14
0.3 0.277 (0.031) 0 (0) 0.032 (0.0002) 0.055 (0.008) 0.35 (0.004) 1.64 (0.01) 0.98
50 0.01 0.01 0.098 (0.007) 0 (0) 0.246 (0.001) 0.090 (0.009) 0.46 (0.004) 2.52 (0.01) 0.87
0.3 0.070 (0.011) 0 (0) 0.166 (0.002) 0.018 (0.039) 0.30 (0.006) 1.70 (0.02) 0.82
0.05 0.01 0.161 (0.022) 0 (0) 0.091 (0.001) 0.116 (0.011) 0.54 (0.002) 4.65 (0.04) 1.04
0.3 0.064 (0.006) 0 (0) 0.032 (0.0001) 0.039 (0.005) 0.36 (0.001) 1.62 (0.004) 0.98
c = 0.7
10 0.01 0.01 — — — — — — —
0.3 — — — — — — —
0.05 0.01 0.129 (0.012) 0 (0) 0.063 (0.001) 0.470 (0.015) 0.44 (0.006) 3.21 (0.05) 1.5
0.3 — — — — — — —
50 0.01 0.01 0.025 (0.004) 0 (0) 0.247 (0.002) 0.317 (0.016) 0.33 (0.01) 2.53 (0.02) 0.88
0.3 0.019 (0.004) 0 (0) 0.213 (0.006) 0.219 (0.131) 0.18 (0.01) 2.18 (0.06) 0.64
0.05 0.01 0.029 (0.003) 0 (0) 0.067 (0.001) 0.368 (0.007) 0.49 (0.003) 3.43 (0.04) 1.42
0.3 0.017 (0.003) 0 (0) 0.033 (0.0003) 0.101 (0.021) 0.31 (0.005) 1.71 (0.01) 0.95
Open in a new tab

Results show the ES dispersal rate (Dobs), the number of fixed loci (Mfix), the mean mutant allele frequency (q), the mean heterosis (I), the mean offspring viability (V), the number of lethal equivalents (Lequ), and the amount of purge (ρ = qexp/q). The genomic mutation rate is U = 1. Values in parentheses are standard deviations over 10 replicates.

With strong drift (small populations and low selection coefficient), synergistic interactions between population size and mutation load induced crashes of the whole metapopulation (the so-called mutational meltdown; Lynch and Gabriel 1990; Lynch et al. 1995a,b; Higgins and Lynch 2001). Mildly deleterious mutations were thus more damaging to the long-term population viability than were more harmful ones, owing to this accumulation process. This outcome agrees well with previous theoretical analyses (Kimura et al. 1963; Bataillon and Kirkpatrick 2000; Whitlock 2002; Glémin et al. 2003; Roze and Rousset 2004), as well as with stochastic simulation studies (Wang et al. 1999; Higgins and Lynch 2001).

Several factors concurred to induce mutational meltdowns in our simulations. First, to ensure reasonable computing times, we had to deal with metapopulations of small overall size, which induced a high drift. In the few simulation runs with 50 demes instead of 10 (Table 4), the mutation load was reduced, which allowed for higher population persistence. Populations that previously underwent early mutational meltdowns now persisted over 10,000 generations.

Second, the genomic mutation rate for mild mutations was set at a fairly high value (U = 1). This value was borrowed directly from experimental Drosophila studies, but might still vary from taxon to taxon (e.g., be lower in Caenorhabditis elegans than in Drosophila; see Keightley and Caballero 1997). The range might actually lie between 0.1 and 1 mutation per genome per generation (see Drake et al. 1998 and Lynch et al. 1999 for reviews and Charlesworth et al. 2004 for recent reanalysis of the Drosophila data). Simulations conducted with a lower genomic mutation rate of U = 0.1 (Table 5) indeed showed a much lower accumulation rate, so that the risks of mutational meltdown were consequently diminished.

TABLE 5.

Dynamics of mildly deleterious with U = 0.1

N s h Dobs Mfix q I V Lequ ρ
c = 0.2
10 0.01 0.01 0.235 (0.063) 65.9 (9.1) 0.089 (0.007) 0.016 (0.021) 0.44 (0.03) 0.91 (0.07) 0.74
0.3 0.178 (0.052) 54.3 (5.6) 0.074 (0.006) −0.007 (0.020) 0.49 (0.03) 0.76 (0.06) 0.21
0.05 0.01 0.229 (0.080) 0.1 (0.2) 0.006 (0.0007) 0.031 (0.006) 0.92 (0.02) 0.32 (0.04) 4.5
0.3 0.268 (0.081) 0 (0) 0.003 (0.0001) 0.005 (0.010) 0.89 (0.003) 0.17 (0.005) 0.97
50 0.01 0.01 0.052 (0.029) 0.1 (0.3) 0.029 (0.002) 0.022 (0.010) 0.92 (0.01) 0.29 (0.02) 2.3
0.3 0.052 (0.020) 0 (0) 0.017 (0.001) 0.004 (0.007) 0.89 (0.01) 0.17 (0.01) 0.94
0.05 0.01 0.055 (0.021) 0 (0) 0.009 (0.0006) 0.034 (0.008) 0.94 (0.003) 0.45 (0.03) 3
0.3 0.069 (0.033) 0 (0) 0.003 (0.0001) 0.002 (0.004) 0.90 (0.005) 0.16 (0.01) 1
c = 0.7
10 0.01 0.01 0.084 (0.031) 58.4 (8.0) 0.087 (0.008) 0.016 (0.042) 0.45 (0.04) 0.89 (0.09) 0.76
0.3 0.071 (0.018) 51.8 (7.9) 0.079 (0.009) −0.021 (0.051) 0.46 (0.04) 0.81 (0.10) 0.20
0.05 0.01 0.079 (0.029) 0.3 (0.4) 0.006 (0.001) 0.087 (0.010) 0.86 (0.04) 0.31 (0.04) 4.5
0.3 0.064 (0.036) 0.1 (0.2) 0.005 (0.002) 0.029 (0.017) 0.80 (0.08) 0.27 (0.11) 0.64
50 0.01 0.01 0.018 (0.005) 0 (0) 0.029 (0.001) 0.078 (0.013) 0.87 (0.01) 0.29 (0.01) 2.3
0.3 0.013 (0.004) 0.1 (0.3) 0.023 (0.003) 0.032 (0.014) 0.82 (0.03) 0.24 (0.03) 0.69
0.05 0.01 0.019 (0.008) 0 (0) 0.006 (0.0003) 0.061 (0.013) 0.92 (0.01) 0.33 (0.02) 4.5
0.3 0.014 (0.006) 0 (0) 0.003 (0.0002) 0.012 (0.017) 0.89 (0.01) 0.17 (0.01) 0.94
Open in a new tab

Results of simulations performed in a metapopulation of 10 demes are shown. Same statistics as in Table 4 are shown. Values in parentheses are standard deviations over 10 replicates.

Finally, the multiplicative fitness model chosen played a role as well. We also performed simulations (not shown here) with an additive model implying nonindependent action of alleles (Wade et al. 2001). This resulted in an intensified selection on the deleterious mutations. Purge was effective over a much wider range of the parameters explored, and populations that previously crashed before 1000 generations (i.e., 737 ± 49 generations for s = 0.01, nd, and N = 10) now persisted for 10,000 generations on average (SD ∼ 3000 generations). Synergistic interactions between deleterious loci are indeed expected to enhance their damaging effect on fitness and increase the purge, thereby limiting their impact on population survivorship in sexual species [although enhancing it in asexual species (Lynch et al. 1993)]. Empirical evidence of epistatic interactions among detrimental loci is scarce (but see Elena and Lenski 1997, Peters and Keightley 2000, Wloch et al. 2001, and Salathe and Ebert 2003 in asexual species and Whitlock and Bourguet 2000 and Rivero et al. 2003 in sexual ones) and remains questionable (West et al. 1998; Trouve et al. 2004). As our simulations underscore, this issue is not a purely technical one, but appears to bear important practical implications for conservation, since the minimal viable population size is bound to depend on the way deleterious mutations interact.

Evolution of dispersal:

All three main selective pressures on dispersal (kin competition, population variability, and inbreeding avoidance) played a role under our settings, but at different extents depending on parameter values. Kin competition, in interaction with dispersal costs, took the leading role in the absence of inbreeding load, as evidenced by the excellent match between simulation results and expectations from game-theoretical models, mostly at large population sizes. At low population sizes or fecundity values, some departures from expectations stemmed from drift and demographic stochasticity. The addition of deleterious mutations to these settings contributed to the evolution of dispersal in two alternative ways, depending on whether parameter values induced a regime of accumulation or one of purge.

Accumulation by drift of mildly deleterious and weakly recessive mutations boosted demographic stochasticity, throwing populations into a dynamic of extinction–recolonization, which in turn increased dispersal rate. More direct selective pressure, however, emerged under regimes of purge. When highly recessive, mildly deleterious mutations segregating at low frequencies had the potential to induce a significant heterosis, thereby boosting dispersal as an inbreeding-avoidance mechanism. But genomic mutation rates also played a role here: the relatively low (but biologically realistic) value of U = 0.03 set for lethal mutations prevented load from reaching equilibrium values high enough to induce a significant heterosis. Since genomic mutation rates vary greatly among organisms (e.g., U ≥ ∼1 in mammals but 0.1 in Drosophila; Drake et al. 1998; Keightley and Eyre-Walker 2000), this result opens the possibility that the role of inbreeding load in driving dispersal may vary among taxa.

Our results thus point to highly contrasted effects of different types of mutation on the evolution of dispersal. While strongly deleterious mutations seem to play no significant role (owing to low genomic mutation rate), the effect of mildly deleterious ones depends on the coefficient of dominance: strongly recessive mutations contribute directly to heterosis and dispersal, but slightly recessive ones contribute indirectly, through the disequilibrium dynamics they foster. More estimates of dominance levels, which are scarce, would be helpful in this context.

Altogether, our results suggest that, under realistic mutation parameters, the additional amount of dispersal driven by inbreeding avoidance, although significant, is not overwhelming, being increased on average by one-third over the value expected from kin-competition avoidance. This conclusion seemingly opposes the results of Morgan (2002) who concluded, from individual-based simulations with similar mutation settings, that deleterious mutations are likely to foster strong dispersal. It is worth noting, however, that this model did not incorporate competitive interactions between kin and assumed no cost to dispersal. Under these conditions, inbreeding-depression avoidance should drive complete dispersal anyway. Our own simulations do evidence a significant effect of inbreeding avoidance independent of kin-competition avoidance, but also suggest that this effect is relatively low.

The point might be made that we underestimated natural levels of heterosis (and thereby the effects of inbreeding load on equilibrium dispersal values), because, owing to our small overall population sizes, mildly deleterious mutations tended to be fixed at the metapopulation level. As already noted, however, for metapopulation sizes >1000 individuals, our heterosis values were comparable to those stemming from the few cases convincingly documented in natural populations (Madsen et al. 1996; Richards 2000; Haag et al. 2002; Marr et al. 2002). It is also worth noting that such studies usually report significant genetic structures or suggest restrained dispersal between populations. From our results, such patterns not only point to an important load of mildly deleterious mutations, but also suggest a strong pressure counteracting the evolution of dispersal, stemming possibly from high costs to dispersal, as already mentioned, but also from high benefits to philopatry (e.g., kin cooperation) and/or other means to achieve inbreeding avoidance (e.g., kin recognition; Lehmann and Perrin 2003).

Indeed, there are also reasons to believe that our conclusions might actually be conservative and to expect an even weaker effect of inbreeding avoidance on dispersal in natural situations. First, as already mentioned, the genomic mutation rate used in our simulations might have overestimated real values, at least for a range of species. Second, we did not include in our model alternative ways of purging load or avoiding inbreeding. As shown by Glémin (2003), for instance, nonrandom mating is expected to purge more effectively than drift, which might further decrease the incentives for dispersal. Inbreeding load might also affect selection for alternative mating strategies. Our results do suggest an advantage for selfing when mutations accumulate at the metapopulation level (see Theodorou and Couvet 2002). The coevolution of dispersal and mating strategies is still a challenging question deserving proper investigations. Similarly, the patterns of kin discrimination are also worth investigating in this context, since kin recognition represents an important alternative to dispersal when it comes to avoiding inbreeding (e.g., Lehmann and Perrin 2003).

It is worth noting in this context that, under normal settings, the system did not achieve boundary solutions in the ES dispersal rates (i.e., dispersal by one sex only, indifferently male or female). Thus, when inbreeding load is allowed to evolve, the combined effects of purge and accumulation limit heterosis sufficiently that, with the parameter values used, the stabilizing effect of kin-competition avoidance was always strong enough to prevent the bistable sex asymmetry in dispersal rate that analytical models suggest as a possible outcome (Motro 1991; Gandon 1999; Perrin and Mazalov 1999). Bistable asymmetry did occur in some of our simulations, but only under parameter values fostering a high level of mutational load (results not shown). Different outcomes might result from investigations on local enhancement and social interactions: the benefits from cooperation might surpass the costs of inbreeding and thus enforce higher philopatry and higher inbreeding loads in local groups, which might possibly induce sex biases in dispersal rate (see, e.g., Perrin and Goudet 2001).

Acknowledgments

V. Reviol provided constant and enthusiastic support for the programing work, and L. Lehmann helped in deriving the analytical model. We thank D. Couvet, S. Gandon, J. Goudet, V. Ravigné, and O. Ronce for helpful discussions of the results. P. Fontanillas, L. Handley, L. Lehmann, and M. Reuter helped to clarify the writing. D. Charlesworth and two anonymous referees made insightful comments on a previous version of the manuscript. This work was supported by grants 31-59442.99 and 31-1000348/1 from the Swiss National Science Foundation.

References

  1. Bataillon, T., and M. Kirkpatrick, 2000. Inbreeding depression due to mildly deleterious mutations in finite populations: size does matter. Genet. Res. 75: 75–81. [DOI] [PubMed] [Google Scholar]
  2. Bengtsson, B. O., 1978. Avoiding inbreeding: At what cost? J. Theor. Biol. 73: 439–444. [DOI] [PubMed] [Google Scholar]
  3. Blouin, S. F., and M. Blouin, 1988. Inbreeding avoidance behaviors. Trends Ecol. Evol. 3: 230–233. [DOI] [PubMed] [Google Scholar]
  4. Charlesworth, B., and D. Charlesworth, 1999. The genetic basis of inbreeding depression. Genet. Res. 74: 329–340. [DOI] [PubMed] [Google Scholar]
  5. Charlesworth, B., H. Borthwick, C. Bartolome and P. Pignatelli, 2004. Estimates of the genomic mutation rate for detrimental alleles in Drosophila melanogaster. Genetics 167: 815–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Charlesworth, D., and B. Charlesworth, 1987. Inbreeding depression and its evolutionary consequences. Annu. Rev. Ecol. Syst. 18: 237–268. [Google Scholar]
  7. Clobert, J., E. Danchin, A. A. Dhondt and J. D. Nichols, 2001. Dispersal. Oxford University Press, Oxford.
  8. Comins, H. N., W. D. Hamilton and R. M. May, 1980. Evolutionarily stable dispersal strategies. J. Theor. Biol. 82: 205–230. [DOI] [PubMed] [Google Scholar]
  9. Crow, J. F., 1993. Mutation, mean fitness, and genetic load, pp. 3–42 in Oxford Surveys in Evolutionary Biology, Vol. 9, edited by D. Futuyama and J. Antonovics. Oxford University Press, Oxford.
  10. Crow, J. F., and M. Kimura, 1970. An Introduction to Population Genetics Theory. Harper & Row, New York.
  11. Drake, J. W., B. Charlesworth, D. Charlesworth and J. F. Crow, 1998. Rates of spontaneous mutation. Genetics 146: 1667–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Elena, S. F., and R. E. Lenski, 1997. Test of synergistic interactions among deleterious mutations in bacteria. Nature 390: 395–398. [DOI] [PubMed] [Google Scholar]
  13. Gandon, S., 1999. Kin competition, the cost of inbreeding and the evolution of dispersal. J. Theor. Biol. 200: 345–364. [DOI] [PubMed] [Google Scholar]
  14. Gandon, S., and Y. Michalakis, 1999. Evolutionarily stable dispersal rate in a metapopulation with extinctions and kin competition. J. Theor. Biol. 199: 275–290. [DOI] [PubMed] [Google Scholar]
  15. Gandon, S., and F. Rousset, 1999. Evolution of stepping-stone dispersal rates. Proc. R. Soc. Lond. Ser. B 266: 2507–2513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Glémin, S., 2003. How are deleterious mutations purged? Drift versus nonrandom mating. Evolution 57: 2678–2687. [DOI] [PubMed] [Google Scholar]
  17. Glémin, S., J. Ronfort and T. Bataillon, 2003. Patterns of inbreeding depression and architecture of the load in subdivided populations. Genetics 165: 2193–2212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Haag, C., J. Hottinger, M. Riek and D. Ebert, 2002. Strong inbreeding depression in a Daphnia metapopulation. Evolution 56: 518–526. [PubMed] [Google Scholar]
  19. Hamilton, W. D., and R. M. May, 1977. Dispersal in stable habitats. Nature 269: 578–581. [Google Scholar]
  20. Higgins, K., and M. Lynch, 2001. Metapopulation extinction caused by mutation accumulation. Proc. Natl. Acad. Sci. USA 98: 2928–2933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Keightley, P., and A. Caballero, 1997. Genomic mutation rates for lifetime reproductive output and lifespan in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 94: 3823–3827. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Keightley, P. D., and A. Eyre-Walker, 2000. Deleterious mutations and the evolution of sex. Science 290: 331–333. [DOI] [PubMed] [Google Scholar]
  23. Kimura, M., T. Maruyama and J. F. Crow, 1963. Mutation load in small populations. Genetics 48: 1303–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lehmann, L., and N. Perrin, 2003. Inbreeding avoidance through kin recognition: choosy females boost male dispersal. Am. Nat. 162: 638–652. [DOI] [PubMed] [Google Scholar]
  25. Lynch, M., and W. Gabriel, 1990. Mutation load and the survival of small populations. Evolution 44: 1725–1737. [DOI] [PubMed] [Google Scholar]
  26. Lynch, M., R. Bürger, D. Butcher and W. Gabriel, 1993. The mutational meltdown in asexual populations. J. Hered. 84: 339–344. [DOI] [PubMed] [Google Scholar]
  27. Lynch, M., J. Conery and R. Bürger, 1995. a Mutation accumulation and the extinction of small populations. Am. Nat. 146: 489–518. [Google Scholar]
  28. Lynch, M., J. Conery and R. Bürger, 1995. b Mutational meltdowns in sexual populations. Evolution 49: 1067–1080. [DOI] [PubMed] [Google Scholar]
  29. Lynch, M., J. Blanchard, D. Houle, T. Kibota, S. Schultz et al., 1999. Perspective: spontaneous deleterious mutation. Evolution 53: 645–663. [DOI] [PubMed] [Google Scholar]
  30. Madsen, T., B. Stille and R. Shine, 1996. Inbreeding depression in an isolated population of adders Vipera berus. Biol. Conserv. 75: 113–118. [Google Scholar]
  31. Marr, A., L. Keller and P. Arcese, 2002. Heterosis and outbreeding depression in descendants of natural immigrants to an inbred population of song sparrows (Melospiza melodia). Evolution 56: 131–142. [DOI] [PubMed] [Google Scholar]
  32. Moore, J., and R. Ali, 1984. Are dispersal and inbreeding avoidance related? Anim. Behav. 32: 94–112. [Google Scholar]
  33. Morgan, M. T., 2002. Genome-wide deleterious mutation favors dispersal and species integrity. Heredity 89: 253–257. [DOI] [PubMed] [Google Scholar]
  34. Morton, N. E., J. F. Crow and H. J. Muller, 1956. An estimate of the mutational damage in man from data on consanguineous marriages. Proc. Natl. Acad. Sci. USA 42: 855–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Motro, U., 1991. Avoiding inbreeding and sibling competition—the evolution of sexual dimorphism for dispersal. Am. Nat. 137: 108–115. [Google Scholar]
  36. Olivieri, I., Y. Michalakis and P. Gouyon, 1995. Metapopulation genetics and the evolution of dispersal. Am. Nat. 146: 202–228. [Google Scholar]
  37. Packer, C., 1979. Intertroop transfer and inbreeding avoidance in Papio anubis. Anim. Behav. 27: 1–36. [Google Scholar]
  38. Packer, C., 1985. Dispersal and inbreeding avoidance. Anim. Behav. 33: 676–678. [Google Scholar]
  39. Packer, C., and A. Pusey, 1993. Dispersal, kinship and inbreeding in African lions, pp. 375–391 in The Natural History of Inbreeding and Outbreeding, edited by N. W. Thornhill. University of Chicago Press, Chicago.
  40. Parvinen, K., U. Dieckmann, M. Gyllenberg and J. A. J. Metz, 2003. Evolution of dispersal in metapopulations with local density dependence and demographic stochasticity. J. Evol. Biol. 16: 143–153. [DOI] [PubMed] [Google Scholar]
  41. Perrin, N., and J. Goudet, 2001. Inbreeding, kinship, and the evolution of natal dispersal, pp. 123–142 in Dispersal, edited by J. Clobert, E. Danchin, A. A. Dhondt and J. D. Nichols. Oxford University Press, Oxford.
  42. Perrin, N., and V. Mazalov, 1999. Dispersal and inbreeding avoidance. Am. Nat. 154: 282–292. [DOI] [PubMed] [Google Scholar]
  43. Perrin, N., and V. Mazalov, 2000. Local competition, inbreeding, and the evolution of sex-biased dispersal. Am. Nat. 155: 116–127. [DOI] [PubMed] [Google Scholar]
  44. Peters, A. D., and P. D. Keightley, 2000. A test for epistasis among induced mutations in Caenorhabditis elegans. Genetics 156: 1635–1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Pusey, A. E., and C. Packer, 1987. The evolution of sex-biased dispersal in lions. Trends Ecol. Evol. 101: 275–310. [DOI] [PubMed] [Google Scholar]
  46. Pusey, A. E., and M. Wolf, 1996. Inbreeding avoidance in animals. Trends Ecol. Evol. 11: 201–206. [DOI] [PubMed] [Google Scholar]
  47. Richards, C. M., 2000. Inbreeding depression and genetic rescue in a plant metapopulation. Am. Nat. 155: 383–394. [DOI] [PubMed] [Google Scholar]
  48. Rivero, A., F. Ballou and S. A. West, 2003. Testing for epistasis between deleterious mutations in a parasitoid wasp. Evolution 57: 1698–1703. [DOI] [PubMed] [Google Scholar]
  49. Ronce, O., F. Perret and I. Olivieri, 2000. Evolutionarily sable dispersal rates do not always increase with local extinction rates. Am. Nat. 155: 485–496. [DOI] [PubMed] [Google Scholar]
  50. Roze, D., and F. O. Rousset, 2004. Joint effects of self-fertilization and population structure on mutation load, inbreeding depression and heterosis. Genetics 167: 1001–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Salathe, P., and D. Ebert, 2003. The effects of parasitism and inbreeding on the competitive ability in Daphnia magna: evidence for synergistic epistasis. J. Evol. Biol. 16: 976–985. [DOI] [PubMed] [Google Scholar]
  52. Simmons, M. J., and J. F. Crow, 1977. Mutations affecting fitness in Drosophila populations. Annu. Rev. Genet. 11: 49–78. [DOI] [PubMed] [Google Scholar]
  53. Taylor, P. D., 1988. An inclusive fitness model for dispersal of offspring. J. Theor. Biol. 130: 363–378. [Google Scholar]
  54. Theodorou, K., and D. Couvet, 2002. Inbreeding depression and heterosis in a subdivided population: influence of the mating system. Genet. Res. 80: 107–116. [DOI] [PubMed] [Google Scholar]
  55. Trouve, S., A. Ding and J. Goudet, 2004. Synergistic epistasis and alternative hypotheses. J. Evol. Biol. 17: 1400–1401. [DOI] [PubMed] [Google Scholar]
  56. Van Valen, L., 1971. Group selection and the evolution of dispersal. Evolution 25: 591–598. [DOI] [PubMed] [Google Scholar]
  57. Wade, M. J., R. G. Winther, A. F. Agrawal and C. J. Goodnight, 2001. Alternative definitions of epistasis: dependence and interaction. Trends Ecol. Evol. 16: 498–504. [Google Scholar]
  58. Wang, J., W. G. Hill, D. Charlesworth and B. Charlesworth, 1999. Dynamics of inbreeding depression due to deleterious mutations in small populations: mutation parameters and inbreeding rate. Genet. Res. 74: 165–178. [DOI] [PubMed] [Google Scholar]
  59. Waser, P. M., S. N. Austad and B. Keane, 1986. When should animals tolerate inbreeding. Am. Nat. 128: 529–537. [Google Scholar]
  60. West, S., A. Peters and N. Barton, 1998. Testing for epistasis between deleterious mutations. Genetics 149: 435–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Whitlock, M., and D. Bourguet, 2000. Factors affecting the genetic load in Drosophila: synergistic epistasis and correlations among fitness components. Evolution 54: 1654–1660. [DOI] [PubMed] [Google Scholar]
  62. Whitlock, M. C., 2002. Selection, load and inbreeding depression in a large metapopulation. Genetics 160: 1191–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Whitlock, M. C., P. K. Ingvarsson and T. Hatfield, 2000. Local drift load and the heterosis of interconnected populations. Heredity 84: 452–457. [DOI] [PubMed] [Google Scholar]
  64. Wloch, D. M., R. H. Borts and R. Korona, 2001. Epistatic interactions of spontaneous mutations in haploid strains of the yeast Saccharomyces cerevisiae. J. Evol. Biol. 14: 310–316. [Google Scholar]
  65. Wolff, J. O., 1992. Parents suppress reproduction and stimulate dispersal in opposite-sex juvenile white-footed mice. Nature 359: 409–410. [DOI] [PubMed] [Google Scholar]
  66. Wolff, J. O., 1994. More on juvenile dispersal in mammals. Oikos 71: 349–352. [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES