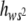Increase of the Spontaneous Mutation Rate in a Long-Term Experiment With Drosophila melanogaster

Abstract

In a previous experiment, the effect of 255 generations of mutation accumulation (MA) on the second chromosome viability of Drosophila melanogaster was studied using 200 full-sib MA1 lines and a large C1 control, both derived from a genetically homogeneous base population. At generation 265, one of those MA1 lines was expanded to start 150 new full-sib MA2 lines and a new C2 large control. After 46 generations, the rate of decline in mean viability in MA2 was ∼2.5 times that estimated in MA1, while the average degree of dominance of mutations was small and nonsignificant by generation 40 and moderate by generation 80. In parallel, the inbreeding depression rate for viability and the amount of additive variance for two bristle traits in C2 were 2–3 times larger than those in C1. The results are consistent with a mutation rate in the line from which MA2 and C2 were derived about 2.5 times larger than that in MA1. The mean viability of C2 remained roughly similar to that of C1, but the rate of MA2 line extinction increased progressively, leading to mutational collapse, which can be ascribed to accelerated mutation and/or synergy after important deleterious accumulation.

DETRIMENTAL mutations occur unceasingly, particularly mild ones, i.e., those with effects that are small enough to allow them to drift in small populations, but sufficiently large to cause an appreciable decline in fitness. This phenomenon has been shown to be potentially relevant to the explanation of some important evolutionary issues and, for instance, sex and recombination could have evolved to protect the genome from the continuous input of deleterious mutations (Kondrashov 1988; Otto and Lenormand 2002). It also affects the amount and nature of the genetic variation that could be maintained in populations and imposes a threat to the survival of those of reduced size (see García-Dorado 2003 and, for a review, García-Dorado et al. 2004).

However, the relevance of the aforementioned processes relies strongly on the properties of detrimental mutations, particularly their rate of occurrence and their distributions of effects in homozygosis and heterozygosis. Pertinent information has been obtained from highly laborious “mutation-accumulation” (MA) experiments, where spontaneous mutations accumulate in lines independently derived from the same genetically uniform origin, which are subsequently maintained in the effective absence of natural selection during a number of generations. The largest data set refers to viability (occasionally, reproductive fitness) in Drosophila melanogaster, although a few other species have also been studied. Earlier results obtained in the 1960s and 1970s by Mukai and co-workers (Mukai 1964, 1969; Mukai and Yamazaki 1968; Mukai et al. 1972) pointed to a high haploid rate of mutations (λ > ∼0.3) showing, on the average, small homozygous effects [E(s) < ∼0.03] and little recessivity [E(h) ≈ 0.4, where h = 0, 0.5, and 1 denote recessive, additive, and dominant gene action, respectively]. Nevertheless, experimental work carried out within the last decade raised questions on the general validity of former estimates, suggesting that mutations arise at a much lower rate but have stronger effects in the homozygous state, which are moderately expressed in the heterozygous state (see reviews by García-Dorado et al. 1999, 2004; Keightley and Eyre-Walker 1999; Lynch et al. 1999).

A long-term MA experiment carried out in our laboratory (Fernández and López-Fanjul 1996; Chavarrías et al. 2001; Caballero et al. 2002; Ávila and García-Dorado 2002) consisted of 200 full-sib MA lines and a large control population (referred to as MA1 lines and C1 control from now on, respectively), all derived from a common isogenic Drosophila melanogaster line. It consistently produced estimates indicating that the rate of occurrence of viability deleterious mutations was one order of magnitude lower than that reported by Mukai, while the average homozygous deleterious effect was larger (∼10%). The data also suggested a smaller degree of dominance, but the corresponding estimates were obtained after 250 generations of mutation accumulation, when natural selection could have removed those lines carrying severely deleterious mutations, which are likely to be the most recessive ones. This may have induced an upward bias in the estimate, which, furthermore, had a considerable standard error [E(h) = 0.33 ± 0.19].

In this article we report the results from a new set of MA lines (MA2) derived from a single line from our previous MA1 experiment. Our aim was to complete the description of the properties of deleterious mutations in the same genetic background, by obtaining more precise estimates of the average degree of dominance at an earlier stage of the process, as well as to investigate the effect of a long period of mutation accumulation on the viability of the MA lines and on the rates of fitness and quantitative mutation. After 46 generations, the rates of decline in mean and increase in between-line variance in MA2 were substantially larger than those calculated in MA1. Furthermore, long-term data indicated substantial instability of the MA2 lines' viability as well as increased mutation accumulation in the corresponding control C2, both compared to those of our previous experiment. These results show that the rates of deleterious and quantitative mutation can increase considerably after substantial mutational deterioration. However, estimates for the average deleterious effect and degree of dominance were in agreement with those formerly obtained.

MATERIALS AND METHODS

Base population and inbred lines:

In a previous experiment (Santiago et al. 1992) a D. melanogaster line isogenic for all chromosomes, obtained by Caballero et al. (1991), was used as a base population for a mutation-accumulation experiment consisting of 200 full-sib mutation-accumulation lines (MA1 lines) and a large control population (C1) maintained in 25 bottles (8 bottles up to generation 200), each with ∼100 individuals per bottle. The isogenic line carried the recessive eye-color marker sepia (se) in the third chromosome as an indicator of possible contamination from wild-type flies. It was also classified as Q (weak P) or M′ (pseudo-M) for the P–M system of hybrid dysgenesis.

At generation 265, one of those MA1 lines (line 85), which had formerly shown good viability, was expanded to be used as the base population of the present experiment. From this new base, 150 full-sib MA2 lines, as well as two large control lines (C2 and C2C, see below), were started and maintained for a further period of 100 (MA2 lines) or 119 (control populations) generations. The original control population (C1) was maintained in parallel, while the remaining MA1 lines were discontinued.

Culture conditions:

Flies were reared in the standard medium formula of this laboratory (brewer's yeast–agar–sucrose). All cultures were incubated at 45 ± 5% relative humidity and maintained under continuous lighting. Flies were handled at room temperature under CO₂ anesthesia. Each inbred MA2 line was maintained by a single pair of parents per generation, kept in a glass vial (20 mm diameter, 100 mm height) with 10 ml medium added, but two spare matings were made and used when the first one failed to reproduce, as in Chavarrías et al. (2001). Oviposition was allowed during 4 days, after which both parents were discarded. This implies that culture densities were low. At emergence, virgin male and female offspring were collected and individual pair matings were made when they were 4 days old.

The original control (C1) as well as the two new control lines (C2 and C2C) were maintained in 25 bottles each (250 ml with 50 ml medium added), using a circular mating scheme to ensure a large population size (∼2500 potential parents per generation), which was considered sufficient to minimize the per generation rate of mutational change due to genetic drift. Controls C1 and C2 were kept at the same temperature as the MA2 lines (25°) and synchronous to them. To detect any possible viability decline in control C2, we kept an additional large control in cold conditions (C2C control), adults being kept at 16°. The number of generations elapsed in control C2C was ∼60% of that in control C2 and in the MA2 lines. However, second chromosomes from C2C control showed drastically reduced viability. This reduction persisted even after being maintained at 25° during four recovery generations although it became small after 10 recovery generations (data not shown), so that it was interpreted as an epigenetic effect. A similar phenomenon has been reported by Houle and Nuzhdin (2004) for cryopreserved controls. In our case, this prevented the use of the C2C control, except for obtaining estimates of the degree of dominance of mutations as explained below.

To make comparisons between lines and controls valid, control flies reared in vials under the same conditions as the MA2 lines were used for evaluation.

Viability assays:

A balancer stock marked by the Cy (Curly wings) and L² (Lobe) genes was used. By generations 41–46, a few L² non-Cy individuals were observed in the stock. In the progeny of crosses between these L² non-Cy individuals and wild ones from the MA experiment, flies were either Cy or L², indicating that the occurrence of L² non-Cy individuals in the stock was due to a reduced expression of Cy in the stock's genetic background, where individuals also carry the L² marked chromosome. Therefore, a different Cy/L² stock was used at generations 77–108. The competitive viability of homozygous (+_i/+_i) or heterozygous (+_i/+_j) genotypes for the second chromosome was obtained from the ratio of wild type (+/+) genotypes in the progeny of an intercross between five Cy/+_i females and five L²/+_i males or five Cy/+_i females and five L²/+_j males, respectively. This ratio was computed as relative to Cy/L² numbers, except for generations 41–46, when it was relative to Cy/+ to avoid bias due to poor Cy expression in Cy/L² genotypes. The five pairs of parents were placed in a vial (with 10 ml medium added) and the females were allowed to lay during 10 days. Thus, viability assays were carried out in highly competitive conditions. Assuming that fitness is multiplicative between loci, log-transformed data are more suitable to compute Bateman–Mukai estimates of the rate λ and average effect E(s) of deleterious mutation, which are based on the additive model, as well as to achieve the normality of the residual errors required by ANOVA. Therefore, in the progeny of each intercross, viability was computed as V = log[no. +/+ individuals/no. Cy/L² individuals] or as V* = log[no. +/+ individuals/no. Cy/+ individuals], where log stands for natural logarithm.

As viability determinations are extremely demanding, they were carried out at different generations for MA2 chromosomes in homozygosis (l/l) and in heterozygosis with chromosomes taken at random from control C2C (l/c), and for C1 or C2 chromosomes in homozygosis (c_i/c_i) and panmixia (c/c). For all purposes, except the estimation of nonlethal inbreeding depression rates, data for specific chromosomes were excluded from the analyses if the viability score departed from the mean by >3 standard deviations. In all experiments, a randomly chosen vial was assigned to each intercross, the position of the vials in the stock room was randomized, and a blind procedure was used for viability determinations. The following experimental designs were used:

1. MA2 chromosomes in homozygosis and in heterozygosis with control C2C chromosomes. These evaluations were performed at generations 41, 77, and 85 for the MA2 lines (generations 25, 44, and 50 for control C2C, respectively). The procedure assumes that each MA2 line is genetically uniform, so that any pair of chromosomes randomly sampled from the same line can be considered to be homozygous, as illustrated in Figure 1A. For each MA2 line, 20 virgin females (l/l) and 20 Cy/L² males were placed together in a bottle. In parallel, 20 virgin control C2C females (c/c) and 20 Cy/L² males were also placed together in each of 64 bottles. From the emerging offspring the following intercrosses were made (each replicated five times in generation 41 and eight times at generations 77 and 85): (1) 5 Cy/l females by 5 L²/l males to evaluate the viability of chromosome l of the ith MA2 line in homozygosis and (2) 5 Cy/c females by 5 L²/l males to evaluate the viability of the same l chromosome in heterozygosis with control chromosomes (c).

2. MA2 chromosomes in homozygosis and control C2 chromosomes in panmixia. These evaluations were performed synchronously for the MA2 lines and the C2 control at generation 46 (Figure 1B). Again, the procedure assumes that MA2 lines are genetically uniform, while the large controls are considered as potentially segregating populations. For each MA2 line, 20 l/l virgin females and 20 Cy/L² males were placed together in a bottle. In parallel, 20 control C2 virgin females and 20 Cy/L² males were also placed together in each of 40 bottles. From the emerging offspring, 5 Cy/l females and 5 L²/l males were crossed to evaluate the viability of MA2 chromosomes in homozygosis. An identical procedure was followed to estimate the viability of C2 chromosomes in panmixia (c/c). Three such crosses were made for each MA2 line and 305 for the control C2.

3. MA2 and control C2 chromosomes in homozygosis. These evaluations were performed synchronously for the MA2 lines and the C2 control at generation 98 (Figure 1C). One hundred crosses were made between 2 Cy/L² virgin females and 2 males (c/c). Five analogous crosses were also made for each MA2 line (l/l males). From each cross, a single L²/+ male offspring was chosen and crossed to 5 Cy/L² virgin females in a new vial, where + stands for the single chromosome sampled from the corresponding control or MA2 line. From the progeny emerging in each vial, 5 Cy/+ virgin females and 5 L²/+ males, all carrying copies of the same + chromosome from the male parent, were crossed in a vial to evaluate the viability of this + chromosome in homozygosis (each cross replicated five times).

4. Control chromosomes (C1 and C2) in homozygosis and panmixia. These evaluations were performed synchronously for the C1 (generation 374) and the C2 (generation 108) controls, and the procedure is illustrated in Figure 1D. For each control population, two Cy/L² virgin females and 2 control males were placed together in each of 50 vials. A single male offspring L²/c_i was chosen from the ith vial and was crossed to 3 Cy/L² virgin females in a new vial. From this vial, 10 L²/c_i male and 10 Cy/c_i virgin female offspring, all carrying copies of the same c_i chromosome from the male parent, were obtained and placed together in a bottle. From the offspring emerging in that bottle, Cy/c_i virgin females and L²/c_i males were chosen and the following intercrosses were made (each replicated five times): (1) 5 Cy/c_i females by 5 L²/c_i males to evaluate the viability of control chromosomes in homozygosis and (2) 5 Cy/c_i females by 5 L²/c_i+1 males, to evaluate the viability of control chromosomes in panmixia.

Figure 1.

(A) Viability determination for MA2 chromosomes in homozygosis and in heterozygosis with control C2C chromosomes. (B) Viability determination for MA2 chromosomes in homozygosis and for control C2 chromosomes in panmixia. (C) Viability determination for MA2 and control C2 chromosomes in homozygosis. (D) Viability determination for control chromosomes (C1 and C2) in homozygosis and panmixia.

Estimates of mutational parameters:

Under certain assumptions (see, e.g., Chavarrías et al. 2001), an upper bound for the rate λ of viability deleterious mutation per gamete and generation and a lower bound for the average homozygous effect of mutations E(s), usually referred to as Bateman–Mukai estimates (Mukai et al. 1972), are given by λ ≥ ΔM²/ΔV and E(s) ≤ ΔV/ΔM, where ΔM and ΔV are the per generation rates of mutational decline in mean and increase in the between-line variance of viability, respectively (or λ_II, ΔM_II, and ΔV_II when referring to the second chromosome). The overall ΔM- and ΔV-values were estimated, respectively, as the difference in mean viability between the lines and the control or the between-line component of variance obtained from standard ANOVA techniques, divided by the number of generations of mutation accumulation in both cases. Standard errors for the components of variance were computed using standard ANOVA techniques. Those for ΔM and ΔV were derived from the variances of the corresponding means and variance components. Since Bateman–Mukai (BM) estimates of λ and E(s) are defined as ratios of variables, their approximate standard errors were obtained by the expansion method (Kendall et al. 1994). Minimum-distance (MD) (García-Dorado 1997) and maximum-likelihood (ML) (Keightley 1998) analyses were also carried out following the procedures described in García-Dorado and Gallego (2003) and using our MD program and an ML program provided by P. D. Keightley.

The average degree of dominance of mutations weighted by their squared homozygous effect, E(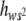), has been estimated by the regression of the heterozygous viability of MA2 chromosomes on the genetic value of the corresponding homozygous viability (Chavarrías et al. 2001).

Estimates of the additive variance for bristle traits in the control populations:

The additive genetic variance of abdominal and sternopleural bristle numbers was independently and synchronously estimated for both C1 and C2 control populations at generations 381 and 115, respectively. It was calculated from the response to one generation of divergent selection carried out in each of 9 lines for abdominal bristle number and in 10 independent lines for sternopleural bristle number per control population. To establish each selected line, 5 males and 5 virgin females were sampled from the corresponding control. They were placed in a vial with 10 ml medium added and discarded 9 days later. From the emerging progeny (generation 0), 25 males and 25 virgin females were obtained and scored for the pertinent bristle trait. The 5 males and the 5 females with the highest score were placed together in a new vial as parents of the upward selected line, and the same was done with the 5 males and the 5 females with the lowest score to obtain the downward selected line. The above adults were discarded 9 days later. From the progeny of each new vial (generation 1), 25 females and 25 males were scored for the bristle trait. At generation t = 0, estimates of the trait's means were computed both for the assayed (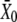, where the subscript denotes generation number) and for the selected individuals ( 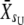and 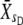, where U and D stand for upward and downward, respectively). At t = 1, the means of scored individuals were also computed in the upward- and downward-selected lines (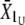, 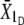). For each line, the additive variance was estimated as V_A = (R/S)V_p, where V_p is the phenotypic variance for the line obtained at t = 0 (pooled over sexes), R is the response to divergent selection (R = 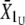− 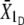), and S is the corresponding selection differential (S = 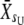− 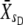), and standard errors for V_A were empirically computed from the sample of estimates (one estimate per line).

RESULTS

The mutational rates of mean decline and increase in variance for second chromosome viability:

The mean viability of second chromosomes from the MA2 lines in homozygosis and the synchronous evaluations for the C2 control (in homozygosis or in panmixia) are given in Table 1 for generations 46 and 98. All flies scored were sepia homozygotes, indicating that no contamination from wild-type flies occurred.

TABLE 1.

Mean (M) and between-line variance (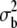) for second chromosome viability of the MA2 lines and their synchronous control

	Generation no.	No. of lines	Trait	MA2 homozygotes	C2 homozygotes	C2 pammixia
M	46	102	V*	−0.278 ± 0.023*		−0.120 ± 0.021
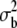				0.009 ± 0.0134 (NS)		−0.006 ± 0.0102 (NS)
M	98	76	V	0.214 ± 0.019*	0.113 ± 0.029
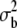				0.013 ± 0.0051**	0.050 ± 0.0296**

Estimates, with their standard errors, obtained at the specified generations for second chromosome viability of different genotypic combinations in the MA2 lines and the C2 control are shown. Synchronous assays are given in the same row. *M significantly different from the mean of synchronously evaluated C2 control (P < 0.005). **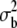 significantly larger than zero (P < 0.001). NS, 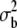not significantly larger than zero (P > 0.05).

First, it should be noted that both the trait assayed and the balancer stock used in generation 46 were different from those in generation 98, thus precluding direct comparisons between the mean viabilities obtained at the earlier and later stages of the MA process. However, the viability differences between the MA2 lines and the C2 control can be validly compared between generations. Thus, the homozygous viability of MA2 chromosomes was significantly smaller than the corresponding control panmictic average (generation 46), but significantly larger than the homozygous viability of control chromosomes (generation 98). This suggests that mutations with large deleterious effect were purged from MA2 lines but segregated at low frequencies in the large control due to their prevailing recessive gene action, causing negligible viability decline in the panmictic control but important depression when homozygous.

The estimates of the between-line component of variance for viability are also given in Table 1 for the MA2 lines and the C2 control. At generation 46, the between-line variance for MA2 chromosomes in homozygosis was not significantly larger than zero, although it was highly significant by generation 98.

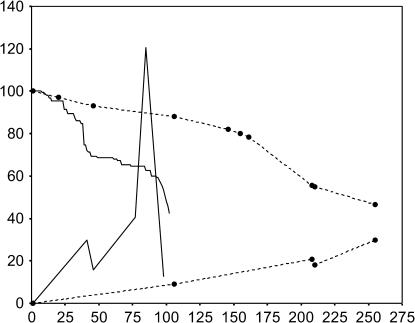
Both the temporal change of the between-line component of variance for MA2 chromosomes in homozygosis (V) and that for the percentage of surviving MA2 lines are shown in Figure 2. Data from our previous MA1 experiment (García-Dorado et al. 2000; Chavarrías et al. 2001) are also presented for comparison. In Figure 2, the between-line variance for egg-to-adult relative viability was adjusted to that of the second chromosome by dividing by 2.5, and the variance components for V* (generations 41 and 46) were averaged and converted to V by multiplying by a scale factor 1.75 (Chavarrías et al. 2001). Thus, Figure 2 is not intended to allow point-by-point comparisons between experiments or between generations within the same experiment. However, it clearly illustrates that the between-line variance for MA2 lines was generally larger and more erratic than that for MA1 lines, despite the more heterogeneous procedures used to obtain estimates for MA1 (standard errors for the between-line variances in Figure 2 are 0.00083, 0.0032, 0.0134, and 0.0124 for MA1 lines and 0.0117, 0.0234, 0.0111, 0.026, and 0.0051 for the corresponding MA2 estimates, ordered according to generation number in both instances). The late reduction in the between-line variance of MA2 lines should not be ascribed to the extinction of those with lowest viability, as the between-line variance at generation 85 for the subset of MA2 lines surviving up to generation 98 was similar to that estimated using the whole set of lines. Figure 2 also shows that, after a short initial period, the rate of line loss became larger in MA2 than in MA1, showing progressive acceleration.

Figure 2.

Percentage of surviving MA lines (starting at ordinate 100) and estimates of the between-line variance (×10⁻³, starting at ordinate 0) plotted against generation number for the previous (Chavarrías et al. 2001, dashed lines) and present experiments (solid lines).

Estimates of mutational parameters for viability:

Mutational parameters for second chromosome viability have been obtained from generation 46 data and are shown in Table 2, together with those calculated in our previous experiment. Before comparing MA1 and MA2 results it should be noted that the direction of the crosses made for the viability assays had an important effect on the outcome, as the relative viability of the Cy/L² genotype in the progeny of the viability evaluations was much higher (and, correspondingly, that of the wild genotype much lower) when evaluated in crosses where the progeny carried both the cytoplasm and the X chromosomes from the marker stock (results not shown), a phenomenon that could be ascribed to a process of coadaptation between the cytoplasm and/or the X chromosomes and the rest of the genome. Maternal effects can be excluded as a cause for this phenomenon, as they should affect equally the survival of wild or marked progeny from the same crossing, thus causing no effect on relative viability. The coadaptation process implies that comparisons should be limited to estimates from those assays where initial crosses were made in the same direction. Retrospectively, this effect was also detected in our previous experiment (Chavarrías et al. 2001), where the average viability of second chromosomes from the panmictic control was 0.447 ± 0.027 (generation 250) or 0.779 ± 0.069 (generation 255), depending upon the direction of the crosses. Due to this reason, only generation 255 results are used for comparison, although joint results for generations 250–255 produced qualitatively similar conclusions.

TABLE 2.

Bateman–Mukai mutational parameters for second chromosome viability (V*)

Parameter	Chavarrías et al. (2001)	Present experiment
ΔMII × 10−2	0.140 ± 0.023	0.344 ± 0.034
ΔVII × 10−3	0.087 ± 0.029	0.197 ± 0.292
λII	0.023 ± 0.011	0.058 ± 0.072
E(s)	0.062 ± 0.023	0.057 ± 0.084

ΔM_II and ΔV_II are, respectively, the estimates of the rates of decline in mean and increase in variance, and λ_II and E(s) are, respectively, the Bateman–Mukai estimates of the rate (lower bound) and average effect (upper bound) of second chromosome mutations, obtained in Chavarrías et al. (2001) from generation 255 data and in the present experiment from generation 46 data.

Estimates of the per generation rates of decline in mean viability and increase in between-line variance were ∼2.5 times larger than those in the previous study. Therefore, the Bateman–Mukai estimate of the rate of mutation in MA2 was also ∼2.5 times larger than that obtained for MA1. The increase of the rate of viability decline was highly significant but that for the rate of increase in variance was not, implying that the increase of the mutation rate was also nonsignificant.

Additional estimates (Table 3) were calculated using the three MA2 lines showing the largest viability at generation 46 as controls for the assays carried out at generation 41 (Mukai's order method). This procedure gave a rate of viability decline that was about one-half of that estimated at generation 46 using control C2 (ΔM_II = 0.0017 ± 0.0031), resulting in a rate of deleterious mutation (λ_II ≥ 0.006 ± 0.011) that was one order of magnitude smaller than the corresponding Bateman–Mukai estimate obtained at generation 46 and in a larger average mutational effect [E(s) ≤ 0.29 ± 0.15]. The smaller ΔM_II estimate obtained using the “order method” should be ascribed to the mutational viability decline in the three top-ranking MA2 lines being larger than that in the panmictic control C2. Therefore, only mutational parameters obtained using the C2 control are further considered.

TABLE 3.

Mutational parameters for second chromosome viability estimated by different methods

Estimation method	λII	E(s)
BM order method	0.006	0.290
BM using control C2	0.065	0.057
MD control supported	0.111	0.034
MD control determined	0.098	0.039
ML	0.036	0.092

Estimates of the rate λ_II and average effect E(s) of second chromosome viability mutations obtained by different methods (BM, Bateman–Mukai; MD, minimum distance; ML, maximum likelihood; see text for further explanation).

MD and ML estimates of the rate and the homozygous effect of mutations have also been obtained and are given in Table 3. When the information of the C2 control on the rate of mean decline ΔM_II was ignored in the MD analysis (“control ignored,” CI–MD), the distance profile showed no minimum and, therefore, CI–MD estimates could not be obtained. Using the information on ΔM_II provided by this control (“control-supported,” CS–MD, or “control-determined,” CD–MD analyses, see García-Dorado and Gallego 2003), the corresponding MD and ML profiles were rather flat, the minimum for the distance was nonsignificant, and the support limit for ML went to infinity. Even so, these approaches gave relatively close estimates: 0.04 ≤ λ_II ≤ 0.11 and 0.03 ≤ E(s) ≤ 0.09. These methods assume gamma-distributed mutational effects and gave estimates for the shape parameter that were ∼2 using MD (2.2 for CS–MD and 1.8 for CI–MD) but went to infinity using ML. These estimates suggest that most of the viability decline could be attributed to mutations with individual effects of the order of the estimated average effect.

In principle, regression estimates of the degree of dominance of deleterious mutations should not be affected by a low-temperature epigenetic effect on the viability of C2C chromosomes (see above), as this will not contribute to the genetic variance between MA2 homozygotes or to the covariance between MA2 homozygotes and heterozygotes. Thus, regression estimates were computed using data from generations 41 or 77–85 and are given in Table 4. The degree of dominance did not significantly depart from zero at generation 41, but was relatively high at generations 77–85. It is worthwhile to note that the average of estimates obtained separately at generations 77 and 85 was substantially smaller than the single estimate obtained using over-generation average viabilities. This difference should be ascribed to the erratic behavior of the homozygous genotypic variance.

TABLE 4.

Estimates of the degree of dominance for second chromosome viability

Generation no.	E() ± SE
41	−0.05 ± 0.16 (NS)
77–85a	0.23 ± 0.08**
77–85b	0.39 ± 0.18*

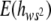is the average degree of dominance of viability mutations weighed by their squared homozygous effect, estimated as the regression of the average heterozygous viability of MA2 chromosomes on the genetic value of the corresponding average homozygous viability. NS, Not significantly different from zero. *Significantly different from zero (P < 0.013). **This standard error, which does not include the between-generation variability for the degree of dominance, implies that the estimate is significantly different from zero (P < 0.0017).

^aAverage of estimates computed separately for generations 77 and 85.

^bEstimate computed using over-generation values for homozygous and heterozygous viabilities.

The inbreeding depression rate for viability in the control populations:

Fifty-five- and 56-sec chromosomes were synchronously sampled from C1 (t = 374) and C2 (t = 108), respectively. From these, 3 C1 (5.5%) and 9 C2 chromosomes (16.1%) were lethal. Viability was assayed synchronously for the 52 nonlethal second chromosomes from C1 and the 47 from C2, and mean viabilities and rates of inbreeding depression are given in Table 5. C1 viability means at generation 250 cannot be directly compared to those at generation 374, as they were not obtained synchronously and are relative to a different balancer Cy/L² stock. However, the rates of inbreeding depression can be compared, that for C1 remaining stable from generation 250 to 374, and that for C2 tripling that for C1.

TABLE 5.

Mean viability and inbreeding depression rate (δ_II), with their standard errors, for nonlethal second chromosomes in both C1 and C2 control populations at the generations specified

	C1 (t = 250)a		C1 (t = 374)b		C2 (t = 108)b
	Homozygosis	Panmixia	Homozygosis	Panmixia	Homozygosis	Panmixia
Mean	0.373 ± 0.025	0.458 ± 0.028	0.347 ± 0.060	0.438 ± 0.038	0.085 ± 0.081	0.366 ± 0.041
δII	0.090 ± 0.037		0.091 ± 0.060		0.2809 ± 0.077

^aComputed from Chavarrías et al. (2001) for nonlethal chromosomes.

^bSynchronous evaluations.

Estimates of the additive variances of bristle number for C1 and C2 control populations:

These estimates are given in Table 6. For both traits, means were significantly larger for C1 (32.25 ± 0.19, 33.72 ± 0.10 for abdominal and sternopleural bristle number averaged over sexes, respectively) than for C2 (28.94 ± 0.48, 28.43 ± 0.27, respectively), suggesting that the effect of accumulated mutations on those traits is, on the average, negative. For sternopleural and abdominal bristle number, the additive variance in C2 was about double that for C1, in agreement with the increase observed for the rates of viability decline in MA2 and for the rate of viability inbreeding depression in the corresponding C2 control.

TABLE 6.

Synchronous estimates of the additive genetic variance for bristle traits accumulated in control populations at the generations specified

Trait	C1 (t = 381)	C2 (t = 115)	Ratio C2/C1
Abdominal	2.10 ± 0.41	4.89 ± 1.32	2.33
Sternopleural	1.34 ± 0.47	2.58 ± 0.42	1.93

DISCUSSION

Increase of the mutation rate:

At generation 255 of our previous experiment (Chavarrías et al. 2001), the rate of viability (V) decline for the second chromosome and the corresponding rate of mutation (ΔM = 0.0037, λ ≥ 0.044, adjusted for the whole genome) were about double those obtained at generations 104–106 (García-Dorado 1997). Nevertheless, the average deleterious effects of mutations were remarkably similar at both moments (0.087 vs. 0.085). This could be taken as an indication that the rate of deleterious mutation for competitive viability may be larger, as the earlier estimate refers to less stressful conditions. However, a larger mutation rate for competitive viability would be at variance with Fry and Heinsohn's (2002) findings of the rate of decline being unaffected by culture density and the mutation rate being larger at low density. Alternatively, the deleterious mutation rate may have increased between generations 105 and 255. However, it should be noted that at generations 208–210 both the rate of decline in mean and increase in variance for noncompetitive viability were comparable to those estimated at generations 104–106 (García-Dorado et al. 2000; Caballero et al. 2002), implying that, if some mutational acceleration occurred, this would apply only to the later stage of the experiment. In any case, MA1 results belong to the spectrum reported for Drosophila (reviewed by García-Dorado et al. 2004), which indicates that the rate of deleterious mutations for genomes sampled from segregating populations is within an interval from 0.005 to 0.05, with average effect E(s) ≈ 0.10.

More recently, Charlesworth et al. (2004) studied the effect of mutation accumulation on the competitive viability of third chromosomes in a replicated experiment. The rate of viability decline was estimated either by using an order control method or from the regression slope of viability on generation number, but these procedures gave substantially different results. The order method provided remarkably uniform rates of viability decline across the three replicates (ΔM_III values ranging from 0.0016 to 0.0022), averaging ΔM ≈ 0.0038 adjusted for the whole genome. The corresponding rates of deleterious mutation per gamete and generation and the average effect of mutations were also relatively uniform, giving average λ = 0.025 and E(s) = 0.15, respectively. However, ΔM and λ could have been underestimated and E(s) overestimated if the lines used as controls in the order method had accumulated a relevant mutational decline. On the other hand, the regression ΔM estimates, averaged over replicates, gave λ = 0.21 and ΔM = 0.0081 for the whole genome and a negative average deleterious effect E(s) = −0.41. Nevertheless, those regression ΔM-values can overestimate the true ΔM-value to an unknown extent if the viability of the marker chromosome used as reference in the viability assay increased during part of the experiment. This possibility is consistent with the high variability of ΔM between replicates, which were initiated at intervals of ∼1 year (ΔM_III ranging from 0.0011 to 0.0067). As a consequence, regression estimates showed considerable variation between replicates [λ_III ranged from 0.0025 to 0.241 and E(s) ranged from −1.27 to 0.064, respectively]. Thus, the data obtained by Charlesworth et al. (2004) can be considered consistent with most results from MA Drosophila experiments, including our MA1 experiment.

Comparisons between the MA1 results and those obtained in the present experiment require the use of the same viability estimates in both instances. In the previous experiment, it was found that the between-line variance for the viability V* of l_i/l_i MA1 chromosomes (relative to the Cy/l_i genotype) underestimated that for the viability V (relative to the Cy/L² genotype), so that the deleterious mutation rate (λ_II ≥ 0.0226) and the average deleterious effect [E(s) ≤ 0.062] for V* may have, respectively, overestimated or underestimated the true viability mutation rate and average effect. Notwithstanding, these V* results can be validly compared to those from the present experiment at generation 46. This comparison using V* gave rates of decline in mean and increase in variance in MA2 ∼2.5 times larger than those calculated in the final period of the former experiment and, therefore, the estimate of the rate of mutation also increased by the same factor while, again, the average deleterious effect remained practically unchanged. The rate of viability decline in MA2 was significantly larger than that in MA1 with p < 4 × 10⁻⁷, but standard errors for the rate of increase in variance and, therefore, for the estimates of mutational rates and average effects, were large. Therefore, this significant increase in the rate of viability decline might also be ascribed to a synergistic increase of the deleterious effects of new mutations when they accumulate upon a genetic background deteriorated by previously accumulated mutations. However, an additional argument supporting the conclusion that the rate of mutation had increased in the early phase of this experiment due to an increased mutation rate in the founder MA1 line is the observed increase in the additive genetic variance of bristle traits in the control C2, by a factor similar to that applying both to the corresponding rate of viability inbreeding depression and to the MA2 lines' rate of viability decline. The proportion of surviving lines fell dramatically by the end of the experiment, suggesting either a further increase of the deleterious mutation rate or synergistic epistatic gene action limited to those genomes that were homozygous for other severely deleterious mutations. Summarizing, our results indicate that the rate of deleterious mutation had increased in the initial phase of the MA2 experiment, but they are also compatible with synergy occurring at later stages.

We have also investigated the accumulation of new genetic variability in two large-size control populations. Control C1 had been kept in 8 bottles up to generation 200 and in 25 bottles thereafter. However, its inbreeding depression rate was the same at generations 250 and 374, implying that, after being maintained in 25 bottles during 50 generations, this population had attained roughly the mutation–selection–drift equilibrium regarding the mutations responsible for the viability inbreeding depression. This C1 nonlethal inbreeding depression rate for the second chromosome was ∼30% the average of published estimates for segregating populations (Temin et al. 1969; Mukai and Yamaguchi 1974; Seager and Ayala 1982; Mukai and Nagano 1983; Kusakabe and Mukai 1984; Kusakabe et al. 2000). Control C2 was also maintained in 25 bottles so that, after 108 generations, it was also expected to be roughly at the mutation–selection–drift balance. By that time, it harbored a viability inbreeding depression rate threefold that detected in C1, which is consistent with the 2.5-fold increase of the rate of viability decline observed in the MA2 lines. On the other hand, homozygous viabilities assayed at generation 98 suggest that the inbreeding depression rate of the control populations was, to a good extent, caused by substantially recessive mutations with large deleterious effects, which can segregate at low frequencies in large control populations but are efficiently purged from MA lines. Therefore, the inbreeding depression rate in the C2 control seems to be partially due to mutations different from those responsible for the rate of viability decline in the MA2 lines, and the fact that both rates increased by a similar factor suggests that they should be ascribed to a general increase in the rate of spontaneous mutation, rather than to synergy.

At the later synchronous evaluation of the viability of controls, the mean of the C2 panmictic genotypes was below that of C1. This could be partly attributed to a viability decline experienced by the MA1-85 line by the time it was used to derive the C2 control. However, it should be noted that this line was chosen on the basis of its high viability value, so that it could be considered an order-method control (Mukai 1964). Thus, in the following we ignore this possible source of viability decline, as well as any unlikely accumulation of beneficial mutations. Consequently, we interpret that the lower panmictic viability of C2 chromosomes was due to a larger viability decline experienced by this control population. However, for such large populations, the rate of viability decline due to fixation should be negligible even at the equilibrium (García-Dorado 2003). Thus, a larger viability decline in C2 must be attributed mainly to a larger segregating mutation load accumulated during the buildup of its new mutation–selection–drift balance and, therefore, the difference in viability between the C1 and C2 controls is expected to overestimate the difference in segregating mutation loads. The equilibrium segregating mutation load for populations with effective sizes >100 has been found to be close to the expected value for infinite populations (García-Dorado 2003), i.e., practically equal to the zygotic mutation rate for log viability (the haploid rate for completely recessive deleterious mutations). This implies that the difference in λ_II between both controls (0.058 − 0.023 = 0.035, Table 2) should be about half the corresponding difference in the panmictic viability of second chromosomes, in good agreement with the estimates reported here [(0.438 − 0.366)/2 = 0.036, Table 5].

An acceleration of the per generation rate of viability decline may have also occurred in other MA experiments and could have resulted in substantial overestimation of the initial rate of mutation. Thus, in Mukai's (1964) experiment, the estimated rate of decline during the first 25 MA generations, adjusted for the whole genome, was ΔM ≈ 0.01 (ΔM = 0.007 using data up to generation 32; Fry 2004). However, this estimate was obtained using a rank-order method that assumed the same initial viability for both the MA lines used as controls and the remaining MA lines. García-Dorado and Caballero (2002) have pointed out that this assumption is inconsistent with the higher viability showed by the control MA lines throughout the experiment, thus suggesting contamination from an external source. They reanalyzed the long-term data from the same experiment (up to generation 60; Mukai 1969), concluding that these were compatible with an early onset of the acceleration of viability decline and with an initial rate of viability decline ΔM = 0.003 estimated from quadratic regression. Using an indirect approach, Fry (2004) also detected an accelerated viability decline in Ohnishi's (1977) experiment, although it should be noted that this is hard to reconcile with the steadily linear increase of the between-line variance (Ohnishi 1977, Figures 5 and 6). On the other hand, synergy has often been found to be limited to heavily loaded genotypes (Rosa et al. 2005 and references therein), which are more likely to appear in the later stages of an accelerated degradation process.

The causes inducing the increased rate of mutation detected in our experiment are unknown. A possible explanation, however, is a corresponding increase of the transposition rate. In our previous experiment, the inferred transposition rate per element copy per generation was ∼10⁻⁴, in excellent agreement with previous data from different genetic backgrounds (Maside et al. 2001). However, the transposition rate is expected to be positively correlated to the number of inserted elements, as documented for copia elements (Pasyukova et al. 1998), which can lead to acceleration after a long mutation-accumulation period. The distribution of the deleterious effects of new transpositions is also unknown. From the regression of fitness on copia number in Drosophila MA lines, Houle and Nuzhdin (2004) obtained an average deleterious effect of 0.0076 per new copia element, but this estimate is compatible with different possible distributions as, for instance, that where 90% of all new insertions occur within nonfunctional DNA, having small undetectable deleterious effects, while the remaining 10% have deleterious effects that follow the distribution estimated in our MA1 experiment. Therefore, the different estimates of deleterious mutation rates and average effects given in the literature may be explained by different transposition rates. Notwithstanding, estimates obtained from data pertaining to the early periods of MA experiments show a much higher consistency, indicating low deleterious mutation rates of the order of 0.02 per gamete and generation and average effects ∼0.1 when obtained from full-sib mating MA lines or somewhat larger effects when derived from MA chromosomes sheltered from selection in the heterozygous state. This is in agreement with the hypothesis of selection regulating both the average number of transposable copies in the genome and the overall transposition rate in natural populations (Maside et al. 2001).

Degree of dominance of mutations:

The regression b of heterozygous on homozygous genotypic values estimates E(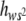), i.e., the average degree of dominance of new deleterious mutations weighed by their corresponding squared homozygous effect. Our b estimates were quite heterogeneous: those obtained at generations 77 and 85 did not differ significantly but their average value (0.234) was significantly larger than that at generation 41 (−0.046). Thus, a temporal increase in E(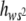) may have occurred. Note that, due to weighing by s², E(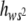) is determined mainly by the h-values (usually very small) corresponding to mutations that are severely deleterious in homozygosis. This implies that E(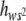) could be well below the unweighed average degree of dominance E(h). However, in inbred MA lines, natural selection acts primarily upon the homozygous effect of mutations, removing those of large deleterious effects that are usually more recessive. This will cause an increase in E(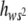) that may be important, depending on the shape of the joint distribution of s and h. For a range of possible values of these parameters, simulation results by Fernández et al. (2004, Table 6) show that b estimates close to zero can be expected in MA experiments if the unweighed estimate of h is relatively small [E(h) ≈ <0.2]. Thus, the temporal increase in b suggests that mutation accumulation was accompanied by increased purging selection against mutations with large homozygous deleterious effects in later stages of the experiment. This corroborates Fernández et al.'s conclusions, indicating that MA experiments may underestimate the rate of largely recessive severely deleterious mutations and may lead to downward-biased predictions for the viability inbreeding depression rates in natural populations. Alternatively, the increase in b could be attributed to accelerated transposition, as suggested by Fry and Nuzhdin (2003). These authors found important overall recessivity for deleterious viability mutations but additive gene action for those caused by copia insertions, although the difference between the corresponding h-estimates did not reach significance.

We should note that the degree of dominance obtained using viability averages over generations 77–85 was larger than the average of estimates obtained separately at each generation. Although the difference was not significant, the result suggests that, due to genotype–environment interaction, over-generation deleterious effects may be less recessive than those estimated at single generations. Note also that, due to between-generation variance for the expression of deleterious effects, viability data obtained at single generations may lead to underestimation of the rate of occurrence of those mutations that have a deleterious average effect over generations, as well as to the overestimation of this effect. Such a possibility has been previously suggested by García-Dorado (1997), who, however, obtained low estimates for the rate of over-generation deleterious mutation for egg-to-adult viability using MA1 data. Our results suggest that such mutations could also have an average over-generation degree of dominance larger than that estimated at single generations, so that the efficiency of natural selection to remove them could still be relatively large.

Taking into account both the aforementioned reanalyses of classical experiments and the estimates obtained in those performed during the last decade (see García-Dorado et al. 2004 for a review), the deleterious mutation rate relevant to the description of the evolutionary properties of natural populations, i.e., that observed at the initial period of MA experiments, fits within an interval from 0.005 to 0.05, excepting the Bateman–Mukai estimates reported by Mukai et al. (1972). In our former experiment, deleterious mutations occurred at a rate belonging to this interval [λ ≈ 0.02 for egg-to-adult viability during the first 100 generations with average effect E(s) ≈ 0.10; λ ≈ 0.04 for competitive viability during the first 250 generations with E(s) ≈ 0.08]. However, the rate of mutations with an effect on quantitative or fitness traits increased in the present experiment by a factor of 2.5. In later generations, this was accompanied by the mutational collapse of the full-sib lines, but caused only minor deterioration in the relatively large control population. These results indicate that the rate of deleterious mutation may increase after important mutational degradation and that synergism of mutational deleterious effects might become an important cause of extinction for very small lines after considerable mutational load has accumulated, but not for populations of moderate size.