Abstract
Estimating seed and pollen gene flow in plants on the basis of samples of naturally regenerated seedlings can provide much needed information about “realized gene flow,” but seems to be one of the greatest challenges in plant population biology. Traditional parentage methods, because of their inability to discriminate between male and female parentage of seedlings, unless supported by uniparentally inherited markers, are not capable of precisely describing seed and pollen aspects of gene flow realized in seedlings. Here, we describe a maximum-likelihood method for modeling female and male parentage in a local plant population on the basis of genotypic data from naturally established seedlings and when the location and genotypes of all potential parents within the population are known. The method models female and male reproductive success of individuals as a function of factors likely to influence reproductive success (e.g., distance of seed dispersal, distance between mates, and relative fecundity–i.e., female and male selection gradients). The method is designed to account for levels of seed and pollen gene flow into the local population from unsampled adults; therefore, it is well suited to isolated, but also wide-spread natural populations, where extensive seed and pollen dispersal complicates traditional parentage analyses. Computer simulations were performed to evaluate the utility and robustness of the model and estimation procedure and to assess how the exclusion power of genetic markers (isozymes or microsatellites) affects the accuracy of the parameter estimation. In addition, the method was applied to genotypic data collected in Scots pine (isozymes) and oak (microsatellites) populations to obtain preliminary estimates of long-distance seed and pollen gene flow and the patterns of local seed and pollen dispersal in these species.
ONE of the major challenges in plant population biology is to describe the relationship between population genetic structure and reproductive patterns of a species. This objective has often been addressed through parentage analysis using neutral genetic markers (Devlin and Ellstrand 1990; Meagher 1991), and recent availability of highly variable genetic markers, such as microsatellites, has greatly increased the efficiency of parentage assignment (Dow and Ashley 1996; Streiff et al. 1999; Gonzalez-Martinez et al. 2002). Parentage inference has now advanced to the point where demonstrating variation in reproductive success among adult plants is no longer sufficient by itself. It is more interesting to identify causes of differential male and female reproductive success. In theory, reproductive patterns are best inferred when parents can be unambiguously assigned through parentage analysis. If, however, genetic discrimination is not complete and/or errors occur in parentage assignment, estimates of parameters describing reproductive patterns in a population may be seriously biased (Roeder et al. 1989). Under these conditions, the population-wide parameters describing a reproductive system (e.g., selection gradients, see Morgan and Conner 2001; Burczyk et al. 2002) are best estimated by applying probability models that account for the genetic composition of offspring in actual progeny arrays and inferring the appropriate model parameters. This method has been used effectively to study male mating success (Adams and Birkes 1991; Burczyk et al. 1996, 2002; Smouse et al. 1999; Morgan and Conner 2001) and female reproductive success (Schnabel et al. 1998) in plant populations.
Estimation of reproductive patterns in plants is further complicated because gene flow (i.e., immigration of seed and/or pollen gametes) from uncensored parents residing outside the study population often contributes to offspring (Ennos 1994; Hamrick and Nason 2000; Morgan and Conner 2001). Methods of simultaneously estimating paternity due to pollen gene flow and selection gradients describing differential fertility of males within populations, by applying mating models to the genetic composition of progeny arrays (seeds) sampled from individual mother plants, have been described and illustrated (Adams and Birkes 1991; Burczyk et al. 1996, 2002; see also Smouse et al. 1999; Morgan and Conner 2001; Wright and Meagher 2004). These procedures can be used only to estimate male components of reproduction at the seed stage and when seeds are sampled from individual, known mother plants. Similar methods, however, can be applied to describe gene flow by seeds and female selection gradients (or effective seed dispersal) within populations (Adams 1992; Dow and Ashley 1996; Schnabel et al. 1998; Godoy and Jordano 2001; Gonzalez-Martinez et al. 2002).
It might be expected that realized gene flow by pollen or seeds (Meagher and Thompson 1987) and selection gradients (female or male fertility) observed in naturally regenerated seedlings may differ substantially from these parameters measured at the seed stage (Dyer and Sork 2001). Several factors such as seed dispersal mechanisms, seed predation, and selection during germination and establishment may influence the genetic composition of naturally regenerated seedlings. For example, if immigrating pollen comes from populations adapted to substantially different environmental conditions, the resulting offspring may not be as fit as offspring derived from local matings. Therefore, revealing patterns and determinants of gene dispersal and reproductive success is fundamental to understanding the genetic aspects of natural regeneration in plant populations (Meagher and Thompson 1987). However, because of the high amount of genetic exclusion power required (Marshall et al. 1998), there have been only a few attempts to study parentage of naturally established seedlings (Meagher and Thompson 1987; Dow and Ashley 1996; Schnabel et al. 1998; Konuma et al. 2000; Kameyama et al. 2001; Gonzalez-Martinez et al. 2002; Isagi and Kanazashi 2002; Jones 2003; Shimatani 2004). Nevertheless, these studies were unable to describe fully the reproductive patterns that led to the establishment of the seedling populations.
In this article we present the seedling neighborhood model (Burczyk et al. 2004), a novel probability model that makes it possible to describe various reproductive factors (i.e., gene flow and selection gradients) influencing the genetic composition and genealogy of naturally regenerating seedling cohorts. We investigate the statistical properties of the model through simulations, focusing on statistical resolution provided by sets of genetic loci of different exclusion probabilities. Finally, we apply the model to preliminary data sets from Scots pine (Pinus sylvestris L.) and oak (Quercus sp.) populations. We also discuss potential applications of the model for investigating reproductive patterns in plant populations.
METHODS
Seedling neighborhood model:
This probability mating model is fashioned after our earlier neighborhood models developed to describe pollen gene flow and mating patterns within populations (Adams and Birkes 1989, 1991; Burczyk et al. 2002). It requires the mapped locations of all sampled seedlings and all potential reproductive adult males and females within a local population, the multilocus genotypes of all seedlings and adults, and allele frequencies of the same species in surrounding (background) populations. The model allows for simultaneous estimation of seed and pollen immigration levels, along with female and male reproductive success parameters (i.e., relative fertilities and seed and pollen dispersal). For bisexual plants it also accounts for the proportion of selfing among the fraction of seedlings originating from local mothers. We assume in this article that parentage of seedlings is of primary interest, but the procedure applies equally well to seeds (embryos) sampled on the ground or in seed traps.
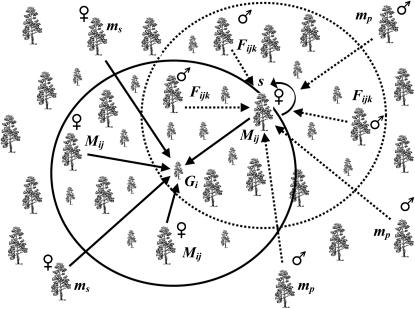
The general idea of the model is outlined in Figure 1. The model assumes that a seedling is mothered either (i) by an unknown female located outside an arbitrarily defined circular area around the seedling (i.e., the seedling's neighborhood, hence the name of the model) due to seed immigration (with probability ms) or (ii) by a specific local female growing within the seedling's neighborhood (with probability 1 − ms). For each seedling with a local mother it is assumed that the paternal gamete came from one of three sources: (i) self-fertilization (with probability s), (ii) migrant pollen from outside of the mother's neighborhood (with probability mp), or (iii) outcrossing with males located within the mother's neighborhood (with probability 1 − s − mp), much like earlier neighborhood models for pollen dispersal (Adams and Birkes 1991; Burczyk et al. 2002). Note that the mother's neighborhood is a circular area surrounding the mother that has the same radius as the seedling neighborhood. The probability of observing the ith seedling having a multilocus diploid genotype Gi, therefore, is
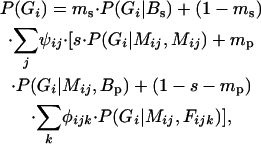 |
(1) |
where Mij and Fijk are the genotypes of the jth mother in the ith seedling neighborhood and of the kth father in the ijth mother neighborhood, respectively. P(Gi | Mij, Mij), P(Gi | Mij, Bp), and P(Gi | Mij, Fijk) are the genetic segregation (or transition) probabilities (Devlin et al. 1988), i.e., the probabilities that the ith seedling has diploid genotype Gi when a mother plant of genotype Mij is, respectively, self-pollinated, pollinated by a distant unknown background male, or pollinated by a neighboring plant having genotype Fijk. P(Gi | Bs) is the transition probability that a seedling immigrating from mothers located outside of a seedling's neighborhood has genotype Gi. Parameter ψij is the relative reproductive success of the jth female in the neighborhood of the ith seedling, and φijk is the relative reproductive success of the kth male within the neighborhood of the ijth female. In species not capable of self-fertilization s = 0, and the terms in the model are simplified.
Figure 1.
The seedling neighborhood model ascribes female and male parentage of a sampled seedling as follows. The mother of the ith seedling comes from an unknown female outside the seedling's neighborhood (circle with solid line) (probability ms) or is a specific (jth) female (i.e., Mij) within the neighborhood [probability (1 − ms)ψij]. If the mother is the jth female within the seedling's neighborhood, the male parent comes from one of three sources: by selfing (if bisexual), with probability s; from an unknown male outside the mother's neighborhood (circle with dashed line) (i.e., background pollen), with probability mp; or by outcrossing to a specific (kth) male (i.e., Fijk) within the mother's neighborhood, with probability (1 − s − mp)φijk. Both seedling and mother neighborhoods have the same radius.
Relative female reproductive success is expressed as
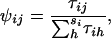 |
(2) |
where τij is a function of one or more factors influencing the reproductive success of the jth female in the ith seedlings neighborhood, and the denominator is the sum over all (si) potential females in that neighborhood (so that 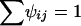 ). Similarly, male reproductive success is
). Similarly, male reproductive success is
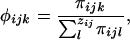 |
(3) |
where πijk is a function of factors influencing the reproductive success of the kth male in the neighborhood of the jth female located within the ith seedlings neighborhood, and zij is the total number of potential fathers in the ijth female's neighborhood.
Although one may use various types of functions for τij and πijk to relate female and male reproductive success to factors influencing reproductive success, here we use an exponential function [τij = exp(ωij); πijk = exp(vijk)] because this assures positivity of the reproductive success parameters ψij and φijk, which can be regarded as relative proportions. Positivity is maintained for any expression for ωij and vijk accommodating various factors affecting reproductive success (Burczyk et al. 1996, 2002; Burczyk and Prat 1997; Bacles et al. 2005). In particular, seed and pollen dispersal can readily be described through exponential distributions. Variation in parental fitness based on relative fecundity surrogates (e.g., number of flowers, plant size) can also be approximated by an exponential distribution (Smouse et al. 1999; Morgan and Conner 2001). For example, if ωij includes two factors, such as the distance of a seedling from potential mothers within its neighborhood and relative size (e.g., height) of the mothers, then we can let ωij = γ1dij + γ2fij, where dij is the distance between a seedling and a potential mother and fij is the mother's relative size. If similar factors are considered for male reproductive success then let vijk = β1dijk + β2fijk, where dijk and fijk are the distance between male and female and the male's size, respectively. The parameters γ1, γ2 and β1, β2, in these cases, describe the strength and direction of the effects of their respective factors. These parameters are often referred to as selection and ecological gradients and they represent the slope of regression of individual fertilities on trait values (see Morgan and Conner 2001; Burczyk et al. 2002). The linear functions ωij and vijk can be further extended to include quadratic terms, making it possible to assess the effects of stabilizing or disruptive selection acting on particular traits influencing reproductive success (Morgan and Conner 2001; Wright and Meagher 2004). The unique feature of the seedling neighborhood model is that it can be applied to simultaneously estimating selection gradients of a given phenotypic trait in both male and female parents, making it possible to evaluate the importance of the trait in both male and female reproductive success.
To estimate the model's parameters the model is “fitted” to observed multilocus genotypic data of seedlings and adults using numerical procedures based on maximum-likelihood methods (see Adams 1992; Burczyk et al. 1996, 2002 for explanations). The likelihood function for a sample of n independently selected offspring individuals is
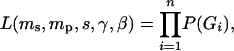 |
(4) |
where γ and β are the vectors of parameters related to female and male reproductive success, respectively. Stated in nontechnical terms, the following can be estimated using these procedures given sufficient data: (1) the proportion of seedlings established from seed by distant (ms) vs. nearby (1 − ms) females; (2) the degree to which various factors such as distance and relative fecundity influence relative reproductive success of females within a local population; (3) the proportion of a mother's offspring within a local population (at the seedling stage) due to self-fertilization (s), pollination by distant males (mp), or pollination by nearby males (1 − mp); and (4) the degree to which various factors such as distance to females and pollen fecundity influence reproductive success of males within local populations.
Simulations:
We wished to explore the efficiency of the model and estimation procedure through computer simulation, which is frequently used to investigate statistical properties of mating models (Marshall et al. 1998; Morgan 1998; Gerber et al. 2000; Morgan and Conner 2001). Each simulation was initiated by generating a bisexual parental population consisting of 200 adults randomly distributed across a square area of 150 × 150 units. Also, the cohort of 500 seedlings was simulated and randomly distributed in the center of the plot across a square area of 30 × 30 units. In this way, drawing a neighborhood of 30 units in radius around seedlings and then the same size neighborhood around potential females resulted in complete neighborhoods located entirely within the generated plot. The average number of adults within a neighborhood of 30 units in radius was ∼25 individuals. Distances between seedlings and potential mothers (dij), as well as distances among adults (dijk, male–female pairs), were calculated and used as factors influencing female and male reproductive successes (γ and β parameters, respectively).
Each parent was assigned a multilocus genotype by randomly sampling alleles from a specified frequency distribution (see below). Alleles were sampled independently within and among loci, so the parental population was in Hardy–Weinberg equilibrium and with linkage equilibrium among loci. The parental generation and the specified frequency distribution were used to generate seedling genotypes. First, the proportion ms of seedlings had their diploid genotypes generated on the basis of the background allelic frequency distribution (same as for adults), which was assumed to represent immigrant seeds from a background source. For each of the remaining seedlings (1 − ms) a female parent was chosen within the seedling neighborhood using a random number generator, with the probability of choosing the jth female given by ψij in Equation 2, and a multilocus egg gamete was determined by randomly sampling alleles from the female parent's genotype. For each seedling whose female parent was within the neighborhood, the source of pollen gamete was determined randomly by the following probabilities: s (self pollen), mp (pollen from the background source), and 1 − s − mp (pollen from a male within the female parent's neighborhood, with the probability of choosing the kth male given by φijk in Equation 3). The pollen haplotype from the specific source was then assigned by randomly sampling alleles from that source, and the genotypes of egg and pollen gametes were combined to form the seedling genotype. The complete set of adult and seedling genotypes was then subjected to the estimation procedure described above.
The potentially large number of parameters and their combinations prevent a comprehensive investigation of statistical properties. For simulations, we used two sets of marker loci varying in their exclusion power. The first set (marker set I) included six loci, each with three alleles at frequencies 0.7, 0.2, and 0.1. This set, with exclusion probability (EP) = 0.8034 (Chakraborty et al. 1988), might be considered typical for isozymes. The second set (marker set II) included six loci with 10 alleles, each with equal frequency (0.1) with EP = 0.9999, resembling a battery of microsatellites.
First we explored the properties of the model and estimation procedure in the simple case where only levels of seed and pollen immigration (ms and mp) were of interest, and there are no selfing (s = 0) or differences in reproductive success (female or male) among parents in the population (i.e., parameters related to female and male reproductive success γ = β = 0). We simulated seedling samples on the basis of true parameter values of seed (ms) and pollen immigration (mp) ranging from 0.2 to 0.8, in various combinations (see Table 1). Second, seedling cohorts were simulated assuming that reproductive success of females and males is a function of seed and pollen dispersal within neighborhoods following an exponential distribution (Table 2). Here, the negative values of γ and β were used to represent the decreasing reproductive success with increasing the dispersal distance. The combination of parameters γ = −0.20, β = −0.10, s = 0.2 was used to represent a case of severely localized seed and pollen dispersal. Here, mean effective numbers of seed and outcross pollen parents (i.e., selfing excluded) within seedling and mother tree neighborhoods were on average Nes = 7.08 and Nep = 15.47, respectively (see Crow and Kimura 1970; Burczyk et al. 2002), as compared to the mean census number of ∼25 individuals. The parameter combination γ = −0.10, β = −0.05, s = 0.1 simulated less restricted seed and pollen dispersal (Nes = 15.40, Nep = 22.03). The seed and pollen immigration levels were set at three categories: (i) ms = mp = 0, fully isolated population with no seed and pollen immigration (i.e., all parents are within neighborhoods); (ii) ms = 0.2 and mp = 0.5, moderate seed and pollen immigration; and (iii) ms = 0.5 and mp = 0.8, extensive seed and pollen immigration. The range of parameter values used for simulations was chosen on the basis of the preliminary analyses of the example data sets (see below).
TABLE 1.
Bias and standard deviations (over 500 replicates, in parentheses) of maximum-likelihood estimates of two immigration parameters (ms and mp) in the seedling neighborhood model obtained from computer-simulated data sets for various combinations of ms and mp and two levels of genetic precision (i.e., where the exclusion probability was either 0.80 or 0.99)
| Parameter values
|
Isozymes EP = 0.80
|
Microsatellites EP = 0.99
|
|||||
|---|---|---|---|---|---|---|---|
| ms | mp | 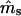 |
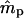 |
fa | 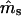 |
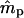 |
fa |
| 0.2 | 0.2 | −0.0031 (0.0681) | −0.0017 (0.1240) | 17 | −0.0002 (0.0183) | −0.0006 (0.0203) | 0 |
| 0.5 | 0.5 | 0.0018 (0.0842) | −0.0282 (0.2036)b | 24 | −0.0002 (0.0232) | 0.0027 (0.0322) | 0 |
| 0.8 | 0.8 | −0.0030 (0.0850) | −0.1439 (0.4553)b | 387 | −0.0003 (0.0195) | −0.0012 (0.0404) | 0 |
| 0.2 | 0.8 | 0.0016 (0.0777) | −0.0089 (0.1062) | 17 | 0.0002 (0.0182) | 0.0004 (0.0200) | 0 |
| 0.3 | 0.7 | 0.0024 (0.0804) | −0.0167 (0.1292)b | 11 | −0.0001 (0.0211) | −0.0003 (0.0246) | 0 |
| 0.4 | 0.6 | 0.0054 (0.0833) | −0.0069 (0.1609) | 15 | 0.0002 (0.0227) | 0.0010 (0.0286) | 0 |
| 0.6 | 0.4 | 0.0021 (0.0847) | −0.0062 (0.2625) | 109 | 0.0000 (0.0229) | −0.0019 (0.0361) | 0 |
| 0.7 | 0.3 | −0.0079 (0.0839)b | 0.0081 (0.3503) | 290 | −0.0002 (0.0217) | 0.0007 (0.0410) | 0 |
| 0.8 | 0.2 | −0.0246 (0.0848)b | 0.0916 (0.5050)b | 615 | −0.0001 (0.0193) | −0.0019 (0.0492) | 1 |
| SE range of simulated bias | 0.0030–0.0038 | 0.0047–0.0226 | 0.0008–0.0010 | 0.0009–0.0022 | |||
ms is the probability that a seedling is the result of seed dispersed from a distant female (outside the neighborhood of the seedling). mp is the probability that a seedling is the result of pollination by a distant male (outside the neighborhood of the female parent). In this case, it was assumed that s = γ = β = 0. See text for details.
Number of times the estimation procedure failed to converge to biologically reasonable estimates of reproductive parameters is shown. Simulations of data sets were continued until 500 gave reasonable estimates.
Bias significant at P < 0.05.
TABLE 2.
Bias and standard deviations (over 500 replicates, in parentheses) of maximum-likelihood estimates of neighborhood model parameters obtained from computer-simulated data sets of various combinations of model parameters and two levels of genetic precision (i.e., where the exclusion probability was either 0.80 or 0.99)
| Parameter values
|
Bias (and SD) of parameter estimates
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ms | mp | s | γ | β | 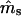 |
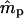 |
ŝ | 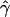 |
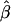 |
fa |
| Isozymes EP = 0.80 | ||||||||||
| 0.0 | 0.0 | 0.1 | −0.1 | −0.05 | — | — | 0.0011 (0.0205) | 0.0001 (0.0105) | −0.0001 (0.0138) | 0 |
| 0.2 | −0.2 | −0.10 | — | — | −0.0012 (0.0240) | −0.0009 (0.0118) | −0.0002 (0.0127) | 0 | ||
| 0.2 | 0.5 | 0.1 | −0.1 | −0.05 | −0.0024 (0.0674) | −0.0087 (0.1082) | −0.0003 (0.0257) | −0.0007 (0.0146) | 0.0027 (0.0387) | 6 |
| 0.2 | −0.2 | −0.10 | −0.0039 (0.0525) | 0.0050 (0.0834) | 0.0026 (0.0308) | −0.0010 (0.0174) | −0.0299 (0.1056)b | 8 | ||
| 0.5 | 0.8 | 0.1 | −0.1 | −0.05 | 0.0058 (0.0809) | −0.0296 (0.1537)b | −0.0013 (0.0377) | −0.0017 (0.0229) | —c | 90 |
| −0.2 | −0.10 | −0.0018 (0.0664) | −0.0081 (0.1199) | −0.0025 (0.0337) | −0.0134 (0.0322)b | —c | 46 | |||
| Microsatellites EP = 0.99 | ||||||||||
| 0.0 | 0.0 | 0.1 | −0.1 | −0.05 | — | — | −0.0008 (0.0133) | 0.0000 (0.0070) | 0.0005 (0.0065) | 0 |
| 0.2 | −0.2 | −0.10 | — | — | −0.0007 (0.0178) | −0.0004 (0.0085) | −0.0004 (0.0071) | 0 | ||
| 0.2 | 0.5 | 0.1 | −0.1 | −0.05 | −0.0001 (0.0183) | −0.0003 (0.0252) | 0.0002 (0.0150) | −0.0002 (0.0074) | 0.0007 (0.0110) | 0 |
| 0.2 | −0.2 | −0.10 | 0.0003 (0.0183) | −0.0007 (0.0251) | −0.0002 (0.0200) | −0.0007 (0.0093) | −0.0003 (0.0129) | 0 | ||
| 0.5 | 0.8 | 0.1 | −0.1 | −0.05 | 0.0003 (0.0232) | −0.0010 (0.0255) | 0.0007 (0.0190) | −0.0002 (0.0092) | −0.0021 (0.0286) | 2 |
| −0.2 | −0.10 | −0.0005 (0.0231) | −0.0004 (0.0255) | 0.0014 (0.0190) | 0.0008 (0.0120) | −0.0023 (0.0297) | 1 | |||
ms is the proportion of seed immigrants. mp is the proportion of pollen immigrants. s is the proportion of self-fertilization. γ and β are parameters of female and male reproductive success, respectively (see text for details).
Number of times the estimation procedure failed to converge to biologically reasonable estimates of reproductive parameters is shown. Simulations of data sets were continued until 500 gave reasonable estimates.
Bias significant at P < 0.05.
The model could not converge with parameter β included in the model.
For each parameter combination 500 simulations were performed. The parameter estimates were obtained numerically on the basis of maximum-likelihood procedures using the Newton–Raphson method (Rao 1973; Kennedy and Gentle 1980). Means and variances of the estimates over the replicated data sets were then compared to the true parameter values.
Example data:
In addition to the simulated data sets, we applied the seedling neighborhood model to actual data obtained from two forest stands: a Scots pine (P. sylvestris L.) stand and a mixed-oak [Quercus robur L./Q. petraea (Matt.) Liebl.] stand. Both are certified seed collection stands located in Poland (Scots pine, Forest District Woziwoda; mixed oaks, Forest District Jamy). In the Scots pine stand, 525 seedlings (5–15 years old) and 313 adults (∼160 years old) were genotyped on the basis of eight allozyme loci (estimated EP = 0.72). In the oak stand, 320 seedlings (1–3 years old) and 450 adults (120 years old) were genotyped on the basis of three microsatellite loci (EP = 0.95). The locations of all seedlings and adults were mapped allowing for a detailed analysis of the effect of seed and pollen dispersal on corresponding male and female reproductive success within each stand. The neighborhood radius around seedlings and putative mothers was set to 40 m in both stands, which included on average 83.8 trees (166/ha) in the Scots pine and 73.9 trees (146.8/ha) in the mixed-oak stands. Such numbers of adults within neighborhoods seemed sufficient for precise estimation of seed and pollen dispersal patterns within neighborhoods (Burczyk et al. 1996). Also, with a 40-m radius, the seedling and subsequent mother neighborhoods were entirely included within the sampled plots of both stands. Reproductive parameters (ms, mp, γ, β, and s) were estimated using the computer program SNM v.1.0, written for this purpose (available from I. J. Chybicki upon request), which employs optimized procedures (Powell's and Newton–Raphson methods) to estimate parameters. The standard deviations of the parameters were derived from the Hessian (variance–covariance) matrix, which is an inherent part of the estimation procedure employed in the SNM program. Additionally, the significance of the parameters γ, β, s was assessed using likelihood-ratio tests (Manly 1992; Morgan and Conner 2001).
RESULTS AND DISCUSSION
Simulations:
Simulations indicated that the seedling model gives reasonably robust estimates of gene flow and reproductive parameters when genetic markers with at least moderately high exclusion probabilities (EP ≥ 0.8) are available (Tables 1 and 2). When individuals within local populations did not differ in female or male reproductive success (s = γ = β = 0), estimates of ms and mp were nearly unbiased; however, the marker set I (isozyme-like) showed high variances of the estimates (Table 1). Notably, while variances of 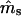 were stable across a range of true ms values, the variances of
were stable across a range of true ms values, the variances of 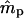 tended to increase with increasing ms. This is because higher ms reduces the number of nonimmigrant seedlings contributing to estimating pollen immigration. The standard deviations of
tended to increase with increasing ms. This is because higher ms reduces the number of nonimmigrant seedlings contributing to estimating pollen immigration. The standard deviations of 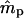 for marker set I appeared to be unacceptably high in most cases, given the sample size used in the simulations (n = 500). However, it is expected that increased sample size will, at least, partly compensate for a lower exclusion probability (Morgan 1998; Morgan and Conner 2001). For marker set II (microsatellite type), the parameter estimates were unbiased and the variances of both
for marker set I appeared to be unacceptably high in most cases, given the sample size used in the simulations (n = 500). However, it is expected that increased sample size will, at least, partly compensate for a lower exclusion probability (Morgan 1998; Morgan and Conner 2001). For marker set II (microsatellite type), the parameter estimates were unbiased and the variances of both 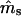 and
and 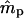 were much lower, although still being larger for
were much lower, although still being larger for 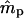 .
.
With some exceptions (marker set I), the seedling model and estimation procedure provided efficient estimates (low bias and variance) in the cases where the simulations assumed reproductive success of individuals within local populations decreased exponentially with distance from the seedling location (females) or mate (males) (Table 2). When we assumed that all seed and pollen parents are local (ms = mp = 0), the variances of 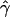 and
and 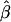 were low and of equivalent magnitude, within a given marker set. However, the variances of both estimates tended to increase with increasing ms and mp. In all cases, mean parameter estimates of both seed and pollen immigration were very close to their true values (i.e., low bias). The means of standard deviations of parameters based on the Hessian matrix for each simulated data set were nearly identical to standard deviations derived from replicate simulations.
were low and of equivalent magnitude, within a given marker set. However, the variances of both estimates tended to increase with increasing ms and mp. In all cases, mean parameter estimates of both seed and pollen immigration were very close to their true values (i.e., low bias). The means of standard deviations of parameters based on the Hessian matrix for each simulated data set were nearly identical to standard deviations derived from replicate simulations.
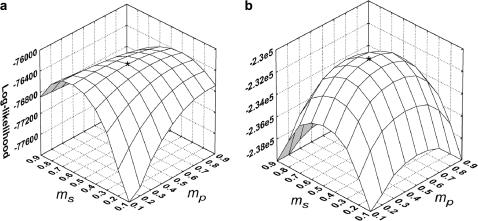
The estimation procedure often failed to converge to reasonable parameter estimates for the simplified data sets with the lower EP, probably due to insufficient genetic resolution. The Newton–Raphson algorithm used in our iterative estimation procedure requires careful choice of initial parameter values for convergence, especially for data sets with less genetic information (Thisted 1988; Morgan and Conner 2001). In our simulations, the parameter values were used as the initial starting points in the iterations. However, the actual parameter values of individual simulated data sets could differ from the expected ms and mp, and if such difference was considerable this led to the lack of convergence, more often for marker set I. We investigated the probability surface (expressed as the log-likelihood) around the true parameter values in the special case where ms = mp = 0.5 and s = γ = β = 0. To obtain smooth graphs, we used a large seedling sample (n = 10,000) (Figure 2). In the case of marker set II (microsatellites), the log-likelihood has a strong peak at the true values of ms and mp (0.50, 0.50). Here, the starting points, if shifted away from the true parameter values, should still converge closely to expected parameter values. However, for marker set I (isozymes), although the peak of the log-likelihood surface corresponds to the expected parameter values, there is a ridge through the maximum along which the gradient is close to zero and the algorithm could stop at any point on this ridge, depending on the convergence criterion. The starting points, if shifted away from the true values, could easily converge to a point on the log-likelihood surface that is not the peak (i.e., where 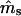 and/or
and/or 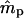 are not close to their true values), especially for small data sets with less genetic information. Note that the slope of the log-likelihood surface is steeper along the ms axis than along mp (Figure 2). The distribution of the log-likelihood around the true parameter values along the ms and mp axes supports our earlier observations, that the variances of
are not close to their true values), especially for small data sets with less genetic information. Note that the slope of the log-likelihood surface is steeper along the ms axis than along mp (Figure 2). The distribution of the log-likelihood around the true parameter values along the ms and mp axes supports our earlier observations, that the variances of 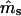 are smaller than those of
are smaller than those of 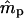 and that these variances are smaller for the microsatellite- than for the isozyme-type genetic markers.
and that these variances are smaller for the microsatellite- than for the isozyme-type genetic markers.
Figure 2.
The approximated log-likelihood surface obtained for a simulated data set based on a large seedling sample (n = 10,000) when the true parameter values for seed (ms) and pollen (mp) immigration are ms = mp = 0.5: (a) low exclusion power genetic markers (EP = 0.80); (b) high exclusion power genetic markers (EP = 0.99).
Empirical seed and pollen gene flow estimates:
The level of seed immigration in the Scots pine population appears considerable; it is estimated that nearly 45% of seedlings resulted from seed flow over distances >40 m (Table 3). In addition, it is estimated that 92% of the seedlings with local mothers resulted from pollination by distant (>40 m) males. These results suggest that only a small percentage (0.55 · (1 − 0.92) · 100 = 4.4%) of the seedlings in this population have both parents that are local. Although 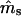 and
and 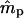 are quite different from zero, their estimated variances are considerable, as are the variances of
are quite different from zero, their estimated variances are considerable, as are the variances of 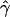 and ŝ. The pollen dispersal parameter, β, could not be estimated, probably due to low frequency of local pollination events (4.4%). Despite the large number of seedlings sampled (525), the precision of these data was greatly compressed by the low exclusion power (EP = 0.72) of the isozyme data set. Nevertheless, the high observed levels of pollen and seed gene flow are not surprising for Scots pine. This species is well known for extensive seed and pollen dispersal. Its pollen sedimentation velocity is among the lowest in conifers and the species has the greatest capability to disperse seeds among temperate forest trees (Geburek 2005). Independent estimates of seed and pollen gene flow obtained in the same population on the basis of seed samples collected in seed traps and directly from mother trees are quite comparable to the results reported above (A. Dzialuk and J. Burczyk, unpublished results).
and ŝ. The pollen dispersal parameter, β, could not be estimated, probably due to low frequency of local pollination events (4.4%). Despite the large number of seedlings sampled (525), the precision of these data was greatly compressed by the low exclusion power (EP = 0.72) of the isozyme data set. Nevertheless, the high observed levels of pollen and seed gene flow are not surprising for Scots pine. This species is well known for extensive seed and pollen dispersal. Its pollen sedimentation velocity is among the lowest in conifers and the species has the greatest capability to disperse seeds among temperate forest trees (Geburek 2005). Independent estimates of seed and pollen gene flow obtained in the same population on the basis of seed samples collected in seed traps and directly from mother trees are quite comparable to the results reported above (A. Dzialuk and J. Burczyk, unpublished results).
TABLE 3.
Estimates of reproductive parameters (SE in parentheses) for a Scots pine (Pinus sylvestris) stand and a mixed-oak (Quercus sp.) stand obtained by applying the seedling neighborhood model and maximum-likelihood estimation procedure to samples of naturally established seedlings
| Reproductive parameter | Pinus sylvestris | Quercus sp. |
|---|---|---|
Seed immigration (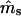 ) ) |
0.4464 (0.1543) | 0.0630 (0.0251) |
Pollen immigration ( ) ) |
0.9225 (0.3936) | 0.6236 (0.0483) |
Seed dispersal effect (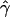 ) ) |
−0.0376 (0.0259) | −0.2027 (0.0124) |
Pollen dispersal effect (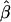 ) ) |
—a | −0.0908 (0.0177) |
| Selfing (ŝ) | 0.0571 (0.0454) | 0.0120 (0.0126) |
| Seedling sample size | 524 | 312 |
| Genetic marker (exclusion probability) | Isozymes (EP = 0.72) | Microsatellites (EP = 0.92) |
Parameter not included in the model.
In the case of the oak stand, we were able to estimate all intended reproductive parameters, but the patterns of gene flow were much different from those estimated for Scots pine. Only ∼6% of seedlings originated from mother trees located >40 m from seedlings (Table 3). Also, seed dispersal within the local population was very limited (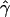 = −0.2027), which means that the majority of seedlings originated from nearby mother trees. On the other hand, pollen gene flow was extensive, as ∼62% of pollen gametes fertilizing local mother trees came from unsampled males situated outside the mothers' neighborhoods. This suggests that a considerable percentage (0.94 · (1 − 0.62) · 100 = 35.7%) of the seedlings in this population have both parents that are local. In addition, while pollen dispersal within neighborhoods followed a negative exponential distribution, it was less restrictive (
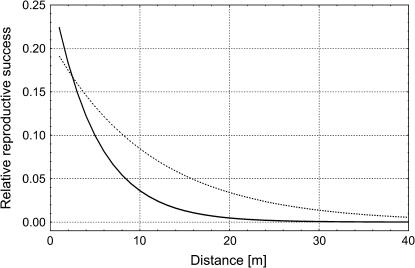
= −0.2027), which means that the majority of seedlings originated from nearby mother trees. On the other hand, pollen gene flow was extensive, as ∼62% of pollen gametes fertilizing local mother trees came from unsampled males situated outside the mothers' neighborhoods. This suggests that a considerable percentage (0.94 · (1 − 0.62) · 100 = 35.7%) of the seedlings in this population have both parents that are local. In addition, while pollen dispersal within neighborhoods followed a negative exponential distribution, it was less restrictive (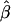 = −0.0908) than seed dispersal (Figure 3). Variances of parameter estimates were low, indicating high precision of the estimation procedure. This was possible because the applied set of microsatellites had relatively high exclusion power (EP = 0.92). The limited seed but extensive pollen dispersal in oaks is consistent with observations in several earlier studies (Dow and Ashley 1996; Streiff et al. 1999).
= −0.0908) than seed dispersal (Figure 3). Variances of parameter estimates were low, indicating high precision of the estimation procedure. This was possible because the applied set of microsatellites had relatively high exclusion power (EP = 0.92). The limited seed but extensive pollen dispersal in oaks is consistent with observations in several earlier studies (Dow and Ashley 1996; Streiff et al. 1999).
Figure 3.
Estimated relationships between relative reproductive success of females and their distance to seedlings (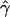 , solid line) and between relative reproductive success of males and their distance to females (
, solid line) and between relative reproductive success of males and their distance to females (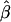 , dotted line) within a local stand (i.e., within neighborhoods) of Quercus petraea/Q. robur in Poland. See text for details.
, dotted line) within a local stand (i.e., within neighborhoods) of Quercus petraea/Q. robur in Poland. See text for details.
Conclusions:
The particular problem in parentage assignment for naturally regenerated seedlings is that it is possible to assign only a fraction of the seedlings to unique potential parental pairs (Meagher and Thompson 1987; Chakraborty et al. 1988). This difficulty is due to insufficient exclusion power of genetic markers and/or parentage with unknown (not genotyped) female and/or male parents (seed and pollen immigration). The two-parent problem, i.e., the problem of determining which of the two identified parents is mother and which is father, also complicates parentage analyses, especially in monoecious species (Meagher and Thompson 1986). The seedling neighborhood model described in this article attempts to overcome these difficulties. The seedling neighborhood model does not assign parentage for offspring but rather models the genealogy of seedlings by reconstructing the two-stage movement of genes through pollen and seeds.
In our description of the model, we defined 1 − ms as the proportion of seedlings whose mothers are within the seedling's neighborhood. In practice, however, one cannot distinguish between the genotypes of male and female parents of a seedling (two-parent problem; Meagher and Thompson 1986). It may happen that in real situations the actual mother of a given seedling could be located outside its neighborhood while the father is located within the immediate neighborhood of the seedling. This may lead to underestimation of seed movement and at the same time to overestimation of pollen movement. Nevertheless, if for a given species seed dispersal is more restricted than pollen dispersal, which is typical in plants (Ennos 1994; Hamrick and Nason 2000), the populationwide ms estimates should approximate the actual proportion of seed immigration.
In this article, we assumed that background allele frequencies are the same for seed and pollen immigration. However, despite little spatial variation in the genetic structure in several natural populations, different modes of seed and pollen dispersal may cause allele frequencies to differ for immigrating seed and pollen pools. Nevertheless, sensitivity of the model to biased background allelic frequencies used in the estimation procedure (Burczyk and Chybicki 2004) decreases with increased exclusion probabilities of the markers. We also assumed that there are no mutations or genotyping errors. However, it might be expected that especially genotyping errors may considerably affect the estimates of seed or pollen immigration (Marshall et al. 1998; Burczyk et al. 2004; Slavov et al. 2005). We will address this issue in a future work.
In our simulations and data examples we did not estimate selection gradients (sensu Morgan and Conner 2001). However, the seedling model can easily accommodate additional parameters that would relate individual reproductive success to individual features, such as plant size, flower fecundity, phenology, or floral characteristics (Burczyk and Prat 1997; Smouse et al. 1999; Wright and Meagher 2004). In addition, application of the seedling model makes it possible to assess how these traits affect female vs. male reproductive success. Another unique feature of the model is that it is possible to estimate rates of selfing at the seedling stage, which may provide new insights into mechanisms determining inbreeding levels in naturally regenerated populations. We believe that applications of this approach will lead to enhanced recognition of the interactions among genetics, ecology, and demography at the population level. Such information is of primary interest in genetic conservation programs, where natural regeneration is the major mode of reproduction.
Acknowledgments
We thank Artur Dzialuk and Magdalena Trojankiewicz for assistance in collecting genotypic data of Scots pine and oak populations. This work was partly supported by research grants from Polish Committee for Scientific Research: 5P06H 042 15 and 3P06L 034 23.
References
- Adams, W. T., 1992. Gene dispersal within forest tree populations. New For. 6: 217–240. [Google Scholar]
- Adams, W. T., and D. S. Birkes, 1989. Mating patterns in seed orchards, pp. 75–86 in Proceedings of the 20th Southern Forest Tree Improvement Conference. Southern Forest Tree Improvement Committee, Charleston, SC.
- Adams, W. T., and D. S. Birkes, 1991. Estimating mating patterns in forest tree populations, pp. 157–172 in Biochemical Markers in the Population Genetics of Forest Trees, edited by S. Fineschi, M. E. Malvolti, F. Cannata and H. H. Hattemer. SPB Academic Publishing, The Hague, The Netherlands.
- Bacles, C. F. E., J. Burczyk, A. J. Lowe and R. A. Ennos, 2005. Historical and contemporary mating patterns in remnant populations of the forest tree Fraxinus excelsior L. Evolution 59: 979–990. [PubMed] [Google Scholar]
- Burczyk, J., and I. J. Chybicki, 2004. Cautions on direct gene flow estimation in plant populations. Evolution 58: 956–963. [DOI] [PubMed] [Google Scholar]
- Burczyk, J., and D. Prat, 1997. Male reproductive success in Pseudotsuga menziesii (Mirb.) Franco: the effect of spatial structure and flowering characteristics. Heredity 79: 638–647. [Google Scholar]
- Burczyk, J., W. T. Adams and J. Y. Shimizu, 1996. Mating patterns and pollen dispersal in a natural knobcone pine (Pinus attenuata Lemmon) stand. Heredity 77: 251–260. [Google Scholar]
- Burczyk, J., W. T. Adams, G. F. Moran and A. R. Griffin, 2002. Complex patterns of mating revealed in a Eucalyptus regnans seed orchard using allozyme markers and the neighborhood model. Mol. Ecol. 11: 2379–2391. [DOI] [PubMed] [Google Scholar]
- Burczyk, J., S. P. DiFazio and W. T. Adams, 2004. Gene flow in forest trees: How far do genes really travel? For. Genet. 11: 179–192. [Google Scholar]
- Chakraborty, R., T. R. Meagher and P. E. Smouse, 1988. Parentage analysis with genetic markers in natural populations. I. The expected proportion of offspring with unambiguous paternity. Genetics 118: 527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, J. F., and M. Kimura, 1970. An Introduction to Population Genetics Theory. Harper & Row, New York.
- Devlin, B., and N. C. Ellstrand, 1990. The development and application of a refined method for estimating gene flow from angiosperm paternity analysis. Evolution 44: 248–259. [DOI] [PubMed] [Google Scholar]
- Devlin, B., K. Roeder and N. C. Ellstrand, 1988. Fractional paternity assignment: theoretical development and comparison to other methods. Theor. Appl. Genet. 76: 369–380. [DOI] [PubMed] [Google Scholar]
- Dow, B. D., and M. V. Ashley, 1996. Microsatellite analysis of seed dispersal and parentage of saplings in bur oak, Quercus macrocarpa. Mol. Ecol. 5: 120–130. [Google Scholar]
- Dyer, R. J., and V. L. Sork, 2001. Pollen pool heterogeneity in shortleaf pine, Pinus echinata Mill. Mol. Ecol. 10: 859–866. [DOI] [PubMed] [Google Scholar]
- Ennos, R. A., 1994. Estimating the relative rates of pollen and seed migration among plant populations. Heredity 72: 250–259. [Google Scholar]
- Geburek, Th., 2005. Sexual reproduction in forest trees, pp. 171–198 in Conservation and Management of Forest Genetic Resources in Europe, edited by Th. Geburek and J. Turok. Arbora Publishers, Zvolen, Slovakia.
- Gerber, S., S. Mariette, R. Streiff, C. Bodenes and A. Kremer, 2000. Comparison of microsatellites and amplified fragment length polymorphism markers for parentage analysis. Mol. Ecol. 9: 1037–1048. [DOI] [PubMed] [Google Scholar]
- Godoy, J. A., and P. Jordano, 2001. Seed dispersal: exact identification of source trees with endocarp DNA microsatellites. Mol. Ecol. 10: 2275–2283. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Martinez, S. C., S. Gerber, M. T. Cervera, J. M. Martinez-Zapater, L. Gil et al., 2002. Seed gene flow and fine-scale structure in a Mediterranean pine (Pinus pinaster Ait.) using nuclear microsatellite markers. Theor. Appl. Genet. 104: 1290–1297. [DOI] [PubMed] [Google Scholar]
- Hamrick, J. L., and J. D. Nason, 2000. Gene flow in forest trees, pp. 81–90 in Forest Conservation Genetics: Principles and Practice, edited by A. Young, D. Boshier and T. Boyle. CSIRO Publishing, Collingwood, Australia.
- Isagi, Y., and T. Kanazashi, 2002. Gene flow analysis in Magnolia obovata Thunb. using highly variable microsatellite markers, pp. 257–269 in Diversity and Interaction in a Temperate Forest Community: Ogawa Forest Reserve of Japan, edited by N. Matsumoto. Springer-Verlag, Tokyo.
- Jones, B., 2003. Maximum likelihood inference for seed and pollen dispersal distributions. J. Agric. Biol. Environ. Stat. 8(2): 170–183. [Google Scholar]
- Kameyama, Y., Y. Isagi and N. Nakagoshi, 2001. Patterns and levels of gene flow in Rhododendron metternichii var. hondoense revealed by microsatellite analysis. Mol. Ecol. 10: 205–216. [DOI] [PubMed] [Google Scholar]
- Kennedy, Jr., W. J., and J. E. Gentle, 1980. Statistical Computing. Marcel Dekker, New York.
- Konuma, A., Y. Tsumura, C. T. Lee, S. L. Lee and T. Okuda, 2000. Estimation of gene flow in the tropical-rainforest tree Neobalanocarpus heimii (Dipterocarpaceae), inferred from paternity analysis. Mol. Ecol. 9: 1843–1852. [DOI] [PubMed] [Google Scholar]
- Manly, B. F. J., 1992. The Design and Analysis of Research Studies. Cambridge University Press, Cambridge, UK.
- Marshall, T. C., J. Slate, L. E. Kruuk and J. M. Pemberton, 1998. Statistical confidence for likelihood-based paternity inference in natural populations. Mol. Ecol. 7: 639–655. [DOI] [PubMed] [Google Scholar]
- Meagher, T. R., 1991. Analysis of paternity within a natural population of Chamaelirium luteum. II. Patterns of male reproductive success. Am. Nat. 137: 738–752. [Google Scholar]
- Meagher, T. R., and E. Thompson, 1986. The relationship between single parent and parent pair genetic likelihoods in genealogy reconstruction. Theor. Popul. Biol. 29: 87–106. [Google Scholar]
- Meagher, T. R., and E. Thompson, 1987. Analysis of parentage for naturally established seedlings of Chamaelirium luteum (Liliaceae). Ecology 68: 803–812. [Google Scholar]
- Morgan, M. T., 1998. Properties of maximum likelihood male fertility estimation in plant populations. Genetics 149: 1099–1103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan, M. T., and J. K. Conner, 2001. Using genetic markers to directly estimate male selection gradients. Evolution 55: 272–281. [DOI] [PubMed] [Google Scholar]
- Rao, C. R., 1973. Linear Statistical Inference and Its Applications, Ed. 2. Wiley & Sons, New York.
- Roeder, K., B. Devlin and B. G. Lindsay, 1989. Application of maximum likelihood methods to population genetic data for the estimation of individual fertilities. Biometrics 45: 363–379. [Google Scholar]
- Schnabel, A., J. D. Nason and J. L. Hamrick, 1998. Understanding the population genetic structure of Gleditsia triacanthos L.: seed dispersal and variation in female reproductive success. Mol. Ecol. 7: 819–832. [Google Scholar]
- Shimatani, K., 2004. Spatial molecular ecological models for genotyped adults and offspring. Ecol. Model. 174: 401–410. [Google Scholar]
- Slavov, G. T., G. T. Howe, D. S. Birkes, A. V. Gyaourova and W. T. Adams, 2005. Estimating pollen flow using SSR markers and paternity exclusion: accounting for mistyping. Mol. Ecol. 14: 3109–3121. [DOI] [PubMed] [Google Scholar]
- Smouse, P. E., T. Meagher and C. Kobak, 1999. Parentage analysis in Chamaelirium luteum (L.) Gray (Liliaceae): Why do some males have higher reproductive contributions? J. Evol. Biol. 12: 1069–1077. [Google Scholar]
- Streiff, R., A. Ducousso, C. Lexer, H. Steinkellner, J. Gloessl et al., 1999. Pollen dispersal inferred from paternity analysis in a mixed oak stand of Quercus robur L. and Q. petraea (Matt.). Liebl. Mol. Ecol. 8: 831–841. [Google Scholar]
- Thisted, R. A., 1988. Elements of Statistical Computing. Chapman & Hall, New York.
- Wright, J. W., and T. R. Meagher, 2004. Selection on floral characters in natural Spanish populations of Silene latifolia. J. Evol. Biol. 17: 382–395. [DOI] [PubMed] [Google Scholar]