Detection of temporal changes in the spatial distribution of cancer rates using local Moran's I and geostatistically simulated spatial neutral models

Abstract

This paper presents the first application of spatially correlated neutral models to the detection of changes in mortality rates across space and time using the local Moran's I statistic. Sequential Gaussian simulation is used to generate realizations of the spatial distribution of mortality rates under increasingly stringent conditions: 1) reproduction of the sample histogram, 2) reproduction of the pattern of spatial autocorrelation modeled from the data, 3) incorporation of regional background obtained by geostatistical smoothing of observed mortality rates, and 4) incorporation of smooth regional background observed at a prior time interval. The simulated neutral models are then processed using two new spatio-temporal variants of the Morany's I statistic, which allow one to identify significant changes in mortality rates above and beyond past spatial patterns. Last, the results are displayed using an original classification of clusters/outliers tailored to the space-time nature of the data. Using this new methodology the space-time distribution of cervix cancer mortality rates recorded over all US State Economic Areas (SEA) is explored for 9 time periods of 5 years each. Incorporation of spatial autocorrelation leads to fewer significant SEA units than obtained under the traditional assumption of spatial independence, confirming earlier claims that Type I errors may increase when tests using the assumption of independence are applied to spatially correlated data. Integration of regional background into the neutral models yields substantially different spatial clusters and outliers, highlighting local patterns which were blurred when local Moran's I was applied under the null hypothesis of constant risk.

1 Introduction

Cancer mortality maps are important tools in health research, allowing the identification of spatial patterns, clusters and disease ‘hot spots’ that often stimulate research to elucidate causative relationships (Jacquez 1998; Rushton et al. 2000). Analysis of mortality maps for a series of time intervals also contributes to a better understanding of temporal trends and can help pinpoint locations where health policy needs to be changed. For example, comparison of maps of mortality rates of cervix cancer from 1950 through 1990 highlighted states that did not follow the national decline because poverty reduced access to health care and to early detection through the Pap smear test in particular (Friedell et al. 1992).

The analysis of spatial patterns and their change in time requires the combination of easy-to-use interactive visualization tools (e.g. see Greiling, this issue) and powerful statistics that can be tailored to the data under analysis and the hypotheses to be tested. In most spatial analysis software a statistical pattern recognition approach has been implemented whereby a statistic (e.g. spatial cluster statistic, autocorrelation statistic) quantifying a relevant aspect of spatial pattern is first calculated. The value of this statistic is then compared to the distribution of that statistic's value under a null spatial model. This provides a probabilistic assessment of how unlikely an observed spatial pattern is under the null hypothesis (Gustafson 1998). Waller and Jacquez (1995) formalized this approach by identifying five components of a test for spatial pattern.

1. The test statistic quantifies a relevant aspect of spatial pattern (e.g. Moran's I, Geary's c, a spatial clustering metric)

2. The alternative hypothesis describes the spatial pattern that the test is designed to detect. This may be a specific alternative, such as clustering near a focus, or it may be the omnibus “not the null hypothesis”.

3. The null hypothesis describes the spatial pattern expected when the alternative hypothesis is false (e.g. complete spatial randomness which corresponds to the absence of clustering in spatial point processes).

4. The null spatial model is a mechanism for generating the reference distribution. This may be based on distribution theory, or it may use randomization (e.g. Monte Carlo) techniques.

5. The reference distribution is the distribution of the test statistic when the null hypothesis is true.

A key step in hypothesis testing is the formulation of the null and alternative hypotheses; see the discussion for case-control point data and regional count data in the recent book by Waller and Gotway (2004). Each null hypothesis corresponds to a particular conceptual model, leading to a specific question being addressed so that different answers are likely depending on the specifics of the null hypothesis. The term “Neutral Model” captures the notion of a plausible system state that can be used as a reasonable null hypothesis (e.g. “background variation”). The problem then is to identify spatial patterns above and beyond that incorporated into the neutral model, enabling, for example, the identification of “hot spots” beyond background variation in a pollutant, or the detection of local spikes in cancer rates beyond broader scale variation in the risk of developing cancer. For situations where health professionals are mostly interested in identifying areas with generally high (or low) disease rates, the focus would be on the detection of cancer clusters above and beyond a null hypothesis of constant risk.

As a rule of thumb one should employ that neutral model or those neutral models that most closely correspond to the spatial pattern expected in the absence of the alternative spatial process. So, for a cluster study one would select those neutral models that specify the risk function deemed most likely in the absence of spatial clustering. Yet, in its most common software implementation the local Moran's I statistic for detection of clusters from aggregate data (Anselin 1995) is based on the “normality” and “randomization” null hypotheses (Waller and Gotway 2004). Under the normality hypothesis all observations follow independent, identically distributed normal distributions. Under the randomization hypothesis, each permutation of the observed values is equally likely. These translate into a null hypothesis of spatial independence of observed rates and, provided the population sizes of areal units (e.g. SEA units) are fairly homogeneous, the assumption of constant or spatially uniform risk. In other words, the neutral model is obtained by a randomization or random shuffling of observed rates, thereby disregarding the spatial pattern of the data and the population size associated with each areal unit which controls the reliability of the measured rates. If ignored, large differences in population size decrease the ability of Moran's I to detect true clustering. Also, as emphasized by Ord and Getis (2001), Type I errors may increase when tests of hypothesis using the randomization assumption are applied to spatially correlated data, leading us to reject the null hypothesis of no clustering more often than we should.

Several modifications of the local Moran's I test of hypothesis have been proposed to take into account heterogeneous population sizes, spatial autocorrelation, and non-uniform risks. For example, Oden (1995), Waldhör (1996), as well as Assunçao and Reis (1992) developed a modified version of the test statistic to account for heterogeneous population sizes in cluster detection. An alternative is to randomly shuffle the counts rather than the rates (i.e. under a heterogeneous Poisson model the cases are allocated to each area using hypergeometric sampling; see Besag and Newell, 1991). A third option is to transform or standardize the rates prior to the application of the test, thereby removing much of the noise due to the small population size; for example, see filters developed by Marshall (1991), Mungiole et al. (1999), and Goovaerts and Jacquez (2004). To account for the fact that observed rates are usually correlated in space, Ord and Getis (2001) introduced a test statistic that detects local hot spots even when global spatial autocorrelation is present, reducing the potential for over-identification of these hot spots. Spatial trends in the observed rates, which might reflect a non-uniform risk, can be incorporated using a reference distribution for the test statistic that is conditional on a known or estimated background spatial trend; see Ord and Getis (1995) and Tiefelsdorf (1998) for further discussion on the conditional distributions of local Moran's I. A non-parametric approach consists of computing the local Moran's I from residuals of a spatial regression model, allowing one to test for clustering of deviations from local expectations based on some model of disease incidence (Cliff and Ord 1981; Tiefelsdorf 2000). A similar approach was adopted by Goovaerts et al. (2003) to identify patches of disturbed soils in hyperspectral imagery; geostatistical filtering was first used to remove regional background and enhance the local signal (i.e. residuals) which was then analyzed for spatial outliers using local Moran's I.

This paper introduces a new approach whereby the spatial or temporal features that the researcher wants to incorporate in the formulation of the null hypothesis are directly accounted for in the generation of neutral models. The key idea is to generate the multiple realizations of the neutral model using simulation techniques developed in the field of geostatistics (Goovaerts 1997) which provides a set of statistical tools for analyzing and mapping data distributed in space and time. In particular, sequential Gaussian simulation (SGS) allows one to generate realizations of the spatial distribution of rates that reproduce the sample histogram and spatial patterns displayed by the data, and also account for any auxiliary data or information on the local trend. Noise caused by small population sizes can be filtered prior to the analysis using geostatistical filtering techniques that account for the pattern of spatial correlation and population sizes (Goovaerts et al. 2005; Goovaerts 2005a).

The objective of this paper is to present a geostatistical approach to generate realistic neutral models and use them for the detection of local clusters and anomalies in cancer mortality rates. Building on the typology recently proposed by Goovaerts and Jacquez (2004), the technique is first introduced within a pure spatial framework that aims to analyze data collected over a single time period. Then, regional background observed at earlier times is incorporated into the neutral model, allowing one to test change in cancer rates above and beyond that observed in the past. The new methodology is illustrated using the space-time distribution of cervix cancer mortality rates recorded over all US State Economic Areas (SEA) with a 5 year resolution. It is worth mentioning that this paper does not pretend to conduct a thorough analysis and interpretation of the space-time pattern of cervix cancer from aggregate data (ecological fallacy), but references to results of prior studies will be made in order to showcase some of the features of the proposed methodology. A simulation-based comparison of the geostatistical approach to the wide range of aforementioned modifications of the local Moran's I, although desirable, is beyond the scope of this paper which reports preliminary results of a recently awarded research project.

2 Methods

2.1 LISA statistic under spatial independence (Model I)

Consider the problem of detecting significant clustering and spatial outliers in the map of cervix cancer mortality rates displayed in Fig. 1 (top graph). For this example, age adjusted mortality rates have been recorded for white females over the period t = 1955–1959 at the aggregation level of State Economic Areas (SEA). Following other studies (e.g. Jacquez and Greiling 2003a, b) these features can be identified using Anselin's (1995) local Moran test implemented in the Cancer Atlas Viewer (Greiling, this issue). The detection approach is based on the so-called LISA¹ (Local Indicator of Spatial Autocorrelation) statistic, which is computed for each SEA unit referenced geographically by its centroid with the vector of spatial coordinates u = (x, y), as:

$$\text{LISA}(\mathbf{u};t)=\left[\frac{z(\mathbf{u};t)-m_t}{s_t}\right]\times \left(\sum _{j=1}^J\frac{1}{J}\times \left[\frac{z({\mathbf{u}}_j;t)-m_t}{s_t}\right]\right)$$ (1)

where z(u; t) is the mortality rate for the SEA unit being tested, which is referred to as the “kernel” hereafter. z(u_j; t) are the values for the J neighboring SEA units that are here defined as units sharing a common border or vertex with the kernel u (1-st order queen adjacencies). All values are standardized using the mean m_t and standard deviation s_t of the N = 506 SEA units at time t. Since the standardized values have zero mean, the LISA statistic takes negative values if the kernel value is much lower or much higher than the surrounding values (i.e. SEA cancer incidence is below the global zero mean while the neighborhood average is above the global zero mean, or conversely), which indicates negative local autocorrelation and the presence of spatial outliers. Clusters of low or high values, which correspond to the presence of positive local autocorrelation, will lead to positive values of the LISA statistic (i.e. both kernel and neighborhood averages are jointly above zero or below zero).

Fig. 1.

Map of cervix cancer mortality (rates per 100,000) for the period 1955–1959 (categories correspond to deciles of the histogram of rates). Bottom graphs show results of local cluster analysis under neutral model I (spatial independence): p-values and the corresponding set of significant outliers and clusters for a 0.009 significance level (Bonferroni adjustment)

In addition to the sign of the LISA statistic, its magnitude informs on the extent to which kernel and neighborhood values differ. Testing whether this difference is significant or not requires knowledge of the distribution of the LISA under the null hypothesis. This distribution can be inferred either analytically under stringent assumptions regarding the distribution of observed rates or empirically using Monte Carlo simulation. In this paper we used the empirical approach as implemented in the ClusterSeer software and Cancer Atlas Viewer (Greiling, this issue). First, the set of observed rates, excluding the kernel value, is sampled randomly and without replacement; in other words all (N-1) observed rates are reassigned at random among the SEA units (randomization assumption). Then, the corresponding “simulated” neighborhood averages are computed. This operation is repeated many times (e.g. L = 999 randomizations) and these simulated values are multiplied by the kernel value to produce a set of L simulated values of the LISA statistic at time t and location u:

$${\text{LISA}}^{\left(l\right)}(\mathbf{u};t\mid \text{Neutral Model}\mathrm{I})=\left[\frac{z(\mathbf{u};t)-m_t}{s_t}\right]\times \left(\sum _{j=1}^J\frac{1}{J}\times \left[\frac{z^{\left(l\right)}({\mathbf{u}}_j;t)-m_t}{s_t}\right]\right)l=1,\dots ,L$$ (2)

with $z^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t)={\mathrm{F}}^{-1}\left[{\mathrm{p}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t)\right]$ F[.] is the sample cumulative distribution function (cdf), and p⁽¹⁾(u_j;t) is a random number uniformly distributed within 0 and 1. This set represents a numerical approximation of the probability distribution of the LISA statistic at u, under the assumption of spatial independence as operationalized by random sampling. Note that in the present paper the randomization was conducted without regard to the heterogeneous population size of SEA units, leading to an implicit null hypothesis of uniform risk of contracting the disease. In particular for tests applied to smaller and less populated geographical units (e.g. counties, census tracts), population size and its impact on the reliability of measured rates should be accounted for; for example, standardized or filtered rates should be used in the analysis.

The last step is to compare the observed LISA statistic, LISA(u;t), to the empirical probability distribution, allowing the computation of the probability of not rejecting the null hypothesis (so-called p-value). Figure 2 (top graph) shows an example for the SEA unit # 57444 identified in Fig. 1, where a p-value of 0.22 is obtained under the null hypothesis of spatial independence. The values have been computed for all the SEA units and mapped in Fig. 1 (bottom graphs), which reveals the existence of significant clusters of high values (High-High: HH) in the Deep South and a few HH clusters across Appalachia, while low values are clustered in the Northern Plain States (Low-Low: LL). A few outliers (Low-High and High-Low) are also identified. The exact number of significant SEA units is listed in the first row of Table 1. An adjusted significance level a α = 0.009356 was used to account for the fact that the multiple tests (i.e. 506 in this study) are not independent since near by SEA units share similar neighbors. This significance level was obtained using the Bonferroni adjustment which divides the significance level α = 0.05 by the average number of neighbors in each test.

Fig. 2.

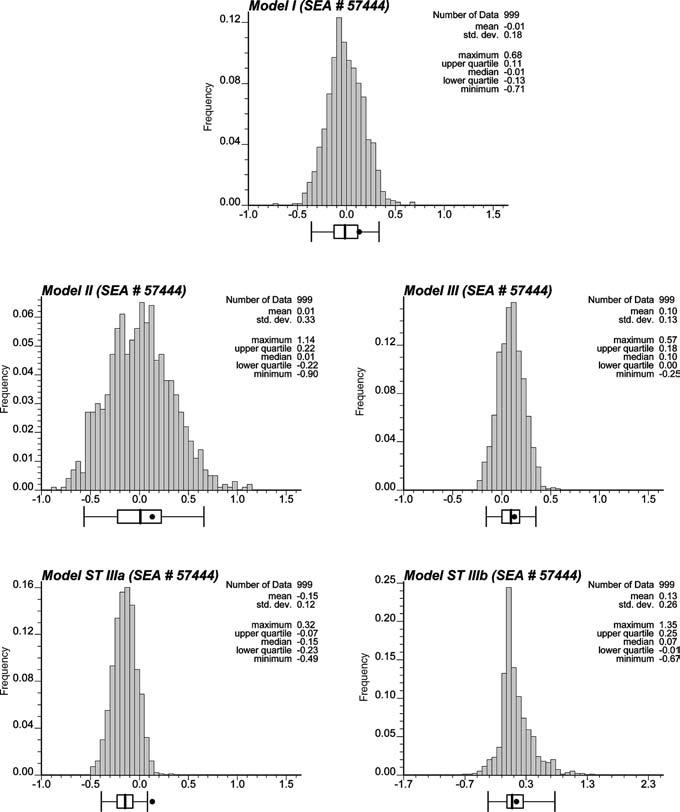
Histograms of the values of the LISA statistic simulated for SEA unit # 57444 (Del Rio, Texas) under different neutral models. The black dot denotes the observed LISA statistic which lies inside the 0.95 probability interval for all models except the space-time model using LISA statistic (8)

Table 1.

Number of significant SEA units for the different types of clusters/outliers and neutral models (cervix cancer for white females). Numbers between parentheses indicate SEA units that have similar classification under the reference Model I (spatial independence). Summary statistics for the p-values are also provided

	Neutral model type
	Model I	Model II	Model III	ST Model III
High-High	11	1(1)	7(0)	18(0)
High-Low	4	0(0)	10(2)	12(0)
Low-High	2	0(0)	5(0)	10(0)
Low-Low	43	7(7)	5(1)	16(1)
Non-Sign.	446	498(446)	479(422)	450(391)
p-value
Mean	0.183	0.255	0.212	0.185
CV	82.0%	54.6%	70.2%	79.7%

2.2 LISA statistic under a spatial neutral model (Model II)

Results in Fig. 1 are based on the null hypothesis that the distribution of cancer mortality rates is spatially random (no autocorrelation) with uniform risk over the study area. According to the typology presented in Table 2, this will hereafter be referred to as Neutral Model type I. The simplistic nature of the assumptions of Neutral Model I is best illustrated by Fig. 3 (top graphs) which shows two maps (realizations) obtained by randomly shuffling the mortality data across the 506 SEA units. The presence of spatial autocorrelation can be detected using the semivariogram (Cressie 1993; Goovaerts 1997) which plots the average squared difference between cancer rates as a function of the separation distance and direction between SEA unit centroids:

$$\widehat{\gamma }(\mathbf{h};t)=\frac{1}{2\sum _{\alpha =1}^{N\left(\mathbf{h}\right)}w({\mathbf{u}}_{\alpha };t)}\sum _{\alpha =1}^{N\left(\mathbf{h}\right)}w({\mathbf{u}}_{\alpha };t){[z({\mathbf{u}}_{\alpha };t)-z({\mathbf{u}}_{\alpha }+\mathbf{h};t)]}^2$$ (3)

where |h| corresponds to the Euclidian distance (spherical distortion of the earth's surface on the continental scale was here disregarded, but could be easily incorporated) between two centroids, and N(h) is the number of data pairs falling within that class of lag distance. All the following discussion can be readily generalized to other distance measures that could be more appropriate to capture contiguity of entities of complex shape (e.g. distance between population-weighted centroids, shortest overland distance, neighbors-based distance). Following previous simulation studies (Goovaerts et al. 2005) and in order to account for the noise induced by small population sizes, each pair has been assigned a weight proportional to the square root of the population size, $\mathrm{w}({\mathbf{u}}_{\alpha };t)=\sqrt{\mathrm{n}({\mathbf{u}}_{\alpha };t)}+\sqrt{\mathrm{n}({\mathbf{u}}_{\alpha }+\mathbf{h};t)}\forall {\mathbf{u}}_{\alpha }$, where n (u_α ; t) is the size of the population at risk in unit u_α at time t. Figure 4 (top graph) shows that cancer data exhibit a range of autocorrelation of about 1,200 km, with slightly larger variability observed along the EW direction for longer distances. Regional background is further revealed when using a geostatistical filtering technique (Goovaerts et al. 2005) to remove the noise and short-range variability of the mortality data while incorporating both the anisotropy (i.e. direction-dependent variability) of the data and population size information, see Fig. 4 (bottom graph).

Table 2.

Typology of neutral models based on the spatial characteristics of the risk being simulated

Risk at time t
Uniform		Heterogeneous
Spatially random	Spatially correlated	Spatially correlated (regional background at t)	Spatially correlated (regional background at t-1)
I	II	III	ST III

Fig. 3.

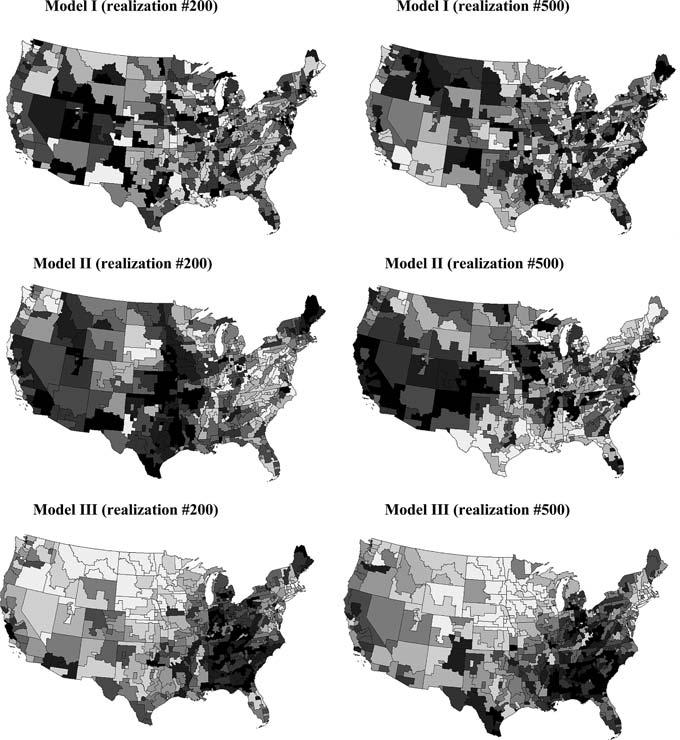
Two realizations of the spatial distribution of cervix cancer mortality data based on the assumption of spatial independence (Model I), reproduction of spatial autocorrelation (Model II), and incorporation of the regional background displayed in Fig. 4 (Model III). The grayscale ranges from white (low rates) to black (high rates), and for each realization categories correspond to deciles of the histogram of simulated rates

Fig. 4.

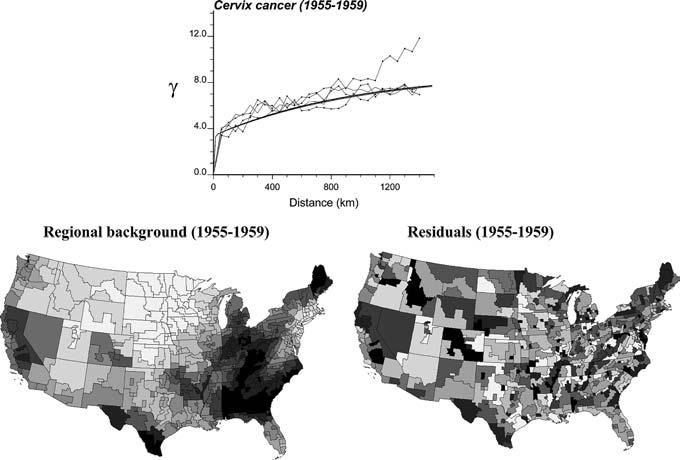
Population-weighted semivariogram for cervix cancer mortality data computed in four directions: N-S, SW-NE, EW, and NW-SE. The semivariogram model (thick solid line) is used by kriging analysis to decompose the original map of mortality rates (Fig. 1) into a smooth map of local means (regional background) and a map of residuals. Grayscale categories correspond to deciles of the histograms of local means and residuals, respectively

A more realistic neutral model would be one that reproduces not only the sample histogram, but also the pattern of spatial correlation observed in the data (Neutral model of type II). Spatial neutral models are here generated using geostatistical simulation, in particular Sequential Gaussian Simulation (SGS) which proceeds as follows (see Goovaerts 1997, p. 380 for more details):

1. Transform the N observed rates (z-data) into a set of standard normal scores $\{\mathrm{y}({\mathbf{u}}_{\alpha };t);\alpha =1,\dots ,N\}$ using the following graphical procedure:

   • The N original data z(u_α; t) are first ranked in ascending order. Since the normal score transform must be monotonic, ties in z-values must be broken, which was done randomly as implemented in GSLIB software (Deutsch and Journel 1998).
   • The sample cumulative frequency of the datum z(u_α; t) with rank k is then computed as $p_k^{\ast }=\mathbf{k}∕\mathrm{N}-0.5∕\mathrm{N}$.
   • The normal score transform of the z-datum with rank k is matched to the $p_k^{\ast }$-quantile of the standard normal cdf: $y({\mathbf{u}}_{\alpha };t)=\phi \left(z({\mathbf{u}}_{\alpha };t)\right)=G^{-1}\left[p_k^{\ast }\right]$ where G[.] is the standard Gaussian cdf.

2. Compute the experimental semivariogram of normal scores by applying expression (3) to normal score data.

3. Fit a permissible function to the experimental semivariogram $\widehat{\gamma }(\mathbf{h};t)$. The modeling was performed by weighted least-square regression using the number of data pairs as weight. All semivariogram models were bounded, that is a sill is reached for a given distance referred to as the range of influence. The covariance model C(h; t) was then derived by subtracting the semivariogram model γ(h; t) from the sill value.

4. Define a random path visiting each location u_α (i.e. SEA unit centroid) only once.

5. At each location u_α, determine the parameters (mean and variance) of the Gaussian probability distribution as:

   $$y_{SK}^{\ast }({\mathbf{u}}_{\alpha };t)-m_Y=\sum _{i=1}^{n\left({\mathbf{u}}_{\alpha }\right)}{\lambda }_i\left[y^{\left(l\right)}({\mathbf{u}}_i;t)-m_Y\right]$$ (4)

   $${\sigma }_{SK}^2({\mathbf{u}}_{\alpha };t)=1-\sum _{i=1}^{n\left({\mathbf{u}}_{\alpha }\right)}{\lambda }_{i}C({\mathbf{u}}_i-{\mathbf{u}}_{\alpha };t)$$ (5)

   where y^(l)(u_i; t) are normal scores simulated at locations previously visited along the random path and located within a search radius from u_α, m_Y is the stationary mean of the variable Y (which is zero following the normal score transform), and C(u_i − u_α; t) is the covariance function of the normal score variable Y at time t for the separation vector ${\mathbf{h}}_{\mathrm{i}\alpha }={\mathbf{u}}_{\mathrm{i}}-{\mathbf{u}}_{\alpha }$. Note that the observed normal scores are not used per se in the kriging system, only the semivariogram model fitted to these scores is used in the simulation procedure (non-conditional simulation). λ_j are kriging weights obtained by solving the following system of linear equations (simple kriging, SK):

   $$\sum _{j=1}^{n\left({\mathbf{u}}_{\alpha }\right)}{\lambda }_{j}C({\mathbf{u}}_i-{\mathbf{u}}_j;t)=C({\mathbf{u}}_i-{\mathbf{u}}_{\alpha };t)i=1,\dots ,n\left({\mathbf{u}}_{\alpha }\right)$$ (6)

6. Draw a simulated value from that distribution and add it to the data set; i.e. $y^{\left(1\right)}({\mathbf{u}}_{\alpha };t)=y_{SK}^{\ast }({\mathbf{u}}_{\alpha };t)+{\mathrm{w}}^{\left(1\right)}\times {\sigma }_{\mathrm{SK}}({\mathbf{u}}_{\alpha };t)$ where w⁽¹⁾ is a random number uniformly distributed within 0 and 1.

7. Proceed to the next location along the random path, and repeat the two previous steps.

8. Loop until all N locations are simulated.

9. Transform the simulated normal scores $\{{\mathrm{y}}^{\left(1\right)}({\mathbf{u}}_{\alpha };t);\alpha =1,\dots ,\mathrm{N}\}$ so that the target histogram (in this case the global distribution of observed rates at time t, F_t[.]) is reproduced:

   $${\mathrm{z}}^{\left(1\right)}({\mathbf{u}}_{\alpha };t)={\mathrm{F}}_{\mathrm{t}}^{-1}\left[{\mathrm{p}}^{\left(1\right)}({\mathbf{u}}_{\alpha };t)\right]$$ (7)

   where ${\mathrm{p}}^{\left(1\right)}({\mathbf{u}}_{\alpha };t)={\mathrm{k}}_{\alpha }∕\mathrm{N}-0.5∕\mathrm{N}$, and k_α is the rank of the simulated normal score y^(l)(u_α; t) in the simulated set.

The procedure is repeated using a different random path and set of random numbers to generate another realization.

Figure 3 (middle graphs) shows two realizations of the spatial distribution of mortality rates generated using this approach. Like the Model I maps (top) the sample histogram is reproduced but in addition these realizations reproduce the pattern of spatial correlation as modeled by the semivariogram of Fig. 4. 999 realizations of Model II were generated and used to compute the LISA statistic defined in Eq. (2). For example, Fig. 2 (left middle graph) shows the distribution of simulated values of the LISA statistics for the SEA unit # 57444. Clearly, the variance of the distribution is much larger than the results obtained under randomization, while the means are very similar and close to zero. The spatial autocorrelation of simulated rates increases the likelihood that the J neighboring values are jointly small or high, causing the neighborhood average, hence the LISA value, to exhibit much larger fluctuations among realizations. Consequently, the probability that the observed LISA statistic lies in the tails of the simulated distribution decreases, leading to a larger p-value (0.34 versus 0.23 for this SEA unit). The same pattern is observed for all units: the average p-values is 0.26 versus 0.18 for Model I. These larger p-values cause a substantial reduction in the size of significant LL or HH clusters (see Fig. 5, top graph), which confirms previous findings regarding the increased risk of type I error when ignoring the presence of spatial autocorrelation in the data. Table 1 indicates that all SEA units significant under Model II were also significant under the assumption of spatial independence.

Fig. 5.

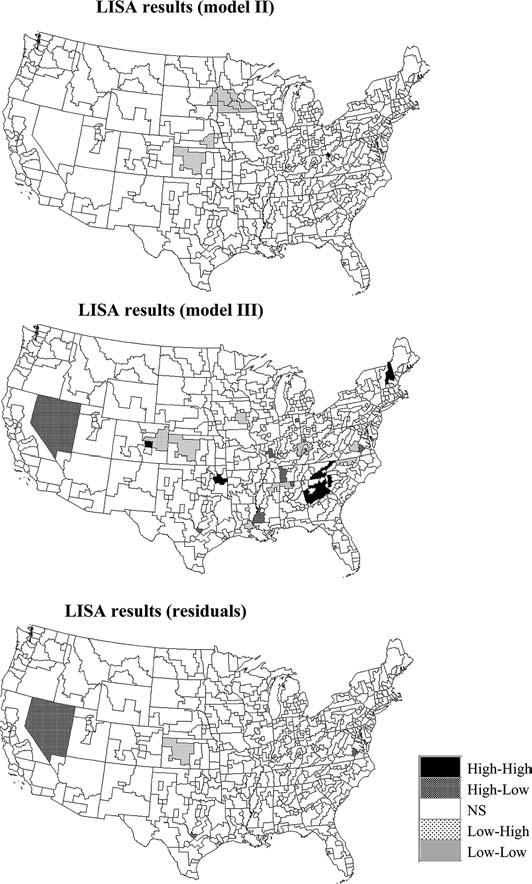
Results of the local cluster analysis conducted using spatially correlated null models of the type displayed in Fig. 3 (Models II and III). For comparison purposes the bottom graph shows the results of the analysis for the map of residuals displayed in Fig. 4 using a neutral model of type II to account for the spatial autocorrelation of the residuals

2.3 LISA statistic under a locally constrained spatial neutral model (Model III)

Additional information, beyond the reproduction of global statistics such as the sample histogram and autocorrelation function, can be included in the generation of neutral models, allowing the testing of more complex null hypotheses. Model III reflects the situation where environmental exposure or other factors make the risk of developing cancer non-uniform. In this instance the researcher wishes to detect spatial pattern above and beyond this non-uniform risk. For example, one might want to detect clusters of melanoma beyond those that are explained by the north-south gradient in solar radiation. In this paper, the regional background of risk is identified with the noise-filtered means of observed rates displayed in Fig. 4. Neutral models are created using the SGS algorithm where the parameters of the local distributions are now estimated using simple kriging with local means to account for the regional background (see Goovaerts 1997, p. 190; Goovaerts and Jacquez 2004, for more details). In short the constant mean m_Y in Eq. (4) is replaced by location-specific means m_Y (u_α; t), which amounts at simulating first the residuals [y(u_α; t)-m_Y(u_α; t)], then adding the regional background. The covariance function of these residuals is used in Eqs. (5) and (6). Note that the local Moran's I is still computed using Eqs. (1) and (2), that is the observed and simulated rates are standardized using the global mean m_t, while the local means are used only in the generation of the neutral models.

Two realizations of neutral model III are displayed at the bottom of Fig. 3, illustrating how the locations of high and small values are now reproduced by these neutral models. This local conditioning reduces fluctuations among realizations, leading to the J neighboring values being consistently either small or large across the realizations. Thus the distribution of 999 simulated LISA values is expected to be narrower than for the two previous models with a shift in the mean. This is illustrated for the SEA unit # 57444 in Fig. 2 (right middle graph). Because this unit is located in a high-valued area, the use of neutral models reproducing the regional background yields larger simulated LISA values (average = 0.1 instead of 0.01). Table 1 also indicates that the p-values are of smaller magnitude (average: 0.21 vs 0.26 for Model II).

The map of significant SEA units in the middle of Fig. 5 bears little resemblance to the maps obtained under neutral models I and II. This is expected since Model III addresses a different question, namely the detection of local departures from the regional background. Therefore, outliers HL and LH are much more frequent on this map than spatial clusters HH or LL. For example, Model III highlights two Low-High outliers in the State of Colorado that went undetected before. While the cancer rates in these units are not much lower than the average rate across the US, they depart significantly from the regional background.

As mentioned in the Introduction, earlier work has examined the computation of local Moran's I from residuals of spatial regression models, allowing one to test for clustering of deviations from local expectations based on some model of disease incidence (Cliff and Ord 1981; Tiefelsdorf 2000). This approach was implemented here by performing the LISA test on the deviations (residuals) from the local means displayed in Fig. 4. Although much of the spatial autocorrelation displayed by observed rates disappears after the removal of the regional background, the semivariogram is not a pure nugget effect, and this residual autocorrelation was accounted for using a neutral model of type II. The map of significant SEA units at the bottom of Fig. 5 is clearly different from the map obtained using Model III. Although the major HL outlier and LL cluster were detected by both approaches, the analysis of residuals leads to much fewer significant SEA units (4 versus 27). It is hazardous to quantify the detection performances of these two techniques in the absence of accurate knowledge regarding the locations and spatial extent of true clusters. Future research using simulated datasets will compare the results of these alternative approaches for taking into account background spatial trend. Note also that the estimation of this regional background by geostatistical filtering is based on the fitting of a semivariogram model to experimental values, which is non-unique although practice has shown kriging results to be robust with respect to small changes in the autocorrelation model.

2.4 Generalization of Model III to account for space-time variability

Model III described in Sect. 2.3 allows one to test change in cancer rates above and beyond a regional background observed at the same time t. The simulation approach can readily be extended to use as local means the regional background observed at a previous time, say (t−1), enabling the testing of whether the spatial pattern has locally changed through time (note that other time lags, e.g. t−2, could be considered as reference spatial patterns, depending on the question to be addressed). While the observed LISA is still computed according to equation (1), the simulated LISA values are obtained as follows:

$${\text{LISA}}_{\mathrm{a}}^{\left(l\right)}(\mathbf{u};t\mid \text{Neutral Model}\mathrm{III})=\left[\frac{z(\mathbf{u};t)-m_t}{s_t}\right]\times \left(\sum _{j=1}^J\frac{1}{J}\times \left[\frac{z^{\left(l\right)}({\mathbf{u}}_j;t\mid t-1)-m_t}{s_t}\right]\right)l=1,\dots ,\mathrm{L}$$ (8)

with ${\mathrm{z}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t\mid t-1)={\mathrm{F}}_{\mathrm{t}}^{-1}\left[{\mathrm{p}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t-1)\right]$ F_t[.] is the distribution of rates observed at time t, ${\mathrm{p}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t-1)=\mathrm{G}\left[{\mathrm{y}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t-1)\right]$ where ${\mathrm{y}}^{\left(1\right)}({\mathbf{u}}_{\mathrm{j}};t-1)$ are normal scores generated using SGS conditionally to the regional background observed at the previous time t–1. The simulation procedure uses the residual semivariogram computed from difference between the normal scores observed at time t and the local means at time t–1, $[\mathrm{y}({\mathbf{u}}_{\alpha };t)-m_Y({\mathbf{u}}_{\alpha };t-1)]$ This space-time test will reveal areas where the ranking of the neighborhood average values in the global distribution changed over time. The procedure is illustrated by including as regional background the age adjusted mortality rates recorded for white females over the previous period 1950–1954.

Figure 6 (top graphs) shows the maps of mortality rates before and after geostatistical smoothing. The smoothed rates are used as local means to generate the neutral models. Two realizations of these models are displayed in Fig. 6 (middle graph), each reproducing a similar location of low and high values (regional background). 999 realizations were generated and the distribution of the simulated LISA values for the SEA unit # 57444 is shown in Fig. 2 (left bottom graph). The major difference between the two time periods is that in 1950–1954 the mortality rate for the neighborhood average was lower than the US mean (9.19 versus 10.13), while the opposite is true for 1955–1959 (10.02 versus 9.26). As a consequence the standardized values of the simulated neighborhood averages are mostly negative, leading to a shift of the empirical distribution to the left (average = −0.15 instead of 0.1) and a p-value which becomes lower than 0.05, indicating a significant change in the pattern of local autocorrelation.

Fig. 6.

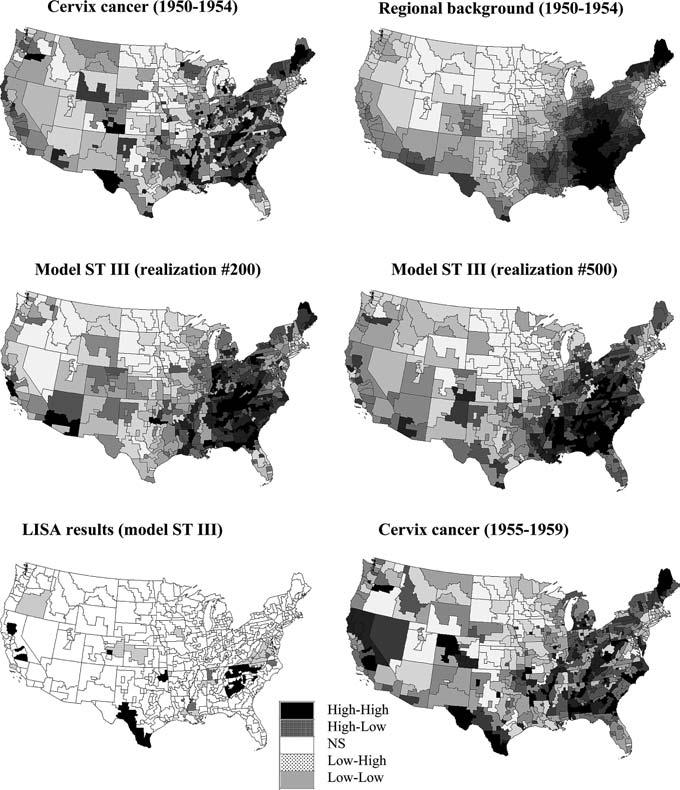
Maps of cervix cancer data for the period 1950–1954 and the regional background obtained by geostatistical smoothing of the short-range variability (top graphs). This regional background is used to generate the two realizations of the neutral model ST III (middle graphs). Bottom maps show the results of the local cluster analysis under this new model, and the distribution of cervix cancer mortality data for the tested period of 1955–1959. For all continuous variables grayscale categories correspond to deciles of the histogram of displayed values

The results for all SEA units are mapped at the bottom of Fig. 6 and summarized in Table 1. Interesting features include the High-High clusters detected for North California and Southern Texas which have experienced an increase in mortality rates between these two periods, while Low-Low clusters in Virginia and Eastern Louisiana corresponds to a significant decrease in mortality over the same period. Yet, the interpretation of these clusters and outliers is not intuitive since their labeling is defined in terms of spatial relationships; e.g. HH denotes a high value surrounded by high values. Important information, such as increase or decrease in rates between times, is not conveyed by this classification. For example the HH clusters detected in Tennessee, North and South Carolina, and Georgia do not reflect the decrease in mortality observed between these two periods. Therefore, we propose a new labeling where H/L would reflect an increase/decrease in standardized rates between times t−1 and t. Thus, a cluster ST-HH would denote a temporal increase in both the kernel value and the neighborhood average, while ST-HL would correspond to the situation where the kernel value would have increased in time while the neighborhood average would have decreased within the same time period. In this way relationships in both space and time can be easily captured and displayed. Note that since this classification is based on values standardized using the global mean at each time t, the change (increase, decrease) actually reflects a change in the ranking of the SEA unit value within the distribution of rates across the US. This new classification scheme is illustrated in the map at the top of Fig. 7 (left graph). Summary statistics listed in Table 4 show a substantial increase in the number of SEA units classified as LL or LH, which is balanced by the decrease in the number of HH and HL units. The newly labeled map indicates that in North California and Southern Texas the rates have either increased or decreased at a slower rate than the average decline over the US, causing the relative rank of the SEA units to climb. This new labeling also highlights the few SEA units in Tennessee, North and South Carolina that have experienced an increase in mortality rates from 1950–54 to 1955–59.

Fig. 7.

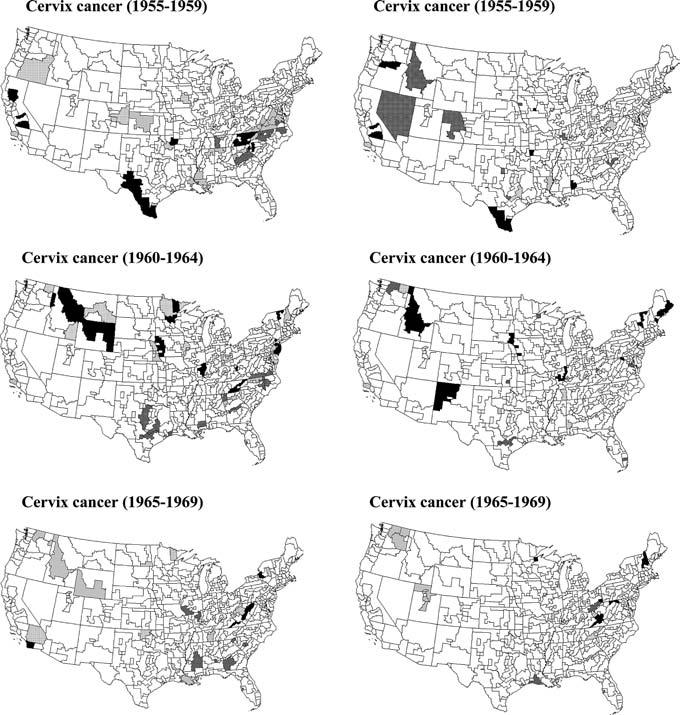
Results of the local cluster analysis under the ST III neutral model for the cervix cancer mortality rates recorded for a series of time periods. Left column corresponds to statistic (8), while right column results are produced by statistic (9)

Table 4.

Number of significant SEA units for the different types of clusters/outliers in cervix cancer mortality data detected using the neutral model ST III with statistic (9). Numbers between parentheses indicate SEA units that have similar classification under Model ST III with statistic (8)

Time period	Type of units
	High-High	High-Low	Low-High	Low-Low	NS
1955–1959	7(4)	10(0)	4(1)	2(0)	483(432)
1960–1964	12(2)	9(2)	8(2)	2(1)	475(433)
1965–1969	8(1)	2(0)	3(0)	7(1)	486(462)
1970–1974	8(0)	3(0)	8(1)	3(0)	484(448)
1975–1979	8(3)	6(1)	3(0)	4(3)	485(448)
1980–1984	9(5)	4(1)	3(0)	1(0)	489(472)
1985–1989	8(4)	10(0)	5(2)	5(1)	478(425)
1990–1994	14(7)	6(1)	5(1)	7(3)	474(421)

Even when using the new classification scheme, the weakness of the LISA statistic (8) is that the kernel value at time t−1 is ignored in its computation; hence only changes in neighborhood average values can be detected. For example, a significant high-high cluster was detected for the SEA unit # 57444, mainly because the kernel value at time t is compared with the smaller neighborhood values recorded at time t−1. To detect actual changes in local spatial patterns across time, we propose to compute the simulated LISA values using the following expression:

$${\text{LISA}}_{\mathrm{b}}^{\left(l\right)}(\mathbf{u};t\mid \text{Neutral Model}\mathrm{III})=\left[\frac{z^{\left(l\right)}(\mathbf{u};t\mid t-1)-m_t}{s_t}\right]\times \left(\sum _{j=1}^J\frac{1}{J}\times \left[\frac{z^{\left(l\right)}(u_j;t\mid t-1)-m_t}{s_t}\right]\right)l=1,\dots ,\mathrm{L}$$ (9)

where the kernel value observed at time t, z(u;t), is now replaced by the simulated value, z^(l)(u;t|t−1), generated conditionally to the regional background observed at the previous time t−1. In other words, the observed LISA statistic (1) will be compared to the distribution of LISA statistics computed from each of the L realizations of the space-time neutral model of type III. Figure 2 (right bottom graph) shows that this new statistic, which accounts for the smaller mortality rate recorded for unit # 57444 at time t−1, leads to a different conclusion (non-significant change). Since both the kernel value and neighborhood average increased from t−1 to t, accounting for the two in statistic (9) clearly reveals that the relationships between these two sets of values did not change over time, hence no significant change in local spatial autocorrelation is found.

Statistic (9) is mapped using the new classification labeling at the top of Fig. 7 (right graph). Except for Southern Texas, the major clusters detected using statistic (8) have vanished because they do not appear significantly unusual under the modified null hypothesis. The summary statistics in Table 4 indicate that the two maps share only 5 SEA units similarly classified as significant, with a smaller proportion of space-time clusters (9 versus 33) detected using the new statistic (9). In particular, statistic (9) leads to fewer significant clusters of decrease in Virginia, which would indicate that the local autocorrelation as measured by the LISA value did not change significantly between these two time intervals.

3 Analysis over multiple time periods

The methodology developed in Sect. 2.4 was applied to the study of the space-time distribution of cervix cancer mortality rates recorded over all US State Economic Areas (SEA) for 9 time periods of 5 years each. Figures 7 and 8 show, for a few time periods, the results of the local cluster analysis using statistics (8) and (9). Classification statistics for all time periods are summarized in Tables 3 and 4. Following Miller et al. (1996), elevated rates among white females tended to cluster across the South, more so in the earlier time period than recently, across Appalachia, parts of the Midwestern states, and the upper Northeast. High rates were also seen in the southern part of Texas, perhaps due to the concentration of Hispanic women, who tend to have elevated risks. Low rates occurred in the lower Northeast, northern Plains, and Rocky Mountain states, which may reflect cultural or religious influences on sexual practices, resulting in reduced transmission of human papillomavirus.

Fig. 8.

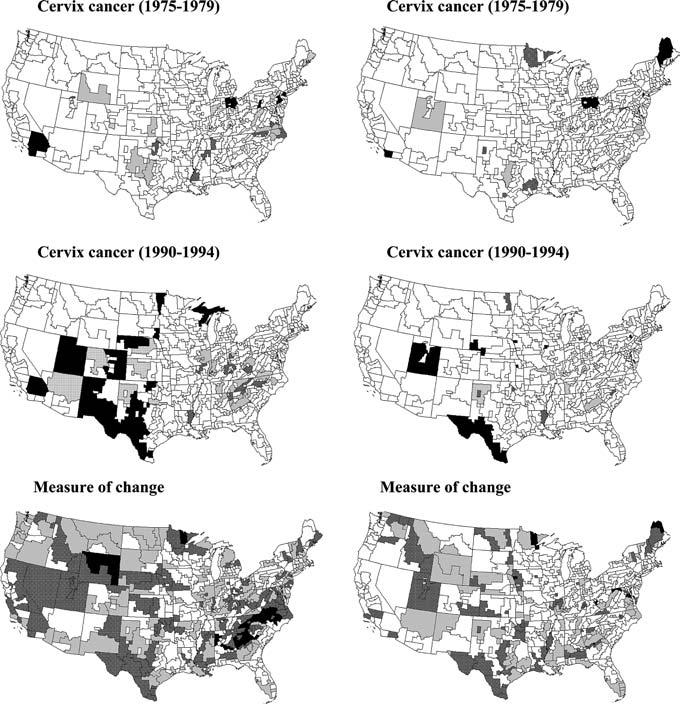
Results of the local cluster analysis under the ST III neutral model for the cervix cancer mortality rates recorded for a series of time periods. Bottom maps show the number of times each SEA unit has been found significant (α = 0.05) over 8 time periods (gray = 2, dark gray = 3–4, black = 5–7). Left column corresponds to statistic (8), while right column results are produced by statistic (9)

Table 3.

Number of significant SEA units for the different types of clusters/outliers in cervix cancer mortality data detected using the neutral model ST III with statistic (8) and the new ST classification scheme. The last column gives the relative change in average mortality rate when compared with the preceding time interval (Grauman et al. 2000)

Time period	Type of units
	High-High	High-Low	Low-High	Low-Low	NS	% change
1955–1959	10	11	12	23	450	−9.3
1960–1964	16	14	15	4	457	−12.1
1965–1969	4	7	7	8	480	−19.2
1970–1974	13	3	8	13	469	−23.1
1975–1979	9	11	9	15	462	−24.1
1980–1984	11	3	7	2	483	−18.1
1985–1989	19	8	16	17	446	−11.9
1990–1994	24	13	8	20	441	−3.5

Mortality from cervical cancer has declined substantially throughout the country; particularly after 1965 (see Table 3, right column). This trend followed the increase in the utilization of Pap smear testing between 1961 and 1966, which allowed early detection of the disease. However, rates in certain areas have decreased less rapidly, mainly due to a relative lack of access to screening programs (Devesa 1995). Looking at the same SEA data presented in this paper, Grauman et al. (2000) detected some change in the geographic pattern over time, with an increasing concentration of relatively high rates in the Appalachian regions of Ohio, West Virginia, Kentucky, and Tennessee in later time intervals and corresponding decreases in high-rates areas across the Deep South. However their analysis was purely visual and could not easily detect changes above and beyond the regional historical background. The series of maps in Figs. 7 and 8 reveal interesting features, such as significant changes (i.e. increase or decrease at a smaller pace than the US average decrease) across Appalachia for the period 1965–1969 and across most of Texas during the last time period of 1990–1994. This illustrates how the technique can be used to identify areas that are lagging or excelling in response to a health intervention such as a screening program.

The information provided by the series of temporal maps is summarized at the bottom of Fig. 8 which displays the number of times each SEA unit has been found significant using a probability level α 0.05. This measure of lack of temporal stability indicates that most units in Southern Texas underwent significant changes over half of the time periods, which might be expected since this part of the country had the highest rates initially. Smaller temporal stability is also observed in parts of Virginia and North Carolina, as well as California. As noticed on the different time-specific maps, the proportion of significant p-values is on average smaller when looking at changes in local spatial autocorrelation, i.e. using statistic (9).

4 Conclusions

Cancer mortality maps are used by public health officials to identify areas of excess and to guide surveillance and control activities. Maps of incidence as well as mortality are used as input to disease clustering procedures whose purpose is to identify local areas of excess. While some controversy revolves around the utility of these techniques, it is indisputable that the finding of a confirmed cancer cluster is often of considerable concern. The accurate quantification of local excesses, as well as regional trends and differences in cancer incidence and mortality, is therefore a problem of considerable practical importance.

Arguably one of the biggest problems facing spatial epidemiology and exposure assessment is that of identifying geographic pattern (e.g. outliers, clusters) above and beyond background variation. Most, if not all, environmental contaminants and diseases with potential environmental causes occur at a background level in the absence of a pollution- or disease-causing process. Nonetheless, this background pattern is typically ignored in spatial analyses that employ null hypotheses of spatial independence and constant risk. Because some spatial dependency is expected at background levels, these null hypotheses often are inappropriate or at least not very interesting to test. The approach presented in the first part of this paper enables researchers to assess geographic relationships using appropriate null hypotheses that account for the background variation extant in real-world systems. An immediate consequence of using more realistic neutral models is fewer significant spatial clusters or outliers, which could reduce unnecessary public alarm and demands for investigation by already stretched state health departments. Similarly, the simulation procedure could easily account for the population size in each SEA unit (i.e., see Goovaerts et al. 2005), which is expected to decrease the number of significant clusters/outliers detected in less populated states.

Another major contribution of this paper is the generalization of neutral models to the detection of space-time clusters through the incorporation in geostatistical simulation of the regional background observed in the past. This new methodology allows one to identify geographic pattern above and beyond background variation displayed in prior time intervals. The new classification scheme also leads to a better visualization of areas where temporal changes have occurred in clusters or distinctly from the surrounding geographical units, as well as the sign and magnitude of these temporal changes. The implementation of this approach in spatial statistical software, such as the STIS (Greiling 2005 this issue), will facilitate the detection of spatial disparities for temporal changes in mortality rates, establishing the rationale for targeted cancer control interventions, including consideration of health services needs, and resource allocation for screening and diagnostic testing.

This paper presented only a few flavors of null hypotheses and statistics to detect clusters in space and time. This is the topic of ongoing research and, for example, Goovaerts (2005b) recently used an environmental exposure model to define the spatial background incorporated in the generation of neutral models. More research is needed to compare the proposed use of geostatistically simulated neutral models with existing analytical or empirical approaches to infer the reference distribution for local Moran's I that is conditional on a known or estimated background spatial trend. In particular, the benefit of our approach over more straightforward local cluster analysis of spatial or temporal regression models should be investigated. Application of the technique to smaller and less populated geographical units will also necessitate a preliminary correction for heterogeneous population sizes. Controlled simulation experiments under different model scenarios should allow a quantification of the power of alternative approaches for cluster detection.