Abstract
Based on the experimentally determined atomic coordinates for RNA helices and the self-avoiding walks of the P (phosphate) and C4 (carbon) atoms in the diamond lattice for the polynucleotide loop conformations, we derive a set of conformational entropy parameters for RNA pseudoknots. Based on the entropy parameters, we develop a folding thermodynamics model that enables us to compute the sequence-specific RNA pseudoknot folding free energy landscape and thermodynamics. The model is validated through extensive experimental tests both for the native structures and for the folding thermodynamics. The model predicts strong sequence-dependent helix-loop competitions in the pseudoknot stability and the resultant conformational switches between different hairpin and pseudoknot structures. For instance, for the pseudoknot domain of human telomerase RNA, a native-like and a misfolded hairpin intermediates are found to coexist on the (equilibrium) folding pathways, and the interplay between the stabilities of these intermediates causes the conformational switch that may underlie a human telomerase disease.
INTRODUCTION
RNA pseudoknot structure is defined as a structure with base pairing between a loop and other regions of the RNA. The simplest RNA pseudoknot is the H-type pseudoknot, where a hairpin loop base pair with a single stranded region outside the hairpin. A simple pseudoknot is composed of two helix stems and two loops that span across the helix stems. RNA pseudoknots play an indispensable role in the structures and functions of many RNAs (1–13). For example, in the translation of many viruses, the downstream pseudoknots play a crucial role to promote the frameshifting (14–20). The biological functions of a pseudoknot are directly related to the folding stability and the conformational changes. In an RNA pseudoknot, the stability and folding thermodynamics are largely determined by the interplay between the loops and the helical stems. For example, pseudoknot folding can be cooperative or noncooperative, which involves several intermediates in the folding process. Some of the folding intermediates may be native-like, or misfolded, which cannot be formed from the native helix stems (21–23). To predict how RNA pseudoknot folds, including the formation of all the possible the native-like and misfolded intermediates and the folding stability and cooperativity, it is essential to have an accurate model that can predict not only the native state, but also all the possible native-like and misfolded states. The availability of such a model would be useful to extract the information about the conformational changes and the folding energetics from the experimentally measured thermal melting curves.
To predict the folding thermodynamics requires (i) the energy parameters for the evaluation of the energy for a given conformation and (ii) the chain entropy. While the energy of a pseudoknot can be obtained from the nearest neighbor interaction model, which gives the energy (entropy) as the sum of the energy (entropy) parameter for each base stack in the helices, the chain entropy calculation requires a model. The evaluation of the chain entropy has become one of the bottlenecks for modeling RNA pseudoknot folding.
For a pseudoknot, the two loops span across the deep and the shallow grooves of the helix stems, respectively (See Figure 1a). The (narrow) deep and the (wide) shallow grooves correspond to the major and the minor grooves of the helix stems, respectively. Therefore, the loop conformations are strongly dependent on the helix that the loop spans across. The stem–loop correlation, such as the volume exclusion makes the loop entropy calculation very complex, because the loop and helix conformations must be treated together when evaluating the loop entropy. As a result of the stem–loop correlation, the conformational entropy of pseudoknots are nonadditive, i.e. the pseudoknot entropy cannot be calculated as the additive sum of the entropies of the helix and the (helix-free) loops.
Figure 1.
(a) A schematic diagram for a simple H-type pseudoknot. Loops L1 and L2 span the deep narrow (major) and the shallow wide (minor) grooves, respectively. (b) The secondary structure for the gene 32 mRNA pseudoknot of bacteriophage T2 and (c) the corresponding atomic structure for P and C4 atoms in the virtual bond representation. The atomic coordinates data are from the NMR structure (PDB ID: 2TPK). (d) The virtual bond representation for the conformation of a nucleotide strand.
Despite the extensive experimental studies on RNA pseudoknot folding thermodynamics (21–29), our ability to quantitatively predict RNA pseudoknot structure and folding stability is very limited (30–34). This is mainly due to lacking of the thermodynamic parameters, especially the chain entropy parameters. The dynamic programming described in Ref. (30) provides an efficient computational algorithm for the structure prediction for pseudoknotted RNAs. Based on ad hoc assumptions, Gultyaev et al. (35) compiled a table for the loop entropies for different loop length and helix length. Later, using the Gaussian chain approximation, Aalberts et al. (36) developed a model to estimate the loop entropies. The model is based on the polymer physics and neglects the atomic details of the loop conformations and the excluded volume interactions. Based on the model, Aalberts et al. performed an analysis for the asymmetry in the pseudoknot structure. Recently, based on the lattice models for chain conformations, Lucas et al. (37) and Kopeikin et al. (38,39) developed theories for pseudoknots and for simple RNA tertiary folds, respectively. These lattice-based physical models can rigorously treat the excluded volume effects but cannot treat atomic details and are thus unable to treat realistic RNA conformations.
In the present study, we present a virtual bond model for RNA pseudoknot conformations and conformational entropy (40–42). The model can account for the atomic details of the conformations. Specifically, we model the helix stems using the NMR measured coordinates (43) and model the loop conformations across the deep and shallow grooves as self-avoiding walks of the nucleotide virtual bonds in a diamond lattice. The atomic coordinates of the helices and the lattice representation for the loops are matched at the loop-helix junction, where steric viability is accounted for. When computing the conformational entropy, we explicitly account for the volume exclusion between different nucleotides. From the statistical mechanical model, we compute the free energy landscapes and the base pairing probability at different temperatures, from which the native and intermediate structures, the equilibrium folding pathways, the folding cooperativity and the stabilities can be obtained. RNA pseudoknots can be classified into several different types. In this study, we treat not only the simple H-type pseudoknots, but also the more complex pseudoknots, e.g. the TYMV and TMV pseudoknot structures.
THEORY AND MODEL
Structural model for pseudoknot
A simple (H-type) pseudoknot consists of two stems (S1 and S2 in Figure 1a) and two loops (L1 and L2 in Figure 1a). In Figures 1b and c, we show the secondary structure and the corresponding positions of the P and the C4 atoms for the gene 32 mRNA pseudoknot of bacteriophage T2 (43). As shown in the Figure, stems S1 and S2 are linked by loops L1 and L2, which span across the deep and shallow grooves, respectively.
The loop conformations are dependent on the helix stems through the chain connectivity and the stem–loop volume exclusion. As a result, the pseudoknot loop entropy is dependent on multiple parameters: the loop entropy is determined not only by the loop length, but also by the helix stem length and structure. Due to the enormously large parameter space (different possibilities for the helix stem length and the loop length), it is practically impossible to rely only on experiments to obtain exhaustively all the possible pseudoknot loop entropies. We need a computational model to calculate the pseudoknot loop entropy. Moreover, to extract the loop entropy parameter from the experiments also requires a model. In this work, we develop a statistical mechanical model to compute the pseudoknot entropy, from which we can obtain the pseudoknot folding free energy landscapes, the folding stability and the conformational changes.
We use the virtual bond model to describe the H-pseudoknot conformations. Since the C-O torsions in the nucleotide backbone have high propensity to be in the trans (t) rotational isomeric state, the P-O5-C5-C4 bonds and the C4-C3-O3-P bonds in a nucleotide backbone can be treated as planar (40). This makes it possible to describe the nucleotide backbone conformations through two effective bonds: the P-C4 and the C4-P bonds. The (i = 1, 2 and 3) and the (i = 1 and 2) in the 5′→3′ direction are called virtual bonds (see Figure 1d). In our model, we use the experimentally determined atomic coordinates to model the virtual bonds of the helix stems. For the loop region, of which the virtual bonds are more flexible, we use self-avoiding random walks in a diamond lattice to model the conformations.
Helix
For the helix stems, we use the P and C4 atomic coordinates in the NMR structure of gene 32 mRNA pseudoknot of bacteriophage T2; see Figure 1c. In gene 32 mRNA pseudoknot, the lengths of stems S1 and S2 are respectively 5 and 7 bp. For helix stems of other lengths, we use the gene 32 mRNA pseudoknot helix as a template to generate the P and C4 atomic coordinates through the virtual bond torsional angles (η,θ) and the bond angles (βP, βC) (42); see Figure 1d. The virtual bond torsional angles (η, θ) in the helix are (170°, 210°) (41) and the bond angles (βP, βC) are (105 ± 5°, 95 ± 5°) for a rigid A-RNA helix (44).
Loop
As shown in Figures 1b and c, loops L1(A8) and L2(U21 → G27) span across the deep narrow and shallow wide grooves, respectively. The two loops have quite different spatial configurations. For example, the loop end–end distance, defined as the distance between the C4 atom at the helix-loop junction and the C4 atom on the other end of the stem, shows different stem length-dependence for the two loops. Shown in Figure 2a are the results from our virtual bond model for the end–end distances, denoted as and for loops L1 and L2, respectively. The two loops show very different behaviors. As the helix stem length is increased, increases monotonically while decreases until stem length S2 = 6 then increases. Our findings here are consistent with the experimental observation (45).
Figure 2.
(a) The C4-C4 end–end distance for the loops for different helix stem lengths. Loops L1 and L2 span across the deep and the shallow grooves of the helix stems, respectively. We obtain the C4 coordinates for short stems using the NMR determined values for the 32 mRNA pseudoknot of bacteriophage T2. For longer stems, we obtain the end–end distance from the helix coordinates generated from the virtual bond model. (b) The entropies for loops across the deep and the shallow grooves. The entropy L2, the loop across the shallow groove, shows a non-monotonic loop length-dependence.
The above intriguing differences in the stem length-dependence of and are due to the different geometries of the narrow and wide grooves. For the deep narrow groove, the minimum distance between the two paired helical strands is between two non-pairing nucleotides separated by a few base pairs apart instead of between two base paired nucleotides. So the minimum end–end distance for L1 occurs when the helix stem S2 has a length of a few base pairs. Moreover, for narrow deep grooves, the minimum end–end distance is small, so L1 can be as short as a single nucleotide, as shown in Figures 1b and c. On the other hand, for the shallow wide groove, the minimum inter-strand distance occurs between two pairing nucleotides and hence the end–end distance of L2 increases monotonically with the helix stem S1. In addition, the minimum end–end distance is large, so a single nucleotide loop cannot form a viable structure for L2.
In our model, we use diamond lattice to configure the loop conformations. This is because the three torsional angles of the diamond lattice bonds (g+, t, g−) represent the typical rotational isomeric states t and g± of a polymer and thus the diamond lattice conformations may well represent the conformational ensemble of a realistic loop. We model loop conformations as self-avoiding walks of the virtual bonds (i.e. the P and the C4 atoms) in the diamond lattice. The bond length of the diamond lattice is equal to the length of a virtual bond 3.9 Å. Furthermore, in order to connect the loop to the helix, we map the P and C4 coordinates of the helices onto the closest diamond lattice sites. Such coarse-grained approach causes a root-mean-square deviation (RMSD) of about 2.2 Å for the helix.
Pseudoknot entropy
At the center of the statistical thermodynamics is the partition function Q, defined as the sum over all the possible structures:
| 1 |
where s denotes a structure. Here a structure is defined by the helices. So a given structure would have fixed loop lengths but can have different loop conformations, which cause different pseudoknot conformations. Ωs denotes the number of pseudoknot conformations accessible to the structure s, and Es is the energy (enthalpy) of s. The sum is for all the possible structures that contain RNA secondary structures and pseudoknotted structures. For a given pseudoknot structure s, Es can be evaluated from the nearest neighbor model using the experimentally measured enthalpy parameters for the base stacks, while Ωs can be obtained from the computational model developed here. Given the fixed coordinates of the helix stems, the entropy of the pseudoknot is determined by the loops. So the main focus for Ωs calculation is to compute the loop entropies in the presence of the fixed helix stems in the structure.
We decompose a pseudoknot into two subunits, each consisting of a stem and the corresponding loop: S1 + L2 and S2 + L1. Due to the loop-helix volume exclusion, the loop entropies are dependent on the length of the corresponding helix stems (namely, stem S1 for loop L2, and stem S2 for loop L1). The strategy in our theory is to first compute the loop entropies for L1 and L2 separately, then combine the subunits to obtain the entropy of the whole pseudoknot.
To ensure the steric compatibility for the connections between the subunits, we configure the P and the C4 atoms in the loop-helix junction regions onto the closest diamond lattice sites. For example, for the pseudoknot structure shown in Figure 1b, we fit the P and the C4 atomic coordinates for C7, G9, A20 and U28 onto the diamond lattice. Furthermore, in order to consider the excluded volume between the loops and helices, we also fit stems S1 and S2 onto the diamond lattice.
We compute the number of conformations for each subunit (S1 + L2 and S2 + L1) separately through exact computer enumeration for the self-avoiding walks in the diamond lattice. We denote the conformational counts as and for the two loops, respectively. If we neglect the excluded volume interaction between the two loops, the pseudoknot conformational count can be computed as
| 2 |
where denotes the number of the conformations of loop Li. Figure 3 shows that the conformational entropy computed from Equation 2 gives accurate results as tested against the exact computer enumeration. From Equation 2, the key for the pseudoknot conformational entropy calculation is to compute the conformational count for the loops.
Figure 3.
Comparison for the calculated conformation entropy from the exact computer enumeration (Times) and the result from Equation 2 (Triangle), where L1 and L2 are the lengths (nt) for the loops across the the deep groove of S2 and the shallow groove of S1, respectively, and Ωs is the number of the pseudoknot loop conformations. The helix lengths for S1 and S2 are fixed at 5 and 7 bp, respectively (See Figure 1b).
In Table 1, we show our results from exact computer enumeration for the two loops. The results are given as the loop entropy parameters defined as the following.
| 3 |
Table 1.
Pseudoknot loop entropies parameters defined in Equation 3.
| Stem size (bp) | Loop size (nt) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| (S2) | L1 (across the deep groove of S2) | |||||||||||
| 2 | — | — | — | 6.2 | 6.4 | 6.4 | 6.6 | 6.8 | 6.9 | 7.1 | 7.2 | |
| 3 | — | 6.4* | 6.4* | 6.4 | 6.6 | 6.6 | 6.8 | 6.9 | 7.1 | 7.3 | 7.5 | |
| 4 | 4.4* | 4.4* | 4.5 | 5.4 | 5.6 | 6.0 | 6.3 | 6.6 | 6.9 | 7.1 | 7.3 | |
| 5 | 2.3 | 4.4 | 4.6 | 5.7 | 6.0 | 6.5 | 6.9 | 7.2 | 7.5 | 7.8 | 8.0 | |
| 6 | 2.3 | 4.4 | 4.8 | 5.8 | 6.0 | 6.5 | 6.8 | 7.1 | 7.4 | 7.6 | 7.8 | |
| 7 | 2.3 | 4.4 | 5.0 | 5.9 | 6.2 | 6.8 | 7.0 | 7.3 | 7.6 | 7.8 | 8.0 | |
| 8 | — | 4.4 | 5.2 | 5.7 | 6.4 | 6.7 | 7.1 | 7.3 | 7.5 | 7.7 | 7.9 | |
| 9 | — | 5.5* | 5.5 | 6.4 | 6.7 | 7.2 | 7.5 | 7.9 | 8.1 | 8.3 | 8.5 | |
| 10 | — | 6.9* | 6.9* | 6.9 | 7.5 | 7.7 | 8.1 | 8.3 | 8.6 | 8.8 | 8.9 | |
| 11 | — | — | — | — | 8.7 | 8.8 | 8.9 | 9.1 | 9.2 | 9.3 | 9.3 | |
| 12 | — | — | — | — | 9.8 | 9.2 | 9.5 | 9.6 | 9.7 | 9.8 | 9.8 | |
| (S1) | L2 (across the shallow groove of S1) | |||||||||||
| 2 | — | — | — | 7.6 | 7.0 | 7.0 | 7.1 | 7.2 | 7.3 | 7.4 | 7.5 | 7.7 |
| 3 | — | 6.5* | 6.5* | 6.5 | 6.6 | 6.7 | 6.9 | 7.1 | 7.2 | 7.4 | 7.6 | 7.7 |
| 4 | — | — | 9.2* | 9.2* | 9.2 | 8.9 | 8.9 | 8.9 | 9.0 | 9.0 | 9.1 | 9.2 |
| 5 | — | — | — | 9.8* | 9.8* | 9.8 | 9.1 | 8.9 | 8.8 | 8.8 | 8.8 | 8.8 |
| 6 | — | — | — | 11.9* | 11.9* | 11.9* | 11.9 | 11.0 | 10.4 | 10.1 | 9.9 | 9.8 |
| 7 | — | — | — | — | 12.4* | 12.4* | 12.4* | 12.4 | 11.4 | 11.0 | 10.7 | 10.5 |
| 8 | — | — | — | — | 12.1* | 12.1* | 12.1* | 12.1 | 11.6 | 11.4 | 11.2 | 11.1 |
| 9 | — | — | — | — | — | 13.7* | 13.7* | 13.7* | 13.7 | 12.6 | 12.0 | 11.5 |
| 10 | — | — | — | — | — | 13.7* | 13.7* | 13.7 | 12.7 | 12.2 | 11.8 | 11.5 |
| 11 | — | — | — | — | — | — | — | — | 15.9 | 14.1 | 13.0 | 12.4 |
| 12 | — | — | — | — | — | — | — | — | 18.7 | 15.8 | 14.2 | 13.2 |
The upper half of the Table gives (−Δ SL1/kB) for loop L1 as a function of the S2 helix stem length and the L1 loop length. The lower half of the Table gives (−Δ SL2/kB) for loop L2 as a function of the S1 helix stem length and the L2 loop length. See Figure 1 for the stem–loop construct of a pseudoknot. The * entries in the Table indicate the long stem and short loop structures that cannot be realized in the diamond lattice but may be viable for a realistic pseudoknot. For these restricted loops, we use the entropies of the minimal loop lengths for the same helix length.
Here is the loop entropy for loop Li, ωcoil (Li) is the number of the corresponding coil conformations for Li. To obtain ωcoil(Li) and , we enumerate the number of self-avoiding loop conformations on the diamond lattice. The volume exclusion between different monomers in the loop and between the loop and the helix (S1 for L2 and S2 for L1) are rigorously accounted for. We note that due to the discreteness of the virtual bond configurations in the diamond lattice, certain conformations with long helix stems and very short loops cannot be realized in the diamond lattice. However, these loops, which are denoted by * in Table 1, may be viable in realistic structures. For these special loops, the conformations would be very restricted, so we assume their loop entropies are equal to the minimal loop entropies.
We denote the loop length by l (nt). For large loops (l > 12 nt), the enumeration of the loop conformations is not possible because of the exponentially increasing computational time. According to the results from the exact computer enumeration for l ≤ 12 nt loops, we fit the following formula for the loop entropies:
| 4 |
where lmin is the minimal loop length to form a H-pseudoknot for the given helix stem (S1 for L2 and S2 for L1). The lmin values for different helix stems are obtained from the experimental data (35,45). The above equations combined with Equation 3 give the loop entropies for a pseudoknot (46–48).
In Table 2, we present our results for (lmin, a, b, c) for L1 (across the narrow groove of S2) and L2 (across the wide groove of S1). To test the accuracy of the above fitted loop entropy formula, in Figure 2b we show the comparison between Equation 4 and the results from the exact computer enumeration. We find that the above fitted formula can indeed provide good approximations for the loop entropies.
Table 2.
The parameters for the loop entropies in Equation 4.
| S2 stem length (bp) | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| lmin | 4 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 5 | 5 |
| a | 0.12 | 0.39 | −2.14 | −2.22 | −2.40 | −2.61 | −1.17 | −1.66 | −1.43 | −0.14 | 0.77 |
| b | 1.96 | 1.92 | 2.15 | 2.11 | 2.18 | 2.21 | 2.03 | 2.09 | 2.09 | 2.06 | 1.84 |
| c | 0.52 | −3.89 | −2.09 | −2.25 | −2.33 | −2.32 | −1.96 | −1.98 | −2.93 | 0.15 | −0.65 |
| S1 stem length (bp) | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| lmin | 4 | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 9 | 9 |
| a | 0.95 | 0.32 | 1.77 | 3.99 | 7.73 | 8.38 | 4.52 | 9.05 | 4.77 | 2.74 | 4.69 |
| b | 1.84 | 1.92 | 1.82 | 1.55 | 1.29 | 1.16 | 1.61 | 1.15 | 1.68 | 2.05 | 1.80 |
| c | −0.67 | −3.90 | −5.76 | −5.86 | −12.67 | −11.45 | −7.58 | −11.45 | −6.78 | 1.38 | −1.11 |
The upper half is for loop L1 and the lower half is for loop L2.
From Table 1 and Figure 2b, we find that the loop entropy shows an intriguing loop length-dependence. As the loop size l is increased, we find that (i) and (ii) for short helix stem S1 would monotonically increase. However, for loop L2 with longer helix stem S1, we find a non-monotonic behavior: first decreases for small l and then increases for large l. Such non-monotonic behavior for L2, the loop spanning across the minor groove, is evident from the exact computer enumeration results (e.g. for stem length S1 = 4 bp in Table 1 and in Figure 2b). In the following, we explain why the pseudoknot loop entropies show such distinctive behavior.
If the helix has zero or weak excluded volume, the loop entropy would increase monotonically with the loop size l, because ωcoil (Li) increases faster with the loop length l than . With the helix stem S2, L1 spans across the deep narrow groove of the helix S2 and can thus have a small end–end distance. For a small end-end distance (compared to the loop length), the probability for the loop to bump into the helix is small, i.e. the excluded volume of the helix is rather weak. Therefore, increases monotonically with l, for L2, which span across the wide shallow groove of helix S1, the loop end–end distance for a long helix S1 can be large. Consequently, for a short loop length l, the volume exclusion between the loop (L2) and the helix (S1) can be very strong. For such case, a small increase of the loop length l can greatly weaken the loop-helix volume exclusion, causing a notable increase in the number of loop conformations . This would result in a decrease in . Therefore, decreases with l for a long S1 stem. For large loops, the loop-helix volume exclusion becomes relatively weak and thus increases with l.
The above excluded volume-caused non-monotonic is supported by the results from the exhaustive computer enumeration. First, the results for S1 = 4 bp in Table 1 shows a non-monotonic loop length-dependence; see also Figure 2b. Second, for longer S1 stems, the loop-helix excluded volume interaction is strong and thus the non-monotonic behavior would be more pronounced. For example, for S1 = 6 bp decreases from 11.9 to 9.8 kB as the loop length l is increased from 7 to 12 nt. This implies a non-monotonic behavior, because for a very large l (≫ end–end distance of the loop), the loop-helix excluded volume interaction is weak, resulting in a monotonically increasing loop entropy.
Though we are lacking in exact computer enumeration data for very large loops due to the extremely demanding computational time for exhaustive enumeration, broad experimental tests presented in the following sections suggest that the loop entropy parameters given in Table 1 and Equation 4 may be reliable for the loop sizes tested. In addition, the entropy parameters derived here might be suffice for biologically significant sequences, which are unlikely to involve very large loops (length ≫12 nt). With the increasing availability of the experimentally measured loop entropy data, further refinements for Equation 4, which is accurate only for short and mid-size loops, can be possible.
Our current model has two advantages. First, the model is based on the virtual bond representation of the atomic P and C4 atoms of the nucleotides, so the model can treat atomic details. Second, the model explicitly accounts for the excluded volume interactions between the helices and the loops and between the loop nucleotides. In the following sections, based on the pseudoknot entropy parameters that we derived, we compute the partition function and the native structure as well as the folding free energy landscape for RNA pseudoknots. Through extensive experimental comparisons on the native structures and the melting curves, we validate the entropy model.
Partition function
In this section, we develop a recursive algorithm (42,49,50) to compute the partition function for all the possible structures that contain pseudoknots and secondary structures.
In order to account for the excluded volume interactions between different structural subunits, we classify different conformational types. A chain segment from nucleotides a to b is connected to the rest of the molecule at the terminal nucleotides a and b. To account for the conformational viability between the chain segments, we classify the conformational types according to the excluded volume near a and b. We assume that a lone base pair is not stable, so we classify structures according to base stacks.
We classify conformations according to whether the terminal nucleotides a and b are involved in base pair or not: the conformation is ‘closed’ if both a and b are involved in base pairing (such as the structures shown in Figures 4b, c and f) and is ‘open’ otherwise (such as the structure shown in Figures 4a and d). It is important to note that for a closed conformation, a and b can either base pair with each other (such as the hairpin structure shown in Figure 4f) or with different nucleotides (such as the pseudoknot structure shown in Figure 4f).
Figure 4.
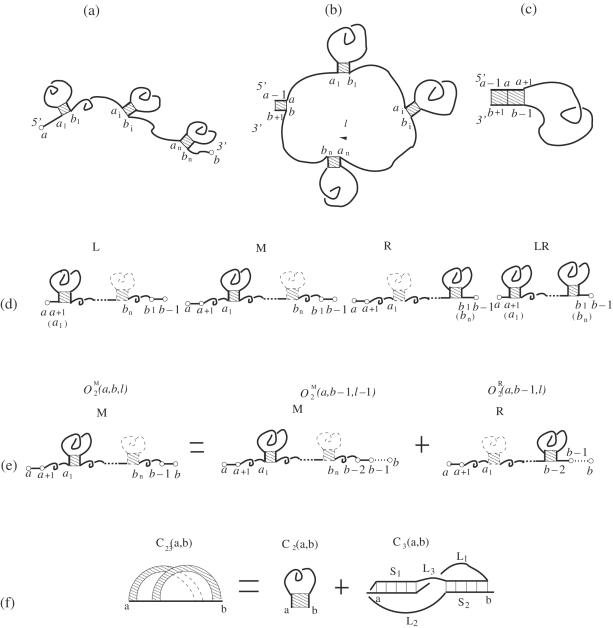
An open conformation (a) and a closed conformation with the closing stack connected to a loop (b) or to a stack (c). The closed conformation in (b) is formed from the open conformation in (a) through the closure of the unstacked loop of length l in (b). (d) The four types of open conformation (L, M, R and LR). (e) The partition function for M-type conformations for a chain from a to b can be computed as the sum of the partition function for a shorter chain from a to b − 1. (f) A closed conformation for RNA secondary structure and pseudoknots. Here we use a polymer graph to represent C23(a,b). The straight dark lines in the polymer graph represent the nucleotide backbone. The curved links represent the base pairs between the nucleotides. The shaded region between two curved links in the polymer graph corresponds to a helix stem.
For convenience, we use the following rules in our notations: C = ‘partition function for the closed conformations’, O = ‘partition function for the open conformations’, subscript ‘2’ = secondary structures, ‘3’ = pseudoknots, ‘23’ = secondary structures + pseudoknots. For example, C2(a, b) and (t = L, R, M and LR) are the partition functions for the closed secondary structures and the open secondary structures for a chain segment from a to b, respectively.
Closed conformations
The partition function for the closed conformations from a to b can be calculated as the sum of the partition functions for all the possible closed secondary structures without pseudoknot C2(a, b) and for all the possible structures with pseudoknots C3(a, b):
| 6 |
C2(a, b) can be calculated from the dynamic program by growing the chain step by step as described in equations 12–16 in the Appendix. C3(a, b) can be computed from the sum over all the possibilities for the helix stem lengths S1 and S2 and the loop lengths L1, L2 and L3 as shown in Figure 4f:
where ΔG(S1, S2, L1, L2, L3) is the free energy of the pseudoknot, which can be obtained from the loop entropy parameters in Tables 1 and 2 and the enthalpy and entropy parameters for the helices. In the Results and Discussion section, we illustrate the detailed calculation of the pseudoknot free energy.
Open conformations
The partition function for the open conformations (with pseudoknots) (t = conformational type L, M, R, LR; see Figure 4d) can be computed from the same recursive relations as the ones that we have derived for the secondary structures; see Equations 13–16 in the Appendix with C2 and O2 replaced by C23 and O23, respectively. From the recursive relations and Equation 17, we can compute efficiently the partition function for any chain segment from a to b.
Total partition function
Through the recursive relation, we can treat not only the simple pseudoknots, secondary structures, but also more complex structures with both secondary structures and pseudoknots (see Figure 5a) and structures with multiple pseudoknots (see Figure 5b). As shown in Figure 4d, we can treat structures with one or more closed conformations connected in series, where each closed conformation can be in the form of a secondary structure or a pseudoknot as shown in Figure 4f, or a mixture of secondary and pseudoknotted structures.
Figure 5.
The density plots for the base pairing probabilities and the predicted stable structures for (a) TYMV and (b) TMV pseudoknots at T = 37°C with the coaxial stacking. The upper diagrams are the corresponding polymer graphs for the predicted native structures. The straight dark lines in the polymer graph represent the nucleotide backbone and the curved links represent the base pairs.
The total partition function Q(a, b) for a chain from a to b is given by the sum of the partition functions for all the different types of conformations:
| 7 |
The first term accounts for the contribution from the unfolded coil state. The computational time scales with the chain length N as O(N6) and the memory scales as O(N2).
RESULTS AND DISCUSSION
Pseudoknot free energy calculation
For a pseudoknot with helix stem lengths S1 and S2 and loop lengths L1, L2 and L3 as shown in Figure 4f, the pseudoknot free energy ΔG(S1, S2, L1, L2, L3) can be computed as the sum of the free energies of the stems, loops and possibly the coaxial-stacking.
| 8 |
Here is the entropy of loop Li (see Equation 3), (i = 1, 2) is the free energy of helix stem Si, and ΔGcs is the free energy of the coaxial stack between the two helices (51).
ΔGassemble in Equation 8 is introduced to account for the entropy change as the two subunits (L1 + S2 and L2 + S1) are assembled into the pseudoknot. In Equation 3 (and Table 1), and are computed with the presence of the helices, therefore, the number of conformations for the assembled pseudoknot can be calculated as Ωs = ωL1 ωL2 as in Equation 2. On the other hand, ωcoil (Li) for L1 and L2 are calculated as two separate chains. As the two (coil) chains are assembled to form a longer chain, due to the different ways for the connection between the two chains, the total number of coil chain conformations is given by ωassemble · ωcoil (L1) · ωcoil (L2), where ωassemble ∼3 × 3 = 9 is the number of conformations for the junction nucleotide (= two virtual bonds, each with three possible orientations) between the two chains. The corresponding free energy for the ωassemble effect is ΔGassemble = kBT ln ωassemble ∼ kBT ln 9 ≃ 1.3 kcal/mol at T = 37°C.
In Equation 8, we have neglected the loop enthalpy and the stability of the single strand segment L3, which is assumed to be short and flexible. From the NMR structural studies (43,52), the two stems in the pseudoknot can be coaxially stacked. Especially for L3 = 0 the two stems can be juxtaposed into coaxial positions and we need to consider the coaxial stacking in the stability calculation.
For a given pseudoknot structure, we obtain (i) the loop entropies (i = 1, 2) from Tables 1 and 2, (ii) the helix free energy from the nearest neighbor interaction model with the enthalpy and the entropy parameters computed from the Turner rule (53), and (iii) the coaxial stacking free energy from the sequence-dependent parameters in Ref. (51).
Using Equation 8, we can compute the free energy for simple H-pseudoknots, such as the T4-35 pseudoknot shown in Figures 6c and 7a. For more complex structures, which involve multiple pseudoknots or a mixture of the pseudoknots and secondary structures, such as the TYMV and TMV structures shown in Figures 5a and 5b respectively, we can estimate the total free energy of the structure as the sum of the free energy of the component structures (pseudoknots, secondary structures). In this section, using T4-35, TYMV and TMV pseudoknots as three representative examples for the different levels of complexity, we show how to compute the pseudoknot free energy using our loop entropy parameters. For all the illustrative calculations in this section, we assume temperature T = 37°C.
Figure 6.
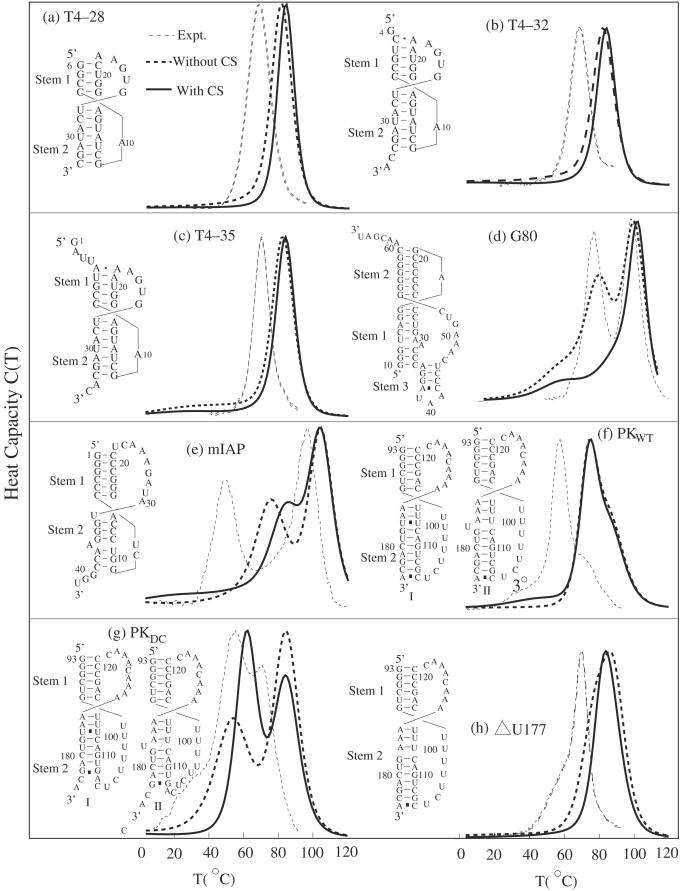
The comparison between the calculated melting curves and the experimentally measured results for eight pseudoknots sequences (a) T4–28, (b) T4–32, (c) T4–35 (24,26), (d) G80 (23), (e) mIAP (27), (f) the telomerase pseudoknot domain (PKWT), (g) (28) and (h) (29) are two mutants of the telomerase pseudoknot domain. The Y-axis is the heat capacity. The calculated melting curves have been normalized such that the theoretical and the experimental curves have the same peak value. The ion conditions are 50 mM NaCl and 1.0 mM Mg2+ for (a), (b) and (c), 1 M KCl for (d), 50 mM KCl for (e), 200 mM KCl for (f), (g) and 200 mM NaCl for (h). Because our calculated enthalpic and entropic parameters for the base stacks are from Turner's rules for 1 M NaCl salt condition, our model generally overestimates the melting temperatures. Results with and without coaxial stacking (CS) are both presented.
Figure 7.
The density plot for the base pairing probabilities, the predicted stable structures, and the density plot for the free energy landscapes for T4–35 pseudoknot at different temperatures. In the free energy landscape F(n, nn), darker color means lower free energy. n and nn denote the numbers of the native and the non-native base pairs, respectively. At T = 70°C, the partially unfolded pseudoknot structure (Z) coexists with the hairpin structure (X).
T4-35 pseudoknot
For the T4-35 pseudoknot shown in Figures 6c and 7a, there are two stems S1 (=5 bp) and S2 (=7 bp) and two loops L1 (=1 nt) and L2 (=4 nt).
(Stems S1 and S2): The nearest neighbor interaction model with the base stack thermodynamic parameters (53) gives the stabilities (in kcal/mol) for stems S1 and S2:
(Loops L1 and L2): (L2, S1) = (4 nt, 5 bp), (L1, S2) = (1 nt, 7 bp). From the lower (upper) half of Table 1 for L2 (L1), we find and .
- (T4-28 pseudoknot): The stability of the T4–28 pseudoknot (without coaxial stacking) at T = 37°C = 310 K (kBT = 0.62 kcal/mol) is equal to:
9
The above calculated free energy is close to the experimentally measured −8.1 kcal/mol in the mixed 3 mM Mg2+ and 50 mM Na+ ion condition (24). If we include the coaxial stacking (through the base stack 5′AG-CU3′), which has (ΔH, ΔS) = (−12.5 kcal/mol, −32.6 cal/mol/K) (51), the pseudoknot stability would be changed to ΔG = −2.5 kcal/mol, which disagrees with the experimental result. Therefore, coaxial stacking is unlikely to play a role in the T4–35 pseudoknot. The NMR studies for T2 pseudoknot (43) indicate that the C7–G16 base pair in the helix–helix junction is over-rotated by 18° compared with a continuous A-form helix. This may result in the disruption of the coaxial stacking in the junction. Therefore, our theoretical prediction is in accordance with the experiment.
TYMV pseudoknot
As shown in Figure 5a, the TYMV pseudoknot consists of two parts: a hairpin denoted as C2-1 from C1 to G15 and a pseudoknot denoted as C3-1 from C16 to A39.
(Hairpin C2-1): The nearest neighbor interaction model gives the stability = −3.9 kcal/mol.
- (Pseudoknot C3-1):
- (Stems S1 and S2): The nearest neighbor model gives the stabilities (in kcal/mol) for stems 1 and 2: and
- (Loops L1 and L2): (L2, S1) = (3 nt, 3bp), (L1, S2) = 3 nt, 6 bp). From the lower (upper) half of Table 1 for L2 (L1), we find and .
- (Pseudoknot C3-1): The stability for pseudoknot C3-1 is equal to
- (TYMV pseudoknot): The total stability for the TYMV pseudoknot is given as below.
where is the coaxial stacking free energy between stem 0 in the hairpin C2-1 and stem 1 in the pseudoknot C3-1. The parameter is from Ref. (51).10
If we include the (5′AG-CU3′) coaxial stacking between stems 1 and 2 within the C3-1 pseudoknot (51), the total stability would become −18.9 kcal/mol.
TMV pseudoknot
As shown in Figure 5b, the TMV pseudoknotted structure consists of three H-pseudoknots (C3-1, C3-2 and C3-3).
(Stems): From the nearest neighbor model and the thermodynamic parameters for the base stacks (53), we obtain the stabilities (in kcal/mol) for the six helix stems (two in each pseudoknot): ; ; ; ; ;
(Loops L1, L1′, L1″): These loops span across the deep narrow grooves of stems 2, 2′, and 2″, with [loop length (nt), stem length (bp)] = [1, 4], [1, 6], and [5, 5], respectively. From the upper half of Table 1, we have ; ;
(Loops L2, L2′, L2″): These loops span across the wide shallow grooves of stems 1, 1′, and 1″, with [loop length (nt), stem length (bp)] = [4, 4], [3, 3], and [7, 4], respectively. From the lower half of Table 1, we have ; ;
(Pseudoknots C3−1, C3−2, C3−3): From the above parameters for the helices and the loops, we use Equation 8 to obtain the stability (in kcal/mol) for each pseudoknot. We have , ,
- (TMV pseudoknot): The stability for TMV pseudoknot is equal to
where ΔGcsij is the free energy of coaxial stacking between stems i and j. The coaxial stacking between C3 − 1 and C3 − 2 is through the 5′AC-GU3′ base stack between stem 2 and stem 1′, and the coaxial stacking between C3 − 2 and C3 − 3 is through the 5′AU-UG3′ base stack between stem 2′ and stem 1″. We note that the coaxial stacking parameter for 5′UA-UG3′ is not listed in Ref. (51), so we use the stacking energy from the Turner rule (53).
The two stems in each H-pseudoknot element may also be coaxially stacking. The coaxial base stack 5′GU-AC3′ between stems 1 and 2 can stabilize C3-1 by −3.5 kcal/mol, anand the base stack 5′UA-UA3′ between stem 1′ and stem 2′ can stabilize C3-2 by −2.2 kcal/mol. For C3-3, however, the coaxial stacking, if formed, would involve a noncanonical base pair (C-A) and would be unstable. So we ignored the coaxial stacking for C3-3. The total extra stability provided by the coaxial stacking within the H-pseudoknot elements (C3-1 and C3-2) could reach (−3.5) + (−2.2) = −5.7 kcal/mol.
Pseudoknot structure prediction
The probability Pij for the formation of a base pair (i, j) can be calculated from the conditional partition function Qij for the ensemble of conformations with base pair (i, j) formed: Pij = Qij/Q. From the distribution of the base pairing probability, we can deduce the stable structures for a given temperature T. Specifically, the structural prediction involves the following two steps. We first compute Pij for all the possible base pairs (i, j). From Pij, we identified the helices as the consecutive (i, j) pairs with large Pij values. For example, the density plot for Pij in Figure 5a for the TYMV pseudoknot has three trains of dark dots (= large Pij's), indicating three stables helices (stems 1, 2 and 3).
We predict the stable structures at T = 37°C for pseudoknot-forming sequences which have known experimentally measured native structures. We quantify the accuracy of our predictions using the sensitivity (SE) and the specificity (SP) parameters (54,55). The SE is defined as the ratio between the number of the correctly predicted base pairs and the number of the base pairs in the experimental determined structure, and the SP is defined as the ratio between the number of the correctly predicted base pairs and the number of base pairs in the predicted structure. A perfect prediction would have (SP, SE) = (1.0, 1.0) and a completely failed prediction would have (SP, SE) = (0.0, 0.0). NMR experiments suggest that the two stems in an H-type pseudoknot can be coaxial (43,52,56) or bent (18,57), so we perform our computations for two cases (with and without coaxial stacking) separately.
Viral ribosomal frameshift signals and viral ribosomal readthrough signals pseudoknots
In Table 3, we summarize the accuracy of our theoretical predictions for the native structures with coaxial stacking for 15 viral ribosomal frameshift signals and 7 viral ribosomal readthrough signals pseudoknots (58). We truncate the sequences and retain only the pseudoknot portions; see Table 3 for the sequences. For the viral ribosomal frameshift signals, BEV, EAV, HCV-229E, LDV-C and RSV sequences are not included because the computational time is demanding for these long (>100 nt) sequences. From Table 3, we find that, except for the BLV and CABYV sequences, our model can give good predictions for all the other 20 sequences. If the second lowest free energy structure is also considered, the predictions for BLV and CABYV would be exact (see Table 3). For BLV, the predicted alternative structure is a hairpin formed through the disruption of the helix stem close to the 3′ end in the native pseudoknot. The hairpin is predicted to be more stable than the native pseudoknot by 0.7 kcal/mol. For CABYV, the model predicts a misfolded hairpin with the helix stem formed by the base pairs from G1495–C1511 to G1501–C1505. The misfolded hairpin is predicted to be 1.6 kcal/mol more stable than the native pseudoknot. The inaccuracy in the predictions for the BLV and CABYV pseudoknots may be caused by the neglected tertiary interactions, such as base triples. The A·(C-G) and C·(C-G) base triples have been found to significantly stabilize the ribosomal frameshifting pseudoknots (18–20), such as ScYLV and BWYV, and may also play important roles in the BLV and CABYV stabilities.
Table 3.
The accuracies of the structure predictions for the viral ribosomal frameshifting signal and the viral ribosomal readthrough signal pseudoknots (58).
| ID | Abbreviation | Length | Truncated sequences | SE | SP |
|---|---|---|---|---|---|
| Viral ribosomal frameshifting signals | |||||
| 1 | BChV | 26 | G1595–C1620 | 1.00 | 1.00 |
| 2 | BLV | 27 | G1604–U1630 | 0.67 | 0.86 (1) |
| 1.00 | 1.00 (2) | ||||
| 3 | BWYV | 26 | C1566–G1591 | 1.00 | 1.00 |
| 4 | BYDV–NY–RPV | 27 | G1706–C1732 | 1.00 | 1.00 |
| 5 | CABYV | 27 | G1494–C1520 | 0.00 | 0.00 (1) |
| 1.00 | 1.00 (2) | ||||
| 6 | EIAV | 35 | G1797–C1831 | 1.00 | 1.00 |
| 7 | FIV | 35 | G1893–C1927 | 1.00 | 1.00 |
| 8 | IBV | 69 | G81–U149 | 1.00 | 0.78 |
| 9 | MMTVgag/pro | 34 | G2090–U2123 | 1.00 | 1.00 |
| 10 | PEMV | 28 | U2042–C2069 | 0.90 | 1.00 |
| 11 | PLRV–S | 26 | G1781–G1806 | 1.00 | 1.00 |
| 12 | PLRV–W | 26 | G1676–G1701 | 1.00 | 0.88 |
| 13 | PRRSV–LV | 59 | G7402–G7459 | 1.00 | 0.95 |
| 14 | PRRSV–16244B | 58 | G7701–G7758 | 1.00 | 1.00 |
| 15 | SRV1gag/pro | 37 | G2337–C2373 | 1.00 | 1.00 |
| Viral ribosomal readthrough signals | |||||
| 16 | AKV–MuLV | 50 | G2261–C2310 | 1.00 | 0.79 |
| 17 | BaEV | 50 | G2607–C2656 | 1.00 | 1.00 |
| 18 | Cas–Br–E–MuLV | 50 | G2239–C2288 | 1.00 | 0.75 |
| 19 | FeLV | 50 | G2196–G2245 | 1.00 | 0.82 |
| 20 | GaLV | 49 | G2202–G2250 | 1.00 | 0.79 |
| 21 | Mo–MuLV | 50 | G1982–C2031 | 1.00 | 0.79 |
| 22 | SNV | 50 | G183–C232 | 1.00 | 0.83 |
The calculations are performed at the standard conditions (1 M NaCl, 37°C). These sequences are truncated to keep the pseudoknot part. In the calculation, we consider the coaxial stacking. The SE is defined as the ratio between the number of the correctly predicted base pairs and the number of the base pairs in the experimental determined structure, and the SP is defined as the ratio between the number of the correctly predicted base pairs and the number of base pairs in the predicted structure (54,55).
As a test, we also predict the pseudoknots without considering the coaxial stacking. We find that removing the coaxial stacking causes no change in the predicted native pseudoknot except for three sequences: PEMV, PLRV-S and FeLV, for which the predicted structures become significantly less accurate with (SE, SP) = (0.60, 0.86), (0.50, 0.40) and (0.57, 0.53), respectively. This clearly shows that the coaxial stacking is an important stabilizing force for these pseudoknots. More specifically, PEMV and PLRV-S are stabilized by the coaxial stacking 5′UC-GA3′ and FeLV is stabilized by the coaxial stacking 5′CC-GG3′. The energy parameter for the 5′UC-GA3′ coaxial stacking is not listed in Ref. (51), so we use the stacking energy parameter from the Turner rule (53). The above two coaxial stacks contribute about −2.3 kcal/mol and −4.1 kcal/mol to the stability of the pseudoknots at T = 37°C, respectively. In addition, the PEMV and PLRV-S may be stabilized by the tertiary interactions (12) such as (C.C-G for PEMV) and (C.G-C for PLRV-S).
Pseudoknots with high binding affinity to the human immunodeficiency virus type 1 reverse transcriptase (HIV-1-RT)
To further test the model, as shown in Table 4, we predict the native structures for 18 pseudoknot sequences [from Figure 2 in Ref. (59)] that have high binding affinity to HIV-1-RT as selected by the SELEX experiments. We find that, except for the sequence 2.9, our model can correctly predict the native structures for all the rest 17 sequences (out of the 18 sequences). For sequence 2.9, our model predicts that an alternative hairpin is more stable than the pseudoknot suggested in the functional studies (59). The theory–experiment difference for sequence 2.9 may come from other stabilizing interactions, such as triple bases (18–20,29) that are neglected in the current model.
Table 4.
The accuracies of the structure prediction for the pseudoknot sequences with high affinity to HIV-1-RT (59).
| ID | Sequence number | Length | SE | SP |
|---|---|---|---|---|
| 1 | 1.1 | 37 | 0.91 | 0.91 |
| 2 | 1.3a | 37 | 0.89 | 0.80 |
| 3 | 2.9 | 34 | 0.63 | 0.42 |
| 4 | 2.4a | 37 | 1.00 | 0.82 |
| 5 | 2.7a | 36 | 1.00 | 0.80 |
| 6 | 2.11 | 37 | 1.00 | 0.80 |
| 7 | 1.7 | 37 | 1.00 | 0.67 |
| 8 | 1.17 | 37 | 0.89 | 0.80 |
| 9 | 2.1b | 39 | 1.00 | 0.80 |
| 10 | 2.10 | 37 | 1.00 | 0.90 |
| 11 | 1.8 | 39 | 1.00 | 0.70 |
| 12 | 1.6 | 37 | 1.00 | 0.78 |
| 13 | 1.9b | 37 | 0.90 | 0.77 |
| 14 | 2.12 | 37 | 1.00 | 1.00 |
| 15 | 2.5a | 41 | 1.00 | 0.91 |
| 16 | 2.6b | 42 | 1.00 | 1.00 |
| 17 | 2.2b | 42 | 1.00 | 0.60 |
| 18 | 2.3a | 45 | 1.00 | 1.00 |
In the calculation, we consider the coaxial stacking.
Because of the use of the more physical entropy parameters, the present model gives more reliable predictions for these sequences (30). If we delete the coaxial stacking in our calculations, we find that the model predicts the same structures as listed in Table 4 except for sequence 2.5a (entry 15 in Table 4), for which the predicted native structure (without coaxial-stacking) has a poor (SE, SP) value of (0.50, 0.50). This clearly demonstrated the importance of the coaxial stacking in stabilizing the native pseudoknot for sequence 2.5a.
In Tables 3 and 4, the SP parameters for some predicted structures are not as good as SE. This is because these sequences (such as IBV) have a long loop L2 across the shallow groove, and our model predicts that some of the nucleotides in the loops can form intra-loop base pairs. These predicted intra-loop base pairs are not explicitly listed in the experimentally measured structures, so the SP values appear to be less optimal.
Pseudoknots PK1 and PK5–PK17
Pseudoknots are found to be functionally active in viral RNAs (45) and ribosomal RNAs (60). A systematic study for the thermodynamic and structural properties of a specific type of short pseudoknots was reported in Refs. (6,52,61,62). These pseudoknots are denoted as PKi (i = 1, 5, 6, … , 17), where PK5-PK17 have the same helix stems but different loops. We here focus on the pseudoknot-forming sequences PK1 and PK5–17 [PK2–PK4 are hairpin-forming (61,62)]. Table 5 shows the results for the accuracies for our predicted native structures for these 14 PKi pseudoknots. All the predicted structures (PK1 and PK5–17) are in exact agreements with the experiments.
Table 5.
The accuracies for the prediction for the melting temperatures for the PK1 and PK5–17 pseudoknots (61,62).
| ID | Abbreviation | Length | SE | SP | Tm (Experiment) | Tm (Prediction) |
|---|---|---|---|---|---|---|
| 1 | PK1 | 19 | 1.00 | 1.00 | 73°C | 83°C |
| 2 | PK5 | 26 | 1.00 | 1.00 | 64°C | 67°C |
| 3 | PK6 | 25 | 1.00 | 1.00 | 63°C | 67°C |
| 4 | PK7 | 25 | 1.00 | 1.00 | 65°C | 67°C |
| 5 | PK8 | 24 | 1.00 | 1.00 | — | — |
| 6 | PK9 | 23 | 1.00 | 1.00 | 59°C | 72°C |
| 7 | PK10 | 25 | 1.00 | 1.00 | — | — |
| 8 | PK11 | 24 | 1.00 | 1.00 | 63.5°C | 68°C |
| 9 | PK12 | 23 | 1.00 | 1.00 | — | — |
| 10 | PK13 | 22 | 1.00 | 1.00 | — | — |
| 11 | PK14 | 22 | 1.00 | 1.00 | 69.5°C | 71°C |
| 12 | PK15 | 22 | 1.00 | 1.00 | 67°C | 71°C |
| 13 | PK16 | 25 | 1.00 | 1.00 | — | — |
| 14 | PK17 | 23 | 1.00 | 1.00 | 66°C | 68°C |
In the calculation, the coaxial stacking is not included. In the experiment, the ion concentration is the mix 5 mM Mg2+ and 50 mM Na+, which may be close to the 1 M NaCl condition used in the calculation. For each of the sequences listed in the Table, we find a single transition in the calculated melting curve.
Our stability calculation can provide useful evidence for the existence/absence of coaxial stacking. For example, without considering the coaxial stacking, our theory predicts a stability of −4.2 kcal/mol for PK5. The predicted result is quite close to the experimental results of −4.9 kcal/mol (optical) or −4.3 kcal/mol (NMR) (62). Adding the coaxial stacking energy −4.1 kcal/mol (5′CC-GG3′) (51) would overestimate the stability. So the PK5 pseudoknot is unlikely to have the full coaxial stacking. On the other hand, the deficiency in the stability without coaxial stacking suggests that we cannot exclude the possibility of partial coaxial stacking (52). For the PK1 pseudoknot, our predicted free energy without coaxial stacking is −6.4 kcal/mol, which is close to the experimental value (−5.4 kcal/mol) (61). Adding the coaxial stacking free energy of −3.0 kcal/mol (5′CG-CG3′) would also over-estimate the stability. Therefore, the coaxial stacking is unlikely to be formed in PK1. Though the predicted results cannot exclude the possibility of partial coaxial stacking, to simplify our calculation, we would not include the coaxial stacking in our further folding thermodynamics calculations for these sequences.
TYMV and TMV pseudoknots
The TYMV and TMV sequences are parts of the tRNA-like structures in viral RNAs (63–65). Their predicted native pseudoknots are more complex than the simple H-pseudoknots discussed above. As shown in Figures 5a and b, TYMV pseudoknot consists of a closed secondary structure (C2-1) and a H-pseudoknot (C3-1), and the TMV pseudoknot includes three H-pseudoknot elements (C3 − i, i = 1, 2 and 3).
Shown in Figures 5a and b are the predicted native structures for the TYMV and TMV pseudoknots at T = 37°C. The predicted structures agree exactly with the experimental results both with and without considering the coaxial stacking within each pseudoknot.
Other pseudoknots
In Figure 6, we show the predicted native structures for other pseudoknot-forming sequences. The predicted structures agree exactly with the experimental measured ones, except for sequences PKWT and PKDC, which, as shown in Figures 6f and g, each has two predicted structures. For both PKWT and PKDC, one of the two predicted structures (structure II) agrees exactly with experiments and the other predicted structure (structure I) is formed through a single nucleotide sliding in the bulge of stem 2 in structure II.
In conclusion, nearly for all the 63 RNA pseudoknots that we have tested, the model can give good predictions as compared with experiments.
Folding thermodynamics
From the temperature-dependence of the partition function Q(T), we can predict the heat capacity melting curve C(T) for a given sequence: We have calculated the melting curves for PK1 and PK5–17 (totally 14) sequences (6,61,62), and other 8 pseudoknot-forming sequences in Figure 6: T4–28, T4–32 and T4–35 (24,26), G80 (23), mIAP (27), the pseudoknot domain of human telomerase RNA (hTR) (PKWT) (28) and its two mutants (PKDC and ΔU177) (29).
Table 5 shows the comparison between the predicted and experimental melting temperatures for PK1 and PK5–17 sequences. The Table shows good theory–experiment agreements. Since our pseudoknot stability calculation and the theory–experiment comparison indicate that the coaxial-stacking is unlikely to exist in these pseudoknots, we do not include coaxial stacking in the melting curve calculation for these sequences.
In Figure 6, we show the theory–experiment comparisons for eight sequences. For these sequences, since the two helical stems can be coaxial or bent, we compute the melting curves with and without coaxial stacking separately. As shown in the Figure, for pseudoknots T4–28, T4–32 and T4–35, the calculated melting curves with and without coaxial stacking give similar results, and the curves without coaxial stacking show slightly lower melting temperatures.
For the G80 and mIAP pseudoknots, however, the predicted results without the coaxial stacking give much better agreement with the experiments, indicating that coaxial stacking may not exist in these pseudoknots. The predicted absence of coaxial stacking is in agreement with the experiments (23,27), which suggest that the two stems are bent in G80 and mIAP.
For PKWT and its mutants PKDC and ΔU177, the predictions with coaxial stacking are better than those without coaxial stacking, suggesting that coaxial stacking may play a role in stabilizing PKWT and its mutant. Moreover, in the experiment (28), the measured stability for the native structure of wild-type at T = 37°C is −17.8 kcal/mol. Our model predicts that, without coaxial stacking, the predicted PKWT structure II in Figure 6f, which agrees exactly with the experimental structure, has stability of ΔGII = −12.3 kcal/mol, and structure I has stability ΔGI = −13.2 kcal/mol. Adding the stability −3.9 kcal/mol for the coaxial stacking (5′UC-GA3′) would give better agreement with the experiment.
Our theory–experiment agreements shown in Table 5 for the melting temperatures and in Figure 6 for the melting curves are not exact. A major problem is the ion effect. Ions play important roles in RNA pseudoknot folding stability (66,67). In our calculations, the enthalpic and entropic parameters for the helix stems are for the 1 M NaCl condition. In the experiments, however, different concentrations of Mg2+/Na+ or K+ mixture are used. For lower experimental ion concentrations, such as 50 mM Na+ and 1.0 mM Mg2+ in Figures 6a–c; 50 mM K+ for Figure 6e; 200 mM K+ for Figures 6f and g; 200 mM Na+ for Figure 6h, the calculated melting temperatures are higher than the experimental results (See Figure 6). Nevertheless, our theory can predict not only the native structures but also the structural transitions as shown in the melting curves.
Coaxial stacking in pseudoknots
Pseudoknots, such as T4–28, T4–32, T4–35, G80 and mIAP that are predicted not to form coaxial stacking all have a short (mostly 1 nt) loop L1 across the deep groove. Short loops tend to form rigid conformations due to the volume exclusion from the helix stem. Such loop-helix interactions can strongly restrict the configurations of the helix–helix connection, such as coaxial stacking. For example, in the gene 32 mRNA pseudoknot of bacteriophage T2 (43), which has a single-nucleotide loop L1, the helix–helix junction is over-rotated compared to the continuous A-form helix, causing the coaxial stacking impossible.
Longer flexible loops can make the formation of coaxial stacking or partial coaxial stacking possible. For example, pseudoknots PKWT, PKDC and Δ U177, which are predicted to have coaxial stacking, all have larger loops. The PK5 pseudoknot, which has flexible loops L1 and L2 with lengths of 4 and 6-nt, respectively, can possibly form partial coaxial stacking.
Free energy landscape and conformational switch
We introduce the free energy landscape to make a direct structure-free energy connection. The free energy F(x) for a macrostate is defined through a structural parameter (or a parameter set) x. Such a macrostate is a collection of conformations described by x. We choose x = (n, nn) = the number of (native, nonnative) base pairs. Here a base pair is called ‘native’ if it exists in the native structure and ‘nonnative’ otherwise. The free energy landscape F(n, nn) can be computed from the following conditional partition function Q(n, nn):
| 11 |
where is the sum over all the possible conformations with n native and nn nonnative base pairs, respectively. The free energy landscape provides a full view for the stability of all the conformations.
T4-derived pseudoknots
For the T4-derived pseudoknots (T4–28, T4–32 and T4–35 in Figures 6a–c), the stability calculation in the previous section shows that the predicted stability without coaxial stacking gives a better agreement with the experiment. So we assume no coaxial stacking for the T4-derived pseudoknots in the free energy landscape calculation. The predicted structures, as shown in Figures 6a–c, agree exactly with the NMR structures (24,26).
Shown in Figure 7 is the temperature-dependent of the free energy landscape and the conformational transitions for T4–35. The pseudoknotted native structure (N) of T4–35 is predicted to be the single predominant state at T = 0°C. As the temperature is increased, stem 1 is partially unfolded at T = 70°C and a resultant native-like hairpin (X) emerges and coexist with the partially unfolded state (Z). At T = 70°C, the intermediate states Z and X are equally stable. This suggests that the first transition from the pseudoknot structure to native-like hairpin X happens at about 70°C, which is close to the 67°C transition temperature observed in the experiment (26). As the temperature is further increased, stem 2 is disrupted and the pseudoknot is fully unfolded. Since stem 2 is only slightly more stable than stem 1, the melting temperatures for the breaking of stem 1 and of stem 2 are close to each other, resulting in an apparent single peak in the melting curve (Figure 6c).
Since the unfolding pathway of T4–35 RNA pseudoknot involves the intermediate states (Z and X), a simple two-state analysis for the experimental data would give inaccurate results for the enthalpic and entropic parameters (24). In fact, a simple two-state assumption may result in an under-estimation for the folding enthalpy. For example, the experiment gives a total folding enthalpy of about −100.7 kcal/mol (26), but the simple two-state assumption gives a enthalpy change of about −78 kcal/mol (24). From the nearest neighbor interaction model (53), we find that the enthalpy change without considering the coaxial stacking is equal to −93.5 kcal/mol, which is close to the −100.7 kcal/mol experimental result (26). If we further consider the contribution of the unpaired terminal nucleotides (5′CA-G5′), which has (ΔH, ΔS)= (−9.0 kcal/mol,−23.4 cal/mol/K) (53), our predicted enthalpy would be −102.5 kcal/mol, which agrees with the experimental result (−100.7 kcal/mol) very well.
G80 and mIAP pseudoknots
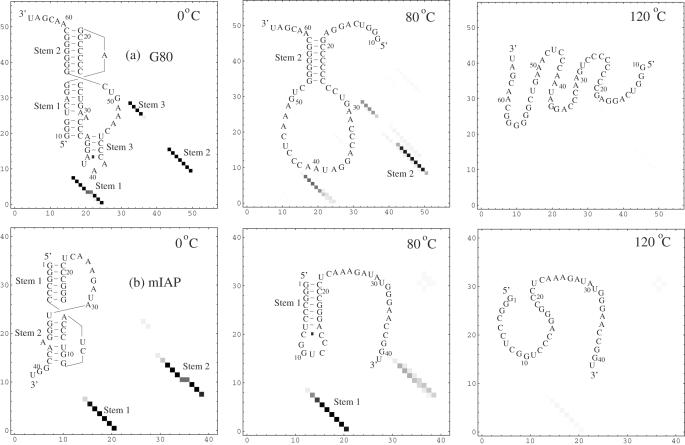
For the G80 and mIAP sequences, two well separated peaks are found in the melting curves (see Figures 6d and e). Our free energy landscape calculation shows that the first peak in the melting curve of G80 (mIAP) corresponds to the pseudoknot → hairpin transition through the disruption of pseudoknot stem 1 (stem 2), while the second transition corresponds to the subsequent unwinding of stem 2 (stem 1) in the hairpin; see Figures 8a and b for the equilibrium unfolding pathways for the two sequences. Experiments show that stem 1 melts before stem 2 for the G80 sequence (23) and stem 2 is disrupted before stem 1 for the mIAP sequence (27). Our predicted pathways are in accordance with the experimental findings. By comparing the unfolding pathways for G80 and mIAP in Figure 8, we find that the pseudoknot can unfold either through unzipping from stem 1 (close to the 5′ end) or from stem 2 (close to the 3′ end).
Figure 8.
The density plot for the base pairing probabilities and the predicted stable structures for (a) the G80 and (b) mIAP pseudoknots at different temperatures.
Human telomerase RNA (hTR) PKWT and the PKDC and ΔU177 mutants
For PKWT (28), our predicted structure II shown in Figure 9 agrees with the experimentally proposed structure (28), and the predicted structure I slightly differs from II by a single-nucleotide shift for the A-U base pairs in stem 2. The melting curve of PKWT (Figure 6f) shows a major peak and a minor shoulder. Our free energy landscape and structural calculations (see Figure 9a) show that the major peak (at lower temperature) corresponds to the formation of two co-existing intermediates: a native-like hairpin structure formed through the disruption of stem 2 and a misfolded hairpin through the complete rearrangement of the base pairs. At T = 80°C, the native-like and the misfolded hairpin intermediates co-exist. The minor shoulder at higher temperature in the melting curve corresponds to the unfolding of the hairpins (28). Our predictions are consistent with the experiment (28), except that an additional minor transition for the disruption of a triple base pairs (28,29) is observed in experiment. Such additional transition is absent in our prediction because the theory does not treat triple base pairs.
Figure 9.
The density plot for the base pairing probabilities and the predicted stable structures for (a) modified telomerase pseudoknot domain (PKWT) in human and (b) its mutant (PKDC) at different temperatures.
As shown in Figure 9, the folding/unfolding of PKWT involves the native-like hairpin intermediate. The pseudoknot → native-like hairpin switch is found to be functionally important in human telomerase RNA (hTR) (28,68,69). The predicted native-like hairpin in Figure 9 is in accordance with the experimentally proposed structure, except that the experimentally proposed hairpin contains tandem base pairs (28,68). The tandem base pairs are not treated in the present form of our model. Experimental mutational studies show that these tandem mismatches have only minor contributions to the hTR function (70).
Our predicted misfolded hairpin in the folding/unfolding of PKWT may also be important for function. Phylogenetic analysis shows that the nucleotides 5′ 107G-111C 3′ and 5′ 115U-119C 3′ in the helix stem of the predicted misfolded hairpin intermediate are highly conserved (>80%) in the published vertebrate telomerase RNA sequences (71). The conserved nucleotides suggest that the misfolded hairpin may serve as the other (hairpin) candidate for the functionally important pseudoknot→ hairpin conformational switch. For the PKDC mutant, the 107GC→ AG mutation would disrupt the most stable base stacking (5′GC-GC3′) in stem 2 of the wild-type (PKWT) and thus destabilize stem 2. As a result, the mutation would cause a decrease in the melting temperature for the disruption of stem 2 (= the first transition in the unfolding process); see Figure 6f for the wild-type PKWT and Figure 6g for the mutant PKDC. In addition, the mutation significantly destabilizes the misfolded hairpin intermediate (see Figure 9a at T = 80°C) that emerges in the unfolding process of PKWT. As a result, the misfolded hairpin is absent in the unfolding process of PKDC.
In contrast, for ΔU177, the deletion of U177 eliminates the 1 nt bulge loop in the (wild-type) stem 2 and thus stabilizes stem 2, which would cause an increase in the transition temperature for the melting of stem 2; see also the melting curves in Figures 6f and h. The prediction agrees with the experiment (29). From the above results for the mutants, we find that the two mutants (107GC→ AG and ΔU177) cause significant changes in the pseudoknot stability. Such changes have been suggested to cause human telomerase diseases (28,29,68,72,73).
Tetrahymena thermophila telomerase RNA pseudoknot
In Tetrahymena thermophila, the telomerase RNA pseudoknot is found to be functionally important. Mutants that disrupt the pseudoknot structure are found to cause low telomerase activity (74). We use the sequences in Figure 1b of Ref. (74) for the predictions. Calculations with and without the coaxial stacking give the same native structures; see Figure 10. Our model predicts that the 71–72G, 84–85C and 84–87C mutations will completely disrupt the pseudoknot structure, and the two compensatory mutations, Comp 1 (71–72G and 84–85C) and Comp 2 (84–87C and 71–74G) can restore the wild-type pseudoknot structure. These predictions are consistent with the experimental results (74). Moreover, the experiments (74) show that the mutants (71–72G, 84–85C and 84–87C) can reduce the telomerase activity to a very low level, which shows that a stable pseudoknot structure is crucial for the functional activity of the telomerase RNA (74,75).
Figure 10.
The density plot for the base pairing probabilities and the predicted stable structures for (a) the telomerase pseudoknot domain in Tetrahymena thermophia and its mutants (b), (c), (d), (e) and (f) at different temperatures. We consider the coaxial stacking in the predictions.
CONCLUSION
Predicting the folding thermodynamics for RNA pseudoknots has been greatly hampered by the lacking of a physical model that can give accurate thermodynamic parameters (especially loop entropy parameters). In the present study, we develop a polymer statistical mechanical model to compute the conformational entropy from first principle. From the rigorous polymer chain conformational count, we derive a set of pseudoknot loop entropy parameters, from which we can compute the pseudoknot partition function and the free energy landscapes and the folding thermodynamics for RNA pseudoknots. Experimental tests for the predicted native structures and the thermal melting curves for a wide range of different pseudoknots show that the model is reliable. Furthermore, from the free energy landscapes and the base pairing probabilities, we predict the equilibrium folding pathways, folding stabilities for RNA pseudoknots. We find that the T4-pseudoknots, the mIAP and the G80 pseudoknots unfold though sequential disruptions of the helix stems without the formation of nonnative intermediates, while the pseudoknot domain of the hTR unfolds through the formation of the native-like and misfolded hairpin intermediates. These folding intermediates are found to be functionally important and mutations that alter the stabilities of these intermediates can cause disease.
Acknowledgments
The authors acknowledge grant support from NIH (GM063732 to S-J.C). Funding to pay the Open Access publication charges for this article was provided by NIH through grant GM063732.
Conflict of interest statement. None declared.
APPENDIX
RNA secondary structure partition function
Closed conformations
For RNA secondary structures without pseudoknots, the hierarchical relationship of the secondary structure results in the following recursive relation for the partition functions (42); see also Figures 4b and c:
| 12 |
where ΔGstack is the free energy of the closing stack formed by the base pairs (a, b) and (a − 1, b + 1)in Figure 4b, and ΔSunstacked(l) is the entropy for a type-t loop of length l (see the central large loop in Figure 4b). C2(x, y) denotes the partition function of the closed conformations from nucleotide x to nucleotide y, denotes the partition function of the type-t open conformations (t = L, M, R, LR) from nucleotide a to nucleotide b shown in Figure 4a.
Open conformations
For RNA secondary structures, can be conveniently calculated recursively from the partition functions for shorter chains (42).
| 13 |
| 14 |
| 15 |
| 16 |
To illustrate the meaning of the above equations, as an example, in Figure 4e we show a diagrammatic illustration for Equation 14.
From Equations 12 and 13–16, the recursive relations for the partition functions for the closed and the open conformations are inter-related. The computation based on the above recursive relations can efficiently give the partition function for any chain segment from a to b:
REFERENCES
- 1.Schimmel P. RNA pseudoknots that interact with components of the translation apparatus. Cell. 1989;58:9–12. doi: 10.1016/0092-8674(89)90395-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pleij C.W.A., Bosch L. RNA pseudoknots—structure, detection, and prediction. Meth. Enzymol. 1989;180:289–303. doi: 10.1016/0076-6879(89)80107-7. [DOI] [PubMed] [Google Scholar]
- 3.Pleij C.W.A. Pseudoknots—a new motif in the RNA game. Trends Biochem. Sci. 1990;15:143–147. doi: 10.1016/0968-0004(90)90214-v. [DOI] [PubMed] [Google Scholar]
- 4.Draper D.E. Pseudoknots and control of protein synthesis. Curr. Opin. Cell Biol. 1990;2:1099–1103. doi: 10.1016/0955-0674(90)90162-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tinoco I., Jr, Puglisi J.D., Wyatt J.R. RNA Folding. In: Eckstein F., Lilley D., editors. Nucleic Acids and Molecular Biology. vol. 4. Berlin: Springer-Verlag press; 1990. pp. 205–226. [Google Scholar]
- 6.Puglisi J.D., Wyatt J.R., Tinoco I., Jr RNA pseudoknots. Acc. Chem. Res. 1991;24:152–158. [Google Scholar]
- 7.ten Dam E., Pleij K., Draper D. Structural and functional aspects of RNA pseudoknots. Biochemistry. 1992;31:11665–11676. doi: 10.1021/bi00162a001. [DOI] [PubMed] [Google Scholar]
- 8.Westhof E., Masquida B., Jaeger L. RNA tectonics: towards RNA design. Folding Des. 1996;1:R78–R88. doi: 10.1016/S1359-0278(96)00037-5. [DOI] [PubMed] [Google Scholar]
- 9.Brion P., Westhof E. Hierarchy and dynamics of RNA folding. Annu. Rev. Biophys. Biomol. Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- 10.Batey R.T., Rambo R.P., Doudna J.A. Tertiary motifs in RNA structure and folding. Angew. Chem. Int. Ed. 1999;38:2327–2343. doi: 10.1002/(sici)1521-3773(19990816)38:16<2326::aid-anie2326>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 11.Tinoco I., Jr, Bustamante C. How RNA folds. J. Mol. Biol. 1999;293:271–281. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
- 12.Giedroc D.P., Theimer C.A., Nixon P.L. Structure, stability and function of RNA pseudoknots involved in stimulating ribosomal frameshifting. J. Mol. Biol. 2000;298:167–185. doi: 10.1006/jmbi.2000.3668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Staple D.W., Butcher S.E. Pseudoknots: RNA structures with diverse functions. PLoS Biol. 2005;3:956–959. doi: 10.1371/journal.pbio.0030213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gesteland R.F., Atkins J.F. Recoding: dynamic reprogramming of translation. Annu. Rev. Biochem. 1996;65:741–768. doi: 10.1146/annurev.bi.65.070196.003521. [DOI] [PubMed] [Google Scholar]
- 15.Liphardt J., Napthine S., Kontos H., Brierley I. Evidence for an RNA pseudoknot loop-helix interaction essential for efficient-1 ribosomal frameshifting. J. Mol. Biol. 1999;288:321–335. doi: 10.1006/jmbi.1999.2689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Plant E.P., Jacobs K.L., Harger J.W., Meskauskas A., Jacobs J.L., Baxter J.L., Petrov A.N., Dinman J.D. The 9 Å solution: how mRNA pseudoknots promote efficient programmed-1 ribosomal frameshifting. RNA. 2003;9:168–174. doi: 10.1261/rna.2132503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Plant E.P., Dinman J.D. Torsional restraint: a new twist on frameshifting pseudoknots. Nucleic Acids Res. 2005;33:1825–1833. doi: 10.1093/nar/gki329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Su L., Chen L., Egli M., Berger J.M., Rich A. Minor groove RNA triplex in the crystal structure of a ribosomal frameshifting viral pseudoknot. Nature Struct. Biol. 1999;6:285–292. doi: 10.1038/6722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kim Y.G., Su L., Maas S., O'Neill A., Rich A. Specific mutations in a viral RNA pseudoknot drastically change ribosomal frameshifting efficiency. Proc. Natl. Acad. Sci. USA. 1999;96:14234–14239. doi: 10.1073/pnas.96.25.14234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cornish P.V., Hennig M., Giedroc D.P. A loop 2 cytidine-stem 1 minor groove interaction as a positive determinant for pseudoknot-stimulated—1 ribosomal frameshifting. Proc. Natl. Acad. Sci. USA. 2005;102:12694–12699. doi: 10.1073/pnas.0506166102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gluick T.C., Draper D.E. Thermodynamics of folding a pseudoknotted mRNA fragment. J. Mol. Biol. 1994;241:246–262. doi: 10.1006/jmbi.1994.1493. [DOI] [PubMed] [Google Scholar]
- 22.Gluick T.C., Gerstner R.B., Draper D.E. Effects of Mg2+, K+, H+ on an equilibrium between RNA alternative conformations of an RNA pseudoknot. J. Mol. Biol. 1997;270:451–463. doi: 10.1006/jmbi.1997.1119. [DOI] [PubMed] [Google Scholar]
- 23.Gluick T.C., Wills N.M., Gesteland R.F., Draper D.E. Folding of an mRNA pseudoknot required for stop codon readthrough: effects of mono- and divalent ions on stability. Biochemistry. 1997;36:16173–16186. doi: 10.1021/bi971362v. [DOI] [PubMed] [Google Scholar]
- 24.Qiu H.W., Kaluarachchi K., Du Z.H., Hoffman D.W., Giedroc D.P. Thermodynamics of folding of the RNA pseudoknot of the T4 Gene 32 autoregulatory messenger RNA. Biochemistry. 1996;35:4176–4186. doi: 10.1021/bi9527348. [DOI] [PubMed] [Google Scholar]
- 25.Nixon P.L., Giedroc D.P. Equilibrium unfolding (folding) pathway of a model H-type pseudoknotted RNA: the role of magnesium ions in stability. Biochemistry. 1998;37:16116–16129. doi: 10.1021/bi981726z. [DOI] [PubMed] [Google Scholar]
- 26.Theimer C.A., Wang Y., Hoffman D.W., Krisch H.M., Giedroc D.P. Non-nearest neighbor effects on the thermodynamics of unfolding of a model mRNA pseudoknot. J. Mol. Biol. 1998;279:545–564. doi: 10.1006/jmbi.1998.1812. [DOI] [PubMed] [Google Scholar]
- 27.Theimer C.A., Giedroc D.P. Equilibrium unfolding pathway of an H-type RNA pseudoknot which promotes programmed-1 ribosomal frameshifting. J. Mol. Biol. 1999;289:1283–1299. doi: 10.1006/jmbi.1999.2850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Theimer C.A., Finger L.D., Trantirek L., Feigon J. Mutations linked to dyskeratosis congenita cause changes in the structural equilibrium in telomerase RNA. Proc. Natl Acad. Sci. USA. 2003;100:449–454. doi: 10.1073/pnas.242720799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Theimer C.A., Blois C.A., Feigon J. Structure of the human telomerase RNA pseudoknot reveals conserved tertiary interactions essential for function. Mol. Biol. 2005;17:671–682. doi: 10.1016/j.molcel.2005.01.017. [DOI] [PubMed] [Google Scholar]
- 30.Rivas E., Eddy S.R. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 1999;285:2053–2068. doi: 10.1006/jmbi.1998.2436. [DOI] [PubMed] [Google Scholar]
- 31.Lyngsø R.B., Pedersen C.N.S. RNA pseudoknot prediction in energy-based models. J. Comput. Biol. 2000;7:409–427. doi: 10.1089/106652700750050862. [DOI] [PubMed] [Google Scholar]
- 32.Dirks R.M., Pierce N.A. A partition function algorithm for nucleic acid secondary structure including pseudoknots. J. Comput. Chem. 2003;24:1664–1677. doi: 10.1002/jcc.10296. [DOI] [PubMed] [Google Scholar]
- 33.Dirks R.M., Pierce N.A. An algorithm for computing nucleic acid base-pairing probabilities including pseudoknots. J. Comput. Chem. 2004;25:1295–1304. doi: 10.1002/jcc.20057. [DOI] [PubMed] [Google Scholar]
- 34.Ren J., Rastegari B., Condon A., Hoos H.H. HotKnots: heuristic prediction of RNA secondary structures including pseudoknots. RNA. 2005;11:1494–1504. doi: 10.1261/rna.7284905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gultyaev A.P., Van Batenburg F.H.D., Pleij C.W.A. An approximation of loop free energy values of RNA H-pseudoknots. RNA. 1999;5:609–617. doi: 10.1017/s135583829998189x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Aalberts D.P., Hodas N.O. Asymmetry in RNA pseudoknots: observation and theory. Nucleic Acids Res. 2005;33:2210–2214. doi: 10.1093/nar/gki508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lucas A., Dill K.A. Statistical mechanics of pseudoknot polymers. J. Chem. Phys. 2003;119:2414–2421. [Google Scholar]
- 38.Kopeikin Z., Chen S.-J. Statistical thermodynamics for chain molecules with simple RNA tertiary contacts. J. Chem. Phys. 2005;122:094909. doi: 10.1063/1.1857831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kopeikin Z., Chen S.-J. Folding thermodynamics of pseudoknotted chain conformations. J. Chem. Phys. 2006;124:154903. doi: 10.1063/1.2188940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Olson W.K. Configurational statistics of polynucleotide chains: an updated virtual bond model to treat effects of base stacking. Macromolecules. 1980;13:721–728. [Google Scholar]
- 41.Duarte C.M., Pyle A.M. Stepping through an RNA structure: a novel approach to conformational analysis. J. Mol. Biol. 1998;284:1465–1478. doi: 10.1006/jmbi.1998.2233. [DOI] [PubMed] [Google Scholar]
- 42.Cao S., Chen S.-J. Predicting RNA folding thermodynamics with a reduced chain representation model. RNA. 2005;11:1884–1897. doi: 10.1261/rna.2109105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Holland J.A., Hansen M.R., Du Z.H., Hoffman D.W. An examination of coaxial stacking of helical stems in a pseudoknot motif: the gene 32 messenger RNA pseudoknot of bacteriophage T2. RNA. 1999;5:257–271. doi: 10.1017/s1355838299981360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Biswas R., Mitra S.N., Sundaralingam M. 1.76 Å structure of a pyrimidine start alternating A-RNA hexamer r(CGUAC)dG. Acta Cryst. D. 1998;54:570–576. doi: 10.1107/s0907444997013097. [DOI] [PubMed] [Google Scholar]
- 45.Pleij C.W.A., Rietveld K., Bosch L. A new principle of RNA folding based on pseudoknotting. Nucleic Acids Res. 1985;13:1717–1731. doi: 10.1093/nar/13.5.1717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jacobson H., Stockmayer W.H. Intramolecular reaction in polycondensations. I. The theory of linear systems. J. Chem. Phys. 1950;18:1600–1606. [Google Scholar]
- 47.Poland D., Scheraga H.A. Occurrence of a phase transitions in nucleic acid models. J. Chem. Phys. 1966;45:1464–1469. doi: 10.1063/1.1727786. [DOI] [PubMed] [Google Scholar]
- 48.Fisher M.E. Effect of excluded volume on phase transitions in biopolymers. J. Chem. Phys. 1966;45:1469–1473. [Google Scholar]
- 49.Chen S.-J., Dill K.A. Theory for the conformational changes of double-stranded chain molecules. J. Chem. Phys. 1998;109:4602–4616. [Google Scholar]
- 50.Chen S.-J., Dill K.A. RNA folding energy landscapes. Proc. Natl. Acad. Sci. USA. 2000;97:646–651. doi: 10.1073/pnas.97.2.646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Walter A.E., Turner D.H. Sequence dependence of stability for coaxial stacking of RNA helixes with Watson-Crick base paired interfaces. Biochemistry. 1994;33:12715–12719. doi: 10.1021/bi00208a024. [DOI] [PubMed] [Google Scholar]
- 52.Puglisi J.D., Wyatt J.R., Tinoco I., Jr Conformation of an RNA pseudoknot. J. Mol. Biol. 1990;214:437–453. doi: 10.1016/0022-2836(90)90192-O. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Serra M.J., Turner D.H. Predicting thermodynamic properties of RNA. Meth. Enzymol. 1995;259:242–261. doi: 10.1016/0076-6879(95)59047-1. [DOI] [PubMed] [Google Scholar]
- 54.Andronescu M., Zhang Z., Condon A. Secondary structure prediction of interacting RNA molecules. J. Mol. Biol. 2005;345:987–1001. doi: 10.1016/j.jmb.2004.10.082. [DOI] [PubMed] [Google Scholar]
- 55.Cao S., Chen S.J. Free energy landscapes of RNA/RNA complexes: with applications to snRNA complexes in spliceosomes. J. Mol. Biol. 2006;357:292–312. doi: 10.1016/j.jmb.2005.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Du Z.H., Hoffman D.W. An NMR and mutational study of the pseudoknot within the gene 32 mRNA of bacteriophage T2: insights into a family of structurally related RNA pseudoknots. Nucleic Acids Res. 1997;25:1130–1135. doi: 10.1093/nar/25.6.1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Shen L.X., Tinoco I., Jr The structure of an RNA pseudoknot that causes efficient frameshifting in mouse mammary-tumor virus. J. Mol. Biol. 1995;247:963–978. doi: 10.1006/jmbi.1995.0193. [DOI] [PubMed] [Google Scholar]
- 58.van Batenburg F.H.D., Gultyaev A.P., Pleij C.W.A., Ng J., Oliehoeck J. Pseudobase: a database with RNA pseudoknots. Nucleic Acids Res. 2000;28:201–204. doi: 10.1093/nar/28.1.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tuerk C., MacDougal S., Gold L. RNA pseudoknots that inhibit human immunodeficiency virus type 1 reverse transcriptase. Proc. Natl. Acad. Sci. USA. 1992;89:6988–6992. doi: 10.1073/pnas.89.15.6988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Göringer H.U., Wagner R. Does 5S RNA from E. Coli have a pseudoknotted structure? Nucleic Acids Res. 1986;14:7473–7485. doi: 10.1093/nar/14.18.7473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Puglisi J.D., Wyatt J.R., Tinoco I., Jr A pseudoknotted RNA oligonucleotide. Nature. 1988;331:283–286. doi: 10.1038/331283a0. [DOI] [PubMed] [Google Scholar]
- 62.Wyatt J.R., Puglisi J.D., Tinoco I., Jr RNA pseudoknots–stability and loop size requirements. J. Mol. Biol. 1990;214:455–470. doi: 10.1016/0022-2836(90)90193-P. [DOI] [PubMed] [Google Scholar]
- 63.van Belkum A., Abrahams J.P., Pleij C.W.A., Bosch L. Five pseudoknots are present at the 204 nucleotides long 3′ noncoding region of tobacco mosaic virus RNA. Nucleic Acids Res. 1985;13:7673–7686. doi: 10.1093/nar/13.21.7673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Mans R.M.W., Pleij C.W.A., Bosch L. tRNA-like structures: structure, function and evolutionary significance. Eur. J. Biochem. 1991;201:303–324. doi: 10.1111/j.1432-1033.1991.tb16288.x. [DOI] [PubMed] [Google Scholar]
- 65.Kolk M.H., van der Graaf M., Wijmenga S.S., Pleij C.W.A., Heus H.A., Hilbers C.W. NMR structure of a classical pseudoknot: Interplay of single- and double-stranded RNA. Science. 1998;280:434–438. doi: 10.1126/science.280.5362.434. [DOI] [PubMed] [Google Scholar]
- 66.Draper D.E., Grilley D., Soto A.M. Ions and RNA folding. Annu. Rev. Biophys. Biomol. Struct. 2005;34:221–243. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 67.Woodson S.A. Metal ions and RNA folding: a highly charged topic with a dynamic future. Curr. Opin. Chem. Biol. 2005;9:104–109. doi: 10.1016/j.cbpa.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 68.Comolli L.R., Smirnov I., Xu L.F., Blackburn E.H., James T.L. A molecular switch underlies a human telomerase disease. Proc. Natl. Acad. Sci. USA. 2002;99:16998–17003. doi: 10.1073/pnas.262663599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Antal M., Boros E., Solymosy F., Kiss T. Analysis of the structure of human telomerase RNA in vivo. Nucleic Acids. Res. 2002;30:912–920. doi: 10.1093/nar/30.4.912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Chen J.L., Greider C.W. Functional analysis of the pseudoknot structure in human telomerase RNA. Proc. Natl. Acad. Sci. USA. 2005;102:8080–8085. doi: 10.1073/pnas.0502259102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Chen J.L., Blasco M.A., Greider C.W. Secondary structure of vertebrate telomerase RNA. Cell. 2000;100:503–514. doi: 10.1016/s0092-8674(00)80687-x. [DOI] [PubMed] [Google Scholar]
- 72.Chen J.L., Greider C.W. Telomerase RNA structure and function: implications for dyskeratosis congenita. Trends Biochem. Sci. 2004;29:183–192. doi: 10.1016/j.tibs.2004.02.003. [DOI] [PubMed] [Google Scholar]
- 73.Marrone A., Walne A., Dokal I. Dyskeratosis congenita: telomerase, telomeres and anticipation. Curr. Opin. Genet. Dev. 2005;15:249–257. doi: 10.1016/j.gde.2005.04.004. [DOI] [PubMed] [Google Scholar]
- 74.Gilley D., Blackburn E.H. The telomerase RNA pseudoknot is critical for the stable assembly of a catalytically active ribonucleoprotein. Proc. Natl. Acad. Sci. USA. 1999;96:6621–6625. doi: 10.1073/pnas.96.12.6621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Blackburn E.H. Telomerase RNA structure and function. In: Simons R.W., Grunberg-Manago M., editors. RNA Structure and Function. NY: Cold Spring Harbor Lab. Press; 1998. pp. 669–693. [Google Scholar]