An Approach to Forecasting Health Expenditures, with Application to the U.S. Medicare System

Abstract

Objective

To quantify uncertainty in forecasts of health expenditures.

Study Design

Stochastic time series models are estimated for historical variations in fertility, mortality, and health spending per capita in the United States, and used to generate stochastic simulations of the growth of Medicare expenditures. Individual health spending is modeled to depend on the number of years until death.

Data Sources/Study Setting

A simple accounting model is developed for forecasting health expenditures, using the U.S. Medicare system as an example.

Principal Findings

Medicare expenditures are projected to rise from 2.2 percent of GDP (gross domestic product) to about 8 percent of GDP by 2075. This increase is due in equal measure to increasing health spending per beneficiary and to population aging. The traditional projection method constructs high, medium, and low scenarios to assess uncertainty, an approach that has many problems. Using stochastic forecasting, we find a 95 percent probability that Medicare spending in 2075 will fall between 4 percent and 18 percent of GDP, indicating a wide band of uncertainty. Although there is substantial uncertainty about future mortality decline, it contributed little to uncertainty about future Medicare spending, since lower mortality both raises the number of elderly, tending to raise spending, and is associated with improved health of the elderly, tending to reduce spending. Uncertainty about fertility, by contrast, leads to great uncertainty about the future size of the labor force, and therefore adds importantly to uncertainty about the health-share of GDP. In the shorter term, the major source of uncertainty is health spending per capita.

Conclusions

History is a valuable guide for quantifying our uncertainty about future health expenditures. The probabilistic model we present has several advantages over the high–low scenario approach to forecasting. It indicates great uncertainty about future Medicare expenditures relative to GDP.

The United States devoted 13.6 percent of its GDP (gross domestic product) to health care in 1998, more than any other OECD nation (Organization for Economic Cooperation and Development 2000). Most of this was funded privately (55 percent), either out of pocket, or through personal or employer-provided health insurance. However, public financing has been steadily increasing since about 1965 when only 25 percent of health expenditures were publicly funded (Health Care Financing Administration 1998). This expansion mainly reflects the founding and growth of the federal Medicare insurance program. Medicare provides basic health coverage for hospital stays, physician visits, and certain outpatient services to those aged 65 and older. It is currently one of the largest federal programs, representing one tenth of the federal budget. As a result of recent legislation imposing some temporary spending freezes, Medicare spending as a percent of GDP has declined for the last two years. But looming on the horizon is a large demographic transformation ushered in by the retirement of the baby boomers and the possibility of dramatic increases in their longevity.

Many forces will influence the future trajectory of health expenditures in the twenty-first century: new medical technologies, policies regarding access to care, the costs of services, the health status of the population, population aging, and the growth of the economy. Some, like population aging, change so slowly as to have little impact in the short-run and can be forecast with high certainty for a number of decades. Others, like health policies, or the costs of a given procedure, can change quickly, and therefore can have large impacts in the short run as well as the long run, and are more difficult to forecast. A forecast of health expenditures will depend on the assumed future course of each of these factors. Needless to say, there is a large amount of uncertainty in the resulting forecasts.

Many people are deeply skeptical of long-run forecasts. Indeed, long-run forecasts of the Medicare system have been criticized as “an enterprise in comparative fantasy” by the former director of the agency responsible for issuing them (cited in White 1999). In our view, however, if a forecast provides a good estimate of the uncertainty surrounding it, then users can decide for themselves whether longer-term forecasts provide information that is of use to them.

Over the past decade, advisory panels to Social Security and Medicare have recommended the use of stochastic methods for dealing with uncertainty (Board of Trustees of the Federal Supplementary Medical Insurance Trust Fund 2001, p. 79). For example, the 2000 Medicare Technical Review Panel on the Trustees Reports noted that “although stochastic modeling is complicated, it can result in enhanced insight into the uncertainty associated with health care cost projections” (Technical Review Panel on the Medicare Trustees Reports 2000, p. 49).

In this paper, we develop stochastic forecasts of Medicare expenditures over the next 75 years. We first discuss our general approach to forecasting each of the main components entering into the overall projection. We then consider problems with the traditional approach to assessing the uncertainty in long-run forecasts of this kind, and describe an alternative approach. Finally, we discuss the results of applying these procedures and approaches to the specific case of the U.S. Medicare system. These methods may be applicable in other countries, despite differences in health care systems.

A Simple Accounting Model

In a simple accounting model, annual health expenditures can be expressed as the sum of the number of people in a given health status times the annual spending associated with that status. Typically, policymakers will be more interested in their expenditures relative to the size of the economy, or GDP, than in the projected expenditures per se. The Health Care Financing Administration (HCFA) projects the gap between the growth rate of health spending per beneficiary and the growth rate of per capita GDP, a point which we will discuss later. For the moment, we note that this approach filters out the effects of uncertainty in the rate of growth of per capita GDP in the future. That is, if we restrict our attention to projecting health care expenditures as a share of GDP, then variations in the rate of growth of per capita GDP affect the numerator and denominator in exactly the same way, and therefore have no effect on the projected share, and can be ignored. In the following sections, we briefly discuss each component of our forecast: health status, population, and annual spending per beneficiary.

Health Status

A population's need for health care depends not only on its size, but also on its health status. How can health status be projected into the future? One straightforward approach notes that health care expenditures are strongly associated with age. This approach implicitly assumes that health status is fixed in relation to age and sex, so that forecasts of population by age and sex can readily be translated into forecasts of aggregate health status. This is roughly the method used in the United States by HCFA for its long-run forecasts of Medicare reimbursements for hospital stays. Unfortunately, the assumption of a fixed age schedule of health status is improbable over a long forecast horizon. In an influential series of articles, Manton and his colleagues (Manton, Stallard, and Liu 1993; Manton and Stallard 1994) construct structural models for health status as a function of demographic characteristics, lifestyle behaviors, and risk factors. However, in order to generate forecasts from these models, one needs to first develop forecasts of the lifestyle behaviors or risk factors, which is a challenging problem. Even then, the highly nonlinear structure of the models might lead to forecast instability.

Some other approaches have projected broad measures of disability based on historical trends. For example, Singer and Manton (1998) project age-specific disability rates based on Activities of Daily Living (ADLs) and Instrumental Activities of Daily Living (IADLs) as measures of the health status of the population, extrapolating trends observed in the Long Term Care Survey data. They forecast a substantial reduction in health care demand among the elderly—enough to offset the effects of population aging on U.S. Medicare spending over the next 75 years.

Some analysts (Lubitz and Prihoda 1984; Fuchs 1984) have noted that the association of health spending with age derives from a more fundamental underlying relationship between age and the fraction of people who are near to death, at least for the older population. Of the people alive at any given age, some fraction will survive for another year, and the remaining fraction will die within the year. These analysts have shown that at least over age 65, there is little variation in health spending with age for those who survive. The strong association of health spending with age is due to the strong association of age with the proportion near death. This observation suggests that instead of holding fixed the relation between health and age, one instead hold fixed the relation between health and time until death. As time passes, life expectancy increases in the population and mortality falls, reducing the proportion of the population near death at any given age, a change that is associated with an improvement in the average health status at any given age.

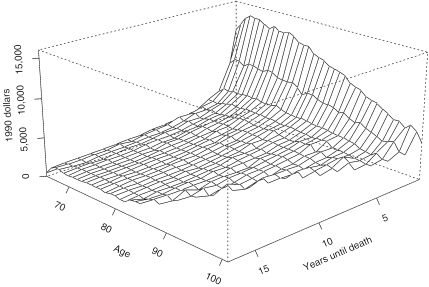
Our approach in this article derives from these empirical studies. Figure 1 shows the association between per capita U.S. Medicare expenditures around 1990 by age and by time until death. These data reflect mainly expenditures for hospital stays and physician visits for the elderly. We must be careful in generalizing from this experience since the same relationship may not exist at younger ages, or for other types of health expenditures such as long-term care and prescription drugs (for example, see Spillman and Lubitz 2000). Here we will apply this approach only to forecasting Medicare expenditures, leaving open the question of whether this method might be more generally applicable.

Figure 1.

Medicare Spending per Beneficiary by Age and Time-Until-Death Source: Author's calculation from data provided by James Lubitz, based on retrospective costs of 1990/91 decedents

The logic of this approach is that health care usage depends on health care needs, which in turn depend on health status. Those who are fewer years from death are presumably less healthy, so time until death can be used as a proxy for health status. For those who die from accidents or violent deaths, this proxy will be useless, but for most people it may be quite good. Indeed, historical data for the U.S. Medicare program over the past two decades indicates that the schedule has been very stable (see Miller 2001). This gives us some confidence that its shape (as opposed to its level) will persist in the future. Miller suggests that the remaining variation in health spending by age, after controlling for time until death, may not be stable, since it may reflect either current medical views about providing health care to seriously ill people at very advanced ages, or current levels of frailty among the elderly, both of which are mutable.

The distribution of the population by time until death is never actually provided in published population projections, but it can be calculated from the information that is ordinarily provided. Combining this with a schedule relating individual health spending to individual time until death, we can calculate the influence of demographic change on health care spending. We assume that the shape of this schedule will be invariant over the projection period, but that its level will increase as health spending rises for a person of a given health status. Similarly, this kind of calculation can be used to standardize data on past health care spending, to purge it of demographic influences. This adjusted series can then be forecasted by some means, and the forecasted series can be used to multiply or shift the schedule of spending by time until death.

Although this approach is appealing in a number of ways, it also has important conceptual drawbacks. After all, health status is in most cases the driving force behind mortality, rather than the reverse. It would be more natural to forecast health status first, and then use it to derive mortality forecasts, rather than the reverse. Our mortality forecast is only an extrapolation of historical trends, with no biomedical content, so the same can be said of the health distribution implied by our mortality projections using the time until death schedule. In defence of this approach, however, we emphasize that our forecasting method for mortality is fairly well established and accepted, has been tested on historical data, and performs well.

If it is problematic to derive implicit forecasts of health status from explicit forecasts of mortality, as if mortality drove health rather than the reverse, then it is equally questionable to forecast mortality as a basis for forecasting health care spending, as if health care expenditures and the services they buy have no influence on mortality. Looked at in this way, our approach appears frankly perverse. Nonetheless, we believe it makes sense. First, there is surprisingly little evidence that health care expenditures influence the trajectory of mortality. If there appeared to be a strong relationship, then we would need to alter our approach. Second, most countries have long time series for mortality, often stretching back one hundred years or more. Comparable historical data do not exist for any country for health status or for health care services. Third, mortality has exhibited a remarkably stable and linear trend over the past century for many industrial countries, at least when measured by the k factor of the Lee-Carter method (Lee and Carter 1992; Lee and Miller 2001; Tuljapurkar et al. 2000). Such trends are sustained despite variations in governmental health policy, the development of new medical technologies such as antibiotics, and the decline of infectious disease. For these reasons, we believe it is reasonable to forecast mortality independently, using the methods we discuss below.

Population

Population projections are available for virtually every country in the world, either from a national statistical agency or lacking that, from the United Nations. We will briefly discuss some issues that arise, since future population aging is expected to be an important force causing rising health care expenditures.

First consider mortality. We believe that official statistical agencies have systematically underprojected mortality declines and gains in life expectancy. In Lee and Miller (2001) we analyzed all past mortality projections by the Office of the Actuary of the U.S. Social Security Administration. We found that in every decade except the 1980s, the actuary underprojected mortality decline. A recent study by the U.S. National Academy of Sciences (2000) confirmed an earlier study by Keilman (1997), finding that official population projections and those of the United Nations consistently underestimated the size of the future elderly population, particularly at the higher ages, due to underprediction of mortality decline.

This tendency may well be continuing. Tuljapurkar et al. (2000), using the Lee-Carter (1992) forecasting method we will describe below, forecasted mortality for the G7 countries out to 2050. Forecasts were generally 1.5 to 4 years or more above the official forecasts by 2050. The analysis of recent mortality trends from age 80 to 100 by Kannisto et al. (1994) indicates more rapid decline at these advanced ages than is projected by official agencies in OECD countries.

In the forecasts we present in the second half of the article, we use the Lee-Carter method (Lee and Carter 1992; Lee and Miller 2001). This extrapolative method fits a model to long historical time series of age specific death rates. It estimates an index of the intensity of mortality, k_t, which can then be forecast using statistical time series analysis. Using the model, the projected age specific death rates can be calculated from k, along with life expectancies and other life table variables of interest. The method produces a probability distribution for each rate and for life expectancy itself for each future year, based on the variability and fitting errors observed in the past. Extensive historical testing of this model on the historical U.S. data, and more limited testing on historical data for Japan, Sweden, France, and Canada, confirm that it would have produced accurate forecasts in the past, relative to the estimated probability bounds.

The Social Security Administration forecasts life expectancy in the United States to reach 83.0 in 2075 in their middle scenario, with low and high scenario forecasts of 79.5 and 87.1. These Social Security forecasts are also used by HCFA and by CBO. We forecast 50 percent more rapid decline in mortality than these official forecasts, with life expectancy in 2075 of 86 years, with a 95 percent probability interval of 82 to 90.

Now consider fertility. In our forecasts, we have constrained the long run mean fertility to equal a pre-specified trajectory, and superimposed the error process derived from the time series analysis (Lee 1993; Lee and Tuljapurkar, 1994). This approach yields fertility forecasts with means corresponding to the pre-specified trajectory, but with uncertainty about that mean. For the mean trajectory, after careful consideration, we chose the middle projection of the Social Security Actuary, with an ultimate total fertility rate (TFR) of 1.95 births per woman, which we believe reasonable. We estimate the variance and autocovariance structure of “innovations” to the fertility process from time series analysis of the historical U.S. TFR.

Immigration can also have an important influence on demographic change, including population aging, although its effect depends strongly on whether and how quickly the fertility of immigrants and their descendants converges to that of the native population. In our population projections we have assumed immigration at the rates projected by the Social Security Administration, that is, net immigration of 900,000 per year. Implicit in the fertility assumption (see above) is the expectation that fertility of immigrants converges fairly quickly to that of natives, as has been the case in the past in the United States.

Health Spending Per Beneficiary

Recent research on costs of treating heart attacks (Cutler et al. 1998) has found that medical price changes have risen at a rate close to that of the general price level, while a cost of living type measure, adjusted for quality changes, has actually risen about 1 percent per year more slowly than the general price level. However, technical progress in medicine constantly replaces older procedures with newer, which are typically more expensive. There is debate over the extent to which the new, more expensive procedures or drugs are really superior to the old, and it appears that policy could exert a powerful influence at this point by slowing the adoption of the new and costlier treatments.

We will not attempt to model and forecast this complicated process. Instead, we will forecast based on observed past trends in actual expenditures, which combine the effects of changes in prices and in the quantity and quality of services consumed. As discussed earlier, future per capita spending depends on health status of the population, and on the spending for each health status category. In our approach, health status is proxied by time until death (without disaggregating by age), and so the relevant spending measure is spending by time until death, rather than spending for treating specific medical conditions, or spending for specific procedures. However, Cutler and Sheiner (2000) found that after controlling for being in the final year of life (that is, within one year of death), disability conditions have an independent effect on health spending, suggesting that a multifactoral model of spending may be more appropriate. We retain the simple time-until-death approach, due to the difficulties in forecasting these disability conditions.

We assume that the schedule of spending by time until death has a fixed shape, and that the level of spending by time until death is determined by multiplying this fixed schedule by a shifting index of spending. Historical estimates of this index can be formed by standardizing the per capita spending in the past for changes in the distribution of time until death in the population. Then the index can be modelled and forecast using some method such as time series analysis.

Both HCFA and CBO analyze and project the gap between the growth rate of health care spending per capita and the growth of GDP per capita (or of wages), rather than health care spending itself. Implicit in this procedure is the important assumption that the gap is independent of the rate of growth of GDP, and therefore that economic growth in general can do nothing to increase or decrease health care expenditures as a share of GDP. It is assumed that more rapid economic growth would simply raise the rate of growth of health expenditures, one-to-one. This assumption is justified in several ways: some regressions of health expenditure growth rates on economic growth rates yield a coefficient near unity; more rapid economic growth would raise the demand for health care; higher wages throughout the economy would force the health care industry to raise wages as well. For present purposes, we will simply rely on the Technical Panel's discussion and conclusion on this matter (see Technical Review Panel on the Medicare Trustees Reports 2000, pp. 27–42.)

The U.S. Medicare system was instituted in 1965, and after erratic variation during the start-up period, a useable series of growth rates is available from 1970 through 2000. These differential rates of growth between per-beneficiary health spending and per-capita GDP fluctuate considerably from year to year, in part reflecting changes in Medicare policy. These year-to-year fluctuations may not be representative of the longer-run uncertainties arising from policy and other sources. Furthermore, we are interested in modelling the underlying trend in health spending due to factors relating to changing technology or medical practice and not those introduced by policy changes in the particular health program. For these reasons, the latest Medicare Trustees Technical Report (Technical Review Panel on the Medicare Trustees Reports 2000, p. 29) suggests that more general data for national per-capita health expenditures be used rather than the specific data on Medicare or any other program. Also, this provides a longer time series and is available for many countries. The mean of this growth rate series is somewhat lower, and its variability is somewhat less, compared to the Medicare index. We subtract the growth rate of GDP per capita from the growth rate of national health care expenditures to form a time series of the gap.

We model and forecast the gap using time series methods. The historical gap series can provide useful information about the variability from year to year in the gap, but not necessarily about the long-run mean trajectory of the gap for the future. For the mean, we think it is important to take into account the views of experts who have made judgmental forecasts reflecting detailed quantitative research into the forces driving spending increases. We take our mean forecast trajectory from the latest forecasts by the Medicare Trustees (issued in March 2001), which were based on the suggestions of the Medicare Trustees Technical Advisory Panel. One might well say that we have outsourced the single most important component of our forecast. This is true, and we can only claim some modest added value on our part, by developing the mechanics of the time-until-death framework, and by putting the forecast in a stochastic context.

We forecast spending using a constrained mean time series model so that the average differential over all simulations mimics the long-run intermediate trajectory of the Trustees. This trajectory starts at the current gap, and trends upward until it reaches a gap of 1 percent over per capita GDP growth in 2025 (Board of Trustees of the Federal Hospital Insurance Trust Fund 2001, p. 9). Our estimated variance structure for the errors in the fitted time series model is then assumed to hold for the forecast period as well. The result is a very wide 95 percent probability interval for the gap between the growth rate of GDP per capita and the growth rate of spending per enrollee, of plus or minus around 5 percent, for a width of 10 percent. However, if we calculate the range for the cumulative average value of the gap, most of this uncertainty cancels out over time, leaving a range only about one-fifth this wide, from 0.1 percent to 1.8 percent. Based on the projected gap and its variance, and ignoring the effects of population aging and changing health status in the population, we can forecast a 95 percent probability interval for U.S. health expenditures as a percentage of GDP in 2075 as 15 percent to 55 percent with a median value of 30 percent in comparison to its 1999 level of 14 percent.

We have now described all the components of the forecasting model. We tested the model in deterministic mode by replicating the Trustees' projection under the Trustees' assumptions, including components such as GDP per capita, old age dependency ratio, and rate of growth of spending per beneficiary.

Policy

For long-run forecasts, the present day details of program structure should not be emphasized; instead forecasts should be based on more fundamental forces influencing expenditures on health care. Our forecasts show the long-term financial consequences of maintaining current policy, or of modifying it in prespecified ways. Because these forecasts are intended to guide policy, it would not make sense to project those policy changes themselves. In this sense, the forecasts are conditional rather than unconditional, since they take the policy assumption as a given.

If instead the forecasts were to be used as a component of comprehensive government budgetary forecasts (for example, see Lee, Tuljapurkar, and Edwards 1998), then it might be useful to make assumptions about future policy changes triggered by rising spending, and in that sense to make unconditional forecasts, intended to represent the forecasters best estimate of what the future will bring, including policy changes.

Dealing with the Uncertainty of Long-Term Forecasts: The Scenario Approach

Traditionally, the uncertainty of long-term forecasts has been assessed through high-cost and low-cost scenarios. The scenario approach begins by choosing high, medium, and low trajectories for each of the key components of the forecast. Experts may be consulted at this stage. For health spending, there would be trajectories for the demography (fertility, mortality, immigration), and then perhaps trajectories for health care spending by age and sex, combining implicit assumptions about health status, treatments offered, and costs of these treatments. The next step is to decide how to bundle together the high or low values of each trajectory. Typically, a high-cost scenario would be composed of the low trajectories for fertility, mortality, and immigration (resulting uniformly in an older population), with the high trajectory for health care spending by age. This would yield the highest ratio of spending to GDP, but not the highest absolute cost—for this, the high trajectories for fertility and immigration would be used. Similarly, a low-cost scenario is constructed. Then the projections corresponding to the trajectories in the two scenarios are taken to bracket the likely outcomes in the future. This approach has certain advantages. Expert opinion is readily incorporated. One can easily study the impact of the assumptions about each component, by varying one trajectory at a time. This may yield analytic insights. The approach is easily explained to policymakers and to the public.

However, the scenario approach also has several serious drawbacks. First, what does it mean that the high–low range is “taken to bracket the likely outcomes in the future”? With what probability are they expected to contain the true outcome? Why are they not twice as wide or half as wide? Only rarely is there an attempt to attach probabilities to scenarios.

Second, the scenario approach implicitly makes extremely strong and highly unlikely assumptions about the correlation of forecast errors. It necessarily assumes perfect correlation of the component trajectories with each other and across time. For example, in the “high-cost” scenario, fertility is lower than in the central forecast in every year, representing a negative forecasting error that is perfectly correlated over time. Per capita health spending is always higher than in the central forecast, which is a positive forecasting error that is perfectly correlated over time. Thus negative forecasting errors for fertility are always perfectly associated with positive forecasting errors in per capita spending, so it is implicitly assumed that there is a perfect negative correlation of forecasting errors for these two variables. Similar statements can be made about any pair of key variables in the forecast. These unrealistic assumptions rule out such possibilities as that fertility might start out low, and then become high, while mortality might do the opposite, with health care spending per beneficiary also wandering around. Some resulting aggregate cost forecasts could pass out of the high–low bounds of the scenarios.

Third, is the high–low range intended to contain annual values or is it calibrated to be no wider than necessary to contain long-run trends? It cannot satisfy both of these criteria at once, since the short-run forecast errors may be large from year to year, but tend to cancel over time. Error cancellation is ruled out by the implicit assumption of perfect intertemporal correlation of errors. In this sense, the scenario approach gives probabilistically inconsistent indications of uncertainty. Since year-to-year randomness may dominate the actual outcomes for the early years of the forecast period, the scenario-based forecasts risk having the actual spending fall outside the high–low range soon after publication. In the case of scenario-based population forecasts, sometimes the actual number of births has fallen outside the high–low range before the publication date of the forecast.

Fourth, and similarly, since there can be either no cancellation of errors across key variables or no reinforcement, depending on whether a perfect negative or positive correlation is assumed, the probability for an outcome to fall within the range for any single variable is inconsistent with the probability that the entire forecast will contain the true outcome.

Ex-post Analysis of Forecast Performance

In some cases, forecast performance and the probability coverage of the high–low range can be evaluated ex post, and used as a basis for assigning probabilities ex ante. Such studies are very useful. However, this kind of ex-post analysis of forecasts is generally restricted to institutional forecasts such as those issued by the United Nations or by the U.S. Social Security Administration, which have compiled a long record and which generally use fairly consistent methods. Examples of such ex-post analysis of population forecasts include Keyfitz 1981; Stoto 1983; Keilman 1997; and National Academy of Sciences 2000; and of Social Security mortality forecasts, Lee and Miller 2001.

Probabilistic Forecasts Based on Constrained Time Series Analysis

A growing literature has developed the use of modified time series methods for demographic forecasting (Alho 1990; Bell 1997; Lee and Carter 1992; Lee and Tuljapurkar, 1994) and for forecasting the finances of the U.S. Social Security system and other government budgets (Lee and Tuljapurkar 2000; Lee, Tuljapurkar, and Edwards 1998). In this article, we extend this approach to forecasting Medicare expenditures.

In the preceding sections, we have indicated how time series models may be fit to historical data series, including the data series of health care or Medicare expenditures in the United States, expressed relative to the growth rate of per capita income or of the wage rate. In some cases, forecasts were generated from the fitted time series model; in others, the mean forecast was taken from subjective expert forecasts, while the forecast error structure was taken from the fitted time series model. Autocorrelations and cross-correlations estimated from the historical data series replace the assumption of perfect correlations used in the scenario approach.

In principle, once the model is fully spelled out as outlined earlier, an analytic solution could be found for the probability distributions of all items of interest in the future. A solution of this sort is presented in Lee and Tuljapurkar (1994) for the population forecast. In practice, however, a far simpler and more flexible approach is to use stochastic simulation to generate a large number of sample paths, one thousand for example, each representing a different future. Then the distribution of the quantities of interest across these one thousand sample paths can be calculated, probability intervals can be found, and so on. For example, a 95 percent probability interval is one that contains the middle 95 percent of sample paths for some quantity in some year. This is the procedure we follow for Medicare.

Forecasts generated through time series analysis have the advantage of objectivity (although subjective judgments about depth of historical period and form of model are certainly required), and of a well-established body of experience in a wide range of applications. However, they also have the disadvantage that they cannot predict profound breaks with the past, even when such breaks in the future may seem likely. Scenario forecasts are the appropriate means to present visions of the future such as a doubling of the human life span. However, such profound changes in a key component of the forecast would often imply a world so different from our own as to render meaningless the basic premises underlying the forecast. We also note that the historical record includes many unexpected events such as the invention of antibiotics, the AIDS epidemic, and the baby boom and bust, and therefore shocks of these magnitudes are already reflected in probabilistic forecasts based on an analysis of the past.

Results of the Probabilistic Forecast of Medicare Finances

Using the techniques discussed in previous sections, we have generated probabilistic population forecasts for the United States from 2000 through 2075, reflecting stochastically simulated fertility and mortality, with deterministic net immigration. These provide us with population counts, disaggregated by age and by time-until-death. Total Medicare expenditures for a given year are the summed products of the number of people in each time-until-death category times the time-until-death schedule of spending. This schedule of spending has a fixed shape, which is multiplied times a projected index of spending. As previously discussed, this index represents the cumulative average differential between the rate of increase in per-beneficiary health spending and the rate of increase in per-capita income. The forecast trajectory of this index is different for each of the ten thousand sample paths. However, the use of a constrained mean time series forecast insures that the average rate of increase over all sample paths is equal to the Trustees' intermediate assumption (long-run average differential of 1 percent). The last step is to calculate the frequency distribution for outcomes of interest using the ten thousand stochastic sample paths representing possible Medicare futures.

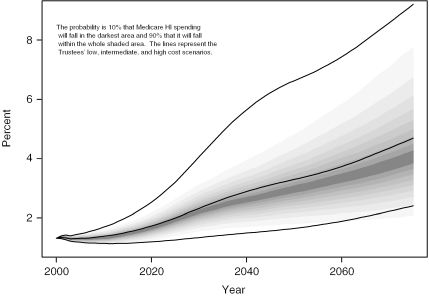
Figure 2 presents the probability deciles for our forecast of Medicare Hospital Insurance (Part A) expenditures as a share of GDP. For comparison, it also shows the low, intermediate, and high cost forecasts issued by the Trustees (2001). The retirement of the baby boom is evident in the accelerated rise in expenditures for all forecasts between 2010 and 2030. Although our faster mortality decline leads us to project more elderly, the Trustees' intermediate forecast (which uses a fixed age schedule of spending) lies quite close to our 50th percentile forecast, a bit below it until 2040, and a bit above it thereafter. Apparently the spending increase due to increasing numbers of elderly is offset by the decreasing proportion near death at each age. Our time-until-death assumption moderates the impact of mortality decline. In a separate analysis using a fixed age schedule of spending, we find spending projections are about 20 percent higher in 2075 than our projections using a fixed time-until-death schedule of spending.

Figure 2.

Medicare Hospital Insurance Program as Percent of GDP: Lee–Miller Probability Deciles and Trustees Scenarios (Excludes Medicare's Supplementary Medical Insurance Program)

Our results are reasonably consistent with those of the Trustees in central tendency. However, we find inconsistency in the probabilities contained within the high–low bounds of the Trustees. While the Trustees claim no probabilistic interpretation for their high–low range, comparison shows that at the end of the forecast horizon in 2075, their high–low range approximates an 89 percent probability interval. But for the first five years, the range covers only about an 85 percent probability, while from 2025 to 2045, it covers 98 percent. Thus the chances of the actual expenditures falling outside the bounds are about seven times as great at the beginning of the forecast horizon as at its middle, and are about four times as great at the end as in the middle. Furthermore, for much of the forecast horizon we find it twice as likely that the actual expenditure will fall below the Trustees' low bound as that it will fall above their high bound.

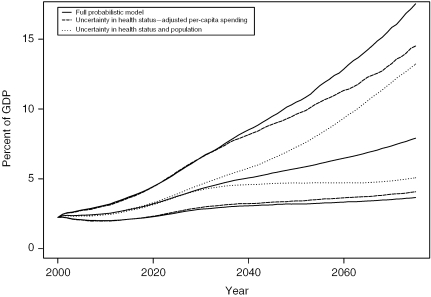
In Figure 3, we have plotted the median and 95 percent probability intervals for the full probabilistic forecast of Medicare expenditures (Hospital Insurance [HI] and Supplementary Medical Insurance [SMI] combined) as well as those forecasts reflecting uncertainty only about growth in health status-adjusted per-beneficiary spending or only uncertainty about population and health status. Summary data behind this plot are provided in Table 1. The median forecast increases from 2.24 percent of GDP initially to 7.91 percent of GDP in 2075, with a 95 percent probability range of 3.66 percent to 17.52 percent. The uncertainty is highly asymmetric, for example 4 percent downward but 9 percent upward in 2075, typical for stochastic budgetary forecasts that have a log-normal probability distribution.

Figure 3.

Medicare (HI and SMI) as a Share of GDP with Lee–Miller 95% Probability Intervals for Various Sources of Uncertainty

Table 1.

Lee–Miller Forecast of Medicare (HI and SMI Combined) As a Share of GDP: Median and 95 Percent Probability Interval

Year	Median	95% Probability Interval
2000	2.24%	n.a.
2001	2.36%	2.26% to 2.47%
2002	2.39	2.22 to 2.58
2003	2.37	2.14 to 2.62
2004	2.38	2.10 to 2.69
2005	2.40	2.08 to 2.77
2006	2.41	2.04 to 2.83
2007	2.42	2.02 to 2.89
2008	2.45	2.02 to 2.97
2009	2.48	2.01 to 3.04
2010	2.51	2.01 to 3.12
2015	2.81	2.11 to 3.72
2020	3.21	2.29 to 4.45
2025	3.75	2.57 to 5.45
2030	4.29	2.83 to 6.53
2035	4.73	2.97 to 7.52
2040	5.07	3.07 to 8.51
2045	5.42	3.14 to 9.48
2050	5.74	3.21 to 10.50
2055	6.10	3.26 to 11.69
2060	6.48	3.33 to 12.86
2065	6.89	3.42 to 14.23
2070	7.36	3.52 to 15.83
2075	7.91	3.66 to 17.52

Further, we note that uncertainty from health status adjusted spending in our stochastic forecast captures almost all the uncertainty until 2050 or so; thereafter, the uncertainty in population and health status begins to matter, particularly for the upside risk. By contrast, uncertainty in population and health status contributes only a small amount until 2040 or so, when uncertain fertility begins to have a growing effect on the labor force and therefore on the tax base and GDP. Uncertainty about mortality has only a slight effect, since it works in both directions: when mortality declines more rapidly, there are more elderly people, but they are healthier—that is, fewer are close to death. By 2075, uncertainty in population and health status account for about 60 percent of the width of the probability interval. Despite this significant contribution from population and health status uncertainty, uncertain spending alone would account for about 75 percent of the probability interval (note that probability ranges are not additive). It follows that one would not go far wrong by ignoring the uncertainty in the population forecast, while concentrating on uncertainty in the health status adjusted spending. This result reflects the great variability in past growth in health spending per beneficiary.

The Trustees (Board of Trustees of the Federal Supplementary Medical Insurance Trust Fund 2001, Appendix D, pp. 79–88) have published a stochastic forecast of SMI over a ten-year horizon (2000 base year, to 2010), based solely on uncertainty in the growth rate of per-beneficiary spending. A detailed comparison to the first ten years of our SMI forecasts shows a near-perfect congruence of the 95 percent bounds after taking into account a difference in the start year data, since as we discussed in connection with Figure 3, the demographic uncertainties have little consequence until many decades into the forecast. This comparison, consistent with the discussion of Figure 3, indicates that short-term stochastic forecasts like that of the Trustees can safely ignore the demographic uncertainty, as they have done.

The Summary Actuarial Balance measure used for assessing long-term imbalance for Social Security can also be used for HI. It is the difference between the present value of taxes and the present value of expenditures, plus the initial Trust Fund balance, minus an amount equal to the final year's expenditures, all expressed as a percentage of the present value of payroll. It can be interpreted as the amount by which the payroll tax for HI would have to be raised now in order for the system to have a Trust Fund balance after 75 years large enough to cover one year's expenditures. This measure depends on the entire course of each stochastic trajectory, whereas the measures we have looked at so far refer only to outcomes in a single year. For HI, we forecast a 75-Year Summary Actuarial Balance of –1.44 percent (the payroll tax for HI would need to be raised by 1.44 percent to achieve actuarial balance by this measure), with a 95 percent probability range of –3.88 percent to +0.13 percent. These compare to the Trustees' projection of –1.97 percent, with a range of =−6.3 percent to +.2 percent. Note that our central forecast is less negative than theirs, and our 95 percent range is only 61 percent as wide as their high–low range. Ours is narrowed by cancellation of forecast errors over the length of the stochastic trajectories, while theirs is not, because the scenario method incorrectly assumes perfect intertemporal correlation of errors. Ours is also narrowed because errors in forecasting mortality are associated with offsetting errors due to changes in time until death.

Now consider a measure similar to the Summary Actuarial Balance for the HI and SMI combined. There is no payroll tax for SMI. About 25 percent of its costs are covered by premiums, with the balance covered mainly by the general fund. Here we assume that premiums continue to cover 25 percent of projected spending, while payments from the general fund remain at the current proportion of payroll. Treating HI finances as above, we can calculate a measure analogous to the Summary Actuarial Balance for the combined programs. The result will tell us the extent to which the HI payroll tax and payments from the general fund would have to be immediately increased relative to payroll in order to achieve actuarial balance over the next 75 years. We find a median imbalance of –3.60 percent, with a 95 percent range of –7.93 percent to –0.92 percent. By this measure, the problem of funding the two parts of Medicare is nearly twice as large as the problem of funding Social Security (Old-Age, Survivors and Disability Insurance—OASDI) over the next 75 years. The HI imbalance by itself is almost as large as the OASDI imbalance.

Conclusion

Long-term forecasting is fraught with uncertainty, and this is particularly so for forecasts of health care spending. This article makes two main contributions. First, it treats the uncertainty of long-term forecasts for health spending more systematically than in the past through a stochastic approach. Second, it uses the relation of health care spending to time until death to incorporate the changing health status of the population in the forecasts. In this way, the steadily declining mortality in the population not only means additional elderly for whom health care must be provided, but also means improving health status of the elderly at each age, and therefore lower spending, other things equal.

For our central forecast, we have drawn on the expert official forecasts, but instead of adjusting for the age composition of the population we have adjusted for its distribution by time until death. Our stochastic forecasts have assumed that these central forecasts are known without error as the true future “expected values,” and we have superimposed on them errors whose size and structure are extrapolated from the historical data as fit by time series models. Since our probability intervals do not reflect uncertainty about the models themselves, they provide a kind of lower bound for the uncertainty of the forecasts.

To summarize our key findings:

• Medicare expenditures are currently 2.2 percent of GDP in the United States. We project them to rise to 8 percent of GDP by 2075. This trajectory stays close to the intermediate Trustees' forecast because our forecast of more rapid mortality decline has offsetting effects on projected health spending, as explained earlier. The increase is due half to population aging and half to increased spending per beneficiary.

• There is a 95 percent probability that Medicare spending in 2075 will fall between 4 percent and 18 percent of GDP. The upward uncertainty is more than twice as great as the downward uncertainty.

• There is substantial uncertainty about the future course of mortality decline. However, the time-until-death approach filters out much of this uncertainty, since there are offsetting effects of mortality decline and the health improvement that causes it. There is no such filtering out of uncertainty about fertility and its effect on the size of the labour force.

• Demographic uncertainty has very little effect on the probability bounds for the forecast for the first forty years or so; only uncertainty about spending-per-beneficiary matters over this period.

• In 2075 the Trustees' high–low range should contain actual expenditures with 91 percent probability. Expenditures are 10 or 20 times more likely to be contained by the range at the beginning or end of the forecast horizon compared to the middle years.

• The cumulative funding imbalance for Medicare Parts A and B over the next 75 years is about twice as great as the imbalance in the Social Security system. Payroll taxes would have to be raised by 4 percent immediately to balance the system over the 75-year horizon.