Effect of hydration on interstitial distribution of charged albumin in rat dermis in vitro

Abstract

At physiological pH, negatively charged glycosaminoglycans in the extracellular matrix may influence distribution volume of macromolecular probes, a phenomenon of importance for hydration of the interstitium and therefore for body fluid balance. We hypothesized that such charge effect was dependent on hydration. Human serum albumin (HSA) (the pH value for the isoelectric point (pI) = 4.9) was made neutral by cationization (cHSA) (pI = 7.6). Rat dermis was studied in vitro in a specially designed equilibration cell allowing control of hydration. Using a buffer containing labelled native HSA and cHSA, the distribution volumes were calculated relative to that of ⁵¹Cr-EDTA, an extracellular tracer. During changes in hydration (H), defined as (wet weight – dry weight) (dry weight)⁻¹), the slope of the equation describing the relationship between extracellular fluid volume (V_x) (in g H₂O (g dry weight)⁻¹) and H (V_x = 0.925 H + 0.105) differed significantly from that for available volumes of cHSA (V_a,cHSA = 0.624 H – 0.538) and HSA (V_a,HSA = 0.518 H – 0.518). A gradual reduction in H led to a reduction in difference between available volumes for the two albumin species. Screening the fixed charges by 1 m NaCl resulted in similar available and excluded volumes of native HSA and neutral cHSA. We conclude that during gradual dehydration, there is a reduced effect of fixed negative charges on interstitial exclusion of charged macromolecules. This effect may be explained by a reduced hydration domain surrounding tissue and probe macromolecules in conditions of increased electrostatic interactions. Furthermore, screening of negative charges suggested that hyaluronan associated with collagen may influence intrafibrillar volume of collagen and thereby available and excluded volume fraction.

The presence of substances such as collagen and glycosaminoglycans (GAGs) create a macromolecular crowding in the space located between the capillary walls and the cells defined as the interstitium, and furthermore limit the space available for plasma proteins and other macromolecules simply due to steric effects. This phenomenon of geometrical, or sterical interstitial exclusion was first described by Ogston & Phelps (1961) and refers to the fact that two solid structures cannot occupy the same confined volume at the same time (for review, see also Bert & Pearce, 1984). The geometrical exclusion phenomenon is relevant only for species with high hydrodynamic sizes such as proteins and not for small molecules such as water, small ions and nutrients. In addition to the steric exclusion, GAGs are negatively charged at physiological pH values and therefore electrostatic factors might also be involved in selectively excluding other negatively charged macromolecules transported through the interstitium (for a reviewed perspective see Taylor & Parker, 2003). As reviewed by Aukland & Reed (1993), interstitial exclusion is thus of importance for interstitial fluid balance, but this phenomenon also influences plasma volume regulation in situations with fluid volume perturbations. The study of exclusion phenomena may also provide information on structural organization of the interstitium since the distribution of a specific probe in the interstitial fluid is determined by size, charge and structural components (Bert & Pearce, 1984; Aukland & Reed, 1993; Wiig et al. 2000). Apart from the physiological importance, the emergence of new therapeutic tools like monoclonal antibodies have made studies of exclusion phenomena of interest from a therapeutic perspective since the interstitium may be a major barrier to drug delivery in tumours (Jain, 1998; Krol et al. 1999; Flessner et al. 2005; Wiig et al. 2005).

In an attempt to further explore the charge effects on interstitial exclusion, and to be able to vary independently the various determinants of exclusion, we turned to an in vitro system using fully swollen dermis as tissue model and albumin as a probe (Wiig et al. 2003). By varying the charge of albumin, an observable graded response on interstitial available volume and thereby also excluded volume fraction was observed. These data suggested that the interstitium acts as a negatively charged matrix and that both collagen and GAGs contribute to volume exclusion in a manner probably dependent on their organization. Later we were able to demonstrate matrix charge effects on exlusion in euhydrated skin and muscle in vivo (Gyenge et al. 2003).

Previous studies have suggested a significant influence of tissue hydration on excluded volume (Parker et al. 1979; Mullins & Bell, 1982; Reed et al. 1989), and we wanted to quantify the effect on interstitial exclusion of altered hydration. More specifically, we asked the question how an increased crowding of interstitial components affects exclusion in relation to differently charged species. To this end we used a specially designed equilibration cell (Bert et al. 1986) enabling us to vary the tissue volumes within wide ranges. Our hypothesis was that an increased crowding would exaggerate the charge effect and lead to an increased relative discrepancy between negatively charged and neural probes as the hydration was reduced.

Methods

The experiments were performed on skin sampled from the back of anaesthetized female Wistar-Møller rats, 202–260 g, fed a standard laboratory diet. All experiments were performed in accordance with recommendations given by the Norwegian State Commission for Laboratory Animals and were approved by the local ethical committee.

Preparation of charge modified albumin

Charge-modified albumin was prepared by a method slightly different from that described by Hoare & Koshland (1967), as described in detail in a previous paper (Wiig et al. 2003). The level of cationization is dependent on the reaction time with increasing positivity with increasing time. We wanted an albumin that was neutral at physiological pH and therefore used a reaction time of 45 min (Wiig et al. 2003). After the charge modification, the albumin solutions were dialysed against distilled water for at least 24 h before radiolabelling.

The pI of native and charge-modified human serum albumin was determined by isoelectric focusing on a vertical mini-gel system (CBS Scientific Company, Inc., CA, USA). Precasted IEF gels (Novex, pH 3–10) were run for 1 h at 100 V, 1 h at 200 V and 30 min at 500 V, fixed for 60 min (12 g TCA and 3.5 g sulfosalicylic acid in 100 ml deionized water) and stained with Novex Colloidal Blue stain. The pH gradient profile was determined using 11 marker proteins with pI ranging from 3.5 to 9.3 (Pharmacia Biotech Broad pI Calibration Kit).

Preparation of radioactive tracer

The native and charge-modified human serum albumins were labelled with ¹²⁵I or ¹³¹I by Iodo-Gen. Briefly, 5 mg 1,3,4,6,tetrachloro-3α,6α diphenylglycouril (Sigma Aldrich Co., product number T0656) was dissolved in 5 ml chloroform and 0.1 ml of this solution was dispersed in a 1.8-ml Nunc vial (Nunc-Kamstrup, Roskilde, Denmark). A film of the virtually water-insoluble Iodo-Gen was formed in the Nunc vial by allowing the chloroform to evaporate to dryness under nitrogen. Then 1.5 mg of albumin dissolved in 1 ml 0.05 m PBS solution, pH 7.5, containing 5 MBq ¹²⁵I or ¹³¹I (Institute for Energy Technology, Kjeller, Norway) and 15 μl 0.01 m NaI was added. The iodinating tube was gently agitated for 10 min before the reaction was terminated by removing the albumin solution. After labelling, unincorporated iodine isotope accounted for 5–10% of the total radioactivity for both tracers as estimated by TCA precipitation. Free iodine in stock solution was removed and kept indistinguishable from background during storage by dialysing the tracer against 1000 ml 0.9% saline containing 0.02% azide. The stock solution was stored in the dark at 4°C and dialysed for at least 24 h before use.

Tissue equilibration cells

To be able to study the effect of hydration on albumin distribution volume we used a modified version of the equilibration cell described in detail by Bert and coworkers (Bert et al. 1986) (for details on construction see Fig. 1 in their publication). This cell was designed to permit equilibration of a disc of tissue with the surrounding fluid while constraining the tissue from swelling. The tissue under study (here dermis) is confined between two fine screens that are supported by two coarse screens again in contact with the cell wall. In the present experiments we controlled the height of the specimen chamber and thereby the amount of swelling by metal spacers with thickness 0.5–1.22 mm placed between the two inner screens. The fine screen allowed a sufficient area of contact to facilitate diffusion between tissue and surrounding fluid. Outside the fine screen there was a reservoir for fluid surrounding the tissue. Uniform concentration throughout the external fluid phase was assured by careful mixing and avoiding air-bubbles within the cell (see below).

Figure 1. Available volumes related to equilibration time.

Available volumes for cationized human serum albumin (cHSA) and native HSA in equilibration cells with maximal swelling restriction (spacer 0.5–0.7 mm) related to equilibration time. For both probes the volumes obtained at different equilibration times did not differ significantly as determined by ANOVA. Values are mean ± 1 s.e.m.

Equilibration experiments

Our method for harvesting of tissue, tracer and buffer preparation corresponds to what was described in a previous paper (Wiig et al. 2003) with minor modifications. Briefly, before harvesting dermis for use in the experiment, a ‘stock’ bathing solution was made from phosphate-buffered saline (PBS) with 0.05% azide, 10 μl serum (ml buffer)⁻¹, 2.5 μl (ml buffer)⁻¹ Protease Inhibitor Cocktail (P8340, Sigma). The mixture of buffer, serum, protease inhibitor and tracers is later referred to as tracer solution. The tracers were ¹³¹I-labelled human serum albumin (HSA; 0.3 kBq ml⁻¹), charge-modified human serum albumin ¹²⁵I-cHSA (see above; 0.15 kBq ml⁻¹) and ⁵¹Cr-EDTA (0.15 kBq ml⁻¹). In previous studies we have alternated between ¹²⁵I and ¹³¹I for probe labelling and shown that the macromolecules behave identically in vitro as well as in vivo irrespective of the type of radionuclide used (Wiig & Tenstad, 2001; Gyenge et al. 2003; Wiig et al. 2003, 2005).

The rats were anaesthetized with pentobarbital, 50 mg kg⁻¹ intraperitoneally, blood was aspirated by cardiac puncture, and the rats were then killed by intracardiac injection of saturated potassium chloride. An area of dorsal back skin was closely clipped and shaved, and a piece of full thickness skin, ∼3 cm × 3 cm, consisting of dermis and subcutis, was excised and the epidermis removed by scraping with a scalpel. Thereafter the dermis and subcutis were separated by careful blunt dissection in the space of natural separation between the layers. The thickness of dermis isolated this way ranged from 0.60 to 0.72 mm as determined with a vernier caliper in 10 samples of skin. After skin separation, two to four pieces of dermis with 10 mm diameter was punched out, placed in the tared equilibration cell and weighed. Then approximately 600 μl of tracer solution was added slowly to avoid inclusion of air bubbles, the cell was reweighed, the port sealed and the cell transferred to the coldroom (4°C) for tissue tracer equilibration. At daily intervals, the cell was rotated to mix the fluid contents, and at day 3, 6 and 8 duplicate 5 μl samples were withdrawn for counting. The radioactivity in these samples was measured so that the approach to equilibrium in the bathing fluid and tissue could be followed.

A fundamental requirement in these experiments is the attainment of steady-state tracer concentration in the tissue. In our previous experiments where the tissue was allowed to swell we established that 5–7 days were sufficient to reach steady state in dermis. Since the tissue hydration in the present experiments was lower, a property that will reduce the hydraulic conductivity of the tissue and diffusion coefficient for albumin (Bert & Pearce, 1984; Granger et al. 1984), we increased equilibration time by terminating the experiments at 8, 11 and 14 days of equilibration. A rising volume with time would indicate the equilibrium was not established. When ending the experiments, as much of the surrounding fluid as possible was withdrawn. The cell was disassembled and the tissue taken out and blotted quickly to remove excess tracer solution while carefully avoiding dehydration. The tissue was then transferred to another vial for counting.

After counting of tissue and bathing solutions at the end of the wash-in period, a wash-out period of 7 days started by soaking the tissue in azide-containing PBS, shown to be sufficient to wash out free tracer from the interstitial fluid (Wiig et al. 2003). Fresh buffer was added at day 2 and 4 of the wash-out period to maintain the tracer diffusion gradient. At the end of the wash-out period the tissue sample was removed from the buffer, carefully blotted as described above, and transferred to a vial for counting of residual activity and later chemical analysis. Counts remaining in the tissue at the end of the wash-out period were constant and were assumed to be unspecifically bound to the tissue and were, after correction for decay, subtracted from the corresponding tissue counts measured at the end of the wash-in period (see Results).

Samples were counted in an LKB gamma counter (model 1282 Compugamma) using window settings of 530–690 keV for ⁵¹Cr, 700–860 keV for ¹³¹I and 120–320 keV for ¹²⁵I. Standards were counted in every experiment and spillover as well as background and decay during the period of measurement were automatically corrected for. After counting, tissue samples were freeze-dried to obtain the dry weight of the tissue.

Characterization of Iodine-labelled isotopes

During tissue equilibration, radiolabel may come off the probes. To check for free radiolabel and whether the probes were changed during equilibration, the tracer solution used for 14 days of tissue equilibration was compared with freshly prepared stock solution by HPLC using a Superdex 200 HR 10/30 column (Amersham Pharmacia Biotech) with optimal separation range of 10–600 kDa. Elution was with 0.005 m phosphate buffer, pH 7.6 in 0.15 m NaCl. Successive fractions of 1.0 ml were collected and counted in the gamma counter.

Composition of the tissue extracellular matrix

The composition of the extracellular matrix is amongst the determinants of the exclusion properties of a tissue. Therefore, the tissue content of collagen, hyaluronan and total glycosaminoglycans (assayed as uronic acid) was measured. Analysis of hyaluronan was performed using a radioassay (HA-test 50, Pharmacia Diagnostics, Uppsala, Sweden) after papain digestion of freeze-dried specimens (Reed et al. 1988).

Uronic acid was measured by the method of Bitter & Muir (1962) utilizing the carbazole reaction to determine hexuronic acid, as described in a previous paper (Reed et al. 1989).

Collagen was determined according to the method of Woessner (1961), based on the determination of hydroxyproline content as described in a previous publication (Reed et al. 1989) assuming a hydroxyproline content of 0.91 μmol (1 mg collagen)⁻¹ (Bert et al. 1986).

Effect of ionic strength

To study the effect of ionic strength on exclusion, we added a group of experiments where 1 m NaCl was used as buffer. Except for NaCl concentration, the composition of the tracer solution in these experiments was similar to that described above.

Calculations

The tissue distribution volumes of tracer were calculated as tracer solution equivalent spaces when a steady-state situation was established, i.e. a stable level of counts in the tissue soaked in tracer solution. When such conditions were established, it was assumed that the tracer concentration in the available space in the tissue was similar to that in the buffer solution. Accordingly tracer distribution volumes (V_t), equivalent to the extracellular fluid volume (V_x) for ⁵¹Cr-EDTA and available volume (V_a) for cHSA and HSA were calculated as:

(1)

Native or charge-modified HSA-excluded volumes (V_e) were found as:

(2)

Only the elutable (i.e. unbound) fractions of the HSA tracers were used in calculation of the distribution volumes (see above). The volumes were related to tissue hydration, i.e. hydration = (wet weight – dry weight)/(dry weight)⁻¹.

Statistics

All tissue and tracer masses were determined by weighing, and volumes and masses are given as masses. Data are given as mean ± 1 s.e.m., and were compared using one-way analysis of variance (ANOVA) and with Tukey tests for multiple comparisons. Slopes of the linear regression curves were compared as described by Zar (1984). Differences were accepted as statistically significant at the P < 0.05% level.

Results

Preparation of tracer

As determined by isoelectric focusing, the pI of the native HSA was 4.9, whereas cationization for 45 min produced cationized HSA (cHSA) having an average pI of 7.6. That the labelled protein had a charge distribution corresponding to that observed from the isoelectric focusing was verified by auto-radiography as demonstrated in a previous publication (Wiig et al. 2003).

Establishment of tissue steady-state levels of tracer

To establish the time needed for tissue equilibration we followed the tissue concentration of tracers during ‘wash-in’. Since the equilibration time may be related to hydration we also investigated whether there was a relationship between the degree of swelling restriction induced by the spacers used in the equilibration cell and the time needed for tissue equilibration. In Fig. 1 we have shown available volumes for the most pronounced swelling restriction induced by spacers between 0.5 and 0.7 mm that may maintain, or actually reduce, tissue fluid content. There was no tendency to a rise in available volume with increasing equilibration time either for cHSA or HSA. Thus, the available volumes for HSA averaged 0.19, 0.20 and 0.15 ml (g dry wt)⁻¹ for equilibration times of 8, 11 and 14 days, respectively. Corresponding, although somewhat higher, numbers were found for cHSA. The ⁵¹Cr-EDTA volumes in these experiments ranged from 1.30 to 1.55 ml (g dry wt)⁻¹. Since there was no tendency to a rise in volume with time (P > 0.1, ANOVA), the respective results from 8, 11 and 14 days of equilibration were pooled.

From previous experience we know that all tracers may not be elutable from the tissue (Wiig et al. 2003). This fraction is assumed to be unspecifically bound to the tissue and not free in the interstitial fluid. If bound tracer is not taken into account, the calculated available distribution volumes will be overestimated and consequently the interstitial exclusion underestimated. We therefore measured the unelutable (i.e. bound) fraction in all individual samples, and found that the amount of such binding increased with charge modification. Thus, for native albumin, the unelutable fraction of tracer was 0.085 ± 0.008 (n = 43) as compared with 0.135 ± 0.013 (n = 43) for cHSA. Bound tracer was subtracted from the total tracer content in each sample and not included in the calculation of available volume. For ⁵¹Cr-EDTA, the unelutable fraction was 0.015 ± 0.002 (n = 43).

Available and excluded volumes

In the present experiments we wanted to test the effect of changes in hydration by restricting the swelling or actually reduce the hydration of the sample. Since the tissue swelling differed, and the amount of dry material (i.e. excluding agents) may be assumed to be constant, we chose to express the absolute available volume as a function of dry weight, i.e. hydration. If samples of dermis are allowed to swell unrestrictedly in the presently used buffer they will reach equilibrium at a hydration averaging 3.09 g water (g dry wt)⁻¹ (Wiig et al. 2003). In the present experiments the hydration thus ranged from 2.85 to 1.02 g water (g dry wt)⁻¹ in cells with spacers of 1.22 and 0.5 mm, respectively. The initial hydration, i.e. calculated from weight after tissue isolation before placing sample in chamber and dry weight after the experiment was 1.658 ± 0.027 g H₂O (g dry wt)⁻¹ (n = 43).

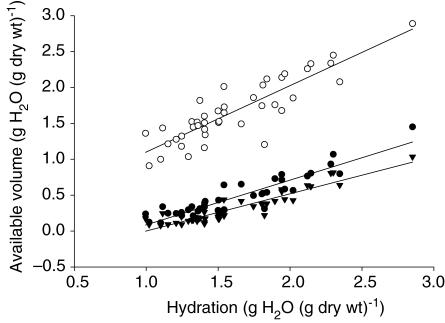
In Fig. 2 we have plotted the absolute available volumes for the extracellular tracer ⁵¹Cr-EDTA and cationized and native HSA as a function of hydration. Inducing a graded reduction in hydration resulted in a reduction in extracellular volume from 2.89 to 0.91 g H₂O (g dry wt)⁻¹. For cHSA and HSA the corresponding reductions in volumes were from 1.45 to 0.12 and from 1.03 to 0.08 g H₂O (g dry wt)⁻¹, respectively. The relationship between hydration (H) and available volume was best described by a linear equation for all volumes. Thus, for ⁵¹Cr-EDTA we found: V_x = 0.925 H + 0.105, R = 0.876 (confidence interval (CI) for slope = 0.762–1.088). For the two albumin probes the corresponding equations were: V_a,cHSA = 0.624 H – 0.538, R = 0.918 (CI for slope 0.538–0.709) and: V_a,HSA = 0.518 H – 0.518, R = 0.928 (CI for slope 0.4521–0.585). The slope of the V_x curve differed significantly from that of that of V_a,cHSA (P < 0.01) as well as from the V_a,HSA curve (P < 0.01). Although there tended to be a significant difference between the slope for the V_a,cHSA and V_a,HSA curves the difference did not reach statistical difference (P = 0.054).

Figure 2. Available volumes related to hydration.

Available volumes for the extracellular tracer ⁵¹Cr-EDTA (○) (V_x) and for cationized (•) (V_a,cHSA) and native (▾) human serum albumin (V_a,HSA) relative to hydration (H) of dermis. Also shown are their respective regression lines: V_x = 0.925 H + 0.105 (CI for slope = 0.762–1.088); V_a,cHSA = 0.624 H – 0.538 (CI for slope 0.538–0.709) and V_a,HSA = 0.518 H – 0.518 (CI for slope 0.4521–0.585). The slope of the V_x curve differed significantly from that of that of V_a,cHSA (P < 0.01) as well as from the V_a,HSA curve (P < 0.01), whereas differences in the slope for the V_a,cHSA and V_a,HSA curves did not reach statistical significance (P = 0.054).

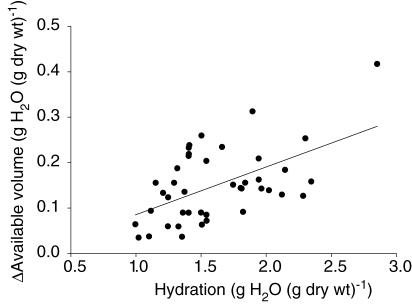
From the curves we get the impression that the difference between the volumes for the two albumin probes is reduced as the hydration decreased. To better visualize such an effect we calculated the difference between the distribution volumes (ΔV_a) and related that to hydration (Fig. 3). We observed that this difference approaches zero as the hydration is reduced, and this relationship is described by: ΔV_a = 0.105 H – 0.020, R = 0.542 (CI for slope = 0.053–0.157). The slope was significantly different from zero (P < 0.01), showing that ΔV_a was reduced as hydration decreased.

Figure 3. Delta available volume for cHSA and native HSA relative to hydration.

Difference in available volume (ΔV_a) for cationionized and native human serum albumin relative to hydration (H). Also shown is the regression line: ΔV_a = 0.105 H – 0.020 (CI for slope = 0.053–0.157). ΔV_a approaches zero as the hydration is reduced. The slope was significantly different from zero (P < 0.01), showing that ΔV_a was reduced as hydration decreased.

Effect of ionic strength

In a previous paper we have shown that increasing the ionic strength abolishes the effect of charge on probe distribution volume in dermis (Wiig et al. 2003). To investigate whether this effect was maintained during changes of tissue hydration we added experiments where the PBS was replaced by 1 m NaCl. Furthermore, we added some experiments where dermis was allowed free swelling in buffer to increase the span of hydration of the tissue. As observed for the previous series of experiments, increasing the salt concentration of the buffer solution strongly affected the distribution volume of the negatively charged native HSA. In these experiments, the hydration was 2.33 ± 0.06 g fluid (g dry wt)⁻¹ (n = 12), significantly lower than the hydration of 3.09 g water (g dry wt)⁻¹ using 0.15 m NaCl (P < 0.001) (Wiig et al. 2003), i.e. the tissue swelled less in the more concentrated buffer. The extracellular fluid volume in these experiments was 0.61 g H₂O (g wet wt)⁻¹ or 2.03 g H₂O (g dry wt)⁻¹. The available volumes of 1.11 ± 0.04 and 1.12 ± 0.04 g H₂O (g dry wt)⁻¹ for cHSA and HSA, respectively, were not significantly different, in agreement with previous experiments (Wiig et al. 2003).

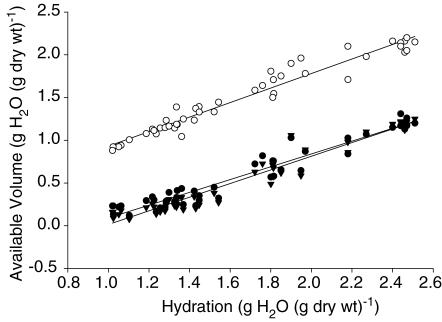
We used 1 m NaCl as buffer in the equilibration cells and varied the hydration as described above. Figure 4 shows the relationship between extracellular fluid volume and the distribution volume of native and charge-modified HSA for hydration ranging from 2.5 to 1.0 g H₂O (g dry wt)⁻¹. During this induced change in hydration, the extracellular volume decreased from 2.15 to 0.88 g H₂O (g dry wt)⁻¹. The range for the available volume for cHSA was 1.26–0.12 g H₂O (g dry wt)⁻¹ whereas the corresponding range for native HSA was 1.25–0.08 g H₂O (g dry wt)⁻¹. The relationship between extracellular volume and hydration (H) can be described as: V_x = 0.850 H + 0.089 with a CI for the slope of 0.791 – 0.909. For the HSA probes the corresponding relationships can be described as; V_a,cHSA = 0.749 H – 0.659 (CI for slope 0.689–0.810) and V_a,HSA = 0.798 H – 0.783 (CI for slope 0.739–0.857). None of the slopes differed significantly from each other.

Figure 4. Available volumes in 1 M NaCl.

Available volumes for the extracellular tracer ⁵¹Cr-EDTA (○) (V_x) and for cationized (•) (V_a,cHSA) and native (▾) human serum albumin (V_a,HSA) relative to hydration (H) of dermis using 1 m NaCl in the equilibration cell. Also shown are their respective regression lines: V_x = 0.850 H + 0.089 (CI for slope = 0.791–0.909); V_a,cHSA = 0.749 H – 0.659 (CI for slope = 0.689–0.810) and V_a,HSA = 0.798 H + 0.783 (CI for slope = 0.739–0.857). None of the slopes differed significantly from each other.

Characteristics of tracer albumin in the buffer

The tracers were run on a HPLC size exclusion column (Superdex 75HR 10/30, Amersham Pharmacia Biotech) to examine whether the cationization affected the hydrodynamic radii of the probes. Charge modification did not affect the size of the albumin molecule. However, the chemical reaction resulted in formation of less than 5% dimer. Free iodine in the stock tracer solution was kept at a level indistinguishable from background by continuous dialysis. After tissue equilibration at the time of start of wash-out, the amount of free ¹²⁵I was below 1.0%, whereas the corresponding value for ¹³¹I was 1.2%. These values were used to correct for free tracer in solution.

Samples of buffer remaining after tissue equilibration for 8–14 days were also applied to a HPLC column. The tracers did not change during their stay for up to 14 days in the buffer, as shown by nearly identical elution patterns of tracer stock solution and buffer after equilibration, in agreement with previous experience (Wiig et al. 2003). Furthermore, the stay in solution during tissue equilibration did not lead to isotope degradation products or an increased amount of dimer cHSA.

Chemical analysis of dermis and buffer

Previously we assayed the composition of dermis and buffer after free swelling to investigate whether the composition changed during the equilibration process (Wiig et al. 2003). Since our present experimental protocol differed and we used longer equilibration times we found it necessary to determine tissue and buffer fluid composition in these experiments too. We measured hyaluronan in dermis before and after equilibration in the tissue equilibration cell and in the buffer itself to see whether the hyaluronan content changed during the equilibration process. In control dermis before soaking in buffer, hyaluronan averaged 1.05 ± 0.10 mg (g dry wt)⁻¹ (n = 9), as compared with 0.95 ± 0.12 mg (g dry wt)⁻¹ after wash-out of tracer in tissue that had been equilibrated for 14 days in the cells (P > 0.6).

To estimate the potential loss of tissue hyaluronan (an exluding agent) to the buffer solution, the total amount of hyaluronan in the buffer solution after equilibration was calculated (concentration in buffer multiplied by buffer volume) and compared with the total amount in the dermis of origin. Such calculations showed that the fraction of buffer hyaluronan amounted to 0.021 ± 0.005 (n = 8) for the samples with lowest hydration (spacer 0.5–0.7 mm) and 0.049 ± 0.006 (n = 9) for the samples with highest hydration (spacer 1.0–1.22 mm) of the total quantity in the dermis of origin.

Uronic acid determined in dermis averaged 2.95 ± 0.25 mg (g dry wt)⁻¹ (n = 10) after soaking in buffer (14 days equilibration time), whereas the concentration in control dermis before soaking was 3.12 ± 0.22 mg (g dry wt)⁻¹ (n = 8; P > 0.45). The fraction of uronic acid in the buffer relative to that in the tissue sample calculated as described for hyaluronan above was 0.012 ± 0.004.

The content of collagen in dermis averaged 630.5 ± 30.4 mg (g dry wt)⁻¹ (n = 8) in control dermis before soaking in buffer, with a corresponding content of 609.6 ± 22.3 mg (g dry wt)⁻¹ (n = 8; P > 0.5) for samples used for buffer equilibration. When assaying for collagen in the tracer solution after the wash-in period the signal was indistinguishable from blank, showing that the collagen concentration in the solution was zero.

Discussion

Whereas we have shown that fixed negative charges in the interstitium affect the distribution volume of a macromolecular probe in fully swollen (oedematous) dermis (Wiig et al. 2003) and in normal skin (Gyenge et al. 2003), it is not known how increased macromolecular crowding and charge density occurring during reduced hydration affects this phenomenon. Here we have used an in vitro tissue equilibration cell where the hydration could be carefully controlled to address these questions. At high and normal levels of tissue hydration there is a significant effect of charge on distribution of albumin, in agreement with our previous study. Surprisingly, increasing the charge density of the interstitium by graded dehydration resulted in a concomitant decrease of such charge effect that was practically abolished at a hydration of 1.0 g H₂O (g dry wt)⁻¹. Below we argue that this may be explained by loss of hydration domains for negatively charged macromolecules in conditions of increased electrostatic interactions. Our data imply that hyaluronan associated with collagen may influence intrafibrillar volume of collagen and thereby available and excluded volume fraction.

Methodological issues

Our previous studies of the exclusion phenomenon have mainly been in intact animals, e.g. (Wiig et al. 1992, 1994; Wiig & Tenstad, 2001), but to be able to independently study the factors that influence probe distribution we recently turned to an in vitro model (Wiig et al. 2003), well aware that such an approach has its limitations. In our previous in vitro study we separated skin into dermis and subcutis in an attempt to measure distribution volumes in two compartments having different composition. Due to a highly variable binding of tracer to subcutis we had to abandon the use of the latter tissue (Wiig et al. 2003). Here we used an approach slightly modified from that described by Bert et al. (1986) enabling us to study macromolecular probe distribution within wide ranges of hydration thereby including the influence of macromolecular crowding. Several questions related to our in vitro approach have been addressed in our previous paper (Wiig et al. 2003), and therefore only specific issues are discussed here.

A fundamental requirement in our approach is that buffer solution albumin reaches steady state with albumin in its available space in the tissue. Since diffusion of macromolecules is strongly dependent on tissue hydration (Granger et al. 1984), this requirement is of particular importance here where the tissue hydration was a key variable and significantly lower than control for many of the samples. Based on the data from Granger et al. (1984) it is reasonable to assume that the equilibration time would be longest in the situation with lowest hydration. We controlled for tissue equilibration by comparing distribution volumes at 8, 11 and 14 days of equilibration in cells with spacers of 0.5–0.7 mm, i.e. containing tissues with lowest hydration, and not different distribution volumes at all equilibration times show that steady-state conditions were attained. Another potential problem may be tissue degradation that may change tissue characteristics and thereby affect probe distribution. Protease inhibitors were used in the buffer to prevent degradation. A HPLC pattern similar to that of normal interstitial fluid and a colour yield in the collagen assay not different from blank in buffer isolated after 14 days of equilibration suggest no tissue degradation. Moreover, HPLC of the buffer after equilibration showed elution patterns of the radiolabelled probes indiscernible from those of stock solutions. Furthermore, the finding of free radiolabel ≤ 1.2% showed that the tracers were stable during the equilibration period and that volume overestimation due to free label was a negligible problem. Unspecific binding of tracer is another potential problem related to our method. In agreement with previous observations (Flessner & Schwab, 1996; Wiig et al. 1994, 2003; Wiig & Tenstad, 2001), this problem was also associated with probe charge since the unelutable fraction of cHSA (pI = 7.6) was significantly higher than that of HSA (pI = 4.9). To avoid overestimation of distribution volumes we therefore eluted all samples, to be able to correct each sample individually, and by doing so get a reliable estimate of tracer albumin, native as well as charge modified, free in the interstitial fluid.

In agreement with previous experience (Gyenge et al. 2003; Wiig et al. 2003), the charge modification gave dimer formation, which will result in a slight increase in average molecular weight of the cationized probe. We have no data on distribution volume for dimer albumin, and it is therefore difficult to quantify this effect. If of importance, such increase in average molecular weight would lead to a potential underestimation of the available volume and thereby of the charge effect on distribution volume, but since the amount of dimer was low (< 5%) we think that this effect is negligible.

Comparison to previous studies

Although there are several studies on albumin distribution volume in skin (for references see Aukland & Reed, 1993; see also Wiig et al. 2003), few have addressed the question of albumin distribution volumes in dermis, and we are not aware of any previous work on the effect of hydration on distribution volume of differently charged macromolecular species. Of most relevance, Bert et al. (1986) studied albumin exclusion in excised human dermis in vitro using a chamber similar to ours to keep hydration constant. In the samples where the hydration was kept at control level, albumin had access to 35% and was thereby excluded from 65% of the total interstitial space. In a more hydrated sample, the available space rose to 51%. If we insert our measured pre-equilibration hydration of 1.66 g H₂O (g dry wt)⁻¹ into the regression equations for the relationship between interstitial fluid volume and albumin space to hydration, we arrive at an average interstitial fluid volume of 1.64 g H₂O (g dry wt)⁻¹ and distribution volumes of 0.50 and 0.34 g H₂O (g dry wt)⁻¹ for cHSA and HSA, respectively, corresponding to available volumes of 31 and 21% of the interstitial fluid volume. Based on the confidence interval for our regression curve for HSA, our available volume is significantly lower than that for human dermis.

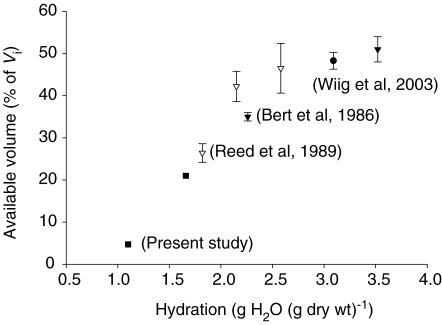
Considering other relevant studies (Bert et al. 1982; Mullins & Bell, 1982; Mullins et al. 1987) and previous (Wiig et al. 2003) and present data from rat dermis led us to suspect that different tissue hydration may explain the present discrepancy. In an attempt to substantiate this assumption, we have compiled data for available volume in dermis as a function of hydration (Fig. 5). In the study of Bert et al. (1986), the hydration of fresh dermis averaged 2.26 g H₂O (g dry wt)⁻¹, i.e. significantly higher than our control value. Indeed, inserting their value for hydration in our derived volume/hydration relationship give an available volume for HSA of 29%, not significantly different from what was found by them. Judging from the compiled volumes it is evident that there is a linear relationship between hydration and available volume for 1.0 < hydration < 3.0 g H₂O (g dry wt)⁻¹, in line with our assumption.

Figure 5. Compiled available volumes relative to hydration.

Compiled available volumes in dermis expressed as percentage of interstitial fluid volume (V_i) relative to hydration. Symbols represent data from the following studies: ▾, Bert et al. 1986; •, Wiig et al. 2003; ▿, Reed et al. 1989; ▪, present study. Values are ± 1 s.e.m. Results for present study derived from regression equations and s.e.m. not shown. For further explanation see text.

Reed and coworkers (Reed et al. 1989) reported excluded volumes of 58 and 74% in normally and dehydrated rat dermis in vivo, both significantly higher than our corresponding volumes for control dermis. Again, the state of hydration at the outset may explain the discrepancy since both data sets fit in with the available volume–hydration relationship shown in Fig. 5.

Physiological implications

The present data have implications for our understanding of fluid distribution within the interstitium of dermis during changes in tissue hydration. The skin contains 30–40% of the total body interstitial fluid volume (Aukland & Nicolaysen, 1981), and is therefore quantitatively important from a fluid balance perspective. As for interstitial exclusion, its magnitude has important consequences in the dynamics of transcapillary exchange. Macromolecular exclusion results in an effective protein concentration in the interstitium that is much higher than the value that would be estimated if it were assumed that all the fluid in the interstitium was available. The physiological importance of the exclusion phenomenon is twofold: a more rapid approach to a new steady state after a change in transcapillary fluid flow and less transfer of interstitial protein to plasma for a given capillary hyperfiltration (Aukland & Reed, 1993). Interstitial exclusion of albumin, the predominant plasma protein, thereby influences plasma volume regulation. First we will discuss the size of the excluded volume per se in relation to excluding structures, i.e. whether domains of excluding agents are overlapping or additive (Bert et al. 1982) and thereafter how the present data may be interpreted in relation to distribution between intra- and extrafibrillar volume.

A quantitative estimate of the charge effect on excluded volume during variation in hydration can be found by comparing the data using PBS and 1 m NaCl. The latter solution will efficiently screen charged sites on fixed tissue elements (and probes), including collagen. In order for the electrostatic forces to be effective, the width of the double electrical layer, i.e. the Debye length, has to be relatively high. In the presence of a strong electrolyte such as 1 m NaCl, however, the double electric layer becomes compressed and shielded, that is, the negative charges of the matrix components are shielded by the positive sodium counter-ions (Bockris & Reddy, 1998). As a result, the effective electrostatic repulsion toward the negatively charged albumin becomes negligible and, as shown in Fig. 4, undetectable.

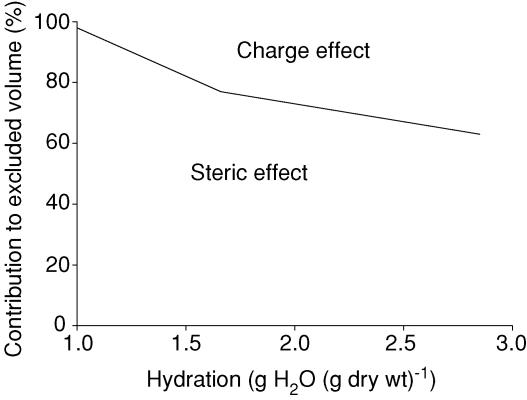
We may apply the initial hydration of 1.66 g H₂O (g dry wt)⁻¹ in the regression equations, use the data for native HSA and assume that the exclusion in PBS (Fig. 2) is the sum of steric and charge effects (i.e. additive) and that numbers for 1 m NaCl (Fig. 4) are representative for steric exclusion only. We then find that steric and charge effects account for 77 and 23%, respectively, of the exclusion in normally hydrated dermis. Choosing our lowest hydration of 1.0 g H₂O (g dry wt)⁻¹ results in excluded fractions due to steric and charge effects of 98 and 2%, respectively. Our highest hydration of 2.85 g H₂O (g dry wt)⁻¹ give corresponding numbers of 63 and 37%, agreeing well with our previous estimates for fully swollen skin (hydration 3.09 g H₂O (g dry wt)⁻¹) (Wiig et al. 2003). The calculations above have been summarized in Fig. 6, and taken together with our finding of a reduced difference between available volume for cHSA and HSA (Fig. 3) clearly show that even if there is some effect of charge at low hydration, such an effect is reduced along with hydration and practically abolished at a hydration of 1.0 g H₂O (g dry wt)⁻¹. There is accordingly an increased importance of steric (i.e. collagen) relative to charge effects on available and excluded volume with reduced hydration of the tissue (Fig. 6).

Figure 6. Relative contribution of steric and charge effects to excluded volume.

Relative contribution of steric and charge effects to excluded volume of native human serum albumin (pI = 4.9) related to hydration of dermis. Calculations based on data for equilibration in PBS (sum of steric and charge effects) and 1 m NaCl (steric effect only). Area below division line represents steric whereas area above line represents charge effect. We notice an increased importance of steric and a reduced importance of charge for exclusion of HSA with reduced hydration.

Alternatively, we may assign excluded volumes to specific tissue elements at low hydration. In human dermis, highly organized collagen will exclude albumin from a volume of 1.57 g fluid (g collagen)⁻¹ (Bert et al. 1982). If the same applies to rat dermis, at a hydration of 1.0 g H₂O (g dry wt)⁻¹ corresponding to an interstitial volume of 0.52 g H₂O (wet wt)⁻¹ where all is excluded for HSA, the measured amount of collagen of 0.63 g (g dry wt)⁻¹ (corresponding to 0.32 g (g wet wt)⁻¹) should alone exclude native albumin from 0.50 g H₂O (g wet tissue)⁻¹. These volumes agree well with figures for relative collagen exclusion above showing a gradually increased importance of collagen as an excluding agent during reduced hydration. There is accordingly no need for overlapping domains or alteration in organization of the collagen fibres to explain our observations, in contrast to some previous in vivo data for skin (Wiig et al. 1992) and tail tendon (Aukland et al. 1997).

Our hypothesis was that increased macromolecular crowding during reduced hydration would result in increased density of charged excluding species and thereby to an exaggerated effect of charge on exclusion. As evident from Fig. 3 the opposite effect was found, calling for an alternative explanation. It is possible that cationization effects on the overall shape of the albumin molecule became apparent in this situation and contributed to our observation, but the similar hydrodynamic radius of cHSA and HSA as estimated by HPLC in the present as well as in a previous study using a different column (Wiig et al. 2005) does not support this notion.

We may assume that the negatively charged GAGs are the main agents responsible for the observed charge effect on exclusion. Native albumin has a significant negative charge (−17) resulting in an electron cloud and a surrounding hydration domain and thus a higher effective Stoke-Einstein radius. When the hydration is reduced and the tissue is compressed, one may intuitively expect increased electrostatic interactions between tissue elements and probes. Actually, considering data in Fig. 4 may indicate the opposite. In the strong electrolyte, the extracellular space was lower than that in PBS for the same hydration, whereas the opposite was found for the albumin probes. These data are indicative of a change in the matrix geometry where the network components tend to collapse. As the polyelectrolyte chains approach each other their hydration domains (that surround the charges) merge and the chains might enter in an anomalous domain where same charges attract instead of repel each other (Bockris & Reddy, 1998).

Structural changes of the gel may also explain the somewhat surprising finding of a difference in slope for the relationship between extracellular fluid and albumin probes using PBS but not 1 m NaCl as vehicle. Whereas the difference between extracellular fluid and available HSA/cHSA space was constant for 1 m NaCl, this difference fell with reduced hydration for PBS, suggesting a charge-dependent redistribution between intra- and extrafibrillar fluid or a structural reorganization of the collagen fibres in the latter case. The extracellular fluid volume may be subdivided into an intra- and extrafibrillar space, and for the extrafibrillar space a given fraction is available for macromolecular probes like albumin (Snowden & Maroudas, 1976; Aukland et al. 1997; Aukland et al. 2001). Our data clearly indicate that during reduction in hydration, fluid is most easily mobilized from the extrafibrillar space, in agreement with studies on cartilage (Maroudas et al. 1991). From other experiments in cartilage it has been shown that the molecular packing density of collagen is influenced by the amount of osmotically active components in the extrafibrillar fluid (Katz et al. 1986) and by electrostatic repulsion (Wachtel & Maroudas, 1998). Collagen has a slight positive charge at physiological pH (Li & Katz, 1976), and since it has close to no net charge, it behaves as a tissue element with effectively no areas with high local charge. One may therefore question how electrostatic interaction may influence fibril packing. Recently Aukland et al. (2001) presented evidence that hyaluronan is located in the intrafibrillar collagen space in tail tendon, a phenomenon which may explain the observed difference in slope. In 1 m NaCl, the hyaluronan charges are screened by the high salt and the intrafibrillar water is constant during variation in hydration. In PBS, however, increased electrostatic interactions during reduced hydration may lead to attraction rather than repulsion of the negatively charged hyaluronan (cf. previous paragraph) again resulting in mobilization of fluid from this space and thereby reduced intrafibrillar water and distance.

In conclusion, we aimed at exploring the effect of charge on excluded volume for albumin in dermis during changes in hydration. Whereas we had expected an increased effect of electrostatic repulsion at reduced hydration, the opposite was found. This effect may be explained by loss of hydration domains surrounding negatively charged macromolecules in conditions of increased electrostatic interactions. Furthermore, screening of negative charge by 1 m NaCl showed that hyaluronan associated with collagen may influence intrafibrillar volume of collagen and thereby available and excluded volume fraction.