Force-dependent chemical kinetics of disulfide bond reduction observed with single-molecule techniques

Abstract

The mechanism by which mechanical force regulates the kinetics of a chemical reaction is unknown. Here, we use single-molecule force–clamp spectroscopy and protein engineering to study the effect of force on the kinetics of thiol/disulfide exchange. Reduction of disulfide bonds through the thiol/disulfide exchange chemical reaction is crucial in regulating protein function and is known to occur in mechanically stressed proteins. We apply a constant stretching force to single engineered disulfide bonds and measure their rate of reduction by DTT. Although the reduction rate is linearly dependent on the concentration of DTT, it is exponentially dependent on the applied force, increasing 10-fold over a 300-pN range. This result predicts that the disulfide bond lengthens by 0.34 Å at the transition state of the thiol/disulfide exchange reaction. Our work at the single bond level directly demonstrates that thiol/disulfide exchange in proteins is a force-dependent chemical reaction. Our findings suggest that mechanical force plays a role in disulfide reduction in vivo, a property that has never been explored by traditional biochemistry. Furthermore, our work also indicates that the kinetics of any chemical reaction that results in bond lengthening will be force-dependent.

The intersection of force and chemistry has been studied for over a century, yet not much is known about this phenomenon compared with more common methods of chemical catalysis (1). There are a number of reasons for this discrepancy, but one of the most important factors remains that it is quite difficult to directly measure the effect of force on a bulk reaction. This difficulty arises because an applied force is not a scalar property of a system; it is associated with a vector. As a result, it is often not possible to directly probe the effect of force on a particular reaction because of heterogeneous application of force and a distribution of reaction orientations (1). To fully quantify the effect of an applied force on a chemical reaction, it is necessary to generate an experimental system where the reaction of interest is consistently oriented with respect to the applied force. Thus, recent advances in single-molecule techniques are particularly well suited to address this problem. The direct manipulation of single molecules allows for the application of force in a vector aligned with the reaction coordinate (2), avoiding the heterogeneity of bulk studies. Earlier works using single-molecule techniques have described the rupture forces necessary to cleave single covalent bonds (reviewed in ref. 1), including Si–C bonds in polysaccharide attachment (3), Au–Au bonds in nanowires (4, 5), and Ni²⁺–NTA attachments (6). However, these studies have not been able to describe the effect of force on the kinetics of these reactions, nor have they examined more complex chemical reactions beyond simple bond rupture.

To test the hypothesis that mechanical force can directly influence the kinetics of a chemical reaction, we studied thiol/disulfide exchange, the reduction of disulfide bonds in a protein (7). The disulfide bond itself is a covalent bond formed between the thiol groups of two vicinal cysteine residues. In the first step of thiol/disulfide exchange, a new disulfide bond is formed between a thiolate anion of the reducing molecule (in this case DTT) and one cysteine on a protein, whereas the sulfur of the other cysteine reverts to the free thiolate state. This reaction has been extensively studied and is known to be important in the function and folding processes of proteins (8–10). This reaction is also of particular interest because it is known that many proteins that are exposed to mechanical stress in vivo contain disulfide bonds (11–13). Thus, the effect of force on this reaction could be of significance in biological systems.

Disulfide bonds have been studied in previous atomic force microscopy (AFM) experiments where a protein molecule is stretched at a constant velocity whereas the applied force varies (force-extension AFM). Most of these experiments could identify the presence or absence of a disulfide bond (14–17) but could not determine when the disulfide reduction reaction occurred. In recent work from our laboratory, we used engineered disulfide bonds to precisely correlate disulfide reduction events with increases in protein contour length, developing a molecular fingerprint for identifying individual chemical reactions (S.R.K.A. and J.M.F., unpublished data). In the present work, we use this fingerprint to investigate the kinetics of thiol/disulfide exchange as a function of pulling force using force–clamp AFM (18, 19). This method provides the only direct means by which to observe the exponential chemical kinetics of thiol/disulfide exchange under a calibrated pulling force. This technique has been used to study the unfolding kinetics (19) as well as refolding (20) of single protein molecules as a function of force, offering insight into the link between protein dynamics and force. By using force–clamp AFM, we directly demonstrate that thiol/disulfide exchange, a bimolecular chemical reaction (21), is catalyzed by mechanical force. The force-dependency of the reaction rate is determined by the structure of the transition state, a result that may be generalized to other chemical reactions. These findings demonstrate that force–clamp AFM is a powerful tool with which to study chemistry at the single-molecule level.

Results and Discussion

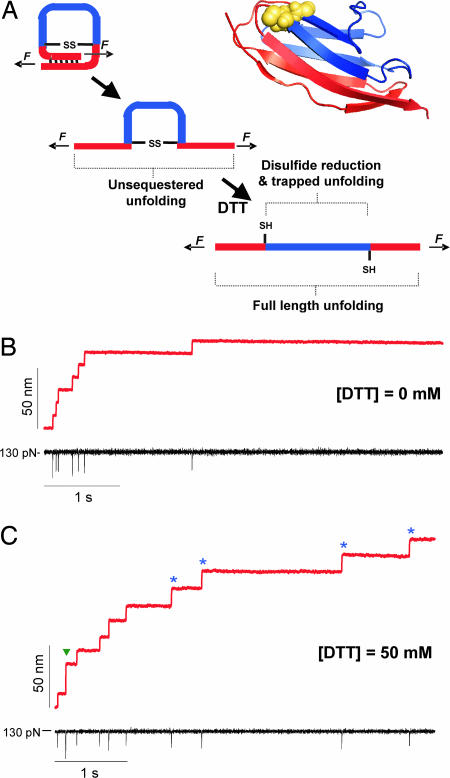
In our studies, we use the 27th immunoglobulin-like domain of cardiac titin (I27), an 89-residue, β-sandwich protein with well characterized mechanical properties (22, 23). Through cysteine mutagenesis, we engineered a disulfide bond in the I27 domain between the 32nd and 75th residues, which are closely positioned in space as determined by the NMR structure of wild-type I27 (Protein Data Bank ID code 1TIT). We constructed and expressed an eight-repeat polyprotein (22) of this modified domain, (I27_G32C–A75C)₈, and used single-molecule force–clamp spectroscopy (19) to manipulate and stretch single polyproteins. Under force–clamp conditions, stretching a polyprotein results in a well defined series of step increases in length, marking the unfolding and extension of the individual modules in the chain (19). Previous work has demonstrated that there is a close correlation between the size of the observed steps and the number of amino acids released by each unfolding event (19). Upon stretching a single (I27_G32C-A75C)₈ polyprotein in an oxidizing environment (Fig. 1B), we observe a series of steps of ≈10.6 nm, which are significantly shorter than those expected for native I27 unfolding (23.6 nm; see Fig. 6B, which is published as supporting information on the PNAS web site). This shortening indicates the formation of the engineered disulfide bond within the protein module. The unfolding of 46 “unsequestered” residues (1–31 and 76–89) has a predicted step size of 10.4 nm at 130 pN (Fig. 6A; see also Supporting Results and Discussion, which is published as supporting information on the PNAS web site), very similar to the observed value. At this stage of unfolding, the disulfide bond in each module is directly exposed to the applied stretching force (Fig. 1A), forming a covalent barrier “trapping” residues 33–74 and preventing complete module unfolding. If the bond were to be ruptured by force alone, we would expect to observe a second step corresponding to the extension of the trapped polypeptide. Yet we do not observe any such steps under these oxidizing conditions (Fig. 1B). This outcome was predicted by previous experimental and theoretical studies (3, 24), where forces <1 nN cannot break a covalent bond. After unsequestered unfolding, the disulfide bond is exposed to the solvent, and thiol/disulfide exchange can occur if DTT is present in solution. In Fig. 1C, we pull a single (I27_G32C-A75C)₈ molecule in the presence of 50 mM DTT. During the first second, we observe a series of steps of ≈10.8 nm as unsequestered unfolding occurs in individual domains. The one step of 24.0 nm denotes a domain with its disulfide reduced before mechanical unfolding, giving a full-length step approximately equal to that for wild-type I27. Such full-length unfolding was rare, however; previous studies have indicated that the disulfide bond in I27_G32C-A75C is particularly solvent-inaccessible in the folded protein (S.R.K.A. and J.M.F., unpublished data). After this first series of steps relating to protein unfolding, which occur over ≈1 s, we then observe a second series of steps of ≈13.8 nm over ≈4 s. The predicted step size for trapped residue extension as determined from force-extension experiments is 13.5 nm at 130 pN (Fig. 6A). In addition, these steps were observed only after unsequestered protein unfolding and only in the presence of DTT. Hence, we conclude that at a pulling force of 130 pN, the 13.8-nm steps monitor the thiol/disulfide exchange reaction as single disulfide bonds are reduced in each protein module, allowing for the extension of the trapped residues.

Fig. 1.

Force–clamp spectroscopy identifies single thiol/disulfide exchange events under a stretching force. (A) An engineered disulfide bond was introduced between the 32nd and the 75th residue of the 27th Ig-like domain of cardiac titin (I27_G32C–A75C). In the ribbon diagram of I27_G32C–A75C, mutated residues 32 and 75 are yellow spheres, residues 1–31 and 76–89 are pictured in red (unsequestered residues), and 33–74, behind the disulfide bond, are in blue (trapped residues). The cartoons on the left depict the three sequential events that take place when we apply a mechanical force to the I27_G32C–A75C protein. Applying a mechanical force first triggers the unfolding and extension of the protein, up to the position of the disulfide bond. We call this initial elongation unsequestered unfolding. If DTT is present in the bathing solution, disulfide bond reduction can occur, allowing for the extension of the trapped residues. (B) Force–clamp experiment showing the stepwise elongation (red trace) of an (I27_G32C–A75C)₈ polyprotein pulled at a constant force of 130 pN (black trace) in the absence of DTT. Seven steps of equal size, ≈10.6 nm, mark the sequential unfolding of the unsequestered region of seven I27_G32C–A75C modules in the polyprotein. The brief downward deflections in the force (black trace) are due to lag in the feedback electronics after each unfolding event. (C) When the same experiment is repeated in the presence of 50 mM DTT, we again observe a series of ≈10.8 nm steps corresponding to the unsequestered unfolding events, followed by several ≈13.8 nm steps (blue stars), which mark thiol/disulfide exchange events and the subsequent extension of the trapped residues. In this trace, we also observe an event with an amplitude of ≈24.0 nm (green arrow), which corresponds to the unfolding of a single fully reduced I27 module.

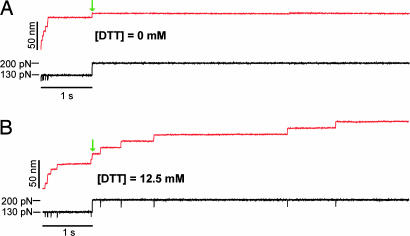
To study the kinetics of disulfide bond reduction as a function of the pulling force, we designed a double pulse protocol in force–clamp. The first pulse to 130 pN allows us to monitor the unfolding of the unsequestered region of the I27_G32C–A75C modules in the polyprotein, exposing the disulfide bonds to the solution. With the second pulse, we track the rate of reduction of the exposed disulfides at various pulling forces. Fig. 2 demonstrates the use of the double-pulse protocol in the absence (Fig. 2A) and in the presence of DTT (Fig. 2B). In both cases, the first pulse elicits a rapid series of steps of ≈10.6 nm marking the unfolding and extension of the 46 unsequestered residues. The second pulse in Fig. 2 increases the stretching force up to 200 pN. Upon application of the second pulse, we observe an elastic extension of the polyprotein by ≈10 nm. In the presence of DTT (12.5 mM), this elastic extension is followed by a series of five additional ≈14.2-nm steps that mark single thiol/disulfide exchange reactions (expected steps of 14.2 nm at 200 pN; see Fig. 6Aand also Table 1, which is published as supporting information on the PNAS web site), whereas no further steps were observed in the absence of DTT (Fig. 2A).

Fig. 2.

A double-pulse protocol separates the unsequestered unfolding from disulfide reduction events. (A) Typical double-pulse force–clamp experiment pulling the (I27_G32C–A75C)₈ protein first at 130 pN for 1 s and then stepping to a force of 200 pN for 7 s (black trace). In this experiment, the first pulse to 130 pN causes a series of seven unsequestered unfolding events (10.6-nm steps). Upon increasing the force to 200 pN (green arrow), we observed an elastic step elongation of the protein. In the absence of DTT, no further steps are observed. (B) Repeating the same experiment in the presence of 12.5 mM DTT, we again observed six unsequestered unfolding events at 130 pN. Upon stepping to 200 pN and after the elastic elongation of the protein (green arrow), we then observed a series of five steps of ≈14.2 nm corresponding to the disulfide reduction events. Notice the rapid exponential time course followed by the unsequestered unfolding events at 130 pN and the much slower reduction events observed during the second pulse at 200 pN.

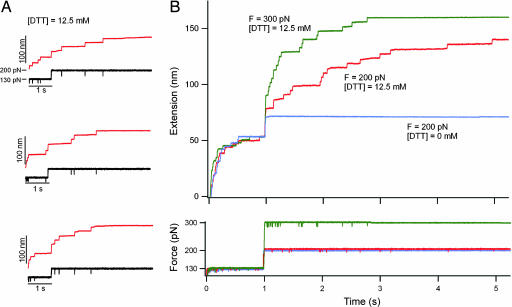
To measure the rate of reduction at 200 pN and at a DTT concentration of 12.5 mM, we repeated many times the pulse pattern shown in Fig. 2B, obtaining an ensemble of single-molecule recordings. Fig. 3A shows three additional recordings demonstrating the stochastical nature of both the unsequestered unfolding and of the thiol/disulfide exchange events. The red trace in Fig. 3B was obtained by simple averaging (19) of these four recordings. The green trace in Fig. 3B was obtained following similar procedures with the second force pulse to 300 pN. By comparison, the blue trace in Fig. 3B corresponds to the averaging of four traces obtained with the second force pulse set to 200 pN and in the absence of DTT. It is apparent from Fig. 3B that protein unfolding during the first pulse to 130 pN is independent of DTT, following a similar exponential time-course in all cases at this force. However, thiol/disulfide exchange during the second pulse appears both DTT- and force-dependent. The double-pulse protocol as shown here effectively separates protein unfolding from the disulfide-bond reduction events. Hence, in the subsequent analysis we ignore the unsequestered unfolding observed during the first pulse and only analyze thiol/disulfide exchange events in the second pulse.

Fig. 3.

Ensemble measurements of the kinetics of thiol/disulfide exchange. (A) Three recordings are shown of single (I27_G32C–A75C)₈ polyproteins that were extended with the same double-pulse protocol shown in Fig. 2B: 12.5 mM DTT, F = 130 pN for 1 s, and then F = 200 pN. The stochastic nature of both the unsequestered unfolding events as well as of the thiol/disulfide exchange events becomes apparent when comparing these recordings. (B Upper) A four-trace average (red trace) of the double-pulse experiments shown in A and Fig. 2B demonstrates the methods used to build up an ensemble of recordings under a set of conditions. Similar four-trace averages are shown for data obtained under two other conditions: 12.5 mM DTT, F = 130 pN for 1 s then F = 300 pN (green trace); and 0 mM DTT, F = 130 pN for 1 s then F = 200 pN (blue trace). Notice that the time course of unsequestered unfolding during the first pulse is similar under all conditions. (B Lower) The averaged force traces are shown.

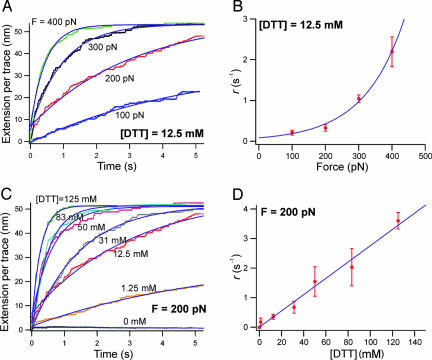
We conducted multiple double-pulse experiments, all with an identical first force pulse to 130 pN lasting 1 s. Fig. 4A shows multiple (>25) trace averages of only the second pulse at four different forces (100, 200, 300, and 400 pN) and at a constant DTT concentration of 12.5 mM. Only traces that included a clear unsequestered unfolding fingerprint in the first pulse and that contained only disulfide reduction events in the second pulse were included in this analysis. By fitting a single exponential to the traces shown in Fig. 4A, we define the observed rate of thiol/disulfide exchange as r = 1/τ_r, where τ_r is the time constant measured from the exponential fits. In Fig. 4B, we show that r is exponentially dependent on the applied force (12.5 mM DTT) ranging from 0.211 s⁻¹ (100 pN) up to 2.20 s⁻¹ (400 pN). Fig. 4C shows the second-pulse averages (>20) of experiments conducted at 200 pN, at different concentrations of DTT (0, 1.25, 12.5, 31, 50, 83, and 125 mM). In Fig. 4D, we show that r has a first-order dependence on the concentration of DTT, demonstrating that the thiol/disulfide exchange reaction in our system is bimolecular.

Fig. 4.

The thiol/disulfide exchange chemical reaction is force and [DTT] dependent. Multiple-trace averages (n > 20 in each trace) of thiol/disulfide exchange events measured by using the double-pulse protocol as a function of force and DTT concentration are shown. Only the second pulse averages are shown; time = 0 s denotes the start of the second pulse. (A) A set of trace averages measured at a constant concentration of DTT (12.5 mM), while varying the force of the second pulse between 100 and 400 pN. Single-exponential fits (continuous lines) measure the time constant, τ_r, of thiol/disulfide exchange. (B) Plot of the rate of thiol/disulfide exchange, r = 1/τ_r, as a function of the pulling force at [DTT] = 12.5 mM. The solid line is an exponential fit to the data. (C) Trace averages measured at a constant pulling force (F = 200 pN) and at various DTT concentrations. (D) Plot of r as a function of [DTT]. The solid line is a linear fit to the data. The linear (first-order) dependence on [DTT] demonstrates that the thiol/disulfide exchange reaction in our system is bimolecular. This reaction can be described empirically from B and D by the simple rate equation r = k(F)[DTT], where k(F) is exponentially dependent on the pulling force and k(200 pN) = 27.6 M⁻¹·s⁻¹ from the linear fit in D.

Given these observations, we derive an empirical relationship r = k(F)[DTT], where k(F) depends exponentially on the applied force and is given by a Bell-like (25) relationship: k(F) = A exp((FΔx_r − E_a)/k_BT). In this equation, A is a constant with units of M⁻¹·s⁻¹, Δx_r is the distance to the transition state for the reaction, and E_a is the activation energy barrier for the thiol/disulfide exchange at zero force. Fitting this equation to the data presented in Fig. 4B, we obtain a value of Δx_r = 0.34 Å and a value of k(0) = 6.54 M⁻¹·s⁻¹, which is similar to the second-order rate constant for DTT reduction of disulfide bonds in insulin at neutral pH [k = 5 M⁻¹·s⁻¹ (26)]. Other studies have found that under certain solution conditions, thiol/disulfide exchange can occur with a second-order rate constant as high as 132,000 M⁻¹·s⁻¹ (27) but also can be up to 6 orders of magnitude slower, in accord with our observations. From the linear fit in Fig. 4D, we see that an applied force alters the second-order rate constant in our system; k(200 pN) = 27.6 M⁻¹·s⁻¹, a 4-fold increase from zero force. Assuming that A ranges from 10⁵ to10¹² M⁻¹·s⁻¹, we estimate E_a to be in the range of 30–65 kJ/mol. The upper values in this range overlap with the calculated energy barriers for a number of thiol/disulfide exchange reactions in solution [60–66 kJ/mol (28)], and each 100 pN of force lowers the energy barrier by ≈2 kJ/mol.

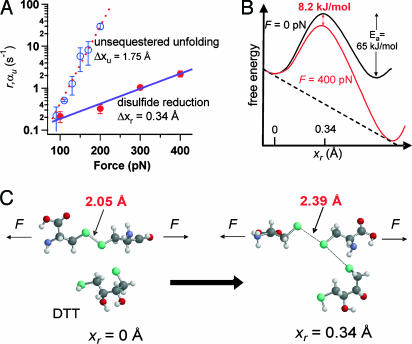
Although our empirical Bell-like model (2, 25) is a useful first approximation to examine our data, it may not hold over all combinations of DTT and force. It also cannot completely describe the effect of a force on the thiol/disulfide exchange reaction. The force constant for an S–S bond, found by vibrational spectrum in the gas phase, is 4.96 N/cm (29). As a result, an applied force of 400 pN will stretch this bond by only 0.008 Å, which is a negligible effect on the geometry of the S–S bond. However, as pointed out by Beyer (30), the reactivity of a stretched molecule is likely to depend on the pulling force despite only minor changes in bond geometry. Furthermore, a reorganization of the energy landscape of the bond is likely to occur during bond lengthening (31). These effects are not accounted for by our model. Hence, further theoretical developments on the effect of a mechanical force on the thiol/disulfide exchange reaction will be required to fully understand our experiments. These limitations notwithstanding, we can still extract useful parameters from our analysis. For example, the sensitivity of the rate of reduction to a pulling force is well represented by the measured value of Δx_r, which can be contrasted to that of unfolding the unsequestered region of the protein. By fitting a single exponential to an average of traces containing solely unsequestered unfolding events of the type shown in Fig. 1B (no DTT), we measured the rate of unfolding, α_u = 1/τ_u, at different pulling forces (see Fig. 7, which is published as supporting information on the PNAS web site). Fig. 5A shows a semilogarithmic plot of both α_u and r as a function of the pulling force. The dashed line corresponds to a fit of α_u(F) = α_u(0) exp(FΔx_u/k_BT) (19), obtaining Δx_u = 1.75 Å for the unsequestered unfolding. The solid line is a fit of the Bell-like model described earlier, where Δx_r = 0.34 Å for the thiol/disulfide exchange reaction. Fig. 5A confirms the difference in force sensitivity between the unsequestered unfolding and the thiol/disulfide exchange reaction, which are two distinct processes occurring within the same protein.

Fig. 5.

Force sensitivity and bond lengthening in the thiol/disulfide exchange chemical reaction. (A) Semilogarithmic plot of the rate of thiol/disulfide exchange, r (filled circles) and of the unsequestered unfolding rate, τ_u (open circles) as a function of the pulling force. The solid line is a fit of the equation r = A(exp((FΔx_r−E_a)/k_BT))[DTT]. The fit gave values of Δx_r = 0.34 Å and E_a = 65 kJ/mol (with A ≈ 10¹² s⁻¹·M⁻¹) for thiol/disulfide exchange. The dashed line fits the unsequestered unfolding rate with α_u(F) = α_u(0)exp(FΔx_u/k_BT) obtaining Δx_u = 1.75 Å. (B) A simple illustration of the energy landscape of the thiol/disulfide exchange reaction under force. Our Bell-like model predicts that the transition state is located at 0.34 Å along the linear reaction coordinate, explaining the relative insensitivity of this reaction as compared with the unsequestered unfolding of the I27 protein. We calculate that applying 400 pN of force reduces the activation energy barrier for thiol/disulfide exchange by 8.2 kJ/mol. (C) Illustration of the thiol/disulfide exchange reaction between a DTT molecule and a disulfide bond under a stretching force. Only the two participating cysteine residues are shown for simplicity. The sulfur atoms are in green. The disulfide bond length increases from 2.05 Å initially (29) (Left) up to 2.39 Å at the transition state of an S_N2 reaction between the DTT molecule and the disulfide bond (Right).

From our measurements above we obtained a preliminary description of the energy landscape for the thiol/disulfide exchange chemical reaction under a stretching force (Fig. 5B). Recent theoretical calculations have proposed that the length of an S–S bond at the transition state of a simple S_N2 thiol/disulfide exchange reaction in solution increases by 0.36 Å (32) or 0.37 Å (28). These values suggest that the value of Δx_r that we have measured experimentally corresponds to the lengthening of the S–S bond during an S_N2 reaction with a DTT molecule (Fig. 5C). Furthermore, in these theoretical studies, varying the reaction mechanism could result in S–S lengthening at the transition state as small as 0.24 Å or as large as 0.78 Å (28). Different values of Δx_r would result in very different sensitivities of the reaction to a pulling force. Hence, we propose that by experimentally measuring the value of Δx_r, as demonstrated here for a single disulfide bond, we can distinguish amongst different types of reaction mechanisms. Conversely, our work also suggests that other bimolecular reactions that result in bond lengthening may be force dependent.

Although we have demonstrated force-dependent thiol/disulfide exchange in an engineered protein, there are many native proteins that contain disulfide bonds and that are exposed to mechanical forces in vivo. Some examples include cellular adhesion proteins such as cadherins (33), selectins (34), and IgCAMs (16). Others are important in maintaining the extracellular matrix, such as fibronectin (35), or in tissue elasticity, such as fibrillin (36) and titin (13). It has been shown that thiol/disulfide exchange in integrin α_IIbβ_III (11) as well as disulfide reduction in von Willebrand factor multimers (37) is necessary for hemostasis and regulating clot formation under high shear forces generated by blood flow. Even the mechanical process of HIV virus fusion and entry into helper T cells has been shown to require disulfide bond reduction in both gp120 of HIV (38) and the CD4 cell surface receptor (39).

We have found that forces >100 pN are necessary to achieve a measurable increase in the rate of thiol/disulfide exchange. Such forces are thought to be toward the high end of the range experienced in biology: single protein complexes may produce forces >100 pN (40), and single selectin–ligand bonds can withstand forces >200 pN (12). Although it is not yet known how often a single disulfide bond in vivo will be exposed to the force levels we explored in this study, it does seem likely that the sensitivity of any particular thiol/disulfide exchange reaction to a pulling force will depend very specifically on the environment surrounding the bond as well as the type of chemical reaction involved. For example, Δx_r is likely to depend on a number of factors that also affect the rate of the thiol/disulfide exchange reaction, including the temperature (41), type of reducing agent (42), pH (42), electrostatics (43), the reaction mechanism (28), and the torsional strain present in the protein structure (21, 44, 45). Any combination of these effects that cause Δx_r to be >1 Å would lead to a near 2-fold increase in reduction rate over just 20 pN of applied force, suggesting that force-catalyzed disulfide reduction may play an important role in vivo.

Materials and Methods

Protein Engineering and Purification.

We used the QuikChange site-directed mutagenesis kit (Stratagene) to mutate residues Gly-32 and Ala-75 in the 27th Ig-like domain of human cardiac titin (22) to Cys residues. Native Cys-47 and Cys-62, which do not form a disulfide bond, were mutated to alanines. We constructed an eight-domain N–C linked polyprotein of this I27_G32C–A75C domain through rounds of successive cloning in modified pT7Blue vectors and then expressed the gene using vector pQE30 in Escherichia coli strain BL21(DE3) as described (22). Pelleted cells were lysed by sonication and the His-6-tagged soluble protein was purified first by immobilized metal ion affinity chromatography (IMAC) and then by gel filtration. The protein was stored at 4°C in 50 mM sodium phosphate/150 mM sodium chloride buffer (pH 7.2).

Single-Molecule Force–Clamp Spectroscopy.

Our custom-built atomic force microscope equipped with a PicoCube P363.3-CD piezoelectric translator (Physik Instruments, Karlsruhe, Germany) controlled by an analog proportional–integral–differential feedback system is described in ref. 19. All data were obtained and analyzed by using custom software written for use in igor 5.0 (WaveMetrics, Lake Oswego, OR). There was ≈0.5 nm of peak-to-peak noise and a feedback response time of ≈5 ms in all experiments. The spring constant of silicon–nitride cantilevers (Veeco, Santa Barbara, CA) was calibrated as reported in ref. 18; the average spring constant was ≈15 pN/nm. All experiments were conducted in PBS buffer with the indicated amount of DTT (Sigma). Buffers were all controlled to pH 7.2. All experiments were conducted over ≈8 h at room temperature (298 K) in an atmosphere open to air. Small changes in active DTT concentration due to evaporation and air-oxidation of DTT did not appear to greatly affect our results, because traces compiled over the course of 1 day's experiment at the same force demonstrated similar single-exponential kinetics. Approximately 5 μl of protein sample (≈0.1 mg/ml) in phosphate buffer was added to ≈70 μl of DTT-containing buffer in each experiment. Single protein molecules were stretched by first pressing the cantilever on the gold-coated coverslide for 3 s at 350–500 pN, then retracting at a constant force. Our success rate at picking up a single molecule was ≈1% of trials. Gold-coated coverslides were used because they resulted in a better success rate than glass coverslides even in the absence of thio-gold bonds. In all force-dependent experiments (Fig. 4A), the molecule was stretched for 1 s at 130 pN and then 5–7 s at the second pulse force. In the concentration-dependent experiments (Fig. 4C), the molecule was pulled at 130 pN for 1 s (0–31 mM DTT) or 140–145 pN for 0.2–0.5 s (50–125 mM DTT; the shorter first pulse times are to reduce thiol/disulfide events during the first pulse), then the force increased to 200 pN for 5–7 s. The interaction between protein and cantilever/coverslide is nonspecific. Thus, in most cases fewer than eight domains were unfolded when a molecule was stretched.

Data Analysis.

The fingerprint of a single (I27_G32C–A75C)₈ was considered to be two well resolved steps of ≈10.5 nm during the first pulse. No traces that included unsequestered unfolding events during the second pulse were included in the analysis. Such mixed spectra were very rarely observed (<1%) at forces of 200 pN or greater because of the very rapid kinetics of unsequestered unfolding at these forces. At a second pulse force of 100 pN, such mixed spectra were observed ≈15% of the time; such traces were not included in the averaging analysis because the unsequestered unfolding steps would corrupt the time course of disulfide reduction. We assume that disulfide reduction in our protein is Markovian (i.e., each reduction event is independent of all others); thus, averaging traces with different numbers of reduction steps will result in invariant exponential kinetics. Error bars in Figs. 4 B and D and 5A were obtained by partitioning the entire set of traces into random subsets (for example, if 20 total single-molecule traces were used, then two subsets of 10 traces each were constructed). These traces in these subsets then were averaged and fit with a single exponential. The rate of thiol/disulfide exchange (Fig. 4 A and B) or rate of unsequestered unfolding (Fig. 5A) was determined as described from the exponential fit. The standard deviation of the rate was then calculated with n = the number of subsets (in the case of the example, n = 2). This value then was used as the magnitude of the error bar shown in the figures.

Abbreviations

AFM

atomic force microscopy

I27

27th immunoglobulin-like domain of cardiac titin.