Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized

Abstract

The cornerstone of autotrophy, the CO₂-fixing enzyme, d-ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco), is hamstrung by slow catalysis and confusion between CO₂ and O₂ as substrates, an “abominably perplexing” puzzle, in Darwin's parlance. Here we argue that these characteristics stem from difficulty in binding the featureless CO₂ molecule, which forces specificity for the gaseous substrate to be determined largely or completely in the transition state. We hypothesize that natural selection for greater CO₂/O₂ specificity, in response to reducing atmospheric CO₂:O₂ ratios, has resulted in a transition state for CO₂ addition in which the CO₂ moiety closely resembles a carboxylate group. This maximizes the structural difference between the transition states for carboxylation and the competing oxygenation, allowing better differentiation between them. However, increasing structural similarity between the carboxylation transition state and its carboxyketone product exposes the carboxyketone to the strong binding required to stabilize the transition state and causes the carboxyketone intermediate to bind so tightly that its cleavage to products is slowed. We assert that all Rubiscos may be nearly perfectly adapted to the differing CO₂, O₂, and thermal conditions in their subcellular environments, optimizing this compromise between CO₂/O₂ specificity and the maximum rate of catalytic turnover. Our hypothesis explains the feeble rate enhancement displayed by Rubisco in processing the exogenously supplied carboxyketone intermediate, compared with its nonenzymatic hydrolysis, and the positive correlation between CO₂/O₂ specificity and ¹²C/¹³C fractionation. It further predicts that, because a more product-like transition state is more ordered (decreased entropy), the effectiveness of this strategy will deteriorate with increasing temperature.

The most abundant protein in nature is d-ribulose 1,5-bisphosphate (RuBP) carboxylase/oxygenase (Rubisco, EC 4.1.1.39) (1). This immense N investment is required to counter the enzyme's pitifully sluggish catalytic performance. Furthermore, Rubisco's tendency to confuse the substrate of photosynthesis, CO₂, with the product, O₂, saddles all aerobic photosynthetic organisms with energy-wasting photorespiration (2). Thus, this single enzyme's efficiency, or lack thereof, dictates the (in)efficiency with which plants use their basic resources of light, water, and N, and currently intense biotechnological effort aims to improve its catalytic properties and to engineer such improvements into crop plants (3, 4). Rubisco's difficulties stem from the inevitable O₂ sensitivity of the 2,3-enediol form of RuBP, to which CO₂ is added during the carboxylase reaction (5), which causes carboxylase/oxygenase bifunctionality (Fig. 1). This difficulty is exacerbated by the need to discriminate between featureless molecules, CO₂ and O₂, that can be bound in Michaelis–Menten complexes only weakly, if at all (2, 6). RuBP oxygenation has been considered to be “an inherent architectural constraint in the structure of life that need not be sustained by, and cannot be reduced by, selective pressure” (7, 8). However, significant natural variation among the kinetic parameters of Rubiscos from various sources seems to indicate responsiveness to selective pressure (9).

Fig. 1.

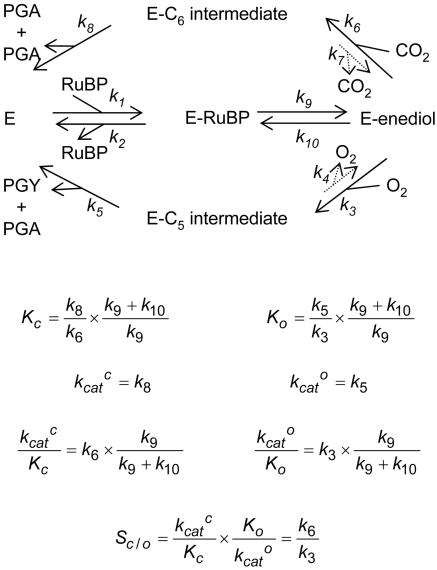
The formal mechanism of the Rubisco-catalyzed addition of CO₂ and O₂ to enolized RuBP (2, 3, 16, 17). The subscripts of the rate constants are those used previously to describe the mechanism (36). The additions of the gaseous substrates are effectively irreversible (i.e., k₇ and k₄ ∼ 0) (19) and, because enolization is readily reversible (6, 37) and [3-²H]RuBP reduces k_cat^c much less than expected for an intrinsic primary ²H effect (except when enolization becomes rate-limiting at unphysiologically low pH) (38, 39), enolization must be much faster than the maximum catalytic rate (i.e., k₈ and k₅ ≪ k₉). Thus the expressions (36) for the apparent Michaelis constants for CO₂ (K_c) and O₂ (K_o), the maximum carboxylation (k_cat^c) and oxygenation (k_cat^o) rates, the ratios between them (k_cat^c/K_c and k_cat^c/K_o), and the specificity for CO₂ relative to that for O₂ (S_c/o) (40) may be simplified as shown. C₆-int., 2′-carboxy-3-keto-d-arabinitol-1,5-bisphosphate; C₅-int., 2′-peroxy-3-keto-d-arabinitol-1,5-bisphosphate; PGA, 3-phosphoglycerate; PGY, 2-phosphoglycolate.

Here we analyze kinetic and isotope-fractionation data obtained from the literature for Rubiscos from a wide diversity of photo- and chemosynthetic organisms and observe clear correlations between the CO₂/O₂ specificity (S_c/o) and other parameters. We use these correlations to argue that, within the “architectural” constraints imposed by the physical and chemical properties of CO₂, the catalytic properties of Rubiscos from various organisms have evolved to match their differing gaseous environments nearly perfectly. We hypothesize that the variations in kinetic properties arise from optimizing an unusual compromise: an advanced product-like transition state for CO₂ addition aids discrimination between CO₂ and O₂, but its strong resemblance to the subsequent six-carbon carboxyketone intermediate causes that intermediate to bind so tightly that it restricts maximum catalytic throughput. This hypothesis may be represented in the form of an energy vs. reaction-coordinate diagram for carboxylation (Fig. 2) based on the sequence of intermediates shown in Fig. 1. The optimum compromise will depend on the CO₂:O₂ ratio in the subcellular environment to which a particular Rubisco is adapted. More discriminatory Rubiscos adapted to lower CO₂:O₂ ratios will be slower. This fundamental insight explains much that was previously inexplicable about Rubisco's kinetics. It predicts the inverse correlation between S_c/o and maximum carboxylation rate (k_cat^c) (10, 11), the extraordinarily tight binding of 2′-carboxy-d-arabinitol 1,5-bisphosphate (CABP), the analog of the carboxyketone intermediate [I] (Fig. 2) and its hydrate [II] (12), the very modest rate enhancement achieved by Rubisco in processing the carboxyketone compared with its nonenzymatic hydrolysis (13), and the positive correlation between S_c/o and ¹²C/¹³C isotope fractionation. It further predicts that the effectiveness of a more product-like transition state in enhancing CO₂/O₂ specificity will deteriorate with increasing temperature. Our hypothesis has extensive ramifications, ranging from the prospects for improving plant productivity by engineering Rubisco to the interpretation of palaeobotanical isotope signals.

Fig. 2.

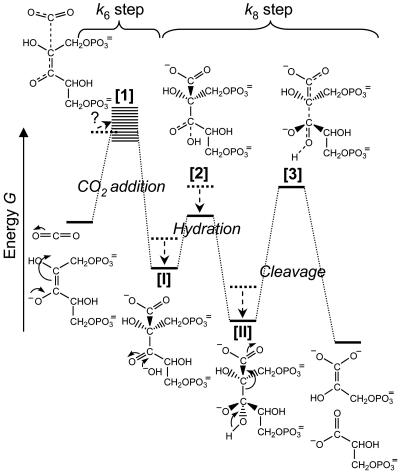
Energetic profile of part of the Rubisco-catalyzed carboxylation reaction, from the carboxylation of the enediolate of RuBP through to the cleavage of the hydrated carboxyketone. Shown are the hypothesized naturally selected shifts (arrows) from a less CO₂-specific Rubisco with a more reactant-like transition state for CO₂ addition (dashed energies) toward a more product-like transition state allowing greater CO₂ specificity (solid energies). The more product-like the transition state for carboxylation [1] is, the more closely it resembles the carboxyketone intermediate [I]. We cannot predict how this will affect the energy level of the whole transition-state-1/active-site complex, so we show a blurred band for the energy at this stage, extending both above and below that of the same transition state in the more reactant-like scenario. Because of their greater resemblance to [1], the carboxyketone intermediate [I] and its gem-diol hydrate [II] are bound more tightly in the more product-like scenario, lowering their energy (see text). As a consequence, the activation energy for cleavage increases, inducing k₈ to decrease. Note that carboxylation and hydration are assumed to be separate steps in this scheme. If they are not, the energetic profiles of CO₂ addition and hydration fuse to one, the hydrated intermediate still having a lowered energy level.

Theory and Discussion

Experimental Basis of the Hypothesis.

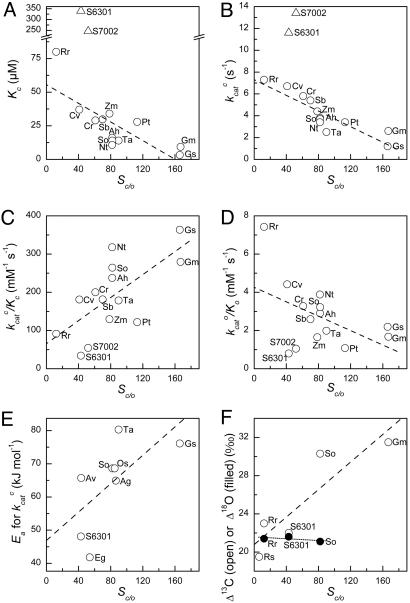
We discuss our hypothesis in terms of the bifurcating multistep mechanism of Rubisco's dual catalytic functions and the forms of the kinetic parameters that may be adduced from it (Fig. 1). Correlations among these kinetic parameters for different Rubiscos from widely varying sources are quite illuminating and form the experimental basis of our hypothesis (Fig. 3). The previously noted (10, 11) negative correlation between S_c/o and k_cat^c is particularly obvious (Fig. 3B), but other correlations are also apparent. The Michaelis constant for CO₂, K_c, also correlates negatively with S_c/o (Fig. 3A) and with a stronger dependency, so that k_cat^c/K_c correlates positively with S_c/o (Fig. 3C). By contrast, k_cat^o/K_o decreases with increasing S_c/o (Fig. 3D). E_a, the Arrhenius activation energy of k_cat^c, increases with S_c/o (Fig. 3E), as does the ¹³C isotope fractionation (Fig. 3F). However, there is no correlation between S_c/o and the fractionation of the ¹⁸O isotope during oxygenation, which is invariant (Fig. 3F). In what follows, we show how these relationships are the expected consequences of evolutionary optimization of the structure of the carboxylation transition state ([1], Fig. 2) along the reactant-/product-like coordinate to suit the CO₂ and O₂ concentrations prevailing in the subcellular environment in which each particular Rubisco functions and has evolved.

Fig. 3.

Natural variation in the kinetic properties of Rubisco in vitro at 25°C. See Table 1 for a listing of the data and their sources. The organisms from which the Rubiscos were isolated were: Ag, Atriplex glabriuscula (C₃ dicot); Ah, Amaranthus hybridus (C₄ dicot); Av, Anabaena variabilis (cyanobacterium); Cr, Chlamydomonas reinhardtii (green alga); Cv, Chromatium vinosum (bacterium); Eg, Euglena gracilis (green alga); Gm, Griffithsia monilis (red alga); Gs, Galdieria sulfuraria (red alga); Nt, Nicotiana tabacum (C₃ dicot); Os, Oryza sativa (C₃ monocot); Pt, Phaeodactylum tricornutum (diatom); Rr, Rhodospirillum rubrum (bacterium); Rs, the bacterial symbiont of the tubeworm Riftia pachyptila; Sb, Sorghum bicolor (C₄ monocot); So, Spinacia oleracea (C₃ dicot); S6301, Synechococcus PCC 6301 (cyanobacterium); S7002, Synechococcus PCC 7002 (cyanobacterium); Ta, Triticum aestivum (C₃ monocot); and Zm, Zea mays (C₄ monocot). Dashed and dotted lines are linear regressions through all of the data except for the cyanobacterial outliers (triangles) in A and B, which were excluded.

Although the trends apparent in the data shown in Fig. 3 are clear, data for individual Rubiscos scatter around the trend lines. This scatter is not large. For example, no Rubisco, even those from the cyanobacterial outliers, has a k_cat^c that falls more than a factor of 2 from the trend line (Fig. 3B). However, it is unlikely to be attributable solely to experimental imprecision. If our hypothesis is correct, some of this scatter may represent optimization currently in progress; that is, adjustment to recent (on the evolutionary timescale) changes in the subcellular CO₂/O₂ environment that is not yet complete.

Closer Resemblance Between the Carboxylation Transition State and Its Product Improves CO₂/O₂ Specificity but Makes the Product Bind Tighter.

The difficulty in binding CO₂ noncovalently limits Rubisco's ability to distinguish between CO₂ and O₂ before covalent chemistry, forcing reliance on transition-state structure as the main determinant of CO₂/O₂ specificity. Our hypothesis is based on the idea that, the more the CO₂ moiety of the transition state resembles a carboxylate group, the easier it will be for the enzyme to distinguish it from a peroxyl group (the O₂ adduct). Thus the more product-like the transition state becomes, the greater S_c/o will be. However, the more the transition state for carboxylation resembles its product, the tighter the carboxylated product (the carboxyketone [I] and/or its gem-diol hydrate [II], Fig. 2) will bind, because the interactions that stabilize the transition state will then tend to stabilize the product also (14). This accords with Rubisco's extraordinary avidity for the analog of the carboxylated intermediate, CABP (K_d <10⁻¹³ M) (15). In further accord, the binding is tighter (as reflected by the half-time for release of CABP from the complex) for the high-S_c/o Rubisco from spinach than for the low-S_c/o Rubisco from Rhodospirillum rubrum (Table 1). This amazing avidity, which rivals that of many transition-state analogs, far exceeds that required to suppress release of an unstable intermediate (12) and is suggestive of a strong resemblance between the intermediate and transition states.

Table 1.

Kinetic data for Rubiscos from various bacteria, algae, and higher plants

	Rubisco CO2:O2 environment	Sc/o	Kc, μM [pH]	kcatc, s−1	Ea for kcatc, kJ mol−1	Δ 13C,* ‰	Δ18O,* ‰	CABP release, t0.5, d
Bacteria
Riftia pachyptila symbiont	Anaerobic	6.2 (42)				19.5 (42)
Rhodospirillum rubrum	Anaerobic	12.3 (43)	80 [7.8] (44)	7.3 (44)		23.0 (25)	21.4 (25)	1.4 (45)
Chromatium vinosum	Anaerobic	41 (46)	37 [8.0] (46)	6.7 (46)
Cyanobacteria
Anabaena variabilis	CCM† present	43 (47)			65.7 (47)
Synechococcus 7002	CCM present	52 (48)	246 [7.8] (48)	13.4 (48)
Synechococcus 6301	CCM present	43 (49)	340 [7.8] (49)	11.6 (49)	48.1 (50)	22.0 (25)	21.6 (25)
Green algae
Euglena gracilis	CCM present	54 (9)			41.8 (51)
Chlamydomonas reinhardtii	CCM present	61 (9)	29 [8.3] (9)	5.8‡
C4 higher plants
Amaranthus hybridus	CCM present	82 (9)	16 [8.3] (9)	3.8§
Sorghum bicolor	CCM present	70 (10)	30 [8.3] (10)	5.4 (52)
Zea mays	CCM present	79 (43)	34 [8.3] (9)	4.4 (52)
C3 higher plants
Triticum aestivum	CCM absent	90 (43)	14 [8.0] (50)	2.5 (50)	80.3 (50)
Oryza sativa	CCM absent	85 (43)			68.6 (53)
Spinacia oleracea	CCM absent	82 (43)	14 [8.3]) (9)	3.7 (52)	68.6 (50)	30.3 (25)	21.1 (25)	530 (15)
Atriplex glabriuscula	CCM absent	87 (54)			64.9 (54)¶
Nicotiana tabacum	CCM absent	82 (55)	11 [8.3] (55)	3.4 (55)
Nongreen algae
Phaeodactylum tricornutum	CCM present	113 (55)	28 [8.3] (55)	3.4 (55)
Griffithsia monilis	CCM absent?	167 (55)	9.3 [8.3] (55)	2.6 (55)		31.5‖
Galdieria sulfuraria	CCM absent?	166 (55)	3.3 [8.3] (55)	1.2 (55)	76.1**

Unless otherwise specified, the data apply to 25°C. Where necessary, S_c/o and K_c values were adjusted using the Henderson–Hasselbalch equation to a common pK_a of 6.25 for the CO₂/HCO₃⁻ equilibrium.

*Unless stated otherwise, the ¹³C and ¹⁸O isotope fractionations were measured with the isolated enzymes in vitro. The limited data for Δ¹⁸O are supported by a recent observation of 21.3‰ for the Δ¹⁸O of the oxygenase reaction of Pisum sativum Rubisco (56).

^†CCM, CO₂ concentrating mechanism that increases the CO₂ concentration in the subcellular environment of Rubisco by 10¹- to 10³-fold above ambient, either by accumulation of CO₂ or HCO₃⁻ directly or by intermediate accumulation and decarboxylation of C₄ dicarboxylic acids.

^‡Determined at 30°C (57) and adjusted to 25°C using the E_a listed for Euglena gracilis.

^§For Rubisco isolated from the related species, Amaranthus retroflexis (52).

^¶E_a for temperatures >15°C.

^‖Inferred from the carbon-isotope fractionation at saturating CO₂ of whole tissues of another temperate floridiophycean macrophyte, Lamanea mamillosa (58).

**For Rubisco isolated from the closely related species Galdieria partita (33).

Tighter Binding of the Carboxyketone Slows Subsequent Catalytic Steps.

Unless there are countervailing imperatives (such as, in this case, the need to distinguish between unbound alternate substrates), such close resemblance would be maladaptive, because it stabilizes the intermediate ([I], Fig. 2), decreasing its energy level and slowing its subsequent processing. The puny rate enhancement achieved by Rubisco in processing the carboxyketone intermediate supports this view. k_cat^c is only 10³-10⁴ times the nonenzymatic rate of hydration or hydrolysis of the same intermediate (13). Arguments based on transition-state theory suggest that rate enhancement is proportional to the ratio between the binding constants of the transition state and the reactants (14); hence, a small rate enhancement is expected if the reactant is already bound so tightly that opportunity for further tightening of the binding in the transition state is limited.

Thus our hypothesis provides a mechanistic explanation for the frequently noted inverse correlation between S_c/o and k_cat^c and the positive correlation with E_a, the Arrhenius activation energy of k_cat^c (= k₈) (Fig. 3 B and E).

A Possible Complication: Hydration of the Carboxyketone.

This consistent picture is complicated somewhat by uncertainty about whether CO₂ addition and hydration of the resulting carboxyketone are concerted in a single transition state or are sequential with separate transition states (16–18) (Fig. 2). If the former is true, intermediate [I] and transition state [2] do not exist, and no complication arises; if the latter is true, the step labeled “k₈” is composed of two elemental steps, namely hydration and cleavage. Rapid borohydride trapping of the six-carbon intermediate after acid denaturation of the enzyme indicates that the on-enzyme equilibrium favors the hydrated gem-diol by at least 20:1 (13). Likely this is required to restrict the reverse decarboxylation tendency of the carboxyketone, which is indeed minimal for all Rubiscos tested (bacterial, cyanobacterial, and higher plant) (19). If so, any enhanced stabilization of the carboxyketone, occasioned by closer resemblance to the transition state for CO₂ addition, would need to be accompanied by similarly increased stabilization of the transition state for hydration ([2], Fig. 2), as well as of the hydrate, itself ([II], Fig. 2). Therefore, k₈ would be reduced in either scenario.

Inverse Correlation Between S_c/o and k_cat^c.

As noted above, the data support this prediction very well (Fig. 3B). Furthermore, they show that the trend reflects the [CO₂]:[O₂] ratio prevailing in the subcellular situation where the Rubisco is located. High environmental [CO₂]:[O₂] ratios can be caused by low or zero [O₂] (in anaerobes) or by the operation of a CO₂-concentrating mechanism (Table 1, column 2). The inorganic mechanisms that actively accumulate CO₂ or HCO₃⁻ in cyanobacteria and algae, and the C₄-dicarboxylic acid pathway in C₄ plants, effectively increase the [CO₂] at the site of Rubisco manyfold above ambient. The strong correlation shown by the data (Fig. 3B) demonstrates that Rubiscos adapted to higher [CO₂]:[O₂] ratios have higher k_cat^c values and lower S_c/o values, in accordance with our hypothesis. Because the ratio between the rates of carboxylation and oxygenation (v_c/v_o) equals S_c/o multiplied by [CO₂]/[O₂], a higher [CO₂]:[O₂] ratio permits an adequate v_c/v_o to be achieved with a lower S_c/o value. This allows a less product-like carboxylation transition state and thus a higher k_cat^c and a lower investment in Rubisco protein.

Correlation with ¹²C/¹³C Fractionation.

The more the carboxylation transition state resembles its product, the shorter the O₂C·····C-2 bond will be and thus the higher its energy and vibrational frequency. The theoretical relationship between this frequency and the kinetic isotope effect for the formation of this bond predicts that the intrinsic ¹²C/¹³C isotope fractionation (Δ) for CO₂ addition should increase as the transition state becomes more product-like (20–23). In accordance with this prediction, highly CO₂-specific Rubiscos show larger ¹²C/¹³C isotope effects (Fig. 3F). Thus, the observed variation among Rubiscos is explained by our hypothesis in terms of variation of the intrinsic ¹²C/¹³C isotope effect resulting from differences in transition-state structure rather than an invariant transition state coupled with varying degrees of reversibility of CO₂ addition (decarboxylation of the carboxyketone [I]) (24) for which the evidence is to the contrary (19).

No Correlation with ¹⁸O/¹⁶O Fractionation.

The nascent carboxylate moiety of the transition state for CO₂ addition has an additional heavy atom, not present in the analogous transition state for oxygenation, which might be exploited for stabilization of the carboxylation transition state (e.g., by H bond interactions) without similar stabilization of the oxygenation transition state. The more the nascent carboxylate approaches a true carboxylate, the greater this opportunity may be. An active site complementary to such an advanced nascent carboxylate may be less complementary to the transition state for O₂ addition, impeding access to that transition state. It may also disfavor the triplet-to-singlet transition that uniquely must occur in the O₂-addition process (2, 16). All of these factors would contribute to an increase in k₆/k₃ [= S_c/o] without necessarily influencing the length and vibrational frequency of the O₂·····C–2 bond in transition state for oxygenation. If so, then in contrast with carboxylation, little interspecific variation of the ¹⁶O/¹⁸O isotope effect should be expected (22), and this is what is observed (25) (Fig. 3F). Furthermore, one might predict that oxygenation would be facilitated by promoting electronic activation of O₂ reactivity, so the ≈10-fold enhancement of k_cat^o/K_o that accompanies replacement of the Mg²⁺ ion naturally present in Rubisco's active site by a Mn²⁺ ion (26) comes as no surprise. We note that the yield of the chemiluminescence emitted by Mn²⁺-Rubiscos during oxygenation also correlates with S_c/o (27, 28). Although such variation in chemiluminescence yield could reflect structural differences affecting quenching of the luminescence, it might also indicate that a higher degree of electronic activation of O₂ is required for oxygenation to occur with higher-specificity Rubiscos, because electronic interactions of O₂ with the active site, or metal, are less favored.

Possible Compensation Mechanisms.

A shorter higher-energy O₂C·····C–2 bond would tend to raise the energy of a more product-like carboxylation transition state, but this might be compensated by more favorable interactions of the active site with the attached O atoms of a more carboxylate-like moiety. Therefore, the effect of a more product-like transition state on k₆ cannot be predicted. The positive correlation between S_c/o and k_cat^c/K_c [= k₆k₉/(k₉ + k₁₀)] (Fig. 3C) suggests either that k₆ is not compromised (and might even be increased) by a more product-like transition state or, if it is reduced, then this reduction is more than compensated by a more favorable equilibrium of the preceding enolization reaction [i.e., increased k₉/(k₉ + k₁₀)]. The latter could be achieved by a more efficient proton abstraction induced by a more strongly basic active-site carbamate (17) but at the cost of increasing the fraction of the enzyme with enediol bound during steady-state catalysis. This would provide more opportunity for the abortive side reactions emanating from the enediol that progressively inhibit the more CO₂-specific higher-plant Rubisco during catalysis and require the ancillary motor protein, Rubisco activase, to be released (29).

No similar compensation can be applied to the k₈ step, however. A more product-like transition state for carboxylation will lead unavoidably to tighter binding of the carboxyketone intermediate, with consequent slowing of its downstream processing.

The Strategy's Effectiveness Deteriorates with Increasing Temperature.

Selecting a more product-like transition state for carboxylation, together with any more favorable interactions with the active site that such a structure may enable, restricts the number of degrees of freedom available to the transition-state/enzyme complex. Therefore, such a more product-like transition-state complex represents an inherently more ordered lower-entropy structure.

Rubisco's CO₂/O₂ specificity has been analyzed in terms of transition-state theory (30, 31), leading to the following expression:

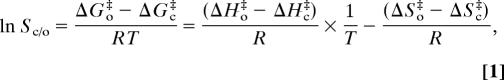where ΔG^‡, ΔH^‡, and ΔS^‡ are the differences in free energy, enthalpy, and entropy, respectively, between the gas reactant and the transition state for its addition in the reaction designated by the subscripts; T is the absolute temperature; and R is the perfect gas constant. Thus an Arrhenius-style plot of ln S_c/o vs. 1/T will have a slope of (ΔH_o^‡−ΔH_c^‡)/R and an ordinal intercept (ln S_c/o at infinite temperature) of −(ΔS_o^‡−ΔS_c^‡)/R. If the transition state for carboxylation becomes more product-like and thus has a lower entropy, but that for oxygenation does not, (ΔS_o^‡−ΔS_c^‡) must increase. Therefore, according to Eq. 1, an increase in (ΔH_o^‡−ΔH_c^‡), resulting from a more product-like transition state for carboxylation will increase S_c/o (as S_c/o = k₆/k₃ and see above), but this is counteracted to some extent by any consequent increase in (ΔS_o^‡−ΔS_c^‡). Furthermore, the impact of the entropy term becomes proportionally greater with increasing temperature. This means that so-called higher-specificity Rubiscos will have higher specificities only at low temperatures; at higher temperatures, the tables will be turned.

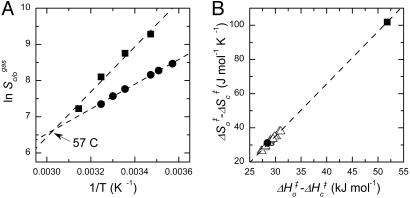
Published data for the influence of temperature on the specificities of the Rubiscos of spinach (32) and the red alga, Galdieria partita (33), clearly exemplify this phenomenon. Although the algal enzyme has a S_c/o value more than twice that of the spinach protein at 25°C, the Arrhenius-style plots cross at 57°C (Fig. 4A). Above this temperature, spinach Rubisco would have the superior S_c/o. The positive correlation between (ΔH_o^‡−ΔH_c^‡) and (ΔS_o^‡−ΔS_c^‡) that leads to this inversion appears to be quite general. Estimates of these parameters obtained from these plots fall on the same regression line as estimates derived by the same procedure for Rubiscos from 15 C₃ higher plants, where well replicated measurements of S_c/o at 15°C, 25°C, and 35°C are available (34) (Fig. 4B).

Fig. 4.

The higher the CO₂/O₂ specificity, the more it is eroded by increasing temperature. (A) Arrhenius-style plots of the specificities of the Rubiscos from spinach (•) (32) and the red alga, Galdieria partita (■) (33). (B) Positive correlation between (ΔH_o^‡−ΔH_c^‡) and (ΔS_o^‡−ΔS_c^‡) (Eq. 1) for these Rubiscos plus those from 15 C₃ higher plants (Δ) (34). To remove variation due to the differing effects of temperature on the solubilities of CO₂ and O₂, data for S_c/o at various temperatures were expressed in terms of the gas-phase partial pressures of CO₂ and O₂ (S_c/o^gas) by dividing the reported values (which were expressed in terms of aqueous-solution concentrations) by the ratio between the aqueous solubilities of O₂ and CO₂ appropriate to the measurement temperature (41). The transformed data for each Rubisco were then fitted to Eq. 1 to obtain the estimates of (ΔH_o^‡−ΔH_c^‡) and (ΔS_o^‡−ΔS_c^‡) and their standard errors. For example, (ΔH_o^‡−ΔH_c^‡) and (ΔS_o^‡−ΔS_c^‡) were estimated to be 28.5 ± 0.6 kJ mol⁻¹ and 31.1 ± 2.0 J mol⁻¹°K⁻¹, respectively, for spinach Rubisco; for G. partita Rubisco, the estimates were 51.8 ± 5.3 kJ mol⁻¹ and 102 ± 17 J mol⁻¹°K⁻¹. The lines shown are linear regressions through all of the data.

Conclusions

Our hypothesis highlights and provides a mechanistic explanation for the critical imperative in Rubisco's evolution for increased catalytic potency and specificity: the need to optimize the compromise between S_c/o and k_cat^c to suit the environmental CO₂ and O₂ concentrations and the prevailing temperature. Further, it raises the possibility that, despite appearing sluggish and confused, most Rubiscos may be near-optimally adapted to their different gaseous and thermal environments. If so, genetic manipulation can be expected to achieve only modest improvements in the efficiency of Rubisco and plant growth. Such improvement would be limited to the magnitude of the scatter apparent in the correlations (Fig. 3), if the scatter represents incomplete optimization (see above). For example, the data for Rubiscos from C₃ plants cluster below the trend line in Fig. 3B, whereas the point for the high-specificity Rubisco from the red alga, Griffithsia monilis, lies above it. If this behavior reflects incomplete optimization, rather than merely experimental imprecision, there may be some opportunity to improve the efficiency of photosynthesis in crop plants at the measurement temperature (25°C) by substituting their natural Rubiscos with one with kinetic properties similar to those of the red algal enzyme (4).

The inability of low-S_c/o high-k_cat^c Rubiscos from anaerobic organisms, such as Rhodospirillum rubrum (Table 1), to support positive carbon gain at current atmospheric CO₂ and O₂ concentrations and temperatures (31, 35) underscores the importance of adaptive optimization of the transition state for CO₂ addition along the reactant-/product-like coordinate. Such adaptation in response to the changing atmosphere and temperature appears to have been instrumental in enabling the expansion of the biosphere to its current size. Furthermore, if that adaptation has always been nearly perfect throughout geologic time, our hypothesis predicts that the average depletion of ¹³C in organic carbon compared with atmospheric CO₂ will have varied from epoch to epoch in response to changes in the atmospheric CO₂ and O₂ concentrations and temperatures. Interpretation of the paleontological isotope record may need to take account of this possibility.

Abbreviations

CABP

2′-carboxy-d-arabinitol 1,5-bisphosphate

RuBP

d-ribulose 1,5-bisphosphate

Rubisco

RuBP carboxylase/oxygenase.