Abstract
A mutation in the epsilon subunit of the human nicotinic acetylcholine receptor (εL78P) is known to cause a congenital slow channel myasthenic syndrome. We have investigated the changes in receptor function that result in the mutant receptor producing prolonged endplate currents, and consequent muscle damage. The rate constants for channel gating and for the binding and dissociation of acetylcholine were investigated by analysis of single ion channel recordings. A conventional mechanism with two non-equivalent binding sites, and variations upon this mechanism, were fitted to data using a maximum likelihood method that uses the Hawkes-Jalali-Colquhoun (HJC) treatment of missed brief events. The mutant receptor produced prolonged activations, bursts of openings that cause a slow decay of simulated synaptic currents. The main reason for the longer bursts of openings seen with mutant receptor was a decrease in the rate of ACh dissociation from diliganded receptors, though the lifetime of individual openings was somewhat increased too. As well as producing long bursts, the mutant receptor also produced many very short openings, though these carry little current. The burst structure for the mutant receptor at low ACh concentration is unusual in that most long bursts appear to start in a very brief monoliganded open state that then usually binds another ACh molecule to produce a long diliganded activation. The first opening is so short that it will usually be missed (together with the shut time that follows it), so the true burst length is likely to be underestimated.
The muscle nicotinic acetylcholine receptor transduces chemical signals in the form of acetylcholine (ACh) released from motor neurones into a voltage change across the membrane of the muscle end plate. The adult form of the receptor is a pentameric complex consisting of two α subunits, and single β, δ, and ε subunits arranged around a central cation-conducting pore. There are two non-identical ACh-binding sites, situated at the interfaces between the α and δ subunits, and between the α and ε subunits (the αδ and αε sites, respectively). In the adult mouse receptor, the two sites are usually assumed to be identical (Akk & Auerbach, 1996; Wang et al. 1997; Salamone et al. 1999; Akk, 2002), although there is some evidence that the ACh dissociation rates (if not the ACh affinity) are different at the two sites (Salamone et al. 1999). However, in adult human (Hatton et al. 2003), fetal mouse (Jackson, 1988; Zhang et al. 1995), and Torpedo (Sine et al. 1990) receptors the sites have been inferred to have different ACh binding properties. The distinction between the two sites is important when considering mutations that could affect one site more than the other.
Mutations in the human receptor have been found to be responsible for slow channel congenital myasthenic syndromes (SCCMS), in which endplate currents decay abnormally slowly. Most patients show varying degrees of weakness that is particularly apparent in the ocular, shoulder, limb, cervical, wrist and finger muscles. The patients fatigue easily and may have breathing difficulties. There is usually degradation of the muscle end plates. Excessive accumulation of calcium has been detected in the endplates of both SCCMS patients (Engel et al. 1982) and a transgenic mouse model (Gomez et al. 2002). It is this calcium overload that is believed to be responsible for the degeneration of junctional folds and apoptosis at subsynaptic end plate nuclei.
Several mutations that underlie SCCMS have been studied in detail using single channel analysis. The primary effect of many mutations is to decrease the rate of agonist dissociation, e.g. αN217K (Wang et al. 1997), αG153S (Sine et al. 1995), εL221F (Hatton et al. 2003), although other mutations, such as αV249F (Milone et al. 1997), have been found that have effects largely, or entirely, on channel gating too.
Here we study the effects of a point mutation in the ε subunit that is responsible for a slow channel congenital myasthenia (Croxen et al. 2002). A single homozygous nucleotide point mutation of thymine to cytosine at position 233 of the mature ε subunit coding region results in the substitution of a proline residue for a leucine residue at position 78 in the protein. The position is within the N-terminal extracellular domain of the receptor but not within the generally accepted ACh binding sites. The mutation was identified originally in a 29-year-old female patient who failed to breathe following a general anaesthetic. Six to seven years earlier she had noticed muscle weakness. Subsequent examinations identified bilateral ptosis, limitation of eye movements, weakness of facial and hand muscles, and weakness of the neck, shoulders and hips. Electromyography showed an abnormally large decrement of response at 3 Hz stimulation. Antibodies to nicotinic receptors were not detected. One of her siblings reported a similar failure to breathe after administration of a general anaesthetic.
In order to understand properly the effects of mutations in the receptor, it is necessary to describe the single channel properties of the receptor in terms of the underlying rate constants that govern the receptor's functions (Colquhoun, 1998). This necessitates identification of a reaction mechanism that describes, to a sufficiently good approximation, the actual physical events that occur during receptor activation. Another reason why it is necessary to postulate a mechanism is that without a mechanism it is, in general, not possible to allow for the fact that brief openings and shuttings will be missed (Colquhoun & Hawkes, 1995). Some preliminary results from this study have been presented in partial form previously (Croxen et al. 2002; Shelley et al. 2003).
Methods
Cell culture and transfections
Human embryonic kidney cells (HEK-293), obtained from either the American Type Culture Collection (ATCC) or the European Collection of Cell Cultures (ECACC), were cultured as previously described (Hatton et al. 2003). For transfection using the calcium phosphate method they were plated onto polylysine-coated coverslips in 30 mm Petri dishes. For each Petri dish, 3 μg of total DNA was used. The DNA consisted of pcDNA3.1 plasmids (Invitrogen) containing inserts encoding the subunits α1, β1, δ, ε, enhanced green fluorescent protein (eGFP) (Invitrogen), and the non-coding plasmid pcDNA3.1 in the ratio of 2: 1: 1: 1: 65: 30. The construction of the plasmids coding for the subunits has been previously described (Croxen et al. 2002). The eGFP and the non-coding pcDNA3.1 plasmids were a gift from Paul J. Groot-Kormelink (University College London). The DNA mix was added to 60 μl of 340 mm CaCl2. This mixture was in turn added dropwise to 66 μl of 2 × Hepes-buffered saline (280 mm NaCl, 50 mm Hepes, 2.8 mm Na2HPO4, pH 7.2 with NaOH). The solution was left for 1 min and then added to the Petri dish. Cells were then incubated overnight at 37°C in 5% CO2 and the medium replaced next morning. Cells were patched between 16 and 56 h following the transfection procedure.
Single channel recording
Steady state single channel recordings were made in the cell-attached configuration at 19°C, from cells that emitted green fluorescence. The extracellular solution contained 142 mm KCl, 10 mm Hepes, 5.4 mm NaCl, 1.7 mm MgCl2, 1.8 mm CaCl2, pH adjusted to 7.4 with KOH. Borosilicate pipettes (GC150F-7.5, Clark Electromedical) were pulled to give a resistance of 8–12 MΩ and their tips coated with 10% Sylgard (Dow Corning). Immediately before patching the pipettes were fire-polished and back-filled with extracellular solution containing ACh chloride. In our cell-attached recordings the membrane potential is unknown, so the holding potential was adjusted to produce openings of 6 pA, which required a membrane potential of approximately −100 mV. Currents were amplified using an Axopatch 200A (Axon Instruments) coupled to a CV 201AU headstage (Axon Instruments). Data were filtered initially at 10 kHz and recorded on digital audio tape (DAT) using a DTR-1204 digital tape recorder (Biologic Science Instruments). Before digitization data were filtered again at 5 kHz to 8 kHz using an 8th order Bessel filter (built in-house), giving a final −3 dB frequency of 4.8 kHz to 6.2 kHz. Data were digitized at 50 kHz to 80 kHz using a CED 1401 interface (Cambridge Electronic Design) and the CONSAM program (I. Vais and D. Colquhoun).
Data analysis
Following an initial inspection of the digitized single channel trace, the amplitudes and the duration of the open and closed states were measured using the SCAN program to give an idealized record. The transitions were fitted with convolved step-response functions using a least-squares criterion (Colquhoun & Sigworth, 1995). A resolution of 20–40 μs was imposed retrospectively on the results; stability plots (program EKDIST) were inspected before further analysis. The duration of an ‘open period’ was defined as the length of time for which the channel remained open (regardless of conductance), the period ending when a shut time longer than the imposed resolution occurs. Bursts were defined as a sequence of openings and shuttings that ends once a shut time longer than tcrit occurs. The tcrit values were chosen so as to ensure that an equal proportion of intervals from both the low and the high components were misclassified (Colquhoun & Sakmann, 1985). In some cases this was not possible due to the bisection algorithm employed not converging. In these cases tcrit was chosen so that an equal number of intervals from the low and high components were misclassified (Magleby & Pallotta, 1983; Clapham & Neher, 1984). The number of intervals fitted for each patch ranged from 2000 to 50 000. For a typical set of fits the mean number of transitions fitted per patch was 17 500 ± 2600.
The open period, shut time, and burst length histograms were fitted empirically with mixtures of n exponential probability density functions (pdfs) using EKDIST.
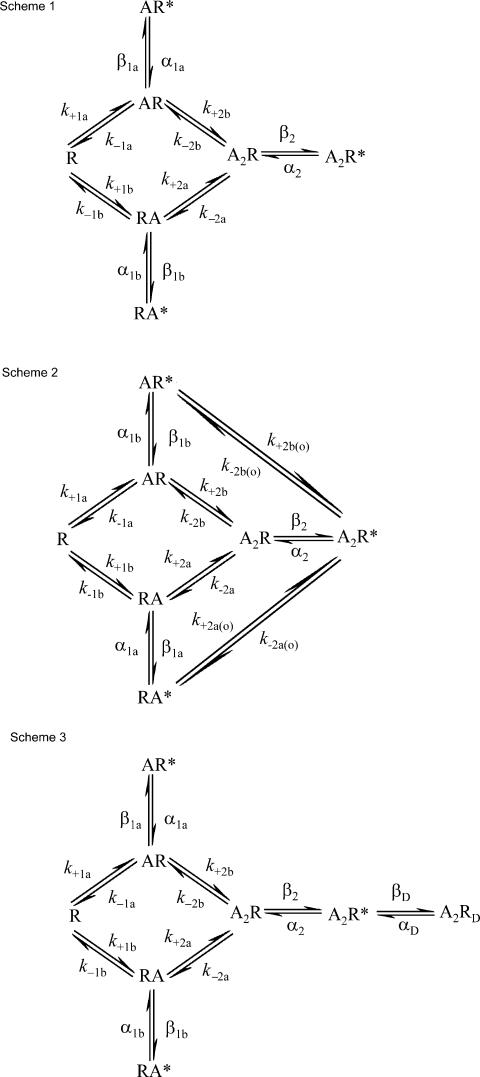
The microscopic rate constants in putative physical mechanisms for receptor activation were estimated using the HJCFIT program, which maximizes the likelihood of the entire sequence of open and shut times, with exact allowance for missed brief events (Hawkes et al. 1990; Hawkes et al. 1992; Colquhoun et al. 1996). For a complete description of the use of the HJCFIT program, and tests of its performance see Colquhoun et al. (2003), Hatton et al. (2003)and Burzomato et al. (2004). Scheme 1, shown in Fig. 4, and some variants of it were used to describe the receptor mechanism. This scheme describes a receptor with two different binding sites, with either of the two different monoliganded forms being able to open, as well as the diliganded form. For all the fits we made the customary assumption that the two binding sites are independent. In other words, we assume that binding of a molecule of ACh to the a-site does not affect binding of a second molecule of ACh to the b-site and vice versa. Using the notation in Fig. 4, this means imposing the following three constraints during fitting.
| (1) |
The additional constraint of microscopic reversibility assures that also:
| (2) |
The number of free rate constants to be estimated in Scheme 1 is thus reduced from 14 to 10.
Figure 4. Reaction schemes used in maximum likelihood analysis of the wild-type and εL78P receptors.
All the schemes describe two different ACh binding sites, and allow both mono and diliganded openings. Scheme 2 allows dissociation of ACh from the diliganded open state, and association with the monoliganded open states. Scheme 3 introduces a short-lived shut state that is accessible only from the diliganded open state.
Estimates of the (microscopic) rate constants in the mechanism were found by HJCFIT, which produced, for the specified resolution (usually 25 μs), plots of the distributions of apparent open and shut times (HJC distributions) for comparison with observations (e.g. Figs 5 and 7). The apparent open and shut times will be longer than the true values, because short (less than the resolution) shuttings and openings are missed. Plots of the mean apparent open time conditional on adjacent shut time (e.g. Figs 5 and 7), again with allowance for missed events, are also produced by HJCFIT, so it can be judged, by comparison with observed values, how well the fitted mechanism describes the negative correlation seen between open times and adjacent shut times (see also Hatton et al. 2003; Beato et al. 2004).
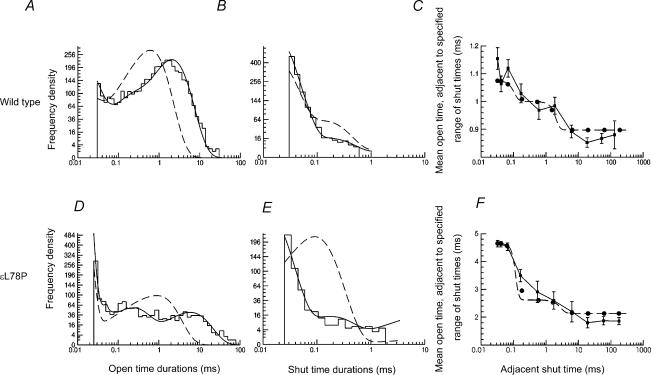
Figure 5. Example of HJC distributions (predicted by fit of Scheme 1) overlaid onto observed open time (A and D) and shut time (B and E) histograms of wild-type and εL78P receptors with 100 nm ACh.
The continuous lines are the HJC distributions calculated from maximum likelihood fitting to the idealized single channel traces. The dashed lines show the distributions of open and shut times that would be predicted if resolution were perfect. The HJC distributions describe the observed open and shut time histograms well. Panels C and F show the conditional mean open time plotted against the adjacent shut time (see Methods). The points with error bars show the experimental observations for each shut time range, the points being joined with continuous straight lines. The circles show the HJC values that are predicted by the fit for the same shut time ranges, and the dashed line shows the continuous theoretical relationship calculated from the HJC distributions.
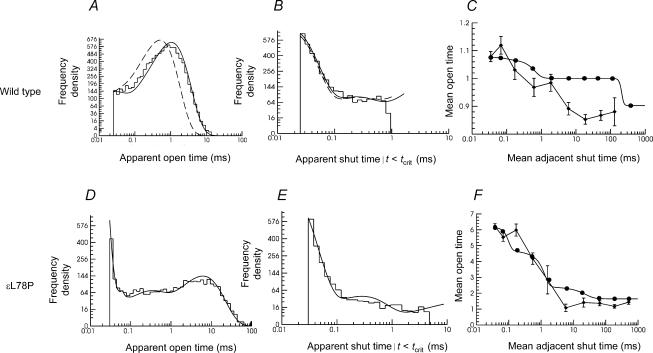
Figure 7. Example of a test of the adequacy of a fit obtained with Scheme 3.
Histograms show the distributions of observed open and shut times from patches with 100 nm ACh for wild-type and εL78P receptors. The HJC distributions of apparent open and shut time with a resolution of 30 μs, calculated from the results of fitting Scheme 3, are overlaid as continuous lines on the histograms, and conditional mean open time plots are shown, as in Fig. 5.
Once values for the rate constants had been estimated then it was possible to predict other properties of the receptor. The macroscopic response to a brief pulse of agonist (Fig. 10), to simulate a synaptic current, was calculated with SCALCS. The ideal (perfect time resolution) properties of bursts of openings were calculated (as in Colquhoun & Hawkes, 1982) with SCBST. The SCBST program was also used to calculate more recondite distributions that proved useful for understanding the receptor activation mechanism. We were interested in calculation of the distribution of the burst length for bursts that contain more than one opening. This was not given explicitly by Colquhoun & Hawkes (1982), but is found easily from their general burst length distribution as a mixture of nine exponential pdfs, six that represent the normal burst length distribution, and three terms that represent the distribution of the open periods durations of the first opening in a burst. These latter three terms all have negative area, and thus act to subtract the distribution of the first opening in a burst from the total burst length distribution. Burst length distributions conditional on the initial open state were also calculated by SCSBT in the same way as the total burst length distribution but substituting the normal steady state initial vector for bursts (ϕb) with a vector that implies that all bursts start in a specified state (Colquhoun & Hawkes, 1982), for example, for start in state 1:
Variability is specified as coefficient of variation, expressed as a percentage, i.e. 100 s/m (C.V.M.). For mean values, s is the standard deviation of the mean (m) (also known as standard error). For rate constants the standard deviation of the estimate was found from the covariance matrix in each fit, but errors here are calculated more conservatively as the standard deviation of the mean from replicate experiments. The mean values of parameters which are a ratio of two rate constants (i.e. equilibrium constants) were obtained by calculating the mean of the ratios from each experiment (rather than as the ratio of means), so the tables do not show exact agreement between mean rate constants and mean equilibrium constants.
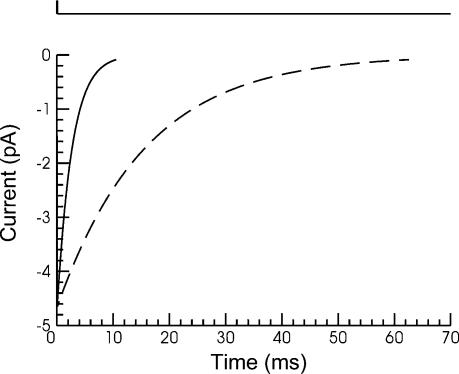
Figure 10. The predicted synaptic currents in response to a 0.1 ms pulse of 1 mm ACh (line at top) for wild-type (continuous line) and εL78P receptors (dotted line).
The currents were calculated from the estimates of the microscopic rate constants obtained from maximum likelihood fitting of Scheme 3; the values are shown in Table 5. The macroscopic decay after removal of ACh is dominated by a single exponential component with a time constant of 2.6 ms for the wild-type receptors and 26.7 ms for the εL78P receptors. The amplitude of the current is that for a single channel.
All of the programs used in this work can be downloaded from http://http://www.ucl.ac.uk/Pharmacology/dc.html.
Results
Open period and shut time durations
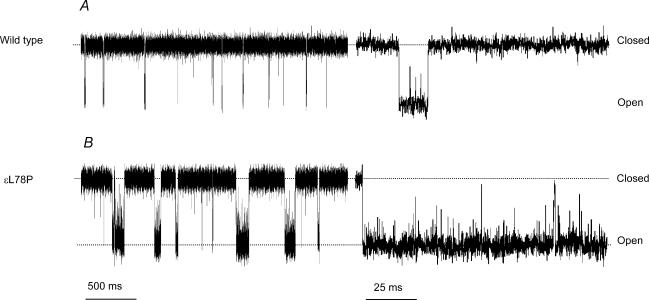
Figure 1 shows examples of the single channel currents recorded from wild-type muscle nicotinic receptors, and from receptors that contain the εL78P mutation. It is obvious to the naked eye from these traces that receptors with εL78P mutation produce bursts of openings that are often longer than those seen in wild-type. This suggests that receptors with this mutation will produce slowly decaying synaptic currents (see Fig. 10 and Discussion). In order to make this impression more quantitative, distributions of open period durations and of burst lengths were fitted empirically (i.e. without reference to any reaction mechanism) with mixtures of exponential pdfs (see Methods). Examples are shown in Fig. 2.
Figure 1. Single channel traces of wild-type (A) and εL78P (B) receptors in the presence of 100 nm ACh at two different time scales.
Openings are shown as downward deflections. The εL78P receptors produce visibly longer activations than the wild-type receptors.
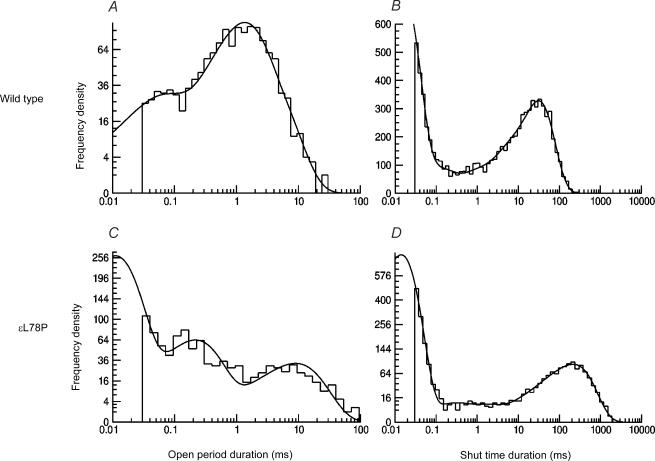
Figure 2. Open period (A and C) and shut time (B and D) duration histograms of wild-type (A and B) and εL78P (C and D) receptors.
The proportion of both very short and very long open time durations are increased in the εL78P receptors. In both cases the open period histograms have been fitted with three exponential components. The wild-type shut time duration histograms were fitted with three exponential components whilst the εL78P receptors were fitted with five exponential components (see Tables 1 and 2 for averaged fits).
The distribution of apparent open period durations for εL78P receptors, with 100 nm ACh, could be fitted adequately with three, and in one case four, exponential components. The values of the individual time constants and their areas are shown in Table 1; the histograms and the fits are shown in Fig. 2. The εL78P receptors contained a greater proportion of short openings compared with wild-type receptors, but an approximate doubling of the slowest time constant meant that the overall mean apparent open time duration was similar for εL78P and wild-type receptors, being 1.17 ms and 1.15 ms, respectively.
Table 1.
The distribution of open period durations for wild-type and εL78P receptors, both with 100 nm ACh
| n | τ1 (ms) | a1 (%) | τ2 (ms) | a2 (%) | τ3 (ms) | a3 (%) | Overall mean open period (ms) | |
|---|---|---|---|---|---|---|---|---|
| Wild-type | 6 | 0.033 | 28.5 | 0.739 | 36.5 | 3.03 | 34.9 | 1.17 |
| ± 48% | ± 27% | ± 30% | ± 31% | ± 26% | ± 26% | ± 15% | ||
| εL78P | 4 | 0.009 | 76.0 | 0.208 | 7.6 | 7.40 | 16.4 | 1.15 |
| ± 33% | ± 21% | ± 3% | ± 58% | ± 8% | 79% | ± 74% |
The results of empirical fitting with a mixture of three exponential pdfs are shown (τ being the time constant, and a the area, for each component). The overall mean, calculated from the fits as Σaiτi, is given in the last column. Errors are specified as c.v.m. (%) (see Methods).
The apparent shut time duration distributions for εL78P receptors could be fitted with four or five components; an example is shown in Fig. 2. The values found for the five component fits are shown in Table 2 and compared with wild-type receptors, both being measured with 100 nm ACh. The εL78P receptors had a greater proportion (a1) of ‘short shut times’ (τ1) compared with wild-type receptors. The proportion of ‘intermediate shut times’ (τ2 for the wild-type, and τ2, τ3, and τ4 for the εL78P receptors) was similar for both.
Table 2.
The distribution of shut times for wild-type and εL78P receptors, both with 100 nm ACh
| n | τ1 (ms) | a1 (%) | τ2 (ms) | a2 (%) | τ3 (ms) | a3 (%) | τ4 (ms) | a4 (%) | τ5 (ms) | a5 (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wild-type | 6 | 0.019 | 62.4 | 0.509 | 3.3 | 385 | 34.4 | — | — | — | — |
| ± 9% | ± 7% | ± 27% | ± 37% | ± 64% | ± 12% | ||||||
| εL78P | 5 | 0.011 | 88.2 | 0.217 | 2.4 | 0.83 | 0.8 | 34.6 | 0.7 | 315 | 7.9 |
| ± 9% | ± 2% | ± 53% | ± 21% | ± 18% | ± 25% | ± 29% | ± 43% | ± 17% | ± 28% |
The results of empirical fitting with a mixture of three exponential pdfs (in the case of wild-type) and five exponential pdfs (in the case of εL78P receptors) are given. Notation as in Table 1.
Burst length durations
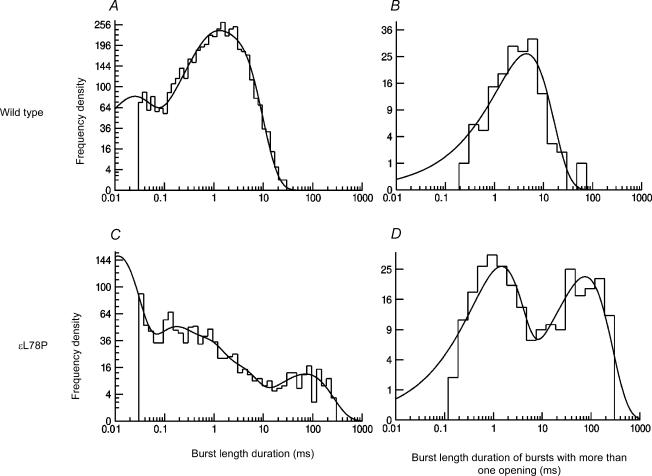
Burst length duration histograms were constructed for wild-type and εL78P receptors. The bursts were defined by fitting the shut time duration histograms with the minimum number of components that described the data adequately. In the case of wild-type receptors this was always three components. For εL78P receptors four or five components were required. In the cases where shut times could be described with three or four components then a tcrit value was specified so as to omit the slowest of the shut time components. In the cases where five shut time components were required then a tcrit was specified so as to omit the slowest two components as it was considered that the mean value of τ4 (35 ms) was too slow to be included within a channel ‘activation’. This component and the ‘smear’ of shut times between 1 and 10 ms in Fig. 2D make the definition of tcrit for the mutant receptor somewhat ambiguous (according to the interpretation of the results given below, these intermediate shut times result largely because brief openings are missed, and are not present in the ideal distribution). Using these criteria gave a mean tcrit of 0.79 ms ± 41% for wild-type channels, and 3.63 ms ± 38% for εL78P channels. Figure 3 and Table 3 show that the distributions of the burst length durations of wild-type and εL78P receptors are very different. The mean burst length of wild-type receptors at 100 nm ACh was 1.41 ms ± 21%, surprisingly similar to the mean burst length duration of εL78P receptors, 1.2 ms ± 32%. Although the εL78P receptors visibly produce longer bursts than the wild-type receptors, the majority of the bursts from εL78P receptors consisted of very short burst length durations (τ1 = 7 μs, area = 84%), and thus there is little change in the overall mean length of bursts. The very short bursts are expected to be mostly isolated single-liganded openings; because they are so short, they will have little influence on the endplate current during physiological activation of the receptors. Virtually all of the synaptic current is carried by multiple diliganded open periods occurring in quick succession, a ‘typical’ burst, because such bursts are much longer than monoliganded openings. Therefore the burst length durations were re-examined by looking at the distribution of only those bursts that contain two or more apparent open periods. The overall mean length of these bursts was eightfold greater for mutant than for wild-type. The wild-type receptor distributions were consistently fitted with a single exponential component, but εL78P receptors required at least two clearly separated exponential components, shown in Table 4 and Fig. 3.
Figure 3. Single channel burst lengths for wild-type (A) and εL78P (C) receptors, fitted empirically with mixtures of exponential pdfs.
Wild-type receptors required three exponential components to describe their burst length distributions, whilst the εL78P required five exponential components. The distributions of burst lengths for those bursts that contain more than one open period are shown for wild-type and εL78P receptors in B and D.
Table 3.
Burst length duration: empirical estimates of time constants and areas found for wild-type and εL78P receptors at 100 nm ACh
| n | τ1 (ms) | a1 (%) | τ2 (ms) | a2 (%) | τ3 (ms) | a3 (%) | τ4 (ms) | a4 (%) | τ5 (ms) | a5 (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wild-type | 4 | 0.032 | 29.7 | 0.615 | 26.2 | 2.860 | 44.1 | — | — | — | — |
| ± 41% | ± 43% | ± 42% | ± 27% | ± 16% | ± 22% | ||||||
| εL78P | 5 | 0.007 | 83.7 | 0.101 | 6.4 | 0.697 | 4.2 | 15.8 | 2.3 | 97.5 | 3.4 |
| ± 22% | ± 9% | ± 15% | ± 46% | ± 16% | ± 55% | ± 86% | ± 55% | ± 51% | ± 60% |
The εL78P receptors required five exponential components to describe their burst properties adequately whilst the wild-type receptors could be described with three exponential components. The mean tcrit values for the wild-type receptors was 0.79 ms ± 41%, and for εL78P receptors was 3.63 ms ± 38%. Errors are specified as c.v.m. (%) (see Methods).
Table 4.
Burst length durations for bursts that contain more than one apparent open period: wild-type and εL78P receptors at 100 nm ACh
| n | Mean burst length (ms) | τ1 (ms) | a1 (%) | τ2 (ms) | a2 (%) | |
|---|---|---|---|---|---|---|
| Wild-type | 4 | 4.06 | 4.06 | 100.0 | — | — |
| ± 9% | ± 9% | ± 0% | ||||
| εL78P | 5 | 33.82 | 1.18 | 39.4 | 55.0 | 60.7 |
| ± 2% | ± 6% | ± 21% | ± 14% | ± 14% |
The distributions of the εL78P receptors are described by two exponential components whilst the wild-type receptors could be described a single exponential component. The tcrit values are as in Table 3. Errors are specified as c.v.m. (%) (see Methods).
Effects of the εL78P mutation on the microscopic rate constants of activation
Fits with Scheme 1
To estimate the rate constants that determine channel activity, maximum likelihood fitting was done by the HJCFIT method. Initially the simplest mechanism (Scheme 1, Fig. 4) was used (see Methods).
No desensitized or ACh-blocked states were included in the scheme as the data were all obtained at low ACh concentrations. We are not investigating desensitization, and it has been shown that there is no need to include it in the reaction scheme in order to estimate the quantities of physiological relevance (Colquhoun et al. 2003). Several constraints were imposed on the rate constants. One of the forward association rates was fixed at a plausible value, because it is not known how many channels are in a cell-attached patch, so the absolute rate of channel activations cannot be known. Therefore it follows that at least one of the initial (binding of a first molecule of ACh) association rate constants cannot be determined. It has been shown (Colquhoun et al. 2003; Hatton et al. 2003) that the quantities of physiological interest can be estimated from low concentration records alone if an association rate constant (k+1a) is fixed. If the value at which it is fixed is incorrect, this will cause errors in the estimates of one monoliganded opening rate constant (β1b) which is in any case ill-defined, and in one affinity constant (Ka). But an incorrect value for k+1a will not cause errors in the diliganded gating rate constants or in any of the dissociation rate constants (Colquhoun et al. 2003; Figs 3 – 5). Therefore k+1a was fixed at a value close to that found in other studies, 1 × 108m−1 s−1 (Salamone et al. 1999; Hatton et al. 2003).
The two agonist binding sites were assumed to be independent, that is binding of ACh to site a is unaffected by the occupancy of site b, and vice versa (see Methods, eqns (1) and (2)). Good fits to single channel data can be obtained with this assumption of independence (Akk et al. 1999; Salamone et al. 1999; Hatton et al. 2003). This is just as well, because if the two sites are not independent it is not possible to get reliable estimates of the rate constants at low ACh concentrations, unless the number of channels in a patch is known (Colquhoun et al. 2003).
Figure 5 shows the HJC distributions overlaid onto (not fitted to) the observed open and shut time histograms and for both wild-type and εL78P channels. The observations appear to be described quite well by the mechanism and fitted rate constants. The most robustly estimated parameters are those that describe the properties of the diliganded receptor. The biggest effect (as might be expected from a mutation near the binding site) is a fourfold slowing of the total rate of ACh dissociation from the diliganded closed receptor, from 16 100 s−1± 6% to 3910 s−1± 9%. Although the εL78P mutation has no substantial effect on the opening rate of the diliganded receptor (β2) (47 900 s−1± 9% compared to 59 100 s−1± 12% for εL78P), the rate of closing of the diliganded receptor (α2) is decreased by about twofold, from 1620 s−1± 6% to 691 s−1± 20%. This means that the individual diliganded openings are about twice as long on average for the εL78P receptors as they are for the wild-type. The reduction in α2 is reflected also as an increase in E2, the efficacy of the gating process for diliganded channels for εL78P, from 30.3 ± 9% to 97.0 ± 14%. The decrease in dissociation rate means that the diliganded but shut channel ACh is relatively more likely to re-open, before the agonist dissociates, thus producing more openings in each channel activation (burst of openings). In addition, each individual opening is longer, on average, too.
Figure 5 shows also the plots of conditional mean open period duration (open periods that are adjacent to shut times in specified ranges) against apparent shut time (the mean of the shut times in each range). The predicted conditional means, calculated as in Colquhoun et al. (1996), agree quite well with the observed values, for both the wild-type and εL78P receptors.
Heterogeneity
Despite the fact that the fit of Scheme 1 to a single concentration (Fig. 5) looks good, this simple scheme is not satisfactory, as previously shown (Salamone et al. 1999; Hatton et al. 2003). The best way to fit a mechanism is to fit simultaneously records made at a range of agonist concentrations. A single set of rate constants should be able to fit the data well at every concentration. This will work well only if the records are homogeneous, and that ideal is not always realized. In this study, heterogeneity was a sufficiently bad problem that we preferred not to do simultaneous fits, but rather to fit each concentration separately.
One problem arose from the fact that an obvious empirical observation, such as the time constant for the main component of apparent open times, was not as constant from one recording to the next as might have been hoped. Another problem arose from the observation of very brief openings in the periods, normally silent, between clusters of openings at high agonist concentrations (see Fig. 1 in Elenes & Auerbach, 2002; and Fig. 2 in Hatton et al. 2003). In native receptors at the endplate, very few such openings are seen, but they seem to have become increasingly common in our recombinant preparations. They are not predicted by any of the mechanisms that have been used so far, and at present we think they are most likely to originate from some sort of atypical channel that contaminates our records to varying extents (R. Lape & D. Colquhoun, unpublished observations).
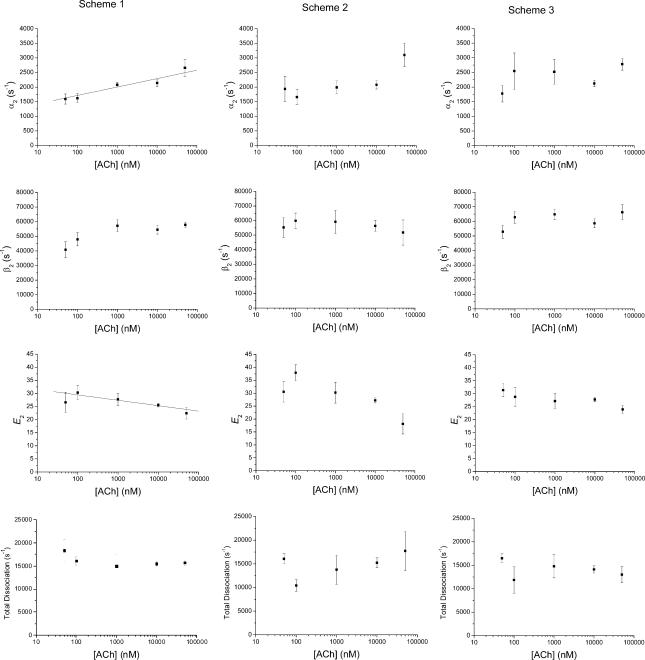
The question arises of how to distinguish between poor fits that result because an inadequate reaction mechanism is being used, and poor fits that result from heterogeneity. Heterogeneity would be manifest as variability in the values of the fitted rate constants, but there is no obvious reason why the values should be correlated with agonist concentration. In fact, when Scheme 1 was fitted, a systematic change in the values of the rate ‘constants’ was found over the concentration range from 50 nm to 50 μm ACh, as shown in Fig. 6 (left column). At high ACh concentrations the estimates of both α2 and β2 appeared to increase slightly. This anomaly suggests that Scheme 1, although it fits well at one concentration (Fig. 5) is not adequate to describe the whole concentration range, as already reported by Salamone et al. (1999) and by Hatton et al. (2003).
Figure 6. Dependence of the estimates of diliganded gating parameters on ACh concentration.
Results found by fitting Scheme 1 (left) Scheme 2 (centre) and Scheme 3 (right). There appears to be some concentration dependence of the estimates of α2 and E2 when Scheme 1 was used. A log-linear least-squares line fitted for α2 gives a slope of 289 (P < 0.05), and for diliganded efficacy, E2(β2/α2) the slope was −0.88 (P = 0.05).
Fits with Scheme 2
In an attempt to improve the fit without introducing more states, we tried Scheme 2 (Fig. 4) in which dissociation of agonist from the diliganded open state is permitted. This increases by two the number of free parameters that must be estimated, because two of the four new rate constants are determined by microscopic reversibility.
Maximum likelihood fitting of Scheme 2 with HJCFIT was tried on 29 patches, at a range of ACh concentrations. Of these, seven patches did not fit well, though these seven patches showed no obvious common properties in ACh concentration, temperature, date of the experiments or tcrit values. For the rest of the patches, as with Scheme 1 there was good agreement between the open and shut time duration histograms and the HJC distributions. The estimates of the diliganded parameters (channel opening and closing rate, and the total rate of ACh dissociation from the diliganded shut state) were similar for both wild-type and εL78P to those obtained with Scheme 1.
The estimates of the rates of ACh dissociation from the wild-type open channels (k−2a(o) and k−2b(o), Schemes 2 and 5) were 86 s−1 and 154 s−1 for the two different sites. These are low compared with the estimate of the rate of channel closing (1660 s−1) and in the same range as those found for dissociation of ACh from the open state of mouse nicotinic receptors using somewhat different methods of single channel analysis (Grosman & Auerbach, 2001). These values imply that, from the open diliganded state, most transitions will involve closure of the pore, rather than dissociation of an agonist molecule. Dissociation from the open channel is much (roughly 40-fold) slower than from the shut channel. However Scheme 2 was still not satisfactory, for two reasons. Firstly, the estimates of the association rate constants for binding to the open channel were implausibly high, of the order of 1010m−1 s−1, and secondly Fig. 6 (middle column) still shows some signs of (non-linear) dependence of the rate constant estimates on concentration.
Fits with Scheme 3
In the light of the imperfections of fits with Scheme 2, we returned to the scheme used previously by Salamone et al. (1999) and by Hatton et al. (2003). This is shown as Scheme 3 (Fig. 4), and differs only from Scheme 1 only by the addition of a short lived shut state accessible from the dilig and ed open state. Maximum likelihood fitting with this scheme yielded estimates of the dilig and ed parameters that were similar to those found with Schemes 1 and 2, namely α2 = 1800 s−1, β2 = 53 300 s−1, E2 = 29.1, total rate of dissociation = 14 900 s−1. Of 29 patches at a range of ACh concentrations, only two did not give good matches between the observed open time and shut time distributions and their corresponding HJC distributions. Moreover, the concentration dependence of α2 seen when fitting to Scheme 1 was not present (Fig. 6, right column). An example of a fit is shown in Fig. 7, and the averaged estimates of the rate constants are shown in Table 5.
Table 5.
Estimates of rate constants from fitting Scheme 3 to data from 100 nm ACh patches
| Rate | Wild-type (n = 5) | εL78P (n = 5) | ||
|---|---|---|---|---|
| α2 (s−1) | 1800 | ± 13% | 1040 | ± 20% |
| β2 (s−1) | 53300 | ± 18% | 74600 | ± 9% |
| E2 | 29.1 | ± 7% | 82.2 | ± 17% |
| α1a (s−1) | 3710 | ± 16% | 4930 | ± 11% |
| β1a (s−1) | 127 | ± 64% | 735 | ± 25% |
| E1a | 0.040 | ± 67% | 0.016 | ± 26% |
| α1b (s−1) | 60900 | ± 21% | 226000 | ± 16% |
| β1b (s−1) | 554 | ± 79% | 4630 | ± 45% |
| E1b | 0.026 | ± 94% | 0.018 | ± 45% |
| k+a (μM−1 s−1) | 996 | ± 40% | 62.9 | ± 48% |
| k-a (s−1) | 11800 | ± 27% | 2760 | ± 20% |
| Ka(μM) | 11.8 | ± 27% | 5120 | ± 96% |
| k+b* (μM−1 s−1) | 100 | 100 | ||
| k−b (s−1) | 3070 | ± 77% | 73.8 | ± 20% |
| Kb(μM) | 30.7 | ± 77% | 0.738 | ± 20% |
| k−a+k-b (s−1) | 14900 | ± 10% | 2840 | ± 20% |
| αD (s−1) | 8720 | ± 56% | 3830 | ± 35% |
| βD (s−1) | 96.5 | ± 35% | 15.7 | ± 32% |
| ED =βD/αD | 0.11 | ± 97% | 0.006 | ± 32% |
The assumption of independence of the two binding sites (see Methods) means that k−2a =k−1a, k−2b =k−1b, k+2b =k+1b, k+2a =k+1a, so the numerical subscript is unnecessary and the rate and constants for a and b sites are denoted simply as k−a, k−b, k+a, and k+b. The asterisk denotes rates that were fixed during the fitting. The total dissociation rate from diliganded receptors, k−a+k−b is given in the table. Note that equilibrium constants were calculated separately for each experiment and then averaged. Therefore the values given differ from the ratios of the mean rate constants, especially when the scatter is large.
The values for rate constants for the diliganded wild-type receptor are in very close agreement with those we found earlier (Hatton et al. 2003). The rate constants for dissociation from the a and b sites (k−a, k−b) are in good agreement too, though the agreement is less good for the association rates (k+a, and k+b), and the rare, and very fast, values for openings of one of the monoliganded states remain elusive (especially β1b), as before. These values are, in any case, susceptible to errors as a result of the atypical short openings that occur in some records (see above). The labels a and b for the two binding sites are arbitrary. In Table 5, the a site has, as in Hatton et al. (2003), been taken as the site which, when singly occupied, gives rise to the longer singly liganded openings (mean lifetime of 1/α1a = 0.27 ms, compared with the mean open time for doubly occupied receptors which is 1/α2 = 0.56 ms). The rate constant for entry into the putative short-lived shut state, A2RD, in Scheme 3 is estimated as βD = 96 s−1 for wild-type and βD = 16 s−1 for the mutated receptor, the former being similar to the values of 32–98 s−1 found by Salamone et al. (1999) and 65 s−1 found by Hatton et al. (2003). However, the rate constant, αD, for leaving this state are around 10 times faster than we found earlier for human receptor (Hatton et al. 2003), and than others have found for mouse receptor (Salamone et al. 1999), so the equilibrium constant for entry into the A2RD state is consequently smaller; the reason for this difference is unknown. Once we have a realistic mechanism, and values for the rate constants, it should be possible to predict the behaviour of the receptor under any circumstances. The values in Table 5 were used to predict the time course of synaptic currents (Fig. 10) and also for calculations that are designed to cast light on the physical basis of the unusually well-separated time constants for the distribution of the length of bursts with more than one opening for the εL78P receptor, that was shown in Fig. 3D.
Bursts with more than one opening
The burst length distribution, unlike that of the apparent open time and shut time, is usually not greatly affected by the inability to detect short events (shorter than 30 μs here). The case of the mutant receptor, εL78P, proved to be an exception to this rule, so the explanation for the shape of the burst length distributions shown in Fig. 3 was investigated by simulation of open and shut times at 100 nm ACh (with the program SCSIM), using the estimated rate constants from Scheme 3 for the εL78P receptor (as in Table 5). The simulation method is explained in greater detail by Colquhoun et al. (2003). Although the burst length distribution is easily calculated in the ideal case of perfect resolution (Colquhoun & Hawkes, 1982; eqn (3.17)), it turned out in this case that the inability to detect brief events had an unusually important effect, so simulation was used. After simulation of the open–shut sequence, a resolution of 30 μs was imposed on the results, as in real experiments. The distributions of simulated open time duration, shut time duration, and of burst length duration, with a resolution of 30 μs, are shown in Fig. 8. The shut time distribution for the mutant receptor (Fig. 8B), like the observed distribution (Fig. 2D) shows a smear of shut times between 1 and 10 ms and an empirical fit gives a component with τ= 12.5 ms, comparable with the observed τ4 = 35 ms. This smear makes the selection of an appropriate tcrit somewhat ambiguous. However, calculation of the ideal shut time distribution from the same rate constants as used for simulation shows that no such intermediate shut times are predicted: virtually nothing is expected between a 0.2 ms component and a 90 ms component. The intermediate shut times that give rise to ambiguity in the definition of tcrit are not ‘genuine’, but arise because many short openings are undetected. For the definition of bursts from the simulated mutant data (Fig. 8C and D), we chose to use the same tcrit value of 3.63 ms that was used for the experimental results (Fig. 3C and D). The distributions of the length of all bursts (Fig. 8C), and the distribution of the length of bursts with more than one opening (Fig. 8D) are similar in shape to those found experimentally (Fig. 3C and D).
Figure 8. The histograms show simulated data for the εL78P receptor.
Open and shut time sequences were generated randomly using Scheme 3, with the values for the rate constants shown in Table 5. After simulation, a resolution of 30 μs, was imposed on the results, as in the real experiments. The distribution of lengths of bursts with more than one opening (D) is seen to show a bimodal shape (using the Sigworth and Sine transformation) that is similar to that of the actual data (compare with Fig. 3). For calculating the simulated burst length distributions, a tcrit value of 3.63 ms was used (as for the experimental data).
In particular, the simulated distribution of the length of bursts with more than one opening (Fig. 8D) has two well-separated components, quite unlike the comparable distribution for the wild-type receptor (Fig. 3B), but similar to the experimental data (Fig. 3D). Quantitatively the agreement is less good, the areas and time constants in Figs 3D and 8D differing by factors of almost 2, perhaps because of the ambiguity in the definition of tcrit that results from so many short openings being missed.
Conditional burst length distributions
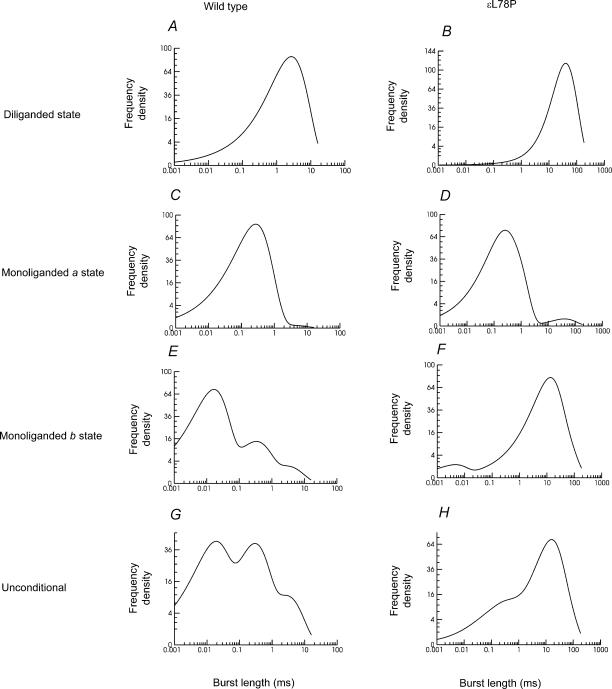
In order to understand better the mechanisms underlying the structure of bursts of openings, we inspected the sort of bursts that are predicted conditional on a burst starting in each of the three open states. These predictions are based on Scheme 3, with the rate constants found in Table 5. They are calculated for perfect time resolution, as described by Colquhoun & Hawkes (1982), using the SCBST program.
At high ACh concentrations, almost all burst of openings will start in the diliganded open state. As shown in Table 6 and Fig. 9, bursts (activations) that start in the diliganded state will have for wild-type a mean length of 2.7 ms with 5.07 openings per burst, whereas for εL78P receptors they will have a mean length of 42 ms with 91 openings per burst. It is these lengthened bursts that underlie the slow decay of the synaptic current, predicted in Fig. 10.
Table 6.
The conditional burst length distributions, and the distributions of the number of openings per burst, for 100 nm ACh
| Conditional on starting in the diliganded open state | Conditional on starting in the a monoliganded state | Conditional on starting in the b monoliganded open state | Unconditional distribution | |
|---|---|---|---|---|
| Wild-type | ||||
| Mean burst length (ms) | 2.73 | 0.26 | 0.14 | 0.44 |
| φ | 0.1 | 0.37 | 0.53 | — |
| a (%) | ||||
| τ= 0.016 ms | — | — | 81 | 43 |
| τ= 0.274 | — | 100 | — | 37 |
| τ= 0.319 | — | — | 16 | 8 |
| τ= 2.69 | 100 | — | 3 | 11 |
| Mean openings per burst | 5.07 | 1.01 | 1.30 | 1.56 |
| a (%) | ||||
| μ= 1.01 | — | 100 | — | 37 |
| μ= 1.17 | — | — | 97 | 51 |
| μ= 4.93 | 100 | — | 3 | 12 |
| εL78P | ||||
| Mean burst length (ms) | 42.1 | 0.48 | 15.8 | 14.0 |
| φ | 2.7 × 10−3 | 0.12 | 0.88 | — |
| a (%) | ||||
| τ= 0.004 ms | — | — | 2 | 1.3 |
| τ= 0.16 ms | — | 42 | — | 5 |
| τ= 0.46 ms | — | 58 | — | 7 |
| τ= 12 ms | — | — | 77 | 68 |
| τ= 30.6 ms | 100 | — | 21 | 19 |
| Mean openings per burst | 90.9 | 1.59 | 65.9 | 58.3 |
| a (%) | ||||
| μ= 1.26 | — | 99.6 | — | 12 |
| μ= 26.2 | −57 | — | 3 | 3 |
| μ= 67.3 | 157 | 97 | 85 | |
The values are calculated from the microscopic rate constants for wild-type and εL78P receptors that were given in Table 5, without allowance for missed events (the ‘true’ distributions). The upper part of the table shows results for wild-type, and the lower part for εL78P receptors. The overall means are given for each sort of distribution. The φ-values give the predicted probabilities that a burst starts in each of the three open states, and are followed by the components of the distribution. Burst length distributions are all given by a mixture of six exponential pdfs because entry into the unliganded R state was the criterion for the end of a burst). The time constants for the exponential components are identical for the unconditional, and all three conditional distributions, so they are given only once, on the left. It is only the areas that vary from one component to another that are tabulated. Many of these components have effectively zero area (indicated by dash) so only those components with areas greater than 1% are shown here. The distributions of the number of openings per burst are mixtures of three geometric distributions (because there are three open states), and again components with very small area are omitted for simplicity.
Figure 9. Burst length distributions calculated without allowance for missed events.
Panels A–F show the distributions conditional on the initial open state of the burst. Panels G and H show the unconditional burst length distributions. As expected, the εL78P data show a larger proportion of very long bursts compared to the wild-type data. Values of the mean burst lengths, time constants and their areas, mean number of openings per burst and initial vectors are given in Table 6.
At 100 nm ACh, when bursts of openings are quite well separated, the first opening in a burst will usually be a monoliganded opening. The initial vector, φb, is calculated from the Q matrix, elements of which are the transition rate constants of the kinetic scheme (Colquhoun & Hawkes, 1982; eqn (3.2)). Values are given for wild-type and the εL78P receptors in Table 6.
Wild-type receptors
For the wild-type, 10% of bursts are predicted to start in the diliganded open state even at 100 nm ACh, and these contribute almost all of the 2.7 ms component in the overall burst length distribution. Bursts that start in the monoliganded a open state have a single principal component, with a time constant of 0.274 ms. This corresponds almost exactly to the predicted lifetime of 0.270 ms for a single monoliganded opening elicited from the a site, as expected, since such bursts are almost all single openings (mean of 1.01 openings per burst). Bursts that start in the monoliganded b state have three principal components. The predominant component has a time constant of 16.3 μs with 81% of the area. This is almost exactly the same duration as a single monoliganded opening from the b site (16.4 μs). The second component has a time constant of 0.32 ms and an area of 16%. The third component has a time constant of 2.7 ms and an area of 3%. The 2.7 ms bursts correspond to bursts that are initiated in the brief monoliganded b state and then proceed via shut states to a sequence of transitions between the diliganded shut and the diliganded open states.
εL78P receptors
For mutant channels, when no short events are missed, it is predicted that virtually no bursts start in the diliganded open state at 100 nm ACh. Most (88%) start in the monoliganded b state, and almost all of these bursts (98%) will lead to long bursts with time constants of 12 ms or 30.6 ms. The monoliganded open state b is so short that it will almost always be missed, and when that happens, the shut time that follows it will not be counted as part of the burst length either. After return from the open state b (RA*, Scheme 3 and Fig. 4) to the adjacent RA state, there will be an average of 1.6 ms before the next open state is entered, omission of which will cause substantial error in the measured burst length. The overall burst length distribution for εL78P receptors contains also about 12% of shorter bursts (τ= 0.16 or 0.46 ms) that are seen to originate from bursts that start in the monoliganded open state a, as shown in Table 6.
Predicted effects of the εL78P mutation on synaptic currents
The values obtained for the microscopic rate constants can be used to calculate the synaptic current that would be produced at the muscle endplate. The SCALCS program was used to calculate the synaptic current using the rate constant estimates from Table 5, the transmitter time course being taken as a 0.1 ms pulse of 1 mm ACh (the results do not depend strongly on the duration of the pulse as long as it is brief). The predicted current is shown in Fig. 10, along with that predicted from the wild-type receptor rate constants.
The wild-type macroscopic current has a predominant decay time constant of 2.6 ms, similar to that found at actual end plates (Cull-Candy et al. 1979). The εL78P receptors have a predominant decay time constant of 26.7 ms, 10-fold slower than the wild-type receptors. The predominant time constant of decay of a macroscopic current is expected to be the same as the slowest time constant of the burst length distribution, when the latter is measured at very low concentration (Colquhoun et al. 1997; Wyllie et al. 1998). The predicted decay is indeed close to this value (Fig. 9, Table 6).
As noted above, the fit to the experimental data (Fig. 3, Table 3) indicated somewhat longer bursts than were predicted by the fit. Possible reasons for this include (a) the ambiguity in the tcrit value, (b) the necessarily limited number of long bursts that are observed at 100 nm, which is reflected in the rather large errors for the time constants and area of the slowest components in Table 3, or (c) some inadequacy of the mechanism we have fitted.
Discussion
Slow channel congenital myasthenic syndrome
Congenital slow channel myasthenic syndromes are caused by mutations in the nicotinic receptor that cause prolonged synaptic currents (e.g. Croxen et al. 2002; McConville & Vincent, 2002; Engel et al. 2003a, b). Many different mutations can cause SCCMS, but there appears to be surprisingly little correlation between the severity of the mutation on channel function, and the severity of the symptoms experienced (e.g. Croxen et al. 1997; Milone et al. 1997). Muscle weakness would necessarily result from degradation of the end plate region. This degradation is thought to be caused by excess Ca2+ entry into the muscle cytosol, which may activate the apoptotic machinery. The source of this Ca2+ could be direct entry through the muscle receptors (Costa et al. 1994), or via the large efflux of Ca2+ from the sarcoplasmic reticulum following the initiation of muscle action potentials by the depolarization of the end plate produced by the receptor activation.
The results here show that the εL78P mutation causes ACh to produce very long activations of the channel, i.e. the channel reopens many times between the time when the first ACh molecule binds, and the time when the last ACh molecule dissociates. Fitting of the single channel results allows it to be predicted that the synaptic current will decay 10-fold more slowly than for wild-type receptors, though no direct measurements have been made on human endplates for this mutation. Nevertheless the symptoms of patients with this mutation are mild compared with those of some other cases of SCCMS. One contributory factor could be a compensatory increase in expression of the fetal γ subunit in damaged endplates (Engel et al. 1996; Ohno et al. 1997).
Mechanisms and rates
Single channel recordings could be fitted quite well with a standard mechanism (Scheme 3, Fig. 4), for the mutant εL78P receptors as well as wild-type. Once the rate constants have been estimated it becomes possible to predict any single channel or macroscopic property of the receptor, whether at equilibrium or not.
The estimates obtained for the diliganded channel opening rate constant, β2, for the human wild-type receptor are similar to those found previously in human and mouse muscle receptors. β2 has been estimated in several studies to be 50 000–60 000 s−1 at 20°C at the mouse receptor (Wang et al. 1997; Salamone et al. 1999), and human receptor (Hatton et al. 2003). The estimate of β2 is similar to that found for frog receptors (30 600 s−1 at 11°C; Colquhoun & Sakmann, 1985), bearing in mind the difference in temperature (the difference corresponds to a Q10 of about 2, a common value for rate constants: Gutfreund, 1995).
The rate constant for diliganded channel closing (α2) for wild-type receptors was estimated as approximately 2000 s−1, in agreement with Hatton et al. (2003) who found 1850 s−1. Mouse receptors also appear to be similar to human receptors. Estimates for α2 in mouse receptors include 1300 s−1 (Akk et al. 1999), 1700 s−1 (Wang et al. 1997), and 2600 s−1 (Salamone et al. 1999). This is again similar to the value of 714 s−1 for frog muscle at 11°C (Colquhoun & Sakmann, 1985), if a Q10 of about 2 is assumed. The equilibrium gating constant (or ‘efficacy’), the ratio of opening to shutting rate constants, E2 =β2/α2, for diliganded channel gating is 25–30 in these and other recent studies.
The total rates of dissociation of ACh from diliganded receptors (which can be measured more accurately than the two separate rates of dissociation from each site) are different in human and mouse. This study estimates this total rate (k−2a+k−2b), to be in the range of 14 900 s−1 (similar to 13 800 s−1 in Hatton et al. 2003) while estimates for the mouse receptor include 36 000 s−1 (Akk et al. 1999), 44 000 s−1 (Wang et al. 1997), and 49 000 s−1 (Salamone et al. 1999). Individually the two sites in both human and mouse have different dissociation rates, values of 18 000 s−1 and 43 000 s−1 are given for the mouse receptor (Salamone et al. 1999).
Although the εL78P receptor produces longer bursts of openings than wild-type, and hence slower synaptic current decay, it also produces many very short openings. Empirical fitting suggested a mean length of 9 μs for these (Table 1) though fitting suggested the openings of the b monoliganded state are even shorter (about 4 μs). A similar discrepancy was seen for homomeric glycine receptors (Burzomato et al. 2004), and it is not surprising since the HJC distribution of observed open times would not be expected to be fitted by exponentials for such short events (Hawkes et al. 1990) because they are too short for the asymptotic distribution, which is a mixture of exponentials, to be valid (Hawkes et al. 1992). Our fits suggest that for the mutant receptor, most bursts will start in this very short-lived open state at low (100 nm) ACh concentrations, though most of these go on to reach the diliganded state and so generate long pathogenic bursts. Most openings that are so short will be missed, so there is an unusually large effect of missed events on the observed burst length distribution, a fact that emphasizes the importance of the exact missed event method used in HJCFIT.
The main reason for the increased burst length of εL78P receptors is that the total dissociation rate for diliganded receptors is reduced fivefold, from 14 900 s−1 to 2840 s−1 (Table 5), the rest of the effect coming from 1.7-fold longer openings (reduced α2) and a 1.4-fold increase in opening rate (β2) in the mutant. It is, perhaps, surprising that a mutation so far from the pore region should affect gating at all. However it must be remembered that the steps labelled as ‘binding’ in the mechanism (Scheme 3) that was fitted actually include everything that occurs before the shut-open conformation change. If there were a substantial change in conformation of the receptor before the channel opened, then it would not be surprising if such a conformation change were affected by mutations in the extracellular region. Exactly this sort of preopening conformation change provides an elegant explanation of observations with glycine receptors (Colquhoun & Sivilotti, 2004; Burzomato et al. 2004), and may also occur in nicotinic receptors (Chakrapani et al. 2004; R. Lape & D. Colquhoun, unpublished observations).
Structure and function
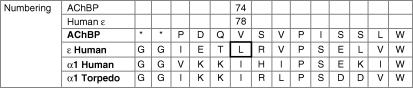
The position of εL78P within the receptor can be guessed by examining the homologous acetylcholine binding protein (AChBP) for which a crystal structure has been obtained (Brejc et al. 2001; Celie et al. 2004). Alignment of the human ε subunit and the AChBP shows that the position εL78 aligns with V74 in the AChBP, as shown in Fig. 11.
Figure 11. Alignment of the amino acid sequences of the human ε and α1 subunits, the Torpedoα1 receptor subunit, and the AChBP.
The site of the point mutation εL78P aligns with V74 of the AChBP (shown framed).
In the structure of AChBP, this position is on the β3 strand which forms part of one of the two twisted β-sheets characteristic of AChBP and of the Torpedo nicotinic receptor, as illustrated in Fig. 12. This position is not in the ACh binding site, nor is it close to the pore region of the channel. However, in the β-sheet, the β3 strand is adjacent to the β5′ strand, which does line the binding site (Brejc et al. 2001). The mutation of a leucine residue to a proline residue in this position would be expected to have several structural effects. First, as proline has a cyclic side chain attached at two points to the peptide backbone, it introduces constraints on the conformation of the backbone. The substitution of a proline at this position would be expected to reduce the flexibility of the β3 strand. In addition, because proline is an imino acid, it lacks a nitrogen-bonded backbone hydrogen which is present on all other amino acids. According to the structure of AChBP, the nitrogen-bonded hydrogen of the valine residue at position 74 is hydrogen-bonded to V105 in the β5′ strand. Therefore the substitution of a proline residue in this position will prevent formation of this hydrogen bond. It may be that the absence of this hydrogen bond significantly reduces the stability of the twisted β sheet, or it may be that an alternative arrangement of hydrogen bonds linking the β3 and β5′ strands occurs. In either case, the changes induced by substitution of a single residue will extend beyond the position of this residue. Following the binding of agonist, there must be movement of many parts of the molecule in order to communicate the effect of the binding to the channel gate (Miyazawa et al. 2003; Chakrapani et al. 2004). It is therefore entirely possible that a mutation such as εL78P can affect gating, despite being so far from the ion-conducting pore.
Figure 12. The homologous residue to εL78P in the AChbp is V74 on strand β3.
The backbone of this residue is hydrogen bonded to strand β5′, which lines the ACh binding pocket. Loops lining the ‘plus’ side of the binding pocket are coloured orange, the ‘minus’ face of the binding site is coloured purple. Hepes is shown in yellow. This image was constructed using RasTop from the crystal structure data of AChBP bound to Hepes, PDB ID number 1I9B. Below (B) is a schematic diagram showing that the replacement of the residue at position 74 with a proline residue will disrupt the hydrogen bonding between the β3 and β5′ strands.
It might be expected that the location of the mutation in the ε subunit would lead to effects on only one binding site. However, effects on both binding sites are seen; dissociation rates are decreased 4-fold at the a site and 42-fold at the b site. This is entirely possible because the ε subunit lies between two α subunits in the arrangement of subunits around the pore. Thus, seen from the extracellular face of the membrane, changes in the ε subunit could be transmitted clockwise to the neighbouring α subunit forming the αε binding site, or anticlockwise to the neighbouring α subunit forming the αδ binding site. Unless a mutation is directly in the αε binding site of the ε subunit it is impossible to predict with any accuracy whether the mutation affects the αε or the αδ binding sites or associated gating steps.
Acknowledgments
C.S. was on the Wellcome Trust four year PhD programme in neuroscience and D.C. was funded by the Wellcome Trust and the Medical Research Council. We are grateful to Professor David Beeson and Dr Martin Brydson (Neurosciences Group, Weatherall Institute of Molecular Medicine, Oxford OX3 9DS, UK) for suggesting this project and for supplying much of the DNA. We also thank Paul J. Groot-Kormelink (University College London) for supply of DNA and help with molecular biology.
References
- Akk G. Contributions of the non-alpha subunit residues (loop D) to agonist binding and channel gating in the muscle nicotinic acetylcholine receptor. J Physiol. 2002;544:695–705. doi: 10.1113/jphysiol.2002.029413. 10.1113/jphysiol.2002.029413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akk G, Auerbach A. Inorganic monovalent cations compete with agonists for the transmitter binding site of nicotinic acetylcholine receptors. Biophys J. 1996;70:2652–2658. doi: 10.1016/S0006-3495(96)79834-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akk G, Zhou M, Auerbach A. A mutational analysis of the acetylcholine receptor channel transmitter binding site. Biophys J. 1999;76:207–218. doi: 10.1016/S0006-3495(99)77190-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beato M, Groot-Kormelink PJ, Colquhoun D, Sivilotti LG. The activation mechanism of α1 homomeric glycine receptors. Journal of Neuroscience. 2004;24:895–906. doi: 10.1523/JNEUROSCI.4420-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brejc K, van Dijk WJ, Klaassen RV, Schuurmans M, van Der Oost J, Smit AB, Sixma TK. Crystal structure of an ACh-binding protein reveals the ligand-binding domain of nicotinic receptors. Nature. 2001;411:269–276. doi: 10.1038/35077011. [DOI] [PubMed] [Google Scholar]
- Burzomato V, Groot-Kormelink PJ, Colquhoun D, Beato M, Sivilotti LG. Single channel behaviour of heteromeric α1β glycine receptors: an attempt to detect a conformational change before the channel opens. J Neurosci. 2004;24:10924–10940. doi: 10.1523/JNEUROSCI.3424-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celie PH, Rossum-Fikkert SE, van Dijk WJ, Brejc K, Smit AB, Sixma TK. Nicotine and carbamylcholine binding to nicotinic acetylcholine receptors as studied in AChBP crystal structures. Neuron. 2004;41:907–914. doi: 10.1016/s0896-6273(04)00115-1. [DOI] [PubMed] [Google Scholar]
- Chakrapani S, Bailey TD, Auerbach A. Gating dynamics of the acetylcholine receptor extracellular domain. J General Physiol. 2004;123:341–356. doi: 10.1085/jgp.200309004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clapham DE, Neher E. Substance P reduces acetylcholine-induced currents in isolated bovine chromaffin cells. J Physiol. 1984;347:255–277. doi: 10.1113/jphysiol.1984.sp015065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D. Binding, gating, affinity, and efficacy: the interpretation of structure-activity relationships for agonists and the effects of mutating receptors. Br J Pharmacol. 1998;125:924–947. doi: 10.1038/sj.bjp.0702164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D, Hatton CJ, Hawkes AG. The quality of maximum likelihood estimates of ion channel rate constants. J Physiol. 2003;547:699–728. doi: 10.1113/jphysiol.2002.034165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG. On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Philos Trans R Soc Lond B Biol Sci. 1982;300:1–59. doi: 10.1098/rstb.1982.0156. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG. The principles of the stochastic interpretation of ion channel mechanisms. In: Sakmann B, Neher E, editors. Single Channel Recording. New York: Plenum Press; 1995. pp. 397–482. [Google Scholar]
- Colquhoun D, Hawkes AG, Merlushkin A, Edmonds B. Properties of single ion channel currents elicited by a pulse of agonist concentration or voltage. Philos Trans R Soc Lond A. 1997;355:1743–1786. [Google Scholar]
- Colquhoun D, Hawkes AG, Srodzinski K. Joint distributions of apparent open times and shut times of single ion channels and the maximum likelihood fitting of mechanisms. Philos Trans R Soc Lond A. 1996;354:2555–2590. [Google Scholar]
- Colquhoun D, Sakmann B. Fast events in single-channel currents activated by acetylcholine and its analogues at the frog muscle end-plate. J Physiol. 1985;369:501–557. doi: 10.1113/jphysiol.1985.sp015912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D, Sigworth FJ. Fitting and statistical analysis of single-channel records. In: Sakmann B, Neher E, editors. Single Channel Recording. New York: Plenum Press; 1995. pp. 483–587. [Google Scholar]
- Colquhoun D, Sivilotti LG. Function and structure in glycine receptors and some of their relatives. Trends Neurosci. 2004;27:337–344. doi: 10.1016/j.tins.2004.04.010. [DOI] [PubMed] [Google Scholar]
- Costa AC, Patrick JW, Dani JA. Improved technique for studying ion channels expressed in Xenopus oocytes, including fast superfusion. Biophys J. 1994;67:395–401. doi: 10.1016/S0006-3495(94)80494-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croxen R, Hatton C, Shelley C, Brydson M, Chauplannaz G, Oosterhuis H, Vincent A, Newsom-Davis J, Colquhoun D, Beeson D. Recessive inheritance and variable penetrance of slow-channel congenital myasthenic syndromes. Neurology. 2002;59:162–168. doi: 10.1212/wnl.59.2.162. [DOI] [PubMed] [Google Scholar]
- Croxen R, Newland C, Beeson D, Oosterhuis H, Chauplannaz G, Vincent A, Newsom-Davis J. Mutations in different functional domains of the human muscle acetylcholine receptor α subunit in patients with the slow-channel congenital myasthenic syndrome. Human Mol Genet. 1997;6:767–774. doi: 10.1093/hmg/6.5.767. [DOI] [PubMed] [Google Scholar]
- Cull-Candy SG, Miledi R, Trautmann A. End-plate currents and acetylcholine noise at normal and myasthenic human end-plates. J Physiol. 1979;287:247–265. doi: 10.1113/jphysiol.1979.sp012657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elenes S, Auerbach A. Desensitization of diliganded mouse muscle nicotinic acetylcholine receptor channels. J Physiol. 2002;541:367–383. doi: 10.1113/jphysiol.2001.016022. 10.1113/jphysiol.2001.016022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AG, Lambert EH, Mulder DM, Torres CF, Sahashi K, Bertorini TE, Whitaker JN. A newly recognised congenital myasthenic syndrome attributed to a prolonged open time of the acetylcholine-induced ion channel. Ann Neurol. 1982;11:553–569. doi: 10.1002/ana.410110603. 10.1002/ana.410110603. [DOI] [PubMed] [Google Scholar]
- Engel AG, Ohno K, Bouzat C, Sine SM, Griggs RC. End-plate acetylcholine receptor deficiency due to nonsense mutations in the epsilon subunit. Ann Neurol. 1996;40:810–817. doi: 10.1002/ana.410400521. 10.1002/ana.410400521. [DOI] [PubMed] [Google Scholar]
- Engel AG, Ohno K, Sine SM. Congenital myasthenic syndromes: a diverse array of molecular targets. J Neurocytol. 2003a;32:1017–1037. doi: 10.1023/B:NEUR.0000020639.22895.28. 10.1023/B:NEUR.0000020639.22895.28. [DOI] [PubMed] [Google Scholar]
- Engel AG, Ohno K, Sine SM. Sleuthing molecular targets for neurological diseases at the neuromuscular junction. Nat Rev Neurosci. 2003b;4:339–352. doi: 10.1038/nrn1101. 10.1038/nrn1101. [DOI] [PubMed] [Google Scholar]
- Gomez CM, Maselli RA, Groshong J, Zayas R, Wollmann R, Cens T, Charnet P. Active calcium accumulation underlies severe weakness in a panel of mice with slow channel syndrome. J Neurosci. 2002;22:6447–6457. doi: 10.1523/JNEUROSCI.22-15-06447.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosman C, Auerbach A. The dissociation of acetylcholine from open nicotinic receptor channels. Proc Natl Acad Sci U S A. 2001;98:14102–14107. doi: 10.1073/pnas.251402498. 10.1073/pnas.251402498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutfreund H. Kinetics for the Life Sciences. Cambridge: Cambridge University Press; 1995. [Google Scholar]
- Hatton CJ, Shelley C, Brydson M, Beeson D, Colquhoun D. Properties of the human muscle nicotinic receptor, and of the slow-channel myasthenic syndrome mutant εL221F, inferred from maximum likelihood fits. J Physiol. 2003;547:729–760. doi: 10.1113/jphysiol.2002.034173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkes AG, Jalali A, Colquhoun D. The distributions of the apparent open times and shut times in a single channel record when brief events can not be detected. Philos Trans R Soc Lond A. 1990;332:511–538. doi: 10.1098/rstb.1992.0116. [DOI] [PubMed] [Google Scholar]
- Hawkes AG, Jalali A, Colquhoun D. Asymptotic distributions of apparent open times and shut times in a single channel record allowing for the omission of brief events. Philos Trans R Soc Lond B. 1992;337:383–404. doi: 10.1098/rstb.1992.0116. [DOI] [PubMed] [Google Scholar]
- Jackson MB. Dependence of acetylcholine receptor channel kinetics on agonist concentration in cultured mouse muscle fibres. J Physiol. 1988;397:555–583. doi: 10.1113/jphysiol.1988.sp017019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magleby KL, Pallotta BS. Burst kinetics of single calcium-activated potassium channels in cultured rat muscle. J Physiol. 1983;344:605–623. doi: 10.1113/jphysiol.1983.sp014958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McConville J, Vincent A. Diseases of the neuromuscular junction. Curr Opin Pharmacol. 2002;2:296–301. doi: 10.1016/s1471-4892(02)00156-x. 10.1016/S1471-4892(02)00156-X. [DOI] [PubMed] [Google Scholar]
- Milone M, Wang HL, Ohno K, Fukudome T, Pruitt JN, Bren N, Sine SM, Engel AG. Slow-channel myasthenic syndrome caused by enhanced activation, desensitization, and agonist binding affinity attributable to mutation in the M2 domain of the acetylcholine receptor α subunit. J Neurosci. 1997;17:5651–5665. doi: 10.1523/JNEUROSCI.17-15-05651.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyazawa A, Fujiyoshi Y, Unwin N. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 2003;424:949–955. doi: 10.1038/nature01748. 10.1038/nature01748. [DOI] [PubMed] [Google Scholar]
- Ohno K, Quiram PA, Milone M, Wang HL, Harper MC, Pruitt JN, Brengman JM, Pao L, Fischbeck KH, Crawford TO, Sine SM, Engel AG. Congenital myasthenic syndromes due to heteroallelic nonsense/missense mutations in the acetylcholine receptor ε subunit gene: identification and functional characterization of six new mutations. Human Mol Genet. 1997;6:753–766. doi: 10.1093/hmg/6.5.753. 10.1093/hmg/6.5.753. [DOI] [PubMed] [Google Scholar]
- Salamone FN, Zhou M, Auerbach A. A re-examination of adult mouse nicotinic acetylcholine receptor channel activation kinetics. J Physiol. 1999;516:315–330. doi: 10.1111/j.1469-7793.1999.0315v.x. 10.1111/j.1469-7793.1999.0315v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelley C, Brydson M, Beeson DMW, Colquhoun D. Single-channel analysis of εL78P, a mutation responsible for slow channel congenital myasthenia. J Physiol. 2003:C44. [Google Scholar]
- Sine SM, Claudio T, Sigworth FJ. Activation of Torpedo acetylcholine receptors expressed in mouse fibroblasts: single channel current kinetics reveal distinct agonist binding affinities. J General Physiol. 1990;96:395–437. doi: 10.1085/jgp.96.2.395. 10.1085/jgp.96.2.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sine S, Ohno K, Bouzat C, Auerbach A, Milone M, Pruit JN, Engel AG. Mutation of the acetylcholine receptor alpha subunit causes a slow-channel myasthenic syndrome by enhancing agonist binding affinity. Neuron. 1995;15:229–239. doi: 10.1016/0896-6273(95)90080-2. 10.1016/0896-6273(95)90080-2. [DOI] [PubMed] [Google Scholar]
- Wang HL, Auerbach A, Bren N, Ohno K, Engel AG, Sine SM. Mutation in the M1 domain of the acetylcholine receptor α subunit decreases the rate of agonist dissociation. J General Physiol. 1997;109:757–766. doi: 10.1085/jgp.109.6.757. 10.1085/jgp.109.6.757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyllie DJA, Béhé P, Colquhoun D. Single-channel activations and concentration jumps: comparison of recombinant NR1/NR2A and NR1/NR2D NMDA receptors. J Physiol. 1998;510:1–18. doi: 10.1111/j.1469-7793.1998.001bz.x. 10.1111/j.1469-7793.1998.001bz.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Chen J, Auerbach A. Activation of recombinant mouse acetylcholine receptors by acetylcholine, carbamylcholine and tetramethylammonium. J Physiol. 1995;486:189–206. doi: 10.1113/jphysiol.1995.sp020802. [DOI] [PMC free article] [PubMed] [Google Scholar]