Abstract
Physiological studies of colour vision have not yet resolved the controversial issue of how chromatic opponency is constructed at a neuronal level. Two competing theories, the cone-selective hypothesis and the random-wiring hypothesis, are currently equivocal to the architecture of the primate retina. In central vision, both schemes are capable of producing colour opponency due to the fact that receptive field centres receive input from a single bipolar cell – the so called ‘private line arrangement’. However, in peripheral vision this single-cone input to the receptive field centre is lost, so that any random cone connectivity would result in a predictable reduction in the quality of colour vision. Behavioural studies thus far have indeed suggested a selective loss of chromatic sensitivity in peripheral vision. We investigated chromatic sensitivity as a function of eccentricity for the cardinal chromatic (L/M and S/(L + M)) and achromatic (L + M) pathways, adopting stimulus size as the critical variable. Results show that performance can be equated across the visual field simply by a change of scale (size). In other words, there exists no qualitative loss of chromatic sensitivity across the visual field. Critically, however, the quantitative nature of size dependency for each of the cardinal chromatic and achromatic mechanisms is very specific, reinforcing their independence in terms of anatomy and genetics. Our data provide clear evidence for a physiological model of primate colour vision that retains chromatic quality in peripheral vision, thus supporting the cone-selective hypothesis.
There exist several reasons for studying the capability of human peripheral vision. Not least is the consideration that valuable comparisons can be made with central visual performance in order to support or reject the premise that similar neural processing mechanisms operate throughout the visual field. These types of study reveal one of the great synergies between visual structure and function in that psychophysical estimates of visual performance can be directly related to cortical magnification (Daniel & Whitteridge, 1961; Cowey & Rolls, 1974; Rovamo et al. 1978). From time to time, physiological investigations of vision raise issues which its own state-of-the-art facilities are unable to resolve. In some cases, appropriately designed functional measurements have the potential to either comment upon or resolve such issues. One of these relates to the functional organization of chromatic mechanisms within the visual system, and we begin by providing an outline of the problem.
Human colour vision is mediated by the linear combination of signals from three different classes of cone photoreceptors sensitive to long (L-cone), middle (M-cone) and short (S-cone) wavelengths. Contemporary models of precortical human colour vision formulate the analysis of colour space as taking place within L/M and S/(L + M) cone-opponent or cardinal mechanisms formed by the convergence of these cone signals (Krauskopf et al. 1982). L/M opponency is mediated by the segregation of L- versus M-cone signals to the centre and the surround of a ganglion cell's receptive field, whereas in the S/(L + M) mechanism the S-cone signals are opposed to a combined L + M-cone signal. In addition there is a third luminance or achromatic mechanism in which ganglion cells receive synergistic L- and M-cone input (De Valois et al. 1966; Derrington et al. 1984; Dacey, 2000). The segregation of these opponent mechanisms is preserved in the lateral geniculate nucleus (LGN) and forms the basis of chromatic input to the primary visual cortex (Derrington et al. 1984; De Valois et al. 2000; Conway, 2001; Chatterjee & Callaway, 2003). Beyond the input to the primary visual cortex numerous psychophysical and behavioural observations indicate that colour processing may not strictly adhere to the cone-opponent model, and may be subjected to various transformations away from cardinal mechanisms (Krauskopf et al. 1986; Lennie et al. 1990; Johnson et al. 2001; Kiper et al. 2001).
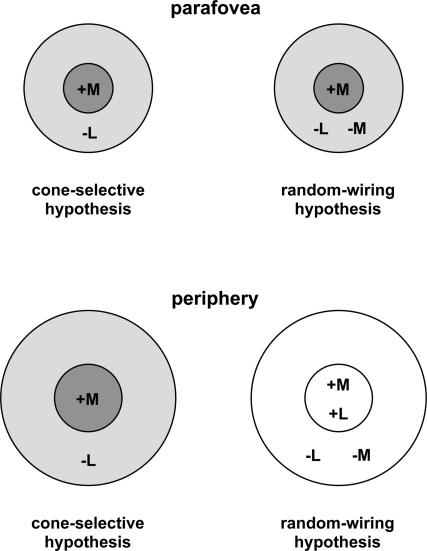
The exact nature of how chromatic opponency is constructed remains contentious. In the parafovea, opponency results automatically due to the fact that the midget ganglion cells' centre receives selective input from a single cone type (e.g. L-cone) via a bipolar cell, whilst the surround receives input either from a different cone type (e.g. M-cone) (selective circuit), or from mixed cone types (non-selective circuit). Both schemes result in colour opponency (Fig. 1, top) due to the fact that the receptive field centre receives its input from a single cone type via a single bipolar cell – the so called ‘private-line arrangement’ (Wiesel & Hubel, 1966; Wassle & Boycott, 1991; Calkins et al. 1994). However, in the peripheral retina, where ganglion cell receptive fields are much larger, both centre and surround gather input from a large number of bipolar cells and the single-cone input to the receptive field centre is lost (Fig. 1, bottom). Physiological studies have produced conflicting views regarding the architecture of retinal projections to ganglion cell receptive fields in the retinal periphery. Many studies, reinforced by computational analyses, have argued that the interneural connectivity within the retina is organized in a non-selective way, and both centre and surround receive mixed spectral inputs (‘random-wiring’ hypothesis) (Shapley & Perry, 1986; Lennie et al. 1991; Dacey, 1996; Mullen & Kingdom, 1996; Dacey et al. 2000; Dacey, 2000). Others suggest that selective connectivity within retinal circuits is maintained (‘cone-selective’ hypothesis) (Reid & Shapley, 1992; Lee et al. 1998; Martin et al. 2001; Reid & Shapley, 2002), although direct comparison between studies is complicated by the different ‘zones’ of eccentricity examined.
Figure 1. Models proposed for L/M chromatic opponency, based on centre–surround receptive field antagonism.
The resulting opponency is determined by the relative weights of the cone input to the centre versus the surround. In the parafovea a ‘private-line’ arrangement exists, where a single cone type (+M here) provides input to the centre of the ganglion cell's receptive field, whilst the surround gets input from another cone type (‘cone-selective’ hypothesis) or from mixed cone types (‘random-wiring’ hypothesis). Chromatic opponency is preserved in both cases. In the peripheral retina midget ganglion cells' receptive fields are much larger and receive convergent input from a number of photoreceptors. The cone-selective hypothesis postulates a selective circuitry where both centre and surround receive input from a single cone type; chromatic opponency is preserved. The ‘random-wiring’ hypothesis postulates mixed input both to the centre and surround of receptive field, resulting in a non-opponent peripheral cell.
Behavioural studies of human colour vision should have the capacity to shed light on this physiological controversy since, in the ‘random-wiring’ hypothesis, chromatic selectivity will be reduced due to a physiological loss of L/M cone opponency, thereby affecting the quality of colour vision in the periphery. Previous behavioural studies have indeed demonstrated a selective, or qualitative, loss of colour sensitivity in peripheral vision (Mullen, 1991; Mullen & Kingdom, 1996, 2002; Newton & Eskew, 2003), in support of the random-connectivity model. Moreover, Mullen & Kingdom (1996) successfully invoked a computational model based on random cone connectivity to account for their measured loss in behavioural colour sensitivity. However, studies of peripheral vision are enormously susceptible to variations based upon the choice of stimuli used. Specifically, stimulus size is the most critical factor, and must be accounted for as a result of ‘cortical magnification’– the fact that progressively less neural resource is assigned to more peripheral regions of visual space. Often, when stimulus size is suitably increased in peripheral vision, foveal and peripheral visual performance can be made equivalent (Daniel & Whitteridge, 1961; Cowey & Rolls, 1974; Rovamo et al. 1978; Virsu et al. 1987). The critical importance of stimulus size in colour vision has long been recognized (Gordon & Abramov, 1977; Noorlander et al. 1983; Abramov et al. 1991), with the ensuing claim that, provided stimuli are enlarged sufficiently, there is no loss of colour discrimination in peripheral vision. Given the physiological importance of the question of whether or not colour discrimination deteriorates in peripheral vision, we chose to investigate the issue using a methodology which makes no a priori assumptions about stimulus size. Whilst this method was adopted in several early studies, it was formalized by Watson (1987) and Johnston (1987) and given the term ‘spatial scaling’. Foveal and peripheral visual performance is measured across eccentricity for a range of stimuli differing only in magnification. If spatial scaling holds true, the resulting data can be simply shifted along the size axis to equate performance across eccentricity.
Our experiments adopt the above method of spatial scaling to examine changes in colour sensitivity as a function of eccentricity. If selective opponency is maintained across the retina, one might expect any differences in chromatic sensitivity across the retina to be merely quantitative. We therefore set out to establish whether differences in chromatic sensitivity, for each of the colour opponent and achromatic mechanisms, are qualitatively or quantitatively different across the visual field.
Methods
The subjects gave written, informed consent to the experiments, and all experiments were carried out in accordance with the Declaration of Helsinki.
Stimuli
Stimuli consisted of isoluminant chromatic or achromatic, horizontally orientated Gabor patches (Fig. 2A), presented within a square wave temporal window of 380 ms duration. Three types of stimulus were used, each one designed to activate a single post-receptoral mechanism, namely either the L/M, the S/(L + M) or the L + M, all defined in the MBDKL colour space (Fig. 2B) (Krauskopf et al. 1982; Derrington et al. 1984). All stimuli were modulated around illuminant C (CIE (0.31, 0.316)) at a mean luminance of 12.5 cd m−2. The achromatic stimuli were defined in terms of their Michelson contrast. Chromatic contrast was defined in a similar manner by considering the proportion of stimulus modulation between the maximum limits defined by the following CIE co-ordinates: 0 deg (0.382, 0.283) and 180 deg (0.238, 0.35) for the L/M stimuli; 90 deg (0.272, 0.228) and 270 deg (0.35, 0.409) for the S/(L + M) stimuli (Fig. 2). It should be noted that the chromatic contrast sensitivities which we present are critically dependent upon this choice of limits. It is therefore inappropriate to use this metric to compare sensitivities between the two chromatic and the achromatic systems, and we duly avoid such a comparison when discussing the results.
Figure 2. Stimuli.
Examples of some of the stimuli used for the experiment (A) and their modulation around the MBDKL colour space (B). All stimuli are magnified versions of each other.
The standard deviation (σ) of the Gabor stimulus envelope was systematically varied in combination with its spatial frequency, such that there were always 0.378 cycles per σ. In other words, all stimuli were magnified versions of each other – conforming to a method of spatial scaling (Watson, 1987). A consequence of this method is that low spatial frequency targets occupy relatively large regions of visual space. The definition of stimulus eccentricity for all stimuli was in relation to the centre of the Gabor patch. Justification for this is that, close to threshold contrast, the parts of the Gaussian-windowed stimuli away from the stimulus centre fall below threshold and the perceptual spatial extent of the patch converges to the peak (Fredericksen et al. 1997). Viewing was monocular using the dominant eye and, for foveal presentations, fixation was central and was aided by a small black fixation cross. Peripheral presentations were always in the nasal visual field so as to avoid the blind spot, and again a small black fixation mark was provided in order to maintain appropriate fixation.
For the chromatic stimuli, isoluminance was determined for each subject individually prior to the experimental procedure, using a minimum flicker paradigm. This not only ensured that any intersubject variability in perceptual isoluminance was accounted for, but that any variation with stimulus condition (specifically stimulus size and eccentricity) was not a confounding factor in the results. It emerged that there was no systematic variation in the isoluminance estimates across any stimulus parameter, with estimates corresponding closely to photometric isoluminance.
Stimuli were presented on a SONY 21-inch FD Trinitron CRT monitor with a frame rate of 120 Hz, and were generated using a video controller (Research Systems VSG2/1) and a Dell Intel Pentium III and Windows 2000 PC.
Procedure
Stimuli were presented using a temporal 2AFC procedure, and the subjects were required to indicate in which of the two intervals the test stimulus appeared. Presentation of each interval was announced with an auditory signal. A method of constant stimuli was adopted – any one of seven different contrast levels could be presented during a trial. The step size between levels was 2 dB. The contrast range was centred so as to provide an adequate coverage of the psychometric function for detection. A total of 20 trials were presented at each of the seven contrast levels. The resulting psychometric function was analysed by logistic regression to provide an estimate of the contrast threshold (75% correct response level). Contrast sensitivity was defined as the reciprocal of contrast threshold. Two of the authors acted as observers (D.W. and C.V.). Each had corrected-to-normal visual acuity.
Results
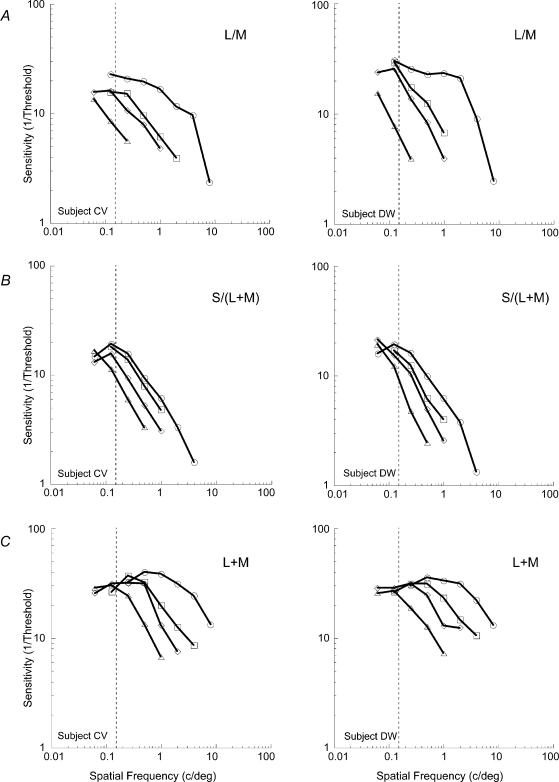
Figure 3 shows contrast sensitivity as a function of spatial frequency for L/M, S/(L + M) and L + M modulation. The foveal data reflect the traditional form of the contrast sensitivity function – sensitivity declining with increasing spatial frequency. Extrapolation of the data to the abscissa reveals the highest resolvable spatial frequencies for the three stimuli which are quantitatively in agreement with previous studies (Mullen, 1985; Anderson et al. 1991; Mullen & Kingdom, 1996, 2002). For the achromatic stimuli there is some evidence of a bandpass shape, with sensitivity declining again at the lowest spatial frequencies. The chromatic sensitivity functions (certainly L/M) are low-pass in shape. In the periphery, lower spatial frequency stimuli (or larger stimuli) are required to obtain sensitivity values equivalent to those at the fovea. This is reflected in the sequential leftwards offset of the functions as eccentricity increases. The eccentricity dependence of the data can be accounted for by applying scaling factors to the peripheral curves in order to superimpose them upon the foveal function (Watson, 1987). If linear spatial scaling holds true, the scaling factors (SF) can be calculated by:
| (1) |
where E is the eccentricity and E2 is a parameter representing the eccentricity at which the stimulus must double in size to maintain performance equal to that at the fovea.
Figure 3. Sensitivity as a function of spatial frequency across eccentricity for the three post-receptoral mechanisms.
Results show the measured chromatic (L/M (A) and S/(L + M) (B)) and achromatic (L + M (C)) visual sensitivity for two subjects (C.V. and D.W.) at 0, 5, 10 and 20 deg eccentricity. Note that progressively lower spatial frequency stimuli are required for the eccentric positions in order to reach the same level of performance as that at the fovea. ○: 0 deg; □: 5 deg; ⋄: 10 deg; ▵: 20 deg. Average standard error approximated to the size of the data points.
An estimated value of E2 was used to shift the peripheral curves along the size (spatial frequency) axis towards the foveal function. A single function was then used to fit the entire data set. The function to describe the scaled colour or contrast sensitivity of the three post-receptoral mechanisms was a version of a contrast sensitivity function used by Rovamo et al. (1993), namely:
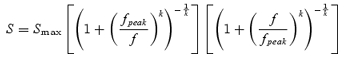 |
(2) |
where Smax represents peak contrast sensitivity (height on the y-axis), fpeak represents the scaled spatial frequency at which the function reaches its maximum and k is a constant which determines the sharpness of the curve at its knee point. The above eqn (2) effectively describes the contrast sensitivity function for luminance-modulated achromatic gratings, which has a band-pass shape. For chromatic isoluminant gratings the spatial contrast sensitivity function is low-pass in shape: sensitivity is constant at low spatial frequencies but decreases at medium and high frequencies (Mullen, 1985; Kelly, 1989). The product in the first bracket of eqn (2) governs the sharpness of the decrease in contrast sensitivity at low spatial frequencies. Since colour sensitivity function is constant in that region, the product of the bracket was set to unity, transforming eqn (2) into:
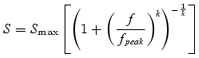 |
(3) |
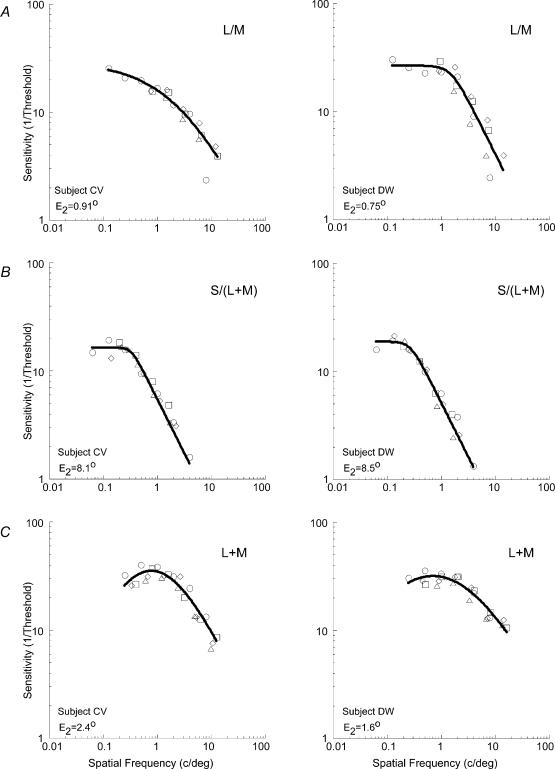
Equation (3) was used to describe all our L/M and S/(L + M) data, while eqn (2) was fitted to all L + M data. Multiple iterations of the application of eqn (1) to each of the three data sets resulted in an E2 value which minimized the sum-of-squares deviation around the curve fitted to the combined data. The resulting scaled data are shown in Fig. 4. The introduction of an appropriate E2 value (equating simply to a horizontal shift of the original data sets) serves to collapse the data across all eccentricities. However, very different scaling factors were found for each of the three mechanisms, each one depending upon the type of modulation. For the L/M mechanism the E2 values were 0.91 deg for subject C.V., and 0.75 deg for subject D.W. For the S/(L + M) mechanism, E2 values were 8.1 deg and 8.5 deg, respectively. The achromatic pathway was found to have an E2 of 2.4 deg and 1.6 deg (C.V. and D.W.).
Figure 4. The data of Fig. 3, scaled to account for eccentricity.
Scaled data of visual sensitivity for the two observers are shown. For each observer, the graphs from Fig. 3A–C were scaled by an estimated E2 value, and the residual variance was calculated with eqn (3) (for A and B) and eqn (2) (for C). The three parameters of the curve fit were allowed to float in order to minimize the residual sum-of-squares deviation of the combined eccentricity data around the curve fit. With an iterative procedure an E2 value was found to minimize the overall residual variance for each observer: C.V. = 97.41%, D.W. = 94.34% (A); CV = 97.19%, DW = 98.31% (B); CV = 92.81%, DW = 92.75% (C). ○: 0 deg; □□: 5 deg; ⋄: 10 deg; ▵: 20 deg. Very different scaling factors were found for the three post-receptoral mechanisms, each depending upon the axis of colour or contrast.
Discussion
For many years, the loss of colour perception in peripheral vision was interpreted as evidence for functional, qualitative differences between central and peripheral visual processing (Moreland & Cruz, 1959). Whilst more recent investigators recognized the critical importance of stimulus size in equating colour perception across the visual field (Gordon & Abramov, 1977; Noorlander et al. 1983), the view of foveal specialization for chromatic sensitivity persists (Mullen, 1985; Mullen & Kingdom, 1996, 2002). As outlined in the introduction, the issue is not merely of empirical interest, but has a critical bearing upon the question of random or selective physiological wiring in chromatic neural pathways. Our view, supported by the data of Figs 3 and 4, is that there exist no sensitivity differences between foveal and peripheral chromatic mechanisms, but that observed sensitivity can be accounted for entirely on the basis of spatial scale (size). Importantly, the spatial scale of the visual system appears to be markedly dependent upon the specific type of chromatic or achromatic mechanism, with the rate of change of scale varying most rapidly with eccentricity for the L/M followed by L + M and finally S/(L + M). The differences represent an order of magnitude in variation, and are therefore not insignificant.
It is quite understandable how psychophysical contrast sensitivity measures can be construed as reflecting a decline in sensitivity with increasing eccentricity. Figure 3 shows a vertical dashed line at a spatial frequency of 0.15 c deg−1– a spatial frequency which could reasonably be considered low enough to provide the periphery with a sufficiently large stimulus to overcome its relatively coarse spatial scale. Examination of sensitivity loss with eccentricity at this spatial frequency predicts a sharp decline for the L/M mechanism followed by a modest decline for S/(L + M) and no decline at all for L + M. This is exactly what previous studies have found (Mullen & Kingdom, 2002, who examined a spatial frequency of 0.3 c deg−1). Clearly, however, these sensitivity observations represent an artefact of the spatial frequency of choice, and the fact that the rate of change of scale with eccentricity varies so markedly between the different mechanisms. For the S/(L + M) mechanism, in particular, even a spatial frequency as low as 0.15 c deg−1 is far from low enough to reveal maximum mechanism sensitivity at higher eccentricities. Rather than concluding that this represents a loss of mechanism sensitivity, our analysis (Fig. 4) shows that spatial scale alone can account for observed performance. In other words, chromatic sensitivity is identical across much of the visual field provided stimulus size is accounted for.
One criticism of the present study is that our data represent only the central 20 deg of the nasal visual field. In our defence, we could point out that the central 20 deg accounts for approximately 70% of the retinal ganglion cell population (Drasdo, 1977; Wassle et al. 1989). However, the absence of data at larger eccentricities is more pragmatic than this. For the L/M stimuli, in particular, more peripheral stimuli require such enormous amounts of size scaling that the physical considerations of display size and observer distance from the display become limiting factors. This difficulty means that it is impossible to present unequivocal evidence that size scaling (horizontal shift) alone accounts for peripheral L/M chromatic sensitivity. Ideally, one would require data in which all peripheral chromatic sensitivity functions had reached a plateau at the same sensitivity level, and we have to acknowledge the absence of asymptotic performance at higher eccentricities for the L/M data. A loss in peripheral chromatic sensitivity (vertical shift) would indeed contribute to the need for a larger horizontal shift of size scale in order to account for the data. Nonetheless, the majority of simple tasks can be equated in absolute sensitivity in peripheral vision through size scaling alone (Rovamo et al. 1978; Levi et al. 1984; Virsu et al. 1987; Watson, 1987), albeit with a diverse variation of scale change between tasks (Whitaker et al. 1992). Our simple size scaling methodology (Fig. 4), and the range of scaling factors which result, is therefore consonant with a body of existing evidence.
The very disparate variation in spatial scale with eccentricity for L/M and S/(L + M) and L + M mechanisms offers behavioural support to the concept that these pathways have distinct neurophysiological origins. Anatomical and physiological studies (Dacey & Lee, 1994; Dacey, 1996; Calkins et al. 1998) provide evidence that the S/(L + M) opponent response arises from a separate pathway originating from a small bistratified ganglion cell type. By contrast, L/M opponency is linked to the ‘midget’ P cells of the retina (Shapley & Perry, 1986; Dacey, 1993, 1999). In turn, the present considerations support the view that the markedly different (over 100-fold) gradients found in previous psychophysical tasks might, at least in part, be due to differences in eccentricity scaling within parallel pathways (Whitaker et al. 1992). This is complementary to the hierarchical viewpoint that variations in magnification factors in different cortical areas contribute to such behaviour. The reason for such diverse mapping of functionality across the visual field seems clear – it is critical in terms of survival, for example, that we possess motion detection mechanisms for stimuli of many sizes in peripheral vision. Hence the observation that the spatial scale for motion changes very slowly across eccentricity (Levi et al. 1984; Whitaker et al. 1992). In contrast, static tasks which require fine red–green colour vision, such as the detection of a distant red fruit against green foliage can safely be accomplished using a strategy of foveation through visual search. One can therefore afford a relatively rapid change in scale of the L/M mechanism with increasing eccentricity, thereby saving neural resource. However, the behavioural reason as to why we should possess a S/(L + M) mechanism whose scale changes by an order of magnitude less rapidly than L/M does not appear immediately obvious.
The differences in scale as a function of eccentricity probably reflect the very different origins of the L/M and S/(L + M) colour systems. It has been proposed (Mollon, 1982) that the opponent system which receives S-cone input may be the current manifestation of an evolutionary older colour pathway that was shared by most (dichromatic) mammals prior to the more recent acquisition of a second system based upon the differentiation of cones into long- and middle-wavelength sensitive receptors. These different evolutionary origins are echoed in the very different: genetic coding of S-cone versus L- and M-cone photopigments (Nathans et al. 1986); physiological processing in separable anatomical pathways (Dacey & Lee, 1994); retinal distributions of cones. Whilst the S-cone density is variable within the central 7 deg, it stabilizes and remains relatively constant beyond this point, in comparison to the L- and M-cone densities, which steadily decrease (Williams et al. 1981; Curcio et al. 1991).
Evidence so far suggests that cone-selective connections for the S/(L + M) pathway are an essential requirement for opponency to be present (Wiesel & Hubel, 1966; Derrington et al. 1984; Dacey, 2000; Mullen & Kingdom, 2002). However, for the L/M pathway the picture is less clear. Midget ganglion cells form the basis of the L/M opponency and no argument seems to be needed to account for the colour-opponent nature of those corresponding to the parafovea, since their receptive field centres are fed by a single cone (Paulus & Krogerpaulus, 1983; Lennie et al. 1991; De Valois & De Valois, 1993; Mullen & Kingdom, 1996). Some studies suggest that peripheral ganglion cells appear to have reduced or no chromatic opponency (Dacey & Petersen, 1992; Dacey, 1993), and have argued that they would therefore demonstrate a reduced L/M chromatic sensitivity (Lennie et al. 1991; Dacey, 1993). Such characteristics are attributed to random cone projections to both the centre and surround of their receptive fields, which receive multiple cone inputs (Paulus & Krogerpaulus, 1983; Lennie et al. 1991; De Valois & De Valois, 1993; Mullen & Kingdom, 1996). According to this ‘random wiring’ model, chromatic sensitivity would be reduced in the periphery. Our results (at least to an eccentricity of 20 deg) are incompatible with the concept of random wiring as they demonstrate the existence of equivalent chromatic sensitivity in the peripheral visual field once spatial scale has been accounted for. The cone-type-specific model predicts that peripheral chromatic sensitivity should match that at the fovea, since selective cone projections to the centre and surround would preserve chromatic opponency (Reid & Shapley, 1992; Martin et al. 2001; Reid & Shapley, 2002). Our results are therefore consistent with previous physiological data (Martin et al. 2001), supporting the ‘cone-selective’ model as the underlying mechanism responsible for chromatic opponency across the retina.
Another criticism might be that the very large E2 values for the S/(L + M) stimuli simply reflect the limitations upon foveal visual performance imposed by optical factors (chromatic aberration) and physiological factors underlying the so-called ‘foveal tritanopia’. We would certainly not deny the relationship between the lack of high-frequency foveal S/(L + M) mechanisms and the optical limitations of chromatic aberration – there is simply no reason to possess neural mechanisms for which retinal stimuli cannot naturally be presented due to the optics of the eye. However, the majority of our S/(L + M) foveal data (Fig. 3B) represent low spatial frequencies which are likely to avoid such problems. Furthermore, the data show no evidence of a sudden drop in foveal performance relative to eccentric data – this type of behaviour would not be compatible with the linear description provided by eqn (1), an equation which provides a good fit to the entire data set (Fig. 4B).
We have shown that achromatic and chromatic contrast sensitivity can be equated across the visual field simply by accounting for the change in scale (size) of the underlying mechanisms. There is no need to invoke a loss of chromatic sensitivity with increasing eccentricity. This suggests that eccentric ganglion cell receptive fields which, for the L/M pathway, draw upon multiple cone inputs to their centre, do so in a cone-specific manner. There is an order of magnitude difference between the eccentricity-related change of spatial scale for the two chromatic mechanisms.
Acknowledgments
P.V.M. is supported by the Wellcome Trust. We are also grateful to the Visual Research Trust and the Colour Group (Great Britain) for financial support.
References
- Abramov I, Gordon J, Chan H. Color appearance in the peripheral retina: effects of stimulus size. J Opt Soc Am A. 1991;8:404–414. doi: 10.1364/josaa.8.000404. [DOI] [PubMed] [Google Scholar]
- Anderson SJ, Mullen KT, Hess RF. Human peripheral spatial resolution for achromatic and chromatic stimuli – Limits imposed by optical and retinal factors. J Physiol. 1991;442:47–64. doi: 10.1113/jphysiol.1991.sp018781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calkins DJ, Schein SJ, Tsukamoto Y, Sterling P. M-cone and L-cone in macaque fovea connect to midget ganglion cells by different numbers of excitatory synapses. Nature. 1994;371:70–72. doi: 10.1038/371070a0. [DOI] [PubMed] [Google Scholar]
- Calkins DJ, Tsukamoto Y, Sterling P. Microcircuitry and mosaic of a blue-yellow ganglion cell in the primate retina. J Neurosci. 1998;18:3373–3385. doi: 10.1523/JNEUROSCI.18-09-03373.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee S, Callaway EM. Parallel colour-opponent pathways to primary visual cortex. Nature. 2003;426:668–671. doi: 10.1038/nature02167. [DOI] [PubMed] [Google Scholar]
- Conway BR. Spatial structure of cone inputs to color cells in alert macaque primary visual cortex (V-1) J Neurosci. 2001;21:2768–2783. doi: 10.1523/JNEUROSCI.21-08-02768.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowey A, Rolls ET. Human cortical magnification factor and its relation to visual acuity. Exp Brain Res. 1974;21:447–454. doi: 10.1007/BF00237163. [DOI] [PubMed] [Google Scholar]
- Curcio CA, Allen KA, Sloan KR, Lerea CL, Hurley JB, Klock IB, Milam AH. Distribution and morphology of human cone photoreceptors stained with anti-blue opsin. J Comp Neurol. 1991;312:610–624. doi: 10.1002/cne.903120411. [DOI] [PubMed] [Google Scholar]
- Dacey DM. The mosaic of midget ganglion cells in the human retina. J Neurosci. 1993;13:5334–5355. doi: 10.1523/JNEUROSCI.13-12-05334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dacey DM. Circuitry for color coding in the primate retina. Proc Natl Acad Sci U S A. 1996;93:582–588. doi: 10.1073/pnas.93.2.582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dacey DM. Primate retina: cell types, circuits and color opponency. Prog Retin Eye Res. 1999;18:737–763. doi: 10.1016/s1350-9462(98)00013-5. [DOI] [PubMed] [Google Scholar]
- Dacey DM. Parallel pathways for spectral coding in primate retina. Annu Rev Neurosci. 2000;23:743–775. doi: 10.1146/annurev.neuro.23.1.743. [DOI] [PubMed] [Google Scholar]
- Dacey DM, Lee BB. The blue-on opponent pathway in primate retina originates from a distinct bistratified ganglion cell type. Nature. 1994;367:731–735. doi: 10.1038/367731a0. [DOI] [PubMed] [Google Scholar]
- Dacey D, Packer OS, Diller L, Brainard D, Peterson B, Lee B. Center surround receptive field structure of cone bipolar cells in primate retina. Vision Res. 2000;40:1801–1811. doi: 10.1016/s0042-6989(00)00039-0. [DOI] [PubMed] [Google Scholar]
- Dacey DM, Petersen MR. Dendritic field size and morphology of midget and parasol ganglion cells of the human retina. Proc Natl Acad Sci U S A. 1992;89:9666–9670. doi: 10.1073/pnas.89.20.9666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel PM, Whitteridge D. The representation of the visual field on the cerebral cortex in monkeys. J Physiol. 1961;159:203–221. doi: 10.1113/jphysiol.1961.sp006803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Valois RL, Abramov I, Jacobs GH. Analysis of response patterns of LGN cells. J Opt Soc Am. 1966;56:966–977. doi: 10.1364/josa.56.000966. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Cottaris NP, Elfar SD, Mahon LE, Wilson JA. Some transformations of color information from lateral geniculate nucleus to striate cortex. Proc Natl Acad Sci U S A. 2000;97:4997–5002. doi: 10.1073/pnas.97.9.4997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Valois RL, De Valois KK. A multi-stage color model. Vision Res. 1993;33:1053–1065. doi: 10.1016/0042-6989(93)90240-w. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Krauskopf J, Lennie P. Chromatic mechanisms in lateral geniculate nucleus of macaque. J Physiol. 1984;357:241–265. doi: 10.1113/jphysiol.1984.sp015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drasdo N. The neural representation of visual space. Nature. 1977;266:554–556. doi: 10.1038/266554a0. [DOI] [PubMed] [Google Scholar]
- Fredericksen RE, Bex PJ, Verstraten FA. How big is a Gabor patch, and why should we care? J Opt Soc Am a Opt Image Sci Vis. 1997;14:1–12. doi: 10.1364/josaa.14.000001. [DOI] [PubMed] [Google Scholar]
- Gordon J, Abramov I. Color vision in the peripheral retina. II. Hue and saturation. J Opt Soc Am. 1977;67:202–207. doi: 10.1364/josa.67.000202. [DOI] [PubMed] [Google Scholar]
- Johnson EN, Hawken MJ, Shapley R. The spatial transformation of color in the primary visual cortex of the macaque monkey. Nature Neurosci. 2001;4:409–416. doi: 10.1038/86061. [DOI] [PubMed] [Google Scholar]
- Johnston A. Spatial scaling of central and peripheral contrast-sensitivity functions. J Opt Soc Am A. 1987;4:1583–1593. doi: 10.1364/josaa.4.001583. [DOI] [PubMed] [Google Scholar]
- Kelly DH. Opponent-color receptive-field profiles determined from large area psychophysical measurements. J Opt Soc Am A. 1989;6:1784–1793. doi: 10.1364/josaa.6.001784. [DOI] [PubMed] [Google Scholar]
- Kiper DC, Levitt JB, Gegenfurtner K. Chromatic signals in extrastriate areas V2 and V3. In: Gegenfurtner K, Sharpe LT, editors. Color Vision: from Genes to Perception. Cambridge: Cambridge University Press; 2001. pp. 249–268. [Google Scholar]
- Krauskopf J, Williams DR, Heeley DW. Cardinal directions of color space. Vision Res. 1982;22:1123–1131. doi: 10.1016/0042-6989(82)90077-3. [DOI] [PubMed] [Google Scholar]
- Krauskopf J, Williams DR, Mandler MB, Brown AM. Higher order color mechanisms. Vision Res. 1986;26:23–32. doi: 10.1016/0042-6989(86)90068-4. [DOI] [PubMed] [Google Scholar]
- Lee BB, Kremers J, Yeh T. Receptive fields of primate retinal ganglion cells studied with a novel technique. Vis Neurosci. 1998;15:161–175. doi: 10.1017/s095252389815112x. [DOI] [PubMed] [Google Scholar]
- Lennie P, Haake PW, Williams DR. The design of chromatically opponent receptive fields. In: Landy MS, Movshon JA, editors. Computational Models of Visual Processing. Cambridge, MA, USA: MIT Press; 1991. pp. 71–82. [Google Scholar]
- Lennie P, Krauskopf J, Sclar G. Chromatic mechanisms in striate cortex of macaque. J Neurosci. 1990;10:649–669. doi: 10.1523/JNEUROSCI.10-02-00649.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi DM, Klein SA, Aitsebaomo P. Detection and discrimination of the direction of motion in central and peripheral vision of normal and amblyopic observers. Vision Res. 1984;24:789–800. doi: 10.1016/0042-6989(84)90150-0. [DOI] [PubMed] [Google Scholar]
- Martin PR, Lee BB, White AJ, Solomon SG, Ruttiger L. Chromatic sensitivity of ganglion cells in the peripheral primate retina. Nature. 2001;410:933–936. doi: 10.1038/35073587. [DOI] [PubMed] [Google Scholar]
- Mollon JD. Color vision. Annu Rev Psychol. 1982;33:41–85. doi: 10.1146/annurev.ps.33.020182.000353. [DOI] [PubMed] [Google Scholar]
- Moreland JD, Cruz A. Colour perception with the peripheral retina. Optica Acta. 1959;6:117–151. [Google Scholar]
- Mullen KT. The contrast sensitivity of human colour vision to red-green and blue-yellow chromatic gratings. J Physiol. 1985;359:381–400. doi: 10.1113/jphysiol.1985.sp015591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullen KT. Color-vision as a post-receptoral specialization of the central visual field. Vision Res. 1991;31:119–130. doi: 10.1016/0042-6989(91)90079-k. [DOI] [PubMed] [Google Scholar]
- Mullen KT, Kingdom FAA. Losses in peripheral colour sensitivity predicted from “hit and miss” post-receptoral cone connections. Vision Res. 1996;36:1995–2000. doi: 10.1016/0042-6989(95)00261-8. [DOI] [PubMed] [Google Scholar]
- Mullen KT, Kingdom FAA. Differential distributions of red-green and blue-yellow cone opponency across the visual field. Vis Neurosci. 2002;19:109–118. doi: 10.1017/s0952523802191103. [DOI] [PubMed] [Google Scholar]
- Nathans J, Thomas D, Hogness DS. Molecular genetics of human color vision: the genes encoding blue, green, and red pigments. Science. 1986;232:193–202. doi: 10.1126/science.2937147. [DOI] [PubMed] [Google Scholar]
- Newton JR, Eskew RT., Jr Chromatic detection and discrimination in the periphery: a post-receptoral loss of color sensitivity. Vis Neurosci. 2003;20:511–521. doi: 10.1017/s0952523803205058. [DOI] [PubMed] [Google Scholar]
- Noorlander C, Koenderink JJ, den Ouden RJ, Edens BW. Sensitivity to spatiotemporal colour contrast in the peripheral visual field. Vision Res. 1983;23:1–11. doi: 10.1016/0042-6989(83)90035-4. [DOI] [PubMed] [Google Scholar]
- Paulus W, Krogerpaulus A. A new concept of retinal color coding. Vision Res. 1983;23:529–540. doi: 10.1016/0042-6989(83)90128-1. [DOI] [PubMed] [Google Scholar]
- Reid RC, Shapley RM. Spatial structure of cone inputs to receptive fields in primate lateral geniculate nucleus. Nature. 1992;356:716–718. doi: 10.1038/356716a0. [DOI] [PubMed] [Google Scholar]
- Reid RC, Shapley RM. Space and time maps of cone photoreceptor signals in macaque lateral geniculate nucleus. J Neurosci. 2002;22:6158–6175. doi: 10.1523/JNEUROSCI.22-14-06158.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rovamo J, Luntinen O, Nasanen R. Modeling the dependence of contrast sensitivity on grating area and spatial frequency. Vision Res. 1993;33:2773–2788. doi: 10.1016/0042-6989(93)90235-o. [DOI] [PubMed] [Google Scholar]
- Rovamo J, Virsu V, Nasanen R. Cortical magnification factor predicts the photopic contrast sensitivity of peripheral vision. Nature. 1978;271:54–56. doi: 10.1038/271054a0. [DOI] [PubMed] [Google Scholar]
- Shapley R, Perry VH. Cat and monkey retinal ganglion-cells and their visual functional roles. Trends Neurosci. 1986;9:229–235. [Google Scholar]
- Virsu V, Nasanen R, Osmoviita K. Cortical magnification and peripheral vision. J Opt Soc Am A. 1987;4:1568–1578. doi: 10.1364/josaa.4.001568. [DOI] [PubMed] [Google Scholar]
- Wassle H, Boycott BB. Functional architecture of the mammalian retina. Physiol Rev. 1991;71:447–480. doi: 10.1152/physrev.1991.71.2.447. [DOI] [PubMed] [Google Scholar]
- Wassle H, Grunert U, Rohrenbeck J, Boycott BB. Cortical magnification factor and the ganglion cell density of the primate retina. Nature. 1989;341:643–646. doi: 10.1038/341643a0. [DOI] [PubMed] [Google Scholar]
- Watson AB. Estimation of local spatial scale. J Opt Soc Am A. 1987;4:1579–1582. doi: 10.1364/josaa.4.001579. [DOI] [PubMed] [Google Scholar]
- Whitaker D, Makela P, Rovamo J, Latham K. The influence of eccentricity on position and movement acuities as revealed by spatial scaling. Vision Res. 1992;32:1913–1930. doi: 10.1016/0042-6989(92)90051-j. [DOI] [PubMed] [Google Scholar]
- Wiesel TN, Hubel DH. Spatial and chromatic interactions in the lateral geniculate body of the rhesus monkey. J Neurophysiol. 1966;29:1115–1156. doi: 10.1152/jn.1966.29.6.1115. [DOI] [PubMed] [Google Scholar]
- Williams DR, MacLeod DI, Hayhoe MM. Foveal tritanopia. Vision Res. 1981;21:1341–1356. doi: 10.1016/0042-6989(81)90241-8. [DOI] [PubMed] [Google Scholar]