Spectrally opponent inputs to the human luminance pathway: slow +M and −L cone inputs revealed by intense long-wavelength adaptation

Abstract

The nature of the inputs to achromatic luminance flicker perception was explored psychophysically by measuring middle- (M-) and long-wavelength-sensitive (L-) cone modulation sensitivities, M- and L-cone phase delays, and spectral sensitivities as a function of temporal frequency. Under intense long-wavelength adaptation, the existence of multiple luminance inputs was revealed by substantial frequency-dependent changes in all three types of measure. Fast (f) and slow (s) M-cone input signals of the same polarity (+sM and +fM) sum at low frequencies, but then destructively interfere near 16 Hz because of the delay between them. In contrast, fast and slow L-cone input signals of opposite polarity (−sL and +fL) cancel at low frequencies, but then constructively interfere near 16 Hz. Although these slow, spectrally opponent luminance inputs (+sM and −sL) would usually be characterized as chromatic, and the fast, non-opponent inputs (+fM and +fL) as achromatic, both contribute to flicker photometric nulls without producing visible colour variation. Although its output produces an achromatic percept, the luminance channel has slow, spectrally opponent inputs in addition to the expected non-opponent ones. Consequently, it is not possible in general to silence this channel with pairs of ‘equiluminant’ alternating stimuli, since stimuli equated for the non-opponent luminance mechanism (+fM and +fL) may still generate spectrally opponent signals (+sM and +sL).

In conventional models of the early visual system, signals from the three types of cones (short- (S), middle- (M) and long- (L) wavelength-sensitive) feed into the luminance channel (L+M) or into the more sluggish chromatic channels (L–M) or (S−(L+M)) (e.g. Schrödinger, 1925; Luther, 1927; Walls, 1955; De Lange, 1958; Guth et al. 1968; Smith & Pokorny, 1975; Boynton, 1979; Eisner & MacLeod, 1980). Discrepancies, such as the observation of a small, inverted S-cone input to luminance have been reported (Stockman et al. 1987, 1991a; Lee & Stromeyer, 1989), but have been typically ignored in order to preserve the utility of the conventional model of luminance (e.g. Lennie et al. 1993).

Failures of the conventional model of luminance

The concept of luminance depends on the context in which it is used. Photometrically, it is defined by the luminous efficiency function, V(λ), which is the effectiveness of lights of different wavelengths in specific photometric matching tasks. Those perceptual tasks now most typically include heterochromatic flicker photometry (HFP) or a version of side-by-side matching, in which the relative intensities of the two half-fields are set so that the border between them appears ‘minimally distinct’ (MDB) (e.g. Ives, 1912; Wagner & Boynton, 1972). This definition of luminance is somewhat narrow, however, since the V(λ) function is strictly appropriate only to the measurement task and to the experimental conditions under which it was measured (e.g. De Vries, 1948; Eisner & MacLeod, 1981; Stockman et al. 1993b).

Mechanistically, the term luminance is applied to the hypothetical visual process in the human visual system that is assumed to signal ‘luminance’, which may have a V(λ)-like spectral sensitivity under limited conditions (see below). A defining property of the luminance channel is that it responds univariantly to lights of different wavelength, and is therefore colour-blind.

In this paper, we describe two phenomena that are not predicted by the conventional model of luminance, and which therefore illustrate the need for a revised model.

(1) Phase delays required for flicker nulls

When detected solely by the luminance channel, two sinusoidally alternating lights that are ‘luminance-equated’ should appear perfectly uniform and non-flickering whatever their chromaticities. In order to eliminate completely the perception of flicker, however, subjects often have to adjust the two lights away from opposite phase. Early estimates of these phase adjustments were relatively small, ranging from less than 9 deg at 6 Hz or 4 deg at 14 Hz (De Lange, 1958), to less than 14 deg between 20 and 55 Hz (Cushman & Levinson, 1983). Phase adjustments as large as 30 deg at frequencies below 9 Hz were found by Walraven & Leebeek (1964), but their data may have been contaminated by rods (see also von Grünau, 1977). More recently, much larger phase differences have been found. Lindsey et al. (1986) and Swanson et al. (1987) reported phase delays between red and green lights of nearly 180 deg at 2 Hz, falling rapidly with increasing frequency to 0 deg by about 13 Hz. The data of Lindsey et al. and Swanson et al. provide the first clear evidence for slow, inverted inputs to the luminance channel that we also find, but they did not initially interpret their results as such. See the Discussion for a more comprehensive review of other work in this area.

The changes in phase delay with frequency that we find under intense long-wavelength adaptation are substantial even at frequencies as high as 25 Hz (see below). They are much too large to be consistent with the conventional model of luminance with two additive L- and M-cone inputs with similar temporal responses.

(2) Frequency-dependent changes in flicker spectral sensitivities

Modulation sensitivity for flickering monochromatic lights varies with wavelength in a way that reflects the spectral sensitivity of the combination of cone signals supporting detection. With the S-cones suppressed by a shortwave auxiliary field, and at those moderate to high temporal frequencies at which the luminance pathway is assumed to predominate, flicker spectral sensitivity is typically characterized as some linear combination of the L- and M-cone spectral sensitivities (e.g. Eisner, 1982; Stockman et al. 1993b). The conventional model of the early visual system predicts that this combination should not strongly depend on flicker frequency (but see Marks & Bornstein, 1973). Yet, we show that flicker spectral sensitivity functions measured on a 658 nm field change dramatically with flicker frequency: as the frequency increases, the functions become shallower, tending away from an M-cone spectral sensitivity function towards that of an L-cone (see Figs 2 and 3). Although an M-cone spectral sensitivity is expected due to selective chromatic adaptation by the background, an L-cone one is not.

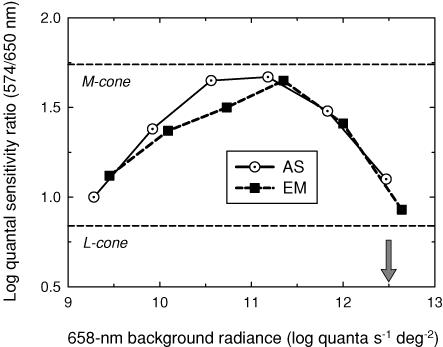
Figure 2. Quantal sensitivity ratios.

Sensitivity ratios for detecting 574 and 650 nm 16 Hz flicker measured as a function of 658 nm background radiance for AS (dotted circles) and EM (filled squares) compared with the 574/650 nm ratios predicted for M-cone (upper dashed line) and L-cone (lower dashed line) detection by Stockman & Sharpe (2000). The arrow indicates the radiance used in the experiments illustrated in Fig. 3.

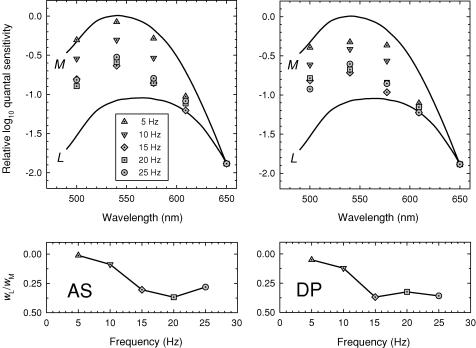
Figure 3. Spectral sensitivities and cone weights.

Upper panels: flicker spectral sensitivities for 5 Hz (triangles), 10 Hz (inverted triangles), 15 Hz (diamonds), 20 Hz (squares) and 25 Hz (circles) flicker compared with the Stockman & Sharpe (2000) M-cone (upper continuous line) and L-cone (lower continuous line) fundamentals. Backgrounds: 12.55 log₁₀ quanta s⁻¹ deg⁻², 658 nm, and 10.32 log₁₀ quanta s⁻¹ deg⁻², 410 nm. Lower panels: ratios of L- and M-cone weights w_L/w_M (see eqn (1)). Subjects: AS (left panels) and DP (right panels).

We might expect large frequency-dependent changes in flicker spectral sensitivity if visual signals with different spectral sensitivities constructively interfere at some frequencies, but, then, because of large phase delays, destructively interfere at other frequencies. As we show below, the changes in spectral sensitivity with frequency are predictable, in part, from the phase delays of the underlying M- and L-cone signals.

Relative cone adaptation

Since light adaptation speeds up the light response of cone photoreceptors (e.g. Baylor et al. 1984) and each cone system can deliver signals with different phase delays, phase and amplitude differences between the M- and L-cone signals will arise if the two cones are in different states of adaptation. Given the large difference in M- and L-cone sensitivity at 658 nm (1.1 log units according to Stockman & Sharpe, 2000), substantial phase differences might be expected on the very intense 658 nm field used in these experiments. Such differences due to selective adaptation have been proposed before (Drum, 1977, 1984). However, because of the effects of photopigment bleaching on the very high intensity field, we expect the adaptive states of the M- and L-cone types to be relatively similar in this experiment. In other work, we find that the adaptive state of the cones monitored by temporal phase delay and amplitude sensitivity measurements reach a roughly asymptotic level above a bleach of about 50% (A. Stockman, M. Langendörfer & L. T. Sharpe, unpublished observations). On the 12.50 log₁₀ quanta s⁻¹ deg⁻², 658 nm field used in the experiment, which bleaches approximately 90% and 50% of the L- and M-cone photopigments, respectively, any phase differences between the M- and L-cone signals caused by adaptational imbalances are likely to be small. In fact, using the data from a binocular phase delay experiment (A. Stockman, M. Langendörfer & L. T. Sharpe, unpublished observations), we estimate that the L- and M-cone phase delays in the current experiment will be on average less than ± 6 deg. Systematic differences caused by differential cone adaptation are found on the lower intensity red backgrounds described in the accompanying paper (Stockman & Plummer, 2005).

Developing a new model

For the initial interpretation of our data, we subscribe to an operational definition of the channel (or channels) that underlie the perception of achromatic flicker. We assume that in its response to flicker this channel produces a colour-blind or univariant percept or output, such that two flickering lights of any wavelength composition can be flicker-photometrically cancelled by adjusting their relative amplitude and phase. This definition consequently excludes those frequencies at which any temporal colour variation is produced that cannot be flicker-photometrically nulled, but we find under the conditions of our experiment that this applies to only low temporal frequencies. Near-threshold, flicker-photometric nulls are generally possible at all frequencies above ca 5 Hz.

In a series of papers on flicker and flicker interactions, of which this is the first, we demonstrate that achromatic flicker perception depends on multiple cone signals with different temporal properties and with different signs. To characterize these signals, we have measured phase delay and modulation sensitivity as a function of temporal frequency, for monochromatic and cone-isolating stimuli, under a variety of adaptation conditions. Here we present data obtained on an intense deep-red field. In these experiments, which were carried out under intense long-wavelength adaptation, we have identified five signals. In the experiments in the accompanying paper, which were measured on less intense fields, we identify two additional signals (see also Stockman & Plummer, 2005).

Nomenclature

For brevity, we will refer to the various contributions to achromatic flicker perception as ‘S’, ‘M’ or ‘L’ (for short-, middle- or long-wavelength-sensitive, respectively), according to the cone type from which the input signals originate, prefixed by either ‘f’ or ‘s’ (for fast or slow), according to the relative phase delay of the input signal, and by either ‘+’ or ‘−’, according to whether the inputs are non-inverted or inverted with respect to the traditional fast signals. The five signals identified in this paper are +fM, +fL, +sM, −sL and −sS (the −sS signal corresponds to the inverted S-cone input previously reported). We use slow and fast here as descriptive terms to distinguish between the two categories of inferred cone signals without implying any underlying mechanism.

Methods

Subjects

Three male observers (the authors: AS, DP and EM) and one female observer (CK) participated in these experiments. All observers had normal colour vision and were experienced psychophysical observers. The main observers were AS and DP. The results for EM and CK (not shown), who measured only a subset of the experiments, were generally similar to those for AS. Informed consent was obtained in writing from each subject. These studies conformed to the standards set by the Declaration of Helsinki, and the procedures have been approved by local ethics committees in the UK and USA.

Apparatus

The optical apparatus was a conventional Maxwellian-view optical system illuminated by a 900 W Xe arc lamp that produced a 2 mm diameter output beam in the plane of the observer's pupil. Target and background wavelengths were selected by the use of 3-cavity, blocked interference filters with half-maximum bandwidths of between 7 and 11 nm (Ealing or Oriel). Infra-red radiation was minimized by heat-absorbing glass. Intensity could be controlled by fixed neutral density filters or variable neutral density filters under computer control.

Sinusoidal modulation of the targets was produced by the pulse-width modulation of liquid crystal light shutters (Displaytech) at a carrier frequency of 400 Hz. Each shutter had rise and fall times of less than 50 µs. The contrasts of the shutters in the test channels were > 300: 1 at the wavelengths used in the experiments.

The position of the observer's head was maintained by a dental wax impression.

Stimuli

Flickering targets of 4 deg in diameter (and in one experiment of 1 and 2 deg diameter) were presented superimposed in the centre of a 9 deg diameter background field. Fixation was central. The background field was 658 nm and delivered 12.50 log₁₀ quanta s⁻¹ deg⁻² at the cornea (5.18 log₁₀ photopic trolands (ph td)). When 500 or 540 nm targets were used, an auxiliary 410 nm background, which delivered 10.80 log₁₀ quanta s⁻¹ deg⁻² (1.93 log₁₀ ph td), was superimposed on the red field in order to prevent any S-cone contribution to flicker perception, which would in any case have been minimal. Subjects light adapted to test and background fields for at least 3 min prior to any data collection. The M-cone and L-cone bleaching levels for these stimuli are approximately 50% and 90%, respectively (Rushton & Henry, 1968; Stockman & Sharpe, 2000).

In the first experiments, flickering targets of 500, 540, 577 or 609 nm were superimposed on a flickering target of 656 nm, and both were presented superimposed in the centre of the larger background field of 658 nm. The 656 nm target is effectively ‘equichromatic’ with the background. Phase settings were made between each of the 500, 540, 577 or 609 nm targets and the 656 nm target. In later experiments, each of the three shorter wavelength targets was paired with a second 656 nm target (so, 500 and 656, 540 and 656 or 577 and 656 nm). Each pair was set to be equal for the L-cones, so that when they were sinusoidally alternated they produced primarily an M-cone flicker signal (given that any S-cone signal was suppressed by the 410 nm background). Phase settings were made between each M-cone-isolating pair and the equichromatic 656 nm light. In other experiments, a pair of 650 and 550 nm lights were set to be equal for the M-cones, so that when they were sinusoidally alternated they produced primarily an L-cone flicker signal. In this case, phase settings were made between the L-cone-isolating pair and the equichromatic 656 nm light.

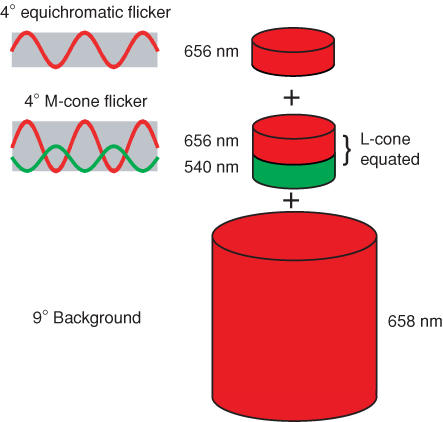
Figure 1 shows an example of stimuli used to measure phase delays between M-cone flicker and equichromatic flicker. The 656 nm light that generates the ‘equichromatic’ signal is superimposed on a pair of sinusoidally alternating L-cone-equated 656 and 540 nm lights that generate an M-cone flicker signal. The three targets are in turn superimposed on the intense 658 nm background. The subject adjusts the phase between the equichromatic flicker and the M-cone flicker.

Figure 1. Stimuli example.

Example of stimuli used to estimate M-cone phase lags. An equichromatic flickering 656 nm light was superimposed on a pair of sinusoidally alternating L-cone-equated 656 and 540 nm lights that generate an M-cone flicker signal, and all three targets were superimposed on the intense 658 nm background. Phase lags were measured between the equichromatic flicker and the M-cone flicker.

Equating the pairs of lights for the L-cones was done experimentally by flicker photometrically nulling each pair on an intense 481 nm background of 11.33 log₁₀ quanta s⁻¹ deg⁻², which effectively isolates the L-cone response (Eisner, 1982). The L-cone spectral sensitivities so obtained agreed with other cone spectral sensitivity estimates (Smith & Pokorny, 1975; Stockman et al. 1993a; Stockman & Sharpe, 2000), so that in subsequent experiments we used the estimates of Stockman & Sharpe (2000). Equating the 650 and 550 nm pair of lights for the M-cones relied mainly on the Stockman & Sharpe (2000) M-cone spectral sensitivity estimate, or before that was available the similar Stockman et al. (1993a) estimate.

We provide further details of the stimuli for each particular experiment below.

Procedures

Subjects interacted with the computer by means of eight buttons, and received feedback and instructions by means of tones and a computer-controlled voice synthesizer. The ability to give subjects simple instructions during the experiment enabled us to adopt more complex testing procedures.

Flicker modulation thresholds were measured by the method of adjustment. Phase settings were also set by an adjustment method. Initially, the two flickering target lights were separately set to just above modulation threshold (typically ca 0.20 log₁₀ above threshold). Next, the two lights were flickered together in counterphase, and the subject's task was to find a flicker null by adjusting their relative phase and modulation. Subjects could advance or retard the phase, or they could reverse the relative phase of one of the lights by 180 deg. Subjects could also adjust the modulation of either flickering stimulus to improve the flicker null (in practice, any adjustments were small). If the null covered an extended range of phase delays, which was usually the case if one of the two signals was weak, subjects were instructed to set the middle of the range.

Except where noted, all data points are averaged from three or four settings made on three or four separate runs.

Calibration

The radiant fluxes of test and background fields were measured at the plane of the observer's entrance pupil with a UDT Radiometer that had been calibrated by the manufacturer against a standard traceable to the National Bureau of Standards. A spectroradiometer (EG&G) was used to measure the centre wavelength and the bandwidth at half-amplitude of each interference filter in situ.

Results

We initially discovered the +sM signal through our investigation of the large and unexpected frequency-dependent effects on flicker spectral sensitivity found on intense red fields (Stockman et al. 1991b). Subsequent measurements of phase delays and modulation sensitivities, first with simple monochromatic flicker and then with cone-isolating flicker, led to the development of models of the interactions between the +sM signal and the +fM and +fL signals, and lastly between the −sL signal and the fast signals. This paper is organized along these chronological lines.

Frequency-dependent spectral sensitivities

Figure 2 shows the effect of increasing the radiance of a deep-red field on the spectral sensitivity for detecting 16 Hz flicker (shown as 574/650 nm sensitivity ratios). Due to the expected selective adaptation of the L-cones by the red field, the spectral sensitivity first changes from an L-cone (or V(λ)) spectral sensitivity (lower horizontal dashed line) to that of an M-cone (upper horizontal dashed line). When the radiance of the deep-red field is increased beyond about 11 log₁₀ quanta s⁻¹ deg⁻², however, there is an unexpected and precipitous fall back towards an L-cone spectral sensitivity.

The change back towards an L-cone spectral sensitivity at high 658 nm radiances was found to be dependent on flicker frequency. Figure 3 shows flicker spectral sensitivities for AS (left panels) and DP (right panels) measured on a 12.50 log₁₀ quanta s⁻¹ deg⁻² background of 658 nm (the level indicated in Fig. 2 by the arrow) at 5 Hz (triangles), 10 Hz (inverted triangles), 15 Hz (diamonds), 20 Hz (squares) and 25 Hz (circles). An auxiliary 10.30 log₁₀ quanta s⁻¹ deg⁻², 410 nm field, was also present to suppress the S-cones and eliminate any S-cone contribution. The functions shown by the continuous lines are the Stockman & Sharpe (2000) M- and L-cone fundamentals. To emphasize the differences between the spectral sensitivity functions, we have vertically aligned them at 650 nm. For both subjects, the flicker spectral sensitivities become shallower as the frequency increases, tending away from an M-cone spectral sensitivity and towards that of an L-cone. To quantify this change, we fitted the spectral sensitivity data with linear combinations of the Stockman & Sharpe (2000) cone fundamentals. That is, we found the best-fitting ratio w_L/w_M in the following equation:

(1)

where Q(λ) is the experimental function, and M(λ) and L(λ) are the M- and L- cone fundamentals with unity peak, k is a scaling constant, and w_L/w_M is the ratio of L- to M-cone weights. (Thus, if w_L/w_M is high the measured spectral sensitivity is close to an L-cone spectral sensitivity, whereas if it is low it is close to that of an M-cone.) The lower panels of Fig. 3 show the weights plotted as the ratio w_L/w_M as a function of frequency. For both subjects, the spectral sensitivity changes from being dominated by M (w_L/w_M = 0.01 and 0.05 for AS and DP, respectively) at 5 Hz, to being strongly influenced by L (w_L/w_M = 0.37 for AS at 20 Hz and 0.37 for DP) at 15 Hz. A reason why the spectral sensitivity is dominated by M at lower radiances will be discussed in the accompanying paper (Stockman & Plummer, 2005c). Here, we are concerned with the change from an M-cone spectral sensitivity back to that of an L-cone at higher frequencies under intense long-wavelength adaptation.

Phase delays for spectral lights

Large frequency-dependent changes in flicker spectral sensitivity might be expected if visual signals with different spectral sensitivities constructively interfere at some frequencies, but then, because of large delays, destructively interfere at other frequencies. To test this possibility, we measured phase lags between signals elicited by a long-wavelength, 656 nm flickering light and a shorter-wavelength flickering light as a function of frequency. Figure 4 shows such data for AS (left panels) and DP (right panels) obtained between 656 nm flicker and 500 nm (circles, upper panels), 540 nm (triangles, upper middle panels), 577 nm (inverted triangles, lower middle panels) or 609 nm (squares, lower panels) flicker. Target radiances were chosen so that 25 Hz flicker at the highest stimulus modulation was, in each case, just visible when the second target was unmodulated.

Figure 4. Phase advances required for flicker cancellation.

Phase advances of 500 nm (dotted circles, upper panels), 540 nm (triangles, upper middle panels), 577 nm (dotted inverted triangles, lower middle panels) and 609 nm (dotted squares, lower panels) flicker required to null 656 nm flicker on a 658 nm background for AS (left panels) and DP (right panels). Targets: 9.58 (500 nm), 9.36 (540 nm), 9.57 (577 nm), 10.05 (609 nm) and 11.25 (656 nm) log₁₀ quanta s⁻¹ deg⁻². Backgrounds: 12.55 (658 nm) and 10.90 log₁₀ quanta s⁻¹ deg⁻² (410 nm, present for the 500 nm target only, to eliminate S-cone flicker detection). The fits of the time delay model are shown as the continuous lines.

The phase advances of the shorter-wavelength flicker required to null 656 nm flicker are plotted relative to the two flickering lights being out of phase (i.e. relative to the prediction of the conventional model). An advance of 180 or −180 deg therefore means that the two lights produce a flicker null when they are physically in phase, while one of 0 deg means that they do so when they are in opposite phase. The continuous lines in each panel of Fig. 4 show the fits of the proposed model, which is introduced below.

A consistent feature of the phase data for AS is that, relative to the 656 nm flicker, the shorter-wavelength flicker is phase-delayed at lower frequencies, and phase-advanced at higher frequencies, with the reversal in sign occurring near 16 Hz. The sizes of the phase advance and phase delay, and the abruptness of the transition from one to the other, increase with the difference in wavelength between the shorter-wavelength target and the long-wavelength reference. At 500 nm, the phase advance changes abruptly by ca 160 deg, while at 609 nm, it changes gradually by only ca 50 deg. The phase data for DP at 577 and 609 nm are comparable to those for AS. In contrast, DP's data at 500 and 540 nm are strikingly dissimilar, since both sets of data increase continuously with frequency and lack the abrupt discontinuity near 16 Hz. (The 500 and 540 nm phase data for DP are continuous across the upper (180 deg) and lower (−180 deg) boundaries of the plot, since a phase angle of θ and θ− 360 deg are equivalent in this plot.)

Though seemingly complex, these phase lag data can be represented by a simple model of signal generation and interaction that incorporate just three or four visual signals. Moreover, the apparently large individual differences in the phase data can be accounted for by variability in a single parameter (the ratio of slow/fast signal sizes, m; see below).

Time delay model

In this model, the 656 nm, equichromatic target is assumed to produce only a ‘fast’ signal (conventional luminance), whereas the shorter wavelength target is assumed to produce both a ‘fast’ signal and a delayed ‘slow’ signal. We assume that, relative to the fast signals, the slow signal has a time delay of Δt. Thus, the phase delay (Δθ) as a function of frequency (ν) is

(2)

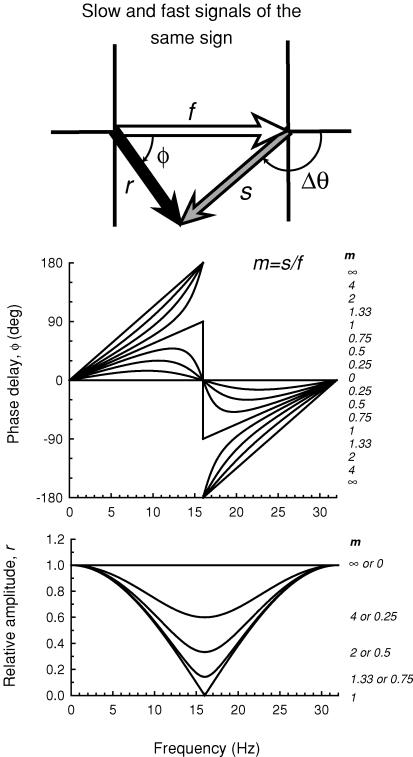
where Δθ is in degrees, ν is in Hz, and Δt is in ms. The model is illustrated in the vector diagram shown in Fig. 5. The shorter wavelength target generates a fast signal, which is represented by the open vector of magnitude f, and a slow signal, which is represented by the grey vector of magnitude s; the two are separated by a phase delay of Δθ. Combining the slow and the fast signals gives rise to the resultant signal represented by the black vector. The magnitude of the resultant is r, the length of the black vector, and its phase lag is ɸ. We assume that the 656 nm target, which is equichromatic with the background, generates only a fast signal. The ratio of the magnitude of the slow to the fast signal (s/f) produced by the short-wave target is referred to as m. The phase delay (ɸ) of the resultant signal is

(3)

where m is the ratio of the slow signal magnitude to the fast signal magnitude, and Δθ is the phase delay between the slow and the fast signals produced by the shorter-wavelength light. Equation (2) can be substituted into eqn (3) to give ɸ in terms of Δt. The magnitude of the resultant signal (r) relative to the size of the slow signal is

(4)

Figure 5 illustrates the effect of varying m on the phase delay, ɸ, of the resultant (upper panel), and on the relative amplitude of the resultant, r (lower panel). A Δt of 31.25 ms (i.e. a phase delay of 180 deg at a frequency of 16 Hz) was used in this example since it is close to fitted values (see Table 1). The largest changes in phase and the smallest relative amplitudes occur at 16 Hz, which is the frequency at which the slow and fast signals produced by the short-wavelength stimulus destructively interfere. When the two signals are equal in magnitude (m= 1), the phase changes abruptly by 180 deg at 16 Hz and the resultant falls to zero. At other ratios of m, the resultant falls to a minimum at 16 Hz, but not to zero. When the slow signal is smaller than the fast (m < 1) the phase lag functions rise and fall, cross 0 deg at 16 Hz, and then rise again. In contrast, when the slow signal is larger than the fast (m > 1), the functions rise with increasing slope below 16 Hz, cross 180 or −180 deg at 16 Hz, and rise with decreasing slope above it. The relative amplitudes (lower panel, Fig. 5) for m and 1/m superimpose.

Figure 5. Phase and amplitude predictions.

Upper diagram: the short-wavelength target is assumed to generate a fast signal, f (open arrow) and a slow signal, s (grey arrow) separated by a phase delay, Δθ, which together give rise to the resultant, r (black arrow), with phase delay, ɸ. Upper panel: phase delay of the resultant signal ɸ for several slow to fast signal ratios, m (continuous lines) for a time delay, Δt, between the slow and fast signals of 31.25 ms (i.e. a delay that causes the two signals to be in opposite phase at 16 Hz). The values of m from top to bottom for the curves < 16 Hz and from bottom to top for the curves > 16 Hz are 8, 4, 2, 1.33, 1, 0.75, 0.5, 0.25 and 0. Lower panel: the relative amplitude of the resultant signal r for several slow to fast signal ratios m (continuous lines). The values of m from top to bottom are 0 or ∞, 4 or 0.25, 2 or 0.5, 1.33 or 0.75 and 1 (plotted in relative terms the amplitude functions for m and 1/m are the same).

Table 1.

Fits of time delay model to phase data for subjects AS and DP

	AS			DP
Wavelength	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.
500 nm	1.00 ± 0.04	30.76 ± 0.41	12.65	4.09 ± 1.29	33.84 ± 0.56	9.23
540 nm	0.90 ± 0.03	30.80 ± 0.19	9.18	1.58 ± 0.18	34.37 ± 0.62	11.97
577 nm	0.69 ± 0.05	30.09 ± 0.54	8.98	0.94 ± 0.06	33.91 ± 0.72	15.25
609 nm	0.43 ± 0.43	29.21 ± 1.00	6.87	0.44 ± 0.03	33.67 ± 0.73	4.64
M-isolating	1.40 ± 0.10	29.71 ± 0.35	10.09	5.91 ± 2.33	33.44 ± 0.48	8.36

m is the slow/fast signal ratio. The slow signal has a time delay of Δt relative to the fast signal.

A comparison of the upper panel of Fig. 5 with the data of Fig. 4 reveals that the model predictions are qualitatively similar to the phase lag data. To find the best-fitting values of Δt and m for each set of phase lag data, we substituted eqn (2) into eqn (3), and used a standard non-linear curve-fitting algorithm (the Marquardt-Levenberg algorithm, implemented in SigmaPlot, SPSS). The best-fitting functions are shown as the continuous lines in each panel of Fig. 4. The best-fitting values of Δt and m with ± their standard errors, and the root mean square (r.m.s.) errors are tabulated in Table 1. Δt is similar for all subjects, and varies little with target wavelength. The values of Δt averaged across target wavelength are 30.22 and 33.95 ms for AS and DP, respectively, so that the corresponding frequencies at which the slow and fast signals produced by the short wavelength target are in opposite phase are 16.55 and 14.73 Hz.

The parameter that accounts for most of the variability with target wavelength and the variability between subjects is the ratio of the slow to fast signal size, m. Indeed, the substantial differences between the phase data for DP and AS at 500 and 540 nm are consistent with the slow signal being more prominent in DP than in AS. The large differences between the subject's phase lag functions are because m exceeds 1 for DP, but not for AS (the values of m for CK and EM are consistent with those for AS).

Phase delays for M-cone-isolating lights

The decline in m as the target wavelength is increased from 500 to 609 nm is likely to result from the growth of an L-cone signal as the L-cones become relatively more sensitive to the target. Indeed, since the 500, 540 and 577 nm targets that we used were roughly M-cone-equated for both subjects, they differ primarily in the L-cone signal that they produce. The decline in m that occurs between 500 and 540 nm for AS and DP (see Table 1) suggests that the 540 nm target (and, in fact, the 500 nm target, see below) must generate a visually significant L-cone signal. The L-cone signal or signals could decrease m in two ways: either by adding to the fast signal produced by the shorter wavelength target or by reducing the slow signal. We will return to this issue below when we consider the modulation sensitivity data.

To assess the influence of the L-cone signal on the phase delays, we repeated the phase measurements with the L-cone signal minimized using a silent substitution technique. Instead of presenting a single 500, 540, or 577 nm target, as before, we paired each of those targets with a second 656 nm target that was equal in its effects on the L-cones. Consequently, when each pair (500 and 656, 540 and 656, and 577 and 656) was sinusoidally alternated, it produced M-cone flicker but little or no L-cone flicker. Given that the L-cone spectral sensitivity varies slightly with eccentricity, the silent substitution was not expected to be perfectly silent over the 4 deg diameter target. Nonetheless, we expected any L-cone modulation to be substantially reduced. We equated the pairs for the L-cones experimentally by flicker photometrically matching them on a 481 nm background of 11.33 log₁₀ quanta s⁻¹ deg⁻², which selectively attenuates the M-cone signals, thus isolating the L-cones. The settings were consistent with those predicted by the Stockman & Sharpe (2000) cone fundamentals. Since the 500, 540 and 577 nm targets are themselves roughly equated for the M-cones, we expect that the phase and modulation sensitivity data should be approximately independent of target wavelength, given, that is, no contribution from the S-cones.

Figure 6 shows the phase setting for AS (top) and DP (bottom) between the 500 and 656 nm (circles), 540 and 656 nm (squares) and 577 and 656 nm (triangles) paired targets and the equichromatic 656 nm target. The use of the paired targets has yielded phase lag data for both AS and DP that are independent of target wavelength, which indicates that as expected there was little or no S-cone influence even at 500 nm. These results suggest that the silent substitution method has effectively isolated the M-cone response for this task across all observers. Moreover, compared with the phase data obtained with single wavelength targets (see Fig. 4), the functions for both subjects are consistent with a decline in the relative size of the fast signal. This result suggests that the L-cone signal that has been lost was either a fast signal (+fL) or a slow signal that opposed the slow M-cone signal (−sL). But, most importantly, these results show that the fast and the slow signals are both generated by the M-cones.

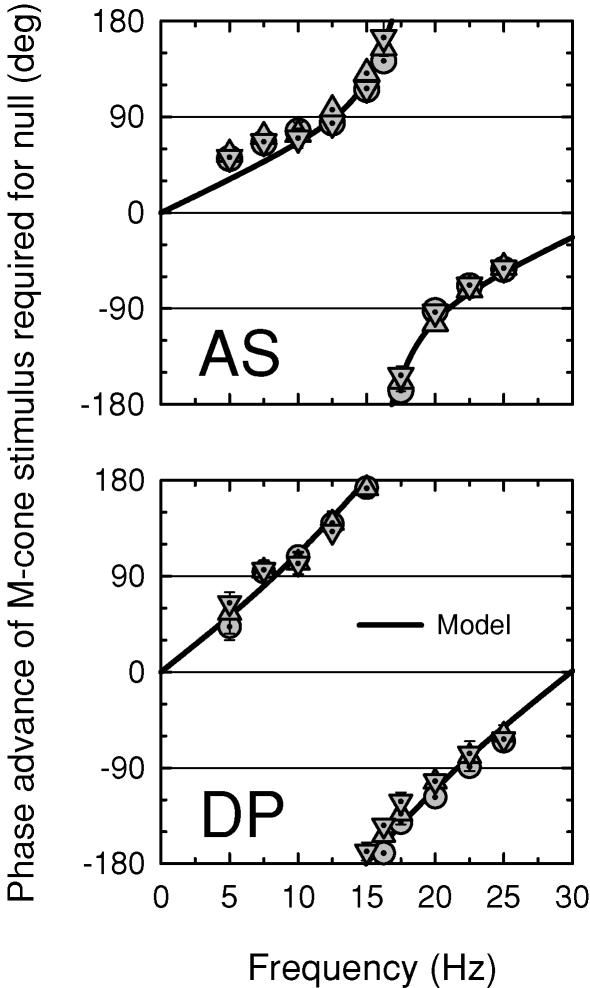
Figure 6. Phase advances of M-cone flickering lights.

Phase advances of sinusoidally alternating, M-cone-isolating pairs of 500 and 656 nm (dotted circles), 540 and 656 nm (dotted triangles), and 577 and 656 nm (dotted inverted triangles) lights, each of which were equal for the L-cones, required to null 656 nm flicker, and mean fits of the time delay model (continuous lines). Subjects: AS (top panel) and DP (bottom panel). The radiances of the combined targets were chosen so that the opposite-phase flicker was L-cone-equated. For AS: 9.70 and 10.21 (500 and 656 nm), 9.48 and 10.38 (540 and 656 nm), 9.66 and 10.61 (577 and 656 nm), and 11.36 (656 nm) log₁₀ quanta s⁻¹ deg⁻². For DP: 9.70 and 10.16 (500 and 656 nm), 9.76 and 10.66 (540 nm), 9.66 and 10.60 (577 and 656 nm), and 11.36 (656 nm) log₁₀ quanta s⁻¹ deg⁻². Backgrounds: 12.55 (658 nm) and 10.90 log₁₀ quanta s⁻¹ deg⁻² (410 nm, present for the 500 nm target only).

We can estimate m and Δt for the paired M-cone-isolating targets by fitting the time delay model to the phase data of Fig. 6 as we did for the phase data obtained with spectral lights. To find the best fit for AS and DP, we averaged the paired-target phase data across target wavelengths. The best-fitting functions are the continuous lines in each panel. The best-fitting parameters and the fitting errors are tabulated in the fifth row of Table 1. For each subject, the m value for the paired targets is higher than for any spectral target. For AS, it is 1.40 compared with 1.00 for the 500 nm target, and for DP, it is 5.91 compared with 4.09 for the 500 nm target. These differences suggest that even the 500 nm target generated a small but perceptually significant L-cone signal. As previously, there are individual differences. The m value for DP is much larger than those for AS (or for CK or EM).

Modulation sensitivity data

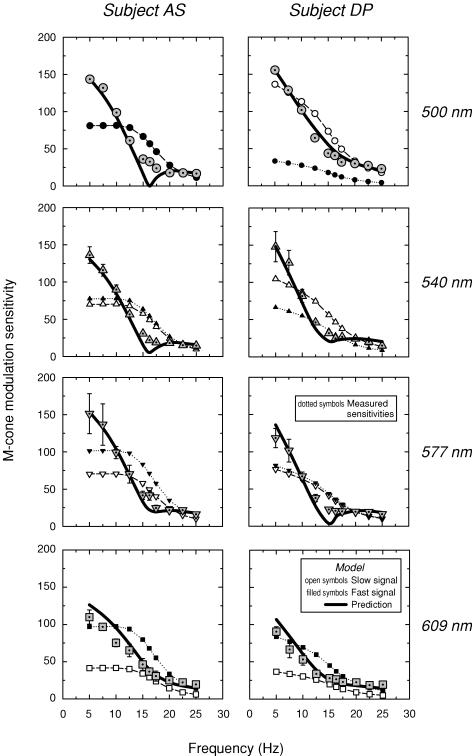
Figure 7 shows the measured modulation sensitivities for the 500 nm (dotted circles, upper panels), 540 nm (dotted triangles, upper middle panels), 577 nm (dotted inverted triangles, lower middle panels) and 609 nm (dotted squares, lower panels) targets for AS (left panels) and DP (right panels), respectively. The modulation sensitivities for both subjects decline with frequency, but are unusual in that they show a rapid sensitivity loss as the frequency approaches 16.25 Hz followed by a much shallower loss at still higher frequencies.

Figure 7. Modulation sensitivities (subject AS).

Modulation sensitivities for AS (left panels) and DP (right panels) obtained with the 500 nm (dotted circles, upper panels), 540 nm (dotted triangles, upper middle panels), 577 nm (dotted inverted triangles, lower middle panels) and 609 nm (dotted squares, lower panels) modulated targets. Conditions as Fig. 4. The predicted modulation sensitivities (continuous lines) are calculated from the assumed slow (open symbols) and fast (filled symbols) modulation sensitivities using parameters obtained from fits of the time delay model to the phase delay data (see Fig. 4). For details, see text.

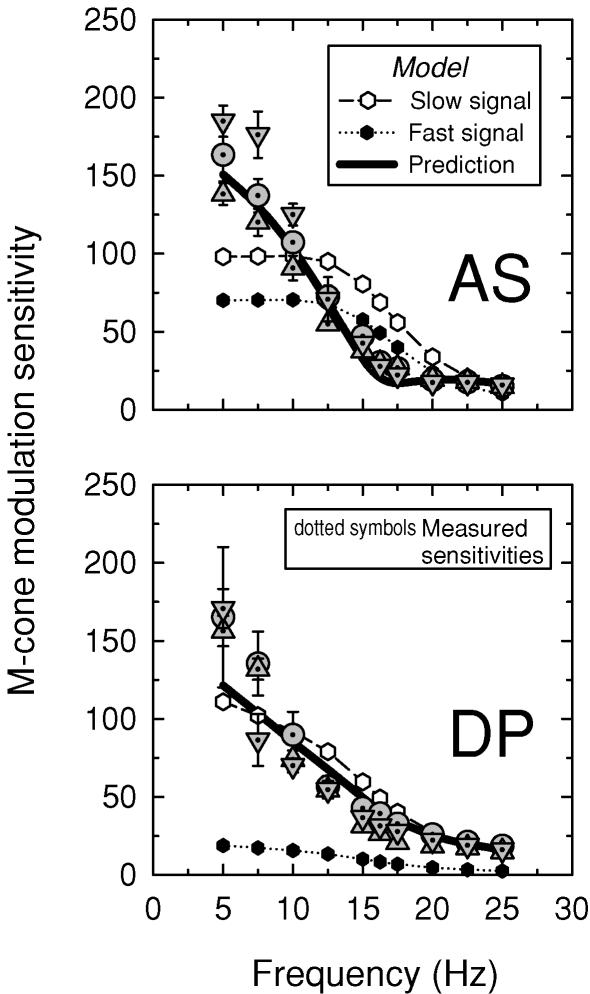
Figure 8 shows the modulation sensitivities for AS (upper panel) and DP (lower panel) measured using the M-cone-isolating sinusoidally alternating 500 and 656 nm (dotted circles), 540 and 656 nm (dotted inverted triangles) and 577 and 656 nm (dotted triangles) stimulus pairs. All three pairs overlie each other fairly well, except at 5 and 7.5 Hz. As for the single stimuli, the sensitivities decline rapidly as the frequency approaches 16.25 Hz. Qualitatively, the results obtained with both the single and the paired targets are consistent with the phase data, which predict some sensitivity loss near 16.25 Hz due to destructive interference between the slow and fast cone signals. It also provides further evidence that the slow and fast signals are both generated by M-cones.

Figure 8. M-cone modulation sensitivities.

Modulation sensitivities for AS (upper panel) and DP (lower panel) obtained with the sinusoidally alternating 500 and 656 nm (dotted circles), 540 and 656 nm (dotted triangles), and 577 and 656 nm (dotted inverted triangles) M-cone-isolating target. Conditions as Fig. 6. The equichromatic target was not modulated. The predicted mean modulation sensitivities (continuous lines) are calculated from the assumed slow (open circles) and fast (filled circles) modulation sensitivities using mean parameters obtained from fits of the time delay model to the phase delay data (see Fig. 6). For details, see text.

We can estimate the magnitudes of the slow and fast signals, s and f, that underlie the modulation sensitivities using the time delay model. Given that the modulation thresholds reflect the magnitude of the resultant, r, and that we know ɸ at each frequency from the phase measurements and Δθ from the model fit (see Table 1), we can use the sine rule, which in this case is

(5)

to calculate the magnitudes of s and f. We obtained plausible and consistent estimates of s and f at low and high frequencies, but inconsistent and sometimes implausibly high values near 15 or 16.25 Hz. These inconsistencies arise when the +sM and +fM signals are close to opposite phase and similar in magnitude, which suggests that they are due to a small residual visible flicker signal that remains even when the slow and fast signals cancel each other (perhaps from non-linear distortion or from another source). As a result of this small residual signal, when s and f are calculated back from r, they are substantially overestimated.

In terms of modulation, the deviations of the modulation sensitivities from the model's predictions (r) are fairly small. We can illustrate this by deriving smoothed mean templates for the slow and fast frequency responses by averaging the estimates of s and f across conditions, interpolating at 15 and 16.25 Hz, and then using the mean templates to calculate back to r. The templates for s and f are shown in Figs 7 and 8 as open and filled symbols, respectively. The predictions for r, the modulation sensitivity, calculated from the templates, are shown as the thick continuous lines. The predictions for r agree remarkably well with the modulation sensitivity data, except, as expected, in the region of self-cancellation between +sM and +fM.

M- and L-cone signals compared and the effect of target size

So far, we have described experiments that used only M-cone-isolating stimuli. For the experiments reported in this section, we added L-cone-isolating stimuli. Again, all phase measurements (M- and L-cone) were made relative to the 656 nm equichromatic stimulus. As a part of this series of experiments, we also varied the target size to determine its influence on the prominence of the slow signal. Targets of 1, 2 and 4 deg diameter were used. We were particularly interested in determining if the slow and fast signals had comparable spatial dependencies.

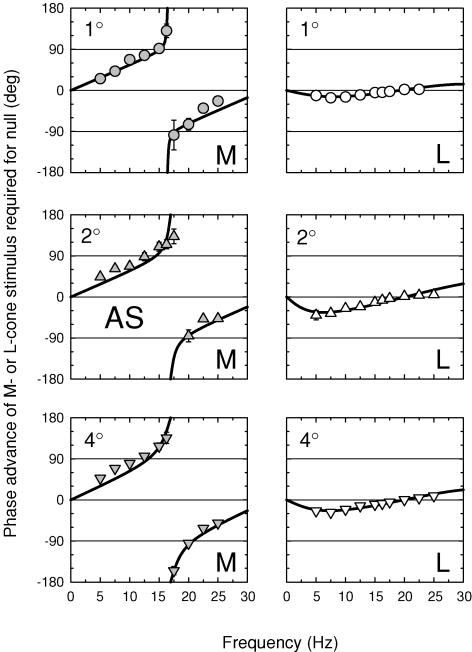
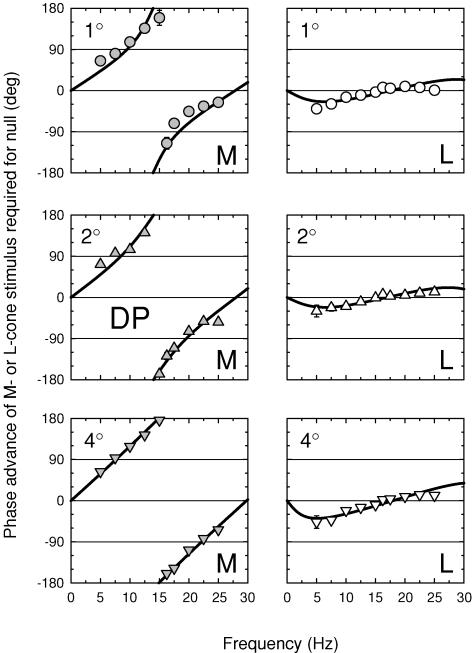
The M- and L-cone phase adjustments required to null the 656 nm equichromatic stimulus are shown in Figs 9 and 10 for AS and DP, respectively, for 1 (top panels), 2 (middle panels) and 4 deg (bottom panels) diameter targets. The three panels on the left of each figure show the M-cone phase lags, while the three right panels show the L-cone phase lags.

Figure 9. M- and L-cone phase advances for three target sizes (subject AS).

Phase advances of M- or L-cone stimuli required to null a 656 nm target presented on a 12.47 log₁₀ quanta s⁻¹ deg⁻², 658 nm background. For the M-cone measurements (left panels, grey symbols), the M-cone stimulus was a sinusoidally alternating L-cone-equated pair of 540 and 656 nm targets of 9.47 and 10.37 log₁₀ quanta s⁻¹ deg⁻² and the equichromatic target was a 656 nm target of 11.36 log₁₀ quanta s⁻¹ deg⁻². For the L-cone measurements (right panels, open symbols), the L-cone stimulus was a sinusoidally alternating M-cone-equated pair of 650 and 550 nm targets of 11.12 and 9.25 log₁₀ quanta s⁻¹ deg⁻² and the equichromatic target was a 656 nm target of 11.41 log₁₀ quanta s⁻¹ deg⁻². The cone-isolating radiances were chosen on the basis of the Stockman & Sharpe (2000) fundamentals. Measurements were made with either 1 (top panels, circles), 2 (middle panels, triangles) or 4 deg diameter (bottom panels, inverted triangles) targets. Subject: AS.

Figure 10. M- and L-cone phase advances for three target sizes (subject DP).

Details as Fig. 9.

The M-cone results for both subjects are similar to those measured before at 4 deg (see Fig. 6). Large phase changes of nearly 180 deg are found at all target sizes, which indicates that the +sM signal still exceeds the +fM signal even for a 1 deg target. As before, we carried out fits of the time delay model to these data. The results of the fits are given in Table 2. For M, the values of Δt are about 30 ms for AS and 35 ms for DP, and the values of m, the slow/fast signal ratios, are consistently greater than one for both subjects. The values of m decline with target size, which suggests that the +sM signal becomes slightly less prominent with reducing target size. It is still, however, equal to or larger than the +fM signal even for the 1 deg diameter target.

Table 2.

Fits of time delay model to M-cone or L-cone phase delay data obtained with cone-isolating targets of 1, 2 and 4 deg diameter for subjects AS and DP

		AS			DP
	Target size (deg)	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.
M	1	1.03 ± 0.10	30.40 ± 0.29	9.97	1.84 ± 0.50	35.90 ± 1.30	22.41
	2	1.12 ± 0.08	29.52 ± 0.80	12.65	3.15 ± 1.11	35.71 ± 0.87	13.87
	4	1.31 ± 0.96	29.50 ± 0.40	12.62	27.96 ± 35.19	33.56 ± 0.33	5.14
L	1	−0.24 ± 0.02	26.00 ± 0.74	1.73	−0.41 ± 0.10	28.44 ± 2.34	9.73
	2	−0.56 ± 0.05	24.84 ± 0.94	5.21	−0.37 ± 0.05	29.61 ± 1.51	5.43
	4	−0.40 ± 0.03	25.08 ± 0.63	2.74	−0.63 ± 0.08	27.79 ± 1.25	7.45

In contrast, the L-cone phase adjustments required for both subjects are much smaller than those of the M-cones. Moreover, the L-cone phase adjustments are consistent with a negative slow L-cone signal (−sL), whereas those of the M-cones are consistent with a positive M-cone signal (+sM). We can apply the same models developed for the M-cone phase data, but with 180 deg subtracted (or added) to the slow signal to incorporate the sign inversion. A vector diagram, and amplitude and phase predictions for the combination of fast and slow signals of opposite polarity are shown in Fig. 2 of the accompanying paper. Thus, eqn (4) becomes:

(6)

Having substituted eqn (6) into the model, we carried out fits, the results of which are also given in Table 2. The values of Δt are slightly smaller than those for the M-cone, but again they show that the slow signal is subjected to substantial delays. The main differences are for m, the slow/fast signal ratios, which are between 0.23 and 0.56 for AS and between 0.37 and 0.63 for DP. Under the conditions of these experiments, then, −sL is consistently smaller than +fL.

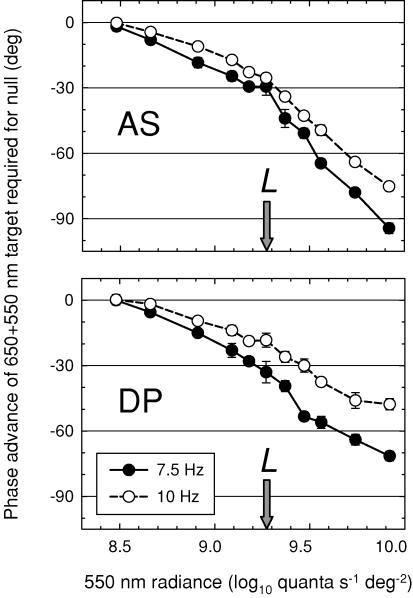
We also carried out a control to ensure that the −sL signal was not an artefact produced by the paired (650 and 550 nm) L-cone-isolating stimulus. Such a stimulus could produce an artefact of the appropriate sign if the opposite-phase 550 nm component more strongly stimulated the M-cones than the 650 nm component, instead of being – as intended − M-cone-equated. (The artefact, in other words, would be a +sM signal, but in opposite phase to the intended L-cone stimulus.) To test this hypothesis, we fixed the radiance of the 650 nm component and measured the phase lag of the pair relative to the 656 nm equichromatic stimulus as a function of the radiance of the 550 nm component. If there is no −sL cone signal, the phase lag should be close to zero when the paired 650 and 550 nm target is correctly equated for the M-cones. Equally important, since the sign of the phase lag is determined by the component that excites the M-cones more, the lag should change sign as M-cone quantal catch equality is reached and then exceeded.

The results of the control experiment are shown in Fig. 11 for AS (top) and DP (bottom) carried out at 7.5 Hz (filled circles) and 10 Hz (open circles). There is no evidence for a change in the sign of the required phase adjustment near the radiances at which the two components should be M-cone-equated (and thus L-cone-isolating), nor indeed is there any evidence that the phase adjustment approaches zero. We conclude that the −sL signal is mainly an L-cone signal.

Figure 11. Control experiment.

Phase advance of a sinusoidally alternating pair of 650 and 550 nm targets required to null a 656 nm target of 11.41 log₁₀ quanta s⁻¹ deg⁻² lag as a function of the radiance of the 550 nm component for AS (top panel) and DP (bottom panel) at frequencies of either 7.5 Hz (filled circles) or 10 Hz (open circles). The paired stimulus was made up of a 650 nm component that was fixed at 11.34 log₁₀ quanta s⁻¹ deg⁻² and an opposite-phase 550 nm component that was varied from 8.48 to 9.87 log₁₀ quanta s⁻¹ deg⁻². The radiance of the 550 nm target at which the two targets are thought to be equated for the M-cones (9.27 log₁₀ quanta s⁻¹ deg⁻²) is indicated in each panel by the arrow. The targets were presented on a 658 nm background of 12.4 log₁₀ quanta s⁻¹ deg⁻².

S-cone phase lags

Thus far we have purposely confined our measurements to M- and L-cone signals, ensuring no S-cone participation by the addition of a short-wavelength background. Of interest, however, is the relationship between the S-cone (−sS) input to luminance (Stockman et al. 1987, 1991a; Lee & Stromeyer, 1989) and the cone signals identified here. In particular, do the slow S-cone signals interact with the other slow cone signals, and do they do so in such a way that the phase lags are additive?

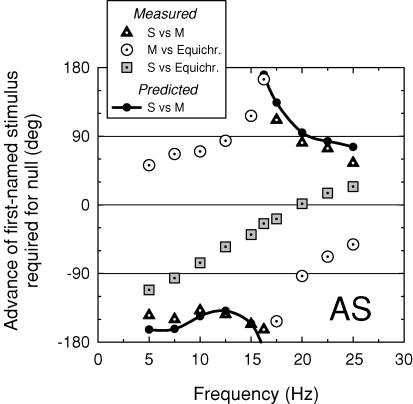
Figure 12 shows phase lags for AS measured between an S-cone-detected 440 nm and an M-cone-isolating paired (577 and 656 nm) stimulus (black dotted triangles), between the M-cone-isolating and equichromatic 656 nm stimuli (open dotted circles), and between the S-cone and the equichromatic 656 nm stimuli (grey dotted squares). Both the M-cone versus 656 nm and the S-cone versus 656 nm phase lags are consistent with previous results. Analysis of the M-cone data suggest mixed +sM and +fM signals (see above), while analysis of the S-cone data suggest a simple −sS signal (one which is inverted in sign, since the function tends towards −180 deg at 0 Hz, and substantially delayed by ca 180 deg at 20 Hz). The S-cone versus M-cone phase lags predicted from the difference between the M-cone versus 656 nm and the S-cone versus 656 nm phase lags are shown by the small filled circles joined by the continuous line. These predicted values agree reasonably well with the measured S-cone versus M-cone phase lags (open triangles), which demonstrates that phase delays between the cone signals are to a first approximation additive.

Figure 12. Phase differences between M- and S-cone and equichromatic flicker.

Phase advances of (i) an S-cone-detected 440 nm target of 9.09 log₁₀ quanta s⁻¹ deg⁻² required to null an M-cone-isolating paired 577 and 656 nm stimulus of 9.66 and 10.61 quanta s⁻¹ deg⁻², respectively (black dotted triangles); (ii) the M-cone-isolating 577 and 656 nm stimulus required to null an equichromatic 656 nm target of 11.36 log₁₀ quanta s⁻¹ deg⁻² (open dotted circles); and (iii) the S-cone-detected target required to null the 656 nm target (grey dotted squares). The filled circles and continuous lines show the phase differences between the S-cone and M-cone stimuli predicted from the phase differences measured between (ii) the M-cone and 656 nm equichromatic stimuli and (iii) the S-cone and 656 nm equichromatic stimuli. The targets were presented on a 658 nm background of 12.40 log₁₀ quanta s⁻¹ deg⁻². Subject: AS.

Discussion

On an intense red field, we find evidence for interactions between at least five different cone signals in the perception of achromatic luminance flicker. Using our nomenclature, these signals are +fM, +fL, −sS, +sM and −sL. Since we monitor the signals from each cone separately, we cannot be sure of any special interdependence between them, but in terms of their properties it seems likely that the +fM and +fL signals are paired as +fM+fL and that the +sM and −sL signals are paired as a spectrally opponent pair +sM−sL. We speculate that the −sS signal is associated with +sM and +sL to give s(M+L−S), another of the classic ‘colour’ channels, but we have no evidence proving or disproving the existence of an +sL signal, which if it were present would be cancelled by the presumably larger −sL signal. These signals are summarized in the model shown in Fig. 13. A spectrally opponent luminance input of the opposite polarity (+sL−sM) will be described in the next paper in this series. The idea that there can be a spectrally opponent signal (SPO) that does not contribute to chromatic perception was raised by Stromeyer et al. (1995) in the context of motion detection.

Figure 13. Postreceptoral model.

A model of the signals underlying achromatic flicker perception that is consistent with the experimental data reported here. On intense red fields, slow, spectrally opponent M-cone (+sM) and L-cone (−sL) signals combine with a slow, inverted S-cone signal (−sS) signal, and the faster, non-opponent M-cone (+fM) and L-cone (+fL) signals usually associated with the luminance channel to predict phase delays, modulation sensitivities and spectral sensitivities as a function of frequency.

Neuroanatomical and physiological considerations are discussed in the next paper (Stockman & Plummer, 2005).

Earlier work

Our preliminary reports of the +sM input (Stockman et al. 1991b) are extended in this paper, while our preliminary reports of a −sM input found on a less intense field (Stockman & Plummer, 1994) are extended in the next paper (Stockman & Plummer, 2005). Since those preliminary reports, we have progressively extended our measurements and refined our analyses in order to present a consistent and simple model of the organization and operation of the postreceptoral human visual system. Subsequent to our initial reports, some of our findings have been replicated, confirming our preliminary conclusions (see below).

As noted above, the phase delay data of Lindsey et al. (1986) and Swanson et al. (1987) were the first clear evidence for slow, inverted inputs to the luminance channel. A clear psychophysical demonstration of an inverted M-cone input to luminance was provided, using M-cone-isolating stimuli, by Stockman & Plummer (1994), who found, in addition to the signal inversion, a delay of 20 ms (a delay that has since been confirmed precisely by Stromeyer et al. 1997). The inverted M-cone input will be covered in more detail in the accompanying paper.

Evidence for a slow M-cone input of the same sign as the faster L- and M-cone inputs was obtained by Stockman et al. (1991b) on an intense red field, which produces M-cone signals that are in phase with the fast signals at low frequencies, but in opposite phase to them near 16 Hz. As a result, the slow and fast M-cone signals destructively interfere (and reduce M-cone sensitivity and change spectral sensitivity) near 16 Hz. Stromeyer et al. (1997) replicated some of our original experiments and analysis, and it is gratifying that in their meticulous study they found a similar M-cone signal on green and on blue backgrounds (Stromeyer et al. 1997).

Stromeyer et al. (1995, 1997) inferred the presence of spectrally opponent +sM−sL and +sL−sM signals from phase data obtained mainly from motion experiments, but also from flicker experiments (see also Stromeyer et al. 2000). Their novel contribution was to observe that +sM−sL signals predominate on shorter wavelength fields. The idea that slow ‘chromatic’+sL−sM signals oppose faster ‘luminance’ signals on longer wavelength fields was proposed several years earlier by Smith et al. (1992) to account for data obtained from macaque magnocellular-projecting (MC) ganglion cells. In their model, Smith et al. assume that the +fM+fL signals are the centre response of the ganglion cell, while the chromatically opponent +sL−sM signals are the surround response. A reduction of the +sM−sL and +sL−sM signals, relative to the +fM+fL signals occurs with increases in spatial frequency, which suggests a spatially opponent surround (Kremers et al. 1993; Stromeyer et al. 1997).

Relative strengths of the inputs

The +sM signal is larger, relative to the +fM signal, than the −sL signal is, relative to the +fL signal. We find evidence for this asymmetry not only on long-wavelength backgrounds, but also on those of short-wavelength, which suggests that this imbalance is not simply a consequence of long-wavelength adaptation (A. Stockman & D. J. Plummer, unpublished observations).

In general, we assume that the weights of the opposing slow signals are approximately balanced (+sM ≈−sL), such that no slow signal is found under equichromatic conditions (when the target and background are of the same wavelength). In contrast, in accordance with the well-known asymmetry of L- and M-cone inputs into the luminance channel, but not into the chromatic channel (see above, and, e.g. Smith & Pokorny, 1975; Stromeyer et al. 1985), we assume that +fL > +fM, but by different amounts in each of our four subjects. If we assume that −sL =+sM, the ratio of +fL to +fM can be calculated from the m ratios for L and M (see Table 2). These values are large, which suggests a substantial suppression of the +fM signal by the long-wavelength field − a conclusion that is consistent with the spectral sensitivity data shown in Figs 2 and 3. A consequence of these relative strengths is that the −sL signals are harder to discern in phase and amplitude data in our subjects than are the +sM signals, since they have a much smaller relative influence if cone-isolating stimuli are used. We predict that in subjects for whom +fM > +fL, the −sL signals will be more prominent.

Other considerations

We have several other considerations. First, we assumed that there are no phase differences between the M- and L-cone signals transmitted through the same type of channel. Although the red field much more strongly adapts the L-cones than the M-cones, under the very intense adaptation conditions of our experiment we assume that the changes in phase have reached their maximum or nearly so (see above). The likely error in this assumption is indicated by the change in Δt when the single shorter wavelength targets were substituted for the L-cone-equated paired targets that stimulated the M-cones. The fact that these changes are small (cf. Tables 1 and 2) suggests that any errors too are small.

Second, the results reported in this paper seem to conflict with the work of Eisner & MacLeod (1981), who obtained 17 Hz flicker photometric spectral sensitivities on red fields that were close to an M-cone spectral sensitivity. Figure 1, which shows the difference in the sensitivity to 16 Hz flicker at 574 and 650 nm, helps to explain both sets of results. On lower intensity backgrounds, the sensitivity difference is close to an M-cone spectral sensitivity, as Eisner & MacLeod found. However, on high intensity backgrounds, the spectral sensitivity reverts back towards L, partly because of self-cancellation between the slow and fast M-cone signals, but also because of a suppression of the +fM signal (A. Stockman & D. J. Plummer, unpublished observations).

Third, because phase differences must be measured relative to another process, we can never be sure of the absolute phase delays of any signal. In these experiments, we use equichromatic flicker as the reference, but we do not know the complexity of its phase behaviour.

Fourth, implicit in the time delay model is the assumption that Δt and m are not frequency dependent; i.e. that the shapes of the logarithmic temporal modulation sensitivities of the slow and fast signals are identical. The ability of such a simple model to account for the data is striking. The phase lag data, however, tend to fall slightly above the predictions of the time delay model at both low and high frequencies, which suggests that m or Δt or both change with frequency. We can account for such changes by passing the slow signal through additional stages of low-pass temporal filtering. One stage of filtering reduces the r.m.s. error by about one half.

Conclusions

Under intense long-wavelength adaptation, multiple cone signals contribute to achromatic flicker perception. These signals, which can be fast (+fM, +fL) or slow and of the same or different sign (+sM, −sL, −sS), constructively and destructively interfere to produce characteristic, frequency-dependent changes in spectral sensitivity, modulation sensitivity and phase delay data. The luminance channel has an achromatic output, but slow spectrally opponent inputs.

The existence of multiple inputs to the luminance channel questions the conventional psychophysical model of the human visual system. It also casts further doubt on the interpretation of the myriad of ‘chromatic’ experiments that have relied on HFP or MDB to silence the luminance channel, since equiluminance only silences a subset of the luminance inputs.