Spectrally opponent inputs to the human luminance pathway: slow +L and −M cone inputs revealed by low to moderate long-wavelength adaptation

Abstract

The luminance pathway has slow (s), spectrally opponent cone inputs in addition to the expected fast (f), non-opponent inputs. The nature of these inputs to luminance flicker perception was further explored psychophysically by measuring middle- (M-) and long-wavelength-sensitive (L-) cone modulation sensitivities, M- and L-cone phase delays, and flicker spectral sensitivities under three conditions of low to moderate long-wavelength adaptation. Under these conditions we find that the luminance channel has fast M- and L-cone input signals (+fM and +fL), and slow, spectrally opponent cone input signals (+sL and −sM). The slow signals found under these conditions are therefore of the opposite polarity to those (+sM and −sL) found under more intense long-wavelength adaptation. At these less intense levels, fast and slow M-cone signals of opposite polarity (−sM and +fM) cancel at low frequencies, but then constructively interfere at intermediate frequencies (ca 12.5–22.5 Hz, depending on adapting level) because of the delay between them. In contrast, fast and slow L-cone signals of the same polarity (+sL and +fL) sum at low frequencies, but then destructively interfere at intermediate frequencies. Importantly, the spectrally opponent signals (+sL and −sM) contribute to flicker nulls without producing visible colour variation. Although its output generates an achromatic percept, the luminance channel has slow spectrally opponent as well as fast non-opponent inputs.

The dominant model of the early visual system is one in which signals from the three cones (short- (S), middle- (M) and long- (L) wavelength-sensitive) feed either into the brisk luminance channel (L+M) or into the sluggish chromatic channels (L–M) or (S−(L+M)) (e.g. Schrödinger, 1925; Luther, 1927; Walls, 1955; De Lange, 1958b; Guth et al. 1968; Smith & Pokorny, 1975; Boynton, 1979; Eisner & MacLeod, 1980). There is a growing body of psychophysical evidence, to which this paper adds, of slow, spectrally opponent and non-opponent inputs into the achromatic luminance channel. In addition to the expected ‘fast’ inputs to luminance (to which we refer as +fM and +fL), we have revealed ‘slow’ signals of the same (+sM) and opposite (−sL) sign on an intense red field (Stockman et al. 2005). In this paper, we report evidence for slow signals (−sM and +sL) on low to moderate intensity red fields that are opposite in sign to those found on the more intense field. The existence of these inputs contradicts the conventional psychophysical model of the human visual system.

The luminance or achromatic channel

The concept of luminance now plays a central role in the design and interpretation of many types of vision research experiments. Mechanistically, it is often defined as a hypothetical visual process with a V(λ) spectral sensitivity that signals luminance, and is often linked – perhaps somewhat simplistically – to the physiological behaviour of the magnocellular pathway. A central, defining property of this channel is that it responds univariantly to lights of different wavelength. Thus two sinusoidally alternating lights that are ‘luminance-equated’ should appear perfectly steady or nulled whatever their chromaticities when detected solely by the luminance channel.

Two failures of the conventional model have led us to develop a new model. First, we find that substantial phase adjustments are often required to produce flicker nulls even at frequencies as high as 20 Hz (see also De Lange, 1958b; Walraven & Leebeek, 1964; Cushman & Levinson, 1983; Lindsey et al. 1986; Swanson et al. 1987; Smith et al. 1992). The frequency dependence of these required phase adjustments is much too large to be consistent with a model of luminance with two simple additive L- and M-cone inputs. Second, large frequency-dependent changes in flicker detection spectral sensitivities accompany the large changes in phase delay. As we demonstrate below, these changes are partly the result of visual signals with different spectral sensitivities constructively interfering at some frequencies and destructively interfering at others (see also the previous paper, Stockman et al. 2005).

Developing a new model

For the initial interpretation of our data, we subscribe to an operational definition of the channel (or channels) that underlie the perception of achromatic flicker. We assume that in its response to flicker this channel produces a colour-blind or univariant percept or output, such that two flickering lights of any wavelength composition can be flicker-photometrically cancelled by adjusting their relative amplitude and phase. This definition consequently excludes those frequencies at which a clear temporal colour variation is produced that cannot be flicker-photometrically nulled. Under the conditions of these experiments, we find that near-threshold, flicker-photometric nulls are generally possible at all frequencies above ca 5 Hz.

In a series of papers on flicker and flicker interactions, of which this is the second, we demonstrate that achromatic flicker perception depends on the complex combination of multiple cone inputs with different temporal properties and with different signs. In this paper, we measured phase delay and modulation sensitivity as a function of temporal frequency for monochromatic and cone-isolating stimuli on a long-wavelength 658 nm background field set at three different radiances from low to moderate intensities. On the basis of this work, we identify four inputs to the luminance channel, but in all we have found seven (see also the previous paper Stockman et al. 2005).

We refer to the various contributions to achromatic flicker perception as ‘S’, ‘M’ or ‘L’ (for short-, middle- or long-wavelength-sensitive, respectively), according to the cone type from which the input signals originate, prefixed by either ‘f’ or ‘s’ (for fast or slow), according to the relative phase delay of the input signal, and by either ‘+’ or ‘−’, according to whether the inputs are non-inverted or inverted with respect to the fast signals. The four signals identified in this paper are +fM, +fL, +sM, and −sL. Slow and fast are used here as descriptive terms to distinguish between the two categories of inferred cone signals, one of which is substantially phase delayed relative to the other, without implying any underlying mechanism.

Methods

Apparatus

The optical apparatus was a conventional five-channel, Maxwellian-view system with a 2 mm entrance pupil illuminated by a 900 W Xe arc. Full details can be found in the previous paper (Stockman et al. 2005).

Stimuli

In all experiments, target stimuli of 4 deg in diameter were presented superimposed in the centre of a steady 658 nm background field of 9 deg in diameter. The observer fixated the centre of the fields. The relatively large target size facilitated flicker threshold and null settings, but comparable results are found with smaller targets (Stockman et al. 2005).

Targets

Single or paired flickering targets of 4 deg diameter were used. Single monochromatic targets of 500, 540, 578 and 610 nm were used for subject AS. We additionally carried out experiments for both subjects in which cone-isolating stimuli were used. These were: (i) sinusoidally alternating M-cone-isolating pairs (540 and 650 nm), which were set to be equal in their effects on the L-cones so that their alternation generated an M-cone flicker signal; or (ii) sinusoidally alternating L-cone-isolating pairs (650 and 550 nm), which were set to be equal in their effects on M-cones so that their alternation generated an L-cone flicker signal. The use of slightly different green targets is of no significance. We used the Stockman & Sharpe (2000) cone fundamentals to calculate pairs of lights that were equally effective for the M- or L-cones, or, before they were available, the similar Stockman et al. (1993) M- and L-cone fundamentals. In control experiments, the relative radiance of some of the pairs of lights was varied to check that cone isolation was near optimal. In general, both AS and DP conform to the standard M- and L-cone spectral sensitivities represented by the above cone fundamentals at the wavelengths used (i.e. ≥ 500 nm). Given, however, retinal inhomogeneities within the central 4 deg, the silent substitution will not be perfect for a 4 deg diameter target. Nonetheless, we should expect the stimuli to modulate predominantly the intended cone type. The single 656 nm target was always used as the reference flicker against which phase delays were measured whether the test flicker was produced by a single or paired target. It was chosen to be similar in wavelength to the primary background. According to our model, this ‘equichromatic’ stimulus generates only fast, +fM and +fL, signals, but this may not always be the case, as we discuss below. See Fig. 1 of the previous paper for an example of M-cone and equichromatic flickering stimuli.

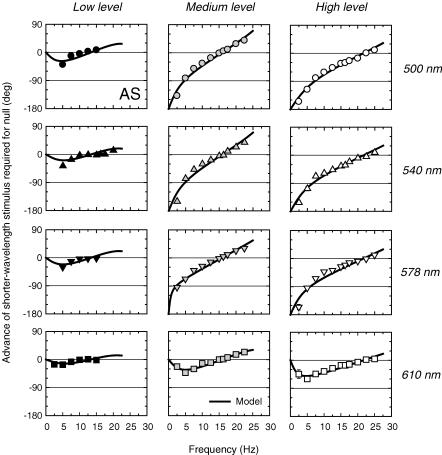
Figure 1. Phase advances of spectral lights required for flicker cancellation on low, medium and high intensity deep-red fields.

Phase advances of 500 nm (circles, upper panels), 540 nm (triangles, upper middle panels), 578 nm (inverted triangles, lower middle panels) and 610 nm (squares, lower panels) flicker required to null 656 nm flicker on 658 nm backgrounds of 8.90 (left panels), 10.16 (centre panels) or 11.18 (right panels) log₁₀ quanta s⁻¹ deg⁻². Target radiances in log₁₀ quanta s⁻¹ deg⁻²: Low level 6.79 (500 nm), 6.73 (540 nm), 6.76 (578 nm), 7.07 (610 nm) and 8.17 (656 nm); Medium level 7.71 (500 nm), 7.50 (540 nm), 7.71 (578 nm), 8.18 (610 nm) and 8.85 (656 nm); and High level 8.34 (500 nm), 8.44 (540 nm), 8.45 (578 nm), 8.79 (610 nm) and 9.86 (656 nm). At the medium and low levels, measurements were made during the cone plateau following a 3 s, 12.20 log₁₀ quanta s⁻¹ deg⁻², 510 nm bleach. At the high level, an auxiliary 410 nm background of 10.30 log₁₀ quanta s⁻¹ deg⁻² was used. Also shown are fits of the time delay model (continuous lines). See text and the previous paper (Stockman et al. 2005) for details of the model. Subject: AS.

The flickering stimuli could be varied in modulation and in phase. Cone modulation for combinations of lights of different wavelength was calculated with the use of the Stockman & Sharpe (2000) cone fundamentals.

Backgrounds

Three 658 nm backgrounds of 8.93, 10.16 and 11.18 log₁₀ quanta s⁻¹ deg⁻² and 9 deg diameter were used. Given the long wavelength of the backgrounds, it was important to ensure that the rods and S-cones were unable to detect the target flicker. Thus, at the higher 658 nm background radiances an auxiliary 410 nm background of 10.30 log₁₀ quanta s⁻¹ deg⁻² was added to suppress the S-cones and saturate the rods. This auxiliary field was not bright enough to alter substantially the relative excitation of the L- and M-cones caused by the 11.18 log₁₀ quanta s⁻¹ deg⁻² red background. At the two lower 658 nm background radiances of 8.93 and 10.16 log₁₀ quanta s⁻¹ deg⁻², the targets were well below S-cone threshold (i.e. the calculated S-cone modulation produced by those lights was far below the S-cone modulation threshold measured with short-wavelength targets), so that an auxiliary 410 nm background was not needed. To suppress the rods at the two lower background radiances, we bleached them by presenting for 3 s a 510 nm background of 12.22 log₁₀ quanta s⁻¹ deg⁻² 3 min prior to any measurements. This background, which is 6.56 log₁₀ scotopic trolands, produces a 7.03 log₁₀ td-s bleach, which bleaches > 99% of the rod photopigment. Measurements were made between 3 and 10 min during the cone plateau following the bleach.

Calibrations were carried out with use of a UDT Radiometer or a spectroradiometer (EG&G). For further details, see the previous paper (Stockman et al. 2005b).

Procedures

Subjects light adapted to the target and background fields for at least 3 min prior to any data collection. Modulation thresholds and flicker thresholds were found by the method of adjustment. Phase differences were measured by a flicker cancellation technique. Subjects first adjusted the modulation of each of the two lights separately (with the other light at zero modulation) until the flicker was just above threshold (typically ∼0.2 log₁₀ units above threshold). They then adjusted the phase difference between the two lights, and if necessary their relative modulation, to find the best flicker null.

Except where noted, all data points are averaged from three or four settings made on at least four separate runs. Other details of the experimental procedures are given in Results.

Subjects

The two primary observers in this work were both male observers (the authors, AS and DP). They have normal colour vision, and are emmetropic. Informed consent was obtained in writing from each subject. These studies conform to the standards set by the Declaration of Helsinki, and the procedures have been approved by local ethics committees in the UK and USA.

For further methodological details, see the previous paper (Stockman et al. 2005).

Results

Phase delays for spectral lights

The phase advances of 500, 540, 578 or 610 nm flickering lights required to null the 656 nm flickering light are shown for subject AS for the low (Fig. 1, left panels), medium (middle panels) and high (right panels) 658 nm background levels (8.93, 10.16 and 11.18 log₁₀ quanta s⁻¹ deg⁻², respectively). Target radiances were chosen so that with the target at maximum modulation 15 Hz flicker was just visible at the low level and 25 Hz was just visible at the medium and high levels. The modulation at each frequency was then set to just above modulation threshold prior to the phase settings (see above).

The phase advances of the shorter-wavelength flicker that were required to produce a null with the 656 nm flicker are plotted relative to the two being opposite in phase (i.e. relative to the prediction of the conventional model of luminance). An advance of 180 or −180 deg therefore means that the two lights produce a flicker null when they are physically in phase, while one of 0 deg means that they do so when they are in opposite phase. The continuous lines in each panel of Fig. 1 are the fits of the time delay model, which is defined in the previous paper (Stockman et al. 2005) and briefly discussed below. These figures can be compared with Fig. 4 of the previous paper.

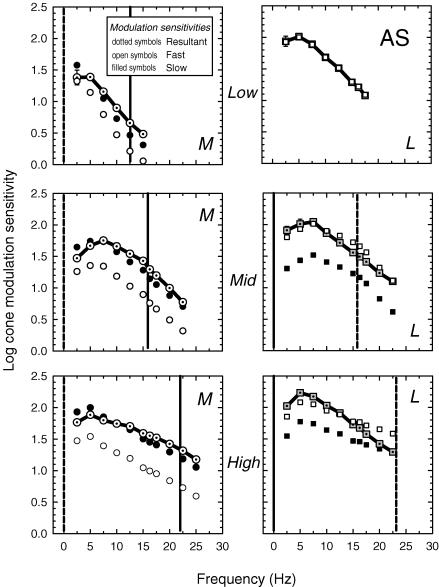
Figure 4. Measured and inferred cone threshold modulations (subject AS).

M-cone (left panels) and L-cone (right panels) modulation thresholds at the low (top panels), medium (middle panels) and high (bottom panels) 658 nm intensity levels. The M-cone threshold measurements (dotted open circles) were made using an L-cone-equated 540 and 656 nm pair of lights, and the L-cone measurements using an M-cone-equated 650 and 550 nm pair. For target and background radiances, see legend of Fig. 3. Also shown are the thresholds for the slow (filled circles) and fast (open circles) M-cone signals, and for the slow (filled squares) and fast (open squares) L-cone signals inferred from the time delay model (for details, see text). The vertical dashed and continuous lines indicate, respectively, the frequency at which the slow and fast signals are assumed to be in opposite phase and in the same phase.

Under all conditions, the shorter wavelength stimulus has to be delayed at lower frequencies in order to improve the null. This means that at those frequencies, the shorter wavelength stimulus produces a signal that is advanced with respect to the equichromatic one. This seeming paradox – that the stimulus more likely to be detected by the less light adapted (and therefore more sluggish) M-cones is advanced – arises because M-cone detection is by multiple mechanisms.

The phase lags obtained with the 500 and 540 nm targets on high or medium intensity red fields clearly tend towards −180 deg as the temporal frequency tends towards 0 Hz. Thus, at low frequencies the two cancelling stimuli are actually in phase with each other. This indicates that the M-cone signal is actually inverted in sign with respect to the signal produced by the equichromatic flicker. The phase advance of the shorter wavelength stimulus continues to decrease with increasing frequency, in many cases becoming a small phase delay at the highest frequencies used in the experiment.

Though apparently complex, the phase lags can be described by simple models of signal generation. We have developed a simple time delay model, which was introduced in detail in the previous paper (Stockman et al. 2005).

Model

In brief, we assume that the 656 nm, equichromatic target predominantly produces a ‘fast’ signal (conventional luminance), unless it is below M-cone threshold (as is the case on the dimmest red background) in which case it will produce an L-cone signal with both slow and fast L-cone components. We make this assumption on the grounds that the intensity variation of a near-flicker-threshold target of the same wavelength as a more intense background produces little or no chromatic modulation. We assume, in other words, that the +sL and −sM signals are approximately equal and therefore cancel under equichromatic conditions. In support of this assumption, the L- and M-cone contrast thresholds for the red–green chromatic channels, as opposed to those for the luminance channel, remain approximately equal under a variety of conditions of chromatic adaptation (Stromeyer et al. 1985; Chaparro et al. 1995; Eskew et al. 1999). If the equichromatic flickering target does generate a slow signal, then the relative strengths of the slow signal will be underestimated for one cone type and overestimated for the other.

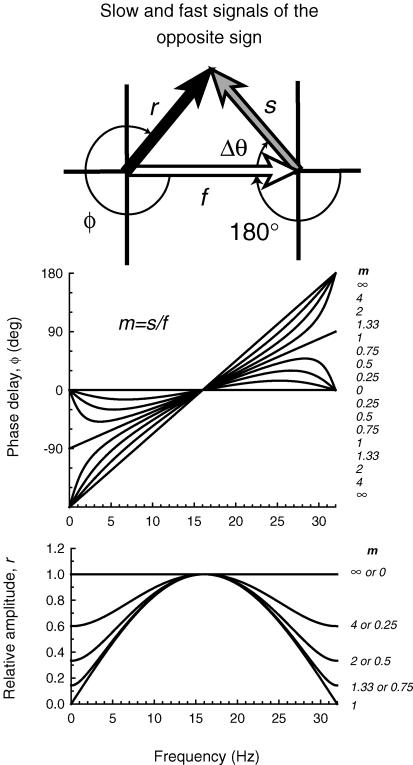
In contrast, we assume that monochromatic targets (which are not equichromatic) and M- or L-cone-isolating targets generate both a ‘fast’ signal and a delayed ‘slow’ signal. We assume that the slow signal has a time delay of Δt relative to the fast signal. Thus, the phase delay (ΔΘ) between them is a linear function of temporal frequency. The ratio of slow/fast signal sizes for the monochromatic or cone-isolating targets is defined as m. Combining the slow and the fast signals gives rise to the resultant signal with magnitude of r, and a phase delay of Φ. The inset of Fig. 2 shows a diagram of the three vectors, in which the slow signal is inverted with respect to the fast. The inversion is equivalent to an additional phase delay or advance of 180 deg. Full equations are given in the previous paper (Stockman et al. 2005).

Figure 2. Phase and amplitude predictions.

Inset diagram: the shorter wavelength (or M-cone) target under low to moderate long-wavelength adaptation conditions is assumed to generate a fast signal, f (open arrow) and an inverted slow signal, s (grey arrow) separated by the phase delay, ΔΘ, which together give rise to the resultant, r (black arrow), with phase delay, Φ. The inversion is equivalent to an extra phase delay of 180 deg. Upper panel: phase delay of the resultant Φ for several slow to fast signal ratios, m, for a time delay, Δt, between fast signals and the inverted slow signals of 31.25 ms (i.e. a delay that causes the two signals to be in opposite phase at 16 Hz). The values of m from top to bottom for the curves < 16 Hz and from bottom to top for the curves > 16 Hz are 8, 4, 2, 1.33, 1, 0.75, 0.5, 0.25 and 0. Lower panel: the relative amplitude of the resultant, r, for several slow to fast signal ratios, m (continuous lines). The values of m from top to bottom are 0 or 8, 4 or 0.25, 2 or 0.5, 1.33 or 0.75 and 1 (plotted in relative terms, the amplitude functions for m and 1/m are the same).

Figure 2 illustrates the effect of varying m on the phase delay, Φ, of the resultant (upper panel), and on the relative amplitude of the resultant, r (lower panel) for the case in which the slow signal is inverted relative to the fast signal. In this example, we assumed a Δt of 31.25 ms (i.e. a phase delay of 180 deg at 16 Hz), because it is close to the fitted values for the middle intensity level (see Table 1, below). The largest phase changes and the smallest amplitudes are found near 0 and 32 Hz, which are the frequencies at which the slow and fast signals are in opposite phase and destructively interfere. Figure 2 should be compared with Fig. 5 from the previous paper.

Table 1.

Fits of time delay model to phase data for low, medium and high 658 nm background levels for subject AS

	Low			Medium			High
Wavelength (nm)	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.
500	0.46 ± 0.11	37.31 ± 2.04	7.91	1.67 ± 0.19	31.59 ± 0.49	8.42	1.99 ± 0.27	23.05 ± 0.44	8.60
540	0.32 ± 0.09			1.72 ± 0.20			1.72 ± 0.19
577	0.36 ± 0.11			1.11 ± 0.08			1.52 ± 0.14
610	0.23 ± 0.09			0.54 ± 0.07			0.77 ± 0.05

m is the slow/fast signal ratio. The slow signal has a time delay of Δt relative to the fast signal. Δt was assumed to be independent of wavelength.

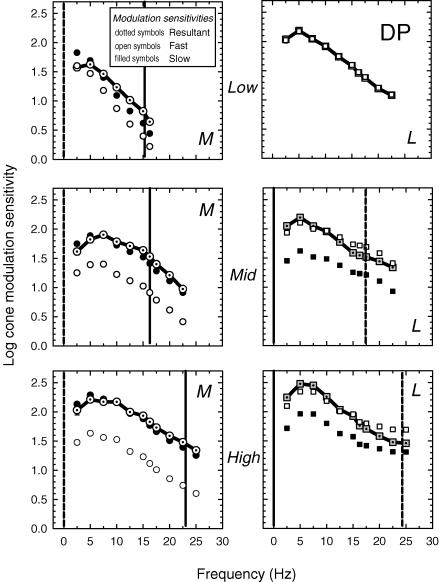
Figure 5. Measured and inferred cone threshold modulations (subject DP).

For target and background radiances, see Fig. 3 legend. Other details as Fig. 4.

A comparison of the upper panel of Fig. 2 with the data of Fig. 1 shows that the model predictions are similar to the phase lag data. Consequently, they can be modelled – at least qualitatively – using the time delay model. To find the best-fitting values of Δt and m for each set of data, we used a standard non-linear curve-fitting algorithm (the Marquardt-Levenberg algorithm, implemented in SigmaPlot, SPSS). Since Δt was found to remain fairly consistent within adaptation levels, we carried out a simultaneous fit in which Δt was constrained to be the same value across all four target conditions at each level. The best-fitting values are tabulated in Table 1, and the best-fitting functions are shown as the continuous line in each panel of Fig. 1.

Phase delays for M- and L-cone-isolating lights

The decline in m as the target wavelength is increased from 500 to 610 nm (see Fig. 1 and Table 1) is due to the relative growth of the signals generated by the L-cones, as they become more sensitive to the target. It would be desirable to know the phase delays, and thus be able to estimate the Δt and m values, for pure M- and L-cone stimuli. Consequently, rather than presenting monochromatic targets as in the previous experiment, we presented targets that stimulated only the M-cones or only the L-cones (see Methods). Phase delays were measured between either M-cone flicker and the equichromatic 656 nm standard, or between L-cone flicker and the equichromatic 656 nm standard.

Figure 3 for AS (left panels) and DP (right panels) shows the additional phase advances of the M-cone (dotted open circles) and L-cone (dotted grey squares) required to null a 656 nm target at the low (top panels), medium (middle panels) and high (bottom panels) 658 nm intensity levels.

Figure 3. M- and L-cone phase advances.

Phase advances of M-cone (open dotted circles) or L-cone (grey dotted squares) flickering stimuli required to null a 656 nm flickering target at low, middle and high levels of the 658 nm background for AS (left panels) and DP (right panels). The lengths of the vertical lines at 1 Hz represent the phase differences between the M- and L-cone signals at 1 Hz inferred from the spectral sensitivity measurements (see Fig. 6). Low level/AS: background 658 nm, 8.86 log₁₀ quanta s⁻¹ deg⁻²; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 6.73 and 7.53 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 8.02 and 6.15 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 8.18 log₁₀ quanta s⁻¹ deg⁻². Low level/DP: background 658 nm, 8.94 log₁₀ quanta s⁻¹ deg⁻²; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 6.78 and 7.58 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 8.06 and 6.19 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 8.25 log₁₀ quanta s⁻¹ deg⁻². Measurements were made during the cone plateau following a 3 s, 12.20 log₁₀ quanta s⁻¹ deg⁻², 510 nm bleach. Medium level/AS: background 658 nm, 10.05 log₁₀ quanta s⁻¹ deg⁻²; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 7.50 and 8.30 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 8.96 and 7.09 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 8.86 log₁₀ quanta s⁻¹ deg⁻². Medium level/DP: background 658 nm, 10.06 log₁₀ quanta s⁻¹ deg⁻²; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 7.53 and 8.33 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 9.00 and 7.13 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 8.75 log₁₀ quanta s⁻¹ deg⁻². High level/AS: background 658 nm, 11.18 log₁₀ quanta s⁻¹ deg⁻²; with a 410 nm, 10.30 log₁₀ quanta s⁻¹ deg⁻² auxiliary; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 8.44 and 9.24 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 10.00 and 8.13 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 9.86 log₁₀ quanta s⁻¹ deg⁻². High level/DP: background 658 nm, 11.20 log₁₀ quanta s⁻¹ deg⁻²; with a 410 nm, 10.30 log₁₀ quanta s⁻¹ deg⁻² auxiliary; M-cone stimulus 540 and 650 nm alternating sinusoidal lights of 8.45 and 9.25 log₁₀ quanta s⁻¹ deg⁻²; L-cone stimulus 650 and 550 nm alternating sinusoidal lights of 10.00 and 8.13 log₁₀ quanta s⁻¹ deg⁻²; equichromatic target 656 nm, 9.86 log₁₀ quanta s⁻¹ deg⁻². Also shown are fits of the time delay model (continuous lines).

Considering the M-cone data first, the phase lags for AS and DP at all three levels are large at low frequencies, clearly tending to a phase advance of −180 deg (i.e. a phase delay of 180 deg) as the frequency tends towards 0 Hz. Comparisons with the predictions of the time delay model shown in the upper left panel of Fig. 2 suggest that the M-cone signal is a combination of a fast signal with a slow, inverted signal of larger magnitude. Fits of the time delay model are given in Table 2, and are shown in Fig. 3 as the continuous lines. The fits are impressive. Δt decreases with level, while m remains consistently high (ca 1.75 at the low level and even higher at the medium and high levels), confirming that the M-cone signal is predominantly a slow, inverted signal.

Table 2.

Fits of time delay model to phase data for the low, medium and high 658 nm background levels using M- or L-cone-isolating stimuli for subjects AS and DP

		Low			Medium			High
	cone stimulus	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.	m	Δt (ms)	r.m.s.
AS	M	1.79 ± 0.50	39.82 ± 2.90	12.77	2.44 ± 0.45	31.48 ± 0.74	7.81	2.87 ± 0.47	22.72 ± 0.51	5.65
	L	0.03 ± 0.02	25.22 ± 7.04	2.45	0.32 ± 0.04	31.63 ± 1.10	4.67	0.49 ± 0.03	21.60 ± 0.42	4.37
DP	M	1.67 ± 0.35	32.70 ± 1.68	13.34	3.15 ± 0.25	30.74 ± 0.23	2.70	4.51 ± 2.25	21.71 ± 0.89	10.15
	L	0.04 ± 0.03	29.94 ± 6.44	2.48	0.33 ± 0.57	28.81 ± 1.49	7.23	0.41 ± 0.05	20.57 ± 0.90	6.98

The L-cone phase delays for both subjects shown in Fig. 3, in contrast to the M-cone data, deviate much less from 0 deg. Moreover, they are always opposite in sign to the M-cone phase delays. Thus, the slow, L-cone signals (which we assume are +sL) spectrally oppose the slow, inverted M-cone signals (−sM). Comparisons with the predictions of the time delay model shown in the upper panel of Fig. 5 of the previous paper suggest that the fast L-cone signal (+fL) is much larger than the slow signal (+sL). Fits of the model are given in Table 2, and are shown as the continuous lines in the figure. At the medium and high levels, the values of Δt are comparable to the M-cone values. The values of m, however, are much smaller than those for the M-cones, ranging from 0.35 to 0.70. The low level adaptation level is unusual because the 656 nm equichromatic target is below M-cone threshold. Since both the reference and the test stimuli are detected only by L-cones, there is no phase lag between them. The results in Fig. 3 can be compared with the 4 deg results measured at the still higher 658 nm level shown in Figs 9 and 10 in the previous paper.

Modulations and modulation sensitivities of the M- and L-cone signals

Figures 4 (AS) and 5 (DP) show the M-cone (dotted open circles, left panels) and L-cone (dotted grey squares, right panels) modulations at threshold for the low (top panels), medium (middle panels) and high (bottom panels) intensity levels. The M-cone data were measured using a pair of sinusoidally alternating 540 and 650 nm lights, the alternation of which generated primarily an M-cone flicker signal, since they were set to be equal for the L-cones. The L-cone data were measured using a pair of sinusoidally alternating 650 and 550 nm lights, the alternation of which generated primarily an L-cone flicker signal, since they were set to be equal for the M-cones.

As expected from previous measurements of the dependence of temporal sensitivity on adaptation (e.g. De Lange, 1958a; Kelly, 1961), the size of the cone signals required to detect flicker modulation increase less steeply with frequency as the adaptation level rises. The M-cone functions show the largest reduction in slope, partly because they are much less light adapted than the L-cones on the dimmest field, and partly because of constructive interference. Constructive interference between the slow and fast M-cone signals near 22 Hz (+fM and −sL) and destructive interference between the L-cone signals (+fL and +sM) produce the seemingly paradoxical result that the M-cone signals at threshold rise less steeply with frequency than those of the L-cones on the high intensity 658 nm background, even though the L-cones are more light adapted.

By assuming that the modulation thresholds reflect the magnitude of the resultant (r), knowing the phase delay of the resultant (Φ) from the phase measurements, and knowing the phase delay between the slow and fast signals (ΔΘ) from the model fits tabulated in Table 2, we can estimate the magnitudes of the underlying slow and the fast signals using simple trigonometric formulas (see the inset of Fig. 2 for a vector diagram). Figures 4 and 5 show the estimated cone modulation thresholds for the slow (filled symbols) and fast (open symbols) signals. Because we use a time delay model, the shapes of the slow and fast modulation sensitivities are identical for every condition.

The vertical dashed line in each panel indicates the frequency at which the slow and fast signals are in opposite phase and thus destructively interfere, while the continuous lines indicate the frequencies at which they are in the same phase and constructively interfere. If the two signals destructively interfere, the measured (resultant) sensitivities are low relative to the sensitivities of the fast and slow components. However, if the two signals constructively interfere, the measured sensitivities are high relative to the components. As a result, the measured L-cone modulation sensitivities at the medium and high levels are paradoxically steeper than the measured sensitivities of the less light adapted M-cones. Nevertheless, the underlying slow and fast L-cone sensitivities are, as expected, shallower than those of the M-cones. At the low level, the L-cone modulation thresholds seem to be dominated by the fast signal, but this an incorrect prediction of the model that arises because the equichromatic stimulus is below M-cone threshold at this level (see above).

Frequency-dependent spectral sensitivities

Our model predicts that the inverted and non-inverted slow signals, which produce such large changes in phase delay, should also distort flicker detection spectral sensitivities in a frequency-dependent way. If we assume that the quantal spectral sensitivity (Q(λ)) is proportional to a vector sum of the Stockman & Sharpe (2000) M-cone (M(λ)) and L-cone (L(λ)) spectral sensitivities, then:

(1)

where a is the relative cone weight, b is a scaling factor, and ΔΘ is the phase delay between the M- and L-cone signals. The effects of the slow and fast signals will be manifested in two ways. First, the phase delay and relative amplitudes of slow and fast cone signals for one cone type will alter its contribution to the spectral sensitivity and thus change a, the relative cone weight. If the slow and fast signals destructively interfere, then the contribution of that cone type to the spectral sensitivity will be relatively reduced, whereas if they constructively interfere, it will be relatively increased. Second, the phase delay, ΔΘ, between the two resultant M- and L-cone signals will also influence the spectral sensitivity. If ΔΘ is near 180 deg, the spectral sensitivity will tend to be spectrally opponent (L–M, under these conditions), whereas if it is close to 0 deg the spectral sensitivity will tend to be spectrally non-opponent (L+M).

For the three adaptation levels, ΔΘ (the phase delay between the M- and L-cone signals) can be obtained from the phase lag data and the model fits shown in Fig. 3. We summarize them in Table 3. From those fits, we should expect the spectral sensitivities to be spectrally opponent at low frequencies (L–M), changing towards non-opponent (L+M) as the frequency is increased.

Table 3.

Phase delays (deg) between the M- and L-cone flicker signals at 1, 10 and 20 Hz for subjects AS and DP

	Freq (Hz)	Low	Medium	High
AS	1	149.2	163.7	170.1
	1 (fitted)	147.1	143.0	141.7
	10	25.3	67.3	101.8
	20	74.3	50.3	32.5
DP	1	152.1	166.4	172.1
	1 (fitted)	146.7	146.0	143.8
	10	41.7	73.6	108.8
	20	36.2	43.9	38.2

Phase delays were estimated from the fits of the time delay model to the phase lags shown in Fig. 3 for the low (column 3), medium (column 4) and high (column 5) 658 nm intensities used to calculate the 1, 10 and 20 Hz flicker detection spectral sensitivities shown in Fig. 6, except s labelled 1 (fitted), which are best-fitting phase lags. See text for details.

Figure 6 shows spectral sensitivities for AS (left panels) and DP (right panels) measured at the low (upper panels), medium (middle panels) and high (bottom panels) levels of the 658 nm background. Flicker frequencies of 1 Hz (dotted circles), 10 Hz (dotted squares) and 20 Hz (dotted triangles) were used. At 1 Hz the flicker sensitivity was measured at more wavelengths in order to locate more accurately the expected dip in sensitivity known as Sloan's notch, which is thought to reflect spectrally opponent processing (e.g. Thornton & Pugh, 1983). We found the best fit of eqn (1) to each of the spectral sensitivities at wavelengths ≥ 500 nm by varying a and b, and fixing the value of ΔΘ at the value estimated from the fits of the time delay model to the phase delay data shown in Fig. 3. The fits are shown in each panel by the dashed lines at 1 Hz and by the continuous lines at 10 and 20 Hz.

Figure 6. Flicker detection spectral sensitivities.

Flicker detection spectral sensitivities for 1 Hz (dotted circles), 10 Hz (dotted squares) or 20 Hz (dotted triangles) for AS (left panels) and DP (right panels) measured at the low (upper panels), medium (middle panels) and high (bottom panels) intensities of the 658 nm background field. The dashed lines at 1 Hz and the continuous lines at 10 and 20 Hz are fits of vector combinations of the Stockman & Sharpe (2000) cone fundamentals to the data, given the phase delay between the M- and L-cone signals determined above with best-fitting L/M cone weights (a in eqn (1)). The continuous lines at 1 Hz are vector combinations of the cone fundamentals with best-fitting phase delays between the M- and L-cone signals (see Table 3) and best-fitting L/M cone weights. For clarity, the 1 Hz and 10 Hz flicker detection spectral sensitivity data have been shifted vertically by 1.5 and 3 log₁₀ units, respectively.

The fits to the 10 and 20 Hz flicker detection data are acceptable for both subjects at all three levels. The fits to the 1 Hz data, however, are poor at both the medium and the high 658 nm adaptation levels. To estimate the values of ΔΘ that are more consistent with the 1 Hz spectral sensitivity data, we fitted eqn (1) to the data and allowed ΔΘ, as well as a and b, to vary. The best-fitting values of ΔΘ are tabulated in Table 3, and the fits are shown by the continuous lines at 1 Hz in Fig. 6. The fitted values of ΔΘ at 1 Hz are about 20–30 deg lower than those inferred from the phase lag measurements. They are shown by the lengths of the vertical lines plotted at 1 Hz in Fig. 3. The fitted and inferred values of ΔΘ at 1 Hz are consistent at the low adaptation level.

Phase lags of 142–146 deg at 1 Hz, rather than the inferred lags of 163–172 deg are still large enough to be consistent with an inverted slow M-cone signal and a non-inverted L-cone signal. We suspect that the discrepancies arise because the expected cancellation between the M- and L-cone luminance signals does not reduce the resultant signal as much as expected, probably because the threshold drop is limited by another signal that does not affect the phase of the luminance signal. We suggest that this signal might be the true chromatic signal, which as we noted above makes flicker nulls impossible to set below ca 5 Hz.

Discussion

On low to moderate intensity red fields, we find clear evidence for interactions between four different cone signals in the perception of achromatic flicker. These signals are, in our nomenclature, +fM, +fL, −sM and +sL. The two fast signals (+fM and +fL) are consistent with the conventional non-opponent inputs to the luminance channel, while the slow signals (+sL and −sM) are spectrally opponent inputs. These spectrally opponent inputs are not associated with a ‘chromatic’ sensation, so are, in a perceptual sense at least, consistent with the traditional view of the luminance channel as an achromatic channel. The inputs are similar to those in the model shown in Fig. 13 of the previous paper, except that the polarities of the slow M- and L-cone inputs are reversed.

The results presented here suggest that our view of the psychophysical, luminance channel as a simple (L+M) channel needs to be revised. Under long-wavelength adaptation, flicker detection and flicker photometry are mediated by a channel with an achromatic output but with spectrally opponent and non-opponent inputs. As we will demonstrate in subsequent work, these inputs are also found under most other conditions of chromatic adaptation.

Receptoral and postreceptoral phase delays

Since light adaptation speeds up the light response of cone photoreceptors (e.g. Baylor et al. 1984), phase and amplitude differences between the M- and L-cone signals will arise if the adaptational states of the M- and L-cone photoreceptors are different. On the red, 658 nm field, to which the L-cones are more sensitive than the M-cones by a factor of ca 12.5 (Stockman & Sharpe, 2000), the L-cones will be significantly more light adapted at most background radiances. Figure 7 for AS (left panels) and DP (right panels) shows the measured phase differences between the M- and L-cone signals plotted as white dotted diamonds, squares and circles, respectively, for the low, medium and high 658 nm intensity levels, respectively (the plotted delays are simply the differences between the M- and L-cone phase delays shown in Fig. 3, above). It is important to understand which portions of these phase delays are due to differential photoreceptor adaptation and which portions are due to postreceptoral differences between the slow and fast pathways. Fortunately, we can use the binocular phase delay measurements to estimate the receptoral differences (A. Stockman, M. Langendörfer, L. T. Sharpe, unpublished observations). They measured pure M-cone phase delays in protanopes using a binocular cancellation technique in which the adaptation state in one eye was fixed, while that in the other eye was varied. The measured M-cone phase delays were found to decrease as the luminance level rose to ca 3.4 log₁₀ photopic trolands (ph td) but then to level off, remaining fairly constant above ca 4.3 log₁₀ ph td. We have used their binocular phase delay data for their primary subject (ML) to predict the M- and L-cone phase delays that should be expected on the three red 658 nm fields used in our experiments. To make the prediction, we first estimated the total effective quanta at λ_max separately for the M- and L-cones for each adaptation condition (i.e. we converted all the target and background radiances to equivalent quanta at the M- or L-cone λ_max using the Stockman & Sharpe (2000) cone fundamentals). Assuming that the quanta at λ_max are equally effective for the M- and L-cones, we then used the M-cone binocular data, similarly estimating the equivalent quanta at λ_max for each level (and, if necessary, interpolating between levels), to estimate the phase delays that should be expected because of differences in photoreceptor adaptation (that is, we estimated the phase delays for the M- and L-cones separately and then took the difference between them). We used those differences to correct the measured phase delays shown in Fig. 7. The corrected delays are shown by the grey dotted symbols in each panel; these are therefore the estimated postreceptoral delays between the slow and fast pathways. The bottom panels compare the three adjusted phase delays for each subject. The corrections are limited to lower frequencies, because binocular phase delays cannot be measured at higher frequencies (presumably because of filtering before binocular convergence).

Figure 7. Receptoral and postreceptoral phase delays.

Estimates of the phase differences between the M- and L-cone signals for AS (left panels) and DP (right panels) that remain after the effects of photoreceptor adaptation are taken into account. Measured phase differences are shown as open dotted circles, diamonds and squares, respectively, for the low (upper panels), medium (upper middle panels), and high (lower middle panels) conditions. The grey dotted symbols in each of these three panels are the phase delays corrected for the effects of relative M- and L-cone photoreceptor adaptation. The lower panels compare the three adjusted functions. The continuous lines in the lower panels are consistent with a time delay of 17.0 ms (AS) or 15.5 ms (DP). See text for details.

The corrected phase delays are similar at the two higher levels, but slightly lower in phase delay at the lowest intensity level. We suggest that the two higher levels reflect the asymptotic phase delays associated with the postreceptoral pathways, while the difference between the lowest and the two higher levels reflects some postreceptoral adaptation. We also suggest that the slopes of the asymptotic phase delays define the actual delay between the slow and fast pathways. The fitted slopes, constrained to go through −180 deg, indicate delays of 17.0 and 15.5 ms for AS and DP, respectively.

Earlier work

The identification of a −sM input and its interaction with the +fM and +fL signals on low to moderate intensity deep-red fields (Stockman & Plummer, 1994) was a follow-up to earlier work in which we identified a +sM input on high intensity red fields (Stockman et al. 1991). Subsequent to these preliminary reports, we have extended our measurements and refined our analyses in order to present a unified working model of the organization and operation of the postreceptoral human visual system. In the previous paper, we described the slow +sM and −sL signals (Stockman et al. 2005), and in this paper we describe the slow +sL−sM signals.

Psychophysical evidence for slow, inverted inputs to the luminance channel can be found in the phase delay data of Lindsey et al. (1986) and Swanson et al. (1987), although the results were not originally interpreted as such. Using M-cone-isolating stimuli, Stockman & Plummer (1994) revealed a slow, inverted cone input (−sM), which they explicitly identified as a luminance input. They found, in addition to the signal inversion, a delay of 20 ms (a delay that has since been confirmed precisely by Stromeyer et al. 1997). Evidence for a slow cone input to luminance of the same sign (+sM) as the faster L- and M-cone inputs was first obtained by Stockman et al. (1991) on an intense red field (see also Stockman et al. 2005). A similar M-cone signal has since been observed on green and blue backgrounds (Stromeyer et al. 1997).

Stromeyer et al. (1995, 1997) inferred the presence of spectrally opponent +sM−sL and +sL−sM signals from phase data obtained mainly from motion experiments, but also from flicker experiments (see also Stromeyer et al. 2000). Their novel contribution was to observe that +sM−sL signals predominate on shorter wavelength fields. But the idea that sluggish ‘chromatic’+sL−sM signals oppose faster ‘luminance’ signals on longer wavelength fields was proposed several years earlier by Smith et al. (1992) to account for data obtained from macaque magnocellular-projecting (MC) ganglion cells.

Working model

Were these slow +sL−sM and −sL+sM signals found only on deep-red fields, they might be dismissed as quirks that occur only when the system is driven outside of its normal operating range by long-wavelength adaptation. However, as the work of others suggests (Lindsey et al. 1986; Swanson et al. 1987; Smith et al. 1992; Stromeyer et al. 1997), and as we demonstrate in these and future papers, the effects of the slow signals are evident under almost all adaptation conditions. Indeed, their presence seems to be an essential and unavoidable property of the human visual system.

In our working model, the luminance channel receives paired +sM and −sL or paired −sM and +sL inputs in addition to the fast +fM and +fL inputs. Because of their opposite signs, these slow signals destructively interfere, so that unless the +sM and −sL and +sL and −sM signals are perfectly balanced and cancel each other completely, one or other pair dominates under a particular set of conditions. Under low to moderate intensity long-wavelength adaptation the −sM and +sL pair dominates, and is revealed in flicker measurements. Under intense long-wavelength adaptation the +sM and −sL pair dominates, and is revealed in flicker measurements (Stockman et al. 2005). Although already substantial in their effects on psychophysical measurements, we speculate that the effects of the slow +sM−sL and +sL−sM signals would be larger still, were it not for the fact that they partially cancel each other.

As noted above, we assume that the weights of the opposing slow signals are approximately balanced (−sM ≈+sL), so that no slow signal is found under equichromatic conditions. This assumption might seem inconsistent with the different slow/fast signal ratios (m) determined for the M- and L-cones, which are tabulated in Table 2. However, the ratios are relative, so that we do not actually know how the sizes of the M- and L-cone signals compare. If we assume that +sM =−sL, then +fL > +fM. A larger +fL than +fM is expected from the asymmetry of L- and M-cone inputs into the luminance channel (e.g. Smith & Pokorny, 1975; Stromeyer et al. 1985), which is also found for subjects DP and AS. This asymmetry is further exaggerated on long-wavelength fields by an additional suppression of the +fM signal (or M-cone luminance input). An overall suppression of +fM contrasts with the relative suppression of the L-cone contribution to flicker sensitivity at 15 or 22.5 Hz previously reported on red fields (Eisner & MacLeod, 1981; Stromeyer et al. 1987, 1997). This paradox may arise because at those frequencies flicker spectral sensitivity can also be altered by constructive and destructive interference between slow and fast flicker signals generated by the same cone type.

It is remarkable that a simple time delay model can account so well for both the phase lag and the modulation sensitivity data. There are some deviations from this model (see above), some of which can be accounted for in a more complex model in which the slow signal is passed through an additional stage of low-pass temporal filtering. Such a model reduces the root mean square (r.m.s.) error of the fits, but is not a substantial improvement over the simpler model presented here.

Achromatic and chromatic channels

The opposition and coexistence of the +sM and −sL signals might be taken to show that the flicker cancellation method that we use is influenced not just by the output of the luminance pathway, but also by the output of a classical red–green chromatic pathway. Yet, two properties of the signals involved argue against such an interpretation. First, the flicker produces an achromatic percept that can be flicker-photometrically cancelled – it does not produce, as might be expected of a red–green chromatic pathway, a chromatic percept. Second, the temporal frequency responses of +sM and −sL extend to moderately high frequencies, well beyond the temporal frequency response of the psychophysically defined chromatic pathway (see, for example, De Lange, 1958a; Wisowaty, 1981). We must conclude that the slow spectrally opponent inputs that we observe produce an achromatic, luminance output.

These slow signals have undoubtedly influenced experimental results many times before. They would have affected, particularly at moderate and high temporal frequencies, most measurements in which ‘chromatic’ sensitivity was determined by measuring the sensitivity to alternating lights matched in luminance (e.g. Ives, 1917; De Lange, 1958b). They probably underlie, for example, parts of the ‘chromatic band’ of the two-band model of heterochromatic flicker of Kelly & van Norren (1977), as well as many other functions measured with equiluminant flicker.

An important question raised by our working model is how the chromatic flicker signals that produce a visible change in colour are related to these slow ‘spectrally opponent’ signals that supposedly feed into the achromatic channel? A clue comes from observations (so far, found under all conditions) that perfect flicker nulls cannot be made at frequencies below 5 Hz, because of the presence of chromatic flicker. These observations suggest that the sensitivity of the true chromatic channels are higher at lower frequencies, but then fall off steeply with increasing frequency, revealing the slow opponent inputs to the achromatic channel that contribute to flicker nulls. Indeed, Wisowaty (1981), who specifically measured the sensitivity for seeing chromatic flicker as a colour alternation, obtained a steeply falling temporal sensitivity function that was much steeper than the functions for detecting the ‘chromatic’ flicker that, we argue, feeds into the achromatic channel (e.g. the functions of Kelly & van Norren, 1977; and filled symbols, Figs 4 and 5, above).

Physiological considerations

Some of the phase and amplitude characteristics that we identify psychophysically can be found not only in the responses of macaque magnocellular (MC) ganglion cells (Smith et al. 1992), but also in the responses of macaque parvocellular (PC) ganglion cells (Gouras & Zrenner, 1979; Lankheet et al. 1998), although other studies of PC responses show smaller temporal-frequency-dependent effects (Derrington et al. 1984; Lee et al. 1989, 1994; Smith et al. 1992; Benardete & Kaplan, 1997). These data suggest that the origin of the slow and fast signals is retinal, and that they can be found in either PC or MC cells or both. However, we should be cautious, since any signals found in the retina will be modified by multiple stages before guiding the observer's response in a psychophysical task. Relating the behaviour of the whole organism to the behaviour of single retinal cells in a simplistic way, although appealing, is often misguided. In particular, the idea that the psychophysical luminance channel is a simple additive L+M channel, which can be related to the behaviour of MC cells (e.g. Livingstone & Hubel, 1987; Kaplan et al. 1990; Lee et al. 1990; see for a review of luminance, Lennie et al. 1993), is an idea that has dominated vision research for many years, but the psychophysical and physiological foundations of the luminance channel have always been weak, and the choice of supporting evidence to some extent selective (see above). The data reported here add more psychophysical weight to the conclusion that the achromatic luminance channel that subserves flicker perception has complex cone inputs. Physiologically, too, new evidence of more complex interactions is emerging. Sun & Lee (2004) recently claimed to find PC signals in the responses of MC cells.

Although a retinal origin for the slow and fast signals has a good deal of support, a cortical origin cannot be ruled out. Indeed, the substantial delay between the slow and fast signals might arise because of differences in the transmission times of parvocellular and magnocellular signals to the cortex, where the two signals might then interact to generate an achromatic flicker signal. Indeed, the parvocellular system is delayed by on average 17 ms relative to the magnocellular system at the level of the lateral geniculate nucleus (LGN) (e.g. Schmolesky et al. 1998), although other estimates at the LGN or cortex are lower at about 10 ms (e.g. Maunsell & Gibson, 1992; Maunsell et al. 1999). These delays are comparable to the delays between the slow and fast signals that we find (see Fig. 7). Moreover, transmission delays are more likely to be consistent with a simple time delay model than other causes of delay.

We conclude that the separation of visual information into channels is not as simple as many hypothesize. Rather than trying to preserve the idea of the visual system as a perfect system that cleanly and separately processes different functional streams of visual information, we should perhaps be thinking of a less tidy system that inherently mixes some of the information across or within different streams. Were we to make the speculative link between psychophysics and physiology, we might suggest that our psychophysical data reflect the mix of spectrally opponent PC and non-opponent MC inputs into an achromatic channel. We might further suggest that the PC inputs, which can be of either polarity (M–L or L–M), are balanced on neutral fields and destructively interfere, thereby reducing the PC signal. On chromatic fields, however, because of selective adaptation, one or other polarity becomes more prominent. On an intense red field, the M–L signal is more prominent, while on a red field of low to moderate intensity, the L–M signal is more prominent. Such an imbalance with chromatic adaptation can be found in PC cell data (e.g. Yeh et al. 1996). A consequence of the above scheme is that the slow signals will be small, and thus hard to identify under the typical experimental conditions that are so pervasive in contemporary vision research (e.g. modulations produced by a monitor around a white point in an equiluminant plane in LMBDKL space; Luther, 1927; MacLeod & Boynton, 1979; Derrington et al. 1984). Our model will be developed more fully in a subsequent paper.

Conclusions

Under long-wavelength adaptation, multiple cone signals contribute to achromatic flicker perception. These signals, which can be fast (+fM, +fL) or slow and of the same or of different sign (+sM, −sL, −sM, +sL and −sS), constructively and destructively interfere to produce characteristic, frequency-dependent changes in spectral sensitivity, modulation sensitivity and phase delay data. The luminance channel has an achromatic output, but slow spectrally opponent inputs in addition to the expected non-opponent inputs.

The implications of these results for much recent and current vision research are fascinating. For one thing, they suggest that the luminance channel cannot be silenced by isoluminant stimuli. Instead, such stimuli not only excite the chromatic channels, but also the slow inputs to the achromatic channel. As a result, the conclusions of some experiments carried out at isoluminance may have to be reconsidered. The unusual properties of perception at isoluminance could be the result of the slow, spectrally opponent inputs to the achromatic channel rather than to the behaviour of chromatic channels per se.