Abstract
Spike frequency adaptation (SFA) is a fundamental property of repetitive firing in motoneurones (MNs). Early SFA (occurring over several hundred milliseconds) is thought to be important in the initiation of muscular contraction. To date the mechanisms underlying SFA in spinal MNs remain unclear. In the present study, we used both whole-cell patch-clamp recordings of MNs in lumbar spinal cord slices prepared from motor functionally mature mice and computer modelling of spinal MNs to investigate the mechanisms underlying SFA. Pharmacological blocking agents applied during whole-cell recordings in current-clamp mode demonstrated that the medium AHP conductance (apamin), BK-type Ca2+-dependent K+ channels (iberiotoxin), voltage-activated Ca2+ channels (CdCl2), M-current (linopirdine) and persistent Na+ currents (riluzole) are all unnecessary for SFA. Measurements of Na+ channel availability including action potential amplitude, action potential threshold and maximum depolarization rate of the action potential were found to correlate with instantaneous firing frequency suggesting that the availability of fast, inactivating Na+ channels is involved in SFA. Characterization of this Na+ conductance in voltage-clamp mode demonstrated that it undergoes slow inactivation with a time course similar to that of SFA. When experimentally measured parameters for the fast, inactivating Na+ conductance (including slow inactivation) were incorporated into a MN model, SFA could be faithfully reproduced. The removal of slow inactivation from this model was sufficient to remove SFA. These data indicate that slow inactivation of the fast, inactivating Na+ conductance is likely to be the key mechanism underlying early SFA in spinal MNs.
In response to sustained supra-threshold input, many classes of neurones, including motoneurones (MNs), exhibit a time-dependent decrease in action potential discharge rate. This phenomenon is termed ‘spike frequency adaptation’ (SFA). SFA is typically divided into two phases: early, occurring over the first hundreds of milliseconds of firing; and late, occurring over tens of seconds or even minutes (Granit et al. 1963; Kernell, 1965; Kernell & Monster, 1982b; Spielmann et al. 1993). In addition, some studies include a third ‘initial’ phase limited to the first few spikes (Sawczuk et al. 1995). The functional role of this fundamental property remains unclear. The shorter initial interspike intervals associated with early adaptation may help to increase the speed of force generation in muscle fibres which can be sustained with lower frequencies (Stein & Parmiggiani, 1979). Later phases of adaptation may contribute to central fatigue during sustained muscular contractions (Kernell & Monster, 1982a).
Interestingly, the mechanisms underlying SFA may be modulated during behaviour. This is evidenced by intracellular recordings from cat lumbar spinal MNs during fictive locomotion where early SFA is not apparent within each step cycle (Brownstone et al. 1992) and late SFA is seemingly reversed during extended bursts of locomotion (Krawitz et al. 1996). Therefore, in order to understand how motor output is produced during behaviour, it is necessary to first understand the underlying mechanisms of repetitive firing and then to study how such mechanisms can be modulated.
The mechanisms underlying SFA are poorly defined. In MNs, considerable attention has focused on the role of the action potential medium afterhyperpolarization (AHP) which is mediated by a calcium-dependent potassium conductance (KCa, SK). It is hypothesized that increased calcium entry during repetitive firing and subsequently greater activation of Ca2+-dependent K+ channels (AHP summation), leads to progressively greater interspike intervals and hence a reduction in firing frequency over time. In support of this hypothesis, AHP summation can be observed in MNs when successive action potentials are stimulated (Ito & Oshima, 1962; Granit et al. 1963; Baldissera & Gustafsson, 1971). Furthermore, MN modelling studies based on these findings have demonstrated that the inclusion of an AHP conductance facilitates simulation of SFA (Baldissera et al. 1973; Kernell & Sjoholm, 1973; Baldissera & Gustafsson, 1974). Evidence for involvement of the AHP in SFA in other cell types includes data from rat hippocampal pyramidal neurones where block of the AHP conductance leads to reductions in adaptation (Madison & Nicoll, 1984).
Despite the focus on AHP summation some studies have demonstrated SFA independent of the AHP. Although such data are lacking for spinal MNs, findings in hypoglossal MNs demonstrate that the AHP contributes to initial but not later phases of adaptation (Viana et al. 1993; Sawczuk et al. 1997; Powers et al. 1999). AHP-independent SFA has also been reported in other neuronal types including substantia gelatinosa neurones (Melnick et al. 2004) and neocortical neurones (Fleidervish et al. 1996). Where SFA has been found to occur in the absence of the AHP, data indicate that conductances which underlie the action potential may be involved in SFA (Fleidervish et al. 1996; Powers et al. 1999; Melnick et al. 2004). In particular, slow inactivation of Na+ currents has been implicated as a contributing factor in SFA (Fleidervish et al. 1996; Powers et al. 1999; Blair & Bean, 2003). Whether sodium channel inactivation is critical for SFA in spinal MNs remains to be determined.
To increase our understanding of the production of repetitive firing in MNs, and hence motor output controlling the extremities, we have investigated the mechanisms underlying SFA in lumbar MNs using whole-cell patch-clamp recordings in mouse spinal cord slice preparations. The aim was to establish which conductances underlie early SFA in spinal MNs. Using a combination of whole-cell patch-clamp recordings and MN modelling we demonstrate that slow inactivation of the fast, inactivating Na+ conductance is likely to be the key mechanism underlying early SFA in spinal MNs.
Methods
Slice preparation
Experiments were performed on spinal cord slices obtained from P8–P14 Swiss Webster or C57BL/6 mice. All procedures were approved by the Dalhousie University animal care committee and conformed to the guidelines of the Canadian Council of Animal Care. One to three days prior to experimentation animals received i.p. injections of Fluoro-Gold (0.04 mg (g body weight)−1; Fluorochrome Inc., Denver, CO, USA) to retrogradely label MNs (Leong & Ling, 1990; Merchenthaler, 1991).
The isolation of the spinal cord and preparation of thin slices was performed as previously described (Carlin et al. 2000a, b). Briefly, animals were anaesthetized with ketamine (500 mg kg−1) and partially submerged in ice-cold water for ∼2 min. Following decapitation and evisceration, the spinal cord was dissected free in a dissecting chamber containing cold (< 4°C) dissecting artificial cerebrospinal fluid (aCSF). The lumbar enlargement was then isolated, glued against a block of agar (2%) and mounted in a vibrating microtome (Vibratome 3000, Vibratome Company, St Louis, MO, USA). Slices (∼250 μm thick) were cut using a sapphire blade (Delaware Diamond Knives, Wilmington, DE, USA) and were immediately placed in warm (∼35°C) recovery aCSF. Following ∼45 min in recovery aCSF slices were transferred to a holding chamber containing recording aCSF at RT (22–24°C). Individual slices were then transferred to a recording chamber (Warner Instruments, Hamden, CT, USA), continuously perfused (3–5 ml min−1) with recording aCSF at RT, where they were visualized with epifluorescence infrared differential interference contrast microscopy using a Leica DMLFSA upright microscope (Leica Microsystems, Richmond Hill, ON, USA) and a DAGE IR-1000 digital camera (DAGE-MTI, Michigan City, IN, USA).
Whole-cell patch-clamp recordings
Whole-cell patch-clamp recordings were made from Fluoro-Gold positive MNs. Patch electrodes (resistance 3–4 MΩ) were pulled on a Sutter P-87 puller (Sutter Instrument Company, Novato, CA, USA) from 1.5 mm o.d. filamented borosilicate glass (World Precision Instruments, Sarasota, FL, USA). Signals recorded using whole-cell patch-clamp techniques were amplified and filtered (4 kHz low pass Bessel filter) using a MultiClamp 700A amplifier (Axon Instruments, Union City, CA, USA). Amplified signals were acquired at ≥ 10 kHz using a Digidata 1322A A/D board and pCLAMP software (Axon Instruments). Series resistance, whole cell capacitance, and input resistance values were calculated using pCLAMP software. All voltage and current-clamp protocols are described in Results. Signals were analysed offline using Clampfit software (Axon Instruments).
All data are reported as means ± s.e.m. Differences in means were compared using Student's t test. Differences in the variance of samples were assessed using an F-test. Values of P < 0.05 were considered significant. Boltzmann fits were performed using Microsoft Excel as described by Brown (2001). Exponential curve fitting was performed using the Levenberg-Marquardt method in Clampfit software.
Solutions and drugs
The dissecting aCSF was sucrose based (Aghajanian & Rasmussen, 1989) and contained (mm): 25 NaCl, 188 sucrose, 1.9 KCl, 10 MgSO4, 26 NaHCO3, 1.2 NaH2PO4, 25 d-glucose, 1.5 kynurenic acid (equilibrated with 95% O2–5% CO2). The recovery aCSF contained (mm): 119 NaCl, 1.9 KCl, 1 CaCl2, 10 MgSO4, 26 NaHCO3, 1.2 NaH2PO4, 20 d-glucose, 1.5 kynurenic acid, 3% dextran (equilibrated with 95% O2–5% CO2). The standard recording aCSF contained (mm): 127 NaCl, 3 KCl, 2 CaCl2, 1 MgSO4, 26 NaHCO3, 1.25 NaH2PO4, 10 d-glucose (equilibrated with 95% O2–5% CO2).
The standard pipette solution for whole-cell patch clamp recordings contained (mm): 140 potassium methane-sulphonate, 10 NaCl, 1 CaCl2, 10 HEPES, 1 EGTA, 3 ATP-Mg, 0.4 GTP (pH 7.2–7.3 adjusted with KOH, osmolarity adjusted to ∼300 mosmol l−1 with sucrose).
For experiments investigating Na+ currents, external and pipette solutions were designed to eliminate Ca2+ and K+ currents. The external solution contained (mm): 115 NaCl, 3 KCl, 30 TEA-Cl, 10 HEPES, 1 MgCl2, 2 CaCl2, 10 d-glucose, 4 4-AP (gassed with 100% O2, pH 7.35 adjusted with NaOH, osmolarity ∼305 mosmol l−1). The pipette solution contained (mm): 100 caesium methane-sulphonate, 30 TEA-Cl, 10 NaCl, 1 CaCl2, 10 HEPES, 1 EGTA, 3 ATP-Mg, 0.4 GTP (pH 7.2–7.3 adjusted with KOH, osmolarity adjusted to ∼295 mosmol l−1 with sucrose).
All drugs were made up as concentrated stock solutions and stored in single use vials (to eliminate freeze thaw cycles) at –20°C. Final concentrations were achieved by diluting stock solutions in aCSF. Stock solutions of apamin, cadmium chloride and iberiotoxin were made up in distilled water. Stock solutions of riluzole and linopirdine were made up in ethanol (final concentration of ethanol, 0.2%). Drug application was via addition to the perfusate.
Modelling
The MN model was built with two compartments (soma and dendrite) using Igor Pro 4.0 (Table 1). Four active conductances were included in the soma compartment. They were fast sodium (gNa), delayed rectifier potassium (gKdr), N-type calcium (gCaN), and calcium-dependent potassium (gKahp) conductances. A leak conductance (gleak) was also included in the soma and dendrite compartments. No active conductance was included in the dendrite compartment. The Hodgkin-Huxley equations for the ionic currents are written as:
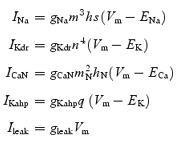 |
where, letters m, h, s, n and q (with or without subscripts) are membrane state variables: m stands for activation of gNa; h for fast inactivation of gNa; s for slow inactivation of gNa; n for activation of gKdr; mN for activation of gCaN; hN for inactivation of gCaN, and q for activation of gKahp. The state variables are defined by the Hodgkin-Huxley type equation:
Steady-state value X∞=α/(α+β) and time constant τ= 1/(α+β).
Table 1.
The model structure
| Diameter (μm) | Length (μm) | RM (Ω cm2) | RA (Ω cm) | CM (μF cm−2) | |
|---|---|---|---|---|---|
| Soma | 12 | 100 | 7000 | 20 | 1.0 |
| Dendrite | 8 | 200 | 7000 | 20 | 1.0 |
Parameters for gNa were based on the results of the present study. A slow inactivation mechanism for gNa with a time constant of 129.2 ms was included. Parameters for other conductances were based on previous modelling (Dai et al. 2002). Small changes in gCaN and gKahp were made to make the AHP amplitude and duration and the frequency–current (f–I) relation of the model comparable to the real MN data (Tables 2 and 3). The densities of maximum conductance for gNa, gKdr, gCaN and gKahp were set to 120, 100, 4, and 1 mS cm−2, respectively. The leak and coupling conductances were chosen so that the properties of the model (input resistance, rheobase, and f–I relation) were comparable to those of the real MNs. The gleak was set to 5.38 × 10−6 mS and 7.18 × 10−6 mS for the soma and dendrite compartments, respectively. Coupling conductance between the soma and dendrite compartments was set to 1.5 × 10−3 mS. The resting membrane potential was set to 0 mV which is equivalent to −60 mV in the real cell. Equilibrium potentials for Na+, K+, and Ca2+ were set as follows: ENa= 115 mV, EK=–10 mV, and ECa= 140 mV. The time step for simulations was 0.02 ms.
Table 2.
Rate constants in Hodgkin-Huxley equations in soma compartment
| Conductance | Forward (α) | Backward (β) | ||
|---|---|---|---|---|
| gNa | ||||
| gKdr | ||||
| gCaN | ||||
| gKahp |
Table 3.
Membrane properties of real MNs and the model MN
| Cm (pF) | Rin (MΩ) | τm (ms) | Em (mV) | Ith (pA) | Imin (pA) | f–I slope (Hz nA−1) | AHP amplitude (mV) | AHP duration (ms) | |
|---|---|---|---|---|---|---|---|---|---|
| MN | 93 ± 12 | 83 ± 17 | 7.7 | − 65 ± 3 | 216 ± 28 | 450 ± 90 | 76 ± 19 | 4.3 ± 0.7 | 113 ± 4 |
| Model | 90 | 80 | 7.0 | − 1.3* | 250 | 330 | 77 | 4.7 | 108 |
Cm: whole cell capacitance. Rin: input resistance. τm: membrane time constant. Em: resting membrane potential. Ith: current threshold (rheobase). Imin: the min current for evoking repetitive firing. In MNs, Ith was calculated using 10 ms current pulses; AHP parameters were measured from single action potentials evoked by single current pulses (amplitude =Ith, duration = 10 ms).
Em= 0 in the model equivalent to −60 mV in the real cell. In the model, AHP parameters were measured from single action potentials evoked by single current pulses (amplitude = 1.5 nA, duration = 2 ms).
The intracellular calcium concentration [Ca2+]i in the soma compartment was defined by the equation (Traub et al. 1991):
where B is a scaling constant in arbitrary units set to −50; τCa is a time constant set to 20 ms; and ICaN is an N-type Ca2+ current.
The membrane properties of the real MNs and modelled MN are shown in Table 3.
Results
Role of K+ currents in SFA
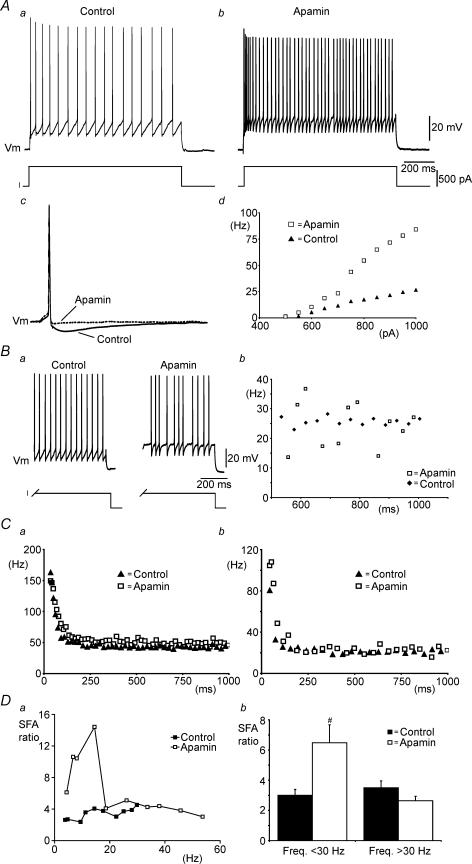
In spinal MNs, the action potential medium AHP is apamin sensitive (Zhang & Krnjevic, 1987). Therefore, to investigate the role of the AHP in the control of MN firing, we used the SK-type Ca2+-dependent K+ (KCa) channel blocker apamin. First, to verify that apamin blocked the action potential AHP in mouse spinal MNs, single action potentials and their accompanying AHPs were elicited in current clamp mode by brief (10 ms) current pulses. Application of apamin (100 nm) blocked the AHP in all MNs tested (Fig. 1Ac) (n = 6) indicating that this concentration was sufficient.
Figure 1. Apamin blocks the AHP and increases variability in steady-state firing frequency, but spike frequency adaptation (SFA) remains.
Aa and b, current-clamp recordings of repetitive firing elicited by current injection (1 s duration) in control (a) and with 100 nm apamin (b). Ac, single action potentials evoked by brief current pulses (10 ms) showing block of the AHP by apamin (dotted line). Ad, steady-state frequency versus injected current plots showing increased excitability in the presence of apamin. Ba, steady-state firing over the last 500 ms of a 1 s current pulse in control and in the presence of apamin. Bb, plot of instantaneous firing frequency versus time for firing during the last 500 ms of a 1 s current pulse showing the greater variability in frequencies in the presence of apamin. Instantaneous frequency versus time plots showing SFA in control and in the presence of apamin during relatively fast (Ca) and slow (Cb) rates of firing (current steps eliciting similar steady-state firing frequencies were chosen for each condition). Da, SFA ratio plotted versus steady-state frequency in control and in the presence of apamin for a single MN. Db, pooled data showing that apamin significantly increases adaptation at lower steady-state firing frequencies (< 30 Hz) (n = 6).
Next, to investigate the role of the AHP in the regulation of firing frequency, longer current steps (1 s duration) were used to elicit repetitive trains of action potentials (Fig. 1Aa). During apamin applications the frequency of repetitive firing was greatly increased (Fig. 1Ab). This increased excitability was associated with a significant increase (155 ± 33%, n = 6) in the slope of frequency versus injected current (f–I) plots (Fig. 1Ad). When periods of steady-state firing (at similar average frequencies) were compared in control conditions and in the presence of apamin it was evident that apamin also significantly increased the variance in instantaneous firing frequency (Fig. 1B) (n = 6). Thus, as suggested previously by Person & Kudina (1972), the AHP plays an important role in controlling firing regularity in MNs.
Despite blocking the AHP, and contrary to predictions from MN models (Baldissera et al. 1973; Kernell & Sjoholm, 1973; Baldissera & Gustafsson, 1974), apamin did not block SFA in MNs. This is best shown by plots of instantaneous frequency versus time for single current steps which elicited similar steady-state firing frequencies in control and in the presence of apamin (Fig. 1C). A similar time course in the decline in instantaneous firing frequency was seen in control and in the presence of apamin (Fig. 1C) (n = 6). To facilitate comparison of adaptation in control conditions and in the presence of apamin, a SFA ratio was calculated. The adaptation ratio equalled Finit/Ffinal, where Finit is the initial instantaneous frequency calculated from the first interspike interval and Ffinal is the final instantaneous frequency calculated form the last interspike interval (Venance & Glowinski, 2003). Interestingly, for steady-state firing frequencies < 30 Hz adaptation ratios were 2-fold greater in the presence of apamin (6.5 ± 1.2, n = 6) compared with control conditions (3.0 ± 0.9, n = 6) (Fig. 1D). When calculated from steps where steady-state firing frequencies were > 30 Hz, there was no significant difference between adaptation ratios in control (3.5 ± 0.5, n = 6) and under apamin (2.6 ± 0.3, n = 6) (Fig. 1D). These data demonstrate that rather than facilitating SFA, the AHP actually limits SFA at low steady-state firing frequencies. In comparison, at high steady-state firing frequencies the AHP has no role in SFA.
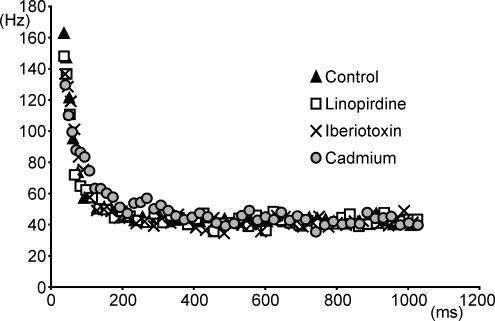
Although apamin appeared to block the AHP completely (Fig. 1Ac), we also investigated whether a remaining apamin-insensitive KCa conductance might contribute to SFA. We first examined the effects of the large conductance (BK-type) KCa channel blocker iberiotoxin (100 nm) (Galvez et al. 1990). Iberiotoxin had no effect on the f–I relationship and SFA remained when the drug was applied suggesting BK-type KCa channels are not involved in adaptation (Fig. 2, n = 5). Next we used the general voltage-activated Ca2+ channel blocker CdCl2 (0.1–0.5 mm) to block all K+ currents which depend on Ca2+ influx via these channels. Like apamin, CdCl2 increased the slope of the f–I relationship (n = 2) while SFA remained (Fig. 2, n = 5), suggesting that neither KCa channels, nor voltage-activated Ca2+ channels, are required for adaptation in MNs.
Figure 2. BK-type Ca2+-dependent K+ channels, voltage-activated Ca2+ channels and M-currents are not required for SFA.
A, instantaneous frequency versus time plots for repetitive firing elicited by single current steps. SFA remains following the application of either the BK type calcium-dependent potassium channel blocker iberiotoxin (100 nm), the general voltage-gated calcium channel blocker cadmium (0.5 mm), or the M-current blocker linopirdine (10 μm). Note, current pulses eliciting similar steady-state firing frequencies were plotted for each condition.
Given that the M-current contributes to SFA in hippocampal pyramidal neurones (Madison & Nicoll, 1984; Aiken et al. 1995) and that the M-current has been observed in turtle spinal MNs (Alaburda et al. 2002), we also examined whether this slowly activating outward current could underlie SFA in spinal MNs. Application of the selective M-current blocker linopirdine (10–25 μm) (Schnee & Brown, 1998) had no effect on the f–I relationship and did not block SFA (Fig. 2; n = 4) indicating that the M-current was also unnecessary for adaptation in MNs.
Persistent Na+ currents
Given that neither the AHP nor activity of the slowly activating outward M-current was necessary for SFA in spinal MNs we hypothesized that a slow decline in inward currents could be involved. The fact that CdCl2 did not block SFA precluded involvement of voltage-activated Ca2+ currents. Therefore, we focused on sodium channels. One possibility is that slow inactivation of a persistent Na+ conductance (GNa,P), which is present in spinal MNs (Schwindt & Crill, 1980; Li & Bennett, 2003), could underlie SFA. Thus, we proceeded to investigate the role of GNa,P in MN firing.
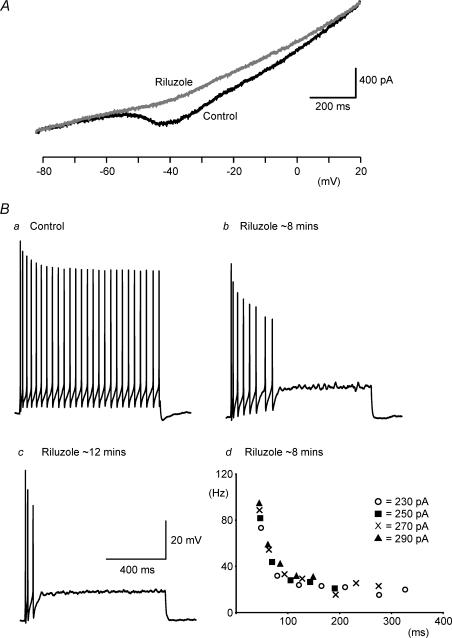
Using voltage-clamp recordings in solutions designed to minimize K+ and Ca2+ currents, persistent Na+ currents were elicited by slow voltage ramps from −90 to +30 mV. This long-lasting current activated near −55 mV and was blocked by the persistent Na+ channel blocker riluzole (10–50 μm; n = 8; Urbani & Belluzzi, 2000) (Fig. 3A). Next, in standard recording solutions, we applied riluzole (10 μm) to investigate the role of the GNa,P in repetitive firing. We predicted that if inactivation of GNa,P contributed to SFA, then riluzole application would lead to a time-dependent reduction of SFA. Conversely, riluzole gradually inhibited repetitive firing and after ∼10–20 min only one to three action potentials could be elicited by sustained current injection (n = 4; Fig. 3B). A similar block of repetitive firing by riluzole has previously been shown in pyramidal neurones of the rat cortex (Urbani & Belluzzi, 2000). Despite inhibition of repetitive firing in our recordings, at all time points following drug application SFA was clearly evident (Fig. 3Bb and c). The preservation of SFA in the presence of riluzole is best illustrated by plots of instantaneous frequency versus time for a range of single currents steps performed ∼8 min after the onset of riluzole (Fig. 3Bd). Taken together these data demonstrate that slow inactivation of a riluzole-sensitive Na+ conductance is unlikely to underlie SFA.
Figure 3. Block of persistent Na+ currents by riluzole inhibits repetitive firing but not SFA.
A, voltage-clamp recordings in solutions designed to isolate sodium currents (see Methods for details) showing the current response to a voltage ramp from −80 to +20 mV (∼70 mV s−1). Under control conditions (dark trace) a persistent inward current is revealed. This current is blocked by the persistent sodium current blocker riluzole (10 μm, light trace). B, I-clamp recordings in standard solutions showing that repetitive firing observed in control (a) is reduced (b) and eventually blocked (c) by riluzole (10 μm). Bd, instantaneous frequency versus time plots showing that although repetitive firing is reduced after 8 min of riluzole application, SFA remains. The different data series represent firing in response to current injection of varying magnitude.
Fast, inactivating Na+ currents
Early studies of SFA in spinal MNs noted an accompanying time-dependent decrease in spike height during sustained periods of discharge (Granit et al. 1963; Kernell, 1965). More recently, SFA has been shown to be associated with both a decline in spike height and decreases in the rate of spike depolarization in hypoglossal MNs (Powers et al. 1999). Since these parameters are most sensitive to the availability of Na+ channels (Hodgkin & Huxley, 1952), it seems plausible that adaptation in MNs reflects a progressive decrease in the available Na+ conductance. A similar mechanism, dependent on slow inactivation of Na+ channels, has been implicated for slow adaptation in neocortical neurones (Fleidervish et al. 1996).
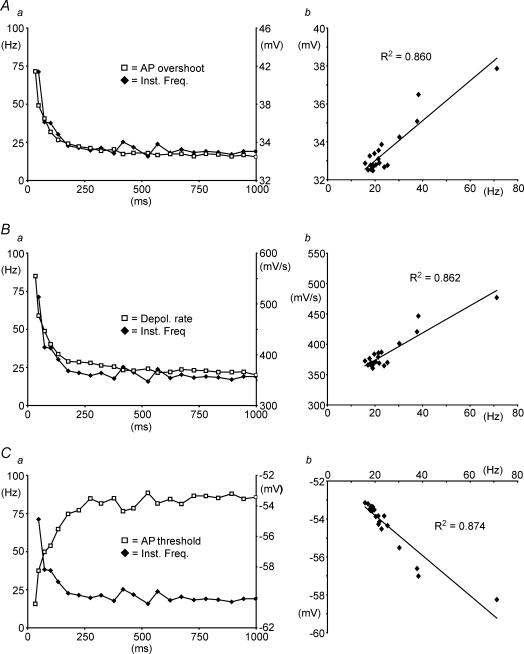
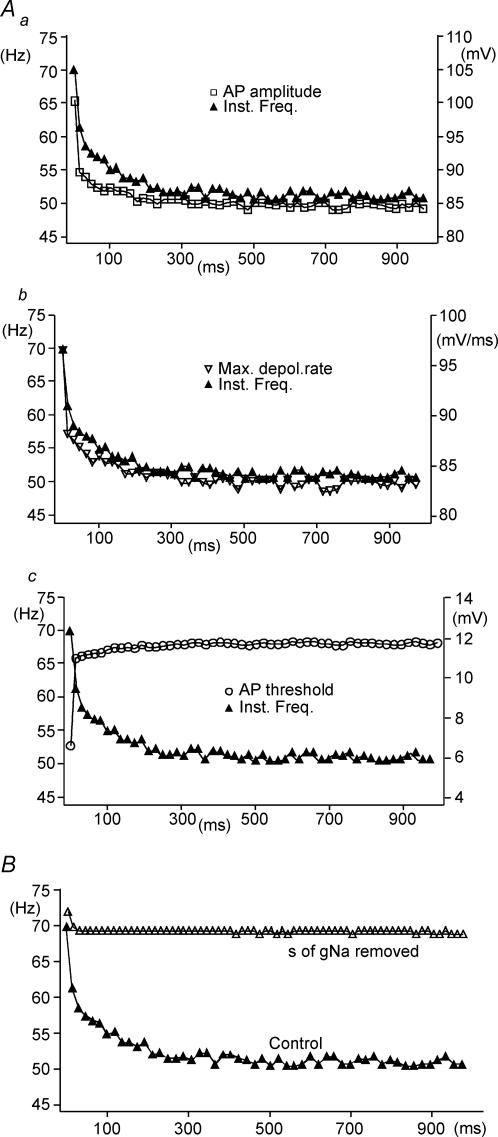
To assess the involvement of Na+ channel availability in SFA in spinal MNs, we first investigated whether parameters associated with Na+ channel availability changed in parallel with reductions in firing frequency in our recordings. Data in all cells tested (n = 4) demonstrated that action potential overshoot (measured as the amplitude above 0 mV) (Fig. 4A) and the maximum rate of depolarization during action potentials (Fig. 4B) were positively correlated with instantaneous firing frequency. In addition, action potential threshold (defined as the voltage at which dV/dt exceeded 10 mV ms−1) was negatively correlated with instantaneous firing frequency (Fig. 4C). The correlation between SFA and a decline in Na+ channel availability suggests that inactivation of Na+ channels plays an important role in adaptation.
Figure 4. SFA correlates with measurements of Na+ channel availability.
Aa, action potential overshoot versus time plotted with instantaneous frequency versus time for a single current pulse (duration 1 s). Ab, action potential overshoot plotted versus instantaneous frequency showing a strong positive correlation. Ba, maximum rate of action potential depolarization versus time plotted with instantaneous frequency versus time. Bb, maximum rate of action potential depolarization plotted versus instantaneous frequency showing a strong positive correlation. Ca, action potential threshold (defined as voltage at which rate of dV/dt = 10 mV ms−1) versus time plotted with instantaneous frequency versus time. Cb, action potential threshold plotted versus instantaneous frequency showing a strong inverse correlation.
To investigate the role of Na+ channel inactivation in SFA further it was necessary to characterize Na+ currents in spiral MNs. Activation of Na+ currents was measured using steps (10 ms) from −60 mV to test potentials ranging from −70 mV to −5 mV (2.5 mV increments) (Fig. 5Aa, inset). Activation of Na+ currents was fitted with the following Boltzmann-type equation:
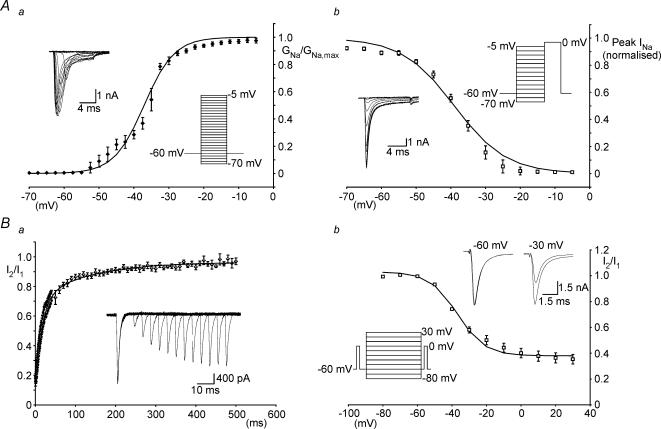
where V½ is the test potential at which GNa is half-maximal, Vtest is the voltage of the activation step and k is the slope of the fitted curve at V½. Averaged data demonstrated that the V½ for Na+ current activation in spinal MNs equalled −37 mV while k equalled 4.3 (Fig. 4Aa, n = 5–8 cells).
Figure 5. Activation and inactivation properties of Na+ currents in spinal MNs.
Aa, peak activation curve for INa fitted with a Boltzmann-type equation (Vhalf=–37 mV, slope = 4.3). Each point is from averaged data (n = 5–8 cells). Ab, steady-state fast inactivation curve for INa fitted with a Boltzmann-type equation (Vhalf=−39 mV, slope = 7.5). Each point is from averaged data (n = 8–14). Ba, time course of recovery of INa from slow inactivation measured using a two-pulse protocol (see results). The graph shows the peak current elicited by the second step (I2) divided by the peak current in response to the first step (I1) plotted versus the time between the two steps. Each point is from averaged data (n = 6). Recovery followed a bi-exponential time course with time constants of 15.7 ms and 129.2 ms. Bb, slow inactivation curve for INa fitted with a Boltzmann-type equation (Vhalf=−37 mV, slope = 8). Each point is from averaged data (n = 7). Insets in Aa, Ab and Bb depict the voltage protocol used and the currents elicited by protocols. Inset in B shows currents elicited by the two-pulse inactivation protocol.
Steady-state inactivation of Na+ channels was then measured using steps to 0 mV (10 ms duration) from prepulses (50 ms duration) ranging from −70 mV to −5 mV (5 mV increments) (Fig. 5Ab, inset). Steady-state inactivation of Na+ currents was fitted with the following Boltzmann-type equation:
where Vcond is the voltage of the inactivating prepulse. Averaged data demonstrated that the V½ for Na+ current steady-state inactivation equalled −39 mV while k equalled −7.5 (n = 8–14).
We then investigated whether Na+ channels in spinal MNs exhibit slow inactivation. This was initially assessed by examining the time course of recovery of Na+ channels from inactivation using a simple two-step protocol (Hille, 2001). Two successive steps from −40 mV to −20 mV were used with the time between steps varied from 0.5 ms to 500 ms (Fig. 5Ba, each point is from averaged data, n = 3–6). For this protocol, low amplitude voltage steps were used from a depolarized potential in an effort to minimize the peak Na+ current and therefore reduce voltage-clamp errors in these relatively long protocols. The recovery from inactivation was measured from the ratio of I2/I1, where I1 and I2 equal the current evoked by the first and second voltage steps, respectively. The relationship between recovery from inactivation and time readily fitted a bi-exponential function which had, at a holding potential of −40 mV, time constants of 15.7 and 129.2 ms. The longer time constant indicates the presence of slow inactivation. Note that the time course of slow inactivation is similar to that of SFA (compare Figs 1C and 5Ba).
Next, the parameters of slow inactivation of Na+ channels were characterized using a protocol modified from Fleidervish et al. (1996) (Fig. 5Bb). It began with an initial step from −60 mV to 0 mV (5 ms duration) to record the maximum current (I1). This was followed by a 2 s inactivating pulse ranging from −80 mV to +30 mV (10 mV increments). After the inactivating pulse the cell was returned to −60 mV for 50 ms to allow sufficient recovery from fast inactivation. A second short step (5 ms duration) to 0 mV was then used to measure the current remaining (I2) (Fig. 5Bb, inset). The degree of slow inactivation at each voltage was calculated from the ratio I2/I1. Slow inactivation of Na+ currents was fitted with the following Boltzmann type equation:
where smin is the minimum fraction of Na+ channel availability as determined by the asymptote of the slow inactivation curve (Fleidervish et al. 1996). Averaged data demonstrated that for slow inactivation of Na+ currents smin equalled 0.38, V½ equalled −37 mV and k equalled −8.0 (n = 7 cells). These data characterize the inactivation properties of sodium conductances in MNs. Furthermore, the properties of slow inactivation of the sodium conductance are such that this process could underlie SFA.
Modelling
To investigate the role of Na+ channels in SFA further we used an existing MN model (Dai et al. 2002), which was adjusted to match mouse MNs (see methods), and included Na+ channel parameters as determined above. As shown in plots of instantaneous frequency versus time, simulation of sustained current injection accurately reproduced SFA in the model (Fig. 6). Furthermore, as seen in MN recordings, both action potential amplitude (Fig. 6Aa) and the maximum rate of depolarization of action potentials (Fig. 6Ab) positively correlated with instantaneous firing frequency, while action potential threshold (again defined as the voltage at which the rate of dV/dt = 10 mV ms−1) negatively correlated with firing frequencies (Fig. 6Ac). These data indicate that the model could faithfully reproduce the repetitive firing properties observed in spinal MNs (Fig. 3).
Figure 6. The MN model exhibits SFA, which correlates with Na+ channel availability, and is dependent on the inclusion of slow inactivation of the Na+ conductance.
Data from computer modelling showing similar results, in response to injection of a single current pulse, as those seen in MN recordings. Aa, action potential amplitude and instantaneous frequency plotted versus time during simulated current injection. Ab, maximum rate of depolarization of action potentials and instantaneous frequency plotted versus time. Ac, action potential threshold (defined as voltage at which rate of dV/dt = 10 mV ms−1) and instantaneous frequency plotted versus time. B, instantaneous frequency versus time plots showing SFA in control conditions when all conductances are included in the model (filled triangles), and the abolishment of SFA when slow inactivation (s) of the Na+ conductance is removed (open triangles).
Next, we used perturbations in the model to investigate which parameters were required for SFA. As noted above, appropriate adaptation in firing frequency was observed when all parameters were included in the model (Fig. 6B, filled triangles). When slow inactivation (s) of the Na+ conductance was removed from the model, SFA was no longer induced by sustained current injection (Fig. 6B, open triangles). These data clearly support the hypothesis developed from MN recordings that slow inactivation of Na+ channels is the main factor required for SFA in spinal MNs.
Discussion
SFA is a fundamental property of MNs. However, the underlying mechanisms of SFA remain poorly understood. A number of mechanisms could underlie early SFA including summation of the AHP, slow activation of outward currents, a slow reduction in inward currents, and/or a reduction in the availability of fast, inactivating Na+ channels which underlie the action potential. In the present study we have shown that early SFA in spinal MNs of the mouse does not rely on the AHP, the slowly activating M-current, or slow inactivation of persistent Na+ currents. Instead, a reduction in the available Na+ conductance over time due to slow inactivation of fast, inactivating Na+ channels is likely to be the key mechanism underlying early SFA.
AHP-independent SFA was demonstrated in the present study by recordings from spinal MNs in which apamin blocked the AHP but not SFA. Consistent with these data, embryonic stem cell-derived MNs do not have a demonstrable AHP conductance but clearly exhibit SFA (Miles et al. 2004). The AHP has also been shown to be unnecessary for early SFA in hypoglossal MNs (Viana et al. 1993; Sawczuk et al. 1997; Powers et al. 1999) and other cell types including substantia gelatinosa neurones (Melnick et al. 2004) and neocortical neurones (Fleidervish et al. 1996). Taken together, these findings indicate that the AHP conductance is not critical to SFA in many cell types (Vergara et al. 1998; Stocker, 2004). Furthermore, contrary to the hypothesis that the AHP is involved in the production of SFA, we observed, at the lower steady-state firing rates, an increase in adaptation following block of the AHP. A similar increase in adaptation upon removal of the AHP has been reported in studies of hypoglossal MNs (Viana et al. 1993; Sawczuk et al. 1997). These data demonstrate that the AHP may be important in limiting the amount of adaptation in MNs. This is likely to reflect limits imposed by the AHP on maximum initial firing rates, particularly at lower MN discharge rates. In addition, the AHP would help to remove Na+ channel inactivation and in doing so limit SFA further.
Slowly activating outward currents including the M-current (Madison & Nicoll, 1984; Aiken et al. 1995) and the net outward current of the Na+–K+ pump (French, 1989) have also been implicated in SFA. Data supporting a role for the M-current in SFA are limited to studies of hippocampal pyramidal neurones (Madison & Nicoll, 1984; Aiken et al. 1995). Findings of the present study, showing that SFA is unaffected by the M-current blocker linopirdine, suggest that the M-current is not necessary for SFA in spinal MNs. Block of the M-current also failed to reduce SFA in a recent study of superior cervical ganglion neurones (Romero et al. 2004). The net outward current of the Na+–K+ pump has been implicated in late stages of SFA (French, 1989); however, the focus of our study was on early adaptation so this was not examined. Previous work in hypoglossal MNs has shown that block of this pump with oubain had no effect on SFA (Sawczuk et al. 1997).
Another outward current that could be involved in SFA is the Na+-dependent K+ current (IK(Na); Schwindt et al. 1989) which contributes to the slow AHP seen at the termination of repetitive firing in various neurones, including rat spinal MNs (Safronov & Vogel, 1996). It is unlikely that IK(Na) underlies SFA in spinal MNs. Firstly, SFA was observed in spinal MNs whether or not there was evidence of a slow AHP (for example, see Fig. 1). Secondly, SFA remains following block of the persistent Na+ current, which should correspondingly reduce IK(Na) (Schwindt et al. 1989). Finally, activation of IK(Na) could not explain the changes in action potential parameters which correlate with SFA. Therefore, it is unlikely that activation of an outward current underlies SFA.
A slow decline in an inward current might also contribute to SFA. An ideal candidate is the persistent Na+ current which is present in spinal MNs (Schwindt & Crill, 1980; Li & Bennett, 2003) and should diminish over time since it undergoes slow inactivation (Fleidervish et al. 1996). Although we showed that the persistent Na+ current could be blocked by riluzole, data did not support a role for this current in SFA in spinal MNs. This is consistent with recent data in hypoglossal MNs where the persistent Na+ current was reduced by phenytoin but SFA remained unchanged (Zeng et al. 2005). Although the persistent Na+ current was not involved in adaptation, it may be required for repetitive firing in spinal MNs (Fig. 3B). These data support the suggestion that a fast persistent inward current is necessary for spike initiation during repetitive firing in motoneurones (Lee & Heckman, 2001). It should be noted that riluzole can also activate TREK-1 and TRAAK leak K+ conductances (Duprat et al. 2000) and could therefore inhibit repetitive firing through activation of these currents. Given that riluzole application did not affect MN input resistance, as indicated by an unchanged current–voltage relationship in the range of resting membrane potential (Fig. 3A), and that activation of TREK-1 and TRAAK currents by riluzole would be minimal at the concentrations used in the present study (10 μm) (Duprat et al. 2000), riluzole-induced activation of leak K+ conductances is unlikely to underlie the inhibition of repetitive firing.
Previous data from some neuronal types have suggested a possible role for slow inactivation of Na+ channels in SFA (Fleidervish et al. 1996; Powers et al. 1999; Blair & Bean, 2003). Data in the present study indicate that slow inactivation of Na+ channels is likely to be critical to early SFA in spinal MNs. Firstly, parameters associated with Na+ channel availability (spike height, rate of action potential depolarization and action potential threshold) correlate with SFA (Fig. 4, present study; Granit et al. 1963; Kernell, 1965; Powers et al. 1999). Secondly, Na+ channels of spinal MNs exhibit slow inactivation from which they recover with a time course similar to that of SFA. Thirdly, in modelling studies, removal of slow inactivation parameters for the Na+ conductance abolishes SFA. We suggest that slow inactivation leads to a progressive decline in the Na+ conductance which is available to generate action potentials and that this leads to a delay in the onset of successive spikes. Further, although we have not studied later phases of SFA (Kernell & Monster, 1982b), it is possible that a similar mechanism underlies these later phases as well: there are multiple time constants for slow inactivation of Na+ channels (ranging from 100 ms to 3 min; Hille, 2001).
Since the pattern of SFA differs in various types of neurones, with some neurones not adapting at all, it seems reasonable to predict that differential expression of Na+ channels, with varying slow inactivation properties, may be an important determinant of cell-specific firing patterns. The expression of different α-subunits of the Na+ channel does vary considerably throughout the CNS, with different α-subunits conveying distinct rates of channel inactivation (for review see Goldin, 2001). In addition, modulation of Na+ channel properties, such as slow inactivation, could serve as an important mechanism for the tuning of firing patterns to suit different states or behaviours. During fictive locomotion in the cat, firing frequencies within each step cycle and over several minutes do not decrease, supporting the suggestion that the mechanisms underlying early and late SFA are modulated during this behaviour (Brownstone et al. 1992; Krawitz et al. 1996). Further, the hyperpolarization of MN action potential voltage threshold during locomotor activity also indicates that fast, inactivating sodium channels may be modulated during this behaviour (Krawitz et al. 2001; Dai et al. 2002). In support of the possibility of modulation, protein kinase C (PKC)-mediated phosphorylation has been shown to modulate the function of fast, inactivating Na+ channels. Specifically, phosphorylation leads to a reduction in the peak Na+ current and slows the inactivation of Na+ channels (Numann et al. 1991; West et al. 1991). Furthermore, receptor (muscarinic)-mediated activation of this PKC pathway, again leading to reduced peak current and slowing of Na+ channel inactivation, has been shown in rat hippocampal neurones (Cantrell et al. 1996). These data suggest that Na+ channels are likely to be targets for neuromodulators and that the modulation of Na+ channel inactivation properties is likely to be an important determinant of firing patterns.
In summary, the present study has demonstrated that SFA occurs in spinal MNs independent of the AHP conductance, the M-current, and persistent Na+ currents. Data demonstrate that slow inactivation of Na+ channels is likely to be the key mechanism underlying SFA in spinal MNs. Such findings highlight the importance of Na+ channel inactivation in determining motor output and suggest that Na+ channel modulation could be important for the control of MN firing patterns during different behaviours.
Acknowledgments
This work was supported by the Canadian Institutes of Health Research and the Nova Scotia Health Research Foundation. G.B.M. is supported by a New Zealand Foundation for Research Science and Technology post doctoral fellowship (DALH0201). R.M.B. is a Dalhousie Senior Clinical Research Scholar.
References
- Aghajanian GK, Rasmussen K. Intracellular studies in the facial nucleus illustrating a simple new method for obtaining viable motoneurons in adult rat brain slices. Synapse. 1989;3:331–338. doi: 10.1002/syn.890030406. [DOI] [PubMed] [Google Scholar]
- Aiken SP, Lampe BJ, Murphy PA, Brown BS. Reduction of spike frequency adaptation and blockade of M-current in rat CA1 pyramidal neurones by linopirdine (DuP 996), a neurotransmitter release enhancer. Br J Pharmacol. 1995;115:1163–1168. doi: 10.1111/j.1476-5381.1995.tb15019.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alaburda A, Perrier JF, Hounsgaard J. An M-like outward current regulates the excitability of spinal motoneurones in the adult turtle. J Physiol. 2002;540:875–881. doi: 10.1113/jphysiol.2001.015982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Regulation of repetitive firing in motoneurones by the afterhyperpolarization conductance. Brain Res. 1971;30:431–434. doi: 10.1016/0006-8993(71)90096-5. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Firing behaviour of a neurone model based on the afterhyperpolarization conductance time course and algebraical summation. Adaptation and steady state firing. Acta Physiol Scand. 1974;92:27–47. doi: 10.1111/j.1748-1716.1974.tb05720.x. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B, Parmiggiani F. Adaptation in a simple neurone model compared to that of spinal motoneurones. Brain Res. 1973;52:382–384. doi: 10.1016/0006-8993(73)90676-8. [DOI] [PubMed] [Google Scholar]
- Blair NT, Bean BP. Role of tetrodotoxin-resistant Na+ current slow inactivation in adaptation of action potential firing in small-diameter dorsal root ganglion neurons. J Neurosci. 2003;23:10338–10350. doi: 10.1523/JNEUROSCI.23-32-10338.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown AM. A step-by-step guide to non-linear regression analysis of experimental data using a Microsoft Excel spreadsheet. Comput Meth Programs Biomed. 2001;65:191–200. doi: 10.1016/s0169-2607(00)00124-3. [DOI] [PubMed] [Google Scholar]
- Brownstone RM, Jordan LM, Kriellaars DJ, Noga BR, Shefchyk SJ. On the regulation of repetitive firing in lumbar motoneurones during fictive locomotion in the cat. Exp Brain Res. 1992;90:441–455. doi: 10.1007/BF00230927. [DOI] [PubMed] [Google Scholar]
- Cantrell AR, Ma JY, Scheuer T, Catterall WA. Muscarinic modulation of sodium current by activation of protein kinase C in rat hippocampal neurons. Neuron. 1996;16:1019–1026. doi: 10.1016/s0896-6273(00)80125-7. [DOI] [PubMed] [Google Scholar]
- Carlin KP, Jiang Z, Brownstone RM. Characterization of calcium currents in functionally mature mouse spinal motoneurons. Eur J Neurosci. 2000a;12:1624–1634. doi: 10.1046/j.1460-9568.2000.00050.x. [DOI] [PubMed] [Google Scholar]
- Carlin KP, Jones KE, Jiang Z, Jordan LM, Brownstone RM. Dendritic L-type calcium currents in mouse spinal motoneurons: implications for bistability. Eur J Neurosci. 2000b;12:1635–1646. doi: 10.1046/j.1460-9568.2000.00055.x. [DOI] [PubMed] [Google Scholar]
- Dai Y, Jones KE, Fedirchuk B, McCrea DA, Jordan LM. A modelling study of locomotion-induced hyperpolarization of voltage threshold in cat lumbar motoneurones. J Physiol. 2002;544:521–536. doi: 10.1113/jphysiol.2002.026005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duprat F, Lesage F, Patel AJ, Fink M, Romey G, Lazdunski M. The neuroprotective agent riluzole activates the two P domain K+ channels TREK-1 and TRAAK. Mol Pharmacol. 2000;57:906–912. [PubMed] [Google Scholar]
- Fleidervish IA, Friedman A, Gutnick MJ. Slow inactivation of Na+ current and slow cumulative spike adaptation in mouse and guinea-pig neocortical neurones in slices. J Physiol. 1996;493:83–97. doi: 10.1113/jphysiol.1996.sp021366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French AS. Ouabain selectively affects the slow component of sensory adaptation in an insect mechanoreceptor. Brain Res. 1989;504:112–114. doi: 10.1016/0006-8993(89)91604-1. [DOI] [PubMed] [Google Scholar]
- Galvez A, Gimenez-Gallego G, Reuben JP, Roy-Contancin L, Feigenbaum P, Kaczorowski GJ, Garcia ML. Purification and characterization of a unique, potent, peptidyl probe for the high conductance calcium-activated potassium channel from venom of the scorpion Buthus tamulus. J Biol Chem. 1990;265:11083–11090. [PubMed] [Google Scholar]
- Goldin AL. Resurgence of sodium channel research. Annu Rev Physiol. 2001;63:871–894. doi: 10.1146/annurev.physiol.63.1.871. [DOI] [PubMed] [Google Scholar]
- Granit R, Kernell D, Shortess GK. Quantitative aspects of repetitive firing of mammalian motoneurones, caused by injected currents. J Physiol. 1963;168:911–931. doi: 10.1113/jphysiol.1963.sp007230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ionic Channels of Excitable Membranes. Sunderland, MA, USA: Sinauer Associates Inc; 2001. [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M, Oshima T. Temporal summation of after-hyperpolarization following a motoneurone spike. Nature. 1962;195:910–911. [Google Scholar]
- Kernell D. The adaptation and the relation between discharge frequency and current strength of cat lumbosacral motoneurones stimulated by long-lasting injected currents. Acta Physiol Scand. 1965;65:65–73. doi: 10.1111/j.1748-1716.1965.tb04081.x. [DOI] [PubMed] [Google Scholar]
- Kernell D, Monster AW. Motoneurone properties and motor fatigue. An intracellular study of gastrocnemius motoneurones of the cat. Exp Brain Res. 1982a;46:197–204. doi: 10.1007/BF00237177. [DOI] [PubMed] [Google Scholar]
- Kernell D, Monster AW. Time course and properties of late adaptation in spinal motoneurones of the cat. Exp Brain Res. 1982b;46:191–196. doi: 10.1007/BF00237176. [DOI] [PubMed] [Google Scholar]
- Kernell D, Sjoholm H. Repetitive impulse firing: comparisons between neurone models based on ‘voltage clamp equations’ and spinal motoneurones. Acta Physiol Scand. 1973;87:40–56. doi: 10.1111/j.1748-1716.1973.tb05364.x. [DOI] [PubMed] [Google Scholar]
- Krawitz S, Brownstone RM, Noga BR, Jordan LM. Can the nervous system overcome a possible central fatigue process – late adaptation. Muscle Nerve. 1996;4(Suppl.):S52. [Google Scholar]
- Krawitz S, Fedirchuk B, Dai Y, Jordan LM, McCrea DA. State-dependent hyperpolarization of voltage threshold enhances motoneurone excitability during fictive locomotion in the cat. J Physiol. 2001;532:271–281. doi: 10.1111/j.1469-7793.2001.0271g.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee RH, Heckman CJ. Essential role of a fast persistent inward current in action potential initiation and control of rhythmic firing. J Neurophysiol. 2001;85:472–475. doi: 10.1152/jn.2001.85.1.472. [DOI] [PubMed] [Google Scholar]
- Leong SK, Ling EA. Labelling neurons with fluorescent dyes administered via intravenous, subcutaneous or intraperitoneal route. J Neurosci Meth. 1990;32:15–23. doi: 10.1016/0165-0270(90)90067-p. [DOI] [PubMed] [Google Scholar]
- Li Y, Bennett DJ. Persistent sodium and calcium currents cause plateau potentials in motoneurons of chronic spinal rats. J Neurophysiol. 2003;90:857–869. doi: 10.1152/jn.00236.2003. [DOI] [PubMed] [Google Scholar]
- Madison DV, Nicoll RA. Control of the repetitive discharge of rat CA 1 pyramidal neurones in vitro. J Physiol. 1984;354:319–331. doi: 10.1113/jphysiol.1984.sp015378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melnick IV, Santos SF, Safronov BV. Mechanism of spike frequency adaptation in substantia gelatinosa neurones of rat. J Physiol. 2004;559:383–395. doi: 10.1113/jphysiol.2004.066415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merchenthaler I. Neurons with access to the general circulation in the central nervous system of the rat: a retrograde tracing study with fluoro-gold. Neuroscience. 1991;44:655–662. doi: 10.1016/0306-4522(91)90085-3. [DOI] [PubMed] [Google Scholar]
- Miles GB, Yohn DC, Wichterle H, Jessell TM, Rafuse VF, Brownstone RM. Functional properties of motoneurons derived from mouse embryonic stem cells. J Neurosci. 2004;24:7848–7858. doi: 10.1523/JNEUROSCI.1972-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numann R, Catterall WA, Scheuer T. Functional modulation of brain sodium channels by protein kinase C phosphorylation. Science. 1991;254:115–118. doi: 10.1126/science.1656525. [DOI] [PubMed] [Google Scholar]
- Person RS, Kudina LP. Discharge frequency and discharge pattern of human motor units during voluntary contraction of muscle. Electroencephalogr Clin Neurophysiol. 1972;32:471–483. doi: 10.1016/0013-4694(72)90058-2. [DOI] [PubMed] [Google Scholar]
- Powers RK, Sawczuk A, Musick JR, Binder MD. Multiple mechanisms of spike-frequency adaptation in motoneurones. J Physiol Paris. 1999;93:101–114. doi: 10.1016/s0928-4257(99)80141-7. [DOI] [PubMed] [Google Scholar]
- Romero M, Reboreda A, Sanchez E, Lamas JA. Newly developed blockers of the M-current do not reduce spike frequency adaptation in cultured mouse sympathetic neurons. Eur J Neurosci. 2004;19:2693–2702. doi: 10.1111/j.1460-9568.2004.03363.x. [DOI] [PubMed] [Google Scholar]
- Safronov BV, Vogel W. Properties and functions of Na+-activated K+ channels in the soma of rat motoneurones. J Physiol. 1996;497:727–734. doi: 10.1113/jphysiol.1996.sp021803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawczuk A, Powers RK, Binder MD. Spike frequency adaptation studied in hypoglossal motoneurons of the rat. J Neurophysiol. 1995;73:1799–1810. doi: 10.1152/jn.1995.73.5.1799. [DOI] [PubMed] [Google Scholar]
- Sawczuk A, Powers RK, Binder MD. Contribution of outward currents to spike-frequency adaptation in hypoglossal motoneurons of the rat. J Neurophysiol. 1997;78:2246–2253. doi: 10.1152/jn.1997.78.5.2246. [DOI] [PubMed] [Google Scholar]
- Schnee ME, Brown BS. Selectivity of linopirdine (DuP 996), a neurotransmitter release enhancer, in blocking voltage-dependent and calcium-activated potassium currents in hippocampal neurons. J Pharmacol Exp Ther. 1998;286:709–717. [PubMed] [Google Scholar]
- Schwindt PC, Crill WE. Properties of a persistent inward current in normal and TEA-injected motoneurons. J Neurophysiol. 1980;43:1700–1724. doi: 10.1152/jn.1980.43.6.1700. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Crill WE. Long-lasting reduction of excitability by a sodium-dependent potassium current in cat neocortical neurons. J Neurophysiol. 1989;61:233–244. doi: 10.1152/jn.1989.61.2.233. [DOI] [PubMed] [Google Scholar]
- Spielmann JM, Laouris Y, Nordstrom MA, Robinson GA, Reinking RM, Stuart DG. Adaptation of cat motoneurons to sustained and intermittent extracellular activation. J Physiol. 1993;464:75–120. doi: 10.1113/jphysiol.1993.sp019625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein RB, Parmiggiani F. Optimal motor patterns for activating mammalian muscle. Brain Res. 1979;175:372–376. doi: 10.1016/0006-8993(79)91019-9. [DOI] [PubMed] [Google Scholar]
- Stocker M. Ca2+-activated K+ channels: molecular determinants and function of the SK family. Nat Rev Neurosci. 2004;5:758–770. doi: 10.1038/nrn1516. [DOI] [PubMed] [Google Scholar]
- Traub RD, Wong RK, Miles R, Michelson H. A model of a CA3 hippocampal pyramidal neuron incorporating voltage-clamp data on intrinsic conductances. J Neurophysiol. 1991;66:635–650. doi: 10.1152/jn.1991.66.2.635. [DOI] [PubMed] [Google Scholar]
- Urbani A, Belluzzi O. Riluzole inhibits the persistent sodium current in mammalian CNS neurons. Eur J Neurosci. 2000;12:3567–3574. doi: 10.1046/j.1460-9568.2000.00242.x. [DOI] [PubMed] [Google Scholar]
- Venance L, Glowinski J. Heterogeneity of spike frequency adaptation among medium spiny neurones from the rat striatum. Neuroscience. 2003;122:77–92. doi: 10.1016/s0306-4522(03)00553-0. [DOI] [PubMed] [Google Scholar]
- Vergara C, Latorre R, Marrion NV, Adelman JP. Calcium-activated potassium channels. Curr Opin Neurobiol. 1998;8:321–329. doi: 10.1016/s0959-4388(98)80056-1. [DOI] [PubMed] [Google Scholar]
- Viana F, Bayliss DA, Berger AJ. Multiple potassium conductances and their role in action potential repolarization and repetitive firing behavior of neonatal rat hypoglossal motoneurons. J Neurophysiol. 1993;69:2150–2163. doi: 10.1152/jn.1993.69.6.2150. [DOI] [PubMed] [Google Scholar]
- West JW, Numann R, Murphy BJ, Scheuer T, Catterall WA. A phosphorylation site in the Na+ channel required for modulation by protein kinase C. Science. 1991;254:866–868. doi: 10.1126/science.1658937. [DOI] [PubMed] [Google Scholar]
- Zeng J, Powers RK, Newkirk G, Yonkers M, Binder MD. Contribution of persistent sodium currents to spike-frequency adaptation in rat hypoglossal motoneurons. J Neurophysiol. 2005;93:1035–1041. doi: 10.1152/jn.00831.2004. [DOI] [PubMed] [Google Scholar]
- Zhang L, Krnjevic K. Apamin depresses selectively the after-hyperpolarization of cat spinal motoneurons. Neurosci Lett. 1987;74:58–62. doi: 10.1016/0304-3940(87)90051-6. [DOI] [PubMed] [Google Scholar]