Abstract
There is growing interest in lithographic technologies for creating 3D microstructures. Such techniques are generally serial in nature, prohibiting the mass production of devices. Soft-lithographic techniques show great promise for simple and rapid replication of arrays of microstructures but have heretofore not been capable of direct replication of structures with closed loops. We demonstrate that 3D microstructures created with multiphoton absorption polymerization can be replicated by using microtransfer molding to afford complex daughter structures containing closed loops. This method relieves many of the topological constraints of soft lithography, paving the way for the large-scale replication of true 3D microstructures.
Keywords: microtransfer molding, multiphoton absorption polymerization, soft lithography
Advances in conventional lithography have been responsible for enormous gains in the power of microelectronic devices in the past few decades. The realization that the same lithographic techniques could be applied to micromachines has led to a parallel revolution in microelectromechanical systems (MEMS) (1, 2). However, the fact that conventional lithographic techniques are limited in their ability to create features with significant structure in the dimension perpendicular to the substrate on which fabrication is performed constitutes a fundamental limitation for the development of MEMS devices.
In further expanding the capabilities of microelectromechanical systems, an important objective is to develop methods that allow for the mass production of arbitrarily complex 3D structures on the wafer scale. For this reason, there has been growing interest in the development of new lithographic techniques, such as LIGA (an acronym from German words for lithography, electroplating, and molding) (3), multiphoton absorption polymerization (MAP) (4–12), and multibeam interference lithography (MBIL) (13–16) for creating complex 3D structures. LIGA and MAP are inherently serial, however. Structures are created on a voxel-by-voxel basis, and so fabrication on the wafer scale is a slow process. Although MBIL is a highly parallel technique, it can only be used to fabricate periodic structures with spatial periods on the scale of the wavelength of the light used. As a result, none of these techniques is suitable for the mass production of arbitrarily complex 3D microdevices.
The first step in conventional lithography is mask writing, which is also a serial process that is relatively slow. Once a lithographic mask has been created, it can be used repeatedly for the rapid, parallel fabrication of devices on the wafer scale. It would be attractive to apply an analogous approach for the mass production of complex 3D structures, by using a technique such as MAP or LIGA to create master structures that can then be replicated in a highly parallel manner.
One potential means of accomplishing such replication is soft lithography. In particular, microtransfer molding (μTM) (17–19) has been used to create wafer-scale replicas of master structures that were created with conventional lithography. Liquid polydimethylsiloxane (PDMS) is poured over the master structures and then cured to create an elastomeric mold. The mold is subsequently filled with a molding material that is cured against a substrate to create a replica of the original structures.
We have previously demonstrated that μTM can be used to replicate 3D structures created with MAP (20). Because of the elastic nature of the PDMS mold, it is possible to replicate a surprising range of structures, including ones with high aspect ratios or substantial overhangs (20, 21). However, structures that have closed loops cannot be released from a mold and therefore cannot be replicated in a single step with μTM. As a result, μTM and related soft-lithographic techniques are considered to be “2.5-dimensional.”
In previous applications of μTM in the creation of 3D structures, the inability to mold closed loops has required that a layer-by-layer approach be adopted (19, 22, 23). Such an approach has a number of drawbacks. There must be as many molds (and molding steps) as there are layers, so registration becomes a difficult task. In addition, at every layer there is a chance for excess molding material to be present on the face of the mold, creating undesired features. It is therefore difficult to create structures with high aspect ratios with multilayer μTM. The range of structures that can be created with this technique is further limited by the requirement that features in each layer be relatively dense to prevent sagging of the mold for the subsequent layer. Also, in any given layer an attachment point for each feature to the previous layer is required for release of the replica from the mold, which precludes the fabrication of moving parts.
Here we introduce a technique, which we call membrane-assisted μTM (MA-μTM), that allows for the soft-lithographic replication of true 3D structures in a single molding step. A technique such as MAP is used to create master structures that have closed loops that are interrupted by thin membranes. In the replication step, we are able to control whether or not the membranes are reproduced. It is therefore possible to create, rapidly and with high fidelity, highly complex daughter structures that can include features such as arches or even interlocked rings
Results
Our method is motivated by the observation that techniques that employ PDMS, such as μTM and microcontact printing (17, 18), do not work well when there are features that are much narrower in one lateral dimension than they are tall, because the PDMS tends to stick to itself (17, 18, 24). We hypothesized that this phenomenon could be used to advantage through the creation of features in the master structure that eliminate closed loops but that have aspect ratios that are too high for easy replication. Consider, for instance, a master structure with an arch in it. The arch forms a closed loop and so cannot be replicated using conventional μTM. However, if the arch includes a thin membrane that passes through its center (Fig. 1A), the mold can be released from the master structure. When a molding material is introduced into the PDMS for replication, the mold has a tendency to stick to itself in the region of the membrane. The use of a viscous molding material that does not wet PDMS strongly also helps to prevent this region of the mold from being filled. When the molding material is cured under these conditions, the membrane will not be replicated. However, because the mold does not contain a closed loop, it can reopen in the region of the membrane to release the replica.
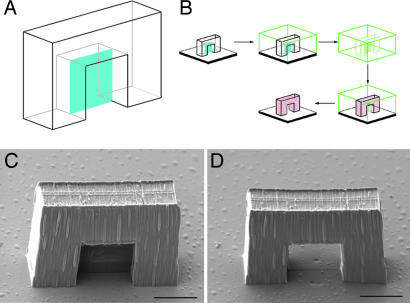
Fig. 1.
Replication of a master structure with a closed loop. (A) Schematic depiction of a master structure for the creation of an arch. The blue plane is the membrane. (B) Procedure for MA-μTM of the arch. After creation of the arch with MAP, it is immersed in PDMS. The elastomer is cured, and the mold is peeled off of the substrate. After gentle compression, the mold is filled with a molding material and pressed against a substrate. After curing of the molding material, the mold is removed, leaving a daughter arch without the membrane. (C) SEM of a master structure for an arch. (D) The corresponding daughter structure to C. (Scale bars: 10 μm.)
A schematic of the procedure for this technique, which we call MA-μTM, is shown in Fig. 1B. We begin by using MAP, following a procedure described in ref. 25, to create a master structure from an acrylic resin. This structure includes one or more membranes that span otherwise closed loops. When fabrication is complete, the excess resin is removed by using ethanol, leaving the solidified structure (Fig. 1C). The procedure for creating the mold has been described in detail elsewhere (20). The mold can be compressed and/or bent to promote self-adhesion of the PDMS in the membrane regions before being filled with the molding material, which is typically the same resin used for MAP fabrication. The mold is pressed against a substrate, and the molding material is photocured. The mold then is removed, leaving a daughter structure in which the membrane is absent (Fig. 1D).
We explored the replication of a wide variety of master structures to demonstrate the effectiveness of MA-μTM. Representative samples of these master structures and the corresponding daughter structures are shown in the scanning electron micrographs (SEMs) in Fig. 2. The master structure in Fig. 2A yields the daughter cantilever in Fig. 2B, which has an overhang that is ≈40 μm long. This overhang is much too long to be replicated by using conventional μTM, but it should be possible to use MA-μTM to replicate considerably longer overhangs.
Fig. 2.
SEMs of master structures with membranes and the corresponding daughter structures. (A and B) Cantilever. (C and D) Divided arch. (E and F) Three bridges. (G and H) Five-turn coil. (I and J) Table. (K and L) Interlocking rings, one of which is free-moving. (Scale bars: 10 μm.)
Shown in Fig. 2C is a master structure that affords the segmented arch daughter structure in Fig. 2D. In Fig. 2E we show a set of master structures that produces the three bridges shown in Fig. 2F. These bridges have spans of tens of micrometers and are separated by similar distances. In Fig. 2G we show a master structure with five membranes that are in relatively close proximity to one another. Replication of this structure yields the five-turn coil shown in Fig. 2H. These examples demonstrate that it is possible to replicate multiple closed loops simultaneously, even when the master structures are far from one another. Other experiments have revealed that the relative orientations of membranes in a master structure do not influence the ability to create a replica with closed loops.
It is also possible to create and replicate master structures in which two or more membranes meet one another. An example of such a master structure is shown in Fig. 2I. There are two membranes underneath the structure that run along the diagonals of the square on the top of the structure. Replication of this master yields the table shown in Fig. 2J. As another example, replication of the master structure in Fig. 2K yields two interlocked links. One link is attached to the substrate, but the other moves freely, which demonstrates that MA-μTM can be used to create moving parts.
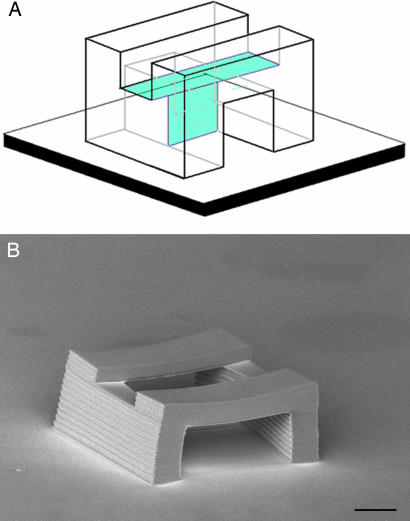
In all of the examples that we have discussed so far, the membranes have been normal to the substrate. The fact that it is possible to replicate master structures with large overhangs (20, 21) suggests that it should be possible to employ membranes that are at a considerable angle to the surface normal. In fact, with appropriately designed master structures it is even possible to incorporate membranes that are horizontal. An example of such a master structure is shown schematically in Fig. 3A. The structure consists of a straight tunnel that runs parallel to the substrate. There is a vertical membrane in the center of the tunnel so that the mold can be released. In addition, there is a horizontal membrane in the roof of the tunnel above the vertical membrane. As shown in Fig. 3B, replication of this master yields a daughter structure that consists of a tunnel with an open “skylight.” Thus, in principle there is no restriction on the orientation of the membranes used in MA-μTM or of the resultant closed loops in the corresponding daughter structures.
Fig. 3.
Replication of a master structure with a horizontal membrane. (A) Schematic depiction of the master structure. The blue planes are the membranes. (B) SEM of the daughter structure. (Scale bar: 10 μm.)
To assess some of the limitations of MA-μTM, we fabricated a number of different master structures that are challenging to replicate. One set of experiments involved straight tunnels of various lengths that were 30 μm wide and 15 μm tall. Each tunnel contained a vertical membrane that was perpendicular to the tunnel halfway down its length. The longest tunnel that we were able to replicate reproducibly had a length of 75 μm; replicas of this structure are shown in Fig. 4A and B. The typical failure mechanism for replication of tunnels is illustrated in Fig. 4C. In this case the roof of the tunnel is thinner, so the portion of the mold that corresponds to the inside of the tunnel is able to adhere to the PDMS above the roof of the tunnel, creating an unintended skylight in the daughter structure. This phenomenon is closely related to PDMS “stamp collapse” that has been studied recently (26–28), and the problem can be alleviated to some extent by making the walls of the tunnel thicker.
Fig. 4.
Limitations in the replication of structures with MA-μTM. (A and B) SEM images of a replicated tunnel that is 75 μm long, 30 μm wide, and 15 μm tall. (C) SEM of a replicated tunnel with the same dimensions but a thinner roof. The area of the mold inside the tunnel has adhered to the area above the roof, creating an undesired skylight in the roof of the replica. (D) SEM of a replica of two parallel bridges that are each 10 μm wide and are separated by 8 μm. (E) SEM of a master structure for two identical bridges that are 5 μm apart. In this case the mold was unable to release, and the piece of PDMS that was torn off can be seen between the bridges. (F) SEM of a replica of two similar bridges with a 5-μm width that are perpendicular to one another. (Scale bars: 10 μm.)
Another set of master structures that we used to test the limitations of MA-μTM was sets of parallel bridges with a height of 15 μm, a span of 30 μm, and a width of 10 μm, each of which had a membrane down its middle. The distance between the two bridges was varied. In this case, the smallest distance between the bridges that allowed us to create closed-loop daughter structures reproducibly was 8 μm, as shown in Fig. 4D. The failure mechanism for smaller gaps is illustrated by the master structure in Fig. 4E. In this case the separation between bridges is 5 μm, and the PDMS in this gap tore off when the mold was released from the master.
We also created master structures in which two bridges, with heights of 15 μm, spans of 30 μm, and widths of 5 μm, were placed at right angles to one another, so that the PDMS would move in perpendicular directions when the mold was released. As shown in Fig. 4F, we had no difficulty in replicating such structures, although presumably if the bridges were wider (i.e., tunnels) there would come a point at which replication would again be problematic.
In some instances it is desirable to be able to make completely faithful replicas of master structures, including the membranes. As discussed above, to ensure that the membranes do not replicate, molds are generally compressed before filling them with the molding material. We used the opposite strategy to make it possible to replicate the membranes. To stretch a mold, the PDMS block is pressed against a vacuum hose to cover the opening of the hose. The region of the mold faces toward the hose and is kept entirely within the opening. A mild vacuum is then applied to bend the PDMS into the hose slightly, which opens the membrane regions in the mold (see the optical micrograph in Fig. 5A Inset). After the vacuum is released, molding material is introduced into the mold immediately, and after curing against a substrate the resultant daughter structure is a faithful replica of the master structure. An example of a replica of a bridge structure with a membrane is shown in Fig. 5A. This process is also fully reversible; if the PDMS block is pressed against the hose with the mold side facing away from the vacuum, the membrane regions are compressed, and the PDMS readheres to itself. The structure in Fig. 5B was made from the same mold as that in Fig. 5A after following this procedure, and the membrane is once again absent, as can also be seen from the Inset optical micrograph of the mold.
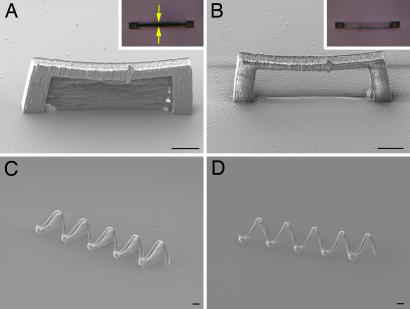
Fig. 5.
Control of membrane replication. (A) SEM of a replica of the master structure for a bridge in which the membrane has been replicated. (Inset) An optical micrograph of the mold, showing that the membrane area of the mold (the region between the two arrows) was open before the molding material was introduced. (B) SEM of a replica without a membrane made from the same mold after compression. (Inset) The optical micrograph shows that the membrane area of the mold is now closed, although the remainder of the mold of the bridge structure is still visible. (C) SEM of a replica of the coil master from Fig. 2G including the membranes. (D) SEM of a replica made from the replica in C after compression of the mold. (Scale bars: 10 μm.)
For mass production of 3D structures, it is desirable to use replication to create additional master structures from an original master. Daughter structures that have closed loops cannot be replicated, so it is necessary to be able to replicate membranes to create second-generation masters. Shown in Fig. 5C is a replica of the structure from Fig. 2G that contains all of the original membranes. As demonstrated by the coil in Fig. 5D, the daughter structure in Fig. 5C is just as effective as the original master structure in the creation of additional daughter structures with closed loops. It is therefore possible to make additional masters from an original master structure.
Discussion
The adhesion of PDMS to itself to prevent the replication of membranes is closely related to the phenomenon of stamp collapse (26–28). Whether the mold will adhere to itself depends on a number of parameters, including interfacial energies and the mechanical properties of the PDMS. The negative membrane is first closed by compression. Whether is stays closed when the pressure is released depends on the PDMS/air interfacial energy, the PDMS/PDMS interfacial energy, and the tension in the deformed PDMS. The last parameter in turn depends on the elastic properties of the PDMS and the thickness of the membrane. Higher PDMS elasticity and thinner membranes both tend to promote continued adhesion. Once the pressure has been released, continued adhesion may either be stable (i.e., a global energy minimum) or metastable (i.e., a local energy minimum) (26–28).
Once the molding material has been introduced into the mold, the energetics of the adhesion change based on the energy of the PDMS/molding material interface. If the molding material wets PDMS strongly, it can wick into the membrane area, causing the membrane to replicate. It is also possible that the adhered PDMS will become metastable upon addition of the molding material, in which case the replication of the membrane will be controlled by the kinetics of wetting of the PDMS by the molding material. Thus, the optimal situation for preventing membrane replication is to have a molding material that is viscous and has a high contact angle on PDMS.
To assess the dependence of the MA-μTM on the molding material, we measured the contact angle of our acrylic resin on PDMS, as well as the contact angles of a number of other resins that are commonly used in μTM: Norland Optical Adhesives 73 and 61 (both from Norland Products, Cranbury, NJ) and Summers Optical J-91 (Summers Optical, Hatfield, PA). The acrylic resin used here had the lowest contact angle of all of the substances investigated, indicating that it represents a worst-case scenario for membrane replication among this group of molding materials. Molding tests confirmed that the membranes did not replicate with any of these materials. In addition, if wicking of the molding material is a problem, the molding material can be introduced while the mold is still under compression, and curing can be performed immediately.
The mechanical properties of the PDMS also play a crucial role in the success of the MA-μTM process. Not only does the high elasticity of the PDMS help to prevent the membrane area from reopening upon introduction of the resin, but it also allows the mold to release from master structures and replicas. The MA-μTM process will be more difficult to perform successfully with molds that are less flexible, including PDMS that is cured at a higher temperature. Conversely, the relatively low curing temperature used here promotes high elasticity in the PDMS, which contributes to the success of the MA-μTM process. Curing the PDMS at an even lower temperature may increase the range of structures that can be replicated successfully by increasing the elasticity and minimizing the shrinkage of the mold. A quantification of the role of the elastic modulus in the success of MA-μTM will be an important issue for further studies.
Another potential limitation of MA-μTM is the creation of seams along the substrate at the position of the membrane in the daughter structures, as seen in some of the replicas in Fig. 2. Employing a molding material with a higher contact angle on PDMS did not affect the appearance of these seams in any reproducible manner. We therefore believe that the mold itself is largely responsible for the seams, either through separation at the surface due to tension within the mold or through a slightly increased membrane thickness near the substrate. This issue also merits further investigation.
Although MA-μTM greatly increases the range of structures that can be replicated, there remain classes of structures for which this technique is not well suited. For example, devices such as photonic crystals that require densely packed closed loops in three dimensions cannot be replicated with this technique. In addition, the minimum inner dimension of a closed loop is currently limited to on the order of 1 μm, although it should be possible to improve on this size significantly given a photopolymer that can create thinner membranes with enough structural integrity to withstand the molding process.
The ability to control the replication of the membranes in a master structure makes it possible to create a large number of closed-loop replicas from a single master structure. Molds degrade slightly with each use (20). As a conservative estimate, it is possible to use a mold at least 20 times before the degradation becomes significant. It is less clear whether there is a limitation to the number of molds that can be made from a single master structure, but we estimate conservatively that this number should be at least 50. Therefore, 50 first-generation daughter structures with membranes can be used to create at least 1,000 second-generation daughter structures without membranes or 2,500 second-generation daughter structures with membranes. Three generations of daughter structures with membranes can be used to create well over 1 million closed-loop daughter structures. Thus, a single master structure can potentially be used to create an almost limitless number of closed-loop daughter structures.
Conclusions
The results presented here demonstrate that many of the topological restrictions that have governed soft lithography to date can be circumvented with MA-μTM. In contrast to previous soft lithographic techniques for creating 3D structures (19, 22, 23), MA-μTM involves only a single molding step, greatly simplifying registration. A single mold can contain structures with vastly different aspect ratios, and the density of features on a substrate can span a broad range. It is also possible to create moving parts with MA-μTM, and as a parallel technique it should be amenable to the rapid production of microstructures on the wafer scale.
We have used MAP to create the master structures reported here, but other 3D lithographic techniques such as LIGA are equally well suited to the task. In addition, it should be possible to use MAP to “retrofit” existing 3D microstructures with membranes such that they can be replicated by using MA-μTM. This technique should open the door for the creation of microelectromechanical systems devices with architectures that have heretofore been inaccessible using mass production techniques.
Materials and Methods
Master structures were fabricated from an acrylic resin (25) composed of 48 wt % ethoxylated (6) trimethylolpropane triacrylate, 49 wt % Tris(2-hydroxyethyl)isocyanurate triacrylate, and 3 wt % Lucrin-TPOL (the photoinitiator). The sample preparation and fabrication procedure have been described in detail (25). Typical fabrication powers were <5 mW at the sample. The membranes were made under the same conditions as the rest of the structure and were usually fabricated last. A typical membrane is on the order of 500 nm thick, whereas the surrounding features that are to be replicated are generally at least a factor of 4 thicker. After fabrication the unexposed resin was washed away with ethanol.
To create a mold, a few grams of Sylgard 184 were mixed in a 10:1 mass ratio of prepolymer to curing agent. The resulting mixture then was centrifuged for several minutes to remove air bubbles. A PDMS form containing a 1 cm × 1 cm × 2 mm well, which had previously been modified with (tridecafluoro-1,1,2,2-tetrahydrooctyl) dimethylchlorosilane, was filled with PDMS and vacuum degassed at 100 mtorr pressure (1 torr = 133 Pa) for ≈1 min. The microstructure then was placed onto this degassed PDMS upside down and maintained at 110°C for 30 min. The PDMS mold then was removed from the PDMS form and carefully peeled off the substrate with tweezers. In most cases the direction of peeling was parallel to the membrane. The same procedure was followed when making molds from replicated structures with the additional step that the replicated polymer be surface modified with (3-aminopropyl)trimethoxysilane, which ensures that the PDMS will cure properly at the polymer interface.
The 1 cm × 1 cm × 2 mm mold containing the shape of the structure was flexed by placing it over the opening of a 12-mm-diameter hose and reducing the pressure in the hose to 60 torr by using a hand pump. If the negative of the structure is on the side of the PDMS that is exposed to vacuum, the mold will flex to open the membrane, whereas if the negative of the structure is on the opposite side of the PDMS, the mold will flex to close the membrane. After slowly releasing the pressure, the mold was restored to its initial shape, and care was taken to no longer flex it. Although any number of materials can be used to create replicas, here we used the same resin that was used for MAP fabrication. A drop of resin was placed between the mold and a piece of acrylate-modified glass and UV cured (365 nm) for 5 min. After the replica was cured, the mold was removed with tweezers.
Acknowledgments
This work was supported by National Science Foundation Grant ECS-0210533.
Abbreviations
- MAP
multiphoton absorption polymerization
- μTM
microtransfer molding
- MA-μTM
membrane-assisted μTM
- PDMS
polydimethylsiloxane
- SEM
scanning electron micrograph.
Footnotes
Conflict of interest statement: No conflicts declared.
References
- 1.Rai-Coudhury P. Handbook of Microlithography, Micromachining, & Microfabrication. Bellingham, WA: SPIE Optical Engineering Press; 1997. [Google Scholar]
- 2.Moore D. F., Syms R. R. A. Electron. Commun. Eng. J. 1999;11:261–270. [Google Scholar]
- 3.Malek C. K., Saile V. Microelectron. J. 2004;35:131–143. [Google Scholar]
- 4.Campagnola P. J., Delguidice D. M., Epling G. A., Hoffacker K. D., Howell A. R., Pitts J. D., Goodman S. L. Macromolecules. 2000;33:1511–1513. [Google Scholar]
- 5.Maruo S., Nakamura O., Kawata S. Opt. Lett. 1997;22:132–134. doi: 10.1364/ol.22.000132. [DOI] [PubMed] [Google Scholar]
- 6.Kawata S., Sun H. B., Tanaka T., Takada K. Nature. 2001;412:697–698. doi: 10.1038/35089130. [DOI] [PubMed] [Google Scholar]
- 7.Cumpston B. H., Ananthavel S. P., Barlow S., Dyer D. L., Ehrlich J. E., Erskine L. L., Heikal A. A., Kuebler S. M., Lee I.-Y. S., McCord-Maughon D., et al. Nature. 1999;398:51–54. [Google Scholar]
- 8.Sun H. B., Kawata S. J. Lightwave Technol. 2003;21:624–633. [Google Scholar]
- 9.Baldacchini T., Fourkas J. T. In: Encyclopedia of Nanoscience and Nanotechnology. Schwarz J. A., Contescu C. I., Putyera K., editors. New York: Marcel Dekker; 2004. pp. 3905–3915. [Google Scholar]
- 10.Witzgall G., Vrijen R., Yablonovitch E., Doan V., Schwartz B. J. Opt. Lett. 1998;23:1745–1747. doi: 10.1364/ol.23.001745. [DOI] [PubMed] [Google Scholar]
- 11.Belfield K. D., Ren X., Van Stryland E. W., Hagan D. J., Dubikovsky V., Miesak E. J. J. Am. Chem. Soc. 2000;122:1217–1218. [Google Scholar]
- 12.Serbin J., Egbert A., Ostendorf A., Chichkov B. N., Houbertz R., Domann G., Schulz J., Cronauer C., Frohlich L., Popall M. Opt. Lett. 2003;28:301–303. doi: 10.1364/ol.28.000301. [DOI] [PubMed] [Google Scholar]
- 13.Yang S., Megens M., Aizenberg J., Wiltzius P., Chaikin P. M., Russel W. B. Chem. Mater. 2002;14:2831–2833. [Google Scholar]
- 14.Ullal C. K., Maldovan M., Wohlgemuth M., Thomas E. L. J. Opt. Soc. Am. A. 2003;20:948–954. doi: 10.1364/josaa.20.000948. [DOI] [PubMed] [Google Scholar]
- 15.Moon J. H., Yang S. J. Macromol. Sci.-Polymer Rev. 2005;C45:351–373. [Google Scholar]
- 16.Chan T. Y. M., Toader O., John S. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2005;71:046605. doi: 10.1103/PhysRevE.71.046605. [DOI] [PubMed] [Google Scholar]
- 17.Xia Y., Whitesides G. M. Angew. Chem. Int. Ed. 1998;37:550–575. doi: 10.1002/(SICI)1521-3773(19980316)37:5<550::AID-ANIE550>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 18.Xia Y., Whitesides G. M. Annu. Rev. Mater. Sci. 1998;28:153–184. [Google Scholar]
- 19.Gates B. D., Xu Q. B., Stewart M., Ryan D., Willson C. G., Whitesides G. M. Chem. Rev. 2005;105:1171–1196. doi: 10.1021/cr030076o. [DOI] [PubMed] [Google Scholar]
- 20.LaFratta C. N., Baldacchini T., Farrer R. A., Fourkas J. T., Teich M. C., Saleh B. E. A., Naughton M. J. J. Phys. Chem. B. 2004;108:11256–11258. [Google Scholar]
- 22.Rogers J. A. In: Three-Dimensional Nanoengineered Assemblies. Orlando T. M., Merhari L., Taylor D. P., Ikuta K., editors. Vol. 739. Warrendale, PA: Materials Res. Soc.; 2003. p. H.1.2.1. [Google Scholar]
- 22.Unger M. A., Chou H.-P., Thorsen T., Scherer A., Quake S. R. Science. 2000;288:113–116. doi: 10.1126/science.288.5463.113. [DOI] [PubMed] [Google Scholar]
- 23.Leung W. Y., Kang H., Constant K., Cann D., Kim C. H., Biswas R., Sigalas M. M., Ho K. M. J. Appl. Phys. 2003;93:5866–5870. [Google Scholar]
- 24.Gates B. D., Whitesides G. M. J. Am. Chem. Soc. 2003;125:14986–14987. doi: 10.1021/ja0367647. [DOI] [PubMed] [Google Scholar]
- 25.Baldacchini T., LaFratta C., Farrer R. A., Teich M. C., Saleh B. E. A., Naughton M. J., Fourkas J. T. J. Appl. Phys. 2004;95:6072–6076. [Google Scholar]
- 26.Zhou W., Huang Y., Menard E., Aluru N. R., Rogers J. A., Alleyne A. G. Appl. Phys. Lett. 2005;87:251925. [Google Scholar]
- 27.Huang Y. G. Y., Zhou W. X., Hsia K. J., Menard E., Park J. U., Rogers J. A., Alleyne A. G. Langmuir. 2005;21:8058–8068. doi: 10.1021/la0502185. [DOI] [PubMed] [Google Scholar]
- 28.Hsia K. J., Huang Y., Menard E., Park J. U., Zhou W., Rogers J., Fulton J. M. Appl. Phys. Lett. 2005;86:154106. [Google Scholar]