Dynamic imaging of coherent sources: Studying neural interactions in the human brain

Abstract

Functional connectivity between cortical areas may appear as correlated time behavior of neural activity. It has been suggested that merging of separate features into a single percept (“binding”) is associated with coherent gamma band activity across the cortical areas involved. Therefore, it would be of utmost interest to image cortico-cortical coherence in the working human brain. The frequency specificity and transient nature of these interactions requires time-sensitive tools such as magneto- or electroencephalography (MEG/EEG). Coherence between signals of sensors covering different scalp areas is commonly taken as a measure of functional coupling. However, this approach provides vague information on the actual cortical areas involved, owing to the complex relation between the active brain areas and the sensor recordings. We propose a solution to the crucial issue of proceeding beyond the MEG sensor level to estimate coherences between cortical areas. Dynamic imaging of coherent sources (DICS) uses a spatial filter to localize coherent brain regions and provides the time courses of their activity. Reference points for the computation of neural coupling may be based on brain areas of maximum power or other physiologically meaningful information, or they may be estimated starting from sensor coherences. The performance of DICS is evaluated with simulated data and illustrated with recordings of spontaneous activity in a healthy subject and a parkinsonian patient. Methods for estimating functional connectivities between brain areas will facilitate characterization of cortical networks involved in sensory, motor, or cognitive tasks and will allow investigation of pathological connectivities in neurological disorders.

The hypothesis that relevant information in the brain is coded by accurate timing of neuronal discharges has received strong support from recent reports of synchronization of neuronal firing within and across areas of the cat visual cortex (1). The synchronization of neural activity, which was modulated by gamma-band oscillations, was shown to depend on stimulus properties like continuity, vicinity, and common motion, and on receptive field constellations (for review, see ref. 2). This and similar findings seem to support the concept that synchronized rhythmic neural firing has a role in solving the binding problem, i.e., the integration of distributed information into a unified representation (1–4).

To investigate cortico-cortical synchrony noninvasively in the human brain, new analysis tools must be developed. In functional magnetic resonance imaging (fMRI) studies, structural equation models have been used to estimate connectivities between brain areas (5, 6). Although this is a very promising approach, it lacks the temporal resolution required to measure oscillatory activity and to observe the expected transient formation of neuronal assemblies (7).

Magnetoencephalography (MEG) and electroencephalography (EEG) have the necessary millisecond resolution to characterize neuronal coupling. Indeed, task-dependent interactions in the frequency domain have been reported between signals recorded by different MEG sensors or EEG electrodes during cognitive (8–12) and motor tasks (13–15). However, these findings are limited to correlations within the measurement device and reveal little on the synchrony between specific cortical areas.

The signal recorded by a MEG sensor or an EEG electrode cannot be directly attributed to the underlying cortical region. The complex relationship between the signal detected by a sensor and an activated brain area is given by the solution of the forward problem (i.e., the calculation of the magnetic field or electric potential generated by a point source). Especially electric potentials (EEG) are smeared out because of the inhomogeneous conductivity structure of the human head. The activity of even a small cortical area is recorded by several sensors, leading to severe spreading in sensor-based measures. The spreading is particularly problematic when describing interdependencies between signals (16–18).

Here, we present an analysis method, dynamic imaging of coherent sources (DICS), that allows studies of cortico-cortical and cortico-muscular interactions by imaging power and coherence estimates within the human brain.

Methods

We employ the cross spectral density matrix as the basic representation of the oscillatory components and their dependencies in MEG/EEG and electromyographic (EMG) signals. In this paper, DICS was applied to MEG data although it can be applied to EEG as well. In the first step, which is identification of the interacting brain areas, we restrict the analysis to linear dependencies. In the next step, the time course for each region of interest is estimated and can be subjected to a more complex (and possibly nonlinear) analysis.

The complex cross spectral density C for signals x(t) and y(t) is computed by using Welch's method of spectral density estimation (19). A Hanning window is applied to the segments of signals x(t) and y(t). The Fourier-transformed X(f) and Y(f) are used to compute the cross spectral density, C(f) = X(f)Y*(f), where Y* denotes the complex conjugate of Y. Finally, C is averaged over successive data segments, which are overlapping by half their segment length.

One element C_i,j of the cross spectral matrix consists of the cross spectral densities of signals i and j. Therefore, C contains the cross spectral densities of all combinations of MEG (and possibly EMG) signals.

Two measures are derived from this matrix. First, the power spectrum of the signal i is represented by the diagonal element C_i,i. It allows identification of frequency bands containing most of the power or those showing task-dependent changes. Second, coherence is the magnitude-squared cross spectrum divided by the power spectra of both time series, viz.

1

Coherence is bounded between 0 and 1, where M_i,j(f) = 1 indicates a perfect linear relation between i and j at frequency f. It is commonly taken as a measure that quantifies the functional coupling between cortical areas (16, 20) based on signals from sensors covering different brain areas. These measures are used to quantify oscillatory components and their interactions in the recorded data.

We propose the use of a linear transformation that acts as a spatial filter (21–24) to compute these measures at any given location in the brain. The method, which is described in detail in the Appendix, represents a linear transformation where the transformation matrix is designed according to the solution of a constrained optimization problem.

In principle, a three-dimensional grid covering the entire brain is defined and two measures are computed at each grid point: first, the estimated power and, second, the estimated coherence with respect to a given reference point. Appropriate strategies for the selection of the reference point are introduced and illustrated in Results. Both measures are derived from the cross spectral density averaged over the frequency range of interest and the solution of the forward problem for the respective grid point.

One of the two measures is then thresholded and displayed together with the individual magnetic resonance images (MRI) (see e.g., Fig. 1). To assess the statistical significance of these measures, power is displayed as a power statistical parametric map (pSPM, see Appendix), and the 99% confidence level is computed for the coherence (25).

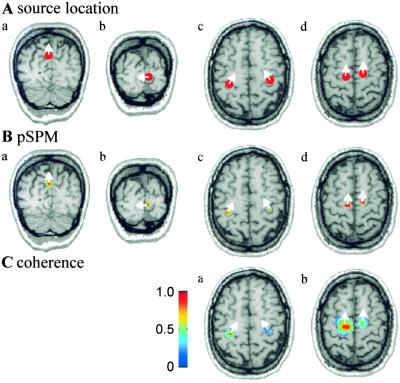
Figure 1.

Simulations. (A) Locations of simulated sources are indicated as red dots on coronal (a and b) and axial (c and d) MR images. (B) pSPMs calculated in the frequency bands 7–9 Hz (a), 11–13 Hz (b), 20–24 Hz (c), and 17–19 Hz (d). The threshold for the pSPMs corresponds to P < 0.001. (C) Coherence estimates are shown with a threshold of 0.23 in the frequency bands 9–11 Hz (a) and 17–19 Hz (b). The reference point in a was the left hand area, as estimated from the pSPM, and in b the left premotor area. Coherence of the reference region with itself is always equal to 1. The white arrows indicate the dominant direction of current flow.

Once coherent brain areas are identified, the time course of their activity is estimated by the spatial filter described in ref. 24. Phase and amplitude information is separated by means of the Hilbert transform (26). The degree of phase coupling between two time series is quantified by the synchronization index ρ (27). The dynamics of phase synchronization ρ and mean amplitude are calculated in a window moving across the data.

Results

We will first demonstrate the efficiency of DICS in identifying the sources of simulated cortical rhythms and their interactions. The effect of the signal-to-noise ratio (SNR) and the level of coherence on the performance of DICS is specifically investigated in the Appendix. We then proceed to test the method in localizing sources of spontaneous cortical rhythms in a healthy, resting human brain. Finally, signals measured from a parkinsonian patient during the tremor phase are analyzed to illustrate the various approaches for evaluating cortico-muscular and cortico-cortical interactions using DICS. The Neuromag-122 (Helsinki, Finland) whole-head MEG system was used for all simulations and measurements.

Simulated Data.

Four source areas of cortical rhythms were simulated, as illustrated in Fig. 1A, to imitate the physiological distribution of spontaneous oscillatory brain activity (28–32). The activity of sources in the parieto-occipital sulcus (Fig. 1Aa) and in the calcarine fissure (Fig. 1Ab) consisted of activity in the 10-Hz frequency range (parieto-occipital sulcus 8 Hz, calcarine fissure 12 Hz). The signals generated in the sensorimotor hand areas (Fig. 1Ac) in both hemispheres were composed of 10-Hz and 22-Hz oscillations. The hand area oscillations had a coherence of 0.25 at 10 Hz but no significant coherence at 22 Hz.

To test the performance of DICS for spatially close source areas in the presence of multiple independent coherences, two premotor sources were added (Fig. 1Ad), which were activated at 18 Hz with a coherence of 0.28. The shortest distances between the sources were 1.8 cm (left hand area to left premotor area), 2.1 cm (right hand area to right premotor area), and 3.0 cm (left to right premotor area).

All time series were obtained by filtering white noise with a narrow band-pass filter at the desired frequencies (center frequency ± 0.5 Hz). A recording time of 100 s was simulated with a sampling rate of 100 Hz. White noise with a maximum amplitude of 30% of the maximum signal was added. Coherence was generated by using the same band-pass filtered noise as a part of both time series. Only the two above-mentioned coherences were significant between any pair of the time series. Power and coherence were computed with a standard grid spacing of 8 mm and interpolated to the MRI resolution of 1 mm. As illustrated by the pSPM representations in Fig. 1B, all of the source areas were separately detected by DICS, including the closely located motor and premotor sources. The error in estimating source location and orientation was below 1.5 mm and 4° for all sources. The simulated coherences between the hand sensorimotor areas and between the premotor areas were accurately identified (Fig. 1C), and no false coherences were detected.

Localization of Cortical Oscillatory Activity.

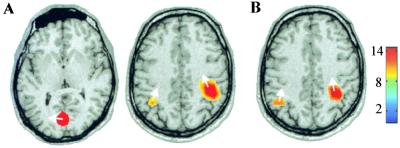
Correct localization of sources of oscillatory activity is a critical measure of the DICS approach because it tests performance of both the cross spectral density matrix and the spatial filter. Here, we estimated the generators of spontaneous brain activity from a 5-min recording of a healthy subject, when he was resting with his eyes open. Fig. 2 displays the pSPMs overlayed on the subject's MR images for the frequency bands 7–12 Hz (Fig. 2A) and 17–23 Hz (Fig. 2B), covering the main peaks of the power spectrum. The results are consistent with the previously reported generators of spontaneous oscillatory activity, as recorded by using whole-head MEG (32). The occipital cortex has been reported to be involved in the generation of the 10-Hz “alpha” rhythm, whereas the “mu” rhythm containing both 10-Hz and 20-Hz components is known to originate from the vicinity of the hand area in the left and right primary sensorimotor cortex.

Figure 2.

Localization of the generators of spontaneous activity recorded from a healthy subject at rest with his eyes open. The strongest pSPMs in the (A) 7- to 12-Hz band and (B) 17- to 23-Hz band are shown, overlayed on axial anatomical MRI slices (P < 0.0001). The color bar defines the relation between color and noise-normalized power.

Localization and Dynamics of Cortico-Cortical and Cortico-Muscular Coupling in Physiological Data.

Because DICS computes coherence to a reference region in the entire brain, the task of identifying a network of coherent brain regions reduces to the problem of detecting at least one member of such a network. In principle, it is possible to test all pairs of grid points for significant coherence, but it is very demanding in computation time. We propose four approaches for selecting reference regions in the brain.

The first strategy is to employ a peripheral signal (e.g., EMG) recorded simultaneously with MEG as the initial reference. A possible peripheral-cortical coupling may thus be identified, and the cortical area showing strongest coherence with the peripheral signal may be chosen as the reference region for further calculations.

In the second strategy, a reference region is defined from the source area of strongest oscillatory activity, i.e., from peaks in the pSPM maps (cf. Fig. 2).

In the third strategy, the most general one, coherences are first calculated between all sensor pairs. The strongest coherence between nonadjacent sensors is selected. A cortical reference region in the neighborhood of one of these sensors is found by the spatial filter approach. A selected reference region can be tested for significant coherence against all points on a grid covering the entire brain.

The fourth strategy uses physiological a priori information to define a reference region. Hypotheses may be tested by selecting reference regions based on knowledge of anatomical structures or pathways or from results of other functional imaging studies.

In the following, we will illustrate these strategies in a patient with idiopathic Parkinson's disease (male, 36 yr), presenting with a predominantly right-sided resting tremor of about 5 Hz at the upper extremity. Spontaneous cortical activity with the subject resting, eyes open, was recorded for 5 min. About 1 min after the beginning of the measurement, the strength of the tremor increased spontaneously, as confirmed by the simultaneously recorded surface EMG from the right flexor digitorum superficialis muscle (FDS).

Strategy 1: Peripheral signals as a reference signal.

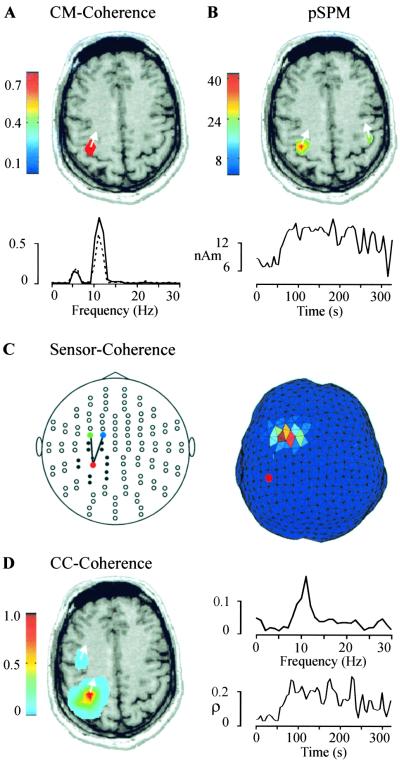
Because an EMG recording was available, the first strategy was applicable. The strongest components in the power spectrum of the EMG were found at 4–6 Hz and at 9–12 Hz. By imaging the cortico-muscular coherence in the 9- to 12-Hz band, we identified the contralateral primary motor cortex (M1) as the area showing highest coherence (Fig. 3A Upper). The step from sensor-based coherence (dashed line in Fig. 3A Lower) to source-based coherence (full line in Fig. 3A Lower) resulted in an increase of 27%, indicating a considerably improved representation of cortical activation by estimating source activity instead of by using sensor recordings.

Figure 3.

Analysis of cortico-muscular (CM) and cortico-cortical (CC) coupling. (A Upper) The spatial distribution of cortical coherence to EMG from the right FDS muscle, with a threshold of 0.78 in the 9- to 12-Hz frequency band. (Lower) The strongest coherence between EMG and an MEG sensor above M1 (dashed line) is compared with the coherence between EMG and M1 itself (full line; 99% confidence level is 0.014). (B Upper) The pSPM in the 9- to 12-Hz band reveals bilateral hand motor areas (P < 0.0001). (Lower) Amplitude of the left M1 activity in the 9- to 12-Hz band is shown as a function of time. (C) Plot of all sensors, flattened onto a plane, with lines connecting the sensors showing highest coherence in the 9- to 12-Hz band (Left). Only coherences between sensor pairs with a distance of more than 6 cm are shown. All sensors at shorter distance to the sensor marked with a red dot are represented by filled circles. (Right). The coherence estimate on the triangulated brain surface is shown for the 9- to 12-Hz range. The reference point is marked with a red dot. (D Left) The spatial distribution of cortico-cortical coherence to M1 is shown with a threshold of 0.07 in the 9- to 12-Hz band. (Right) A peak at 11 Hz is evident in the coherence spectrum between M1 and PM (Upper). The synchronization index ρ between M1 and PM increases abruptly when tremor strength increases at about 60 s (Lower; 99% confidence level is 0.04).

Strategy 2: Maximum of the pSPM.

The pSPM in the 9- to 12-Hz frequency range was computed to identify the area in the brain with the strongest power. The peak of the pSPM (Fig. 3B Upper) is in the same location as the maximum of cortico-muscular coherence (Fig. 3A Upper) and leads to the selection of the same reference region. The right M1 area also showed oscillatory activity (Fig. 3B Upper) that, however, was not coherent with the EMG signal of the right FDS muscle. The amplitude of the left M1 activity in the 9- to 12-Hz band exhibits a marked increase at the time of increased tremor strength at about 60 s (Fig. 3B Lower).

Strategy 3: Sensor-based search.

The most general approach for the definition of a reference region is based on coherences between all sensor pairs. This approach is ideal for planar gradiometers, which detect the strongest signal directly above an activated cortical area. When a coherent sensor pair has been determined (Fig. 3C Left), a triangulation of the brain surface is used to estimate which cortical areas gave rise to the coherence in the sensor signals. The spatial filter was used for an iterative search on two cortical patches closest to the selected sensors. First, the triangulation node closest to one of the selected sensors (red, Fig. 3C Left) is taken as the reference point, and coherence is computed to all points in the second cortical patch (Fig. 3C Right). The point in the second patch showing highest coherence is now taken as the reference point, and coherence is computed to all points in the first patch. After the iterations have converged to two points showing maximum coherence on the brain surface, the iteration is extended into the brain volume in spherical regions surrounding the surface points. This approach also led to the selection of left M1 as a reference region.

Strategy 4: Physiological a priori information.

With the fourth strategy, we identified the hand area of the left primary motor cortex in the anatomical MRI scan as represented by a knob-like, Ω-shaped structure (33). This approach yielded the same reference region as obtained from strategies 1 to 3.

Studying cortico-cortical interactions.

The reference region M1 can now be tested for significant coherence to other brain areas. The results are illustrated in Fig. 3D, which shows a color coded representation of cortical coherence to the M1 area in the 9- to 12-Hz band. The coherence of M1 with itself (which is equal to one by definition) accounts for most of the coherence. Nevertheless, a second well separated premotor area (PM) shows significant coherence to M1.

The time courses of M1 and PM were calculated by using a spatial filter. Fig. 3D (Upper Right) illustrates that the coherence between M1 and PM is largely restricted to the 9- to 12-Hz band. Both time series were also subjected to a synchronization analysis. The synchronization index ρ was calculated in 10-s windows with 5-s overlap. Phase synchronization between M1 and PM increases at the time of enhanced tremor activity (Fig. 3D Lower Right).

The delay between M1 and PM activity in the 9- to 12-Hz band was computed at the times of strongest phase synchronization (for a detailed description of the method, see ref. 34). In this particular case, the delay was 0 ms (standard deviation 5 ms), which suggests a zero lag interaction between M1 and PM or a common pacemaker. In contrast, directional information flow was evident in the cortico-muscular coupling where M1 activity preceded EMG by 16 ms (standard deviation 3 ms), in agreement with cortico-muscular conduction times to forearm muscles as determined in transcranial stimulation studies (35).

Discussion

We present a method, dynamic imaging of coherent sources or DICS, for the localization of oscillatory brain activity and the identification of coherent brain areas using a frequency domain implementation of a spatial filter. It can be used for imaging the spatial distribution of power and coherence in chosen frequency bands. It is especially suited for analyzing oscillatory components in continuously recorded electromagnetic signals.

We have used a two-step procedure. First, we identify the coherent brain areas. Second, we analyze the time courses of their activity. The first step requires the selection of a reference region by one of four strategies, which are based on (i) a peripheral signal, (ii) maximum power, (iii) the coherence between sensors, or (iv) physiological a priori information. A number of reference regions can then be tested for significant coherence to other brain areas. The four approaches are complementary and may each lead to the detection of different interacting areas. For example, a weak but significant coherence between brain areas may lead to a nonsignificant sensor coherence and to failure of strategy 3. It may, however, be identified by a correct a priori choice of the reference region (strategy 4). On the other hand, by choosing the reference region according to the strongest oscillatory brain areas (strategy 2), one could miss regions that are highly coherent but have low power. These regions could be detected by strategy 3.

Locations of neuronal populations generating oscillatory activity have been previously estimated and their time behavior investigated by various methods (e.g., refs. 36–39). In contrast, the main purpose of DICS is the detection of coherent neuronal populations and characterization of their dynamic interactions. pSPMs are mainly used as one strategy of choosing a reference region. Nevertheless, the estimation of pSPMs and coherence is done conveniently within the same conceptual and methodological framework.

The time course of activity in the regions of interest is computed by applying a spatial filter. Because the resulting time series can be taken as estimates of the activity in a brain region, the final interpretation of the results is considerably facilitated. For studying dynamical features of power and neural interactions in the second step, we used the instantaneous amplitude and the synchronization index. Both measures are derived from the Hilbert transform and do not require stationarity of the data (27). Application of any other nonlinear or linear analysis on the time courses of the neuronal activations is equally feasible.

Simulations demonstrate the ability of the present algorithm to accurately estimate the location of coherent brain areas in a range of SNR and coherence expected in physiological data. Because DICS is applied to unaveraged data, coherences between brain areas as high as 0.95 used in the simulations seem unlikely.

Employing DICS on recordings of spontaneous activity in a healthy subject and a parkinsonian patient resulted in the localization of the generators of oscillatory activity and the characterization of cortico-muscular and cortico-cortical coupling, which are consistent with results of previous studies.

In the healthy subject, pSPM peaks in the 10-Hz and 20-Hz frequency ranges were in accordance with the locations of the known generators of the alpha- and mu-rhythm. In the parkinsonian patient, we identified the cortical area showing highest coherence to the FDS muscle. We were able to trace yet further functional connectivities by taking this area as reference point for a cortico-cortical coherence analysis. This approach led to the detection of PM showing coherence to M1. The synchronization analysis revealed an increase in M1–PM synchronization at the time of enhanced tremor activity consistent with involvement of these areas in parkinsonian resting tremor (27, 40).

In conclusion, we have introduced an analysis method that makes it possible to directly study dynamics of coherent brain areas based on electromagnetic recordings of human brain activity, and demonstrated its applicability on real data. The present approach is barely biased by the user or by assumptions on the source model. Access to identified brain areas instead of MEG sensors or EEG electrodes will enhance the information content in studies of cortico-muscular interactions. Most importantly, cortico-cortical interactions and their time courses can now be evaluated to address the intriguing questions of perceptual binding in the human cortex and, more generally, of coupling within distributed cortical networks during rest or task performance in physiological and pathological conditions.

Abbreviations

DICS

dynamic imaging of coherent sources

MEG

magnetoencephalography

EEG

electroencephalography

pSPM

power statistical parametric map

EMG

electromyography

FDS

flexor digitorum superficialis

SNR

signal-to-noise ratio

FWHM

full width at half maximum

PM

premotor cortex

Appendix

Methodological Details of DICS.

DICS employs a linear transformation defined by the matrix A, which, when applied to the measured data, passes the activity in a specific frequency band of the sources at position r with unit gain, while suppressing contributions from all other sources. These characteristics can be formulated as a minimization problem:

2

where ℰ{} denotes the expectation value and the matrix D contains the Fourier transformed data. I is the unit matrix, α is the regularization parameter, and the columns of L(r) contain the solution of the forward problem for two orthogonal tangential unit dipoles at r. The constraint ensures that the desired signal is passed with unit gain. By minimizing the corresponding Lagrange function, the frequency-dependent solution can be derived in analogy with ref. 41:

3

with C_r(f) = C(f) + αI, where C(f) is the cross spectral density matrix at frequency f or averaged across a frequency band centered at f, and superscript T indicates the matrix transpose. The last two terms in Eq. 3 represent a weighting of L(r), with the inverse of the cross spectral density matrix. The bracket contains a scaling of the coefficients, which emerges from the constraint in Eq. 2.

The cross spectrum estimates between the four tangential source combinations at locations r₁ and r₂ at frequency f are then represented by the 2 × 2 matrix

4

In the case r₁ = r₂, C_s is a 2 × 2 matrix containing the power estimates

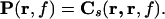5

The corresponding equation for the cross spectral density to an external reference signal can be computed according to

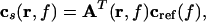6

where c_ref(f) is the cross spectral density between the reference signal and all MEG signals. From Eq. 5, it is evident that the power estimate can thus be computed efficiently from the solution of the forward problem and the cross spectral density matrix.

If the singular values of C_s, λ₁ ≫ λ₂, the cross spectrum can be attributed to sources with fixed orientations, determined by the singular vectors corresponding to λ₁. We can then reduce the matrices in Eqs. 4 and 5 to scalars by estimating the cross spectral density along the dominant direction, which leads to the expression

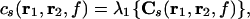7

where λ₁{} indicates the larger singular value of the expression in braces.

Analogously, the power in the dominant direction is

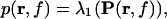8

and we obtain the coherence from Eqs. 7 and 8 as

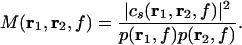9

If λ₁ ≫ λ₂ does not hold, the trace of the 2 × 2 matrix is used instead of the largest singular value.

To obtain the spatial distribution of the power, p(f) is computed on a regular grid covering the entire brain, and, following the approach of refs. 23 and 24, the ratio of source power to noise projected by the spatial filter is displayed. The projected noise is computed in analogy to Eq. 8, where the cross spectral density matrix is replaced by the noise cross spectral density matrix. The noise-normalized power is F-distributed, with degrees of freedom corresponding to the number of values used for the computation of C. The thresholded image, color-coded according to noise-normalized power, is referred to as pSPM (42). Sources are identified from local peaks in the pSPM. The corresponding orientations are computed from the eigenvectors of the matrix C_s.

If a large grid spacing is chosen to ensure fast computation, sources may be missed or incorrectly estimated if their true location is too far apart from a grid point. This problem is avoided by increasing the regularization which leads to a spatially wider representation of the source.

Time courses are computed for selected regions of interest with a spatial filter (24) for the dominant orientation and an orthogonal direction. The spatial resolution is higher for the narrowband data used for imaging power and coherence than for broadband data used for the estimation of the time course. The number of sources is usually reduced in narrowband data, which increases the spatial resolution. For the computation of phase synchronization, a narrow-band time course is estimated with a spatial filter of high spatial resolution.

The Dependence of DICS Performance on SNR and on the Level of Coherence.

The performance of spatial filter methods that use the spatial data covariance matrix degrades in the presence of correlated sources although correlations of 0.5 seem tolerable (24). To investigate the performance of DICS under various conditions, we carried out simulations that revealed, in agreement with ref. 24, that level of coherence and the SNR are decisive parameters also for DICS.

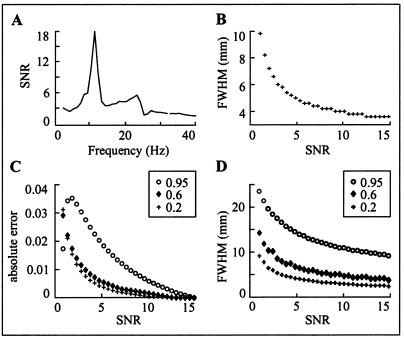
We define SNR as the ratio of the frobenius norms of the cross spectral density matrices of signal and noise. A typical SNR range in physiological data is illustrated in Fig. 4A, with spontaneous brain activity in a resting subject (eyes open) as signal and with recordings without a subject as noise. The peaks correspond to alpha- and mu-rhythm.

Figure 4.

Testing the performance of DICS. (A) The SNR of spontaneous activity, estimated as the ratio of the frobenius norms of the cross spectral density matrices of data measured from a resting subject (signal) and without a subject (noise). (B) The pSPM FWHM in millimeters plotted for SNR in the range 1 to 15. (C) The absolute error in the coherence estimation for three different coherences (0.2, 0.6, and 0.95) is plotted as function of SNR. (D) The dependence of FWHM of coherence on SNR for three different coherence values (0.2, 0.6, 0.95).

Fig. 4B displays the dependence of the spatial resolution on SNR. In the simulations, sensor positions and conductivity model for the head were taken from the measurement of the parkinsonian patient. The noise data were taken from recordings without a subject. Location and orientation of the simulated point source was taken from the M1 source (Fig. 3). The M1 activity was simulated by using bandpass filtered noise (12 ± 0.5 Hz), and the pSPM was computed in the 10- to 14-Hz range along the line connecting the M1 and PM areas with a resolution of 0.15 mm. The pSPM showed a peak at the true source location. Note that the number of contiguous grid points where the effect of a point source can be seen depends on the grid spacing, threshold level, and amount of regularization applied according to Eq 3. The width of the peak changes with SNR and is quantified by the full width at half maximum (FWHM) for the SNR range from 1 to 15. The curve in Fig. 4B shows a steep decrease for low SNR (<5) whereas only small improvement is evident for high SNR beyond about 12.

A further simulation was performed to test the accuracy of the coherence estimate. Coherence was simulated at 12 Hz between the M1 and PM area (see Fig. 3D). The angle between source orientations was 30°. Fig. 4C illustrates the absolute error in the coherence estimation as a function of SNR for three different coherences (0.2, 0.6, and 0.95). High coherence results in a larger absolute error, compared with medium (0.6) and moderate (0.2) coherence.

Fig. 4D illustrates the effect of SNR on the minimum distance between sources that can still be separated. Two sources are defined as separable if there is no overlap in their FWHM ranges of coherence computed along the line connecting M1 and PM. The minimum distance required to separate two sources increases sharply for the highest coherence. However, even highly coherent and spatially close neuronal populations can be identified when the SNR is high. After estimating the SNR from real data, simulations can be used to quantify the expected uncertainty of the coherence estimate.