Abstract
PURPOSE The health care system in the United States is inherently hierarchical. Patients are “nested” within physicians who in turn are “nested” within practices. Much of the research data gathered in practice-based research networks (PBRNs) also have similar patterns of nesting (clustering). When research data are nested, statistical approaches to the data must account for the multilevel nature of the data or risk errors in interpretation. We illustrate the concept of multilevel structure and provide examples with implications for practice-based research.
METHODS We present a selection of multilevel (hierarchical) models and contrast them with traditional linear regression models, using an example of a simulated observational study to illustrate increasingly complex statistical approaches, as well as to explore the consequences of ignoring clustering in data. Additionally, we discuss other types of outcome data and designs, and the effects of clustering on sample size and power.
RESULTS Multilevel models demonstrate that the effects of physician-level activities may differ from clinic to clinic as well as between rural and urban settings; this variability would be undetected in traditional linear regression approaches. Study conclusions differed when the data were analyzed with multilevel methods compared with traditional linear regression methods. Clustered data also affected sample size; as the intraclass correlation increased and the patients per cluster increased, the required number of patients increased dramatically.
CONCLUSIONS Recognizing and accounting for multilevel structure when analyzing data from PBRN studies can lead to more accurate conclusions, as well as offer opportunities to explore contextual effects and differences across sites. Accommodating multilevel structure in planning research studies can result in more appropriate estimation of required sample size.
Keywords: Practice-based research network; cluster analysis; clustered data, multilevel models; data analysis; models, statistical; data interpretation, statistical
INTRODUCTION
Many studies conducted in practice settings collect patient-level data (such as blood pressure measurements) as the dependent variable. Usually, such data have a hierarchical structure, with patient-level measures clustered (nested) within physicians and multiple physicians clustered within the same practice. (For definitions of the statistical terms we use in this article, see Table 1 ▶.) When analyzing such data, it is important to recognize hierarchical/multilevel structure and account for similarities among individuals within groups.1–6 Traditional statistical methods, such as logistic or linear regression analysis, assume that observations are uncorrelated; however, in the case of hierarchical/multilevel data (also called clustered or nested data), these assumptions are unrealistic. Individual observations (eg, patient-level blood pressure measurements) that are clustered within a higher-level unit share a common environment and may be more similar than observations from individuals in different higher-level units. In health care settings, patients treated by a particular clinician receive care in a common treatment setting that is influenced by clinician characteristics and philosophy, and that may differ from one clinician to another; clinicians within the same practice share a common practice environment that is influenced by the practice setting and other characteristics. Ignoring group membership can result in erroneous conclusions, as demonstrated in studies from educational settings.7 The choice of analytic methods for clustered data can have major implications for research by practice-based research networks (PBRNs), which almost always involves sampling patients from multiple physicians and clinics. Investigation of the effects of macrolevel characteristics on individuals has been carried out in educational and organizational research but is relatively new in health research.1–9
Table 1.
Glossary of Terms
| Multilevel/hierarchical/clustered/nested data: Data that have some inherent group membership (eg, students within schools, patients with clinics) or hierarchical structure |
| Multilevel models/hierarchical linear models (HLMs): A type of statistical procedure belonging to the class of general linear models, adapted for analysis of clustered data |
| Analysis of variance (ANOVA): A statistical procedure used to compare means of a continuous outcome variable for more than 2 groups, classified by 1 or more categorical variables; for example, comparison of patient scores on a functional health survey for 4 non-overlapping diagnostic groups by 2 sex categories |
| Analysis of covariance (ANCOVA): An extension of ANOVA in which the means of a continuous outcome variable are compared across groups, as described above, adjusting for 1 or more continuous covariates; for example, comparison of patient scores on a functional health survey for 4 nonoverlapping diagnostic groups, adjusted for age |
| Fixed effects: A condition in which the levels of a factor include all levels of interest to the researcher (eg, sex: male or female) |
| Intraclass correlation coefficient (ICC): A measure that describes the extent to which individuals within the same group are more similar to each other than individuals in different groups |
| Random effects: A condition in which the levels of a factor represent a random sample of all possible levels (eg, clinics) |
| Linear regression analysis:Simple linear regression analysis assesses how a continuous outcome variable (or dependent variable) changes per unit change in a predictor variable (or independent variable). Multiple linear regression analysis assesses the relationship between 1 dependent variable and more than 1 independent variables. |
| Residual variance: The remaining variance in the outcome variable (dependent variable) after accounting for all predictors (independent variables) and random effects of interest |
Most statistical procedures involve understanding sources of variance among experimental units (eg, people). Traditional approaches (ie, ordinary least squares [OLS]) such as analysis of variance and multiple linear regression analysis ignore dependencies within groups, but advances in analytic approaches (general linear mixed models, hierarchical linear models, random regression modeling) and computing software1–8,10 can account for the multilevel structure of the data and also for the random variation associated with sampling higher-level units, such as physicians or practices.
In a simple 2-level model, the sources of variance are within-groups and between-groups. Using a PBRN context with patients sampled from clinics, the total variation in patient outcomes can be partitioned into 2 variance components: within-clinics variance (ie, variance among patients in the same clinic) and between-clinics variance (ie, variance between patients in different clinics). When patients within groups are very similar to each other, we have less information than we would have from the same number of patients obtained in a simple random sample (ie, an unclustered sample). An important measure that describes these dependencies in the data is the intraclass correlation coefficient (ICC); this statistic measures the extent to which individuals within the same group are more similar to each other than they are to individuals in different groups. We will explain this measure more fully in the next section. Issues around violations of distributional assumptions such as nonindependence of measures have long been recognized, but technical advances that make such complex analytic methods accessible are fairly recent.8–13
In this article, we illustrate the concept of multilevel (hierarchical) structure and analytic approaches, using a specific example from the health field with data simulated to maximize clustering effects, and we contrast multilevel methods with traditional methods. We include an overview of modeling approaches for studies with continuous outcomes and hierarchical structure. We cover 2-level models in detail, illustrating the conceptual ideas behind multilevel approaches and contrasting them with traditional methods. The analyses progress from simple to complex, with 2 traditional models and 5 multilevel models (also called hierarchical linear models [HLMs]). The models described below can be adapted or extended to cover most research designs common to PBRNs. We include an additional statistical model for studies with dichotomous or binary outcomes and briefly discuss other applications. Finally, we address issues pertaining to power and sample size for clustered data, and give some examples.
ILLUSTRATION OF TRADITIONAL AND MULTILEVEL ANALYSES FOR A PBRN STUDY
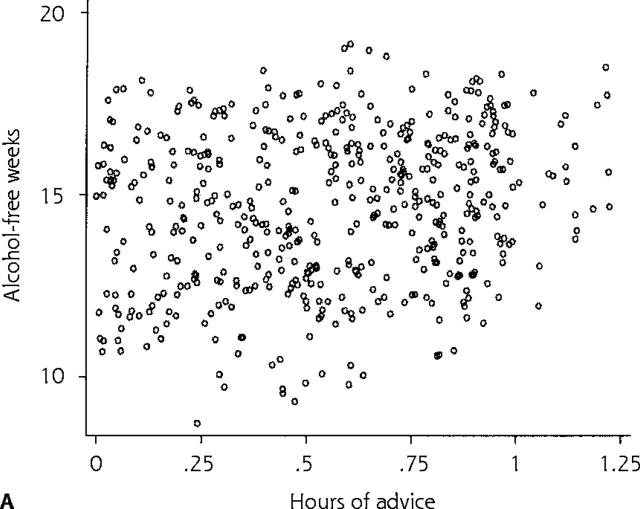
We use a hypothetical observational PBRN study and a simulated database to illustrate the results obtained with different traditional and multilevel models in a context with large between-clinic differences. The purpose of the study was to examine the effect of time spent by physicians giving advice to patients regarding alcohol consumption on their alcohol consumption during 1 year. The data set consists of 500 patient-level observations. Patients were randomly sampled from 1 physician in each of 5 clinics (100 patients per physician), with 3 clinics located in an urban area and 2 in a rural setting. The dependent variable, a continuous variable, was the number of alcohol-free weeks per patient during 1 year. The independent variables included the number of hours per year of physician advice each patient received (a patient-level variable) and clinic location, classified as urban or rural (a clinic-level covariate). The 500 patients in this study reported an average of 14.61 (SD, 2.12) alcohol-free weeks during the past year (Table 2 ▶). Figure 1a ▶ illustrates the distribution of number of alcohol-free weeks by physician advice over all clinics in a scatter plot.
Table 2.
Study Results Obtained With Differing Models
| Description of the data | |||
| Variable | Description | Mean (SD) | Range |
| yij | Number of alcohol-free weeks in 1 year for patient i from clinic j | 14.61 (2.12) | 8.7–19.1 |
| xij | Total hours of physician advice per year for patient i from clinic j | 0.56 (0.30) | 0.002–1.23 |
| wj | Urbanicity: urban = 1; rural = 0 | 0.6 | 0–1 |
| Notation | |||
| i | Indexes patients within a clinic | 1–100 | |
| j | Indexes clinics | 1–5 | |
| HLM model 1: random-effects ANOVA model | |||||
| Fixed effects | Estimate* | SE | t | df | Pr > t |
| γ00 (grand mean) | 14.61 | 0.79 | 18.46 | 499 | .000 |
| Random effects | Estimate* | Pr(H0: τ= 0) | |||
| τ00 (between-clinic variance) | 1.76 | .000 | |||
| σ2 (residual variance) | 1.41 | ||||
| REG model 1: traditional linear regression model 1† | ||||
| Fixed effects | Estimate* | SE | t | Pr> t |
| β0 (γ10) – slope | 1.31 | 1.23 | 1.07 | .345 |
| β1 (γ00) – intercept | 13.87 | 1.19 | 11.69 | .000 |
| σ2 (residual variance) | 2.1 | |||
| HLM model 2: random-intercept model | |||||
| Fixed effects | Estimate* | SE | t | df | Pr> t |
| γ10 (slope) | 2.38 | 1.05 | 2.26 | 498 | .024 |
| γ00 (average intercept) | 13.27 | 1.30 | 10.24 | 4 | .000 |
| Random effects | Estimate* | Pr(H0: τ= 0) | |||
| τ00 (variability in clinic intercepts) | 3.47 | 0.000 | |||
| σ2 (residual variance) | 1.65 | ||||
| HLM model 3: random-coefficients model | |||||
| Fixed effects | Estimate* | SE | t | df | Pr> t |
| γ10 (average slope) | 2.96 | 0.89 | 3.31 | 4 | .040 |
| γ00 (average intercept) | 12.80 | 1.32 | 9.74 | 4 | .000 |
| Random effects | Estimate* | Pr(H0: τ= 0) | |||
| τ00 (variability in intercepts across clinics) | 10.71 | .000 | |||
| τ11 (variability in slopes across clinics) | 4.74 | .000 | |||
| τ01 (covariance between intercept and slope) | −7.10 | ||||
| σ2 (residual variance) | 1.18 | ||||
| HLM model 4: intercept as outcome model | |||||
| Fixed effects | Estimate* | SE | t | df | Pr> t |
| γ10 (slope) | 2.34 | 0.23 | 10.03 | 497 | .000 |
| γ01 (difference between urban and rural intercept) | −3.26 | 0.51 | −6.36 | 3 | .000 |
| γ00 (rural intercept) | 15.25 | 0.42 | 36.67 | 3 | .000 |
| τ00 (variability in clinic intercepts after adjusting for urban or rural location) | 0.55 | .000 | |||
| σ2 (residual variance) | 1.28 | ||||
| HLM model 5: intercept and slope as outcomes model | |||||
| Fixed effects | Estimate* | SE | t | df | Pr> t |
| γ11 (difference in slope between urban and rural areas) | 3.97 | 0.50 | 7.94 | 3 | .000 |
| γ10 (average slope in rural areas) | 0.67 | 0.44 | 1.54 | 3 | .220 |
| γ01 (difference in intercepts between urban and rural areas) | −5.53 | 0.83 | −6.67 | 3 | .000 |
| γ00 (average intercept in rural areas) | 16.15 | 0.60 | 26.77 | 3 | .000 |
| Random effects | Estimate* | Pr(H0: τ= 0) | |||
| τ00 (variability in intercepts after adjusting for urbanicity) | 1.51 | .000 | |||
| τ11 (variability in slopes after adjusting for Urbanicity) | 0.28 | .092 | |||
| τ01 (covariance between intercept and slope) | −0.44 | ||||
| σ2 (residual variance) | 1.39 | ||||
| REG model 2: traditional regression model 2 | ||||
| Fixed effects | Estimate* | SE | t | Pr> t |
| HLM = hierarchical linear model; H0 = null hypothesis; ANOVA = analysis of variance; REG = regression; Pr = probability. | ||||
| * Estimated number of alcohol-free weeks during the past year. | ||||
| † Residual variance = 2.0813. | ||||
| Slope | ||||
| γ11 (urban – rural) | 1.48 | 1.13 | 1.30 | .226 |
| γ10 (rural) | 0.83 | 0.49 | 1.71 | .163 |
| Intercept | ||||
| γ01 (urban – rural) | −4.04 | 1.01 | −4.01 | .016 |
| γ00 (rural) | 16.05 | 0.67 | 23.94 | .000 |
Figure 1.
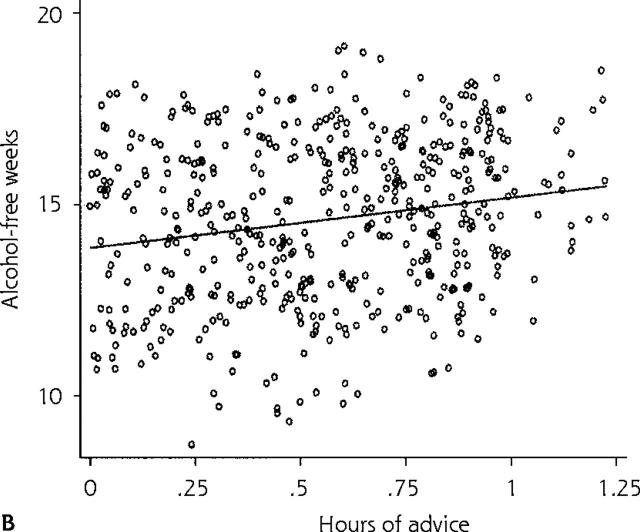
(a) Scatter plot of patient number of alcohol-free weeks during 1 year vs physician number of hours of advice per year. (b) Fitted line based on predictions for the whole data set using REG model 1 (traditional linear regression model 1).
Traditional Models
HLM Model 1: Random-Effects Analysis of Variance
The simplest multilevel model is a 1-way analysis of variance (ANOVA) with clinic random effects; the assumption is that we have sampled from a population of clinics (just as we typically sample from a population of patients). In contrast to the overall mean and SD of number of patient alcohol-free weeks reported in Table 2 ▶, this model estimates the mean number of alcohol-free weeks (γij) for each clinic and decomposes the total variance in that number (γij) into the between-clinic (level-2) and within-clinic (level-1) variance components, that is, variability due to differences in the mean number of alcohol-free weeks for the 5 clinics and variability in the number of alcohol-free weeks for patients within the same clinic. (A detailed description of this statistical model and the others we discuss is given as supplementary data in the Supplemental Appendix, available online only at http://www.annfammed.org/cgi/content/full/3/Suppl_1/S52/DC1.)
The ICC reflects the extent to which patients within the same clinic are more similar to each other than they are to patients in different clinics. It is the proportion of the total variance that is due to differences among clinics. ICCs are very important in planning studies and analyzing data that have hierarchical structure, which is common to most practice-based research. Obviously, the degree to which individuals within a practice are more similar than individuals in different practices depends on the outcome of interest, as well as other factors, and will vary from one study to another.
The results from applying the random-effects ANOVA model to the alcohol data set are given in Table 2 ▶ (see HLM Model 1). Note that the variance is now decomposed into a between-clinic variance (1.76) and a within-clinic (residual) variance (1.41). The estimated ICC indicates that the ratio of the between-clinic variance to the total variance is about 55%, calculated as ICC = 1.76/(1.76 + 1.41), suggesting that patients within clinics are more similar to each other than to those at other clinics. (ICC ranges from 0 to 1 [or 0% to 100%], with higher values representing stronger clustering effects.)
REG Model 1: Traditional Linear Regression Model 1
The most commonly used analytic approach to our hypothetical problem would be the simple linear regression model (online Supplemental Appendix, see REG model 1). This model is essentially a patient-level model, but one can visualize it as a 2-level model with fixed effects; that is, the mean number of alcohol-free weeks among patients without any physician advice—intercept (β0)—is the same for all clinics, and the effect of physician advice on patient alcohol-free weeks, per unit of time spent—slope (β1)—is also the same across all clinics.
The results from applying this model to the alcohol data set are shown in Table 2 ▶ (see REG model 1). These results indicate that, on average, 1 additional hour of physician advice is associated with an increase of 1.31 alcohol-free weeks; however, this increase does not reach statistical significance at the 5% level, so these results would lead us to conclude that physician advice does not impact patient alcohol consumption. The residual variance in number of alcohol-free weeks after adjusting for hours of advice (σ2) is about 2.1. Figure 1b ▶ shows the predicted regression line for the entire data set based on this model. Robust regression methods, which involve only a slight modification of traditional linear regression analysis, address some of the problems described above and can be used as sensitivity analyses when the emphasis is primarily on fixed effects.10
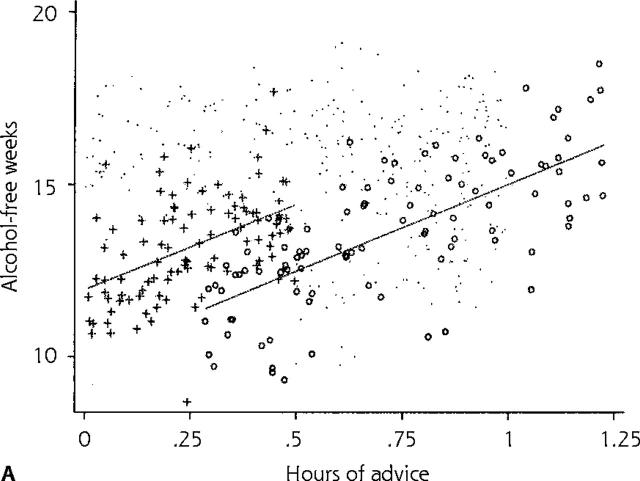
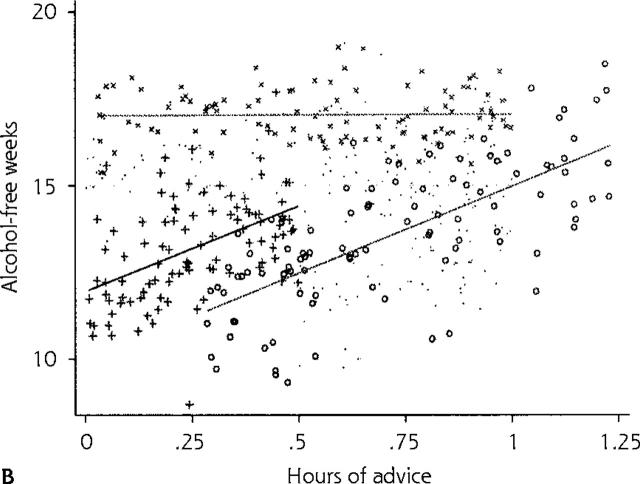
Careful exploration of the data reveals that the mean number of alcohol-free weeks without any physician advice—intercept (b0)—may be different in different clinics (Figure 2a ▶). This baseline heterogeneity across clinics is illustrated in the figure, which shows the traditional model 1 fit individually for 2 clinics. Further exploration of the data reveals that the effect of physician advice—slope (b1)—may also vary across clinics (Figure 2b ▶), suggesting that physicians’ advice (per unit of time spent) is more effective at some clinics than at others. This figure illustrates the model fit of the traditional model 1 in a third clinic, which suggests that besides differences in mean number of alcohol-free weeks without any physician advice (variation in intercepts), there are also differences in the effect of hours of physician advice (variation in slopes) on patient number of alcohol-free weeks across clinics.
Figure 2.
Fitted lines based on predictions for individual clinics using REG model 1 (traditional linear regression model 1). (a) Lines for 2 clinics. (b) Lines for 3 clinics.
Multilevel Models
Multilevel models provide a way to account for variation in intercepts and slopes across clinics (level-2 units) without having to apply the traditional model 1 separately for each clinic. The random-intercept model, which allows for variation in intercepts across clinics, is a simple model in the series of HLMs, whereas a more advanced model, the random-coefficients model, accounts for variation in both intercepts and slopes across clinics. These models are described below and in the online Supplemental Appendix. Researchers can use a variety of statistical programs to analyze multilevel data:
HLM (Raudenbush, Bryk, Cheong, and Congdon; available at http://www.ssicentral.com/hlm/hlm.htm)
MLWIN (Centre for Multilevel Modelling, Institute of Education, London, England; available at http://multilevel.ioe.ac.uk/index.html)
SAS – Proc Mixed (SAS Institute, Cary, NC; available at http://www.sas.com)
WinBUGS (MRC Biostatistics Unit, Cambridge, United Kingdom; available at http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml)
HLM Model 2: Random-Intercept Model
The random-intercept model accounts for the variation across clinics in the mean number of alcohol-free weeks without any physician advice (online Supplemental Appendix, see HLM model 2); however, the effect of physician advice (per unit of time spent) is still constrained to be the same for all clinics (ie, the slope is fixed). This model is equivalent to a 1-way analysis of covariance (ANCOVA) with random effects (intercepts).
Statistical packages for multilevel modeling allow for estimation of all parameters in this model, including the random effects, and enable us to test whether there is significant variation among clinics, after adjusting for patient- and clinic-level covariates. This test helps us to determine whether it is necessary to retain a clinic-level random effect. The results from applying the random-intercept model to the alcohol data set are shown in Table 2 ▶ (see HLM model 2). The ICC (ratio of the between to the total variance) is about 68%, indicating that patients within clinics are very similar to each other compared with patients in different clinics. Consequently, after accounting for differences among clinics, the estimate for the residual variance (s2) is reduced to 1.65. Moreover, the estimate of the effect of physician advice, per unit of time spent, on patient alcohol-free weeks—slope (γ10)—is now 2.38 alcohol-free weeks per unit time spent and is statistically significant at the 5% level. From these results, we would conclude that time spent by physicians advising patients on alcohol consumption does have an effect on their alcohol consumption (it is also possible to gain in precision but lose in significance). In this case, wherein between-clinic differences are large, the gain in efficiency with the HLM estimator provides 2 advantages over the traditional models:(1) it can affect policy decisions by influencing the significance of the estimates, and (2) it reduces the instability in point estimates of parameters because of the tighter error variance.
HLM Model 3: Random-Coefficients Model
In the random-coefficients model, we allow both the intercept and the slope to be specified as random variables (Figure 2b ▶ showing individual regressions for each clinic), thus accounting for variability in both the mean number of alcohol-free weeks without any physician advice (intercepts) and the effects of physician advice (slopes) across clinics. As a result, if clinics were analyzed in separate linear regression models, estimates for intercepts and slopes could be quite different from one clinic to the next. These differences are ignored when data from different clinics are combined in a simple linear regression model or even in a random-intercepts model, and ignoring them can result in incorrect conclusions, such as erroneously concluding that physician advice does not affect patient alcohol consumption. (Note: It is possible to estimate clinic differences using a combination of indicator variables and interaction effects in traditional linear regression, but this practice is not recommended because the assumption of independence is still violated, power is severely hampered, and too many terms may be required for the sample size.)
The online Supplemental Appendix (see HLM model 3) gives details of the random-coefficients model, and Table 2 ▶ (see HLM model 3) shows the results obtained when this model is applied to the alcohol data set. We can see that there is significant variability in the mean number of alcohol-free weeks without any physician advice across clinics, as well as variability in the effect of physician advice on alcohol consumption across clinics (reject the null of H0: τ= 0). The average slope in the entire study population is estimated to be 2.96 and is statistically significant at the 5% level. Also, the covariance parameter estimate, which describes the relationship between the intercepts and slopes, is negative (τ01 = −7.10). It is therefore possible that physician advice in clinics with a higher baseline number of alcohol-free weeks may have less impact than in clinics with a lower one (a possibility that should be tested more rigorously to determine whether it is a real clinical effect).
More-Complex Models
In the previous HLMs, we have allowed the intercept and the slopes to be random (vary across clinics) in order to account for the variability in mean number of alcohol-free weeks without physician advice and the variability in the effects of physician advice across clinics. The next logical step is to try to explain these differences among clinics using characteristics of the level-2 units (clinics).
HLM Model 4: Intercept as Outcome Model
With the intercept as outcome model, we want to see if variability in the mean number of alcohol-free weeks without any physician advice across clinics (intercepts) can be explained by clinic-level characteristics such as urban or rural location of the clinic (online Supplemental Appendix, see HLM model 4). Like HLM model 2, this model assumes that the effect of physician advice on alcohol consumption (slope) is the same across clinics.
The results for the intercept as outcome model are given in Table 2 ▶ (see HLM model 4). The results show that the mean number of alcohol-free weeks without any physician advice (ie, xij = 0) is about 15.25 for patients in rural clinics, whereas it is about 3.26 weeks lower for patients in urban clinics. This difference is statistically significant at the 5% level. Moreover, urbanicity of the clinic explains about 84% of the variance in the intercept. This observation suggests that a substantial amount of the variability in baseline number of alcohol-free weeks across clinics can be accounted for by urban or rural location; nevertheless, the variability in the intercepts is still significant even after adjusting for clinic location.
HLM Model 5: Intercept and Slope as Outcomes Model
In the intercept and slope as outcomes model, we try to explain both the variability in the baseline number of alcohol-free weeks (intercepts) across clinics and the variability in the effect of physician advice on alcohol consumption across clinics (slope) by clinic- level characteristics such as urban vs rural location of the clinic (online Supplemental Appendix, see HLM model 5).
Study results obtained when the intercept and slope as outcomes model is applied to the alcohol data set are given in Table 2 ▶ (see HLM model 5). The results show that after adjusting for urbanicity of clinics, the remaining variability in slopes is not statistically significant (P = .092) at the 5% level (although it is significant at the 10% level). The researcher may decide to retain the random slope or may choose to specify the slope as nonrandomly varying. The results also show that the effect of physician advice on alcohol consumption is nonsignificant in rural clinics (0.67 alcohol-free weeks per hour of physician advice, P = .220), but there is a significant difference in this effect between urban and rural clinics (difference of 3.97 alcohol-free weeks per hour of physician advice, P = .000). For urban clinics, an additional hour of physician advice is associated with an increase of 4.64 (ie, 3.97 + 0.67) additional alcohol-free weeks on average.
REG Model 2: Traditional Regression Model 2
In a traditional patient-level model, a main effect for physician advice, a main effect for urbanicity, plus an interaction term (physician advice × urbanicity) would be used to study how urban vs rural location moderates the effect of physician advice on alcohol-free weeks (online Supplemental Appendix, see REG model 2). This approach allows the intercept and the slope to vary for urban and rural locations but is problematic if there is significant variability among intercepts and slopes of clinics within location type. The results for the traditional regression model 2 are shown in Table 2 ▶ (see REG model 2). Unlike the intercept and slope as outcomes model above (HLM model 5), this model shows that the difference in the effect of physician advice on alcohol consumption between the urban and rural clinics is nonsignificant. Had we used this model, we would have concluded that physician advice was ineffective for rural clinics and that the effect of physician advice in urban clinics did not differ from that in rural clinics.
How Important Are Modeling Decisions in PBRN Studies?
Can different analytic approaches affect an investigator’s conclusions about the outcome? The results in Table 2 ▶ show that decisions about the potential effectiveness of physician time spent advising patients on alcohol consumption may vary with the choice of analytic approach. Had the researchers ignored the hierarchical structure of the data and used traditional analytic approaches, they would have erroneously concluded that physician advice had little or no influence on patient alcohol consumption behavior. On the other hand, all the HLMs that assess the relationship between physician time advising patients on alcohol consumption and patient behavior lead to the conclusion that physician advice is effective, at least in some settings. An important limitation of the hypothetical study should be mentioned at this point. Because variability among clinic intercepts and slopes is estimated using clinic-level information, ideally, the number of level-2 units (clinics) should be much greater than 5. Several of the references cited below include discussions about how many level-2 units should be sampled.1–5
APPLICATIONS TO OTHER FORMS OF DATA AND INTERVENTIONS
Randomized Controlled Trials
The variety of HLMs described above can be readily extended to study different types of interventions and data that have some sort of group structure, such as clustering of patients within clinics. In intervention studies that are carried out in PBRNs, it is often necessary to randomize at the clinic level to avoid contamination and minimize difficulties in implementing interventions. This setup naturally leads to the use of multilevel modeling. For example, suppose we want to test an intervention to assist patients in their daily management of type 2 diabetes. The intervention might involve patient education and support from their primary care clinicians and be implemented at the practice level in 20 practices, with 10 randomized to the intervention and 10 to provision of usual care. We wish to control for patient characteristics, so patient-level covariates will be included in the level-1 model. We would allow the intercept and slope to vary randomly across practices and then try to explain this variability using the intervention variable as a level-2 characteristic (as in HLM model 5, the intercept and slope as outcomes model).
Longitudinal Models
Longitudinal models, in which individuals are observed at multiple instances over time, are actually another kind of hierarchical structure, in which level-1 represents the individual’s observations over time, and the level-2 units are the patients themselves. These models are discussed in detail elsewhere.6,7
Dichotomous Dependent Variables
Other forms of outcome data can be analyzed using hierarchical generalized linear models (HGLMs), also called generalized linear mixed models (online Supplemental Appendix, see HGLM model). For example, many health outcomes are dichotomous or binary rather than continuous (eg, a patient was tested for a particular condition, a patient achieved a target hemoglobin A1c level). Suppose in the example above, the intervention for diabetes included a physician education component designed to encourage primary care physicians to screen for hyperlipidemia among diabetic patients. The patient-level outcome is whether the patient was screened (yes or no) within a designated time period after the intervention. We want to control for patient characteristics and test whether the intervention is effective at encouraging physicians to screen their diabetic patients. In the traditional approach to this analysis, we might use a logistic regression model; however, the assumption of independence of observations is violated because of the clustering of patients within clinics. One alternative approach (there are other possible approaches13) adapts the hierarchical linear model by using a link function at level 1 that is appropriate to the distribution of the outcome variable.5
Higher-Level Data Structure
Finally, it is straightforward to extend a 2-level hierarchy to a hierarchy of 3 or more levels. Interested readers are referred to Bryk and Raudenbush1 for a detailed description of these models. A number of useful statistical references are given below.8–12
OTHER ISSUES
Measurement and Variable Specification in Multilevel Models
Characteristics of patients, physicians, and practices constitute a set of interrelated factors that can be conceptualized and measured at different levels of a hierarchical system. In multilevel modeling, researchers must pay careful attention to the specification of variables, with measurement at the appropriate level. Some measurement issues that are specific to multilevel models differ from those of traditional psychometric approaches, focusing instead on level of measurement, ways of operationalizing higher-level constructs, and empirical support for types of composition processes for aggregating lower-level data to form macrolevel variables. Variables that provide information about higher-level units (eg, clinicians or settings) can be measured directly or created from measures aggregated from lower-level units (eg, patients). Researchers must exercise caution, however, in avoiding aggregation bias when creating variables and in interpreting results because meaning and functional relationships in multilevel models may be different at lower and higher levels of the hierarchy.1 In the example on counseling about alcohol consumption, the effect of average (aggregated) time spent on such advice in a clinic may reflect a clinic’s awareness of the importance of health counseling or a general emphasis on alcohol (ie, a contextual effect) as opposed to the effects of individual physician time spent counseling individual patients.
Power
In the data analysis on alcohol consumption, the ICC is quite high, but even a relatively small ICC can have adverse effects on power, requiring a larger sample size. Using the Donner et al formula8 for the variance inflation factor (VIF), which is also referred to as the design effect,4 we can determine adjusted sample size requirements in the presence of clustering. If an unclustered design for a randomized controlled trial requires n patients per group to detect the desired effect size with adequate power (eg, 80% power) and α = .05, then the VIF allows us to adjust the sample size for a positive ICC. If we sample m patients per cluster clinic, then we must inflate the sample size by a factor of (1 + (m − 1)ICC). Table 3 ▶ gives a range of sample size corrections for cluster designs with a starting sample size of 100 patients per treatment condition and varying numbers of patients per cluster (clinic) and ICC. It is readily apparent from this table that sample size requirements for clustered designs can be drastically affected by large cluster sizes and increasing ICCs.
Table 3.
Examples of Sample Sizes for Group-Randomized Designs
| Original Sample Size* | No. of Clinics | No. of Patients per Clinic (m) | ICC | VIF | Adjusted Sample Size* |
| 100 | 25 | 4 | .00 | 1.0 | 100 |
| 100 | 29 | 4 | .05 | 1.15 | 115 |
| 100 | 33 | 4 | .10 | 1.30 | 130 |
| 100 | 10 | 10 | .00 | 1.0 | 100 |
| 100 | 15 | 10 | .05 | 1.45 | 145 |
| 100 | 19 | 10 | .10 | 1.90 | 190 |
| 100 | 5 | 20 | .00 | 1.0 | 100 |
| 100 | 10 | 20 | .05 | 1.95 | 195 |
| 100 | 15 | 20 | .10 | 2.9 | 290 |
| 100 | 4 | 25 | .00 | 1.0 | 100 |
| 100 | 9 | 25 | .05 | 2.2 | 220 |
| 100 | 14 | 25 | .10 | 3.4 | 340 |
m = designator for number of patients per cluster to be used in calculations; ICC = intraclass correlation coefficient; VIF = variance inflation factor.
*Number of patients per treatment group.
CONCLUSIONS AND RECOMMENDATIONS
PBRN research generally involves sampling patients from multiple practice sites and often involves group randomization approaches to intervention studies. Data resulting from such approaches are inherently hierarchical. Recognizing the need for adjustments to study design and data analysis in the presence of clustering can allow PBRN investigators to arrive at more accurate conclusions and to more appropriately estimate sample size requirements. Methodologic advances also offer rich opportunities to explore contextual effects by using models that incorporate characteristics of clinicians and clinics as well as those of patients.
Conflicts of interest: none reported
REFERENCES
- 1.Bryk S, Raudenbush A. Hierarchical Linear Models: Applications and Data Analysis Methods. 2nd ed. Thousand Oaks, Calif: Sage Publications; 2002.
- 2.Atikin M, Anderson D, Hinde J. Statistical modeling of data on teaching styles. J R Stat Soc. 1981;144:419–461. [Google Scholar]
- 3.Hedeker D, Gibbons R, Flay B. Random regression models for clustered data: with an example from smoking prevention research. J Clin Consult Psychol. 1994;62:285–296. [DOI] [PubMed] [Google Scholar]
- 4.Murray DM. Design and Analysis of Group-Randomized Trials. New York, NY: Oxford University Press; 1998.
- 5.Littell R, Milliken GA, Stroup WW, Wolfinger RD. SAS System for Mixed Models. Cary, NC: SAS Institute; 1996.
- 6.Willett JB. Questions and answers in the measurement of change. In: Rothkopf E, ed. Review of Research in Education. Washington, DC: American Educational Research Association; 1988:345–422.
- 7.Strenio JLF, Weisberg HI, Bryk AS. Empirical Bayes estimation of individual growth curve parameters and their relationship to covariates. Biometrics. 1983;39:71–86. [PubMed] [Google Scholar]
- 8.Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. London, England: Oxford University Press; 2000.
- 9.Raudenbush SW. Magnitude of teacher expectancy effects on pupil IQ as a function of the credibility of expectancy induction: a synthesis of findings from 18 experiments. J Educ Psychol. 1984;76:85–97. [Google Scholar]
- 10.Singer J. Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. J Educ Behav Statistics. 1998;24:323–355. [Google Scholar]
- 11.Hedeker D. Multilevel models for ordinal and nominal variables. In: Leeuw JD, Kreft I, eds. Handbook for Quantitative Multilevel Analysis. Dordrecht, the Netherlands: Kluwer; in Press.
- 12.McCullagh P, Nelder JA. Generalized Linear Models. London, England: Chapman and Hall; 1983.
- 13.Hardin JW, Hilbe JM. Generalized Estimating Equations. Boca Raton, Fla: Chapman and Hall/CRC; 2003.