Selectin receptor–ligand bonds: Formation limited by shear rate and dissociation governed by the Bell model

Abstract

We have studied the principles that govern the formation and dissociation of an adhesive bond between a cell moving in shear flow and a substrate and tested different theories of how force affects bond dissociation. Viscosity relates the kinematics of fluid movement (shear rate, units of time⁻¹) to shear stress (units of force/area, the product of shear rate and viscosity). At different medium viscosities, the formation of receptor–ligand bonds between a cell in the flowstream and P-selectin on the vessel wall showed a similar efficiency as a function of shear rate but not of shear stress. Therefore, bond formation was a function of shear rate and hence of the kinematics of receptor and ligand movement. By contrast, the kinetics of bond dissociation was a function of shear stress and hence of force on the bond. The different requirements for bond formation and dissociation allowed dissociation kinetics to be measured at higher forces on the bond by increasing medium viscosity. Data over an extended range of forces on the bond therefore could be collected that enabled five different proposed equations, relating force to bond dissociation, to be compared for fit to experimental data. The relationship proposed by Bell [Bell, G. I. (1978) Science 200, 618–627] fit the data significantly the best and also predicted an off-rate in the absence of force that best matched an independent measurement [Mehta, P., Cummings, R. D. & McEver, R. P. (1998) J. Biol. Chem. 273, 32506–32513].

Here we study both the principles that govern the formation of an adhesive bond between a cell moving in shear flow and a substrate and those that govern dissociation of this bond by the force that is applied to the bond as a consequence of the hydrodynamic force acting on the cell. The resistance of molecular bonds to rupture is of key importance to understanding cell–cell adhesion. For many adhesion molecules including selectins, a key function of the adhesive bond is to resist forces in the body that would otherwise break cell–cell contact (1). The “strength” of a receptor–ligand bond or multiple bonds is not a simple function of affinity, because bonds have “mechanical properties” that affect their ability to resist applied force. Whereas affinity is related only to the net energy change of a bond, mechanical properties are a function of the shape of the energy landscape in the transition states of bond formation and dissociation.

Specific physical models have been proposed to describe the effect of force on receptor–ligand association and dissociation. Bell proposed a model (2) that uses an exponential relationship that had been demonstrated experimentally for the rupture of materials (3). In the Bell model, k_off = k_off⁰ exp(σF/kT) where k_off⁰ is the k_off in absence of force, σ is the distance range of the bond potential-energy minimum, F is the force on the bond, k is Boltzmann's constant, and T is absolute temperature. The Bell model predicts that the dissociation rate, k_off, increases exponentially with force on the bond. Using a similar thermodynamic approach based on the Gibbs free energy, the Hookean spring model was developed by assuming that the receptor–ligand bond has a spring-like mechanical property with an overall bond spring constant, κ, and a spring constant for bond formation, κ_ts (4, 5). According to this theory, the adhesion bonds can be classified as “catch bonds” (κ − κ_ts < 0) that strengthen with applied force: “ideal” bonds (κ = κ_ts) that are unaffected by force, and “slip bonds” (κ − κ_ts > 0) that weaken with bond stretching. For the slip bonds, the k_off can be written as k_off = k_off⁰ exp((1 − κ_ts/κ)F²/2κkT), where 1 − κ_ts/κ is the fraction of bond strain that is devoted to bond dissociation. Thus, the Hookean spring model predicts that the dissociation rate of the slip bonds increases exponentially with the square of force. Recognizing that in the Bell model all features of the energy landscape are lumped into one parameter, the length σ, Evans and Ritchie introduced a different model in which the dissociation rate follows a power law at low forces in the vicinity of f_β = kT/σ, k_off = a(F/f_β)^b (6). They also introduced further equations for a model with a deep harmonic well and a model that incorporates spontaneous dissociation at zero force. Although there are now at least five models for the response of receptor–ligand bonds to applied force, the models have yet to be compared for their fit to experimental data.

Selectins are an almost ideal experimental system for studying adhesive-bond interactions; because a small number of receptor–ligand bonds is involved, the force on the bond can be estimated with reasonable accuracy, and bond formation-breakage events can be detected by monitoring cell movement in a flow chamber. For cells in flow, the formation of an adhesive receptor–ligand interaction can be detected as an abrupt halt in the motion of a cell that had been free in flow, and bond dissociation can be detected as the subsequent resumption of hydrodynamic motion of the cell. These events have been operationally termed “transient tethers” (7). They occur at selectin or ligand densities on the substrate that are too low to support rolling (1, 7, 8) and below the shear threshold required for rolling through L-selectin (1). The first-order kinetics of transient tether dissociation and independence of these kinetics from selectin or ligand density suggest that they represent single receptor–ligand bonds (1, 7). By contrast, the kinetics of stepwise movement during rolling have been demonstrated to represent the dissociation of multiple, clustered bonds (8). The k_off⁰ values measured for P-selectin (7) and L-selectin (1) are in excellent agreement with subsequent BIAcore measurements using purified molecules (9, 10), providing further evidence that transient tethers represent dissociation of single receptor–ligand bonds.

Previous work has demonstrated how bond-dissociation kinetics varies with applied force for selectins (1, 7, 11–14, unpublished observation) and an antibody (15). The data demonstrate an increase in dissociation kinetics with applied force and better fit an exponential than a linear increase in k_off with force on the bond (1). However, it has not been possible yet to distinguish between different models of the effect of force on bond-dissociation kinetics, all of which are exponential.

Determination of the response of k_off to an extended range of forces on the tether bond is crucial for comparisons between different models of how force affects bond dissociation. Cells form transient tethers to the substrate over a limited range of wall shear stresses that limit the dynamic range over which tether dissociation kinetics can be measured (1, 7, 11). Transient tether formation drops off rapidly at higher shear. The basis for this dropoff is not known. We hypothesized that transient tether formation would be limited by the time that the receptor and ligand were in proximity to one another rather than by the force exerted on nascently formed bonds, i.e., by shear rate (s⁻¹) rather than by shear stress (force/area). Shear stress equals viscosity times shear rate. By varying viscosity, we demonstrate that tether formation indeed is related to shear rate rather than to shear stress. Moreover, variation of viscosity has allowed us to extend the range of forces over which the kinetics of transient tethers can be measured and to demonstrate a significantly better fit to the Bell model than to other models of bond dissociation with applied force.

Materials and Methods

Cells and Substrates.

Neutrophils were prepared as described (16). P-selectin purified from human platelets (17) was a gift from R. McEver (University of Oklahoma, Oklahoma City, OK). A polystyrene Petri dish was coated with an ≈5-mm spot of 20 μl of a purified P-selectin 1.65 mg/ml stock diluted 1:10,000, 1:20,000, and 1:40,000 in PBS (pH 9.0) supplemented with 0.1% octyl β-glucoside for 1 h at 37°C. Substrates then were washed and quenched with 2% (vol/vol) human serum albumin for 1 h at 37°C to block nonspecific binding sites.

Flow Assay.

P-selectin substrates were assembled as the lower wall in a parallel wall-flow chamber and mounted on an inverted phase-contrast microscope (16). Hanks' balanced salt solution with 10 mM Hepes, pH 7.4, containing 2 mM Ca²⁺ and no Mg²⁺ was supplemented with 0, 3, and 6% (wt/vol) of Ficoll (400,000 M_r, Sigma) to increase the viscosity. The viscosities of the media were measured as 1.0, 1.8, and 2.6 cP (1 P = 0.1 Pa⋅s), respectively, at room temperature by a Ubbelohde viscometer (Cannon Instrument Co., State College, PA). Neutrophils were resuspended in the buffers and perfused through the flow chamber at different flow rates as indicated. Microscopic images of cells under flow were recorded on Hi-8 videotape using a Nikon plan 20×-objective microscope.

Determination of Duration of Transient Tethering Events.

The duration of transient tethers on P-selectin was analyzed by a computerized imaging system consisting of a Pentium computer with MVC 150/40-VL boards (Imaging Technology, Bedford, MA) (15). Cells interacting with the substrate were detected by discriminating their velocity from the hydrodynamic velocity distribution of cells free in flow near the wall of the flow chamber. Sufficient videotape was analyzed to obtain 100–500 transient tethering events at each shear rate except at the highest shear rate, at which over 30 events were obtained. The duration of these events was plotted as the natural log of the number of cells that remained bound as a function of time after initiation of tethering. The most rapidly dissociating 90% or more of tethered events were used to determine k_off as the negative slope of the plot.

Determination of Force on the Tether Bond.

During the lifetime of a transient tether, the instantaneous force on the tether bond f_b varies because of membrane-tether extension from the cell body (18). Therefore, we used a previously described set of equations (18, 19) to estimate f_b: θ = arctan(R/l) + arccos((L² + l²)/(2L(R² + l²)^1/2)); f_b cos θ = F_s = 32.05τR²; f_bl sin θ = T_s + RF_s = 43.91τR³; and f_b = F₀ + k₂dL/dt, where τ is the shear stress, R is the radius of the cell, L is the length of the microvillous tether, l is the length of the lever arm, T_s and F_s are the torque and force, respectively, imposed by shear flow on the cell, and k₂ is the tether extension constant that equals 11 pN s/μm. The threshold force F₀ for elongation of the membrane tether between the neutrophil and the substrate is 45 pN (18); because f_b exceeded F₀ under our experimental conditions, the lever arm l increased and f_b slightly decreased with time. We calculated f_b numerically as a function of time during each video-frame interval after tethering (8) at each shear stress and viscosity. The average force on the bond, F_b, and the SD of f_b were calculated from f_b over the time interval during which the percentage of tethered cells decreased from 100 to 10%. F_b was used in relationships between force on the bond and dissociation kinetics. The lever arm previously measured on P-selectin at 0.5 dyn/cm² (1 dyne = 10 μN) of 3.06 ± 0.53 μm (1) is in good agreement with the estimate from tether elongation (18) of 3.4 μm; the corresponding estimates of F_b differ only 8%. The rate of increase in l, dl/dt, was calculated by using the same set of equations as described above for estimating f_b and averaged over the same time period as for F_b. The average dl/dt was calculated as a percentage of the hydrodynamic velocity of cells measured in Fig. 1. This percentage was higher for cells in 6% (wt/vol) Ficoll than for cells in 0% Ficoll and ranged from 2.5 to 9.2%. Therefore, the static equations used here overestimated the dynamic force on the bond by <10% (20).

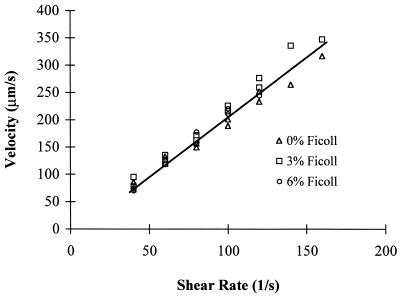
Figure 1.

Hydrodynamic velocities of neutrophils near the substrate at different viscosities. Neutrophils were infused into the flow chamber in Hanks' balanced salt solution/Hepes buffer containing 2 mM Ca²⁺ and 0, 3, and 6% Ficoll. The velocity of the cells was measured in the microscopic focal plane near the lower wall of the flow chamber.

Tethering Frequency.

The frequency of neutrophil tethering to P-selectin was determined as the number of tethering events per second and normalized by the number of cells in the field of view in the focal plane near the wall of the substrate. The number of tethering events at 0.033 s, as determined by the linear fit of the kinetics of the first 90% of transient tethers to dissociate, was used to calculate the tethering frequency.

Results

We evaluated the influence of shear stress and shear rate separately on the formation and dissociation of tether bonds between neutrophils in shear flow and P-selectin immobilized on the lower wall of a parallel wall-flow chamber. We altered viscosity, which alters shear stress (units of force/area, the product of shear rate and viscosity) but not shear rate (units of time⁻¹). Ficoll (400,000 M_r), a highly branched polymer of sucrose, was used to increase viscosity because of its low contribution to osmolarity, and because its wide use in density separation of leukocytes has shown that it has little if any effect on these cells. Gravitational sedimentation of neutrophils in the flowstream is influenced by medium viscosity and density; therefore, it was important to verify that the cells we studied were a similar distance from the bottom wall of the flow chamber. We measured cell velocity, because it increases rapidly with distance from the wall (19, 20). Cells within the microscopic focal plane near the lower wall of the flow chamber traveled at a velocity that was related directly to shear rate but independent of medium viscosity (Fig. 1). Therefore, the cells studied in media of different viscosities were similar in distance from the substrate.

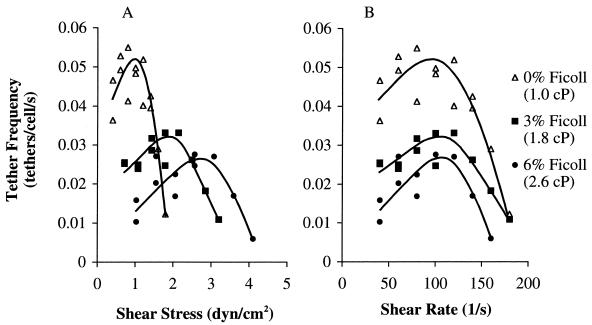
The formation of receptor–ligand bonds in shear flow, visualized as transient tethering of cells to the P-selectin substrate, was measured at different viscosities. The frequency of formation of transient tethers was plotted as either a function of wall shear stress (Fig. 2A) or wall shear rate (Fig. 2B). As flow rate increased, tether frequency increased to a peak then decreased. At different viscosities, the maximal tethering was reached at approximately the same shear rate, ≈100 s⁻¹ (Fig. 2B), but at different shear stresses (Fig. 2A). This result demonstrates that tethering is regulated by shear rate and hence kinematics, not shear stress. The peak tethering efficiency at ≈100 s⁻¹ was decreased at higher viscosity (Fig. 2B). This decrease may be because when kinematics brings the receptor and ligand within the zone where interaction is possible, their interaction is limited by their rate of diffusion, which is decreased at higher viscosity.

Figure 2.

Frequency of tethering in shear flow of neutrophils to P-selectin at three different viscosities. Transient tether frequency on P-selectin diluted 1:40,000 was determined as the number of tethering events per second divided by the number of cells in the field of view near the wall of substrate in Hanks' balanced salt solution/Hepes buffer containing 2 mM Ca²⁺ and 0, 3, and 6% of Ficoll. The same data are plotted vs. wall shear stress (A) and shear rate (B).

Because tether formation is related to shear, whereas tether dissociation is related to force on the tether bond and hence to shear stress (see below), increased viscosity allowed transient tether-dissociation kinetics to be measured at an extended range of forces. In standard medium, transient tethering was detected up to a wall shear stress of 1.8 dyn/cm² (Fig. 2A). By contrast, in medium with 3% Ficoll, sufficient tether events were obtained up to 3.2 dyn/cm²; in 6% Ficoll, measurements could be extended up to 4.1 dyn/cm² (Fig. 2A).

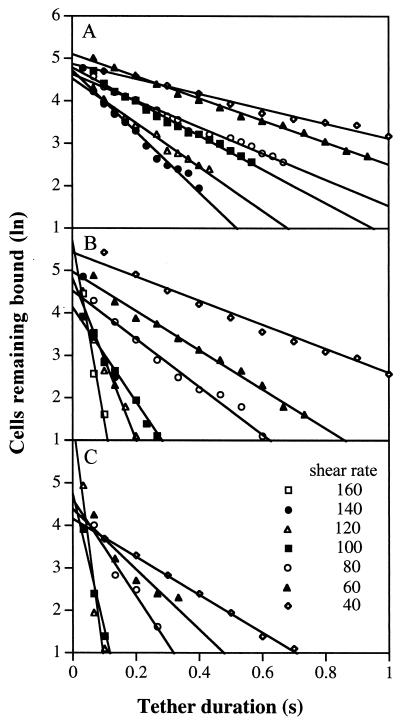
The duration of transient tethers was determined over a wide range of shear rates at each viscosity, and the natural logarithm of the number of cells remaining bound was plotted as a function of tether duration (Fig. 3). k_off values are equal to the slopes of these plots. Importantly, a large range of k_off values was measured: from 2.5 s⁻¹ at 0.4 dyn/cm² to 11.7 s⁻¹ at 1.8 dyn/cm² in medium alone; from 2.6 s⁻¹ at 0.7 dyn/cm² to 69 s⁻¹ at 3.2 dyn/cm² in 3% Ficoll, and; from 4.5 s⁻¹ at 1 dyn/cm² to 52 s⁻¹ at 3.1 dyn/cm² in 6% Ficoll. In 6% Ficoll at 3.5 and 4.1 dyn/cm², sufficient tethered cells were obtained at 0.033 s, but few cells remained bound at 0.067 s. Therefore, we omitted the estimates of k_off (109 s⁻¹ at 3.5 dyn/cm²) from the curve fitting described below; however, the same conclusions on significant differences between theories were obtained when this value was included.

Figure 3.

The kinetics of dissociation of transiently tethered neutrophils at different viscosities. The number of cells remaining transiently tethered as a function of time after tether initiation was measured on P-selectin at 1 (A), 1.8 (B), and 2.6 cP (C). Lines show the fits to first-order dissociation kinetics by the method of least squares.

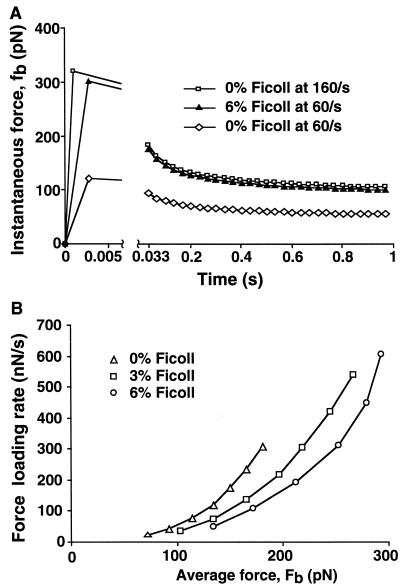
It has been emphasized that the rate at which force is loaded can be an important variable that affects receptor–ligand dissociation (6). In many other techniques in which forces are applied to bonds, such as atomic-force microscopy, the force increases with time until bond dissociation. In our system, force is loaded during the brief period between tethering and movement of the cell downstream by a distance that is defined by the initial length of the membranous tether (microvillus) that links the molecular tether bond to the cell body. Based on the measurement of this initial length as 0.35 μm, the distance moved downstream is 1.8 μm (18). Using this distance and the hydrodynamic velocity (Fig. 1), the time required for force loading can be calculated to be less than 0.005 s under the range of shear rates used here (Fig. 4A, first time point). We have estimated the range of the force loading rates under our experimental conditions (Fig. 4B). The higher the shear rate, the faster the loading; and the higher the viscosity, the higher the force that is loaded (Fig. 4 A Left and B). After initial force loading, the amount of force decreases with time (Fig. 4A). The decrease is because at forces on the membranous tether of >45 pN as experienced here, the tether elongates at a defined rate (18). The resulting increase in the lever arm results in turn in a gradual decrease in the instantaneous force on the tether bond (Fig. 4A). We calculated the instantaneous force on the bond, f_b, at each video-frame interval (0.033 s) by using this correction for membrane-tether elongation (8, 18). The average force on the bond, F_b, was calculated over the time period during which 90% of the cells dissociated at each wall shear stress. The coefficient of variation in f_b over this period is small (15%). Therefore, it is reasonable to fit our measurements of k_off to F_b, the average of f_b (see Materials and Methods). Furthermore, dynamic and static estimates of F_b differed by <10% (see Materials and Methods).

Figure 4.

Instantaneous force on the bond and rate of force loading. (A) Instantaneous force, f_b. The first time point is at the time when the peak force is loaded, as determined by the hydrodynamic velocity of the cell and the lever arm (see text); thereafter, f_b is shown after each video-frame time interval (0.033 s). (B) Force loading rate. The rate was calculated as described in the text.

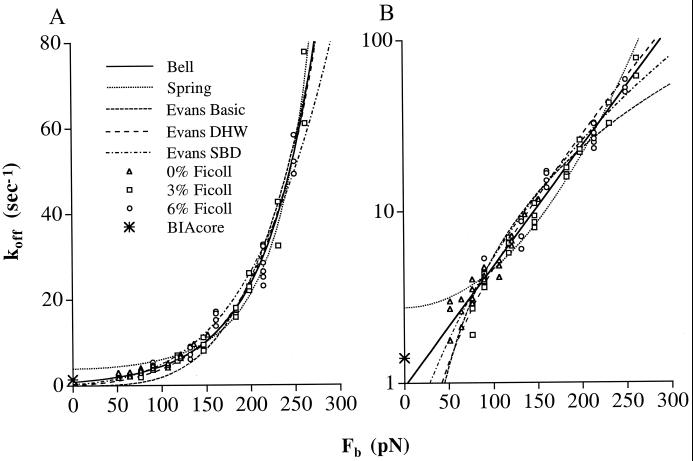
We plotted k_off as a function of F_b (Fig. 5) to test different theories of how force affects bond dissociation (see Discussion). The k_off data obtained at 0, 3, and 6% Ficoll (triangles, squares, and circles in Fig. 5, respectively) overlap extensively and are in excellent agreement in these overlap regions when plotted as a function of F_b, which is related to wall shear stress. Thus, the dissociation kinetics are related to shear stress not shear rate. Furthermore, the kinetics were independent of loading rate. Note that when comparing the same F_b at different concentrations of Ficoll, and hence at different viscosities, the force loading rates differ (Fig. 4B). Therefore, the extensive agreement in k_off values as a function of F_b when measurements are made at different viscosities (Fig. 5) demonstrates that under our experimental conditions, the rate of force loading has little influence on k_off measurements. We conclude that it is reasonable to fit our data to different theories on the relationship between F_b and k_off.

Figure 5.

Fit to five theoretical predictions of the effect of F_b on k_off. (A) Arithmetic fit. (B) Logarithmic fit, using the difference between the logs of the predicted and observed k_off values. The k_off data of tethered neutrophils on P-selectin measured in 0, 3, or 6% Ficoll are plotted vs. the average force on bond, F_b. The pooled data of k_off at different viscosities were fit to the indicated theoretical models. DHW, deep harmonic well; SBD, spontaneous bond dissociation.

Discussion

We have addressed important issues about the formation and dissociation of selectin–ligand bonds between leukocytes in laminar shear flow and the wall of a flow chamber. Variation in viscosity played a key role in these studies. Viscosity is of profound importance in shear flow, because it relates the kinematics of fluid movement (shear rate in units of time⁻¹) to the hydrodynamic forces (shear stress, in units of force/area) that are experienced by objects in contact with the fluid.

Previously, it was observed that there was a cutoff in flow rate above which transient tethers did not form (1, 7). As flow rates were increased, the frequency of transient tethers to the substrate was observed to increase to a peak and then decrease (1) (in contrast to the current study, transient tether frequency was divided by the transport velocity, which alters the shape of the curves, because velocity increases with shear). The cutoff or peak in tethering has been reported previously in terms of wall shear stress values; however, it has not been known whether shear stress or shear rate was the relevant variable. Hypothetically, either could be limiting. For example, shear stress could be limiting if nascent bonds were formed but then were broken, because there was some force threshold at which bond breakage suddenly increased and became too fast for bond formation to be detected. On the other hand, shear rate could be limiting if bonds were not formed, because the high velocity of the cell relative to the substrate provided insufficient time for a collision between a receptor and ligand to result in formation of a stable receptor–ligand bond (21, 22). Our measurements at different viscosities show similar peaks in tether frequency and upper and lower thresholds as a function of shear rate but not of shear stress. Thus, receptor–ligand bond formation depends on shear rate not shear stress. The velocity of cells relative to the substrate is related directly to shear rate, whereas the force on the receptor–ligand bond is related directly to shear stress. Therefore, the findings suggest that the velocity of the receptor relative to the ligand and not the force on the bond dominates the rate of formation of tether bonds.

Shear enhances formation of selectin–ligand bonds (8, 23, 24). It has been proposed that the velocity with which selectins contact their ligands is important both to increase the collision probability (8, 22) and to overcome a repulsive barrier (8). The decrease in rate of tethering at higher shear further suggests that time is essential for the molecular contact to develop into bond formation. The balance of these two effects gives the maximum tethering of neutrophils to P-selectin at a shear rate of 100 s⁻¹. We previously found that shear-enhanced bond formation is essential for the stability of rolling, i.e., for the maintenance of rolling in contrast to firm adhesion or detachment despite wide variation in wall shear stress and in selectin or ligand density on the vessel wall. Shear-enhanced bond formation also accounts for the relative insensitivity of rolling velocity to variation in the same parameters (8). The current study showed that above a shear rate of 100 s⁻¹, bond formation was no longer enhanced with increasing shear and instead decreased. This shear rate of 100 s⁻¹ corresponds to a hydrodynamic velocity of approximately 200 μm/s for a cell close to the flow-chamber wall. Because bond formation is not enhanced above this point, this velocity can be considered a theoretical maximum rolling velocity; the same principles of bond formation apply for transient tethers and rolling tethers (8). In agreement with this upper limit, the fastest rolling seen in the parallel-plate flow-chamber system, through L-selectin, approaches this limit with reported velocities of up to 125 μm/s (25) and 140 μm/s (26, 27).

Previously, it has been possible to demonstrate an exponential, as opposed to a linear, increase of k_off with applied force but not to discriminate between different theories of how force affects k_off (1). In this study, a computerized real-time image-analysis system (15) allowed us to collect a larger amount of data with higher accuracy than in our previous studies with manual data analysis. Furthermore, varying viscosity enabled us to measure the kinetics of transient tethers over an extended range of wall shear stress and hence force on the tether bond. In this study, we have made over 70 k_off value determinations ranging from 1.7 s⁻¹ to 69 s⁻¹ based on over 9,000 tether-duration measurements in a force range from 50 to 260 pN. The dynamic range of off-rates of 40-fold and improvements in estimation of F_b enable meaningful comparisons between experimental data and different theories of the mechanical properties of receptor–ligand bonds.

As reviewed in the introduction, at least five different models have been proposed for how force affects the dissociation of receptor–ligand bonds. We fit these models to our data by using arithmetic fits that weight more the data at high F_b (Fig. 5A and Table 1 Left), and log fits that weight measurements at low and high F_b similarly (Fig. 5B and Table 1 Right). The Bell model (2) proposes that k_off = k_off⁰ exp(F_bσ/kT). The exponential term in this relationship was derived empirically from measurements of the lifetime until fracture of solids (3). The Bell model fit our data well (χ² = 19, df = 68), and statistical F tests of variances showed that the fit was significantly better than with all other models (P = 3.6 × 10⁻² to 3.6 × <10⁻¹⁰). The Bell model yields k_off⁰ = 0.84 ± 0.08 s⁻¹ (estimated value ± asymptotic standard error) and a bond interaction range σ = 0.68 ± 0.02Å. In the Hookean spring model (4), k_off = k_off⁰ exp(f_κF_b²/κkT). This model raises the intriguing possibility of catch bonds that paradoxically dissociate more slowly as force is applied (4). The fit to the Hookean spring model yields a slip bond with k_off⁰ = 3.9 ± 0.2 s⁻¹ and the value of the bond spring constant divided by the fractional spring slippage κ/f_κ = 2.9 ± 0.1 N/m; however, this model fits the data less well than the Bell model with P values ranging from 0.036 to <10⁻¹⁰ depending on whether fits are arithmetic or log (Table 1). Two of the Evans and Ritchie (6) models do not incorporate the possibility of bond dissociation in absence of force. Of these, the deep harmonic well model, k_off = c(F_b/f_β)exp(F_b/f_β), where f_β = kT/σ, fit the data the best, although significantly less well than the Bell equation (Table 1). This model yields f_β = 85.5 ± 3.3 pN, σ = 0.48 ± 0.02Å, and c ≈ 1.0 ± 0.15. Evans and Ritchie introduced an intrinsic repulsive force f_i to yield spontaneous bond dissociation: k_off = d(f_i/fβ + F_b/f_β)^b, where k_off⁰ = d(f_i/f_β)^b. This model yields f_i = 110 pN, b = 4.3, and k_off⁰ = d(f_i/f_β)^b = 0.31 s⁻¹ and is not as good of a fit to the data as the Bell model (Table 1). However, it is still possible that power law models might model bond dissociation more accurately at orders of magnitude higher forces, as has been proposed (6). In the range of forces we have examined, the experimental data show that the spring model gives k_off values that change too much with change in force, yielding an over-bent curve; whereas the power laws yield k_off values that change too little with force, with under-bent curves (Fig. 5).

Table 1.

Comparison between the Bell model and other models for fit to experimental data on effect of force on P-selectin tether dissociation (k_off)

Theoretical model	df	Fit to koff				Fit to ln(koff)
		koff0, s−1	σ, Å	χ2	P (F-test) versus Bell*	koff0, s−1	σ, Å	χ2	P (F-test) versus Bell*
									(T − M)2/T	(lnT − lnM)2/lnT
Bell	68	0.84	0.68	19	—	0.95	0.66	18	—	—
Spring	68	3.9	—	35	3.6  × 10−2	2.75	—	49	<1  × 10−10	7.8  × 10−6
Evans Basic	68	0	—	366	<1  × 10−10	0	—	90	<1  × 10−10	<1  × 10−10
Evans DHW	68	0	0.48	37	3.9  × 10−4	0	0.45	36	2.4  × 10−6	<1  × 10−10
Evans SBD	67	0.31	0.37	30	6.2  × 10−10	0.40	0.35	34	<1  × 10−10	3  × 10−6

DHW, deep harmonic well; SBD, spontaneous bond dissociation. 

^*F test of χ_i² values of all data points: χ_i² = (T − M)²/T, or if indicated χ_i² = (lnT − lnM)²/lnT, where T = theoretical k_off and M = measured k_off. The F test (29) comparing the variances of the Bell model to each of the other models was done using the data analysis tools of excel. 

The k_off⁰ values described above, i.e., k_off in the absence of force, are all derived by fitting theoretical relationships to experimental data on k_off in the presence of force. It is therefore of interest that k_off in the absence of any significant applied force has been determined directly by measuring the dissociation of purified, monomeric P-selectin and P-selectin glycoprotein ligand with surface plasmon resonance, as 1.4 s⁻¹ (9). This k_off⁰ value was not used in curve fitting and therefore provides an independent evaluation of how well the different models fit the data, particularly in the low force regime. The k_off⁰ values predicted by the linear fit to the Hookean spring, Bell, and Evans models with spontaneous dissociation at zero force are 3.9 s⁻¹, 0.84 s⁻¹, and 0.31 s⁻¹, respectively. Therefore, the BIAcore measurement of 1.4 s⁻¹ agrees better with the Bell model (difference of 1.7-fold) than the other two models (differences of 2.8- and 4.5-fold). The Bell model also fits best when k_off⁰ is estimated with log fits.

Since the Bell model was first proposed in 1978 (2), at least four other models have been put forward to explain how force affects receptor–ligand dissociation (4–6); however, experimental data that enable meaningful comparisons between these models have been lacking. We have now obtained such data. We find that the Bell model fits the data significantly better, as determined with a statistical F test of variances, than four other models. Furthermore, the Bell model predicts a k_off⁰ value that best matches the experimentally observed value for bond dissociation in the absence of force. There was no theoretical justification for the exponential relationship that Bell proposed; instead, it was based on an experimentally determined relationship observed in the fracture of materials such as aluminum and Plexiglas (3). We now provide empirical support for the use of this exponential relationship for the dissociation of receptor–ligand bonds. In our experimental system, force is applied on receptor–ligand bonds as a consequence of the hydrodynamic force acting on transiently tethered cells in a parallel wall-flow chamber. This system mimics how forces are exerted on selectins and their ligands in binding of leukocytes to blood vessel walls in vivo. In the future, it will be important to make further comparisons between biophysical models of bond dissociation using other receptor–ligand pairs, other experimental systems for applying forces to receptor–ligand bonds, and other force regimes.