Dynamics of site juxtaposition in supercoiled DNA

Abstract

Juxtaposition kinetics between specific sites in supercoiled DNA is investigated at close to physiological ionic conditions by Brownian dynamics simulations. At such conditions, supercoiled DNA is interwound, and the probability of spatial site juxtaposition is much higher than in relaxed DNA. We find, however, that supercoiling does not correspondingly increase the rate of juxtaposition at these physiological conditions. An explanation to this unexpected finding emerges on analysis of the juxtaposition dynamics. We note that although a particular site i₁ in supercoiled DNA is often in close proximity (juxtaposed) to another site i₂, the change of i₂ occurs very slowly and depends largely on internal slithering of opposite segments of the DNA superhelix. Such slithering results in long correlations between successive values of i₂; these correlations increase the average time of juxtaposition between two DNA sites. Random collisions between sites located on different superhelix branches—although increasing in importance with DNA size—contribute less substantially to site juxtaposition at high salt than slithering for DNA up to 6 kb in length.

Supercoiling affects virtually all biological processes involving DNA; these reactions include transcription (1–4), replication (5), and chromosome segregation during cell division (6, 7). As a result of extensive study during the past three decades (8–10), we now appreciate many physical facets of supercoiled DNA, especially equilibrium properties. In contrast, the dynamic properties of these molecules are much less understood, largely because of a lack of suitable experimental techniques. This explains why most of our current knowledge of supercoiled DNA dynamics comes from Brownian dynamics (BD) simulations (11). This computational approach is based on the bead model of the double helix and on the Langevin equation, which describes motion of small particles in viscous media. BD makes possible simulations of long-time processes of large DNA in solution (12–17). The reliability of BD simulations for double-stranded DNA has been established for linear and circular DNA molecules through quantitative agreement with available experimental data (13–15, 17–20). In particular, simulations for small supercoiled molecules have shown that characteristic times of relaxation processes related to bending deformations are in the range of 1 μs to 10 ms (18, 19, 21, 22).

Here we report analysis of BD simulations focusing on juxtaposition kinetics involving specific sites along supercoiled DNA. Juxtaposition is a prerequisite for many biochemical reactions, such as site-specific recombination and transcription initiation, which bring together in space two linearly distant DNA sites. To date, only one experimental approach, based on competitive site-specific recombination, has been suggested to study the dynamics of site juxtaposition in supercoiled DNA (23–25). Results of such experiments show, however, that juxtaposition is not a rate-limiting step in recombination; thus, only an upper bound on juxtaposition time can be established (24, 25). Much earlier, Benjamin and Cozzarelli proposed two mechanisms for site juxtaposition in supercoiled DNA: random collision of different parts of supercoiled molecules and slithering (also random) of two sites along the axis of the interwound superhelix (26). Theoretical estimates by Marko and Siggia based on polymer statistical mechanics have suggested that slithering is very slow, and hence site juxtaposition in long DNA (kilobase order) must occur by random collisions (27). However, their analysis did not account for branching of the interwound superhelix. Later revisions by Marko based on a simple model showed that indeed DNA branching can accelerate juxtaposition via slithering substantially (28). Still, these conclusions are based on highly simplified models of superhelix dynamics and must be tested on realistic representations of supercoiled DNA.

Our group has recently applied BD simulations to study site juxtaposition (19). In our first work, the large computations involved restricted us to low salt conditions, where the computations are less time consuming (19). Because conformational properties of supercoiled DNA depend dramatically on the ionic conditions in solution (10, 29–34), it was not clear how general our conclusions were regarding the importance of random molecular reorientation to juxtaposition kinetics. Since then, algorithmic improvements have made possible a study of juxtaposition at close to physiological ionic conditions (about 0.2 M monovalent ions in solution). Unexpectedly, we find that the dynamic properties of supercoiled DNA depend on ionic conditions even stronger than equilibrium properties, so the conclusions regarding juxtaposition kinetics made for low salt concentration are not valid for high salt concentrations, even qualitatively. Here we report a detailed kinetic analysis of site juxtaposition in supercoiled DNA at near physiological ionic conditions. We establish physical times for DNA juxtaposition and identify the dominant juxtaposition mechanism at high salt concentration by analyzing the relative importance of slithering and random collisions to juxtaposition events.

Methods of Computations: DNA Model.

Our wormlike chain DNA model (19, 35) follows that of Allison et al. for linear DNA (13–15) and its extension by Langowski and coworkers (18, 36, 37) to supercoiled DNA. Namely, a closed DNA molecule of n Kuhn statistical lengths is represented by kn straight elastic segments of equilibrium length l₀. To define torsional deformations, a body-fixed coordinate (bfc) frame of unit vectors f_i, v_i, u_i is attached to each chain vertex so that u_i is directed along the segment i. The chain energy consists of the following five terms.

1. The stretching energy is computed as

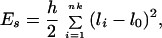1

where l_i is the actual length of segment i, and h is the stretching rigidity constant. E_s is a computational device rather than an attempt to account for the actual stretching elasticity of the double helix (13). We choose h = 100k_BT/l₀², where k_BT is the Boltzmann factor so that the variance of l_i is close to l₀²/100 for this value of h.

2. The bending energy, E_b, is specified by angular displacements θ_i of each segment i relative to segment i + 1:

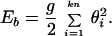2

The bending rigidity constant g is defined so that the Kuhn statistical length corresponds to k rigid segments (38). It was shown previously that equilibrium properties of supercoiled conformations do not change, within the accuracy of the simulations, if k ≥ 10 (39). The value k = 10 used here corresponds to g = 4.81 k_BT and l₀ = 10 nm when using 100 nm for the Kuhn length (40).

3. The energy of electrostatic intersegment interaction, E_e, is specified by the Debye–Hückel potential as a sum over all pairs of point charges located on the chain segments. The number of point charges placed on each segment, λ, is chosen to approximate well continuous charges with the same linear density. The value of λ increases as the Debye length, 1/κ, decreases. We choose λ = 5 for [Na⁺] = 0.2 M, because simulation results do not depend on λ as long as λ ≥ 5. For [Na⁺] = 0.01 M, λ = 2 is sufficient. The energy E_e is specified as

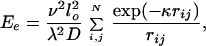3

where ν is the effective linear charge density of the double helix, D is the dielectric constant of water, N = knλ is the total number of point charges, r_ij is the distance between point charges i and j. The value of ν was equal to 40.9 e/nm for [Na⁺] = 0.2 M and 2.43 e/nm for [Na⁺] = 0.01 M (41). The electrostatic potential is replaced by excluded volume potential for r_ij < 2 nm, that is, in the region of physical overlapping of the double helix segments (see below).

The electrostatic interaction contributes to both the bending rigidity of the double helix and the volume interaction between chain segments separated along the chain contour. Because the first effect is already accounted for in the experimentally measured value of bending rigidity constant, the interaction between charges located at adjacent segments was not included in Eq. 3.

4. The energy of torsional deformations, E_i, follows ref. 18. With Euler angles α_i,i+1, β_i,i+1,γ_i,i+1 describing the transformation from the bfc frame i to i + 1, β_i,i+1 coincides with the bending angle, θ_i of Eq. 2, and the torsional angle between frames i and i + 1 is the sum φ_i,i+1 = α_i,i+1 + γ_i,i+1. Thus E_i is expressed as

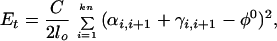4

where C is the DNA torsional rigidity constant, and φ⁰ is the equilibrium twist of one model segment. Because the value of φ⁰ does not affect the simulation results, we used φ⁰ = 0. The value of C was set to 3⋅10⁻¹⁹ erg⋅cm (38, 40). Together with the writhe, Wr, the torsional deformation ΔTw = Σ_{i = 1}^kn (φ_i,i+1 − φ⁰) of the initial conformation specifies the linking number difference, ΔLk = Wr + ΔTw, for a particular simulation run.

5. The energy of the short-range repulsion between DNA segments, E_ν, is added to the energy function to prevent passing one segment through another. We exclude such events to maintain a fixed topology of the model chain by specifying E_ν as

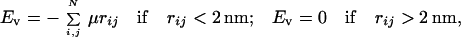5

where the summation in Eq. 5 is performed over the same pairs of points as in Eq. 3. The value of μ is 35 pN. With this setting, the frequency of segment passing events is less than 10⁻⁷ per simulation step, even in torsionally stressed chains. We monitor the segment passing events as described in ref. 19.

To account for hydrodynamic interactions of the DNA with solvent, we position beads of radius a at each vertex of the chain. These beads are used only to define the hydrodynamic interaction and thus do not affect equilibrium properties of the model chain. We used the Rotne–Prager diffusion tensor to specify the hydrodynamic interaction (42). The value of a was equal to 2.24 nm and was chosen to provide the experimentally measured values of the translational diffusion (sedimentation) coefficients of circular DNA (21, 33, 43).

BD Simulations.

We use the second-order BD algorithm (44), with modifications to improve efficiency (19, 35) involving less frequent updating of the diffusion tensor than the systematic forces (e.g., every 10 timesteps). The numerical accuracy is not comprised, whereas the central processing unit time is reduced on average by a factor of four on our SGI R10K/195 MHz processor (19, 35, 37). Further improvements and numerical analysis of the accuracy of the BD method were described recently (45, 46). A verification that our current BD code reproduces the same equilibrium properties of supercoiled DNA as Monte Carlo simulations is detailed in the supplemental data on the PNAS web site (see www.pnas.org).

At each timestep Δt (600 ps here), the beads and the associated coordinate frames also rotate around the local axis of each segment. The torsional deformation of the chain is treated as described in ref. 14. About 5 h of computing are required on our SGI processor to simulate 1 ms of a 3-kb supercoiled DNA; 24 h are required for 6-kb DNA.

Results

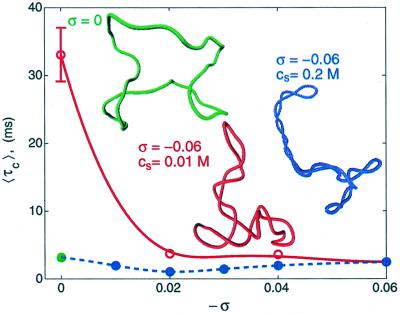
Monte Carlo simulations have previously shown that the degree of supercoiling strongly affects the equilibrium probability of juxtaposition of specific sites separated along the DNA contour (39, 47). This conclusion is intuitive, because there are many more pairs of juxtaposed sites in each conformation of supercoiled DNA than in typical conformations of relaxed molecules (see examples of DNA conformations in Fig. 1). This simple relation, however, does not mean that supercoiling increases the rate of juxtaposition in general. At low salt concentration, this acceleration holds: we found that the rate of juxtaposition is two orders higher in tightly supercoiled DNA than in relaxed molecules for [Na⁺] = 0.01 M (19). However, conformations of supercoiled DNA at the low salt and at near-physiological ionic conditions (0.2 M monovalent ions and a few millimolars of magnesium ions) are very different (Fig. 1) (31, 39). The major structural element of supercoiling at high salt concentration, the interwound superhelix, is highly irregular and sometimes nonexistent at low salt concentration. It is not surprising that, at low salt, transient distortions of the interwound superhelix, rather then slithering of the opposite segments of the superhelix, are the dominant contributors to the juxtaposition process. A different picture was found here at close to physiological ionic conditions.

Figure 1.

Effect of supercoiling on the juxtaposition time. Computed dependencies of 〈τ_c〉 on σ correspond to 0.2 M (●) and 0.01 M (○) monovalent ions. Data were obtained for 3-kb DNA and 600-bp separations between the chosen sites along the chain contour. Typical simulated conformations of supercoiled DNA (σ = −0.06, 0.2 M (blue) and 0.01 M (red) concentration of monovalent salt ions) and relaxed DNA (green) are also shown. For σ = 0, conformations depend weakly on ionic conditions.

We consider two points of the molecule juxtaposed if the distance between them is less than or equal to r₀. We set r₀ to 10 nm, close to the average size of proteins that interact with two DNA sites simultaneously, unless otherwise stated. At high salt, we found the average juxtaposition time, 〈τ_c〉, to be nearly proportional to l/r₀ if r₀ is in the range of 5–15 nm (data not shown); thus, as long as r₀ is chosen in this range, our conclusions do not change. For a DNA molecule at given conditions (salt and supercoiling), 〈τ_c〉 depends only on the separation of the chosen sites along the molecular contour, d. We calculated 〈τ_c〉 for various values of d for each BD trajectory started from a selected conformation over the simulated equilibrium set. A trajectory is continued until all selected pairs of the chain vertices juxtapose (as defined by r₀). Because there were many pairs of vertices in each model chain for a particular value of d, we obtain data for many pairs at each simulation run. Several independent runs starting from different initial conformations were performed for each set of parameters to improve the statistics.

Fig. 1 shows computed 〈τ_c〉 data for 3-kb circular DNA as a function of the superhelix density, σ, the linking number difference normalized for DNA length; see ref. 10, for example. We see that at high salt concentrations, 〈τ_c〉 is virtually independent of σ. This result is strikingly different from corresponding data obtained for low salt concentration, also shown in Fig. 1. In the latter case, a decrease of 〈τ_c〉 by 1.5–2 orders of magnitude is observed as | σ | increases from 0 to 0.06. Thus, the data at high salt do not correlate with the two orders increase in the probability of site juxtaposition (39, 47).

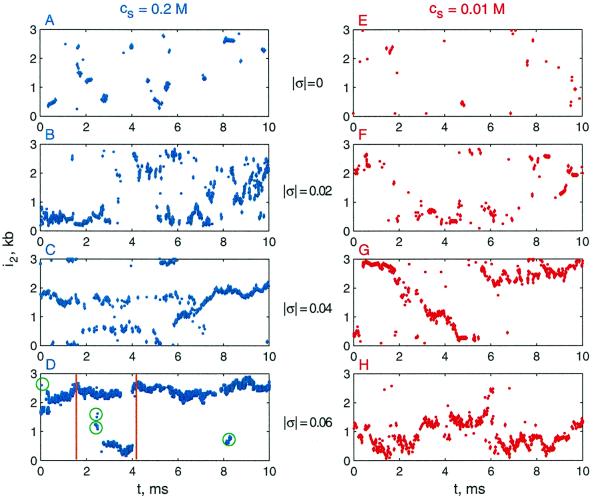
To understand this departure, we next inspect the juxtaposition kinetics. Consider the juxtaposition of a particular site, i₁, with other sites along the DNA. Usually at any time moment, t, no more than one other site, i₂, is juxtaposed with i₁. A plot of the dependence of i₂ on t contains ample information about the dynamics of the juxtaposition. Typical plots for different combinations of σ and salt concentration are shown in Fig. 2. We see that site i₁ very often lacks juxtaposed sites for relaxed DNA (σ = 0, Fig. 2 A and E). For low salt concentrations, the electrostatic repulsion between DNA segments makes juxtapositions even less probable (compare Fig. 2 A and E). As | σ | increases, juxtaposition frequencies increase systematically (Fig. 2 B–D and F–H). At rare moments, more than one site may be juxtaposed with i₁.

Figure 2.

Juxtaposition of a selected site with other sites of DNA molecule as a function of time. The coordinate of the second site, i₂, was recorded over one BD trajectory. Simulations for DNA molecules 3 kb in length were performed both for physiological (Left) and low (Right) salt concentrations, with different σ values (as noted). The circled points in D correspond to collisions between sites separated along the superhelix axis (“random collisions”); all other points in the panel result from juxtapositions across the superhelix axis.

Another salient feature evident from these plots is that, as  σ  increases, strong correlations between successive values of i₂ emerge. The interwound conformations of the superhelix are responsible for this correlation. If a supercoiled molecule adopts only interwound conformations (this is a good approximation for conditions that correspond to Fig. 2D), site i₁ is nearly always juxtaposed with another geometrically related site, i₂. The slow slithering of the opposing DNA segments continuously changes i₂, explaining the plot. Such random slithering is slow because it requires coordinated displacements of large segments of the double helix. This mechanism is thus strikingly different from the nearly independent random collisions between sites in relaxed DNA. However, random collisions of DNA sites that belong to different branches of supercoiled DNA occur for supercoiled DNA as well. Although these events are rare (circled points in Fig. 2D), they contribute significantly to 〈τ_c〉, because there is a very short correlation between values of i₂ for such collisions.

Fig. 2D illustrates that the very long correlation between successive values of i₂ increases 〈τ_c〉 (i.e., decelerates juxtaposition) for supercoiled conformations. On the other hand, the higher probability of site juxtaposition in supercoiled conformations decreases 〈τ_c〉. These opposite effects make the overall influence of supercoiling on 〈τ_c〉 uncertain. It is thus not surprising that the combined effect depends drastically on ionic conditions (see Fig. 1).

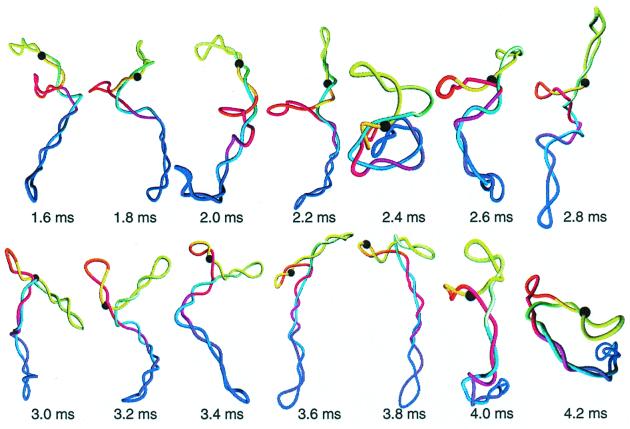
Because long correlations in the values of i₂ increase 〈τ_c〉, any interruption of such continuous changes would decrease juxtaposition times. At low salt concentrations and/or low supercoiling, transient distortions of the interwound superhelix coupled with rearrangements of interwound conformations dominate. Although as | σ | increases (Fig. 2 E–H), the frequency of such global distortions decreases, and the intervals of continuous changes of i₂ lengthen, such distortions occur even at σ = −0.06 at low salt (19). At physiological ionic conditions, the second interrupting mechanism, namely superhelix branching, affects 〈τ_c〉 as follows. As site i₁ passes through a branchpoint, the change of i₂ is equal to the size of the branch (Fig. 2D). Snapshots taken from a simulated BD trajectory illustrate such events (Fig. 3). Because the average length of one branch is about 1.5 kb (47), branching becomes crucial for site juxtaposition in supercoiled molecules longer than 5 kb.

Figure 3.

Dynamics of the site juxtaposition in supercoiled DNA. Snapshots represent the part of the simulation trajectory shown in Fig. 2D (σ = −0.06, [Na⁺] = 0.2 M). Site i₁ is shown by a large black sphere. The actual simulated orientation of the molecule was rotated to enhance connection between successive conformations.

Fig. 2D and corresponding snapshots (Fig. 3), as well as many other similar series we analyzed, confirm that slithering in interwound superhelices is the major mechanism for site juxtaposition in highly supercoiled DNA a few kilobases in length at near physiological ionic conditions. The contribution to 〈τ_c〉 from collisions of different parts of the interwound superhelix is less important than from slithering, although the contributions from the collisions increase with the site separation d. The fraction of the first juxtapositions that occur by collisions of different parts of the interwound superhelix is shown in Fig. 4 as a function of d. The algorithm used for the analysis is described in the supplemental data (see www.pnas.org). Unlike juxtapositions at low salt, extensive distortions of the interwound superhelix do not occur at these ionic conditions.

Figure 4.

The contribution from collisions of different parts of the interwound superhelix to the first collision between two sites as a function of the separation between the sites, d. The simulation results for supercoiled DNA (σ = −0.06, [Na⁺] = 0.2 M) 3 kb (○) and 6 kb (●) in length are approximated by the solid line.

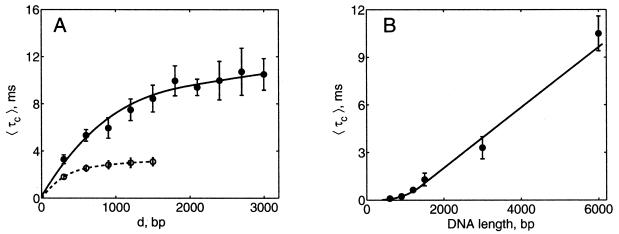
The dependence of 〈τ_c〉 on the separation between the sites along DNA contour, d, and on the total DNA length, L, is shown in Fig. 5. Although 〈τ_c〉 is nearly proportional to d for p < d < L/5 (where p is the persistence length of DNA), 〈τ_c〉 is nearly independent of d in the range L/4 < d < L/2 (Fig. 5A). The dependence of 〈τ_c〉 on L plotted for d = L/2 (Fig. 5B) thus represents well all values of d comparable to L.

Figure 5.

Dependence of 〈τ_c〉 on the separation between the sites along DNA contour, d, and on the total DNA length, L. Results of BD simulations correspond to highly supercoiled DNA, σ = −0.06, at physiological ionic conditions. (A) Dependence of 〈τ_c〉 on d for DNA molecules 3 (--) and 6 (—) kb in length. (B) 〈τ_c〉 as function of DNA length is shown for d = L/2.

Site juxtaposition is certainly one of the slowest processes in supercoiled DNA. The values of 〈τ_c〉 are one to two orders larger than the relaxation time of writhe or the radius of gyration in supercoiled molecules (Table 1). The relaxation of the number of branches in the interwound superhelix is the only other process with a rate comparable to the rate juxtaposition for supercoiled DNA a few kilobases in length. The corresponding relaxation time for branching, 〈τ_b〉, is also shown in Table 1. The value of 〈τ_b〉 decreases with DNA length, however, because the relaxation of the number of branches occurs locally and more or less independently at each region of long DNA. Thus for longer molecules, 〈τ_b〉 should be much shorter than 〈τ_c〉.

Table 1.

The average time of juxtaposition, 〈τ_c〉, for sites separated by half of the DNA length; relaxation time for the number of branches, 〈τ_b〉; and relaxation time of the radius of gyration, 〈τ_R〉, for supercoiled DNA at physiological ionic conditions, σ = −0.06

DNA length, bp	〈τc〉, ms	〈τb〉, ms	〈τR〉, ms
3,000	3.3  ± 0.7	2.9  ± 0.6	0.12
6,000	11  ± 2	1.0  ± 0.3	0.35

Discussion

Our BD simulations reveal that at physiological ionic conditions, DNA supercoiling does not affect notably the average time of juxtaposition of two DNA sites separated along the chain contour. This conclusion was highly unexpected, because supercoiling increases the equilibrium probability of juxtaposition by two orders of magnitude (39, 47), as well as the juxtaposition rate at low salt concentrations (19). Our analyses showed that both the equilibrium and dynamic properties of supercoiled DNA at high salt concentrations are determined by DNA's interwound conformations. The probability of juxtaposition is much higher in supercoiled DNA, simply because at any given time there are many more juxtaposed pairs of sites in an interwound superhelix than in a random-coil conformation of relaxed DNA (see Fig. 1). This factor favors faster site juxtaposition in supercoiled DNA. However, interwound superhelices slow down changes of the pairs that are juxtaposed at a particular instant, and this decreases the rate of site juxtaposition. In relaxed DNA, site juxtaposition occurs by their random collision in three dimensions, and the probability of finding a particular pair of juxtaposed sites does not depend on past conformations separated by 100 μs or so. In interwound superhelices, in contrast, very long correlations between successive conformations exist, so the probability of juxtaposition between two specific sites in DNA a few kilobases in length can depend on the initial conformation for more than 10 ms. This correlation results from the slow slithering motion of opposing superhelix segments. Still, site juxtaposition by slithering in supercoiled molecules a few kilobases in length is on the time scale of milliseconds, not seconds, as initially suggested in ref. 27. The alternative mechanism of juxtaposition, collision between sites located in different branches of the superhelix, is less important than slithering for the DNA molecules 1.5–6 kb in length studied here but may become dominant for longer molecules, as was suggested by Marko and Siggia (27). It should be noted, however, that for many enzyme systems, these two types of collisions are not equivalent (48).

The DNA model used in our simulations quantitatively describes all of the dynamic properties of DNA measured experimentally and lends confidence in our simulation results. Still, there are few experimental data on the dynamics of the internal motion in DNA molecules to be used for reference. Although BD simulations successfully describe the kinetics of fluorescence depolarization (13) and dynamic light scattering (15), the internal motion that determines the rate of these processes is fundamentally different from the slithering motion that defines the rate of site juxtaposition in supercoiled DNA under near physiological ionic conditions. Although the recent successful modeling of the dynamic light scattering for supercoiled DNA (20) is a step in the right direction, it is not clear how critical these experimental data are to the rate of slithering motion.

One important assumption in our model may affect our estimates of juxtaposition times. The model considers the double helix as intrinsically straight; thus its minimum energy conformation corresponds to a straight line. This is certainly an approximation, as DNA is well known to have intrinsic sequence-dependent curvature (49, 50). Still, it was shown that equilibrium conformational properties of long DNA can be described well without explicit modeling of intrinsic curvature, because this intrinsic bending can be considered a contributor to the measured DNA persistence length (51, 52). The estimates show, nonetheless, that the situation may be different for some dynamic properties (36, 53). Although intrinsic curvature can be easily incorporated into our model, an uncertainty in the value of intrinsic curvature for a specified DNA sequence does not allow us to estimate its effect on the rate of site juxtaposition unambiguously. At present, we can only state that intrinsic curvature can decrease the juxtaposition rate.

Finally, it is interesting to speculate how the data obtained in our work can be extrapolated for larger DNA molecules. It was noted by Marko and Siggia (54) that the rate of site juxtaposition by slithering motion in the interwound superhelix should be very low for long DNA molecules, because this rate is proportional to L³. This conclusion did not account, however, for superhelix branching, which reduces 〈τ_c〉 greatly for DNA molecules longer than a few kilobases. Branching should reduce the dependence of 〈τ_c〉 on L from 〈τ_c〉 ∝ L³ to 〈τ_c〉 ∝ L² (28). Although our simulation results (Fig. 5B) do not allow us to determine the exponent unambiguously, analyses suggest an exponent value close to 2. We found that at physiological ionic conditions, DNA supercoiling does not affect 〈τ_c〉 notably for 3-kb DNA. Because for linear or relaxed circular chains 〈τ_c〉 ∝ L^2.2 (55, 56), our conclusions regarding the independence of 〈τ_c〉 on σ should be valid for a wide range of DNA lengths. If 〈τ_c〉 ∝ L², it follows that for a circular DNA 100 kb in length—a typical size of topological domains in prokaryotic DNA (57)—〈τ_c〉 is in the range of a few seconds. This estimate suggests that site juxtaposition may become a rate-limiting step for some biochemical reactions that require juxtaposition of two sites along a large DNA molecule.

Abbreviations

BD

Brownian dynamics

bfc

body-fixed coordinate