Isotopic evidence for large gaseous nitrogen losses from tropical rainforests

Abstract

The nitrogen isotopic composition (¹⁵N/¹⁴N) of forested ecosystems varies systematically worldwide. In tropical forests, which are elevated in ¹⁵N relative to temperate biomes, a decrease in ecosystem ¹⁵N/¹⁴N with increasing rainfall has been reported. This trend is seen in a set of well characterized Hawaiian rainforests, across which we have measured the ¹⁵N/¹⁴N of inputs and hydrologic losses. We report that the two most widely purported mechanisms, an isotopic shift in N inputs or isotopic discrimination by leaching, fail to explain this climate-dependent trend in ¹⁵N/¹⁴N. Rather, isotopic discrimination by microbial denitrification appears to be the major determinant of N isotopic variations across differences in rainfall. In the driest climates, the ¹⁵N/¹⁴N of total dissolved outputs is higher than that of inputs, which can only be explained by a ¹⁴N-rich gas loss. In contrast, in the wettest climates, denitrification completely consumes nitrate in local soil environments, thus preventing the expression of its isotope effect at the ecosystem scale. Under these conditions, the ¹⁵N/¹⁴N of bulk soils and stream outputs decrease to converge on the low ¹⁵N/¹⁴N of N inputs. N isotope budgets that account for such local isotopic underexpression suggest that denitrification is responsible for a large fraction (24–53%) of total ecosystem N loss across the sampled range in rainfall.

Coherent patterns in N isotope composition across forests and soils suggest that natural abundance isotopes can provide critical information on the N cycle across broad geographic areas. Tropical forests, which are highly productive and play an important role in the Earth's climate system (1), are among the most ¹⁵N-enriched of the terrestrial biomes (2); however, the ¹⁵N/¹⁴N of plant and soil pools in tropical forests decrease systematically with increasing rainfall across tropical forests (3–8). This latter trend has garnered considerable attention because it implies a coupling between climate and the N cycle; however, the underlying cause remains unclear. The decline in forest soil ¹⁵N/¹⁴N with increasing rainfall has been attributed to: (i) changes in the ¹⁵N/¹⁴N of atmospheric N inputs (9, 10) such as biological N₂ fixation or rainfall and cloud deposition, (ii) preferential leaching of isotopically light N to stream waters (3–8, 11), or (iii) gaseous losses of isotopically light N to the atmosphere (3–8, 11).

Here, we examine these hypotheses in a series of tropical montane rainforests on Mt. Haleakala, Maui, HI; we also identify the mechanism(s) responsible for the elevation of soil ¹⁵N/¹⁴N relative to atmospheric N₂. At this location, Schuur and Matson (6) characterized a sequence of six tropical forests, across which mean annual precipitation (MAP) varies from 2,200 to 5,050 mm, thus spanning the majority of tropical rainforest MAP worldwide (12). Ecosystem state factors (13) such as bedrock (≈400,000-year-old basaltic tephra), plant composition (trees dominated by Metrosideros polymorpha), mean annual temperature (16°C), topographic relief (slope of <5%), and elevation (1,270–1,370 m) are relatively constant across the gradient (6). The forests have never been cleared for timber or agriculture (6), are composed of species native to Hawaii, and have thus far escaped modern increases in anthropogenic N deposition. Because N pools equilibrate within 20,000 years of development in Hawaii (14, 15), the internal N pools in these ≫20,000-year-old forests should be at steady state with respect to N inputs and losses.

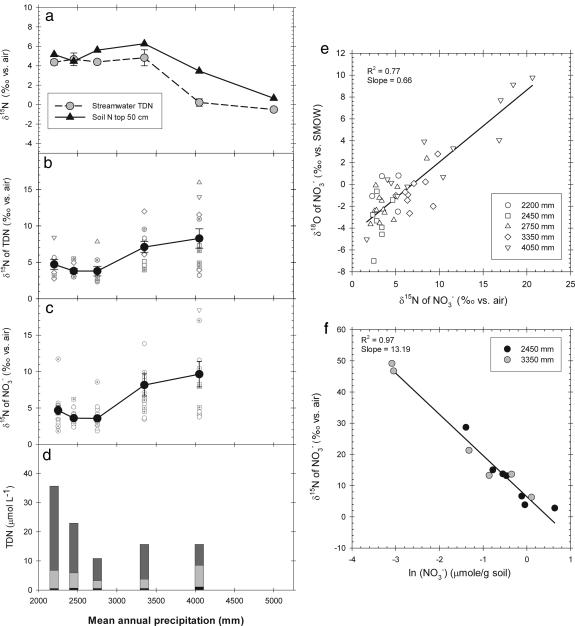
In the soil N of most of these forests, Schuur and Matson (6) have observed the high ¹⁵N/¹⁴N characteristic of the mean of the tropical forest biome (2). Moreover, they observed that the integrated ¹⁵N/¹⁴N of the top 50 cm of soils decreased with MAP, with the steepest change occurring between the sites with 3,350 and 4,050 mm of MAP (Fig. 3a). Together with a similar decrease in plant ¹⁵N/¹⁴N with rainfall along this gradient (6), these trends mimic the patterns observed for forests worldwide (4, 7).

Fig. 3.

Nitrogen isotope ratios and chemistry in rainforest soils. (a) ¹⁵N/¹⁴N of the top 50 cm of bulk soil (14). (b and c) ¹⁵N/¹⁴N of TDN (b) and of NO₃⁻ (c) in soil solution from a 35-cm depth. (d) Soil solution N species. Symbols are the same as in Fig. 2. (e) Relationship between soil solution nitrate ¹⁵N/¹⁴N and ¹⁸O/¹⁶O across all sites. (f) ¹⁵N/¹⁴N of NO₃⁻ vs. the natural logarithm of soil NO₃⁻ concentration in a series of cores designed to eliminate processes other than denitrification, such as nitrification (by addition of N serve) and plant uptake (by removal of plant roots) (see Supporting Materials and Methods).

Results and Discussion

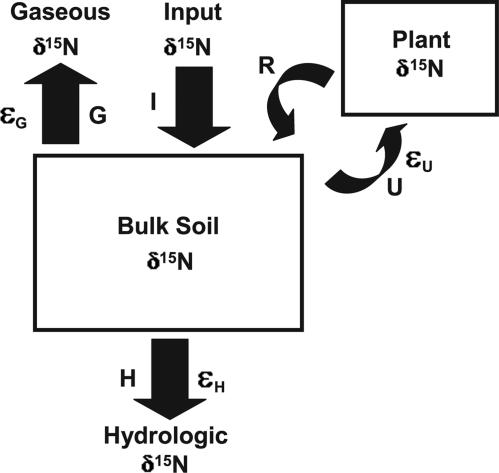
We measured over 4 years (14 events distributed across seasons and hydrological conditions) the ¹⁵N/¹⁴N of NO₃⁻ and of total dissolved N (TDN) in precipitation and cloud water inputs, in stream water losses, and in soil waters and extracts. In Fig. 1 we show that the assumption of steady state N pools permits us to exclude effects of plant N uptake, because this process only impacts bulk soil N isotopes under transient conditions such as net N accumulation (7). On the basis of previous work (11), we assume that the N contributed by biological N₂ fixation has a ¹⁵N/¹⁴N close to that of air [i.e., its δ¹⁵N is 0‰, where δ¹⁵N (per mil, ‰, vs. air) = (¹⁵N/¹⁴N_sample/¹⁵N/¹⁴N_air − 1)·1,000)]. Combining these constraints on N isotope budgets with the isotope data for bulk soils and plants from Schuur and Matson (6), we test the competing hypotheses for the elevation of the ¹⁵N/¹⁴N in these forests relative to atmospheric N₂ and for the observed ¹⁵N/¹⁴N decrease in soil and plant N with increasing MAP (Fig. 1).

Fig. 1.

Conceptual model of controls on forest ¹⁵N/¹⁴N; soil N and plant N are boxed. I, nitrogen input flux to the forest; H and G, hydrologic leaching and gaseous fluxes, respectively; U and R, plant fluxes (uptake and return, respectively). ε_U, ε_H, and ε_G are effective (i.e., expressed) isotope effects for plant uptake and external hydrologic and gaseous losses, respectively [ε (in ‰) = (¹⁴k/¹⁵k − 1)·1,000, where k is the rate constant]. Under steady-state conditions, the N inputs into plants must balance the losses from it. Hence, the same flux-weighted δ¹⁵N that plants take up (U) is returned to the soil (R), resulting in no net change in soil δ¹⁵N by plant uptake processes. By contrast, losses of N to the external environment that fractionate against soil N isotopes (i.e., ε_H or ε_G) can lead to an elevation in soil δ¹⁵N relative to inputs. Consequently, at steady state, soil N isotopes can be modeled independently of plants: δ¹⁵N_soil = δ¹⁵N_inputs + ε_H·(H/(H + G)) + ε_G·(G/(H + G)). In this study, we test which of the following best explains the soil δ¹⁵N variation across a rainfall sequence of tropical forests: (i) the δ¹⁵N of inputs, (ii) N isotope discrimination during hydrologic leaching (ε_H), or (iii) discrimination during gaseous N loss (ε_G).

Elimination of Two Competing Hypotheses.

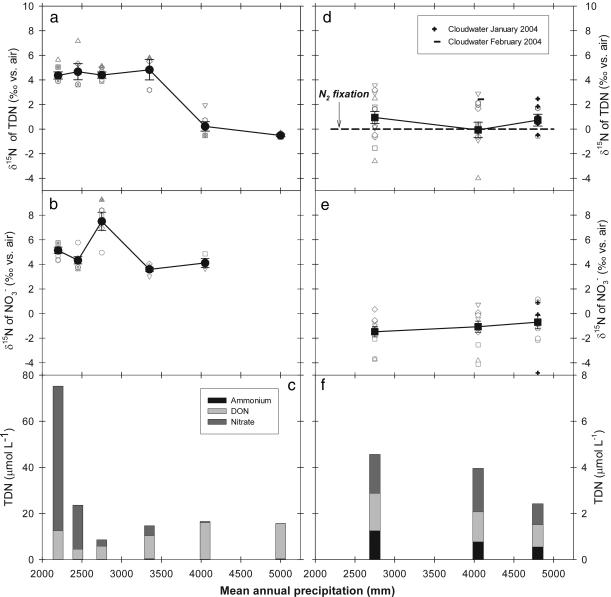
Neither the forms of N in bulk deposition nor its ¹⁵N/¹⁴N changed systematically with rainfall (Fig. 2d and f). Concentrations of all dissolved N forms were exceedingly low (<3 μmol per liter) in the rainfall but did not change in relative contribution across the sequence (Fig. 2f). The ¹⁵N/¹⁴N of TDN in deposition was statistically indistinguishable from 0‰ across the sequence (one-tailed t test, P > 0.15; n = 42) and thus similar to the isotopic ratio of N₂ fixation (indicated by the dashed line in Fig. 2d). In addition, cloud water ¹⁵N/¹⁴N did not differ significantly from either bulk deposition or N₂ fixation (one-tailed t test, P > 0.10; n = 6) (Fig. 2d). Thus, we found no evidence for our first hypothesis: that a trend in the ¹⁵N/¹⁴N of N inputs explains the decline in soil ¹⁵N/¹⁴N with rainfall.

Fig. 2.

Nitrogen isotope ratios and chemistry of small streams and atmospheric inputs across the rainforests. (a and b) In stream water, the ¹⁵N/¹⁴N of TDN (a) and of NO₃⁻ (b) are shown. (c) Stream water N species. (d and e) In atmospheric N inputs (precipitation and cloud water), the ¹⁵N/¹⁴N of TDN (d) and of NO₃⁻ (e) are shown; a δ¹⁵N of 0‰ for N₂ fixation (11) is indicated in d. (f) Precipitation N species. Open gray symbols represent individual observations from 2001–2004 (see Supporting Materials and Methods); filled symbols connected by solid lines represent means ± 1 SE.

The ¹⁵N/¹⁴N of bulk soil (and thus of forest-integrated N) was substantially elevated relative to inputs across all but the two wettest forests (Fig. 3a). Such a difference between inputs and internal pools requires a pathway of preferential ¹⁴N loss from forests receiving <4,050 mm of MAP, which acts to elevate forest ¹⁵N/¹⁴N above the ¹⁵N/¹⁴N of the inputs to these forests (Fig. 1). However, we found no evidence for our second hypothesis: that the trend in soil ¹⁵N/¹⁴N was caused by decreasing isotopic fractionation of N leaching losses with increasing rainfall (3–8, 11). The forms of dissolved N in stream water losses changed sharply with rainfall: NO₃⁻ dominated in streams draining drier forests (<2,750 mm of MAP), whereas DON (TDN minus inorganic N) was the most important form of N in streams draining wet forests (Fig. 2c). This pattern indicates that NO₃⁻ accumulates in the drier forests to the point where NO₃⁻ leaching occurs, whereas only DON leaks from the wet forest ecosystems. Despite this shift in N forms, the ¹⁵N/¹⁴N of stream water TDN changed in a manner similar to the trend in bulk soils (Figs. 2a and 3a). In fact, we found only slight differences in ¹⁵N/¹⁴N between stream losses and soils, most notably in forests with >2,500 mm of MAP, where the δ¹⁵N of stream water TDN was 1–2‰ lower than soils. This isotopic difference between streams and soils, if anything, should cause an increase (rather than the observed decrease) in ¹⁵N/¹⁴N forest soils with increasing MAP.

Given that these forests can be assumed to be in steady state with respect to total N inputs and losses (14, 15), the ¹⁵N/¹⁴N of total losses must balance that of total inputs (Fig. 1). The ¹⁵N/¹⁴N ratios of leaching losses were consistently higher (ANOVA, P < 0.001; n = 53) than those of inputs at all but the two wettest sites (Fig. 2 a vs. d), indicating a pathway other than hydrologic loss for preferential ¹⁴N removal. The only remaining explanation is the process central to our third hypothesis: gaseous N loss. The most likely cause of such fractionating gaseous N loss is denitrification, which is known to strongly favor loss of ¹⁴N over ¹⁵N, especially in NO₃⁻ -rich soils (9, 11). Ammonia volatilization is unlikely, owing to the acidic (pH of 3.2–4.2) and NH₄⁺ -poor soil conditions of our forests (6).

Evidence for Denitrification.

Examination of the isotope ratios of NO₃⁻ and TDN in local soil solutions and extracts indicates that soil denitrification was an important process in these forest soils. In both soil extracts and lysimeter samples, the δ¹⁵N of NO₃⁻ was substantially elevated above the ≈0‰ average input (Fig. 3c and Fig. 6, which is published as supporting information on the PNAS web site; see also ref. 16). The ¹⁵N/¹⁴N of soil water TDN (Fig. 3b) tracked this ¹⁵N enrichment in NO₃⁻, with highest values and greatest range in the ¹⁵N/¹⁴N in the wetter forests. This similarity in ¹⁵N/¹⁴N between NO₃⁻ and TDN indicates that dissimilatory microbial reduction of NO₃⁻ to NH₄⁺ (17) or some other aspect of internal cycling could not explain the local ¹⁵N enrichment in NO₃⁻ . Previous work indicates that, under the nutrient conditions that characterize these forests, plant uptake of dissolved inorganic N does not appear to discriminate between the N isotopes (11).

¹⁵N/¹⁴N and ¹⁸O/¹⁶O ratios of NO₃⁻ in soil solutions were highly correlated (R² = 0.76; n = 44; P < 0.0001) within and across forests (Fig. 3e). Such a correlation has previously been found in terrestrial systems only when denitrification contributes actively to N loss (18, 19); it is caused by discrimination against both ¹⁵N and ¹⁸O during NO₃⁻ reduction. Moreover, the slope of the relationship (0.66) was similar to that associated with denitrification in groundwater systems (0.49–0.67) (18, 19).

Soil extracts (2 M KCl) indicated that the ¹⁵N/¹⁴N ratios of extracted NO₃⁻ were markedly elevated relative to those of extracted NH₄⁺ in all but the shallowest forest soils (16). Without denitrification, NO₃⁻ that accumulates in soils would be lower in ¹⁵N/¹⁴N than NH₄⁺ as a consequence of fractionation during nitrification of NH₄⁺ to NO₃⁻ (9). Moreover, the soil extracts revealed decreasing NO₃⁻ concentrations and sharply increasing ¹⁵N/¹⁴N ratios from shallow to deep soils (Fig. 6). The most dramatic trends occurred in the wettest sites, where profiles of soil O₂ availability (6) show sharp declines with depth, approaching levels that favor anaerobic metabolism. To our knowledge, our measurement of a δ¹⁵N of 180‰ for NO₃⁻ extracted from soil at a 35-cm depth in the 4,050-mm MAP forest is the highest δ¹⁵N ever reported from a natural soil system. This parallel decline in NO₃⁻ concentration, increase in the ¹⁵N/¹⁴N and ¹⁸O/¹⁶O of NO₃⁻, and decrease in O₂ availability with soil depth is highly suggestive of active denitrification (16).

Finally, the presence of measurable NO₃⁻ in soil extracts and soil solutions from wet forests (>2,750 mm; Fig. 3d), coupled with the virtual absence of NO₃⁻ in streams draining the same forests (Fig. 2c), suggests that denitrification occurred along the path of water flow from local soil solutions to watershed streams.

Scale Dependence of Isotopic Imprint.

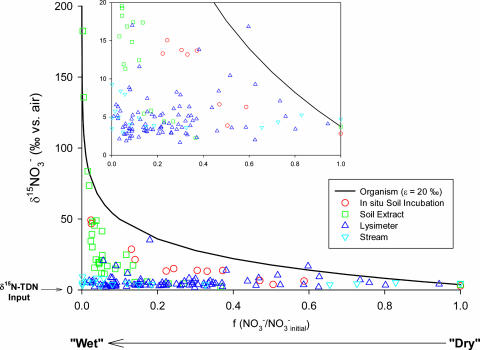
Although denitrification raises the ¹⁵N/¹⁴N of soil N in our forests relative to atmospheric inputs, we have not yet resolved why this isotope ratio in soil organic matter decreases systematically with rainfall, especially because the greatest ¹⁵N enrichment of NO₃⁻ and TDN in soil waters and soil extracts is observed in the wettest forests. We must consider how the isotope effect of denitrification, a local process, is expressed at the largest scales, in the streams and bulk soils. Partial consumption of NO₃⁻ (“open-system kinetics”) leaves behind ¹⁵N-enriched NO₃⁻, which can diffuse out of the zone of ongoing denitrification and enter the larger plant–soil N cycle. Complete NO₃⁻ consumption (“closed-system kinetics”) would cause underexpression of the isotope effect at larger scales (21, 22), because little or no ¹⁵N-rich NO₃⁻ would escape the zone of denitrification to elevate the ¹⁵N/¹⁴N of the larger plant–soil system.

We found evidence of such scale dependence of isotope effect expression in our sites. When we plot δ¹⁵N vs. the fraction of NO₃⁻ consumed locally (see the legend of Fig. 4 for the calculation method), we find that the expressed isotope effect of denitrification decreased with increasing scale: the theoretical organism-level isotope effect (23, 24) (black line in Fig. 4) > local soil solution extracts (circles and squares) > water intercepted below rooting zones (triangles) > first-order watershed streams (inverted triangles). Moreover, the scale-dependent isotope effect underexpression was greatest in the wettest sites. Soil extracts and soil waters showed the greatest (and most variable) ¹⁵N enrichment of NO₃⁻ and TDN in the wettest sites (Figs. 3 b, c, e, and f and 6), but the stream waters and bulk soils, which integrate over the ecosystem-scale N budget (Fig. 1), displayed little to no ¹⁵N enrichment relative to inputs in these sites (Figs. 2 a and b and 3a). The absence of detectable NO₃⁻ in streams from the wettest forest provides a final indication that denitrification consumed NO₃⁻ locally, preventing isotopic expression at the watershed scale. We conclude that increasingly complete NO₃⁻ consumption by denitrification causes the observed decline in ecosystem ¹⁵N/¹⁴N with increasing rainfall.

Fig. 4.

Isotopic expression of denitrification across sampling scales. The x axis is f, the fraction of nitrate remaining, which is the ratio of measured NO₃⁻ to the estimated initial NO₃⁻ concentration. We estimated the initial NO₃⁻ concentration and ¹⁵N/¹⁴N as follows: for the incubation experiment (see Supporting Materials and Methods and Fig. 3f), we used the highest extractable NO₃⁻ concentration and its corresponding ¹⁵N/¹⁴N; for soil extracts, we used the mean of the five highest NO₃⁻ concentrations and their corresponding ¹⁵N/¹⁴N; for lysimeters, we used the mean of the five highest soil water NO₃⁻ concentrations and their corresponding ¹⁵N/¹⁴N; for streams, we used the mean of the five highest stream water NO₃⁻ concentrations and their corresponding ¹⁵N/¹⁴N. The organism-level isotope effect line was calculated using an approximate form of the Rayleigh equation, δ¹⁵NO₃⁻ = δ¹⁵NO₃⁻ _initial − ε·(ln(f)) (20), and an intrinsic ε of 20‰ (23, 24).

An Isotope-Balance Approach for Reconstructing Pathways of N Loss.

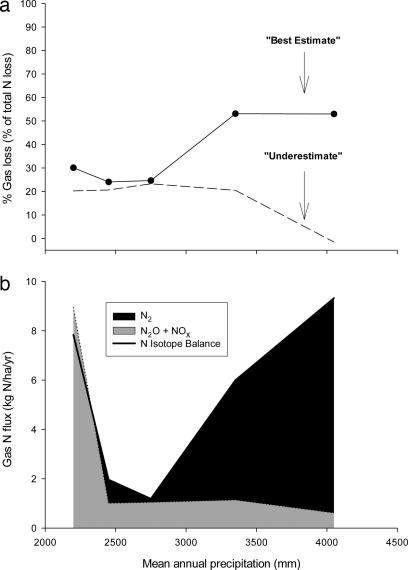
We apply an isotope-balance approach to partition the relative magnitudes of gaseous vs. hydrologic N losses across forests. We present two calculations, which derive from the same mass-balance equation but differ in the degree to which they incorporate the above findings of isotopic underexpression (see the legend of Fig. 5; see also Supporting Materials and Methods, which is published as supporting information on the PNAS web site). In the most conservative case, we assume no isotopic underexpression of denitrification [i.e., the ecosystem-level isotope effect is taken as 20‰ (23, 24)], which allows us to place a lower bound on the proportion of N loss by means of denitrification. This calculation (Fig. 5a) shows that denitrification constitutes ≈20% (and hydrological losses constitute ≈80%) of total N losses in sites with <4,050 mm of MAP. However, the fraction of N lost to denitrification drops to 0% in the 4,050-mm MAP site because, as discussed above, the organism-level isotope effect of denitrification is not expressed in streams draining our wettest forests. Given our evidence for underexpression of the denitrification isotope effect (Fig. 4), we believe that this calculation shows the lower limit of the true importance of gaseous N loss in the wettest sites.

Fig. 5.

Partitioning of N losses by isotope balance. (a) The fraction of total N loss by gaseous N using stream and lysimeter isotope data. The following equation was solved for the fraction of total N loss by gaseous N using stream and lysimeter isotope data: δ¹⁵N-TDN_deposition (i.e., 0.47‰) = δ¹⁵N_gas·(f_gas) + δ¹⁵N_TDN·(1 − f_gas), where f is the fraction of loss. In the “underestimate,” δ¹⁵N_gas was estimated as the weighted-mean δ¹⁵N of NO₃⁻ in stream water minus an ε of 20‰ (23, 24), and δ¹⁵N-TDN was taken from the stream water; in the “best estimate,” δ¹⁵N_gas was estimated as the weighted-mean δ¹⁵N of NO₃⁻ in deep soil waters minus an ε of 13.2‰, and δ¹⁵N-TDN was taken from the soil waters (Fig. 2f). (b) Estimated rates and forms of gaseous N loss. Fluxes were calculated by applying a linear regression for the relationship between rainfall and evapotranspiration to estimated stream flow (31). Also shown are in situ fluxes of NO_x and N₂O from ref. 26 and P. A. Matson, personal communication. The N₂ flux is estimated as the difference between total gas flux based on the N isotope balance and the N₂O and NO_x fluxes measured by chambers.

In the second calculation, we seek to account for local isotopic underexpression of denitrification by using the ¹⁵N/¹⁴N of NO₃⁻ from soil solutions collected from beneath the plant-rooting zone, coupled with an empirically determined denitrification isotope effect to derive the δ¹⁵N of gaseous N loss (see the legend of Fig. 5). The field-calibrated isotope effect was intended to match the degree of underexpression observed at scales of soil waters: we used in situ cores, removing the effects of plant N uptake (by excluding plant roots) and nitrification (by additions of N serve, i.e., nitrapyrin) (Supporting Materials and Methods). The ¹⁵N/¹⁴N of NO₃⁻ in these core incubations displayed a strong relationship of ¹⁵N enrichment with the logarithm of the NO₃⁻ consumed, consistent with consumption of a closed NO₃⁻ pool (ref. 20 and Fig. 3f). The slope (13.2‰) of this relationship (n = 13; R² = 0.97; P < 0.0001) identifies an empirical isotope effect that is lower than the organism-level isotope effect (of ≈20‰; refs. 23 and 24); this result offers further evidence of heterogeneity in isotope expression within our soils.

Applying this empirical isotope effect to the soil water TDN-δ¹⁵N data (as opposed to the stream TDN-δ¹⁵N data in the calculation), we calculate that denitrification accounts for 24–53% of total N losses across our forests (Fig. 5a, circles connected by solid line). The estimates for the three driest sites (≈25%) are almost identical to the stream-based approach. However, for the 3,350- and 4,050-mm MAP sites, denitrification increased substantially above the stream-based estimates to ≈50% of total N losses.

By combining these calculations with estimates of dissolved N losses, we can derive total fluxes of both gaseous and hydrological N losses. In Fig. 5b we show that total gas N fluxes (≈2–9 kg of N per hectare per year) are appreciable when compared with the range of total N inputs (including biological N₂ fixation, rain, and cloud water deposition) of <6 kg of N per hectare per year in Hawaiian forests which are not immediately downwind of active volcanoes (25, 15). In the drier forests, our fluxes do not differ substantially from short-term, chamber-based measures of oxidized N (Fig. 5b; ref. 26 and P. A. Matson, personal communication). However, in wet forests, our estimates are ≈10 times higher than chamber-based measurements. This difference could be caused by episodic denitrification (e.g., linked to rainfall events) that is not captured by chamber methods. Alternatively, and perhaps more likely, denitrification is converting almost all of the NO₃⁻ to N₂ in the wettest sites, consistent with expectations for denitrification under low-O₂ conditions (27).

Conclusions

We conclude that the pattern of decreasing ecosystem ¹⁵N/¹⁴N with increasing rainfall cannot be explained by changes in N inputs (9, 10) or preferential leaching of ¹⁴N to streams (3–8, 11). Rather, gaseous N loss is the major influence on forest ¹⁵N/¹⁴N across the climate gradient, with denitrification acting as a dominant pathway. In the drier sites, incomplete nitrate consumption by denitrification causes the elevation of bulk soil ¹⁵N/¹⁴N relative to atmospheric N₂ and the measured N inputs to the forests. In the wettest sites, complete denitrification prevents its isotopic expression at larger scales, explaining why the ¹⁵N/¹⁴N ratios of bulk soil N and stream losses decrease with rainfall and converge on the ¹⁵N/¹⁴N ratios of the inputs. Our findings provide evidence that denitrification can be a major vector of N loss from tropical rainforests (i.e., ≈24–53% of total N loss), with a large impact in overall forest N balances. To the extent that these findings apply generally to tropical forests, they identify a poorly resolved pathway in the global N budget.

Methods

We collected bulk deposition in polypropylene funnels connected with silicon tubing to high-density polyethylene bottles. We sampled cloud water by an active collector mounted on a telescoping tower 15 m above the ground (25). We collected soil water from silica gel lysimeters at a 35-cm depth by using slight vacuum pressure (32 cm of Hg) over 72 h (14). Streams were sampled with syringes. Samples were immediately filtered through precleaned glass fiber filters (Gelman A/E, 1.0-μm nominal pore size). Chemical methods for the following were as described in ref. 14: ion chromatography for NO₃⁻, colorimetry for NH₄⁺, and persulfate oxidation followed by colorimetry or furnace combustion for TDN. The ¹⁵N/¹⁴N and ¹⁶O/¹⁸O ratios of NO₃⁻ were analyzed by using the denitrifier method (28, 29); ¹⁵N/¹⁴N of TDN was analyzed by persulfate oxidation followed by the denitrifier method (30). (See Supporting Materials and Methods.)

Abbreviations

TDN

total dissolved N

MAP

mean annual precipitation.