To walk or to fly? How birds choose among foraging modes

Abstract

We test the predictive value of the main energetic currencies used in foraging theory using starlings that choose between two foraging modes (walking versus flying). Walking is low-cost, low-yield, whereas flying is the opposite. We fixed experimentally, at 11 different values, the amount of flight required to get one food reward, and for each flight cost value, we titrated the amount of walking until the birds showed indifference between foraging modes. We then compared the indifference points to those predicted by gross rate of gain over time, net rate of gain over time, and the ratio of gain to expenditure (efficiency). The results for the choice between modes show strong qualitative and quantitative support for net rate of gain over time over the alternatives. However, the birds foraged for only a fraction of the available time, indicating that the choice between foraging and resting could not be explained by any of these currencies. We suggest that this discrepancy could be accounted for functionally because nonenergetic factors such as predation risk may differ between resting and foraging in any mode but may not differ much between foraging modes, hence releasing the choice between foraging modes from the influence of such factors. Alternatively, the discrepancy may be attributable to the use of predictable (rather than stochastic) ratios of effort per prey in our experiment, and it may thus be better understood with mechanistic rather than functional arguments.

Optimal foraging theory is founded on the proposal that foraging decisions maximize fitness-related currencies (1–3). In the absence of complicating factors such as predation, nutrition, or variance, research focuses on the theoretical and empirical investigation of different currencies based on combinations of energy and time. Depending on circumstances, a variety of combinations may be expected to maximize fitness, but although theoretical models abound, studies providing rigorous empirical discriminations are scarce. This scarcity of precise experimental evidence challenges the status of optimality as a predictive framework in animal decision-making. Here we present a precise quantitative discrimination between energetic currencies, using preferences of starlings (Sturnus vulgaris) choosing among two foraging modes.

We focus on the three energetic currencies that dominate the literature: Gross rate of energy over time (b; gain/time), net rate of energy over time (net; b minus metabolic rate c), and efficiency (effy; the ratio of b or net to c). These currencies' theoretical justifications and descriptive performances have been analyzed in some detail (see refs. 4–12). In brief, efficiency is favored when expenditure has a negative impact on fitness (for instance, if heat dissipation is constrained and the time available is not), and net rate is favored when expenditure is harmless but time is limited. Gross rate is more difficult to justify, but in some situations it approximates net rate and may be easier to implement as a controlling mechanism (13, 14). Because these ideas have been discussed extensively elsewhere, but precise experimental tests are limited, our emphasis is on the empirical distinction among them.

We conducted experiments in which starlings chose between two foraging modes (walking and flying) that resulted in low-yield, low-expenditure and high-yield, high-expenditure, respectively. We fixed the amount of flying required to get a reward, and we titrated the amount of walking required to get the same reward until the subject showed indifference. The three currencies make very different predictions for the amount of walking that yields the same currency value as a given amount of flying. This is shown graphically in Fig. 1. Under natural circumstances, starlings use foraging modes that differ in yield and expenditure (e.g., fast walk with superficial pecks; slow walk with ground probing and digging; and hawking insects by flight), and hence they are likely to have evolved appropriate evaluation mechanisms to handle these choices.

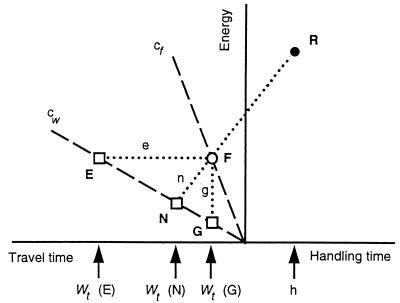
Figure 1.

Indifference between foraging modes with different rates of expenditure (walking and flying) according to three currencies. The slopes of the dashed lines c_f and c_w represent energy expenditure rates during flying and walking, respectively. Reward size (R) is assumed to be fixed. Point F shows the energy expenditure and travel time flying to obtain one reward. In the experiments, F was fixed but the subjects' choices determined the travel time walking at the point of indifference. To equalize gross rate (G), time walking [w_t (G)] should equal time flying, (line g). To equalize net rate (line n), time and energy walking correspond to point N. Finally, to equalize efficiency, energy expenditure walking and flying are equal (E, line e).

Methods

We used four wild-caught, experimentally naïve starlings, housed and tested in individual aviaries (5.10 m long × 2 m high × 0.5 m wide) in the Department of Zoology, University of Oxford, U.K. Except for three extra mealworms each day, the birds obtained all of their food from the experimental protocol. Each aviary had three recording perches, one “central” and two “foraging” (“near” and “distant”). The central perch was placed 0.35 m from the near perch and 4.65 m from the distant perch. The three perches were 1.30 m above the floor, but an elevated platform made it possible for the starlings to walk between the central and near perches. The distant perch could be reached by flight only. Food rewards with a mean weight of 0.09 g were delivered to either of two hoppers placed 0.05 m from each of the foraging perches. Food consisted of a mixture by weight of 90% turkey starter crumbs and 10% Orlux (a commercial mixture for soft-billed birds; ORLUX Vogelroedens, Roeselare, Belgium). Water was always available at both sides of the cage. For a fuller description of this set-up, see ref. 7.

Daily Routine.

The birds were on a 12-hr light/12-hr dark cycle, switching at 0700 and 1900 h. The experimental schedule started at 0700 and stopped at 1700 h, when the birds were weighed to the nearest 0.01 g and given three mealworms as a dietary supplement, and the cages were cleaned.

Foraging Schedule.

The birds were trained to gain each food reward by flying or walking a number of times between the central perch and either the distant or near perches until food was delivered. A reward was delivered after the starlings walked between the central perch and the near perch r_w times or after the starlings flew between the central perch and the distant perch r_f times. A BBC microcomputer running spider software (15) ran the schedule and stored the data. Cue lights placed next to each perch guided the birds through the schedule. We refer to a perch as being “primed” when its light is on and the computer program sets it as an active input and “unprimed” when neither condition applies. When the bird landed on a primed perch, it became immediately unprimed and the schedule advanced, either by delivering a reward or by indicating with other lights which perch or perches were now primed.

We use the term cycle to describe the events required to obtain a reward (7). There were “forced” and “free” cycles. In forced cycles, only one of the foraging perches was active so that the animal could not choose whether to walk or fly. A forced cycle started when the bird first landed on the primed central perch after consuming the previous reward. At this point, the central perch was unprimed and one of the two foraging perches was primed. When the bird landed on the primed foraging perch, this perch was unprimed and the central perch was primed again. After a preset number of repetitions, a light next to the feeder beside that foraging perch switched on for 5 s while the food dispenser delivered the reward. In a free cycle, the central place was primed in the same way after a reward, but once the bird landed on it, both foraging perches were primed. The first visit to one of the foraging perches expressed the subject's choice, and from then on the cycle continued as it did in forced cycles.

Each trial consisted of four consecutive cycles. The first two cycles of each trial were forced (one walking and one flying, in random order) and served to expose the bird to the current values of the schedule, while the third and fourth cycles were free. The number of walks per reward (r_w) was modified by an approximation to 10% between trials, depending on whether in the two free cycles the bird chose to walk (new r_w = Integer (1.10 × old r_w + 0.5)), to fly (new r_w = Integer (0.90 × old r_w + 0.5)), or one of each, respectively (new r_w = old r_w).

Treatments.

We manipulated the number of flights required per food item in 11 different treatments, from 1 flight per reward to 11 flights per reward. All birds experienced the treatments in the same order (i.e., 6, 10, 2, 9, 3, 7, 11, 4, 1, 8, and 5 flights per reward) and for the same duration. Change between treatments occurred when visual inspection of the data indicated that r_w was stable for most birds. The predictions were computed once the whole experiment was over.

The last 40 trials before stopping were used to assess the equilibrium r_w. Pilot analyses showed that all conclusions were robust with respect to this choice of sample size. Treatments lasted between 4 and 7 days (see details below).

To examine the total daily economy as a function of treatment, we focused on three theoretical possibilities. As effort per reward varied, the subjects could have defended (i) total daily intake (reaching the same number of trials and hence flying and walking in direct relation to the programmed manipulations), (ii) total net gain (increasing the number of trials as effort per reward increased, because greater expenditure is then required per reward), or (iii) total expenditure (decreasing the number of trials as effort per reward increased).

We recorded the number of daily trials, r_w in each trial and the duration of flights, walks, and perching events to the nearest centisecond.

Energy Parameters.

Flight metabolism.

Our estimates of flight costs takes into account two effects of body mass: the change in BMR (basal metabolic rate) and the change in power required during flight itself. Metabolic intensity during flight for distances of less than 6 m in starlings was estimated by Westerterp and Drent (16) as being approximately 39 ± 20.7 BMR (mean ± 95% c.i.). For BMR we used earlier respirometry measurements (7). We corrected for each treatment the flight cost (c_f, rate of energy expenditure flying), incorporating the cost of carrying different body mass:

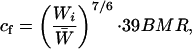1

where W_i is the body weight for the last day of treatment i (i = 1–11), and W̄ is the body weight average across treatments for the same bird (17).

Walking metabolism.

The cost of walking (c_w, rate of energy expenditure walking) was calculated with the equation

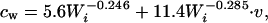2

where v is the walking speed (m/s) and c_w is expressed in J/s (18, 19).

Perching metabolism.

The perching cost (c_p, rate of energy expenditure perching) was calculated with the Aschoff and Pohl equation (20) for the activity phase as

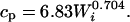3

Body mass used in Eqs. 1–3 was 5% less than that measured at dusk each day because the foraging activity was performed when birds were lighter than they were at the end of the foraging period and because body mass varies approximately 10% during a day (7).

Energy content of rewards.

The caloric value of the food used is 19.47 kJ/g (7). The assimilation efficiency for this kind of food approximates 74.4% (21). Therefore, effective food energy density was taken to be 14.49 kJ/g, and the value of one 0.09 g reward (v_p) was estimated as 1.30 kJ.

Foraging Currencies.

All three currencies were computed per foraging cycle walking and per foraging cycle flying. We use throughout the suffix “x” in symbols that are valid for either foraging mode, and then we replace it with either “w” or “f” when we refer to walking or flying, respectively.

Gross rate.

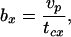4

where t_cx is the cycle duration. t_cx includes the time spent in the repeated journeys to gain one food item plus the time spent handling the food, and is given by

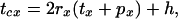5

where r_x is the number (doubled to include return trips) of journeys between the central and the foraging perches, t_x is the duration of a single journey, p_x is the time perching between journeys, and h is the time spent handling a reward (same for both travel modes).

Net rate.

Net rate is the difference between b and the rate of energy expenditure (c). The latter is given by

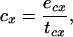6

where e_cx is the energy expenditure per foraging cycle, and it is calculated as

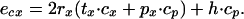7

We assume that metabolic rate during handling equals that during perching between journeys. Combining Eqs. 4–7, we get

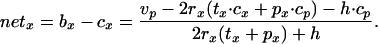8

Notice that as r_x tends to infinity, net_x tends toward the ratio −(t_x·c_x + p_x·c_p)/(t_x) + p_x), namely the rate of energy loss associated with working for food unsuccessfully in mode x. These asymptotic values are different for walking and flying.

Efficiency.

This is the ratio of gain to expenditure, and thus has no dimensions. Its expression is

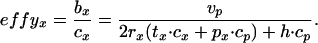9

Replacing b for net in the numerator has no consequences for determining the maximizing policy between the two modes.

For any number of flights per foraging cycle (r_f), equalization of each currency predicts a different number of walks per foraging cycle (r_w). If gross rate is equalized, then

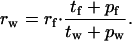10

That is, r_w is proportional to r_f and the proportionality is given by the ratio between the durations of single journeys in the two modes, including perching times.

From Eq. 8, we get that when net rate is equalized between walking and flying, the predicted number of walks per foraging cycle is

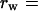11

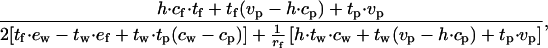where e_w and e_f are the energy expenditures in one single journey including the expenditure during perching (e_w = c_p t_p + c_w t_w and e_f = c_p t_p + c_f t_f).

By replacing the numerator and the constant expressions in the two terms of the denominator by the symbols α, β, and γ, respectively, this cumbersome equation can be written as

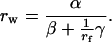11a

This form of Eq. 11 serves to see clearly its nonlinearity on r_f and also to point out that the equation is only meaningful in the range 1 ≤ r_f < γ/−β. For realistic parameters, β is negative and γ is positive.

Equalization according to efficiency is derived from Eq. 9 as

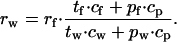12

The results predicted by each currency according to Eqs. 10–12 were compared with the equilibrium values of r_w.

Sensitivity Analysis.

Because the predictions depend on assumptions about incompletely known quantities, it is crucial to examine their sensitivity to these assumptions. The least precisely known parameters were the costs of flying, walking, and perching, and the energy content of the food. We computed the predictions resulting from three values of each parameter, the best estimates and these estimates plus or minus 25%. Given that we tested four parameters each taking three values, we ended with a total of 3⁴ = 81 predictions for each bird and treatment. We then computed the mean and dispersion of these predictions to have a measure of the range of predictions compatible with each model. The result of this analysis is shown at the end of Results. We explored alternative sensitivity analyses, including modifying each parameter on its own, but they led to conclusions similar to those to be reported later, and hence will not be presented.

Results

General Response to the Protocol.

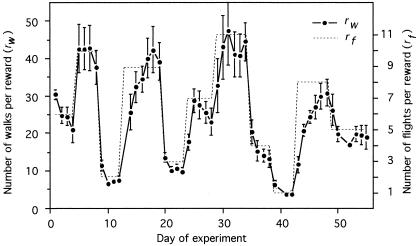
Starlings quickly modified their preference for walking according to r_f (Fig. 2), demonstrating that the titration procedure did operate as planned. For all birds, r_w was highly correlated with r_f (r_s = 0.99, 0.98, 0.96, 0.95, for each bird. r_s = Spearman's rank correlation coefficients; for all birds P < 0.001, n = 11 treatments).

Figure 2.

Temporal relationship between the mean (±SE) number of walks per cycle resulting from the titration (r_w, left) and number of flights per cycle (r_f, right) in each treatment.

Unless stated otherwise, the average variables described in the following sections are expressed as mean (±SD) across the four individual means of each bird, hence with n = 4.

Overall Daily Economy.

Birds completed greater daily distances flying and walking when r_f increased (0.62 ≤ r_s ≤ 0.82; for all birds P < 0.001, n = 11 treatments; see Fig. 3A). Of the 8 h available for foraging, they spent on average 28.6 ± 0.2 min foraging in the flying mode (a mean distance of 3196 m) and 54.7 ± 1.3 min foraging in the walking mode (a mean distance of 1072 m), and they perched the rest of the time. These values indicate that the time available for foraging was not a constraint for total intake.

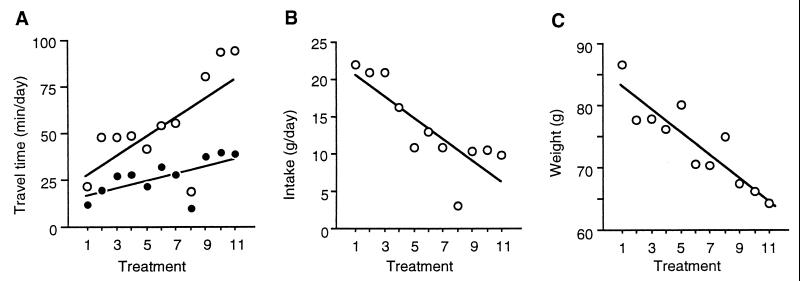
Figure 3.

Total daily economy. Mean daily time foraging in walking (A, open symbols) and flying (A, solid symbols) modes, intake (B), and body mass (C).

Mean daily intake was 13.5 ± 2.6 g (range 10.8–16.9), but it correlated negatively with r_f (r_s = −0.67, −0.74, −0.89, and −0.78; all P < 0.022, n = 11 treatments; see Fig. 3B). This means that although starlings walked and flew more each day when r_f increased, they did not regulate or increase daily intake between treatments.

Mean body mass was 73.7 ± 3.2 g (range 71.4–77.8), but body mass also decreased as r_f increased (−0.88 ≤ r_s ≤ −0.94; all P < 0.001, n = 11 treatments; see Fig. 3C). In summary, when r_f was larger, starlings walked and flew more but ate less, and hence, body mass decreased.

Travel Times and Costs.

Mean walking velocity was 0.69 ± 0.25 m/s, and mean flight velocity was 4.22 ± 0.26 m/s. These speeds differed significantly among individuals but were not significantly different between treatments (Table 1). Table 1 also shows that the time perching between flights and between walks was significantly different between birds, but handling time was not. Mean walking cost was 1.9 ± 0.4 J/s (range 2.6–1.3 J/s, r_f from 1 to 11), and mean flight cost was 31.4 ± 1.0 J/s (range 40.4–24.7 J/s, r_f from 1 to 11), while perching cost was 1.1 ± 0.1 J/s (range 1.2–0.9 J/s, r_f from 1 to 11).

Table 1.

Observed mean travel, perching, and handling times across birds and treatments (n = 44), and results of the ANCOVA test of individual differences in mean travel and perching times

	df	Walking		Flying		Perching between				Handling
						Flights		Walks
		F	P	F	P	F	P	F	P	F	P
Mean ± SE, s		0.6 ± 0.1		1.1 ± 0.0		1.4 ± 0.2		1.0 ± 0.2		28.3 ± 1.1
Bird	3,36	6.0	0.01	7.2	<0.01	8.0	<0.01	4.5	0.01	1.1	0.43
rf	1,36	0.5	0.51	1.4	0.25	12.3	<0.01	2.0	0.17	2.5	0.10
Bird × rf	3,36	0.9	0.46	0.5	0.70	0.6	0.63	0.4	0.73	0.4	0.73

The number of flights per foraging cycle (r_f) was defined as a covariable and the bird was defined as a random factor. To compute overall means, the time duration for each bird and treatment was defined as the median for that data set, so that each of the 44 numbers entered in the mean was a median from a sample size of between 300 and 1,500 data points. 

Choice Between Foraging Modes: The Currencies.

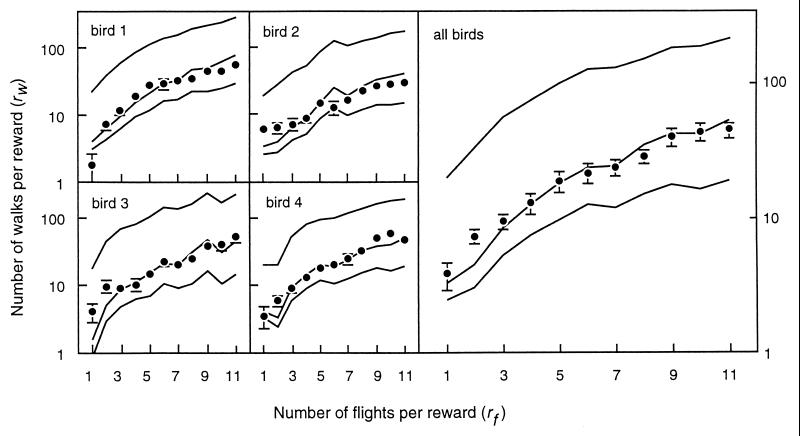
Fig. 4 presents our main result, including the predictions of the three currencies and the observed equilibrium r_w for each value of r_f. Although we present individual results with their standard deviations, successive determinations of r_w are not independent (because of the titration method they differ at most by 10%), and hence the error bars for individual data are only an indication of variability. In all birds, the net rate of energy intake was the best predictor, and the only one that fell within one standard deviation of the observed results. Gross rate of energy intake underpredicts r_w, and efficiency overpredicts it in all birds.

Figure 4.

Observed (solid circles, mean ± SD) and predicted (lines) number of walks per cycle (all birds plot shows mean ± SE). Net rate (middle lines) was the best predictor. Efficiency (top lines) overestimated r_w and gross intake (bottom lines) underestimated it.

Sensitivity Analyses.

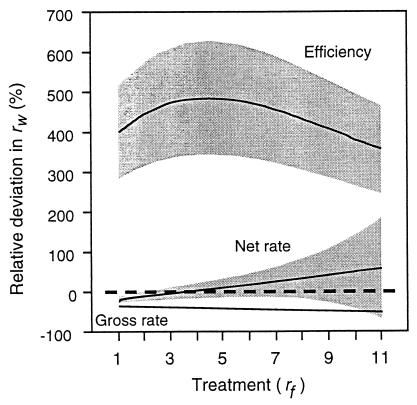
The robustness of our results with respect to each energetic assumption is shown in Fig. 5. This analysis is not relevant to gross rate because this currency depends only on foraging times, and these were measured directly. While the assumptions affect the value of the predictions, none of the changes would have altered the main conclusion drawn from Fig. 4: net rate is an accurate predictor after any of these changes, and by far a better one than either of the other currencies. We conclude that our margin of error in parameter values is not a serious difficulty for any of our conclusions.

Figure 5.

Sensitivity analysis. Effect on predictions after modifying the energetic parameters to 75%, 100%, and 125% of the best estimates. We calculated all scores of relative deviation (100 × [(predicted − observed)/observed]) per bird and treatment. These values were averaged and the means are shown as lines. Shaded areas show one standard deviation of the mean difference.

Discussion

In our experimental setup, starlings could obtain food by using a high-yield, high-cost mode (flying) or a low-yield, low-cost mode (walking). The amount of flight necessary to obtain a food item was fixed during each treatment, while the amount of walking was adjusted by titration until the birds chose both modes equally often. By comparing the results of the titration with the equilibrium predicted by the three most influential energetic currencies used by foraging theorists (i.e., gross and net rates of gain per time unit and energy gained per unit of expenditure), we established that net rate of energy gain is the only currency that accounts for the choice between foraging modes, and that it does so in a precise and quantitatively accurate manner. Although the predictions do depend on the assumptions made to parameterize the models, the advantage of net rate over its competitors does not.

The predictive superiority of net rate over gross rate and efficiency is not surprising, but its accurate quantitative fit is. It is hard to conceive that natural selection would favor a currency that entirely ignores energy expenditure or one that entirely ignores time (5). However, from a biological point of view, net rate could also be questioned because it assigns no cost to a high metabolism (provided it leads to higher gains). Net rate has also been found to be a better predictor than its alternatives in the case of delivery loads and patch residence times when starlings are feeding young (4) and when exploiting depleting patches in the laboratory (22). Given that it is a simple, state-independent currency (although it does take into account mass costs), this performance is remarkable. When factors such as predation risk (23), nutrition (24), incomplete information (25, 26), or environmental stochasticity (27) also differ among modes, static energetic models that do not include these factors must necessarily be insufficient, but even then, they should still be useful as the baseline models. Dynamic, state-dependent models such as those extensively investigated by Houston and McNamara (28, 29) incorporate these extra dimensions, but their quantitative testing requires knowledge of ecological parameters, such as mortality rates during foraging modes, which are not measurable under experimental laboratory conditions.

There is an important issue that deserves discussion in relation to our results. While net rate maximization gave a precise account of the choice between foraging modes, it failed to predict the choice between foraging and resting. The birds spent only a small proportion of the day working, even when they were losing body mass at the harder working regimes (see also ref. 7). Incomplete compensation of increasing price of food has been also described in rats working in closed economies (for instance, see ref. 30). Because the net gain during foraging was positive even under the harsher treatment, overall net energy gain would have been maximized by continuous foraging, or at least by foraging for sufficient time to maintain the net gains of the easier, shorter flight conditions. This observation confirms and expands the results that we have reported elsewhere (7): starlings do have a complex repertoire of responses to alterations in ecological conditions, including alterations in nonbehavioral dimensions such as nocturnal energy expenditure or digestive efficiency. There is no trivially obvious reason why net rate should be so good at predicting choice of mode, patch exploitation, or load delivered to the nest and yet fail to predict the time spent foraging.

From a functional point of view, it is logical to speculate that there may be some selective force that distinguishes foraging (regardless of the foraging mode) from other activities, for instance if foraging increases vulnerability to predation over resting but walking and flying are equally dangerous. In this case, a purely energetic currency would not account for when foraging occurs, but it could explain foraging choices during foraging. We are not in a position to test this idea.

An alternative hypothesis is that the mechanism of choice may have evolved to maximize energetic gain under normal ecological conditions but produces unintended side effects on circumstances that may be infrequent in nature. To develop this point, we focus on the fact that we used fixed, rather than stochastic, ratios of effort (flight or walk) per reward. This means that (in contrast with natural foraging) the birds could anticipate that a reward would not be obtained in the initial journeys to the foraging perches, and hence they may have avoided the food sources for some time before starting to forage. The degree of aversiveness (and hence of the pause before starting to forage again) should be positively related to the anticipated effort or time to reward, with the consequence that interreward interval should increase more than strictly imposed by the schedule (31). This is supported by evidence that modifying the feeding schedule from fixed to stochastic while preserving the mean ratio of effort per reward eliminates the drop in body mass associated with greater work loads (32). Under this interpretation, the failure of net energy gain to account for the proportion of time foraging would be attributable to postreinforcement pauses that occur as an epiphenomenon of deterministic foraging schedules. The pauses before foraging starts, however, should affect both foraging modes, and once the bird overcomes the motivational threshold to start foraging, the choice between modes should be free from this interference, hence the best energetic currency should operate in full.

In conclusion, we report strong experimental support for the notion that the mechanism of choice between foraging modes in starlings is designed so as to maximize the net rate of energy gain per unit of time, and we also report the failure of this currency to account for the decision to shift from inactivity to foraging. Although there is no shortage of hypotheses to solve this discrepancy, these remain speculative for the time being.