Receptor-Receptor Coupling in Bacterial Chemotaxis: Evidence for Strongly Coupled Clusters

Abstract

Receptor coupling is believed to explain the high sensitivity of the Escherichia coli chemotaxis network to small changes in levels of chemoattractant. We compare in detail the activity response of coupled two-state receptors for different models of receptor coupling: weakly-coupled extended one-dimensional and two-dimensional lattice models and the Monod-Wyman-Changeux model of isolated strongly-coupled clusters. We identify features in recent data that distinguish between the models. Specifically, researchers have measured the receptor activity response to steps of chemoattractant for a variety of engineered E. coli strains using in vivo fluorescence resonance energy transfer. We find that the fluorescence resonance energy transfer results for wild-type and for a low-activity mutant are inconsistent with the lattice models of receptor coupling, but consistent with the Monod-Wyman-Changeux model of receptor coupling, suggesting that receptors form isolated strongly-coupled clusters.

INTRODUCTION

The chemotaxis network of Escherichia coli shows remarkable sensitivity to small changes in attractant levels over 3–4 orders of magnitude of concentration. In fact, E. coli have been shown to respond to <10 nM of added chemoattractant, corresponding to the binding of ∼10 molecules of attractant (3). This sensitivity is more than expected from the dissociation constants for ligand binding, which have been measured both directly (4–7) and indirectly (8) to lie in the 1–100 μM range.

To explain enhanced sensitivity, Bray et al. (9) proposed the idea of conformational spread, in which the activity of a receptor is influenced by the activity of its nearest neighbors. Conformational spread is supported by direct observations of receptor clustering at the cell poles (10), by measurements both of receptor cooperativity (2) and interactions between receptors of different types (1), and by theoretical models (2,8,11–18). However, it is not understood how receptors are coupled, either mechanically at the level of protein-protein interactions or topologically in terms of the interaction network.

E. coli contains five chemotaxis receptors: two high-abundance receptors, Tar and Tsr, and three low-abundance receptors, Tap, Trg, and Aer (involved in aerotaxis). The receptors form homodimers and each homodimer can bind one molecule of attractant. In vitro crystallization studies suggest these homodimers form complexes of three homodimers, termed “trimers of dimers” (19). Large-scale clustering is enhanced by the linker protein CheW and by the kinase CheA (10,20). Receptors transduce the external signal, or ligand concentration, into the activity of CheA, which phosphorylates the diffusible signaling protein CheY. Phosphorylated CheY then binds to the flagellar motor and changes the motor bias, inducing the cell to change directions. Receptors have specific modification sites, which are methylated and demethylated by CheR and CheB, respectively, as part of the adaptation system. Methylation influences the activity of receptors, but it does not significantly change the dissociation constants for ligand binding (4–6).

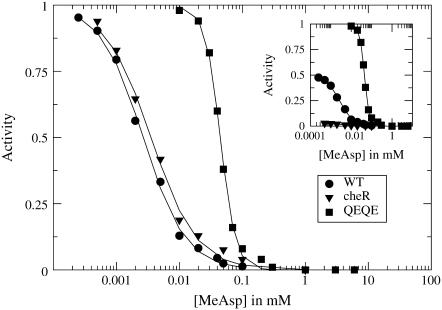
Recently, Sourjik and Berg measured dose-response curves for a variety of adaptation mutants using in vivo fluorescence resonance energy transfer (FRET). Specifically, they measured the rate of phosphorylation of CheY, i.e., the activity of the receptor system, in response to steps of chemoattractant. Fig. 1 shows data from Sourjik and Berg (1,2) for wild-type E. coli and two adaptation mutants: cheR and QEQE. The cheR strain lacks the protein required for receptor methylation, so all receptors are highly demethylated. The QEQE mutant strain was engineered to have no adaptation system (cheRcheB), leaving receptors as synthesized with two glutamates (E) and two glutamines (Q) at the modification sites (glutamines are functionally similar to methylated glutamates), and modified to express Tar receptors at six times the native level. The data appears to show two regimes of behavior: In one regime are wild-type and the cheR mutant with low-to-moderate activities and nearly the same low inhibition constant K_i, which we define to be the ligand concentration at half-maximal activity. In the other regime is the QEQE mutant, with a significantly higher K_i, as well as a high activity and high cooperativity, or Hill coefficient.

FIGURE 1.

Dose-response curves showing receptor activity as a function of attractant (MeAsp) concentration for various E. coli strains, obtained by Sourjik and Berg using in vivo FRET. Results are shown for wild-type (WT) and cheR strains, which express wild-type levels of both Tar and Tsr receptors (1), and a cheRcheB strain (QEQE), which expresses six times the wild-type level of Tar receptors (2). Receptor activity is shown normalized by the activity at zero MeAsp concentration and is shown unnormalized in the inset (lines are guides to the eye).

In this article, we compare in detail two fundamentally distinct models of receptor coupling: weakly-coupled extended one-dimensional and two-dimensional lattice models and the Monod-Wyman-Changeux (MWC) model of isolated strongly-coupled clusters. We study how receptor coupling affects the dose-response curves in each model and identify features in the Sourjik and Berg FRET data that distinguish between the models. Specifically, we find that the nearly-same low K_i observed for wild-type and the cheR mutant is inconsistent with extended lattice models of receptors, but consistent with the MWC model, thus suggesting that E. coli chemotaxis receptors form isolated strongly-coupled clusters.

MODELS

Bacterial chemoreceptors have two states, an active and inactive state, and binding of ligand favors the inactive state. We consider only one type of ligand binding to one type of receptor, e.g., the binding of MeAsp to the Tar receptor, and we assume both ligand binding and receptor conformational switching to be in equilibrium. The partition function for such a two-state receptor is

(1)

where E_on and E_off are the energies of the active and inactive states (all energies are in units of the thermal energy k_BT), [L] is the ligand concentration, and and are the ligand dissociation constants of the active and inactive states, respectively (8). Since ligand binding favors the inactive state, < The partition function contains four terms, corresponding to active receptor with or without bound ligand, and inactive receptor with or without bound ligand.

The average activity A, i.e., the probability of the receptor being in the active state, is

(2)

where f is the free-energy difference between active and inactive states,

(3)

The offset energy, Δε ≡ E_on − E_off, is the energy difference between active and inactive states in the absence of ligand.

The Sourjik and Berg data of Fig. 1 can be qualitatively explained if receptor modification simply decreases the offset energy Δε (8,13) without affecting the dissociation constants for ligand binding, the latter being supported experimentally by in vitro studies (4–7). The two regimes of behavior, described in the Introduction, are distinguished by whether this offset energy Δε is positive or negative (8). The low-activity regime has Δε > 0 and includes the cheR mutant. Assuming and the activity for a single receptor, Eq. 2, becomes

(4)

Thus, in this regime, the activity is initially low hence the name low-activity regime, and the inhibition constant The high-activity regime has Δε < 0 and includes the QEQE mutant. Assuming and the activity is given by

(5)

Therefore, in this regime, the activity is initially high hence the name high-activity regime, and i.e., the inhibition constant increases exponentially with |Δε|. Wild-type has and shares features of both regimes. It has intermediate activity and i.e., only twice the inhibition constant found in the low-activity regime.

The model for a single receptor does not explain the enhanced sensitivity (i.e.,) of the wild-type and cheR strains or the enhanced cooperativity of the QEQE mutant. We will explore how receptor coupling can account for these features, and, in particular, we will compare isolated strongly-coupled clusters, described by the MWC model, to extended lattices of more weakly-coupled receptors, described by the Ising model.

Monod-Wyman-Changeux (MWC) model

The MWC model (21) assumes receptor clusters of size N, in which the receptors are either all active or all inactive. The partition function of such a cluster is

(6)

The probability that a cluster is active is

(7)

where f is given by Eq. 3. This basic formulation of the MWC model is equivalent to that described in Sourjik and Berg (2) and shares the essential features of the MWC models of Keymer et al. (8) and Mello and Tu (18), which were extended to account for multiple receptor types.

Lattice models

We consider one-dimensional and two-dimensional lattice models, describing a single extended lattice of receptors with nearest neighbors interacting with Ising coupling energy J > 0, favoring neighbors in the same activity state. Letting σ_i = +1 and σ_i = −1 represent the active and inactive states of the receptor at site i, the free energy of a lattice of N receptors is given by

(8)

where 〈i, j〉 denotes nearest neighbors. The partition function is then

(9)

where {σ} denotes all possible activity states of the receptors.

For an infinite one-dimensional lattice, there is an analytic solution for the activity (22),

(10)

All one-dimensional lattice results reported in this article were calculated from Eq. 10. All two-dimensional lattice results reported in this article were calculated by Monte Carlo sampling for a 50×50 square lattice of receptors, using the Metropolis algorithm. For the lattice sizes of interest, ≃10,000 receptors, finite-size, and boundary-condition effects are negligible. For the two-dimensional lattice, the only significant effect on our results of changing the lattice geometry from a square lattice to triangular or honeycomb lattices is to rescale the coupling J.

There is a phase transition in the two-dimensional but not in the one-dimensional lattice model. We restrict the coupling energy J in two dimensions to be below the critical value for a two-dimensional square lattice. For coupling energies above the critical value, the receptors favor one of the activity states even when there is no free-energy difference between these states, resulting in hysteresis, which has not been experimentally observed.

Receptor coupling causes the activities of nearby receptors to be correlated. For lattice models, an effective cluster size N_eff is measured by the correlation length ξ, which is a function of the coupling energy J and free-energy difference f, and is calculated from the receptor-receptor correlation function 〈σ₀σ_k〉 ∼ e^−k/ξ. The correlation length can be calculated analytically in one dimension (23); for f = 0, for J ≫ 1.

Activity versus free-energy difference f

In the above models, given a value of the MWC cluster size N or the Ising coupling J, receptor activity is solely a function of the free-energy difference f; i.e., ligand concentration [L] and offset energy Δε enter our equations only through the free-energy difference f between active and inactive states of a single receptor, defined by Eq. 3. This dependence of activity on free energy is supported experimentally by the scaling property of E. coli dose-response curves for wild-type cells adapted at different ambient ligand concentrations (1): these curves collapse onto a single curve when plotted as a function of f instead of [L] (8).

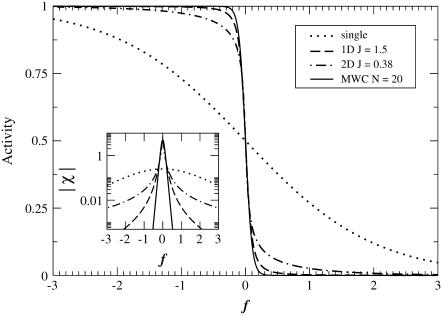
The above models of receptor coupling determine families of activity versus f curves, parameterized by N or J. Examples of such curves are shown in Fig. 2 for a single receptor, a one-dimensional lattice with J = 1.5, a two-dimensional lattice with J = 0.38, and an MWC cluster with N = 20; for the latter three, values of J and N were chosen to give roughly equal slopes at f = 0 for comparison. (Shown in the inset to Fig. 2 is the derivative of the activity curve, the susceptibility, χ = dA/df.) For f < 0, the activity is high, whereas for f > 0, the activity is low. Receptor coupling sharpens the transition at f = 0. From Fig. 2, it is apparent that the main differences between the models for coupled receptors lie in the tails of the transitions. These deceptively small differences have important consequences for experiment, which will be explored in the remainder of this article.

FIGURE 2.

Receptor activity as a function of free-energy difference f between active and inactive states for a single receptor, a one-dimensional lattice of receptors with Ising coupling J = 1.5, a two-dimensional lattice of receptors with Ising coupling J = 0.38, and an MWC cluster of size N = 20. The inset shows the magnitude of the susceptibility χ = dA/df versus f on a semilog scale. Energies are measured in units of the thermal energy k_BT.

Relation to magnetic notation

The partition function describing two-state receptors (Eq. 1) can be directly mapped onto the partition function for a two-state magnetic system. The active and inactive states correspond to the spin states σ = +1 and σ = −1, respectively, and the free-energy difference f corresponds to the magnetic field splitting −2μB. The average receptor activity A is related to the magnetization m = 〈σ〉 by A = (m + 1)/2, and the receptor susceptibility χ is related to the magnetic susceptibility χ_m by χ = − χ_m/4.

RESULTS

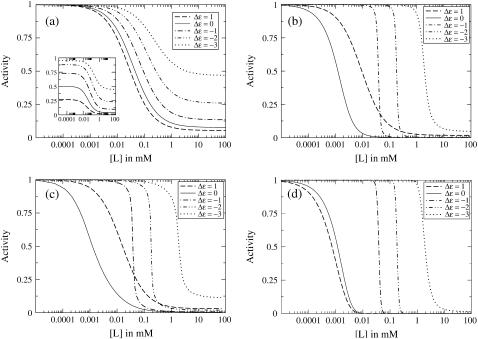
Fig. 3 shows receptor activity as a function of ligand concentration for different models of receptor coupling. We consider a single receptor (Fig. 3 a) and three models of coupled receptors (Fig. 3, b–d): a one-dimensional and a two-dimensional lattice model and the MWC model. For each model, results are shown for receptors with five different offset energies Δε. We have chosen the values of the Ising coupling J and the cluster size N to give comparable inhibition constants K_i for Δε = 0; specifically, we chose J = 1.5 for the one-dimensional lattice, J = 0.38 for the two-dimensional lattice, and N = 20 for the MWC model. The plateaus seen for large ligand concentrations, particularly visible in Fig. 3 a, are due to the finite value of K_D^on, as [L]→∞, implying a finite activity.

FIGURE 3.

Receptor activity as a function of ligand concentration for receptors with various offset energies Δε for (a) a single receptor, (b) a one-dimensional lattice of receptors with Ising coupling J = 1.5, (c) a two-dimensional lattice of receptors with Ising coupling J = 0.38, and (d) an MWC cluster of receptors of size N = 20. Receptor activity is normalized by its value at zero ligand concentration and is shown unnormalized for a single receptor in the inset to panel a. The dissociation constants for receptor-ligand binding are = 0.02mM and = 0.5 mM, and energies are measured in units of the thermal energy k_BT.

Comparing Fig. 3 a for a single receptor to Fig. 3, b–d, for coupled receptors, we see that coupling decreases the inhibition constant K_i for the low- and intermediate-activity regimes (Δε ≥ 0), and sharpens the transition, without changing K_i, for the high-activity regime (Δε < 0). We can understand, on a qualitative level, why receptor coupling has these different effects in the two regimes as follows. The majority of receptors will always be in the thermodynamically favored state, i.e., the state with the lower free energy. Since receptor coupling biases receptors to be in the same state, it effectively acts to further favor the state with the lower free energy. In the low-activity regime (Δε > 0), the inactive receptor configuration is favored and coupling allows the binding of one ligand to spread further inhibition to many receptors, which causes the low K_i and high sensitivity to ligand. In contrast, in the high-activity regime (Δε < 0), the active state is favored for small [L], but adding ligand eventually favors the inactive state. When the active state is favored, receptor coupling acts to keep the receptors active, but when the inactive state becomes favored, receptor coupling acts to inactivate the receptors. Thus receptor coupling sharpens the transition in the high-activity regime.

Fig. 3, b and c, shows that there is little difference between the dose-response curves for the one-dimensional and two-dimensional lattice models for the selected values of J. This is not surprising because the coupling energies are both chosen to be in the weak-coupling regime J < J_c, where the two models have similar behavior.

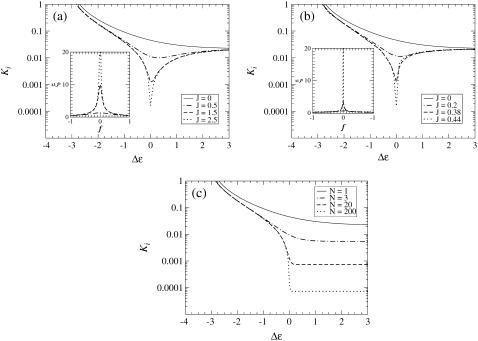
Comparing Fig. 3, b and c, with Fig. 3 d reveals a striking difference in the Δε = 1 curve between the two lattice models and the MWC model. In the lattice models, the inhibition constant K_i for Δε = 1 is significantly increased from the K_i for Δε = 0, whereas in the MWC model, the Δε = 1 and Δε = 0 curves have approximately the same low K_i. Fig. 4 emphasizes this important difference by showing K_i as a function of Δε for each of the models. Here we clearly see that, in the lattice models, K_i only attains its low value for Δε = 0, but, in the MWC model, K_i attains its low value for all Δε ≥ 0.

FIGURE 4.

Inhibition constant K_i versus receptor offset energy Δε for (a) a one-dimensional lattice of receptors, (b) a two-dimensional lattice of receptors, and (c) MWC clusters, for various values of the Ising coupling J and MWC cluster size N. The dissociation constants for receptor-ligand binding are = 0.02 mM and = 0.5 mM, as in Fig. 3. Insets to panels a and b: correlation length ξ versus free-energy difference f for one-dimensional and two-dimensional lattices, for the same parameters as in the main panels.

How can we understand the behavior of K_i versus Δε for the various models? First we consider why receptor coupling decreases K_i relative to in all models in the intermediate-activity regime (). The inhibition constant K_i measures the ligand concentration that is needed to inhibit the activity by a factor of two from the activity at zero ligand concentration. Adding ligand inhibits activity by increasing the free-energy difference f between the active and inactive states of each receptor. In the MWC model, where the activity is given by Eq. 7, for Δε = 0 the required change δf_1/2 to inhibit activity by a factor of two is determined by

(11)

(since the initial activity for Δε = 0 is 1/2), which implies Thus the required free-energy change per receptor to inhibit activity by a factor of two is inversely proportional to the cluster size N. According to Eq. 3, the ligand concentration required for this change of free energy, which is the K_i-value by definition, is (assuming ), and therefore K_i is decreased by a factor of the cluster size N. Similarly, for the one-dimensional lattice model, one also finds that δf_1/2 and K_i are decreased by the effective cluster size Intuitively, therefore, when receptors act as clusters, the inhibition constant K_i is reduced relative to by a factor of the cluster size.

Next we consider why K_i is significantly reduced for all Δε ≥ 0 in the MWC model, but only for in the lattice models. This dramatic difference in behavior of K_i is a consequence of the differences in the tails of the transitions of the activity versus f plot in Fig. 2. For large f (e^f ≫ 1), the activity in the MWC model falls off as A ∼ e^−Nf, whereas the activity in the one-dimensional lattice model falls off as A ∼ e^−f. Consequently, the required change δf_1/2 to inhibit activity by a factor of two becomes yielding in the MWC model, and yielding in the one-dimensional lattice model.

The different behaviors of K_i for Δε > 0 seen in Fig. 4 can also be understood intuitively in terms of the cluster size in each model. The cluster size N in the MWC model is fixed from the outset, but in the lattice models, the effective cluster size N_eff is set by the correlation length ξ, which is a function of both the coupling J and the free-energy difference f. The insets to Fig. 4, a and b, show ξ as a function of f for several values of J for the one-dimensional and two-dimensional lattice models, respectively. Even for large values of J, the correlation length is only large for Thus in the absence of ligand, where f = Δε, only close to Δε = 0 is the effective cluster size N_eff in the lattice models large, causing K_i to be small.

We can gain intuition for the strongly-peaked behavior of the correlation length ξ as a function of f in lattice models by the following heuristic energy argument, given for the one-dimensional lattice model, but easily generalized to two dimensions. Assume the free-energy difference f is positive, biasing receptors to be in the inactive state. Starting with all receptors inactive, compare the free-energy cost to activate a single receptor with that to activate a cluster of receptors. For a one-dimensional lattice, the free-energy cost ΔF₁ to activate a single receptor is

(12)

The energy cost ΔF_n to activate a cluster of n receptors is

(13)

Thus the activation of single receptors will dominate the activation of clusters of size n for n|f| ≥ 1, limiting the correlation length to In other words, for large enough f, receptors in the lattice models behave like individual uncoupled receptors, rather than as clusters.

In Fig. 3 we saw that in addition to decreasing the inhibition constant K_i for the low- and intermediate-activity regimes (Δε ≥ 0), receptor coupling also sharpens the inhibition transition for the high-activity regime (Δε < 0). The sharp transition for the high-activity regime is a signature of receptor cooperativity, i.e., clusters of coupled receptors bind ligand and switch from active to inactive all at once. To quantify the sharpness of this transition, we define the receptor response R as the change in activity caused by a relative change in ligand concentration,

(14)

For calibration, if receptor activity were given by a Hill function with Hill coefficient h,

(15)

then the maximum receptor response would be R_max = h/4. For MWC clusters of size N with the activity is given by a Hill function with h = N and K_i = e^−ΔE

(16)

The inhibition constant K_i does not depend on N, but the maximal receptor response is proportional to N. Similarly, for the one-dimensional lattice model, one also finds that the maximal receptor response R_max is proportional to the effective cluster size N_eff. Thus a large maximal response R_max is associated with a large cluster size.

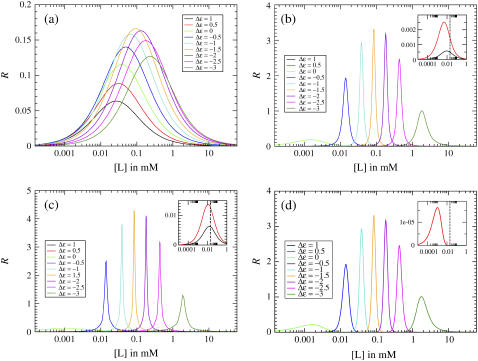
Fig. 5 shows the response R for different values of Δε for a single receptor, for one-dimensional- and two-dimensional lattices, and for MWC clusters. For a single receptor, R is always ≪1. Receptor coupling provides a larger maximal response (by as much as a factor of ∼20 for the values of J and N shown), but at the cost of narrowing the range of response. Comparing the models of coupled receptors in Fig. 5, b–d, we see that R differs greatly from model to model for the low-activity regime (Δε > 0), but the models give similar results for the high-activity regime (Δε < 0).

FIGURE 5.

Receptor response R = |dA/d log [L]| for (a) a single receptor, (b) a one-dimensional lattice of receptors with Ising coupling J = 1.5, (c) a two-dimensional lattice of receptors with Ising coupling J = 0.38, and (d) an MWC cluster of receptors of size N = 20, as in Fig. 3. Response curves are shown for different values of the offset energy Δε. The insets show the receptor responses for the low-activity regime (Δε > 0) on a smaller scale with indicated by a dashed line; the receptor response for Δε = 1 in panel d is too low to be visible.

We can better understand the receptor response R by factoring it as

(17)

where χ ≡ dA/df is the susceptibility of receptor activity A to the free-energy difference f, and

(18)

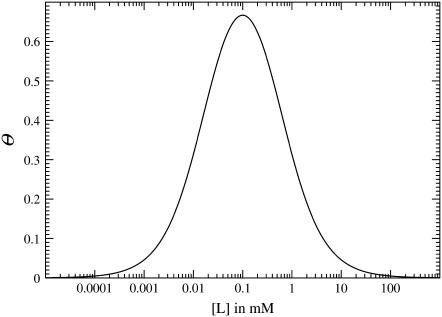
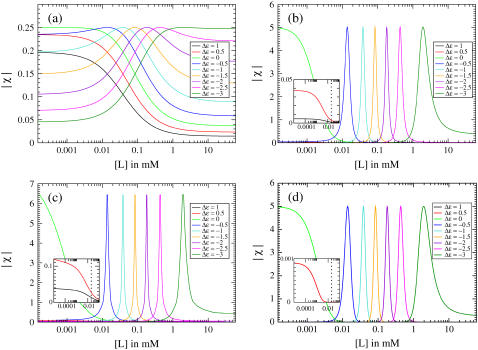
is the difference in receptor occupancy between the active and inactive conformational states at ligand concentration [L]. The occupancy difference θ is independent of the receptor-coupling model, depending only on the dissociation constants for ligand binding, and simply creates a window over which the response is nonzero, as shown in Fig. 6. All of the model-dependent features of the receptor response R come from the susceptibility χ, which is shown in Fig. 7.

FIGURE 6.

Receptor-occupancy difference between active and inactive states θ = df/d log [L]. The dissociation constants for receptor-ligand binding are = 0.02 mM and = 0.5 mM, as in Fig. 3.

FIGURE 7.

Receptor susceptibility χ = dA/df for (a) a single receptor, (b) a one-dimensional lattice of receptors with Ising coupling J = 1.5, (c) a two-dimensional lattice of receptors with Ising coupling J = 0.38, and (d) an MWC cluster of receptors of size N = 20, as in Fig. 3. Susceptibility curves are shown for different values of the offset energy Δε. The insets show the susceptibility for the low-activity regime (Δε > 0) on a smaller scale with indicated by a dashed line; the susceptibility for Δε = 1 in panel d is too low to be visible.

In the low-activity regime (Δε > 0), the low susceptibilities χ and resulting low responses R for coupled receptors are due to the low absolute activity. The absolute activity is low because, as mentioned above, coupling acts to further favor the thermodynamically favored state, which in this regime is the inactive state. The positions of the peaks approximately correspond to the inhibition constants K_i and thus are lower for the MWC model than for the lattice models, as explained above.

In the high-activity regime (Δε < 0), the high susceptibilities and resulting high responses are due both to the high absolute activities and to the receptors acting cooperatively as clusters. The maximum susceptibility occurs at f = 0 for all models, as shown in the inset to Fig. 2. Receptors with different Δε reach f = 0 at different values of ligand concentration and are therefore sensitive over different ranges. Since both MWC and lattice models can have large cluster sizes when both models can produce large maximal susceptibilities and responses, explaining the similarity of the models for Δε < 0.

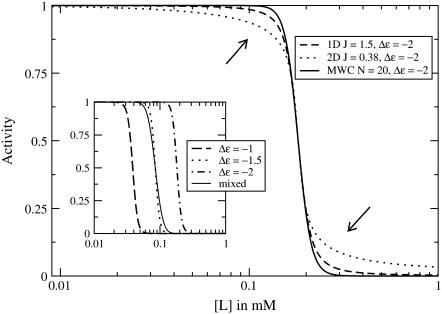
Subtle differences between the models are also present in the high-activity regime. Specifically, the differences in the tails of the activity versus f transitions, as seen in Fig. 2, carry over to the tails of the activity versus [L] transitions, as shown in Fig. 8. These transitions are less steep in the lattice models than in the MWC model because the cluster size in the lattice models is greatly diminished for f ≠ 0. The two-dimensional lattice model has fewer steep transitions than the one-dimensional lattice model because the correlation length ξ is a more sharply peaked function of f in two dimensions than in one dimension, as shown in the insets to Fig. 4.

FIGURE 8.

Receptor activity as a function of ligand concentration for receptors with offset energy Δε = −2 for a one-dimensional lattice with Ising coupling J = 1.5, a two-dimensional lattice with Ising coupling J = 0.38, and an MWC cluster of size N = 20. The curves have approximately the same slope at [L] = K_i, but deviate in the tails of the transition, as indicated by the arrows. (Inset) Effect of having a mixture of receptor modification states. Receptor activity as a function of ligand concentration for MWC clusters of size N = 20 for homogenous clusters with offset energies Δε = −1, Δε = −1.5, and Δε = −2, and for mixed clusters with Δε = −1 and Δε = −2.

These differences in the high-activity regime are masked for receptors having a mixture of modification states. In the QEQE strain in the Sourjik and Berg experiment (Fig. 1), all the receptors are in the same modification state by construction; however, receptors in wild-type E. coli presumably have a mix of modification states, due to ongoing methylation and demethylation by the adaptation system. Since different modification states lead to significantly different inhibition constants K_i in the high-activity regime, averaging over these modification states effectively smoothes the transition. The inset to Fig. 8 compares activity curves for homogenous MWC clusters with the activity curve for an ensemble of MWC clusters with an equal-probability binomial mix of two modification states. The mix of receptors reduces the Hill coefficient to from for homogenous receptors. In the MWC model in the low-activity regime, having a mixture of modification states has little noticeable effect since the shape and inhibition constant K_i of the activity curves are essentially independent of Δε.

DISCUSSION

An interesting result of the Sourjik and Berg FRET studies is the similarity between the dose-response curves for wild-type and the cheR mutant. Although the absolute receptor activities for these strains differ by a factor of ≃16, implying their receptors have different modification levels, their inhibition constants K_i are very similar and are significantly lower (by a factor of ≃10) than the ligand-dissociation constant of the inactive state, We find the low values and close similarity of the inhibition constants K_i for different levels of activity to be inconsistent with an extended lattice model of receptor coupling. In lattice models, high sensitivity, i.e., low K_i, is only achieved for receptors in a modification state such that receptor activity is in the absence of ligand, i.e., This is because a low value of K_i results from receptors acting together as clusters, and the effective cluster size in lattice models is only significant when the free-energy difference f between active and inactive receptor states is near zero. In contrast, the MWC model naturally accounts for low unvarying K_i values because cluster size is fixed and independent of the free-energy difference f. The Sourjik-Berg FRET data therefore indicate that chemotaxis receptors in E. coli form strongly-coupled clusters.

Receptor coupling is physiologically important because for receptors in the low- and intermediate-activity regimes (Δε ≥ 0), coupling enhances sensitivity to ligand by lowering the inhibition constant K_i by a factor of the cluster size. For receptors in the high-activity regime (Δε < 0), receptor coupling amplifies the response R, also by a factor of the cluster size. However, this amplification comes at the cost of narrowing the range of response for a given Δε. The adaptation system overcomes this limitation by actively adjusting Δε via receptor methylation. In effect, E. coli dynamically chooses the response curve whose peak best matches the ambient ligand concentration (see Fig. 5). By combining receptor clustering with adaptation, E. coli achieves the best of both worlds: high response over a broad range.

In both the MWC and lattice models, the effect of receptor coupling is contained in the activity A versus free-energy difference f curves (compare to Fig. 2). The main feature of these curves is the transition from high to low activity, and the main difference between the MWC and lattice models lies in the tail of this transition. The tail decays asymptotically as A ∼ e^−Nf in the MWC model and as A ∼ e^−f in the lattice models. This fundamental difference can be intuitively understood in terms of the behavior of the cluster size as a function of f in each model. The cluster size is fixed in the MWC model, but is strongly peaked at f = 0 in the lattice models, as shown in the insets to Fig. 4. The consequences for experimental dose-response curves are:

1. The different behaviors of K_i in the low-activity regime, as shown in Fig. 4.

2. A steeper inhibition transition for MWC clusters than for extended lattices in the high-activity regime, as shown in Fig. 8.

The assumption in the MWC model that all receptors in a cluster have the same activity state and switch simultaneously can only be an approximation. The coupling energy between receptors in a cluster is necessarily finite and so receptors must occasionally act independently. How does relaxing the strong coupling approximation of the MWC model change our results? A lattice model can be continuously turned into an MWC model by arbitrarily assigning clusters of fixed size N and then increasing the coupling energy J between receptors inside a cluster and decreasing the coupling energy J_B between receptors on the boundaries of different clusters. The MWC model is the limit J → ∞ and J_B → 0. If the cluster size N and coupling energy J are thought of as variables, there must be a crossover regime where the behavior of the correlation length ξ as a function of the free-energy difference f changes from being sharply peaked, as in lattice models, to being constant, as in the MWC model. (Equivalently, in terms of the activity versus f plot, there must be a crossover regime where the activity curves change from falling off as A ∼ e^−f, as in lattice models, to falling off as A ∼ e^−Nf, as in the MWC model.) From the energy argument given earlier in Eqs. 12 and 13, we expect the crossover to occur when the free-energy cost ΔF₁, to excite a single receptor, is equal to the free-energy cost ΔF_N to excite a cluster of size N. By generalizing the energy argument to a lattice with coordination number z, and setting the coupling energy on the boundary J_B to zero, we find the crossover occurs when Therefore, for strong enough coupling J, the activation of isolated clusters will always be favored over the activation of single receptors, and the receptors will behave like MWC clusters.

Another assumption in our model is that the MWC cluster size (or Ising coupling energy J) is constant, i.e., does not change dynamically upon stimulation with ligand. To address the dynamics of clustering, recent experiments have investigated the activity dependence of receptor-receptor interactions and receptor localization after addition of attractant and for different receptor modification states (24–29). Crosslinking experiments have shown that a large addition of attractant causes a significant decrease in crosslinking efficiency in the periplasmic domain (24) of the Tar receptor, but no significant change in crosslinking efficiency in the cytoplasmic domain (25). Fluorescence microscopy studies have shown either no activity dependence (24) or slight activity dependence (26,27) of polar localization of the major receptors. So far, these results suggest that addition of attractant causes microscopic receptor conformational changes, which can be best interpreted as switching from active to inactive states, rather than as dynamical changes in cluster size. Nevertheless, for the minor receptors there are indications that inactive receptors cluster less well than active receptors. As the sole receptors in a cell, minor receptors cluster only when modified to favor higher activity (28). Also, a significant decrease in the polar localization of the minor receptor Trg was observed upon addition of saturating amounts of attractant, followed by fixation (29). Our analysis of (major) receptor dose-response curves strongly supports the stability of clusters, at least over times that are long compared to signaling response times (<1 s); if the MWC cluster size decreased significantly as a function of receptor activity, then the high sensitivity in the low-activity regime, i.e., for the cheR mutant, would be lost. In the future, we expect that rapid probes of receptor-receptor interactions in vivo, such as homo FRET (30), will help clarify the dynamics and determinants of cluster size.

Fitting the MWC model to the Sourjik and Berg data (1) indicates a cluster size of ≃15 (8). This is surprisingly small compared to the ≃10,000 receptors that have been experimentally observed to cluster at the cell poles (10). From a signal-processing standpoint, receptors would optimally be spread out over the entire cell surface so as to be as uncorrelated spatially as possible (31,32). Our findings thus raise the question of why clusters are not distributed more uniformly. One possibility is that assembly of clusters is a limiting process and requires receptor concentration at the cell poles. Another possibility is that receptor clustering is important to localize the cytoplasmic proteins, e.g., CheY, CheA, and CheZ, at the cell poles (33,34).

Other examples of higher-order oligomerization of receptors in signal-transduction systems are known, including ryanodine receptors (35,36) and rhodopsin (37), and more are likely to be discovered. This article has attempted a quantitative investigation into how receptor coupling can enhance sensitivity and response in signal-transduction, and how different topologies of receptor coupling can be distinguished by measurements of dose-response curves.