Two-Dimensional Infrared Spectroscopy Displays Signatures of Structural Ordering in Peptide Aggregates

Abstract

In the presence of lipid bilayers, the hexapeptide AcWL₅ forms membrane-bound aggregates dominated by β-secondary structure and is thus a useful model for the onset of peptide aggregation in membrane environments. Two-dimensional infrared (2D IR) spectra in the amide I region for aggregates of AcWL₅ peptides with single isotopic labels provide new insight into the residue-level structural ordering of the aggregated peptides. Separation of spectral information along two axes provides clear indications of the band frequencies and relative intensities, which together are an indication of extended amide coupling networks across structural regions of a particular size. The lowered anharmonicities, relative to free peptide, and the narrow, homogeneous lineshapes of the 2D IR peaks indicate the delocalization of vibrational modes through an ordered structure whose flexibility varies with relative peptide concentration. Crosspeaks between delocalized transitions can be used to estimate the strength of the coupling interactions between neighboring residues. The sensitivity of 2D IR spectra to residue-level structural ordering shows that 2D IR spectroscopy is a powerful technique for probing structures formed during the onset of peptide aggregation.

INTRODUCTION

The molecular structure of peptides in small soluble or membrane-bound aggregates is of fundamental importance in understanding the onset of protein aggregation processes. Small, soluble peptide aggregates have been implicated as the possible toxic actor in amyloid-related pathologies (1), but the structure of such small aggregates is not easily determined by experimental methods currently in use; rather, most studies have focused, with much recent success, on determining the structure of the end product of aggregation pathways, the insoluble amyloid fibrils (2,3). Concurrently, evidence has emerged which suggests that lipid membranes may promote the earliest stages of amyloid protein aggregation, particularly membranes containing reactive lipid species resulting from oxidative degradation (4,5). Therefore, it is of considerable interest to understand the structure of proteins that aggregate in the lipid milieu.

The synthetic peptide AcWL₅ adopts a disordered structure in free aqueous solution, but in contact with a lipid bilayer it partitions into the bilayer and forms aggregates that are dominated by β-secondary structure (6). As such, AcWL₅ is a useful model system for investigating the formation of small membrane-bound aggregates. The thermodynamics of the aggregation process were determined, and the high β-secondary structure content of the aggregates is evident by infrared absorption spectroscopy, but the exact structural details of the aggregates are still to be determined. A selective isotopic labeling scheme, in which single peptide backbone carbonyls are labeled with ¹³C, was recently used in tandem with spectral simulations from a vibrational excitonic model to propose antiparallel β-sheet secondary structure for the membrane-bound aggregates (7).

A new spectroscopic tool capable of providing site-specific structural information is two-dimensional infrared spectroscopy (2D IR) (8). The 2D IR spectra of peptides contain unique information that can be used to determine both average structures and structural distributions. By spreading information collected by pulsed infrared laser techniques along two frequency dimensions, overlapping infrared features can be separated; in addition, the vibrational anharmonicities of specific bands, the mechanical couplings between molecular vibrations, and the line-shape parameters of resonances in the infrared absorption spectrum can be obtained. Each of these features of 2D IR spectra has a particular dependence on peptide local environment (including solvation and aggregation state) and secondary structure.

Here we report the 2D IR spectra of the isotopically labeled AcWL₅ aggregates. The isotopic labeling scheme for AcWL₅ is denoted by the following, where (L*) indicates the ¹³CO-labeled amino acid: UL, unlabeled AcWL₅ peptide; L2, AcW(L*)LLLL; L3, AcWL(L*)LLL; and L4, AcWLL(L*)LL. In this study, the 2D IR spectra show features that are diagnostic of extended antiparallel β-structure and that indicate the extent of vibrational delocalization and overall structural ordering of the aggregates.

MATERIALS AND METHODS

Peptides

Unlabeled and labeled forms of AcWL₅ were synthesized by ordinary solid-phase methods and purified as reported previously (6). A single ¹³C₁-labeled leucine residue (Cambridge Stable Isotopes) was placed at amino acid positions 2, 3, or 4 in each of the labeled forms (L2, L3, and L4, respectively).

Nonlinear infrared spectra

The 2D IR spectra presented here are generated by the optical analog of the NMR homonuclear COSY pulse sequence: three short pulses (k₁, k₂, and k₃) arrive in succession, separated by times τ (coherence time, between k₁ and k₂) and T (waiting time, between k₂ and k₃), and the generated photon echo evolves in time t after k₃. Double half-Fourier transformation of the resulting echo signal along τ and t yields a two-dimensional spectrum (plotted against ω_t and ω_τ) that is dependent on T. In this study, 2D IR spectra (shown in Fig. 1) were generated from heterodyned photon echo signals collected in the (−k₁ + k₂ + k₃) phase-matched direction using frequency(ω_t)-domain spectral interferometry (9) with the signal dispersed by a 50-grooves/mm grating blazed at 6 μm (Jobin-Yvon/SPEX, Edison, NJ) onto a 64-element MCT array detector (InfraRed Associates, Stuart, FL). The three ∼100-fs infrared pulses incident on the sample and the fourth weak heterodyning pulse (local oscillator) were generated using an existing laser system (10). The local oscillator was set to arrive ∼1500 fs before the photon echo signal. Unless otherwise specified, all pulses were polarized in the same direction, i.e., where 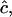and are the polarization indices of the four pulses (k₁, k₂, k₃, and local oscillator) defined formally in the Appendix.

FIGURE 1.

Real 2D IR correlation spectra for AcWL₅ peptides at peptide/lipid ratios 1:8 and 1:5. All contours are drawn at intervals of 1/15 of the strongest spectral peak.

All reported spectra were collected at a waiting time of T = 250 fs to avoid contributions from nonresonant signals (at near-zero T) and distortion of the spectra by relaxed-state contributions (at longer T). Some minor dependence of the 2D IR spectra on T was observed: beyond T = 250 fs, a dynamic averaging out of the small residual inhomogeneous distribution was noted. Data in the rephasing (k₁ comes first, positive τ) and nonrephasing (k₂ comes first, negative τ) quadrants were collected separately. The rephasing signal was cleaned of residual signal from the scattering of k₁ by the heterogeneous sample medium into the photon echo beam direction using inverse Fourier transformation to the t domain. The signal phases of each quadrant were corrected by a global fit of the one-dimensional infrared pump-probe spectra to the 2D IR data projected onto the ω_t axis. The 2D IR correlation spectra were generated by adding the phase-adjusted rephasing and nonrephasing spectra.

Contour maps for the real 2D IR correlation spectra in the amide I frequency region for UL, L2, L3, and L4 are presented in Fig. 1: the labeled peptides' spectra are shown at two different peptide concentrations (1st and 2nd columns). Contours are drawn at increments of 1/15 of the strongest peak. Strong, positive-going (red) peaks corresponding to the strong absorption bands in the linear (FTIR) spectra appear along the diagonal: for UL there is one strong peak, for the labeled peptides there are two (see FTIR spectra in Paul et al. (7)). Out-of-phase, negative-going (blue) peaks appear shifted to lower frequency along the ω_t axis: these peaks correspond to the anharmonically shifted v = 1→v = 2 transitions. In these spectra, the strong diagonal features have tails extending in both frequency directions. Weak features appearing off the diagonal (and often interfering with the long tails of the diagonal peaks) include positive and negative crosspeaks at frequencies indicating coupling between the diagonal bands. Other spectral contours are due to background noise (ripple-like features) and non-amide I signals from the lipid (for example, in the high-frequency region of the high-concentration L2 spectrum).

Vibrational lifetimes were determined from heterodyned transient grating signals collected in the same experimental geometry as above: in these experiments k₁ and k₂ arrived together (τ = 0) and T was varied from 0 to 5 ps to probe the persistence of excited-state populations. The absolute signal for each peak along ω_t was plotted versus T, and this transient was fit using a least-squares algorithm (Microcal Origin, Northampton, MA) to a single exponential function with a small constant baseline shift. The transient grating decays included oscillations due to contributions from combination tone coherences; these damped oscillations, at the difference frequency of the two main spectral peaks, and decaying with the average of the two peaks' T₁ lifetimes, were included in the fits when necessary.

Sample preparation

The 20-mM peptide stock solutions were prepared in MeOD (Cambridge Isotope Laboratories, Andover, MA). Lipid vesicle stock suspensions were prepared by mixing synthetic dimyristoylphophatidylcholine in 5 mM HEPES-D₂O buffer at pD = 7.4 and extruding through a 100-nm polycarbonate filter. The extruded vesicle suspension was assayed for phosphate (11) and adjusted to a concentration of 20 mM with HEPES-D₂O buffer. Samples for spectroscopic study were prepared by mixing 1 part of the peptide stock to either 5 or 8 parts of the lipid vesicle stocks, and incubating at room temperature overnight. Because small volumes are prepared in vials with much larger capacities, only trace amounts of MeOD remain in these samples at the time of study. Peptide-vesicle suspensions were placed between two CaF₂ windows with a Teflon spacer of pathlength 12 μm, with an approximate optical density of 0.02 at the peak of the strongest band (∼1600 cm⁻¹).

Calculations and spectral simulation

Simulation of the exciton levels for model parallel and antiparallel sheets was carried out using the Frenkel Hamiltonian described previously (7). Linear infrared spectra were calculated from these levels as in the previous work. The procedures for simulation of 2D IR spectra are described in detail in the Appendix.

Density functional calculations on small model systems were used to provide coupling constants as inputs to the excitonic Hamiltonian; for a glycine dipeptide and for an antiparallel dimer of triglycine, geometries were optimized and frequencies and vibrational couplings were calculated at level B3LYP/6–31 + G** as in Paul et al. (7).

RESULTS AND DISCUSSION

The linear amide I infrared spectra of unlabeled AcWL₅ aggregates (UL) consist mainly of two bands: the lower-frequency band is roughly 10 times more intense than the weaker, high-frequency band. On single isotopic substitution of each AcWL₅ peptide strand (L2, L3, or L4), the strongest of these two bands splits in two with the strongest component at lowest frequency. All of the amide I transitions are spatially delocalized and excitonic in nature; we refer to the intense lowest-frequency bands of the labeled aggregates as the “labeled bands” because they are downshifted from their split “unlabeled” counterparts by approximately the isotope shift expected for substitution of ¹³C=¹⁶O for ¹²C=¹⁶O.

A remarkable feature of the linear infrared spectra (7) of the labeled aggregates is that the lowest-frequency, “labeled” amide I band is the strongest band in the amide I region, despite a fivefold preponderance of unlabeled peptide groups. This “intensity borrowing” by the labeled band is a consequence of the magnitudes and topology of the coupling between amide I modes. The resulting delocalized vibrational excitations are modeled as vibrational excitons; a Frenkel exciton Hamiltonian was previously used to simulate the linear infrared spectra of labeled AcWL₅ aggregates (7). The relative participation of each coupled leucine amide I mode in the strongest observed amide I transitions as predicted by the excitonic model applied to an idealized L2 antiparallel aggregate of three strands is shown in Fig. 2. The “labeled” band is dominated by the isotopically subsituted residues but the significant participation of many other residues is also predicted.

FIGURE 2.

Calculated participation fractions for all residues of a three-strand L2 antiparallel aggregate in the low-frequency infrared absorption bands. (Upper) The higher-frequency “unlabeled” band at ∼1630 cm⁻¹. (Lower) The “labeled” band at ∼1600 cm⁻¹. Label positions at leucines 2, 7, and 12 are shown in bold.

As noted previously (7), near-identical infrared spectra would be expected for aggregates of all labeled AcWL₅ peptides if the aggregates were dominated by parallel, in-register β-structure; the changing frequencies and intensity patterns with different label positions indicate dominance of an antiparallel-like structure. The essential difference that arises between IR spectra of isotopically labeled parallel and antiparallel sheets is related to the amide I exciton topology. In an unlabeled antiparallel sheet, the most strongly dipole-allowed transition is always to the state at the bottom of the exciton band, then isotopic substitution pushes out an intense band to lower frequency. In an unlabeled parallel sheet, the strongest transition involves levels higher in the exciton band, so the levels that are pushed to lower frequency by isotopic substitution have weaker transitions. The disposition of exciton levels for parallel and antiparallel AcWL₅ structures is shown in Fig. 6 of Paul et al. (7).

FIGURE 6.

Simulation of projected (pump-probe) spectra for the two sizes (three strands versus nine strands) of simulated L2 aggregates (whose single-exciton band structures are shown in Fig. 4). The 2D IR spectra were calculated with energy disorder to give all contributing transitions finite spectral widths, and all signals were summed to the ω_t axis. The difference in frequency between corresponding positive and negative peaks is proportional to what would be the anharmonicity in an experimental spectrum.

However, since the spectral features in the L2, L3, and L4 spectra remain qualitatively similar in their shapes and intensities, we conclude that the antiparallel aggregates do not exhibit perfect strand registry. Perfect registry for AcWL₅ aggregates would result in direct through-H-bond coupling of all the labeled amide I modes in one of the labeled peptides and thus lead to a qualitatively different excitonic band structure than in the other labeled peptides, whose labeled amide I modes are all coupled through H-bonds to unlabeled modes. For the structural model used in AcWL₅ simulations, in-register L3 aggregates have the ¹³C labels lined up (see Fig. 3). If the ¹³C labels were aligned, the “labeled” spectral band would not be able to “borrow” as much spectral intensity from the unlabeled amide I modes. In all spectral simulations of structures in which the ¹³C labels are aligned, for either parallel or in-register antiparallel structures, the low-frequency labeled band is predicted to be weaker than the unlabeled band. The labeled band is the strongest in the experimental amide I infrared spectra of L2, L3, and L4. The intensity patterns and band frequencies observed in the FTIR spectra, and more dramatically in the 2D IR spectra (see Table 1), suggest that changing the location of the isotopic label only changes the fraction of ¹³C amide I modes in direct interaction with other ¹³C modes.

FIGURE 3.

Model structures for in-register L2 and L3 antiparallel aggregates showing isotopically labeled carbon atoms (black circles). All labeled amide I modes are coupled to other labeled modes through H-bonds in the case of in-register L3, whose simulated spectrum does not match the experimental spectrum.

TABLE 1.

Frequencies and relative 2D IR peak intensities for AcWL₅ peptides

Sample	Unlabeled frequency ω01 (/cm−1)	Diagonal peak intensity versus labeled band
Aggregated at P/L = 1:8
L3	1628	1/2
L2	1629	1/3
L4	1635	1/6
Aggregated at P/L = 1:5
L2	1631	1/6
L3	1634	1/6
L4	1633	1/5
Unaggregated in MeOD
L2 main	1651	5

Lack of perfect stand registry in AcWL₅ aggregates is not particularly surprising given the lack of specificity in the residue-to-residue interstrand contacts. Imperfect strand registry does not necessarily mean that the residue-level secondary structure is disordered; indeed, the linear IR spectra of the AcWL₅ aggregates indicate an overwhelming dominance of β-secondary structure.

The 2D spectra at different peptide/lipid ratios indicate a concentration dependence of the frequencies and intensity patterns. The 2D IR correlation spectra for only two concentrations of peptide (Fig. 1) are considered here, so we are unable to make systematic conclusions about concentration effects. In the experimental 2D IR spectra, the “labeled” to “unlabeled” band intensity ratio is larger for aggregates formed at 1:5 peptide/lipid relative concentrations than at 1:8. The frequency splitting between the “unlabeled” and “labeled” band maxima is also larger for 1:5 peptide/lipid. However, the “labeled” band frequency is not significantly decreased for 1:5 peptide/lipid.

Simulations of linear infrared spectra (7) for aggregates of isotopically substituted AcWL₅ predict that as the vibrational excitons are delocalized over more strands, the frequency split between the labeled and unlabeled bands should increase, whereas the unlabeled band weakens in relative intensity. This prediction agrees qualitatively with the spectral differences observed for aggregates at 1:5 and 1:8 peptide/lipid relative concentrations. The exciton simulations also predict that for larger exciton sizes, the exciton bandwidth should increase, and thus the “labeled” band frequencies at the bottom of the band should decrease. This prediction is not borne out by the experimental spectra. The experimental exciton bandwidth does not exceed the value predicted by spectral simulation for a three-stranded aggregate.

The differences in low-frequency band splitting and relative band intensities may suggest larger aggregates at higher peptide concentration; however, the exciton bandwidth appears to not be significantly increased at higher peptide concentration. Differences in either the distribution of aggregate sizes or the residue-level structural disordering of the aggregates at the two different peptide concentrations are possible reasons for the qualitative disparity between exciton simulation and experiment. A distribution of aggregate sizes should lead to inhomogeneously broadened transitions caused by the distribution of sizes. The presence of residue-level structural inhomogeneity would limit the ability of vibrational excitons to delocalize over the entire structure and modulate the effects of aggregate size on the excitonic bandwidth in any particular aggregate; in addition, small changes in the mean residue-level structure would change the shape of the exciton band and thus the frequencies and intensities of the infrared-active transitions. Further discussion of the role of structural ordering in the context of particular 1D and 2D infrared spectral features appears below.

Two features available only in the 2D IR correlation spectra indicate the extended and ordered residue-level structure of the aggregates: the vibrational anharmonicities and the narrow, clearly resolved lineshapes (Table 2). A third feature of the 2D IR spectra reports on the residue-to-residue interactions between amide I vibrators: the intensity of the crosspeaks (Table 3).

TABLE 2.

Diagonal band frequencies, anharmonicities, and linewidths (from fitting horizontal spectral slices), and vibrational lifetimes (from transient gratings)

Vibrational band	Frequencyω01 (/cm−1)	AnharmonicityΔi (/cm−1)	Vibrational lifetime T1 (/fs)	T1 linewidth contribution 1/2πcT1 (/cm−1)	Spectral full width at half-maximum (/cm−1)
Aggregated at P/L = 1:8
UL	1624	8	1050	5.0	7
L3 unlabeled	1628	9	1100	4.8	7
L3 labeled	1597	8	1200	4.4	6
L2 unlabeled	1629	8.5	1200	4.4	7
L2 labeled	1602	9	770	6.9	6
L4 unlabeled	1635	9.5	700	7.5	9
L4 labeled	1602	9	900	5.9	8
Aggregated at P/L = 1:5
L2 unlabeled	1631	12	650	8.2	11
L2 labeled	1600	10	700	7.6	10
L3 unlabeled	1634	12	650	8.2	11
L3 labeled	1599	10.5	630	8.4	10
L4 unlabeled	1633	10	640	8.3	10
L4 labeled	1599	9	600	8.8	10
Unaggregated in MeOD
L2 unlabeled	1651	15.5	–	–	–
L2 labeled	1613	13	–	–	–

TABLE 3.

Approximate crosspeak intensities relative to diagonal labeled peak intensity

Sample	Labeled/unlabeled	Labeled/high	Unlabeled/high
UL	N/A	N/A	–
L3	1/10	–	1/100
L2	1/10	–	1/100
L4	1/15	–	1/150
L2	1/30	–	1/100
L3	–	–	–
L4	–	–	1/100

Anharmonicities

Vibrational anharmonicities are manifested in 2D IR correlation spectra as the frequency difference (along the ω_t axis) between the positive peak for the v = 0→v = 1 transition and the neighboring out-of-phase negative peak for the v = 1→v = 2 transition. For example, the 2D IR spectrum for UL (Fig. 1 A) shows two peaks, one for the low-frequency β-sheet v = 0→v = 1 band at (ω_t = 1632 cm⁻¹,ω_τ = 1632 cm⁻¹) and its anharmonically shifted counterpart at (ω_t = 1624 cm⁻¹,ω_τ = 1632 cm⁻¹). The anharmonicity of the amide I mode of the single isotopically labeled leucine residue as determined by 2D IR (spectrum in Fig. 4) of nonaggregated L2 in MeOD is 13.5 ± 1.5 cm⁻¹, and the signal from the remaining unlabeled leucines shows an average anharmonicity of 15.5 ± 0.5 cm⁻¹. A definitive determination of the anharmonicity in the unaggregated case is not straightforward, as spectral fitting of both slices of the 2D spectrum and the pump-probe spectrum (the projection of the 2D spectrum on the ω_t axis) involves assumptions about the structural distribution and the lineshape components of the v = 0→v = 1 and v = 1→v = 2 transitions. Diagonal vibrational anharmonicities for the two strong peaks in the aggregated 2D IR spectra, determined from fitting pump-probe spectra, are shown in Table 2.

FIGURE 4.

The 2D IR correlation spectrum for L2 in MeOD.

The observed anharmonicities for the labeled amide I bands and the main low-frequency collective β-sheet band are all 11 cm⁻¹ or less. Delocalization of vibrational modes due to the coupling network is a likely explanation for this reduction of anharmonicities in the aggregates as compared to the free peptide. The effect of the delocalization of vibrations on the anharmonicity is easily seen from a simple example relevant to pairwise interactions between amide I modes in β-sheets. 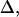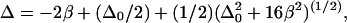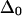If the splitting between a pair of parallel, head-to-tail-oriented transition dipoles is 2β, then the difference between the v = 0→v = 1 and v = 1→v = 2 transition frequencies, is given by where is the anharmonicity of each uncoupled mode (12). 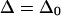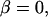Clearly, when but 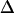approaches as the ratio becomes large. Thus, the observed anharmonicity for a pair of coupled vibrations can vary between 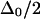and depending on the extent of vibrational delocalization.

Using simpler arguments, for an ensemble of n coupled vibrators, the average anharmonicity is estimated to be 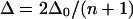(13). In a more explicit numerical model for the vibrational response in β-sheets (14), the apparent anharmonicity of the delocalized low-frequency amide I transition observed for extended antiparallel sheets is predicted to scale approximately as 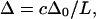where c is a constant and 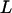is the participation length, a measure of the number of sites accessed by delocalized excitonic states (greater L means greater delocalization). In each of the above examples of modeled coupled vibrators, increased coupling leads to decreased apparent vibrational anharmonicities as measured by energy differences between out-of-phase transitions in the v = 0→v = 1 and v = 1→v = 2 regions. Thus the decreased experimental anharmonicities of the AcWL₅ aggregates' amide I modes suggest that the transitions contributing to the 2D IR signals for both the labeled and unlabeled amide I bands are from collective and delocalized vibrational modes, which result when many vibrators of similar frequencies are coupled.

An additional factor is that in extended structures, the zero-order anharmonicity, of amide I modes may be smaller than in short peptides or disordered structures like that of AcWL₅ in MeOD. Recent results for single amide I modes in a model helix (15), as well as recent theoretical work (16), suggest that the zero-order amide I anharmonicity can be significantly smaller than the conventional value of 16 cm⁻¹ (17) before excitonic effects are taken into account. However, the small diagonal anharmonicities observed for AcWL₅ spectral bands appear to be at least partially due to delocalization of vibrational excitations. All 2D spectral simulations (detailed below) were performed with zero-order anharmonicities of 16 cm⁻¹. No significant changes in the simulated spectral shapes and amplitudes were obvious for other choices of 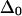greater than 12 cm⁻¹.

Vibrational two-exciton modeling (see Appendix) of the AcWL₅ system, using ab initio calculated coupling for the nearest-neighbor amide units and transition charge coupling for the rest, predicts that apparent band anharmonicities should decrease as the delocalization length increases. The modeled excitonic band structure for two sizes (three versus nine strands) of L2 in-register antiparallel aggregates are shown in Fig. 5, and projections of 2D IR spectra generated from these states are shown in Fig. 6. The modeling results indicate that increasing the delocalization length augments the total exciton bandwidth. States at the very bottom of the exciton band show anharmonicities closest to the free peptide value, whereas states at the top have near-zero anharmonicity. A qualitatively similar dependence of anharmonicity on frequency within the exciton band was predicted for α- and 3₁₀-helices (18). In the case of antiparallel β-aggregates, the model predicts that for all delocalization lengths, the two bands with strong transition dipole intensity (corresponding to the labeled and main bands in the 2D IR spectra) will exhibit similar anharmonicities, which are reduced from the free peptide value by an amount depending on size of the aggregate. Fig. 6 shows that for an antiparallel aggregate of three strands, the model for L2 predicts apparent spectral anharmoncities near 12 cm⁻¹, a reduction of ∼25% compared to the input 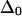of 16 cm⁻¹; for nine strands, the predicted anharmonicity is near 4 cm⁻¹, a reduction of ∼75%. The experimentally observed anharmonicities for the two strong diagonal bands in the 2D IR spectra (Table 2) show substantial reductions of the anharmonicity and, assuming that 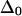are 12 cm⁻¹ or greater, place the delocalization length in the aggregates between three and nine strands (closer to three). We note that the aggregate size in our samples could exceed the delocalization length; the lowered anharmonicities are a probe of local ordering within antiparallel sheets and not necessarily of whole-aggregate size.

FIGURE 5.

Simulated exciton states for two different sizes (three strands versus nine strands) of ideal L2 aggregates, with predictions of transition dipole intensity and spectral bands. The zero-order states include hydrogen-bonded and free carbonyls for both unlabeled and ¹³C-labeled leucine residues.

A further prediction of the exciton model is that for all delocalization lengths, the anharmonicity of states near the top of the exciton band approaches zero. This is the likely explanation for the absence of the high-frequency feature at 1675–1780 cm⁻¹ from the 2D IR spectra, despite its weak presence in the linear spectra: vibrations with zero anharmonicity do not produce a 2D IR signal because of complete destructive interference between the out-of-phase v = 0→v = 1 and v = 1→v = 2 transitions.

All AcWL₅ experimental band anharmonicities are larger for 1:8 peptide/lipid compared with 1:5 peptide/lipid. The prediction of the model (and the simpler treatments mentioned above) is that the anharmonicities should decrease with increasing delocalization length. The model structure includes no registry errors or residue-level structural disorder. The anharmonicities suggest that the aggregates at higher peptide concentration are more structurally disordered at the residue level than their counterparts at lower peptide concentration. The reduction in delocalization length of the excitons is perhaps due to constraints imposed by solvation or other influences as the aggregates outgrow or destabilize their membrane interface-localized environment.

2D lineshapes

Transitions that partially overlap in linear IR spectra are often resolved in 2D IR spectra. The 2D IR lineshapes of typical amide I bands are defined by population relaxation and the structural distribution and its dynamics. A distinct advantage of 2D IR spectroscopy is that it separates the inhomogeneous and homogeneous contributions to the linewidth. In the limit that the correlation function of the inhomogeneous distribution of vibrational frequencies has fast and slowly varying parts, the spectrum becomes built up from a fixed distribution of homogeneously broadened transitions. The fixed distribution of structures spreads the 2D IR spectrum along the diagonal. The homogeneous contributions result in Lorentzian lineshape contributions characterized by tailing in the ω_t and ω_τ directions (19–21).

A contributor to the homogeneous linewidth is the vibrational lifetime (T₁ in Table 2): longer vibrational lifetimes lead to more narrow vibrational absorption bands. T₁ lifetimes for each vibrational resonance from transient grating experiments (see Materials and Methods) are in the range of 0.7–1.1 ps, slightly longer than those observed for solvated peptides in the range of 0.6 ps (22,23). An extended β-aggregate that is partially intercalated into a membrane-like detergent could exhibit extended amide I vibrational lifetimes in the hydrophobic, water-free local environment of the membrane due to new structural constraints, as recently observed in a membrane-bound dipeptide (24). The population lifetimes measured here for AcWL₅ resonances are slightly shorter than, but similar to, the recently measured T₁ for a single amide I vibration of a membrane-bound helical peptide (25). The expected contribution of T₁ to the homogeneous linewidths for AcWL₅ is calculated in Table 2.

The lineshapes of the two strong resonances in the AcWL₅ 2D IR spectra are very clear, and they are remarkably narrow for amide I transitions. The diagonal peaks (including the v = 0→v = 1 and v = 1→v = 2 components) have lineshapes that are close to Lorentzian; the linewidths determined from fitting horizontal spectral slices (for an example, see Fig. 7) are collected in the last column of Table 2. The experimental linewidths are dominated by vibrational population lifetimes, with only small inhomogeneous contributions. Convolution of T₁-defined Lorentzian bands with narrow Gaussian distributions, followed by refitting with Lorentzians, indicates that the observed spectral bands could have small underlying Gaussian components up to a full-width at half maximum of 3 cm⁻¹. With such small inhomogeneous contributions, the experimental bands would still have approximately Lorentzian shapes.

FIGURE 7.

Slices of 2D IR correlations spectra along ω_t axis at specified values of ω_τ for aggregated L2 peptides (dotted lines), with Lorentzian fits to the diagonal spectral bands (solid lines).

The 2D lineshapes are much narrower and show a much smaller inhomogeneous contribution than those reported recently for a membrane-bound dipeptide (24). Based on comparison of the lineshapes observed for AcWL₅ to the other recent 2D results for amide I vibrations near membranes (24,25), the membrane environment is not the direct cause of the narrow amide I lineshapes observed here. The very small inhomogeneous lineshape contribution likely reflects a highly ordered residue-level secondary structure.

Aside from the limited structural distribution of amide units in the aggregates, additional narrowing of the amide I peaks to near the limit set by T₁ relaxation could be caused by the delocalization of vibrational excitations in the peptide aggregates. The coupling beween the carbonyl groups in the aggregate structure causes the excitations to jump from site to site. If the differences in the site energies are smaller than the excitation exchange energies, then the inhomogeneous distribution would not be sensed by the excitations. In other words, delocalization of the vibrational excitations can average out the inhomogeneous linewidth. In an excitonic model, the inhomogeneous contribution to the spectral linewidth depends on the ratio (26), where 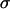characterizes the frequency distribution (the uncoupled inhomogeneous width) and is the coupling between basis sites. As increases, the excitonic states become more delocalized, and the inhomogeneous width contribution to the lineshape vanishes as approaches zero. In this line-narrowed limit, there could be structural heterogeneity at the residue level but its contribution to the lineshape would not be observed because it is averaged out by jumping of the vibrational excitations from site to site. The AcWL₅ aggregates' spectra appear to be close to the motionally narrowed limit. To approach this limit, the residue-level structural distribution must be restricted versus that of a free peptide. These issues were tested by simulations.

Vibrational exciton modeling of the linear infrared spectra for a three-stranded L2 aggregate with varying Gaussian energy disorder in the zero-order vibrational states (which is a way to include residue-level structural disorder) predicts that the observed spectral bands in AcWL₅ aggregates will be narrowed compared to the zero-order distribution of energies. Fig. 8 shows the full widths at half maximum (FWHM) for a Voigt profile with a constant homogeneous contribution of 6 cm⁻¹, the simulated lowest-frequency band in a three-strand UL aggregate, and the simulated lowest-frequency (labeled) band in an L2 aggregate plotted against the variance of the inhomogeneous (Gaussian) contribution. If there were no spectral narrowing, the simulated spectral widths would equal the width of the Voigt profile. The reductions in simulated spectral widths are the expected narrowing based on the model. For a homogeneous linewidth contribution of 6 cm⁻¹ (the approximate lifetime contribution plus estimated smaller effects from dephasing) and a narrowed linewidth of 7 cm⁻¹, the spectral narrowing predicted by the model is between 1 and 3 cm⁻¹. This indicates that although narrowing removes most of the inhomogeneous lineshape contribution to the spectra, the prenarrowed distribution of energies is in fact quite limited (σ = 1.5–3.5 cm⁻¹) according to Fig. 8. The model predicts that the width of the low-frequency band in the UL spectrum will be narrowed slightly more than the labeled band in the L2 spectrum, but this difference is too small to be observed in the experimental 2D spectra.

FIGURE 8.

FWHM linewidths plotted against the variance of the Gaussian inhomogeneous energy distribution for a Voigt profile (solid line), the simulated low-frequency amide I band for a UL three-stranded aggregate (triangles), and the simulated labeled amide I band for a L2 aggregate (squares). The reductions in spectral FWHM of the simulations compared to the Voigt profile are spectral narrowing due to excitonic averaging out of the inhomogeneous distribution.

These simulations demonstrate that although there is some residue-level structural disorder in the AcWL₅ aggregates that is not sensed by the 2D IR spectra, the residue-level secondary structures have a much narrower distribution than other peptides that have been studied (8,9,17,22–25). A small inhomogeneous lineshape component is further diminished by excitonic effects.

The 2D IR linewidths of the aggregates at 1:5 peptide/lipid are slightly larger than those at 1:8. The population lifetimes are decreased at the higher concentration. The spectral bandwidths are still dominated by T₁, with larger but still minor (less than Gaussian FWHM 4.5 cm⁻¹) inhomogeneous contributions, indicating that spectral narrowing due to delocalization also affects the spectra at higher peptide concentration.

Although slices through the high-concentration 2D IR spectra for L2, L3, and L4 (Fig. 1, right) at the band maxima in ω_τ can still be fit with Lorentzian peaks (as in Fig. 7, right, for L2), there is a noticeable increase in the tilt of the main peaks along the diagonal. This tilt is evidence of increased inhomogeneous broadening (27). The greater inhomogeneous contribution to the lineshape at higher peptide concentration could result from several factors. Assuming similar vibrational coupling constants, the greater inhomogeneous contributions to the 2D lineshapes could mean that the aggregates observed at 1:5 peptide/lipid are less structurally ordered at residue level than their counterparts at 1:8, although they maintain the same mean antiparallel sheet structure. It could also mean that a slightly greater range of aggregate structures (and sizes) is populated at higher peptide concentration. Heterogeneity of aggregate size and heterogeneity of mean structure both contribute to the inhomogeneous width in ways that would not be averaged out by excitonic effects. All of the AcWL₅ aggregate spectra display very narrow inhomogeneous widths, suggesting that both of these nonexcitonically narrowed factors are only minor spectral contributors.

Crosspeaks

The intensity of a crosspeak in a 2D IR spectrum is directly proportional to the geometric mean of the infrared cross sections of the two coupled modes and to the off-diagonal anharmonicity that is the signature of vibrational coupling between them. Crosspeaks may still be seen when one of the contributing diagonal components is very weak. Since amide I-amide I coupling constants are dependent on secondary structure, the crosspeak intensities can be used as structural determinants (8,28). In the case of the excitonic vibrational bands observed for AcWL₅ aggregates, the intensity of crosspeaks is sensitive to the couplings between pairs of single amide I modes. In well-ordered β-aggregates there are two strong coupling interactions between amide I vibrations: the interstrand (through-H-bond) and intrastrand (through-covalent bond) couplings between nearest-neighbor pairs. In aggregates of isotopically substituted AcWL₅ peptides, ¹³C-labeled amide I modes are coupled intastrand to unlabeled modes and interstrand to a mixture of other labeled and unlabeled modes. Ab initio and semiempirical model calculations by different groups show the interstrand coupling constant for β-secondary structure to be between −5 and −10 cm⁻¹ (7,19,29–32), depending on the method and details of the structure.

Approximate crosspeak intensities versus the intensities of the labeled diagonal band are reported in Table 3. Part of the challenge in clearly characterizing the crosspeaks arises from their interference in the spectra with the strong Lorentzian tails from the diagonal peaks. Furthermore, although strong photon echo signals are collected from samples with small optical densities here, the spectral signal-to-noise ratio is affected by residual nonecho signals due to light scattering from the heterogeneous medium that pollute and distort the weak crosspeak spectral regions. The Materials and Methods section describes how most of this scattering signal is removed, but some residual signal does pollute the final 2D IR spectra and reduce the effective signal-to-noise ratio.

Simulation of the aggregates' 2D IR spectra to approximate the experimental crosspeak intensities was carried out by using a vibrational two-exciton model (18) for in-register L2 antiparallel β-aggregates with three strands. Specific details of the 2D spectral simulation appear in the Appendix. The choice of coupling parameters affects the overall shape of the exciton band and not just the crosspeak intensities, so these simulations are used as only a qualitative guide to assess the coupling parameters. The simulated 2D IR spectra were not least-squares fitted to the experimental data and were not expected to reproduce all aspects of the spectra.

A transition charge coupling of −10 cm⁻¹ between two interchain amide units across a C=O…H–N hydrogen bond generates a crosspeak between the labeled and unlabeled amide I transitions in simulated 2D IR spectra that is too strong to agree with experiment. The intensity ratio of the crosspeak to the strongest diagonal peak for simulated L2, when the transition charge coupling of −10 cm⁻¹ is used for the through-H-bond coupling constant, is ∼1:6. By reducing the interstrand nearest-neighbor coupling by half to −5 cm⁻¹, the ratio decreases to ∼1:30, which is in the range of the observed crosspeak intensities.

Density functional calculations for a β-structured glycine dipeptide at the level of B3LYP/6-31G* give a nearest-neighbor coupling constant of +3.3 cm⁻¹ for through-covalent-bond, intrastrand coupling (7). Using the same density functional method for a hydrogen-bonded glycine tripeptide dimer in antiparallel sheet conformation, the nearest-neighbor, through-hydrogen bond coupling constant is estimated to be −5.5 cm⁻¹. Excitonic simulation of the 2D IR spectrum for L2 using the DFT-calculated through-hydrogen-bond coupling constant of −5.5 cm⁻¹ provides approximate agreement with the experimental crosspeak intensities in the 2D IR spectra.

More extensive spectral simulation (see Appendix for full details) using the vibrational two-exciton model (18) reveals the sensitivity to the vibrational coupling parameters of the transition energy difference between the two two-exciton states that gives the apparent mixed-mode anharmonicity. We chose to examine this mixed-mode anharmonicity in the crosspeak region of the “labeled” and “unlabeled” strong transitions. The mixed-mode anharmonicity can be written as a power series expansion of all the coupling terms in the β-sheet system:

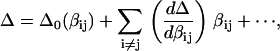(1)

where is the reference mixed-mode anharmonicity and β_ij is a bilinear coupling constant. We numerically evaluated the sensitivity of Δ with respect to all the significant coupling constants in a three-stranded antiparallel β-sheet of AcWL₅, namely the nearest-neighbor coupling through-hydrogen-bond across strand, the second nearest coupling across strand (nonbonded), and the nearest- and the second-nearest-neighbor coupling through-covalent-bonds on the same strand. It was found that the slope in the first case is the largest in magnitude: = −0.4 or −0.3, given 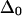= 16 or 12 cm⁻¹; the remaining three slopes are all within the range ±0.11. The mixed-mode anharmonicity between “labeled” and “unlabeled” transitions is most sensitive to the coupling between two amide units that are hydrogen-bonded across different strands. This sensitivity is physically reasonable: both the “labeled” and “unlabeled” transitions originate from the low-frequency strong exciton transition of β-sheets, in which hydrogen-bonded amide units have their amide I motions in-phase. The two-exciton simulations also show that the mixed-mode anharmonicity 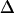can be quite sensitive to the zero-order anharmonicity 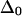used in the exciton model. In the unlikely event that 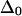is <10 cm⁻¹ or >20 cm⁻¹, the predicted mixed-mode anharmonicity would decrease dramatically.

Although the highest-frequency β-sheet bands are absent from the 2D IR spectra because of the small anharmonicity of states near the top of the exciton band, weak crosspeaks can be observed between the diagonally absent high-frequency band and the strong, low-frequency bands. Polarization-dependent 2D IR experiments using the “cross-polarization” conditions (where 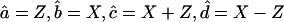) developed previously (10) for elimination of diagonal peaks from conventional 2D IR spectra, confirm the presence of these weak crosspeaks (Fig. 9). In addition, the presence in the cross-polarized spectra of the crosspeaks between the strong low-frequency bands and the absent high-frequency feature indicates that the transition dipoles for both the labeled and the unlabeled bands are oriented nearly perpendicular to the transition dipole for the high-frequency band. This observation agrees qualitatively with polarized FTIR studies of AcWL₅ aggregates bound to a membrane oriented in a Langmuir trough (6). In generalized β-sheets (33), the low-frequency infrared bands have transition dipoles oriented parallel to the H-bond axis and perpendicular to the peptide strands, whereas the high-frequency bands are oriented parallel to the peptide strands. Polarized FTIR results in Wimley et al. (6) showed that the AcWL₅ aggregates' interstrand H-bonds are oriented parallel to the membrane surface. The perpendicular arrangement of transition dipoles for the low- and high-frequency infrared bands as suggested by cross-polarized 2D IR supports the excitonic description of the aggregates' amide I modes, in which delocalized in-phase (low-frequency) and out-of-phase (high-frequency) linear combinations of amide I modes appear with perpendicular transition dipole orientations.

FIGURE 9.

Absolute-value rephrasing-quadrant (k₁ arrives first) 2D IR spectra for L2 and L3 aggregates at 1:8 peptide/lipid ratio collected with pulses polarized at 0, π/2, π/4, and 3π/4 (the cross-polarized conditions designed to eliminate diagonal pathways). Remaining diagonal signals are likely due to true diagonal signals from imperfect beam polarizations and contributions from near-diagonal two-exciton pathways.

CONCLUSIONS

The features of amide I linear infrared (FTIR) spectra of isotopically labeled AcWL₅ aggregates that display residue-level structural ordering and the resultant delocalization of amide I vibrational excitations are the spectral frequencies and band intensity ratios. On the basis of these spectral features and their dependence on the isotopic labeling scheme, some general conclusions were made about the secondary structure of the aggregates. However, as is often the case for amide I IR spectra of peptides, the linear IR spectra exhibit a broad absorption envelope within which specific features are not clearly resolved. The 2D IR spectra of the same aggregates exhibit clear, unique features which are unambiguous signatures of the delocalization of vibrational excitations in aggregates with well-ordered secondary structures.

Frequencies and relative band intensities, decreased anharmonicities relative to free peptide, and narrowed lineshapes (which are otherwise obscured in the linear IR spectra) provide unmistakable evidence of vibrational delocalization in AcWL₅ due to structural ordering and vibrational coupling of neighboring amide units. The total exciton bandwidth levels off at the value anticipated by simulation for a delocalization length of three strands. The 2D spectral simulations yielding the diagonal anharmonicities suggest a delocalization length slightly longer than three strands. The narrowed lineshapes do not provide a firm estimate of the delocalization length, since the lineshapes are dominated by homogeneous contributions; rather, the narrowed lineshapes show that the ratio σ/β is small due to a combination of structural order (small σ) and many coupling interactions (large β). The anharmonicities and lineshapes of the diagonal 2D IR bands and the delocalization of vibrational excitations that they indicate are not a direct probe of aggregate size, but they are sensitive to the residue-level structure adopted by the aggregates and to the rigidity and fluctuations of this structure.

The 2D IR crosspeaks contain, in their intensities and polarization dependences, the most specific atomic-level description of the aggregated structure. Since the isotopic labeling scheme's effect on band frequencies and relative intensities reveals an antiparallel structure for AcWL₅ aggregates, the crosspeaks in these 2D IR spectra report characteristic coupling constants associated with antiparallel β-sheets. In addition, since the amide I-amide I coupling constants for parallel and antiparallel sheets should be different, systematic comparison between crosspeaks in 2D IR spectra of β-aggregates or other extended β-sheets with parallel and antiparallel structures could eventually provide a general spectroscopic means to distinguish between parallel and antiparallel β-structure in systems displaying extended β-sheets.

The 2D IR spectral signatures of β-aggregation are important in this particular case because they can report on both the residue-level and global structure of small peptide aggregates; similar studies of the onset of aggregation in physiologically important peptides will form a new experimental basis for understanding aggregate formation and perhaps the structural basis for the toxicity of small aggregates. The 2D IR measurements are also of general importance because they provide a spectroscopic basis for diagnosing ordered β-secondary structure in the vicinity of ¹³C-isotopically labeled amide groups in any peptide or protein. Monitoring spectral changes in β-structured peptides and proteins by 2D IR will provide an important new probe of protein structure and dynamics in a wide variety of systems; the unique ability of 2D IR to monitor the onset of aggregation at the level of small, still-soluble aggregates is demonstrated here. In particular, 2D IR could be a useful probe of the structure of the small “dimers” and “trimers” of Alzheimer's-related peptides recently shown to influence neurological function (1).

APPENDIX: THE PROCEDURE FOR COMPUTING SIMULATED 2D IR SPECTRA

Numerical simulations were used to analyze the 2D IR spectra of AcWL₅ aggregates in the amide I region. Such systems of amide I modes are highly degenerate and exciton models are appropriate to estimate their 2D IR spectra. Here we use the method originally introduced for helical structures (18). The one-exciton Hamiltonian for s strands of five units was chosen as follows for 5s coupled harmonic oscillators:

(A1)

where ɛ_m is the vibrational frequency of the relevant transition of the mth amide unit; this frequency was chosen to be dependent on the location of the residue in the structure (whether or not it is hydrogen-bonded to solvent). The set of site energy fluctuations 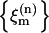for a given 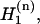chosen to represent the energy disorder, was randomly selected from an uncorrelated Gaussian distribution of width σ, the inhomogeneous linewidth parameter used in the text. The correlation of one- and two-quantum energy fluctuations could be varied. In our simulation, each one-quantum energy and its overtone energy are strictly correlated. The intersite interaction terms 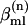involve through-bond and through-space interactions between sites m and l obtained from density functional calculations described above. The ensemble properties were obtained by averaging over n.

The transitions between the 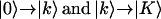manifolds of vibrational states (where the lower-case k indices correspond to the whole set of N one-exciton states and upper-case K to the set of N(N + 1)/2 two-exciton states at roughly twice the frequency, where N = 5s) were obtained by diagonalization of the two-quantum Hamiltonian in the site basis:

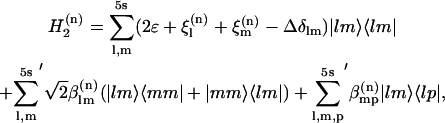(A2)

where 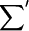omits terms with equal pairs of indices. A state with two amide I excitations, one at l and the other at m, is labeled as 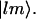The site anharmonicity, Δ₀, only appears in the single-site overtone states, signified here as 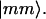The transition dipole moments 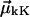between one-exciton states 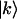and two-exciton states 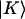were calculated by invoking a harmonic approximation:

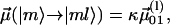(A3)

where 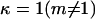or In the exciton picture, essentially all the interband transitions become allowed as a result of the anharmonicity that induces a redistribution of the transition dipole strengths among the excitonic states.

The 2D IR spectra 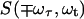originate from rephasing 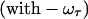and nonrephasing Liouville pathways. These pathways are illustrated in Fig. A1. Therefore the overtone and combinations are labeled by K (K = k + k'). The overall profile of a 2D IR spectrum was determined by contributions from the orientational prefactor and the signal strength. Spectral simulation based on the diagrams of Fig. 1, and at fixed T, incorporates population relaxation and a fixed inhomogeneous distribution. General expressions for 2D IR spectra in this Bloch limit can be written as:

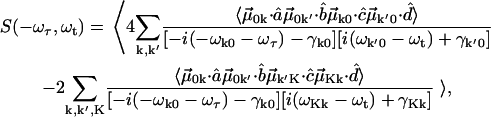(A4)

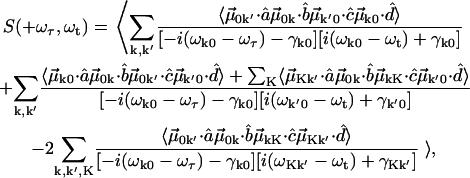(A5)

where the numerators are the orientation factors, written for a given sequence of laboratory fixed-pulse polarizations 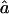to and molecule frame transition dipole directions given by the indices. Each of the terms is a Fourier transform of a field from molecules responding in the manner of one of the diagrams in Fig. A1. The γ_Kk are the homogeneous widths of the individual transitions at ω_Kk, which in the present case are dominated by the population relaxation time: 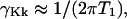and chosen equal for all the transitions. An ensemble average of Eq. A1 over the resonance frequencies was carried out to simulate the inhomogeneous broadening and accompanying localization as manifest in the Hamiltonians given above. The total 2D IR rephasing signal has two parts: one includes only the 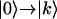transitions (pathways R₁, R₂, R₄, and R₅₎ and the other includes both 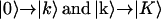transitions (diagrams R₃ and R₆). The first term contributes to the positive peaks on diagonal (when k′ = k) and off diagonal (when k′ ≠ k), and the second term contributes to all the negative peaks. 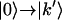The total 2D IR nonrephasing signal has three parts: the first includes only the and transitions (R₇ and R₈), which contribute to the positive diagonal peaks; the second term (R₉) contributes to the positive peaks on the diagonal (when k′ = k) and off diagonal (when k′ ≠ k); the third term (R₁₀ and R₁₁) contributes to all the negative peaks. The simulated 2D IR correlation spectra were obtained by adding the equally weighted rephasing and nonrephasing spectra.

FIGURE A1.

Feynman diagrams for pathways contributing to the 2D IR spectral simulations.