Mismatches and Bubbles in DNA

Abstract

Single mismatches in the DNA double helix form nucleation sites for bubbles. Although the overall melting temperature of the duplex is affected to different degrees depending on the probe length, the statistical weights of the bubble states around the defect are always strongly affected. Here we show experimentally that a single mismatch has indeed a dramatic effect on the distribution of intermediate (bubble) states in the melting transition of DNA oligomers. For probe lengths in the range 20–40 bases, the mismatch transforms a transition with many intermediates into a nearly two-state transition. One surprising consequence is the existence of a regime where the sensitivity of a mismatch detection assay based on monitoring intermediate states would increase with probe length. Our results provide experimental constraints on how mismatches should be implemented in models of DNA melting, such as the widely used thermodynamic nearest neighbor model, to which we compare our data.

INTRODUCTION

The greater conformational freedom of single strands (ss) compared to double strands (ds) drives the melting transition of DNA, promoting localized strand separation, or the formation of “bubbles” (1–6). Intermediate states in conformational transitions are notoriously difficult to pinpoint experimentally, but recent work has revisited the properties of DNA bubbles, through experiments which took advantage of a new method based on quenched states (7), and theoretical models based on a “reduced degrees of freedom” description (8,9). It was found that internal bubbles have a nucleation size of ∼20 basepairs (bp), whereas there is no nucleation threshold for bubbles opening from the ends of the molecule; correspondingly, the statistical weight of intermediate states decreases for decreasing length L of the molecule, but vanishes only for L ≈ 1 bp (10–12). Mismatches in the base pair sequence reduce the overall stability of the duplex, and indeed standard assays for single nucleotide polymorphism (SNP) detection are based on revealing the temperature shift of the melting curve of the mismatched oligomer with respect to the matched one (13). However, this method uses a global criterion (the melting profile) to detect a local defect. But locally, mismatches affect the nucleation of bubbles, so in principle a better approach would be to focus on the bubble states. Here we show that a single mismatch in a DNA oligomer makes a dramatic difference in the statistical weights of intermediate states, transforming a transition characterized by many intermediates into a nearly two-state transition. Thus even though the midpoint of the transition, T_m, may be little affected by a single mismatch, especially if the probe is long, the amount of intermediates present is drastically different. In principle this observation could form the basis for an improved SNP detection assay (a topic of continued interest (14–18)); however, we have not yet succeeded in developing a practical assay. On the other hand, our measurements unveil an interesting and unexpected regime where the effect of a single mismatch on the melting transition increases with the length of the molecule. These results are consistent with our previous work on bubble nucleation (11), but they represent new findings which, for instance, are not immediately predicted by the widely used thermodynamic models (the nearest neighbor (NN) model (19)) of DNA melting.

MATERIALS AND METHODS

The method by which we monitor bubble formation and measure the statistical weights of the bubble states is based on comparing two different “melting curves” for the same sample. The first is the standard melting curve obtained by monitoring ultraviolet (UV) absorption around 260 nm; properly normalized, this gives the fraction of unpaired bases f in the sample. Actually, the change in UV absorption upon melting is due to both base unpairing and base unstacking, and both phenomena must be included for a complete description of the UV melting curves (20,21). However, the unpairing and unstacking transitions are somewhat separated in temperature (the midpoint of the unstacking transition occurring at higher temperature relative to the unpairing transition), so the UV absorption measurements still express approximately the fraction of unpaired bases f, in the temperature range below the critical temperature T_c for complete strand separation. The second “melting curve” in our method monitors the fraction of molecules p, which have undergone complete strand separation. The fraction p is obtained by a method based on quenched states, which we described previously (7,10,11). Briefly, the oligomers to be studied are designed to be partially self-complementary, so the single strands can form hairpins. First the probe is hybridized to the target (Fig. 1 A). Then the sample is heated to a temperature T within the transition region; at this stage we have in general a mixed population of partially and completely open molecules. Finally the sample is rapidly quenched to ∼0°C. Under the dilute conditions of the experiment, the completely dissociated strands form hairpins (hp), whereas the partially open molecules close again as duplexes (ds). After the quench, we have therefore a mixed population of hairpins and duplexes; the fraction of hairpins represents the fraction of dissociated molecules at the temperature T before the quench, p(T). This fraction is determined by gel electrophoresis from the relative intensities of the hp and ds bands (Fig. 1 B). Under the dilute conditions of the assay, hp + hp → ds recombination after the quench and in the gel is slow enough to allow the measurements in practice: the data confirm that if the heating temperature T before the quench is high enough (so that the sample is entirely dissociated), the measured hp fraction is close to 1.

FIGURE 1.

(A) To obtain the dissociation curve p, we have developed a method based on quenched states of partially self-complementary probes. The probe-target hybrids are heated to an intermediate temperature T_i within the transition range, then quenched to ∼0°C. Strands which were completely dissociated at temperature T_i form hairpins after the quench, whereas molecules which were in partially open (intermediate) states close again as duplexes. The final mixture of hairpins and duplexes is separated by gel electrophoresis. The fraction of hairpins after the quench represents the fraction p of completely dissociated molecules at temperature T_i . (B) Example of a gel (3% agarose), corresponding to L24. The gel runs from right to left. The slow (fast) band corresponds to the duplexes (hairpins). The numbers on the right of the lanes give the temperatures to which the aliquots were heated before quenching. The intensities of the hairpin (hp) and duplex (ds) bands (shown in the density profiles to the right, where the numbers are proportional to the areas under the peaks) are used to calculate the fraction of open molecules p. (C) Two further examples of agarose gels, corresponding to L13 (left) and L40 (right). (D) Example of a polyacrylamide gel, corresponding to L24.

Experiments were carried out as follows: 20 μL aliquots (A_i: i = 1, 2, …, 8) of the sample (target hybridized with the probe) in PCR tubes were heated to the desired temperatures T_i for 3 min in a water bath, then quenched in chilled water. A_i was run on the ith lane of a 3% agarose gel, which was stained with Ethidium Bromide and photographed with a digital camera (Fig. 1 B). While developing this method, we often had a control lane in the gel containing a DNA ladder, to verify that the position of the ds and hp bands were consistent with that expected based on the lengths of the duplex and hairpins (unpublished data). Sometimes we also employed polyacrylamide gels, to get a higher resolution picture. In that case, 10 μL aliquots (A_i: i = 1, 2, …, 15) were used; after quenching, the aliquots were run on a ready-made 15% polyacrylamide gel and then stained with SYBR-Gold.

For all gels, the integrated intensities of the duplex (slow) and hairpin (fast) bands were determined from the digital pictures. In the absence of any recombination after the quench, the fraction of open molecules p at each temperature T_i is given by:

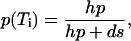(1)

where hp and ds are the intensities of hairpin and duplex bands in the lane i. If the gels show that even at the highest temperature (chosen well above the midpoint of the transition, where we expect p = 1) ds ≠ 0, then some degree of hp + hp → ds recombination has taken place after the quench. We take this into account through the simplest model, where the recombination rate is proportional to the concentration of hairpins squared (two body collisions); this leads to a correction factor γ in the normalization of p (10):

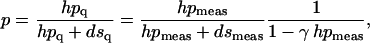(2)

where the subscript q means “quenched” (i.e., the value of the quantity right after the quench), and meas means “measured.” The factor γ is found from the band intensities in the gel, by enforcing p = 1 at high temperature. In the experiments we observe that the ratio hp_meas / (hp_meas + ds_meas) saturates (at a value close to 1) for high enough temperatures; this limiting value is used to compute the factor γ, by enforcing p = 1 in Eq. 2. The same value of γ is then used in Eq. 2 to analyze all lanes of the gel (i.e., the same γ is used for the different temperatures T_i). For example, for the data set of sequences L13 and L24, the ds band completely disappears at the highest temperature points (Fig. 1 C). This gives hp_meas / (hp_meas + ds_meas) = 1 for the highest temperature points, so γ = 0 in this case. However, for sequence L40, hp_meas / (hp_meas + ds_meas) ≈ 0.47 at the highest temperature points which gives 1 / (1 − γ hp_meas) ≈ 2 for those points. In general, longer sequences lead to more recombination and a more important factor γ. Also, there may be differences between agarose and polyacrylamide gels in this respect: for instance γ = 0 for L24 in Fig. 1 b (agarose gel), whereas in Fig. 1 D (polyacrylamide gel) γ is close to, but not exactly, zero as the duplex band does not completely disappear at the highest temperature. Agarose is generally a better medium for these experiments.

With the above analysis, p is extracted assuming that the fluorescent intensity of a band in the gel is proportional to the amount of DNA in the band, with the same proportionality constant for hp and ds bands. We confirm this by noting that the sum of the intensities of the two bands (hp + ds) is the same for all lanes in the gel, even though the relative intensities change according to the different temperatures before the quench. More generally, p can also be extracted in a manner independent of the relation between hp and ds fluorescence, by comparing hp bands (or ds bands) across lanes.

Synthetic DNA oligonucleotides were purchased from Qiagen salt free and were not further purified. In previous (unpublished) experiments we compared the f and p melting curves obtained from salt-free and HPLC-purified oligomers, for two different sequences of lengths 42 and 48. We concluded that there was no significant difference in the measured melting curves between purified and unpurified oligomers. The polyacrylamide gel in Fig. 1 D gives an idea of the typical level of impurities.

In this study we use probes of three different lengths: L13, L24, and L40; probes were hybridized to targets (exact or single mismatch complementaries) in 1:1 ratio at an oligomer concentration of 200 μM, by heating the mixture to 90°C and cooling slowly. UV absorption measurements were performed with a Beckman Coulter DU-640 spectrophotometer with temperature-controlled cell (800-μL samples in standard quartz cuvettes; temperature increase rate was 0.5°C per minute). For the quenching measurements, sample volume was 20 μL in PCR tubes. All experiments were performed at a DNA duplex concentration of 1 μM, in phosphate buffered saline (PBS) at an ionic strength of 50 mM (with 45.7 mM sodium chloride, 1 mM potassium chloride, 3.3 mM phosphate buffer, no Mg²⁺). During annealing, the high concentration of oligomers (200 μM) and the slow cooling process result in a sample in the duplex form. In contrast, in the experiments the low oligomer concentration (1 μM) and the rapid quench process lead to the formation of hairpins from completely open molecules. In all cases both melting curves (f and p) were obtained at the same DNA concentration (1 μM).

After the quench, the sample consists of a mixture of hairpins and duplexes, which we separate by gel electrophoresis. The fraction of hairpins p represents the fraction of completely dissociated molecules at the temperature T_i before the quench, i.e., p is an equilibrium quantity. At temperatures well below T_m, the fraction of completely open molecules is zero, and all the unpaired bases contributing to the UV absorption signal come from the partially open molecules. At temperatures well above T_m, p saturates to 1. We normalize the f curve such that p = 1 coincides with f = 1 (see Fig. 2). Since p = 1 corresponds to the critical temperature T_c of complete strand separation, the rise of f for f > 1 is due to unstacking in the ss (20), whereas for f ≤ 1, f represents approximately the fraction of unpaired bases.

FIGURE 2.

Melting curves for three sets of sequences. (Open symbols) melting curves obtained from UV absorption, representing the fraction of open base pairs f. (Solid symbols) dissociation curves obtained from the quenching method, representing the fraction of completely dissociated molecules p. (Circles) no mismatch; (triangles) one mismatch. (A) L13 (a sequence of length 13 bp) and L13M (the same sequence with one mismatch); (B) L24 and L24M; the two sets of triangles for p-L24M refer to data obtained from the agarose gels (p-L24M1), and the polyacrylamide gel (p-L24M2), for the same sample; (C) L40 and L40M. In all cases, a single mismatch transforms the transition into an essentially two-state process (f = p).

The distance between the two melting curves, σ = f − p, represents the fraction of bases in the bubble states, and thus quantifies the presence of intermediate states. More precisely, σ is the total fraction of bases which are 1), unpaired and 2), not part of a completely dissociated strand (see the relation between f and p below). For a two-state transition, σ = 0, i.e., the two melting curves coincide. If there are bubble states, σ > 0, i.e., p < f. In our previous work (10) we reported measurements of the average fractional length 〈ℓ〉 occupied by bubbles (the average is over the subset of partially open molecules), using the relation f = p + (1 – p) 〈ℓ〉. Keeping the terminology we employed then, here we use the term “bubble” (or “intermediate state”) to denote in general partial separation of the two strands; there are then two kinds of bubbles: bubbles opening “from the ends” and bubbles opening “in the middle.”

The oligomer sequences used in the study are given below. We studied sequences of three different lengths L, with and without a single mismatch. For example, L13 is a completely complementary sequence of length 13 bp, and L13M is the same sequence except with one mismatch (underlined).

• L13: GCCGCCAGGCGGC − 3′

• CGGCGGTCCGCCG − 5′

• L13M: GCCGCCAGGCGGC

• CGGCGGACCGCCG

• L24: TAT TTGCAGCGGCCTGGCCGCTGC

• ATAAACGTCGCCGGACCGGCGACG

• L24M: TAT TTGCAGCGGCCTGGCCGCTGC

• ATAAACGTCGCCGGTCCGGCGACG

• L24C: GCC CGTATTAGTCCTGGCGGCTGC

• CGGGCATAATCAGGACCGCCGACG

• L40: GCCTC CGTCCCGCGGGACGGAGGCAGGCCAAGTGGCGCGG

• CGGAGGCAGGGCGCCCTGCCTCCGT CCGG TTCACCGCGCC

• L40M: GCCTCCGTCCCGCGGGACGGAGGCAGGCCAAGTGGCGCGG

• CGGAGGCAGGGCGCCCTGCCTCCGT CCGC TTCACCGCGCC

RESULTS

We studied DNA oligomers of three different lengths L, for each length analyzing the completely complementary sequence and the same sequence except for the presence of one mismatch. The mismatch is in different positions with respect to the middle of the molecule in the three cases: in this study we do not focus on effects arising from the location of the mismatch. On the contrary, we want to show that the results described below are robust with respect to the position of the defect. In Fig. 2 we display the melting curves: the filled symbols are the p curves, representing the fraction of completely dissociated molecules (obtained from the quenching method), the open symbols are the f curves, representing the fraction of unpaired bases (obtained from the UV absorption measurements). For L13, the presence of the mismatch lowers the midpoint of both melting curves (f and p) by ∼10°C. The transition for L13 is already close to two-state (p ≈ f), and becomes indistinguishable from two-state (p = f) with the mismatch. For L24 and L40, the mismatch has almost no effect on the midpoint of the f curves, but a dramatic effect on the midpoint of the p curves. A single mismatch turns a transition with many intermediate states (p < f) into an almost two-state transition (p ≈ f). The magnitude of the effect is remarkable, especially in the case of the 40mer, where the oligomer length is considerable and the mismatch is not in the middle.

Now suppose we want to detect the mismatch without comparing with the melting curves of the matched oligomer. We can just compare the f and p curves for the oligomer in question: if p ≈ f there is a mismatch, if p ≪ f there is not. The relevant quantity for mismatch detection is then σ = f − p, displayed in Fig. 3. The surprising result is that with this method, the sensitivity to a single mismatch Δσ = σ(mismatch) − σ(match) actually increases with probe length, at least in the regime of lengths from 13 to ∼40 (in comparing L24 and L40, note that for L40 the location of the mismatch is far from the middle, which presumably tends to reduce Δσ).

FIGURE 3.

The parameter σ = f − p, calculated from the curves of Fig. 2 by interpolating between the points for the p-curves and subtracting from the f-curves. σ represents the total fraction of bases in a bubble state. (Solid circles) one mismatch; (open circles) no mismatch. (A) L13 and L13M, (B) L24 and L24M, (C) L40 and L40M.

DISCUSSION

A single mismatch introduces a localized defect in the double helix structure; the ideal detection method should therefore be sensitive to the local conformation. Here we study how the presence of the mismatch affects the typical duplex conformation at different temperatures. We find that the probe oligomer melts away from the target strand essentially in a two-state transition, instead of melting by gradually unzipping from the ends. The reason for this is not obvious. Qualitatively, we may argue that the defect introduces two “extra ends” in the middle of the molecule, which becomes effectively shorter, and melts through a transition which is closer to two-state. However, we could also reason that the defect lowers the barrier for bubble formation, and so should promote intermediate states. To make progress, we need to understand the effect of a mismatch on the local pairing, stacking, and elastic energies in the duplex. This interesting question is probably best explored through a combination of experiments and statistical mechanics models (12).

To be able to measure the dissociation curves p, we use sequences which are partially self-complementary. The question then arises whether the results obtained reflect the “special” nature of these sequences. In particular, one may ask whether the hairpin melting transition influences the behavior of the measured duplex melting curves f. We have examined this question, first by comparing the melting curves measured by UV absorption for the duplex and the hairpin (Fig. 4). The hairpin melts at lower temperature compared to the duplex (which is the reason why by careful annealing we can prepare ds samples predominantly in the duplex state, as shown by the gels in Fig. 1); the midpoints of the two transitions being separated by ∼5 and ∼10°C for the 24mer and the 40mer, respectively. At the midpoint of the duplex transition, the hairpins are ∼80% melted in both cases. Thus we expect the influence of the hairpins on the duplex f curves to be small. We have confirmed this by comparing the duplex melting curves (f) for L24 and a control L24C, the sequence of which is a permutation of the sequence of L24, such that there is no self-complementarity. As seen in Fig. 5, the two melting curves are identical in the region f ≤ 1, which is the region in question for this study. The marked difference in the two melting curves for f > 1 is, we believe, an interesting phenomenon which we may address in future work; however, it is immaterial to the conclusions of this study.

FIGURE 4.

Comparison of the normalized (UV absorption) melting curves f for the ds sample (reporting on the melting of the duplex) and the ss sample (reporting on the melting of the hairpin). The concentrations are such that in both samples there is the same weight of DNA (the ds sample is at 1 μM, the ss sample at 2 μM). (A) L24; the midpoint of the transition is ∼5°C lower for the hairpins (triangles); (B) L40; the midpoint of the transition is ∼10°C lower for the hairpins.

FIGURE 5.

Comparison of the normalized (UV absorption) melting curves f for L24 and the control oligomer L24C. The sequence of L24C is a permutation of the sequence of L24, with no significant self-complementarity.

The method presented here measures intermediate states, so it is sensitive to the defect driven formation of bubbles. In contrast, present SNP detection methods, based on the signal from a FRET pair on adjacent probes (see e.g., LightCycler Products from Roche Molecular Diagnostics), are sensitive to the conformation at the site of the fluorescent probes, which can be far away from the mismatch and the bubble. The present technique detects bubble nucleation driven by the defect, irrespective of the position of the defect. The dissociation curves p with and without mismatch are significantly different in all cases, whereas this is not true for the melting curves f (Fig. 6). The quantity Δp (difference of the dissociation curves with and without mismatches), displayed in Fig. 6 for the three cases, shows that the method can detect the presence of the mismatch irrespective of the location of the mismatch and length of the probe, within the range of defect location and probe lengths studied. A surprising property of the method is that, by the measure of σ, the ability to detect a single mismatch increases with probe length, at least in the regime 13 < L < 40.

FIGURE 6.

The difference in the melting curve with and without mismatch, for the two different measurements Δf and Δp, shown for the three sets of sequences: (A) L13 and L13M, (B) L24 and L24M, (C) L40 and L40M. The filled circles represent Δf, difference of the UV melting curves with and without mismatches. The open circles represent Δp, difference of the dissociation curves with and without mismatches. The curves are interpolated from the experimental data.

In summary, we find that for probes of length ∼20 bases and up the more discriminating measurement for mismatch detection is the complete strand dissociation curve p, not the usual melting curve f. This is visually rendered in Fig. 6, where we plot the difference in the melting curve with and without mismatch, for the two different measurements, Δf and Δp. Our results also explain the reason for the steepness of the melting curves obtained spectroscopically from DNA-gold aggregates (14), as those are essentially p curves (the spectroscopic signal is sensitive to the melting of the aggregate, i.e., the complete strand separation of the DNA linkers), which are steeper than the corresponding f curves (see Fig. 2), for lengths of order 20 and up (i.e., in the presence of significant amounts of intermediates).

Apart from the possible technological relevance, the results above represent new findings in the study of the DNA melting transition. Our measurements reveal the drastic effect that a single mismatch has on bubble nucleation, and thus the nature of the melting transition. In contrast, present thermodynamic models do not describe this aspect well. Specifically, these experimental results are not well reproduced by an off-the-shelf application of the NN model. We investigated this point by obtaining the melting curves (f and p) for our 24mer and 40mer sequences, from the two strands hybridization web server (19), which is based on the NN model (22) and also takes into account hairpins (as sequence L13 is exactly symmetric, we cannot directly use the server in this case). The p curve is calculated from the duplex concentration curve.

Comparing Fig. 7 A (the server) with Fig. 2 B (the experiment), we see that the server does not predict the drastic difference in the occurrence of intermediate (bubble) states between the matched and mismatched sequences. Although the f-curve for the matched case (f-L24) is correctly predicted, the p-curve is not. In the mismatch case, both melting curves (f and p) do not agree with the experiments. Similar differences are evident when comparing Fig. 7 B to Fig. 2 C. In general, the server predicts p-curves which are softer than the experimental curves, although this may be a consequence of the strand dissociation entropy term used by the server, which is extracted from data at 1 M salt.

FIGURE 7.

Melting curves f and p, obtained from the hybridization web server (19) for the two sets of sequences: (A) L24 and L24M, (B) L40 and L40M. The server is based on the NN model and takes into account hairpin formation. Symbols are the same as in Fig. 2.

In conclusion, the experimental measurements could be used to refine the models' parameters and improve the accuracy of the server, which is a most useful tool for designing sequences for experiments with DNA.