The Effect of Salt on Self-Assembled Actin-Lysozyme Complexes

Abstract

We present a combined experimental and computational study of the bundling of F-actin filaments induced by lysozyme proteins. Synchrotron small-angle x-ray scattering results show that these bundles consist of close-packed columnar complexes in which the actin is held together by incommensurate, one-dimensional arrays of lysozyme macroions. Molecular dynamics simulations of a coarse-grained model confirm the arrangement of the lysozyme and the stability of this structure. In addition, we find that these complexes remain stable even in the presence of significant concentrations of monovalent salt. The simulations show that this arises from partitioning of the salt between the aqueous and the condensed phases. The osmotic pressure resulting from the excess concentration of the salt in the aqueous phase balances the osmotic pressure increase in the bundle. These results are relevant for a variety of biological and biomedical problems in which electrostatic complexation between anionic polyelectrolytes and cationic globular proteins takes place, such as the pathological self-assembly of endogenous antibiotic polypeptides and inflammatory polymers in cystic fibrosis.

INTRODUCTION

In the presence of multivalent counterions, highly charged, stiff polyelectrolytes, including double-stranded DNA (1), filamentous actin (2), and the fd virus (3), exhibit a tendency to form bundles. This phenomenon, which cannot be explained within the framework of mean-field approaches such as the Poisson-Boltzmann theory (4,5), has attracted widespread experimental and theoretical attention (6–8). It is the purpose of this work to extend these investigations to situations in which the role of the multivalent ions is taken over by significantly larger charged species. In this case, excluded-volume interactions become more prominent and the occurrence of polyelectrolyte-macroion complexation is governed by the interplay between these short-range potentials and the electrostatic interactions. Such complexes are found in a variety of biological systems, including DNA-dendrimer complexes for nonviral gene therapy (9) and antimicrobial binding in cystic fibrosis (10).

Specifically, we investigate the electrostatic complexation of F-actin with lysozyme, which can be viewed as a prototypical system of oppositely charged “rod-like” and “sphere-like” objects, with charge distributions and dimensions that are well-known from molecular biology (11). By means of small-angle x-ray scattering (SAXS), we demonstrate that the actin filaments are arranged on a close-packed lattice and that the lysozyme occupies the voids between the filaments. From the peaks in the scattering intensity we infer a specific arrangement. By means of complementary molecular dynamics (MD) simulations of a coarse-grained but accurate model system we demonstrate that this arrangement indeed yields the most stable structure. In addition, the x-ray measurements indicate that the lysozyme molecules are aligned in a regular manner along the actin filaments, in a way that is incommensurate with the actin charge distribution. We show that a similar arrangement arises in the simulation of our model system. To investigate the structure and stability of this complex under physiological conditions, we systematically vary the bulk concentration of monovalent salt. Surprisingly, the actin-lysozyme complexes retain their stability up to considerably higher salt concentrations than would be expected from conventional arguments based on counterion release or differential screening. Using simulations to determine salt partitioning between the aqueous and the condensed phases, we explain the observed trends from the osmotic pressure exerted by the aqueous phase.

In cystic fibrosis, the accumulation of viscous mucus in pulmonary airways is the primary cause of long-term bacterial infections, respiratory failure, and eventually death. One of the contributing causes to these long-term infections is the pathological self-assembly of endogenous antibiotic polypeptides from the immune system by adventitious anionic polyelectrolytes, such as F-actin and DNA, which are released by lysed neutrophils during the inflammatory response to airway infections (12). The interactions responsible for this self-assembly are largely electrostatic, since such antibacterial globular proteins are usually cationic (e.g., lysozyme, β-defensin, and lactoferrin). More important, this self-assembly process results in the loss of antimicrobial function in the airways. We examine the actin-lysozyme complexes as a prototypical system, and aim at a fundamental understanding of antibacterial binding in the airways.

A brief account of this work has been presented in Sanders et al. (13). Here we provide a detailed discussion of our computational and experimental approach, as well as a considerably more detailed analysis of the simulation results.

METHODOLOGY

Experimental methods

Monomeric actin (G-actin) (molecular weight (MW) 43,000) is prepared from a lyophilized powder of rabbit skeletal muscle (Cytoskeleton, Denver, CO). The nonpolymerizing G-actin solution contains a 5-mM Tris buffer at pH 8.0, with 0.2 mM CaCl₂, 0.5 mM ATP, 0.2 mM dithiothreitol, and 0.01% NaN₃. G-actin (2 mg/ml) is polymerized into F-actin (linear charge density λ_A ≈ 1e/2.5 Å at pH 7.0) by the addition of monovalent salt (100 mM KCl final concentration). Human plasma gelsolin, an actin severing and capping protein (14) (Cytoskeleton), is added at a gelsolin:actin monomer molar ratio of 1:370 to restrict the length of the F-actin polymers to ∼1 μm. The filaments are treated with phalloidin (MW 789.2, Sigma Aldrich, St. Louis, MO) to prevent actin depolymerization. F-actin gels are ultracentrifuged at 100,000 g for 1 h to pellet the filaments. After the removal of the supernatant buffer solution, the F-actin is resuspended in ultrapure H₂O (18.2 MΩ; Millipore, Billerica, MA).

Lyophilized hen egg white lysozyme (MW 14,300; Sigma Aldrich) is dissolved in ultrapure H₂O and allowed to equilibrate overnight. Stock solutions of NaCl and KCl are prepared by mixing in ultrapure H₂O. To ensure uniform mixing and to decrease error associated with pipetting small volumes, lysozyme is premixed with monovalent salt solutions in 500-μl aliquots. The isoelectric complexes are prepared by flame sealing F-actin with lysozyme-monovalent salt solutions in 1.5-mm quartz capillaries (Hilgenberg, Malsfeld, Germany) and mixing thoroughly by centrifugation. The approximate sample volume in the capillary is 30 μl. The final F-actin concentration is 5.5 mg/ml and the final lysozyme concentration is 2.3 mg/ml. A series of samples are prepared, with the final monovalent salt concentration ranging from 0 to 500 mM.

SAXS measurements are performed using the in-house x-ray source located in the Frederick Seitz Materials Research Laboratory (Urbana, IL), beamline 4-2 at the Stanford Synchrotron Radiation Laboratory (SSRL, Palo Alto, CA), and BESSRC CAT beamline 12-ID-C at the Advanced Photon Source (APS, Argonne National Laboratory, Argonne, IL). For the in-house experiments, incident Cu Kα radiation (λ = 1.54 Å) from a Rigaku (The Woodlands, TX) rotating-anode generator is monochromatized and focused using Osmic (Auborn Hills, MN) confocal multilayer optics, and scattered radiation is collected on a Bruker AXS (Madison, WI) 2D wire detector (pixel size 105 × 105 μm²). For the SSRL experiments, incident synchrotron x-rays from the eight-pole wiggler are monochromatized to 8.98 keV using a double-bounce Si(111) crystal (λ = 1.3806 Å) and focused using a cylindrical mirror. The scattered radiation is collected using a MAR Research (Evanston, IL) charge-coupled device camera (pixel size 79 × 79 μm²). For the APS experiments, incident x-ray wavelength is set at λ = 1.033 Å by a double-crystal Si(111) monochromator and focused using a flat-focusing monochromatic mirror. The scattered x-rays are collected using a two-dimensional mosaic CCD detector (pixel size 79 × 79 μm², MAR Research). The sample-to-detector distances are set such that the detecting range is 0.03 < q < 0.25 Å⁻¹, where q = (4π sin θ)/λ, λ is the wavelength of the incident beam, and 2θ is the scattering angle. The 2D SAXS data from all set-ups have been checked for mutual consistency.

Typically, the precipitated F-actin-lysozyme complex is compacted into a dense pellet during mixing. These pellets consist of many coexisting domains of actin bundles locally oriented along different random directions, as indicated by the “powder averaging” of the diffraction pattern and the associated loss of orientational information. To minimize these effects, a small (300 × 300 μm²) x-ray beam is used to obtain diffraction information on locally aligned domains within the pellet.

Simulation model

To study the structure and stability of the actin-lysozyme complex we perform MD simulations of the complex in the microcanonical ensemble, using a modified version of the Moldy package (15). We also carry out grand-canonical Monte Carlo simulations of monovalent salt to complement the MD results, as described in the following section. In both cases, electrostatic interactions are treated by means of the Ewald summation (16), and excluded-volume interactions are represented by a steep repulsive pair potential of the form k_BT(σ/r)¹², where k_B is Boltzmann's constant, T the absolute temperature, and r the center-to-center distance between two particles. We define the effective radii of particles such that at contact the excluded-volume interaction pair energy is k_BT. Thus, σ is the sum of the effective radii of the two interacting particles. Both the excluded-volume potential and the real-space term of the Ewald sum have a cutoff distance chosen to optimize the Ewald technique as described in (16). Water is treated implicitly as a continuum with dielectric constant ɛ_r = 80. Polarization effects resulting from a different dielectric constant of the solute are not taken into account.

To carry out efficient simulations of actin-lysozyme complexes, we avoid a computationally expensive all-atom representation and adopt instead a simplified model which nevertheless faithfully reproduces the excluded-volume interactions and charge distributions of the molecules involved. In this model, salt ions are treated as spherical particles with a hydrated radius of 3.3 Å (17). We only consider the effect of monovalent salt in this study. The lysozyme protein is represented in a coarse-grained fashion as a rigid dumbbell consisting of two overlapping spheres with diameter 25 Å and charge +4.5e. The lysozyme mass was chosen to be 143 times the salt ion mass. The spheres have a center-to-center distance of 20 Å, so that the dumbbell structure approximates the known dimensions of lysozyme, which has an ellipsoidal shape of 26 × 26 × 45 Å. This shape becomes important at high densities where it can strongly influence the packing properties, and such high densities may indeed arise due to localization of the lysozyme within the bundle. Although the net charge of lysozyme (+9e at neutral pH) arises from a combination of positive and negative charges, the choice of equal charge on both spheres is reasonable, given the relatively homogeneous charge distribution obtained when the electrostatic potential around this molecule is computed (18).

A similar coarse-grained approach is used in the treatment of actin. The structure of the G-actin monomer has been determined to atomic resolution (19). Holmes et al. (20) exploited the known monomer structure to develop an atomic model for F-actin, where the arrangement of monomers along the filament was iteratively improved by fitting computed intensities to experimental x-ray diffraction data from highly aligned F-actin gels. Crystallographic measurements of G-actin indicate that it can be naturally decomposed into four subdomains (19), which can be accurately represented by spheres (21). Thus, a sequence of such four-sphere units can be fitted to the atomic model for F-actin, in a way that reliably captures the F-actin structure (22). The charge on each sphere is obtained by summing the charges of all the atoms within the Voronoi cell containing the sphere center, which gives charges of −6.75e, −6.05e, +0.59e, and + 2.06e, respectively. This leads to a filament with net negative charge, although positively charged domains do occur. In the F-actin model that we use in our simulations, successive monomers are separated along the filament axis by a distance of 27.5 Å, and are rotated with respect to each other by 166.7° about this axis. Thus, over a repeat unit of 13 monomers the filament undergoes six full turns.

The actin filaments are assembled into a parallel, hexagonally coordinated bundle. This is accomplished by using an elementary simulation cell in the shape of a prism in which two opposite faces are 60–120 rhombuses. A 2 × 2 regularly spaced array of parallel filaments with a length of six repeat units (78 monomers per filament) is placed in the simulation cell, which is replicated under periodic boundary conditions (see Fig. 1). The periodicity of the array may introduce finite-size effects. To minimize these effects, we have chosen the largest simulation cell that is feasible for our computational resources. During each simulation, the actin molecules are held rigid at a fixed separation, effectively ignoring their rotational degrees of freedom. This is justified by the observation that the largest actin separation we consider is 25 nm, which is <0.25% of the persistence length (∼10 μm). Mutual sliding, axial rotations, and changes in the helical symmetry of the actin filaments are also not considered. Because lysozyme is highly charged, and because it has a much lower mobility than the salt ions, we expect it to be closely associated with the actin, and thus it is reasonable to assume that all of the lysozyme resides in the bundled phase. Since in the experiments the actin-lysozyme complexes are isoelectric, we set the concentration of lysozyme in the complex to satisfy the electroneutrality condition. This leads to 352 lysozyme molecules in the simulation cell. For systems with added salt, the number of salt ions is computed from the desired concentration, and ranges up to 8770 for the largest system reported here. Simulations are carried out for systems with salt concentrations (within the bundle) of 0, 5, 10, 15, 25, 40, and 50 mM, at actin-actin separations ranging from 99 Å to 250 Å. Every MD simulation run has an initial equilibration stage in which the temperature is rescaled at every step to T = 298 K. The duration of this initial stage varies, depending on the number of ions in the simulation, from 100,000 to 600,000 time steps. The time step is 0.01113 t₀, with the time scale t₀ = (k_BTm⁻¹ℓ⁻²)^−1/2, where m is the mass of a salt ion and ℓ = 1 Å is the length scale. The duration of the production run also varies—ranging from 300,000 to 3 million time steps—so as to produce good statistics for every system size. Furthermore, to obtain better statistics and further reduce finite-size effects when performing structural measurements, some runs are carried out with a simulation cell that is twice as long, containing 12 repeat units (156 monomers per filament).

FIGURE 1.

Schematic illustration of the actin arrangement in the simulations. Each disk represents the cross section of a single filament. The actual simulation cell (shaded) contains 2 × 2 filaments, and is replicated periodically to create a hexagonal packing. Each filament is represented by a coarse-grained model that mimics the actual shape and charge distribution of F-actin. In the direction along the filaments (out of the plane), the simulation cell is repeated periodically after 78 monomers, which corresponds to six full actin repeat units.

The grand-canonical Monte Carlo simulations used to determine the osmotic pressure of aqueous salt solutions at fixed chemical potential (see the following section) involve solutions of monovalent salt, at a variety of chemical potentials. Adopting a convention similar to the approach of Valleau and Cohen (23), we introduce a shifted chemical potential,

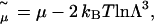(1)

where μ is the chemical potential that appears in the grand partition function and 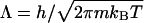is the thermal de Broglie wavelength. The factor 2 in Eq. 1 arises because the chemical potential pertains to a salt molecule. In our simulations, 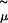ranges from −26.15 k_BT to −19.13 k_BT. All trial moves consist of insertions or deletions of a neutral pair of ions. The volume of the system is fixed, and average concentrations in the range 4–120 mM are obtained, corresponding to a range of 200–5000 ions in the system. The simulations have an initial equilibration period of 2 million trial moves and a subsequent production run length of 20 million moves.

Determination of osmotic pressure

The stability of an actin bundle is determined by mechanical equilibrium, which implies that the pressure is equal in the aqueous and bundled phases. To obtain the pressure P from simulations we apply the virial theorem, which gives the virial tensor as (24)

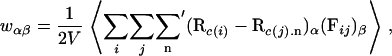(2)

where i and j index the N atomic sites of the system, c(i) gives the index of the molecule to which i belongs, n denotes a vector pointing from the central cell to a periodic copy, α and β are tensor indices, w is the virial tensor, V is the volume of the system, R_k.n is the position of the periodic copy of molecule k reached by n, and F_ij is the force exerted by site i on site j. The prime indicates omission of terms with c(i) = c(j) if n = 0. Thus, intramolecular forces (including forces that arise from the rigid molecule constraints) are never computed when evaluating the virial.

The pressure is usually obtained as one-third of the trace of the virial tensor, plus a kinetic contribution ρk_BT, where ρ is the overall density. However, since our model only allows expansion and contraction in the lateral plane, i.e., perpendicular to the bundle axis, we employ only the corresponding lateral components of the stress tensor when computing the pressure. The actin filaments are held fixed during the simulation, so they do not contribute to the kinetic term in the pressure. Moreover, the forces exerted by the actin filaments on each other do not affect the evolution of the system and need not be computed during the simulation, but they do contribute to the virial. This contribution, involving the lateral components of the forces between particles on different filaments, is computed separately and later added to the virial. Because the MD simulations employ the microcanonical ensemble, the average temperature of the runs will drift slightly despite the initial equilibration period. On average the temperature drift ΔT was 2.4 K, and the largest value we observed was ΔT = 9.5 K. To compare results from different simulation runs, we add a correction term of the form (∂P/∂T)_VΔT to the pressure, where the thermal pressure coefficient (∂P/∂T)_V is computed as described in (25,26).

We adopt the convention of considering water a solvent and actin and lysozyme solutes, to define the osmotic pressure Π of the complex. Within the continuum approximation, the effect of water on solute-solute interactions is accounted for via the relative electric permittivity ɛ_r. Thus, the pressure we obtain via the virial theorem corresponds directly to the osmotic pressure Π of the solutes (27). We assume that the concentration of actin and lysozyme in the aqueous phase is negligible, so that in the absence of salt the actin-lysozyme complex is surrounded simply by bulk water. In this case, no osmotic pressure is exerted by the aqueous phase and mechanical equilibrium demands that the osmotic pressure of the bundled phase also equal zero. Indeed, recalling the thermodynamic definition of pressure,

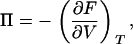(3)

we see that the criterion for stability is Π = 0 and ∂Π/∂V < 0, which describes a minimum in the free energy F. A similar approach has been used earlier to study the stability of bundles of rod-like polyelectrolytes condensed via counterions (see Lyubartsev et al. (3) and Deserno et al. (28)). Equation 3 is not affected by our use of the microcanonical ensemble, since for each run the pressure is obtained at the same temperature.

One noteworthy point is that all our simulations apply to a bundle in excess water, i.e., there is no external solvent pressure acting on the complex. This is different from, e.g., a lamellar phase with fixed water content (29), where the external pressure can permit coexistence of two phases (to be located via a Maxwell construction) that both have a positive pressure. Unlike what is claimed by Deserno et al. (28), this does not apply to a bulk phase of charged polyelectrolytes, which will permit solvent exchange and thus does not have a fixed water content. However, it would be possible to exert an external pressure by means of an additional component that is unable to penetrate the bundle, such as the polyethylene glycol that was used to condense DNA by Lerman (30) and Rau et al. (31).

The relation between the pressure obtained from our simulations and the osmotic pressure of the solutes in the presence of water is an identity, limited only by the approximations arising from our implicit model for water. Such an identity would not hold if in our simulations we modeled the water explicitly, since the virial would contain contributions involving explicit interactions with water molecules. One way to obtain the osmotic pressure Π in this case would be to determine the total pressure of both the aqueous and the bundled phases, and then subtract the former from the latter.

These considerations become important in the presence of salt, which generally will distribute unevenly between the two coexisting phases. Since we model the salt explicitly, there is now an osmotic pressure Π_salt exerted by salt in the aqueous phase and the osmotic pressure of the bundle is the difference of the pressure P_sim obtained from simulation and the external osmotic pressure arising from the salt (32). The osmotic pressure in the aqueous phase can be obtained by means of simulations that treat the salt molecules grand-canonically, so that the bundle is brought into equilibrium with a salt reservoir at a given chemical potential μ_salt (33). Here, however, we have adopted a different strategy. For a given concentration of salt in the bundle—which we simulate via molecular dynamics—we apply the Widom particle-insertion method (16) to determine μ_salt. Since our MD simulations are carried out in the microcanonical ensemble, we must account for temperature fluctuations when computing the excess chemical potential 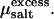The proper average to collect is

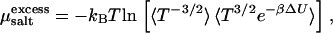(4)

where ΔU is the change in energy resulting from the insertion of a pair of monovalent particles with opposite charges (34,35) and β = (k_BT)⁻¹. The salt chemical potential then follows from 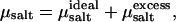where 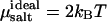ln ρ_salt + 2 k_BT ln Λ³, with ρ_salt the average number density of the salt. The shifted chemical potential (cf. Eq. 1) of the salt in the condensed phase is thus given by 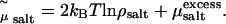By performing grand-canonical Monte Carlo simulations of bulk salt at 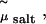we obtain the concentration of salt in the aqueous phase and the corresponding pressure Π_salt. This yields the osmotic pressure Π = P_sim – Π_salt and we can apply the same criterion as before to study the stability of the actin-lysozyme complex with added salt.

RESULTS AND DISCUSSION

Experimental

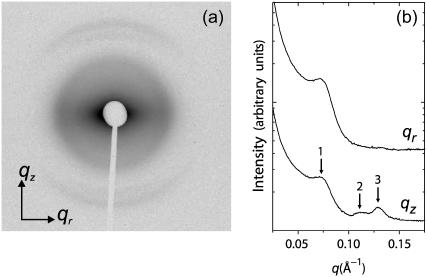
A representative 2D diffraction pattern for partially aligned isoelectric actin-lysozyme bundles is shown in Fig. 2 a. The actin rods are aligned along the q_z axis and are powder-averaged in the plane perpendicular to the q_z axis. The software program FIT2D (36) is used for the analysis of the 2D SAXS patterns. Traces along q_r and q_z (Fig. 2 b) are produced by integrating the 2D SAXS image over 45° wedges in χ, centered about the q_r and q_z axes, where q_r = q cos χ, q_z = q sin χ. An examination of the slice along the equatorial (q_r) direction shows the actin-actin close-packed bundling peak at q = 0.07 Å⁻¹. This peak corresponds to a nominal inter-actin spacing of ∼90 Å and can be compared with the ∼75 Å inter-actin spacing of close-packed actin measured in actin bundles condensed by small divalent ions (37) as well as in actin-cationic membrane complexes (38). (We observe one diffraction peak from the in-plane ordering of actin, so it is not strictly possible to assign a unique surface unit cell to it. The value of the inter-actin spacing depends on the precise form of the unit cell. For example, if we assume that the actin is organized into a hexagonal lattice, then this observed peak would correspond to the q₁₀ diffraction for a columnar lattice, with a lattice parameter 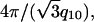and the inter-actin spacing would be ∼15% larger than this value, or 104 Å.) Approximating lysozyme as an ellipsoid with the above-mentioned dimensions of 25 Å and 45 Å along its minor and major axes, respectively, we can see that the actin spacing of 90 Å is quantitatively consistent with a columnar actin lattice uniformly expanded by lysozyme in threefold interstitial sites, aligned with its long axis parallel to the actin rods. The expanded spacing is necessary to accommodate the lateral dimensions of the lysozyme. Along the meridional (q_z) axis, a weak actin form factor peak at 0.113 Å⁻¹ can be observed. The most interesting feature along q_z, however, is the strong correlation peak appearing at 0.130 Å⁻¹. This peak cannot be generated by the actin helix, or by any conceivable deformation of the actin helix. This peak is observed only in actin condensed with lysozyme and corresponds to a distance of ∼48 Å, which is essentially the length of lysozyme along its major axis from crystallographic data (39). This is consistent with the data along q_r and is strong additional evidence for a self-assembled actin-lysozyme structure in which lysozyme is close-packed along the long axis of the actin bundles. Schematic representations (40) of a condensed actin and lysozyme bundle are shown in Fig. 3.

FIGURE 2.

(a) Synchrotron 2D x-ray diffraction pattern of partially aligned actin-lysozyme bundles, formed in a solution containing 150 mM NaCl. (b) One-dimensional integrated slices along the q_z and q_r directions with arrows marking the actin-actin close-packed bundling peak (1), the actin helix form factor (2), and the lysozyme-lysozyme correlation peak (3).

FIGURE 3.

Proposed structure of actin-lysozyme composite bundles (end and side views). Lysozyme is close-packed in threefold symmetric sites between actin filaments. The representations are low-resolution density maps.

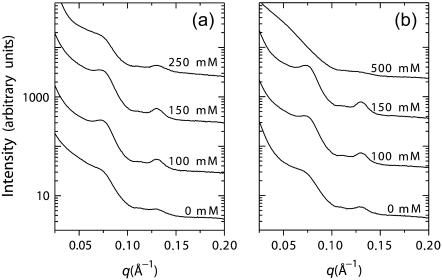
A series of SAXS measurements are performed on actin-lysozyme complexes at increasing monovalent ion concentrations. An increase in the intensity of the actin-actin bundling peak is observed with increasing [KCl] up to ∼150 mM (Fig. 4 a). At higher monovalent salt concentrations, the trend reverses, and a weakening of the close-packed bundling peak is observed. The same results are seen using NaCl (Fig. 4 b), which indicates that this is not a cation-specific binding effect. Whereas the destabilization of the complexes at high salt concentrations is not surprising, the salt levels up to which they retain their stability is unexpectedly high. A number of explanations can be suggested for this counterintuitive behavior. It is possible that the actin-actin and lysozyme-lysozyme repulsions are screened faster than the lysozyme-actin attractions with increasing salt concentrations, due to the shape asymmetry between actin rods and lysozyme spheroids (41). This argument is cognate with the well-known arguments from the body of literature on polyampholytic protein adsorption on polyelectrolytes, which suggest that salt can enhance binding between oppositely charged macroions by screening out the repulsive interactions between like charges on the protein and on the polyelectrolyte, without significantly affecting attractive “contact” interactions (18,42–44). Furthermore, since actin and lysozyme have similar surface charge densities, entropic effects from counterion release upon binding may be especially important. The applicability of all of these arguments, however, depends strongly on the salt concentration around the actin and lysozyme. Thus, it becomes essential to establish how salt is partitioned between the bundle and the surrounding bulk.

FIGURE 4.

Series of diffraction data showing the evolution of bundle structure as a function of (a) KCl and (b) NaCl, with maximum bundling seen at ∼150 mM.

Simulation results

Bundle stability

In Fig. 5, we show the osmotic pressure of the bundled phase as a function of actin-actin separation L, for a salt-free system. The curve is nonmonotonic, crossing zero at L ≈ 100 Å and asymptotically approaching zero as the separation increases. This asymptotic behavior arises because the system approaches infinite dilution in the limit of large L. At small separations the osmotic pressure rises abruptly, because the system is nearly close-packed in the lateral plane and repulsive excluded-volume interactions dominate. In view of the coarse-grained model adopted here, the predicted stable actin-actin separation agrees quite well with the value of ≈90 Å obtained from the experiments. We can compute the difference in Helmholtz free energy per actin repeat unit, f, between two systems at different separations, by numerically integrating Eq. 3,

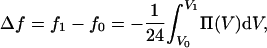(5)

where V₀ and V₁ are the initial and final volumes of the simulation cell, which are set by our choice of L, and the factor 1/24 comes from the number of actin repeat units inside a simulation cell. The inset of Fig. 5 shows the result of performing this integration, with f₀ corresponding to a separation of L = 99 Å. From this curve we see that the depth of the free energy minimum is ∼28 k_BT per actin repeat unit, indicating that once the bundle has formed it is very unlikely to dissolve again.

FIGURE 5.

Osmotic pressure Π of a hexagonally coordinated bundle of actin filaments and lysozyme proteins in excess (salt-free) solution, as determined from MD simulations. Negative pressure implies a contracting bundle, whereas Π = 0 corresponds to a stable bundle. The zero crossing at a separation near 100 Å is comparable to the experimental result of 90 Å (cf. Fig. 3). The inset shows the variation of the free energy per actin repeat unit upon increase of the actin separation in the bundle. For further discussion, see the text.

In the presence of salt, the determination of bundle stability becomes somewhat more involved. As described above, in “Determination of osmotic pressure”, we perform MD simulations at fixed salt concentration in the bundle, c_bundle. Thus, to determine coexistence, the bundle pressure P_sim must be balanced by the corresponding osmotic pressure of salt Π_salt in the aqueous phase. The appropriate bulk salt concentration follows from the condition for chemical equilibrium, 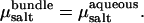Accordingly, for a given value of c_bundle, we determine P_sim(L) and 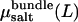as a function of actin separation L. Comparison to the bulk pressure Π_salt obtained from grand-canonical simulations at chemical potential 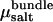yields a unique zero crossing,

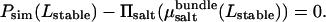(6)

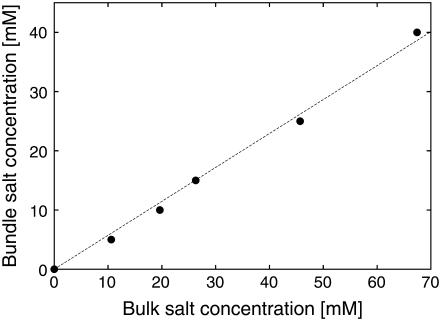
This condition determines the stable separation L_stable, the corresponding salt chemical potential, and hence the concentration in the aqueous phase. We find that the stability criterion can be satisfied for bundle salt concentrations up to 40 mM, corresponding to bulk salt concentrations of 67 mM. Fig. 6 summarizes the results for all values of c_bundle, illustrating that there is a significant partitioning of salt between the bundled and aqueous phases: The concentration in the bundle is systematically suppressed to approximately half the bulk salt concentration. Since the osmotic pressure of the bundle rises more rapidly as a function of salt concentration than the pressure of an aqueous solution at the same concentration, the salt partitioning contributes in an essential manner to the bundle stability, allowing the osmotic pressure Π_salt to balance the bundle pressure P_sim as salt concentration increases. Evidently, the exclusion of salt from the bundle is in turn driven by a complex interplay of entropic effects and electrostatic interactions. For c_bundle = 50 mM, the stability criterion can no longer be satisfied, causing the bundle to disintegrate if the bulk salt concentration is raised above ∼70 mM. This value is lower than the maximum stable concentration found in the experiments. Whereas there are many inherent approximations in the simulation model that may be invoked to explain this discrepancy, there is one particular trend that ultimately destabilizes the bundles in the simulations, but is not observed in the experiments. Namely, for the points shown in Fig. 6 we find that the stable actin-actin separation increases slightly as a function of salt concentration, ranging from L_stable ≈ 100 Å to L_stable ≈ 116 Å for the range of salt concentrations shown. Although all values in this range are relatively close to the experimental result, the steady rise of L_stable disagrees with the SAXS data, which show an essentially constant peak position with increasing salt concentration (Fig. 4). Possibly, the swelling in the simulations occurs because of the lack of atomistic detail in the excluded-volume envelope of actin or because actin degrees of freedom have been ignored. Such degrees of freedom might allow the experimental bundles to accommodate more salt without the swelling that is observed in simulations. On the other hand, at sufficiently large salt concentrations, swelling would also be expected in the experimental system, although possibly only over a very narrow concentration range before destabilization. Certainly, the increase of the average actin-lysozyme separation in the swollen bundle diminishes the attractive electrostatic contribution to the osmotic pressure, rendering the complex unstable. Despite these differences, we consider our observation of salt partitioning as a confirmation and explanation of the experimental results and a central finding of the simulations presented here. In fact, owing to the swelling of the complexes, the simulations presumably overestimate the salt concentration within the bundle, since an increased bundle separation decreases the relative volume occupied by the actin and lysozyme. The mechanism identified here should affect the stability of a variety of self-assembled complexes that are driven by electrostatic interactions, especially those involving oppositely charged macroions with charge densities of similar magnitude, where the tendency toward counterion release is large.

FIGURE 6.

Equilibrium distribution of salt between bundled and bulk phases, obtained from simulations via the procedure described in sections entitled “Determination of osmotic pressure” and “Simulation results”. The plot shows that in a stable actin-lysozyme complex the salt concentration is approximately half the bulk concentration. Error bars are of the order of the symbol size and the dotted line is a guide to the eye.

Lysozyme distribution

The model we have established for actin-lysozyme complexes also permits the study of structural properties, such as the distribution of salt ions and lysozyme molecules within the complex. Such information can provide the basis for further comparison to experiment and may yield insight into the relative importance of competing energetic and entropic effects.

In Fig. 7 we show plots of the lateral lysozyme distribution for a system without added salt. These plots are generated by projecting the center of mass of each lysozyme molecule onto a plane perpendicular to the bundle axis, and averaging over the duration of the simulation run. Fig. 7 a corresponds to a bundle at the equilibrium actin-actin separation L_stable ≈ 100 Å. The lysozyme clearly has a pronounced tendency to occupy the threefold interstitial sites of the hexagonal actin lattice, corroborating our interpretation of the SAXS data in Fig. 2. Interestingly, there is also a slightly enhanced lysozyme concentration in the twofold bridging sites between pairs of neighboring filaments. This observation is remarkable since, at this separation, the excluded-volume repulsion of the actin filaments intrudes upon the bridging regions, effectively reducing the free volume available to lysozyme. In fact, the helical symmetry of the actin leads to an excluded-volume envelope with a rather convoluted shape. To distinguish any structure in the lysozyme distribution due to this shape, Fig. 7 b shows a bundle at the same actin-actin separation, but with all species neutral. The homogeneous lysozyme distribution obtained in this case demonstrates the dominant role of electrostatic interactions. The importance of these interactions can also be seen by comparing the actin excluded volume (white regions) in Fig. 7, a and b. In the absence of charged species the excluded volume is larger and the helical symmetry, which leads to the rough hexagonal shape of the white regions in Fig. 7 a, is much less pronounced. This reconfirms the strength of the electrostatic attraction between actin and lysozyme, and also makes it important to ensure that, during the simulation, the lysozyme is not trivially “frozen” in place. By measuring the mean-square displacement of lysozyme, we have explicitly confirmed that it indeed travels freely, with a diffusivity that is significantly higher along the filament axis than in the lateral plane.

FIGURE 7.

Contour plots showing the lysozyme distribution in actin-lysozyme complexes without added salt, projected in the plane perpendicular to the bundle axis. Darker shading corresponds to higher concentrations, and the same shade corresponds to the same concentration in all four plots. In the equilibrium configuration (a), lysozyme is predominantly located in the threefold interstitial regions. By contrast, in a slightly expanded lattice (c), corresponding to the minimum osmotic pressure in Fig. 5, lysozyme is depleted from these regions and occupies the bridging regions instead. (b and d) Counterparts of panels a and c, respectively, in the absence of electrostatic forces. These control graphs confirm the important role of electrostatic interactions in the actual lysozyme distributions.

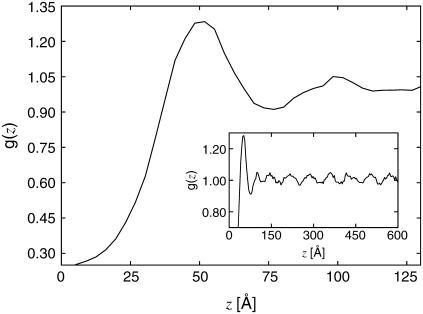
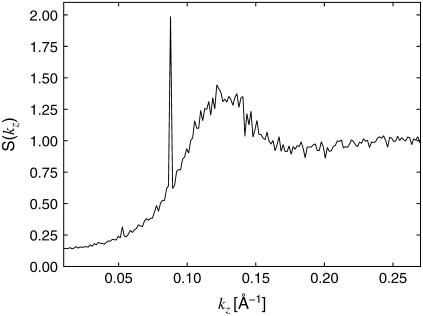
Since the lysozyme resides preferentially in the threefold interstices of the actin lattice, it is of interest to study the distribution of lysozyme in these regions along the filament axis. Fig. 8 shows the lysozyme-lysozyme (center-of-mass) pair correlation function g(z) along the actin axis. To avoid cross-correlations between regions, g(z) is computed independently for each region and then averaged. The pair correlation shows a strong first peak at z = 50 Å, in agreement with the experimentally observed lysozyme-lysozyme periodicity of 48.3 Å, indicating that despite strong mutual electrostatic repulsion the lysozyme molecules are indeed relatively close-packed. However, as shown in the inset of Fig. 8, g(z) also exhibits a strong periodicity at larger separations. To visualize this periodicity more clearly, we present the Fourier transform, S(k_z), of g(z) in Fig. 9. There is a broad peak centered around k_z ≈ 0.126 Å⁻¹, corresponding to the short-distance peak in g(z), and a much sharper peak centered at k_z ≈ 0.088 Å⁻¹, corresponding to order with a period of ∼71.5 Å.

FIGURE 8.

Lysozyme-lysozyme pair correlation function along the filament axis. The plot corresponds to a system without added salt at the stable actin-actin separation. The first peak occurs at z = 50 Å. The inset is a larger portion of the same function, showing the long-range periodicity, with period 71.5 Å.

FIGURE 9.

Fourier transform of the lysozyme-lysozyme pair correlation function g(z) along the filament axis, for the same system as in Fig. 8. The broad peak is centered at k_z ≈ 0.126 Å⁻¹, which corresponds to a periodicity of z = 50 Å in the lysozyme distribution. The sharp peak at k_z ≈ 0.088 Å⁻¹ corresponds to a periodicity of z = 71.5 Å.

Further analysis of the lysozyme distribution in the presence of salt provides important additional information. At the stable actin separation, the lysozyme now remains present in significant concentrations in the bridging regions between pairs of actin filaments. We view this as an artifact, resulting from the swelling of the actin bundles (not occurring in the experiments) in the presence of salt, which leaves more room to accommodate the lysozyme in these regions. However, if the lysozyme correlations are probed in these regions, they only exhibit the broad maximum around k_z = 0.126 Å⁻¹, whereas the sharp maximum is completely absent. On the other hand, the distribution in the threefold interstitial regions still exhibits both features, although the sharp maximum is weakened considerably, owing to the decreased lysozyme concentration in these regions. Furthermore, analysis of S(k_z) in the bridging regions in the salt-free case reveals that the short-distance peak persists whereas the peak at k_z = 0.088 Å⁻¹ is replaced by peaks at 0.0176 Å⁻¹ and 0.035 Å⁻¹. All sharp peaks result from the actin periodicity 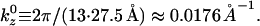Note that 0.035 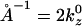and 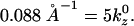These observations indicate that the broad maximum, which also corresponds to the experimental observations, is a robust feature, confirming that the lysozyme is aligned with its long axis along the filaments. On the other hand, the sharp maxima are features that arise from the perfect periodicity of our model system of filaments that lack rotational degrees of freedom.

It is also possible to study the lysozyme distribution of bundles with larger actin-actin separations, which may arise as intermediate states during the process of bundle formation, provided that the lysozyme can relax on the timescale of motion of the actin filaments. Fig. 7 c shows the projected lysozyme distribution for a bundle with a lattice spacing of L = 116 Å, which corresponds to the minimum of the osmotic pressure curve in Fig. 5. As the osmotic pressure is negative at this separation, the bundle is actually contracting at this stage. Although the difference in lattice spacing, compared to the equilibrium configuration, is small—even when compared to the size of lysozyme—the lysozyme distribution is qualitatively different. The threefold interstitial regions are depleted, and instead the lysozyme occupies the bridging sites. Fig. 7 d demonstrates that, as with the stable system, this lysozyme distribution is dominated by electrostatic effects. “Contact” interactions between the lysozyme and actin are maintained despite the loss of entropy associated with the localization of lysozyme in the bridging regions.

SUMMARY AND CONCLUSIONS

We have presented a detailed comparison of experimental and computational results for the structural properties of isoelectric complexes of filamentous actin and lysozyme. The numerical results, which are obtained by means of molecular dynamics simulations of a coarse-grained model that explicitly incorporates the charge distribution on the actin, confirm the thermodynamic stability of close-packed bundles of actin filaments that are held together by lysozyme. The small-angle x-ray scattering results indicate that the lysozyme proteins are arranged in a regular manner along the filaments. The structure factor computed in the simulations exhibits a similar feature, which arises from the contact peak between the proteins that are oriented with their long axis along the bundle axis. At larger separations the simulations predict a specific pattern for the lysozyme distribution reflecting the periodicity of the actin filaments. These long-range features are not observed in the experiments and may arise because of artificial periodicities imposed by the rigid actin structure employed in the simulations. The central finding of this study is the stability of the actin-lysozyme complexes in the presence of comparatively high concentrations of monovalent salt. Although model-specific effects prevent the simulations from reproducing this phenomenon up to the same salt concentrations as employed in the experimental work, they clearly identify an important mechanism responsible for the enhanced stability of the complexes. Upon increasing salt concentration in the aqueous phase that coexists with the condensed phase, salt partitioning occurs, leading to a considerably lower salt concentration within the bundle than in the aqueous phase. This concentration difference leads to an excess osmotic pressure on the bundle that counteracts the pressure arising from the salt ions confined in the bundle. In view of the generic nature of this mechanism it is potentially relevant for a wide range of electrostatically driven complexation phenomena. Important parameters that will be investigated in future research include the actin surface charge density (which can be controlled by variation of the pH) as well as the macroion charge.