Swelling-Activated Pathways in Human T-Lymphocytes Studied by Cell Volumetry and Electrorotation

Abstract

Small organic solutes, including sugar derivatives, amino acids, etc., contribute significantly to the osmoregulation of mammalian cells. The present study explores the mechanisms of swelling-activated membrane permeability for electrolytes and neutral carbohydrates in Jurkat cells. Electrorotation was used to analyze the relationship between the hypotonically induced changes in the electrically accessible surface area of the plasma membrane (probed by the capacitance) and its permeability to the monomeric sugar alcohol sorbitol, the disaccharide trehalose, and electrolyte. Time-resolved capacitance and volumetric measurements were performed in parallel using media of different osmolalities containing either sorbitol or trehalose as the major solute. Under mild hypotonic stress in 200 mOsm sorbitol or trehalose solutions, the cells accomplished regulatory volume decrease by releasing cytosolic electrolytes presumably through pathways activated by the swelling-mediated retraction of microvilli. This is suggested by a rapid decrease of the area-specific membrane capacitance C_m (μF/cm²). The cell membrane was impermeable to both carbohydrates in 200 mOsm media. Whereas trehalose permeability remained also very poor in 100 mOsm medium, extreme swelling of cells in a strongly hypotonic solution (100 mOsm) led to a dramatic increase in sorbitol permeability as evidenced by regulatory volume decrease inhibition. The different osmotic thresholds for activation of electrolyte release and sorbitol influx suggest the involvement of separate swelling-activated pathways. Whereas the electrolyte efflux seemed to utilize pathways preexisting in the plasma membrane, putative sorbitol channels might be inserted into the membrane from cytosolic vesicles via swelling-mediated exocytosis, as indicated by a substantial increase in the whole-cell capacitance C_C (pF) in strongly hypotonic solutions.

INTRODUCTION

Volume regulation in hypotonic media is a near-ubiquitous property of animal cells. In response to a sudden decrease in the external osmolality, the initial cell swelling activates various volume-sensitive pathways in the plasma membrane that mediate the release of ions (K⁺ and Cl⁻) and small organic osmolytes, such as carbohydrates, amino acids, etc., from the cytosol. The net efflux of cytosolic solutes through volume-sensitive channels, along with osmotically driven water loss, allows the cells to recover their original isotonic volume. The process of restoration of the normal cell size under continuous hypotonic stress is known as regulatory volume decrease (RVD) (1,2). Despite extensive studies, it is still a matter of controversy whether common or separate volume-sensitive pathways are used by inorganic ions and organic osmolytes during RVD (3–7).

Hypotonically induced cell volume changes are associated with large and rapid changes in cell surface area and membrane organization (8,9). The hypothesis is that the activity of volume-sensitive channels is regulated by the cell surface organization and particularly by membrane structures, such as microvilli (2,10). Valuable insights into the mechanisms of channel activation upon hypotonic stress have been obtained by studying the relationship between the ion channel activity and electrically accessible membrane surface area, from parallel current and capacitance C_C (pF) recordings on patch-clamped cells. Thus, molluscian neurons reversibly increase or decrease their C_C and, consequently, their surface area as they swell or shrink in hypo- or hypertonic solutions (11). In the gland cells of dogfish, hypotonicity causes a marked increase in C_C, which occurs even faster than both membrane conductance increase and hyperpolarization (12). In contrast, human T-lymphocytes exhibit a slight decline in C_C during moderate hypotonic swelling and Cl⁻ current induction (13).

So far, most electrophysiological studies have addressed volume-sensitive anion channels, whereas less data are available on the mechanisms of swelling-activated fluxes of neutral organic osmolytes. An alternative approach for studying changes in the electrical properties of cells subjected to hypotonic stress is single-cell electrorotation (ROT) (14). This is a noninvasive method that allows the dielectric analysis of cells freely suspended in solutions, whose osmolality can be varied over wide ranges by using appropriate concentrations of both inorganic and organic osmolytes (8,15). Moreover, ROT is particularly suitable for studying cells suspended in solutions containing a neutral carbohydrate (sorbitol, inositol, trehalose, etc.) as the major osmolyte, whose membrane permeability can be assessed simultaneously from the volumetric cell response (16).

In this study on Jurkat cells, we explored the relationship between the hypotonically induced changes in cell surface area and membrane permeability to the monomeric sugar alcohol sorbitol, the disaccharide trehalose, and cytosolic electrolyte. To this end, we used video microscopy and the ROT technique to monitor the cell volume as well as the area-specific membrane capacitance C_m (μF/cm²) and whole-cell capacitance C_C (pF) of cells exposed to an acute hypotonic challenge. The osmolality of external solutions containing either sorbitol or trehalose as the major solute was adjusted to 200 or 100 mOsm. Under mild hypotonic stress (200 mOsm), the cells accomplished RVD due to the volume-regulatory release of cytosolic electrolyte, whereas the plasma membrane permeability for both sorbitol and trehalose remained very poor. In contrast, extreme swelling in a strongly hypotonic solution (100 mOsm) led to substantial sorbitol uptake by cells due to a dramatic increase of sorbitol permeability, as evidenced by RVD inhibition. Unlike sorbitol, trehalose did not permeate the plasma membrane even under severe hypotonic conditions. The different osmotic thresholds for activation of electrolyte release and sorbitol influx suggest the involvement of separate swelling-activated pathways. Whereas the electrolyte efflux occurred obviously by pathways preexisting in the plasma membrane, putative sorbitol channels were apparently inserted into the plasma membrane from cytosolic vesicles via swelling-mediated exocytosis, as suggested by a substantial C_C increase in strongly hypotonic solutions.

MATERIALS AND METHODS

Cells

All experiments were performed on Jurkat cells, a human leukemic cell line, obtained from the American Type Culture Collection (ATCC, Manassas, VA). The cells were cultured in RPMI 1640 based complete growth medium (CGM) containing 10% fetal calf serum (PAA Laboratories, Linz, Austria) at 37°C under 5% CO₂ (16). The cells were kept in the exponential growth phase by passaging them three times weekly. These nearly spherical, anchorage-independent cells do not strictly adhere to a solid substrate.

Hypotonic carbohydrate solutions

Both sorbitol and trehalose of the highest purified grade were purchased from Sigma (Taufkirchen, Germany). In volumetric experiments, carbohydrate solutions of osmolalities 100, 200, and 300 mOsm (mosmol/kg) were used containing either sorbitol or trehalose as the major osmolyte. The conductivity of carbohydrate solutions was adjusted to 10–140 μS/cm by the addition of HEPES-KOH (pH 7.2). Conductivity and osmolality were measured with a digital conductometer (Knick, Berlin, Germany) and a cryoscopic osmometer (Gonotec, Berlin, Germany).

Cell volumetry

Cell volume changes were measured by video microscopy, using a flow chamber designed for rapid exchange of media, and according to the setup described elsewhere (16). The transparent body and floor of the chamber were made of poly(methylmethacrylate) (plexiglass) and a 0.15-mm thick glass coverslip, respectively. Before measurements (10–15 min), an aliquot of cells suspended in isotonic CGM (∼280 mOsm) at a density of ∼10⁵ cells/ml was injected into the flow chamber and the cells were allowed to settle and to adhere to the chamber floor. To enhance cell adhesion, the coverslip was pretreated for 5–10 min at room temperature with 0.5 mg/ml poly-D-lysine (Sigma) (13). The chamber was placed on the stage of a microscope (Olympus, Hamburg, Germany) and the cells were viewed with a 20× objective. Images of cells were taken 1 min before and at various time intervals (20–60 s) up to ∼15 min after medium exchange. The cross-section areas of 8–10 cells per microscopic field were determined. At each time interval, the volume (V) of an individual cell (Fig. 1) was evaluated from its cross-section area by assuming spherical geometry. Because of the very weak (and apparently punctual) attachment, the cells retained their nearly spherical shape. The cell volume was normalized to the original isotonic volume (V₀) as: ν = V/V₀. The mean ν values (±SE) for a given experiment were calculated from a sequence of ∼50 images and plotted against time after the change from isotonic to hypotonic medium (200 or 100 mOsm).

FIGURE 1.

Fast swelling and regulatory volume decrease (RVD) of a Jurkat cell in 100 mOsm trehalose-substituted medium. The photographs show the same cell before (A, isotonic CGM) and after (B–D) an acute hypotonic challenge, at the indicated time intervals. In isotonic CGM (A, t ≤ 0), the cell radius r was 7.4 μm, corresponding to the original isotonic volume V₀ ≈ 1.7 pL. Upon medium replacement at time zero, the cell swelled to V_max ≈ 3.1 pL (r ≈ 9.0 μm) within 2 min (B) and then shrank gradually to its isotonic size within 10–15 min (C–D).

Rotation chambers and driving fields

Electrorotation (ROT) spectra were measured in a microstructured four-electrode chamber, described in detail earlier (17). The microchamber is arranged as a planar array of circular electrodes of 60-μm diameter, 140-nm thickness, and 300-μm electrode spacing. The electrodes were driven by four 90° phase-shifted, rectangular signals from a pulse generator (Hewlett-Packard, Boeblingen, Germany) with 2.5- to 4.8 V_PP amplitude over the frequency range from ∼100 Hz to 150 MHz. A sample of cell suspension (50–70 μl) was added to the rotation chamber, and a coverslip was placed gently over its center. The cell rotation was observed using the Olympus microscope. ROT spectra were monitored by decreasing the field frequency in steps (five frequency points per decade). At each field frequency, the rotation speed of lone cells located near the center of the chamber was determined using a stopwatch. The ROT spectra, i.e., frequency dependencies of the ROT speed Ω (rad/s), were normalized to the field strength of 100 V/cm.

Measurements of the field frequency f_c1 that induced fastest antifield cell rotation of cells were performed by the contrarotating fields (CRF) technique (14). Unlike the regular ROT described above, the CRF method uses two rotating fields applied in rapid succession. The fields are of equal amplitude (∼100 V/cm), but of opposite directions and differing frequencies f_L and f_H. The ratio f_L/f_H (≈4) is kept constant, and the switching rate between the fields is much faster than the mechanical time constant of the cell. When the geometric mean frequency f_G = (f_L × f_H)^0.5 is scanned through the rotation region, the resulting response to CRF is proportional to the differential of the regular ROT spectrum. Thus, finding f_c1 is simply a matter of changing f_G until the cell stop rotating (i.e., ∂Ω/∂f =0). This was made by means of a CRF generator arranged to display f_G directly (12). The CRF technique allows rapid and accurate f_c1 measurements, with an acquisition time of a few seconds. In the CRF experiments, ∼10 μl of cell suspension was added to a macroscopic four-electrode chamber described in detail previously (8). The spacing of the planar electrodes (mounted at right angles to each other) was ∼1.2 mm. The chamber is open at the top for rapid sample replacement. During CRF measurements, the cells were viewed with an inverted Leitz-Labovert microscope through a 100× oil-immersion objective for optimum resolution. Cell radii were determined with a calibrated eyepiece micrometer. Conductivity within the chamber was monitored by a conductometer connected to two opposite electrodes.

ELECTROROTATION THEORY

ROT and related AC electrokinetic techniques are increasingly being exploited as powerful tools for the characterization, handling, and manipulation of biological cells (18–22). AC electrokinetic phenomena are based on the electrostatic interaction of the applied field E with the induced cell dipole μ that arises mainly from the free charges that accumulate at the membrane interfaces. In a rotating field, the phase shift between E and μ produces a torque and therefore results in cell rotation. The theory of electrorotation was given in full detail in previous publications (14,17,23,24). Here we will only summarize the basic assumptions and list the equations that allow the evaluation of electrical cell properties from experimental ROT data. Jurkat and other mammalian cells can be approximated very accurately by the simplest single-shell spherical model (8,17), which considers the cell as a conductive sphere (cytosol) surrounded by an insulating layer corresponding to the plasma membrane.

It is well known that the frequency-dependent cell rotation speed Ω(f) is fully determined by the imaginary part of the complex cell polarizability χ*, and is given by:

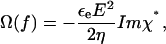(1)

where E is the applied field strength, ɛ_e and η are the dielectric permittivity and dynamic viscosity, respectively, of the external medium. Taking into account that the cell radius a is usually much larger than the membrane thickness d (a ≫ d), the complex polarizability χ* of a spherical single-shelled cell can be expressed as follows:

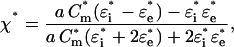(2)

where the complex permittivity is defined as ɛ* = ɛ − jσ/ω, with ɛ and σ for the real permittivity (F/m) and conductivity (S/m) of the medium (subscript “e”) and cytosol (subscript “i”); j = (−1)^0.5; ω = 2πf is the radian field frequency. The complex area-specific membrane capacitance is given by: C_m* = C_m − jG_m/ω, where C_m (F/m²) and G_m (S/m²) are the real membrane capacitance and conductance per unit area, respectively. In this study, only the cytosolic properties (σ_i and ɛ_i) were derived by fitting the combination of Eqs. 1 and 2 to the experimental ROT spectra, using the nonlinear regression package of Mathematica. For these calculations, we reduced the number of unknown parameters by treating the term ɛ_eE²/(2η) (Eq. 1) as a scaling factor (25) and by using the mean C_m and G_m values obtained by the CRF technique (see below).

The ROT spectra of single-shelled cells can also be presented as a superposition of two Lorentzian peaks caused by the Maxwell-Wagner dispersions at the outer and inner interfaces of the plasma membrane:

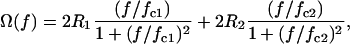(3)

where R₁ and R₂ are the magnitudes of the two rotational peaks centered at f_c1 and f_c2, respectively. The two ROT peaks are usually widely separated: f_c1 ≪ f_c2. The characteristic frequencies (f_c1 and f_c2) and ROT magnitudes (R₁ and R₂) combine the applied field strength, all conductivities, permittivities, and some other parameters of the external medium, membrane, and cytosol (23,26).

Given that σ_l ≫ σ_e ≫ σ_m and the cell radius a is much larger than membrane thickness d, the single-shell model gives the following relationship between the f_c1, σ_e, area-specific membrane capacitance C_m (μF/cm²), and conductance G_m (mS/cm²):

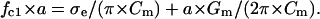(4)

Eq. 4 was used in this study for the evaluation of C_m and G_m from the f_c1 data obtained by the CRF technique, after long-term hypotonic stress.

For sufficiently large external conductivities (e.g., σ_e = 50–150 μS/cm), the second term in the right-hand side of Eq. 4 is much smaller than the experimental f_c1 × a values of most mammalian cells and can be neglected. Therefore, the following equation can be used to approximate the area-specific capacitance:

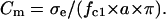(5)

Based on Eq. 5, accurate C_m values can be obtained from continuous f_c1 measurements on individual cells using the CRF technique. From the C_m and radius data, the whole-cell capacitance C_C for each cell can also be calculated as

(6)

In contrast to the antifield peak (described by f_c1 and R₁), which is mainly determined by the capacitive membrane charging and cell size, the cofield rotation (f_c2 and R₂) is primarily due to the cytosolic polarization, whose characteristic frequency is given by

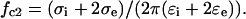(7)

As seen from Eq. 7, the cofield peak shifts to lower frequency with decreasing cytosolic conductivity σ_i.

RESULTS

Cell volumetry

The initial and secondary cell volume changes were studied by video microscopy after rapid transfer of Jurkat cells from isotonic culture medium (CGM) to iso- or hypotonic solutions containing either sorbitol or trehalose as the major solute. For each sugar, the solution osmolality was adjusted to 300 (isotonic), 200, or 100 mOsm. Upon substitution of CGM by an isotonic sugar solution (Fig. 2, solid circles), the cells shrank slowly to a final relative volume ν_end of 0.8–0.9 at ∼15 min after medium exchange. This isotonic shrinkage occurred presumably due to the loss of cellular osmoticum driven by the steep concentration gradient in low-salinity media used here.

FIGURE 2.

Changes of the relative volume (ν = V/V₀) in Jurkat cells in response to sorbitol- and trehalose-substituted solutions (A and B, respectively) of different osmolalities. The cells were bathed initially (t < 0) in an isotonic saline solution (∼280 mOsm) and then exposed at time zero to solutions having osmolalities of 300, 200, or 100 mOsm as indicated by the numbers close to the data points. Each data point represents the mean ± SE of eight to nine independent determinations. Note that in the presence of trehalose, RVD was observed over the entire hypotonicity range (B, open symbols). RVD also occurred in slightly hypotonic solutions of sorbitol (A, 200 mOsm, open squares), but was completely inhibited at 100 mOsm (A, open circles).

In hypotonic sorbitol or trehalose solutions, the cells first swelled within 1–2 min from their original isotonic volume V₀ to the maximum volume V_max. As expected, the relative magnitudes of initial swelling, defined as ν_max = V_max/V₀, increased with decreasing osmolality (Fig. 2).

Independent of the sugar used, 200 mOsm solutions allowed regulatory volume decrease (RVD) in Jurkat cells (Fig. 2, open squares). After the fast initial swelling phase in these weakly hypoosmotic media, the cells shrank gradually despite persisting hypotonicity and recovered their original isotonic volume (ν₀ ≈ 1) within 5–10 min. Thereafter the cell volume continued to reduce modestly to reach a stationary value slightly below ν₀ (ν_end ≈ 0.9).

Further reduction of the osmolality resulted in different effects of sorbitol and trehalose on the secondary volume changes of Jurkat cells (Fig. 2, open circles). At 100 mOsm (Fig. 2 B), application of the disaccharide trehalose induced complete RVD within ∼15 min upon acute hypotonic challenge. RVD also occurred in 50-mOsm trehalose solution, but at a lower rate than at higher osmolalities (data not shown). The RVD disappeared in 100 mOsm sorbitol (in contrast to trehalose) as indicated in Fig. 2 A (open circles).

Electrorotation of cells after long-term hypotonic treatment

The f_c1 frequencies giving rise to maximum antifield rotation (see Eq. 4) of cells were measured in sorbitol- and trehalose-substituted media of different osmolalities, using the CRF technique. Before f_c1 determinations, the cells were incubated in a 300 (isotonic), 200, or 100 mOsm sugar solution for 15–30 min. These experimental conditions were similar to those used for long-term volumetric determinations of ν_end (Fig. 2). For each cell, the f_c1 value, the radius (a) and the external conductivity (σ_e) were recorded, and the product f_c1 × a was plotted versus σ_e. In these experiments, σ_e was varied from ∼10 to 70 μS/cm (Fig. 3, circles). Within this conductivity range, linear relationships between f_c1 × a and σ_e were observed for various experimental conditions. Therefore, the mean values of the area-specific membrane capacitance (C_m) and conductance (G_m) could be extracted by fitting Eq. 4 to the CRF data, as illustrated by the lines in Fig. 3. The fitted C_m and G_m values for each cell sample (N = 180–420 cells) are summarized in Table 1.

FIGURE 3.

Cumulative plots of the radius-normalized f_c1 values (f_c1 × a) of Jurkat cells versus the external conductivity σ_e. The measurements were performed after long-term (15–30 min) incubation of cells in solutions of various osmolalities. The solutions contained sorbitol (A) or trehalose (B) as the major osmolyte. The f_c1 data were obtained either by the CRF technique (circles) or were deduced from the ROT spectra (squares), as shown in Fig. 4. The straight lines are the least-square approximations of Eq. 4 to the CFR data sets, each containing 120–420 cells. Note that according to Eq. 4, the slope of the fitted line is inversely proportional to the area-specific membrane capacitance C_m. For sorbitol-treated cells (A), the steep slope determined at 100 mOsm (open symbols) implies that the C_m value is smaller than the C_m value in isotonic 300 mOsm medium (solid symbols). In contrast, cells suspended in 100 and 300 mOsm trehalose (open and solid symbols, respectively) exhibited similar C_m values. Table 1 summarizes the fitted C_m and G_m data for all experimental conditions.

TABLE 1.

Electrical properties of Jurkat cells incubated for 15–30 min in sorbitol- and trehalose-substituted solutions of different osmolalities

Osmolyte	Sorbitol	Sorbitol	Sorbitol	Trehalose	Trehalose	Trehalose
Osmolality, mOsm	100	200	300	100	200	300
Cm, μF/cm2	0.73 ± 0.01	0.94 ± 0.05	1.35 ± 0.04	1.42 ± 0.05	1.22 ± 0.04	1.40 ± 0.05
Gm (mS/cm2)	9.8 ± 1.5	n.d.	3.5 ± 2.9	16.2 ± 4.5	5.8 ± 3.5	8.2 ± 4.1
Number of cells (CFR)	420	120	180	300	300	180
σi (mS/cm)	2.8 ± 0.2	5.7 ± 0.3	11.0 ± 1.0	4.0 ± 0.2	5.8 ± 0.5	8.4 ± 0.7
ɛi/ɛ0	138 ± 5	110 ± 9	149 ± 12	122 ± 18	104 ± 12	106 ± 10
Number of measurements	11	12	12	10	13	9

C_m and G_m are the mean values (±SE) determined by curve fitting to the CRF data (Fig. 3). σ_i and ɛ_i are the means (±SE) evaluated from the ROT spectra of individual cells (N = 9–13 cells).

As indicated in the table, the CRF technique yielded similar C_m values of 1.35 ± 0.04 and 1.40 ± 0.05 μF/cm² for Jurkat cells incubated in 300 mOsm (isotonic) sorbitol- and trehalose-substituted media. Prolonged hypotonic stress in 100 mOsm sorbitol solution led to a marked reduction of C_m to 0.73 ± 0.01 μF/cm², whereas the C_m value of 1.42 ± 0.05 μF/cm² measured after 15–30 min incubation in 100 mOsm trehalose solution was similar to that in isotonic media. Strongly hypotonic sorbitol- and trehalose-substituted media gave also significantly higher G_m values (9.8 and 16.2 mS/cm², respectively) than corresponding isotonic solutions (3.5 and 8.2 mS/cm²). Note that apart from changes in the electrical properties, there was also an ∼1.8-fold increase of the cell volume after ∼15 min incubation in 100 mOsm sorbitol solution compared to isotonic conditions (Fig. 2 A, open circles). In contrast, the isotonic and long-term hypotonic cell volume values in trehalose-substituted media were similar (Fig. 2 B).

ROT experiments were further extended to account for the possible changes in the electrical properties of the cytosol induced by long-term hypotonic stress. To this end, complete ROT spectra were measured over the frequency range from a few kHz to 150 MHz. ROT spectra recorded in sorbitol- and trehalose-substituted media of two different osmolalities, but of the same conductivity are shown in Fig. 4, A and B, respectively. Before recording of the ROT spectra, the cells were incubated for 15–30 min in either isotonic (300 mOsm) or strongly hypotonic media (100 mOsm), denoted in Fig. 4 by solid and open symbols, respectively.

FIGURE 4.

Typical rotation spectra of Jurkat cells in sorbitol- (A) and trehalose-substituted media (B) of different osmolalities, but of the same conductivity of 140 μS/cm. ROT spectra were measured after 15–30 min incubation in 300- and 100-mOsm solutions (solid and open symbols, respectively). For each sugar, ROT spectra of 9–13 cells were measured at each osmolality. Continuous curves are best fits of the single-shell model. The fitted parameters are given in Table 1. The characteristic frequencies (f_c1 and f_c2) with corresponding rotation amplitudes (R₁ and R₂) are defined in the text (Electrorotation theory).

In accordance with the single-shell model (Eq. 3), the ROT spectra measured at various experimental conditions exhibited two symmetrical Lorentzian peaks (Fig. 4). Field frequencies below ∼1 MHz induced antifield rotation with the characteristic frequency f_c1 due to the capacitive membrane charging (Eq. 53). The mean f_c1 values varied only slightly (48–49 kHz) among the four samples. Note that although the ROT spectra were measured at a much higher conductivity (σ_e ≈ 140 μS/cm) than those used for CRF determinations (σ_e ≈ 10–70 μS/cm), the f_c1 × a values derived from the ROT spectra (Fig. 3, squares) matched well the extrapolated regression lines to the corresponding data obtained by means of the CRF technique (Fig. 3, circles).

The ROT spectra exhibited a cofield peak (f_c2) at frequencies above 1 MHz. In isotonic 300 mOsm solutions of either sugar (Fig. 4, solid circles), this cytosolic peak generally occurred at much higher frequencies (with the mean f_c2±SE of 66.7 ± 2.5 and 61.1 ± 3.0 MHz for sorbitol and trehalose, respectively) than in corresponding 100 mOsm media (17.5 ± 0.9 and 29.0 ± 1.5 MHz, Fig. 4, open circles). Since the ROT spectra were measured at the same external conductivity σ_e of ∼140 μS/cm, the observed shift of f_c2 to lower frequency implies that prolonged hypotonic challenge led to a significant reduction in the cytosolic conductivity σ_i (see Eq. 7).

The electrical properties of the cytosol, including ɛ_i and σ_i, were derived for each cell sample by fitting the single-shell model to the ROT spectra of individual cells. In carrying out the nonlinear least-square fit, the number of unknown parameters was reduced by using the corresponding C_m and G_m values obtained by the CRF method (Fig. 3). The solid fitted curves in Fig. 4 illustrate that the simplest single-shell model approximates very accurately the experimental spectra. The fitted ɛ_i and σ_i values for each cell sample are given in Table 1. Taken together, the linear dependence of f_c1 × a on σ_e (Fig. 3) and the reasonable agreement of the experimental ROT spectra with the theory (Fig. 4) obviously justify, retrospectively, the use of the nondispersive single-shell model for the analysis of the dielectric properties of Jurkat cells.

Note that apart from their large size, cells incubated in 100 mOsm sorbitol exhibited a much faster electrorotation (R₁= −13 rad/s and R₂ = 6 rad/s) than under other experimental conditions. As shown in Fig. 4, in 100 mOsm trehalose R₁ and R₂ were 5.7 and 3.0 rad/s, respectively, after RVD had been completed. Values of R₁ and R₂ in isotonic sorbitol or trehalose media were R₁ ≈ −6 and R₂ ≈ 3 rad/s. The lower rotation speed can be explained by the increased hydrodynamic resistance of these cells caused by their rough surface due to the large number of membrane folds and microvilli (see Discussion).

Time-resolved measurements of membrane capacitance

As seen in Table 1, ROT spectra in combination with the CRF method (Figs. 3 and 4) allowed detailed dielectric analysis of both membrane and cytosol after prolonged hypotonic stress. However, due to the long acquisition time, the experimental approaches used above do not provide sufficient temporal resolution for continuous monitoring of membrane capacitance, which is expected to vary rapidly in hypotonically treated cells undergoing large volume and related surface excursions. The acquisition of C_m data can be accelerated if G_m is not resolved. To this end, we monitored the f_c1 and radius (a) of individual cells at a sufficiently large external conductivity (σ_e ≈ 100 μS/cm; see Materials and Methods). By substituting the measured f_c1, a, and σ_e data into Eqs. 5 and 6, the apparent area-specific membrane capacitance C_m (μF/cm²) and the whole-cell capacitance C_C (pF) were calculated and plotted versus time (Fig. 5).

FIGURE 5.

Changes of the area-specific (C_m (μF/cm²), A and B) and whole-cell capacitance (C_C (pF), C and D) of Jurkat cells during hypotonic stress. The cell samples were originally (t < 0) exposed to isotonic CGM. At zero time the cells were transferred to 200 or 100 mOsm medium (open squares and circles, respectively) containing sorbitol (A and C) or trehalose (B and D) as the major osmolyte. At various time intervals after acute hypotonic challenge, the cell radius a, the characteristic frequency f_c1 of maximum antifield electrorotation and the medium conductivity σ_e were recorded for individual cells (N = 15–20). From these data, the mean C_m and C_C values (±SE) were calculated using Eqs. 5 and 6. The initial capacitance values (t = 0, solid symbols) represent the data derived from the CRF experiments performed correspondingly in isotonic 300 mOsm media (see Fig. 3, Table 1).

Fig. 5, A and C, shows the time courses of C_m and C_C changes in Jurkat cells exposed to hypotonic sorbitol solutions. The corresponding data for trehalose-substituted media are shown in Fig. 5, B and D. In these experiments, cells were bathed initially in isotonic CGM (∼10⁷ cells/ml) and were then rapidly transferred (at t = 0) into hypotonic sugar solutions (final cell density ∼10⁵ cells/ml). The hypotonic C_m and C_C data were acquired (as described above) at the indicated time intervals after acute hypotonic challenge, starting at t = 1–1.5 min with ∼30-s intervals. The C_m and C_C values at zero time (Fig. 5, solid symbols, t = 0) represent the data derived from the CRF experiments performed in isotonic 300-mOsm media (Fig. 3 and Table 1).

Independent of the sugar composition and medium tonicity (200 or 100 mOsm), the hypotonic shock reduced markedly the C_m value from its original isotonic level of ∼1.4 μF/cm² to nearly the same minimum of 0.7–0.8 μF/cm², as indicated by the dashed and dotted lines in Fig. 5, A and B. Comparison of the C_m changes with the corresponding volumetric curves in Fig. 2 reveals that both the fast initial C_m drop and cell swelling accomplished within the same time of 1–1.5 min after hypotonic exposure.

In contrast to the initial C_m decrease, the rate and magnitude of the secondary C_m changes were strongly associated with the ability of cells to undergo RVD. During RVD in 200 mOsm sorbitol (Fig. 2 A, open squares), C_m increased gradually from the minimum value of 0.8 μF/cm² to ∼1.1 μF/cm² at 15 min (Fig. 5 A, open squares). In trehalose-substituted media (both 100 and 200 mOsm), in which RVD also occurred (Fig. 2 B, open symbols), C_m increased even faster and approached its original isotonic value of 1.4 μF/cm² at 10–15 min after hypotonic shock (Fig. 5 B). Without RVD there were no secondary C_m changes. Thus, after the fast initial swelling and drop in C_m upon application of 100 mOsm sorbitol, cell volume and C_m (∼0.8 μF/cm²) did not change significantly during the following 15 min incubation (Figs. 2 A and 5 A, open circles).

Unlike C_m, the whole-cell capacitance C_C changed—if at all—only slightly in response to the mild osmotic shift from 300 to 200 mOsm in sorbitol or trehalose solutions (Fig. 5, C and D, respectively, open squares). There was a small initial C_C increase from 8.2–8.3 to ∼9.5 pF within the first 2–2.5 min. After that, C_C did not change (Fig. 5 C, squares) or decreased slowly to its isotonic level (Fig. 5 D, squares).

A more severe hypotonic shift to 100 mOsm caused significant C_C alteration in both sorbitol- and trehalose-substituted media. In 100 mOsm sorbitol, C_C increased from an isotonic value of ∼8.2 pF (t ≈ 0) to a maximum value of ∼11.5 pF at t ≈ 2.5 min (Fig. 5 C, circles). The initial C_C increase in 100 mOsm trehalose was even larger (up to ∼14.5 pF after 3 min; Fig. 5 D). Note that the initial C_C changes were somewhat slower (i.e., within 2.5–3 min) than the initial C_m and volume responses (1–1.5 min, Figs. 2 and 5, A and B). Longer incubation (3–15 min) in strongly hypotonic solutions caused little further C_C change.

DISCUSSION

Small organic solutes, including sugar alcohols, amino acids, etc., can contribute significantly to the total intracellular osmolality and thus to the osmoregulation of cells (27–29). Hypotonically treated cells exhibit both diffusion-driven release and uptake of organic solutes, with the net solute flux being governed by the imposed concentration gradient. This suggests that the organic osmolyte pathways are bidirectional (1,30–33).

There is a large body of evidence that the swelling-activated transport of anions and a spectrum of structurally dissimilar organic osmolytes occurs through a common channel, such as the volume-sensitive organic osmolytes and anion channel (3,32). On the other hand, there is also evidence from a number of studies that the swelling-activated transport of organic osmolytes and inorganic anions uses separate pathways (4–7). The controversial results may in part be explained by differences in experimental conditions regarding the magnitude of the acute osmotic challenge, medium composition, and cell type. In this study, the combination of the two noninvasive methods (volumetry and ROT) allowed detailed analysis of the complex relationship between the membrane permeability for different solutes (including trehalose, sorbitol, and electrolyte) and electrically accessible membrane area. Whereas the volumetric data provided information on the size-selectivity and osmotic thresholds of swelling-activated pathways, the cell capacitance measurements by ROT were useful for monitoring membrane flattening and extension caused by cell volume changes in hypotonic media.

Osmotic thresholds for electrolyte and sorbitol permeability

The volumetric data given in Fig. 2 reveal a dramatic difference between the effects of sorbitol and those of trehalose on the secondary cell-volume changes. Independent of the hypotonicity (200 or 100 mOsm), trehalose-substituted media allowed complete RVD of Jurkat cells (Fig. 2 B). RVD also occurred in slightly hypotonic solutions of sorbitol (200 mOsm), but it vanished in a more diluted sorbitol medium (100 mOsm, Fig. 2 A). The cytosolic conductivity data presented in Table 1 demonstrate that RVD is obviously caused by a release of electrolytes from the cells. In 100 mOsm sorbitol (i.e., without RVD), the intracellular conductivity dropped even more dramatically from 11 mS/cm in isotonic medium to 2.8 mS/cm. Inhibition of RVD in such media can be envisaged by an osmotically equivalent influx of sorbitol through volume-sensitive channels conducting monomeric sugars but being impermeable for oligosaccharides (such as trehalose). This explanation is consistent with previous direct chromatographic determination of intracellular sugars in hypotonically stressed cells (16) and with results of other authors. For example, monomeric carbohydrates and other solutes, including amino acids (taurine) and organic and inorganic anions (SCN⁻, I⁻, etc.) inhibited RVD completely via the swelling-activated uptake of these molecules by cells through volume-sensitive channels (31,34). Thus, it seems to be justified to use RVD inhibition as an indicator of osmotically mediated membrane permeability for extracellular sugars. According to the volumetric data in Fig. 2, the osmotic threshold for the swelling-activated uptake of sorbitol by Jurkat cells was between 100 and 200 mOsm. This threshold osmolality was lower than that for the electrolyte release as indicated by the ability of Jurkat cells to accomplish RVD in 200 mOsm hypotonic sorbitol solution as well as in trehalose-substituted media over the whole osmolality range.

Different osmotic thresholds for activation of the release of inorganic ions and organic osmolytes have also been observed in radioisotope flux studies on various mammalian cells. In rat myocytes exposed to half-isotonic medium ³⁶Cl⁻ efflux was more rapid than taurine efflux (35). Furthermore, the efflux of chloride anions from human intestine cells (probed with ¹²⁵I⁻) has been activated by a very mild hypotonic shift from 320 to 290 mOsm, whereas the release of organic osmolytes (³H-taurine) required a more pronounced hypotonic challenge (<225 mOsm) (7). Similarly, in rat hepatocytes, taurine efflux has been unaffected by reduction of the osmolality from 300 to 240 mOsm, whereas osmolalities <215 mOsm dramatically increased the efflux rate of this solute (33).

Three possible mechanisms are conceivable for the finding of different osmotic thresholds for sorbitol and electrolyte permeation through the Jurkat cell membrane. First, there are swelling-activated channels with a unitary permeability increasing gradually with stretching of the cell surface area. A second explanation would be that electrolyte and sorbitol use separate pathways, both of which are permanently present in the plasma membrane but distributed unevenly between the different membrane regions (i.e., in the plane plasma membrane or shaft and tip of microvilli as suggested by Lange (10)). Activation of either pathway occurs above a critical level of hypotonic swelling and related membrane flattening due to retraction of microvilli. A third explanation would be that electrolyte and sorbitol use separate pathways, i.e., the electrolyte pathway is permanently present in the plasma membrane, whereas the sorbitol channel is inserted into the plasma membrane from internal membranes by an exocytosis-like mechanism activated by strong hypotonic challenge (27).

The first mechanism seems to be unlikely because even strong membrane expansion in a 50-mOsm solution did not render the cell membrane permeable to trehalose (unpublished data). A decision between the second and third mechanism can be made by correlation of the observed changes in area-specific capacitance (C_m) and in the whole-cell capacity (C_c) of hypotonically stressed cells with structural changes of the plasma membrane.

Osmotically induced electrical and structural membrane changes

Liposomes and cells with a planar plasma membrane (e.g., erythrocytes) usually exhibit a capacitance per unit area C_m value ranging typically between 0.6 and 0.8 μF/cm² (15,36). In most mammalian cell types, however, the plasma membrane is not smooth under physiological conditions (300 mOsm). It exhibits surface extensions such as invaginations and microvilli not observable under the light microscope. Therefore, the true total membrane area is greater than that calculated on the basis of the cell radius (a). The presence of microvilli can reliably be detected by an increase of the apparent area-specific capacity C_m. The structural interpretation of the higher values of C_m detected in both electrophysiological and dielectric studies is actually well established in the literature (2,8,13,24,37). Accordingly, the C_m value of 1.35–1.4 μF/cm² obtained here was by ∼1.8-fold larger than the C_m value of a planar membrane. This means that in isotonic media, ∼50% of the electrically accessible membrane surface of Jurkat cells must be attributed to microvilli. It is interesting to note that the isotonic C_m of Jurkat cells measured here by electrorotation matches exactly the C_m values of 1.35 ± 0.47 and 1.4 ± 0.2 μF/cm² determined for this cell line by means of the dielectrophoresis (24) and patch-clamp techniques (13), respectively.

Independent of the osmolality and nature of the sugar, the fast initial swelling gave rise to a rapid decrease of C_m to the value of a planar membrane. The C_m reached its minimum level ∼1–1.5 min after acute hypotonic challenge (Fig. 5, A and B), indicating that the initial changes of cell volume and C_m occurred on a similar timescale (t_max ≈ 1.5–2 min (Fig. 2)).

In cells undergoing RVD, not only the cell volume but also C_m returned gradually toward their normal isotonic levels. This partial or even complete recovery of C_m apparently reflects the restoration of original or microvilli-like structures during RVD. In agreement with our electrical data, scanning electron microphotographs of isolated rat hepatocytes have also revealed a decrease in the density and length of microvilli within 1 min of exposure to 200 mOsm and an almost complete recovery of the original surface morphology during RVD (10). Similarly, an increase in the number of microvilli has been detected in human lymphocytes after RVD (38). Without RVD (e.g., in 100 mOsm sorbitol (Fig. 2 A)), the C_m of ∼0.8 μF/cm² remained unchanged for the 2–15 min following hypotonic shock (Fig. 5 A), indicating that long-lasting hypotonic swelling did not allow regeneration of microvilli.

The consistence of the structural and electrical data suggests that flattening of the plasma membrane via retraction of microvilli is the main trigger for the activation of electrolyte release, but not for sorbitol influx. Even complete unfolding of microvilli was not sufficient for the activation of sorbitol pathways. This stands in contrast to the second, but not the third, mechanism discussed above. The third mechanism, i.e., insertion of sorbitol channels from the cytosol into the stretched plasma membrane, is also strongly supported by the whole-cell capacitance (C_C) data.

The C_C kinetics given in Fig. 5, C and D, reflect changes in the total, i.e., electrically accessible, membrane area. Mild hypotonic stress (200 mOsm) increased C_C only slightly, if at all (Fig. 5, C and D). This is expected if the increase in cell surface is achieved exclusively by microvilli unfolding. In contrast, the dramatic increase in C_c at 100 mOsm (Fig. 5, C and D) must be due to incorporation of additional endomembrane material via exocytosis, as suggested elsewhere (8,9). Thus, we are driven to the conclusion that putative sorbitol-conducting channels observed at this hypotonic stress apparently arise from incorporated endomembrane material, e.g., from cytosolic vesicles. A similar mechanism is discussed by Czekay et al. (27) who found that in hypotonically treated rat renal inner medullary collecting duct cells, the fusion of cytosolic vesicles (containing sorbitol transporters) with the plasma membrane resulted in a rapid increase in sorbitol permeability.

CONCLUDING REMARKS

Electrorotation is obviously a powerful technique for noninvasive characterization of both transient and long-term changes in the electrical properties of cells undergoing volume regulation in hypotonic solutions. The data reported here have evinced that conflicting data and interpretations in the literature can partly be traced back to the hypotonic conditions to which the cells were subjected. We have demonstrated that electrolytes and monomeric sugars use distinct pathways that are activated by different hypotonicities, as also suggested by several authors (4–7,39). Although the electrolyte pathways seemed to be preexistent in the plasma membrane, the putative sorbitol channels were obviously inserted into the membrane from cytosolic vesicles by an exocytosis-like mechanism. Although this study focuses on the hypotonically induced uptake of sorbitol by Jurkat cells, similar regulatory mechanisms of swelling-activated fluxes of other small organic osmolytes can also be operational in different cell types.

The response of cells to hypotonic shock is not only of physiological but also of biotechnological interest. Thus, strongly hypotonic sugar solutions are useful in the production of therapeutically relevant hybrid cells via electrofusion, and also for electrotransfection of mammalian cells (18,40). In addition, development of cell-based biosensors for screening of pharmaceuticals and other compounds (e.g., ATP) is facilitated if hypotonic solutions are applied (41,42). Hypotonic sugar solutions have also an increasing potential in cryopreservation of rare and valuable mammalian cells and tissues (43).