Novel Changes in Discoidal High Density Lipoprotein Morphology: A Molecular Dynamics Study

Abstract

ApoA-I is a uniquely flexible lipid-scavenging protein capable of incorporating phospholipids into stable particles. Here we report molecular dynamics simulations on a series of progressively smaller discoidal high density lipoprotein particles produced by incremental removal of palmitoyloleoylphosphatidylcholine via four different pathways. The starting model contained 160 palmitoyloleoylphosphatidylcholines and a belt of two antiparallel amphipathic helical lipid-associating domains of apolipoprotein (apo) A-I. The results are particularly compelling. After a few nanoseconds of molecular dynamics simulation, independent of the starting particle and method of size reduction, all simulated double belts of the four lipidated apoA-I particles have helical domains that impressively approximate the x-ray crystal structure of lipid-free apoA-I, particularly between residues 88 and 186. These results provide atomic resolution models for two of the particles produced by in vitro reconstitution of nascent high density lipoprotein particles. These particles, measuring 95 Å and 78 Å by nondenaturing gradient gel electrophoresis, correspond in composition and in size/shape (by negative stain electron microscopy) to the simulated particles with molar ratios of 100:2 and 50:2, respectively. The lipids of the 100:2 particle family form minimal surfaces at their monolayer-monolayer interface, whereas the 50:2 particle family displays a lipid pocket capable of binding a dynamic range of phospholipid molecules.

INTRODUCTION

High density lipoproteins (HDL) represent a heterogeneous population of particles with apolipoprotein (apo) A-I as the major protein (1–5). ApoA-I appears to be secreted principally in a lipid-free form (6,7). HDL biogenesis then proceeds with the formation of discoidal HDL particles by addition of cell membrane-derived phospholipid and cholesterol (8,9).

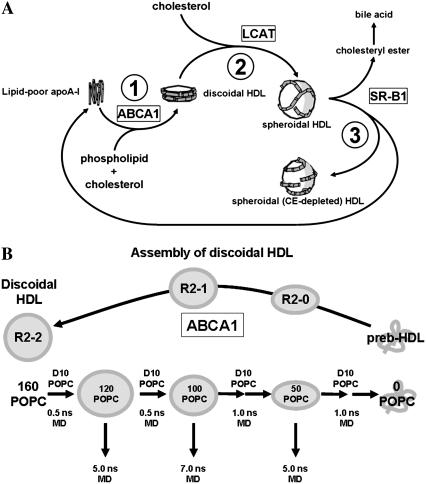
ApoA-I-containing lipoproteins in the form of HDL are inversely correlated with the risk of coronary artery disease and atherosclerosis. Of the possible mechanisms that have been suggested to explain this protective role of apoA-I, a process called reverse cholesterol transport is most completely understood at the molecular level. Reverse cholesterol transport consists of three relatively well-understood steps (Fig. 1 A). First, the transmembrane transport protein, ATP-binding cassette transporter A1 (ABCA1) (2), is required for the assembly of newly synthesized (lipid-poor) apoA-I into discoidal HDL, resulting, as a consequence, in cholesterol efflux from cells. Second, the activation of the enzyme lecithin/cholesterol acyl transferase (LCAT) (10) by apoA-I is necessary for esterification of the cholesterol molecules of HDL and leads to the conversion of discoidal to spheroidal (circulating) HDL. Third, interaction of spheroidal HDL with receptors, such as the scavenger receptor B, type I (3), leads to cholesterol uptake by the liver and excretion into the bile. This interaction results in remodeling of the spheroidal HDL particle, a process that regenerates lipid-poor HDL. Also, plasma enzymes and transfer proteins remodel lipid-poor and discoidal HDL particles (11,12). Thus a fuller understanding of reverse cholesterol transport demands knowledge of the detailed structure of the various HDL particles and the intermediates in their assembly. In this article, we use molecular dynamics (MD) to explore the structural nature of possible intermediates in the assembly of discoidal HDL from lipid-poor apoA-I during step 1 of reverse cholesterol transport (Fig. 1 A).

FIGURE 1.

HDL assembly. (A) Pathways of HDL assembly in reverse cholesterol transport. (B) Relationship of discoidal HDL assembly to the S/R method of particle size reduction.

Atomic resolution structural information on HDL is limited because, being a supramolecular assembly of proteins with lipids, HDL is dynamic. A detailed understanding of the lipid-associated structure of apoA-I is crucial because the lipid environment in HDL modulates apoA-I structure and function. The conformation of apoA-I is highly flexible since apoA-I exists in different states: lipid-free, lipid-poor, and discoidal or spherical lipoproteins of different size. The size of discoidal complexes is determined primarily by the number of apoA-I molecules per particle, but analysis of reconstituted HDL disks formed between apoA-I and phospholipids has revealed several discrete sized particles in complexes containing a constant number of apoA-I per particle (13).

The common lipid-associating motif in apoA-I is the amphipathic α-helix (14,15). The structure of apoA-I has been studied previously through MD simulations using different models, the picket fence (16,17) and the double belt (18,19). The structure of the lipoprotein core of cholesteryl esters has also been recently studied by means of MD simulations (20). This lab proposed in 1999 an atomic resolution double belt model for discoidal HDL that consisted of two of the lipid-associating domains of apoA-I arranged as continuous antiparallel amphipathic helixes around a bilayer disk containing 160 POPC molecules to form a 106 Å diameter particle (21). Although the initial derivation of this model depended critically upon certain features of the x-ray structure (22), the entire model can be derived a priori from profound constraints imposed on the conformation and orientation of lipid-associated proteins by the lipid bilayer. These constraints are: i), the amphipathic structure of apoA-I, ii), flat planar discoidal (bilayer) HDL geometry, iii), helical curvature dictated by the difference between the low dielectric constant of the lipid and the high dielectric constant of the solvent (23), and iv), the critical role of salt bridges in determining the specific antiparallel association of A-I monomers into the dimer (21). Each apoA-I monomer formed a curved, flat amphipathic α-helical ring with 11/3 (∼3.67) residues per turn (termed an 11/3 α-helix) in which the hydrophobic surface faced inward toward the lipid disk. The general features of the double belt model have been confirmed by several laboratories using physical chemical methods (24,25).

Using nondenaturing gradient gel electrophoresis, we recently showed that dimyristoylphosphocholine (DMPC) disks containing two apoA-I molecules, the R2 complexes, display two types of size heterogeneity: i), The most obvious form of size heterogeneity was the quantization of disks into five distinct, fairly monodisperse particles (26), with maximal Stokes diameters of 98 Å (R2-1), 106 Å (R2-2), 110 Å (R2-3), 114 Å (R2-4), and 120 Å (R2-5). This was termed stepwise heterogeneity. ii), The more subtle form of size heterogeneity that we described was a seemingly smooth increase in size of each of the individual particles with increasing DMPC/apoA-I molar ratios, a process termed continuous heterogeneity (26).

We further showed that the Stokes diameters of R2-1 and R2-2 are independent of the N-terminal 43 residues (the flexible domain) of apoA-I, whereas the flexible domain is necessary and sufficient for the formation of the three larger complexes. On the basis of these results, the conformation of apoA-I on the R2-2 disk was modeled quite satisfactorily as an amphipathic helical double belt extending the full length of the lipid-associating domain with N- and C-terminal ends in direct contact (27). Full length apoA-I on the flexible domain-dependent disks (R2-3, R2-4, and R2-5) model as the R2-2 conformation extended on the disk edge by one, two, or three of the 11-residue tandem amphipathic helical repeats (termed G1, G2, and G3), respectively, contained within the flexible domain (26).

A structural explanation for the size of the smallest of the disks, R2-1, requires a conformational change in the apoA-I belt. It was proposed at that time that R2-1 represented the R2-2 conformation with an antiparallel 15–18 residue pairwise segment of helixes hinged off the disk edge (a hinged-domain); several lines of indirect evidence were listed to support the model. The hinged-domain hypothesis was initially proposed as a general mechanism to explain the size heterogeneity of DMPC/apoA-I discoidal complexes (13). This hypothesis stated that one or more amphipathic α-helical segments of apoA-I undergo conformational changes to hinge off or on to the disk edge (13,26).

The hinged-domain model became more problematical when we observed that a particle even smaller than the R2-1 particle, a 78 Å Stokes diameter particle termed R2-0, results when apoA-I particles are reconstituted in vitro using palmitoyloleoylphosphatidylcholine (POPC), rather than DMPC (L. Li, J. Chen, F. Gu, J. C. Patterson, A. Catte, and J. P. Segrest, unpublished results). The specific problem faced was that a hinged-domain explanation for R2-0 required the hinging off additional antiparallel helical segments, a model that was difficult to conceptualize.

Thus, to explore the structural basis for the stepwise heterogeneity represented by R2-1 and R2-0, MD simulations were used to study the molecular nature of these discrete particles. A series of progressively smaller model HDL particles was formed by the removal of POPC molecules from the initial 106 Å disk, representing R2-2, created by a double belt rotamer of the lipid-associating domain of apoA-I (residues 41–243) (21,26). Fig. 1 B is a schematic diagram of the general strategy employed for particle size reduction. Because of data suggesting that the R2-1 and R2-0 particles have stoichiometries of ∼100:2 and 50:2 POPC/apoA-I, respectively (L. Li, J. Chen, F. Gu, J. C. Patterson, A. Catte, and J. P. Segrest, unpublished results), the two particles with these molar ratios were simulated for additional periods of time.

If discoidal HDL assembly represents a reversible process (a likely possibility; see Discussion), then a particle reduction strategy should provide useful structural information about the mechanisms of assembly of nascent HDL (Fig. 1 B). Because there is a good model for discoidal HDL and no comparable model for lipid-free apoA-I, lipid removal was a better strategy for study of HDL assembly than lipid addition.

During our particle reduction experiments, the predicted detachment of a hinged domain from the disk edge failed to materialize (18,26). Rather, the belt remained attached to the disk edge, although there was a major and progressive conformational change in the apoA-I belt. Thus the lipid structure was twisted out of the plane of the original disk into a saddle-shaped structure, to an extent that was unexpected and, to our knowledge, unprecedented for a nonrepetitive, bounded lipid structure. Further, the relatively short simulation time required for these conformational changes indicated a rapid convergence of the protein-lipid supramolecular structures in the system.

MATERIALS AND METHODS

Generation of model structures

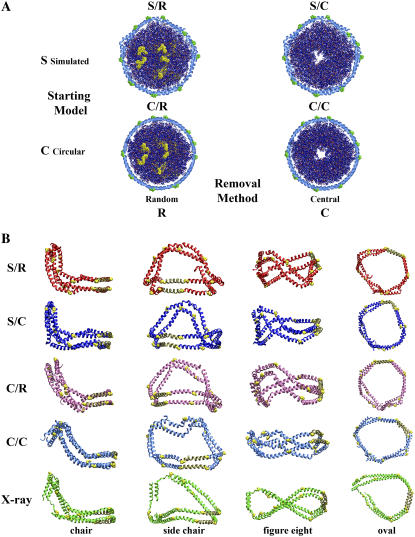
Two starting structures were used in this work (see Fig. 2 A). The first consisted of a de novo created circular Δ40 apoA-I double belt surrounding a planar POPC bilayer with lipid coordinates obtained from a previous simulation of the liquid-crystalline phase (27) (model C). The second is the final structure from a 10 ns simulation of C (model S) (Z. Su, J. P. Segrest, and S. C. Harvey, unpublished data). The POPC molecules were removed by deleting the relevant coordinates from the Protein Data Bank file of each simulated structure. Two methods were used to decrease the number of POPC in the two starting disk models. The first involved a somewhat randomized removal methodology (removal condition R), consisting of a procedure to refrain, as much as possible, from both removing lipids from the disk edge and creating transbilayer holes. The other method, central bilayer removal (removal condition C) involved removing lipids strictly from the center of the circular disk's bilayer. Both removal methodologies removed 10 POPC molecules in incremental steps, 5 from each side of the bilayer. To choose the structure with the minimum numbers of transbilayer holes, before applying the R method, 13 different starting structures with different selected POPC molecules were visually inspected at each particle reduction step until the particle contained 40 lipids. Model HDL particles with 30, 20, and 10 POPC molecules were chosen by inspecting two different starting structures. The structure with the fewest and smallest transbilayer channels was selected (28).

FIGURE 2.

Use of particle reduction method B to test convergence of protein conformation to the x-ray crystal structure. (A) Particle reduction method B displayed in a 2 × 2 table showing the two different 160:2 starting models (S, previously simulated and C, circular) subjected to two different removal conditions (R, random and C, central). POPC molecules removed are denoted in yellow for the removal condition R and are not shown for the removal condition C. (B) Four different views of apoA-I from the four different MD simulations produced by the particle reduction method B compared with four comparable view of the AB apoA-I pair from the tetrameric x-ray structure. (Top row) S/R, red; (second row) S/C, blue; (third row) C/R, mauve; (fourth row) C/C, blue (this model required a longer simulation time than the other three, 4 vs. 0.5 ns); and (bottom row) AB apoA-I pair from the tetrameric x-ray crystal structure, green. All structures are shown in ribbons representation, helix 5 segments (residues 121–142) are shown in tan in all representations, and prolines are space filling in yellow in all representations.

Energy minimization

After each removal step, all chosen model HDL particles were subjected to 5000 steps of energy minimization to remove steric clashes. The energy-minimized model HDL particles were then solvated using the Solvate plug-in of visual molecular dynamics (VMD) (29) in a cubic periodic water cell extending at least 25 Å beyond the lipid headgroups and the protein molecules. The solvated systems were then subjected to 25,000 additional steps of conjugate gradient energy minimization to reduce steric contacts between water molecules and the lipoprotein complexes. The final model systems with protein, lipid, and water molecules had a total number of atoms ranging from ∼312,000 atoms for the model HDL particle with 150 POPC molecules to 206,000 atoms for the model HDL particle with 50 lipid molecules (including hydrogen atoms).

Molecular dynamics simulations

All simulations were performed using NAMD (30) on three shared high-performance computer clusters at the University of Alabama at Birmingham (UAB). All model HDL particles with 160–100 POPC molecules were simulated for at least 0.5 ns, whereas those with 90 POPCs or less were simulated for at least 1.0 ns. The CHARMM 22 and 27 force fields were used for protein and lipid molecules, respectively. Nonbonded van der Waals and electrostatics interactions were truncated using a cutoff distance of 12 Å. The pressure was held constant at 1 atm for all simulations using Berendsen's pressure bath (31). Velocity reassignment was carried out every 1 ps during the first 30 ps of simulation, increasing the temperature in the simulation from 30 to 310 K, after which the temperature was held constant using Berendsen's temperature bath. Coordinate trajectories were updated every 10 ps of simulation and all 50–100 structures were used for analysis. The particle mesh Ewald (PME) treatment of long-range electrostatic interactions for model HDL particles with a number of POPC molecules ranging from 160 to 120 (only for model S and removal condition R) led essentially to the same results as those performed without PME.

To be certain that the key particle sizes were equilibrated, five different particles chosen inside the SR pathway were simulated for longer times: 120:2 for 5 ns, 100:2 for 7 ns, 50:2 for 5 ns, 30:2 for 3, ns and 10:2 for 3 ns. All five MD simulations were performed at 310 K and 1 atm using the PME treatment of long-range electrostatic interactions.

Root mean-square deviations

The root mean-square deviations (RMSDs) were employed to verify that each simulated model HDL particle was equilibrated. RMSDs of all protein atoms and all atoms of POPC molecules of every model HDL particle were measured over the entire trajectory using the structure obtained after the first 30 ps of the MD simulation (the first structure at 310 K) as a reference.

We also performed structural alignments of four simulated model HDL particles with the x-ray crystal structure of lipid-free apoA-I using the average position of the alpha carbons from the last 20% of each trajectory. The standard way of measuring RMSDs give high values because proteins in our simulated structures bend (see Fig. 1 of Supplementary Material) in the opposite direction from the x-ray crystal structure.

Improved RMSDs were obtained by reindexing the x-ray crystal structure to include a 22-residue shift in each protein chain. Also, the index values for the A chain were switched with those of the B chain. The net result is that residues 122–143 (helix 5) in the crystal structure were compared to residues 100–121 (helix 4) in one chain and residues 144–165 (helix 6) in the other chain of the simulated structures (see Fig. 2 of Supplementary Material). This gave lower RMSD values for three of the simulated structures (S/R, S/C, and C/R), but somewhat higher values for the C/C simulation.

Solvent-accessible surface areas

The solvent-accessible surface area (SASA) of POPC hydrophobic groups, represented by carbon and hydrogen atoms of the fatty acyl chains (palmitoyl and oleoyl chains), without including the carboxyl group, were measured over the entire trajectory and averaged over the last 20% of each trajectory.

Best-fitting surfaces and fit parameter

The data used in the numerical fits for the particle with a clear saddle-shaped monolayer interface, 100:2, were generated in three ways. First, the coordinates for the methyl carbons of the POPC molecules were recorded at every 10 ps of the 7 ns simulation for the 100:2 POPC/apoA-I particle. Then only the coordinates for the average atomic positions that were within 0.2 Å of the coordinates of the average atomic positions in the other leaflet were kept, generating a set of 2193 points. Second, the average coordinates for the methyl carbons of the POPCs were recorded for the last 2 ns of simulation for the 100:2 POPC/apoA-I particle; this generated a data set of 200 points. Finally, the atoms in each leaflet from the 200 point set that were within 4.5 Å of atoms in the opposing leaflet were kept, generating a data set of 78 points.

These data point sets were then numerically fitted to surfaces from three different families using a least-squares algorithm (32). The sum of the squares of distances from each point to the surface was minimized over a number of parameters. The distance was taken as the closest point distance (i.e., perpendicular offsets, also known in the linear case as total least squares). For Enneper's minimal surface, the seven parameters were three rotation parameters, three translations, and a scaling parameter. For the catenoid, one of the rotation parameters could be dropped thanks to the symmetry. For the hyperbolic paraboloid, an additional parameter involving the ratio of the two principal axes was added.

Code for nonlinear least-squares fitting with perpendicular offsets was developed specifically for this project under Maple 10, since ready-made code was not available. The code uses a Maple built-in routine (from the Optimization package) to find the closest point, and a conjugate gradient method to minimize the sum of square residues.

The quality of the fit is measured by a fit parameter:

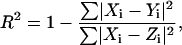where are the data points, 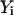is the point closest to 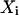on the surface, and 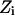is the point closest to 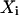on the best-fitting plane (again with perpendicular offsets).

It is important to note a number of facts regarding R². First, this fit parameter is different from the usual correlation coefficient in linear regression:

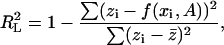where 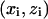are the data points with 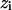the vertical coordinate, 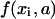is a linear (or nonlinear model) depending on parameters 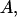and 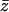is the average of 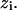Next, it should be observed that although the numerator of the fraction in 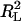is the sum of square residues with vertical offsets, the denominator can be viewed as the sum of square residues from the best fitting horizontal plane. Since in the case of perpendicular offsets there is no preferred vertical direction, that has been replaced by simply the best-fitting plane. Now, if a rotation is performed so that this best-fitting plane becomes horizontal, then the denominators in R² and 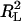become equal (although the numerators are still different) and the linear regression coefficient becomes zero. Thus, we may view R² as a substitute for 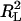in the case of perpendicular offsets once the latter one has been calibrated to zero. Finally, if the family of surfaces admits scaling, then since after scaling by a sufficiently large parameter, any surface becomes indistinguishable from a plane, it follows that the numerator of the fraction in R² is always smaller than the denominator, and hence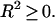

Triangulation of surfaces for calculation of areas and surface normals

To calculate the bilayer surface area per lipid molecule, we used VMD and modified Tool Command Language scripts from the VMD script library (33). The original script uses the phosphorus atoms of each lipid headgroup from a single side of the bilayer, projects their three-dimensional coordinates onto an approximate best-fit plane, and determines a Delaunay triangulation of those two-dimensional points eliminating any triangle with a side greater than a cutoff threshold (chosen to be 40 Å), to draw an approximation of the lipid surface using the original coordinates and the derived set of triangles. The adapted script takes the same set of derived triangles and sums their area using the original coordinates of phosphorus atoms.

Since this calculation of the bilayer surface area per lipid molecule ignores the area between the phosphorus atoms and the protein, it will be an underestimate. To compensate, for each leaflet the triangulation above was also performed including the Cα of each residue at position 3 (referring to the third position within the tandem 11/3 α-helical motif in the lipid associating domain of apoA-I; see Segrest et al. (21)) of the corresponding protein chain. The mean position of residue 3 represents a first approximation of the edge of the headgroup surface. Here again our areas are calculated with the original coordinates of phosphorus atoms.

This calculation in turn will be an overestimate of the mean bilayer surface area per lipid. To find a compromise between these under- and overestimates, we reasoned that the total triangulated area is approximately equal to the correct area minus half of the contribution to the area coming from the lipids in contact with the protein (annular lipids), leading to the following equation:

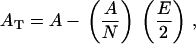where A_T is the total triangulated area, A the total correct area, (A/N) the correct area per lipid with N the total number of lipids, and E the number of annular lipids. Solving for A gives A = A_T/(1 – E/(2 × N)).

Deuterium order parameters profiles

The order parameters can be calculated easily for flat lipid bilayers (18) and can yield valuable structural information. The deuterium order parameter is given by

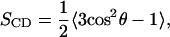where θ is the angle between the C-H bond and the bilayer normal.

However, this calculation was not trivial because we were dealing with curved lipid bilayers and thus we could not use a single normal to represent the lipid bilayer. To overcome this problem, methods for finding the local normals to the lipid surface were developed. Using a modified version of the script described in the previous paragraph, we were able to assign a different normal to each phosphorus atom of the model HDL particle, by taking each normal to be the normalized vector sum of all the normals of the triangles surrounding the atom. The order parameters for the sn-1 and sn-2 chains of POPC molecules were calculated, averaging them for both C-H bonds and all lipids for a given methylene group. This parameter was calculated every 10 ps during the simulation, and the reported results are averages over the last 40% of each trajectory. Further, the different orientational order of the annular lipids, defined as POPC molecules with a phosphorus atom within 6.8 Å of any protein atom, were monitored and compared versus that of central lipids (those in the bulk of the lipid bilayer). The 6.8 Å was chosen from the P-P radial distribution functions and it corresponds to the first minimum in the P-P radial distribution functions (data not shown).

Electron microscopy

Human plasma apoA-I was purified according to the procedure described previously (26). Reconstituted HDL particles at different POPC/apoA-I molar ratios were prepared by the sodium cholate dialysis procedure. To make homogenous R2-0, R2-1, and R2-2 particles, the molar ratios of POPC/Δ43apoA-I at 50:2 and 100:2 and POPC/Δ43apoA-I at 160:2 were used, respectively. The Stokes diameters of these particles were determined by nondenaturing gradient gel electrophoresis as described previously (26) and by electron microscopy in this study.

The complexes had adsorbed to hydrophilic, carbon, and Formvar-coated grids. Samples were negatively stained for 20 s with 2% phosphotungstic acid, pH 7.0. Digital images were taken using a Philips CM-30 electron microscope equipped at 80 keV accelerating voltage. For quantification, at least 10 arbitrarily selected fields were chosen and more than 200 particles were measured.

RESULTS

Two methodologies for generation of smaller structures

Two sets of computations were performed.

Reduction methodology A

The S/R methodology (S = previously simulated apoA-I and R = randomized deletion POPC in increments of 10 molecules) was used to create a series of supramolecular assemblies with 160–0 POPC in increments of 10 molecules.

Reduction methodology B

Two starting structures (S and C = initially circular apoA-I) were coupled with two methods for removing POPC in increments of 10 molecules (R and C = deletion of central lipids) to obtain four different simulation methodologies (S/R, S/C, C/R, and C/C) for generating disks with 160–120 lipids (Fig. 2 A).

The particle structures converge and the protein conformation approximates the x-ray crystal structure

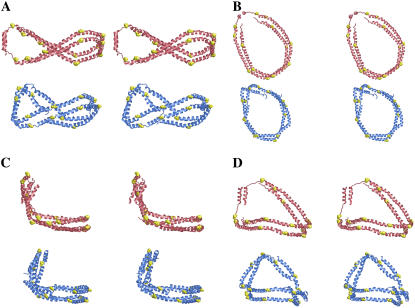
In reduction methodology A, as the particles decreased in size beyond the 150:2 particle, they adopted conformations that were less like the flat double belt structure and increasingly more nonplanar, twisted, ellipsoidal, and double helical. The 120:2 particle resulting from reduction pathway A was simulated for an additional 5 ns using PME and the resulting protein belt compared to the x-ray structure of the AB dimer (22). Fig. 3 and Table 1 show clearly that the two structures are remarkably similar, especially for helixes 3–7 (residues 88–186).

FIGURE 3.

Relaxed eyed stereo comparison of 120:2 particle simulated for 5 ns by S/R method with x-ray crystal structure of Δ43 apoA-I. Four different views of the AB dimer of the tetrameric x-ray crystal structure of Δ43apoA-I (red) are compared with four views of the Δ40 apoA-I dimer of the 120:2 model HDL particle (blue): (A) figure eight view, (B) top view, (C) front chair view, and (D) side chair view.

TABLE 1.

RMSD (Å) of alignment of α-carbons of protein component of 120:2, 100:2, and 50:2 particles with apoA-I x-ray crystal structure

	Particle
X-ray	S/R 5ns (50:2)	S/R 7ns (100:2)	S/R 5ns (120:2)	S/R	S/C	C/R	C/C
Helixes 4–6	7.3	5.1	4.2	3.7	4.3	5.1	4.7
Residues 99–164
Helixes 3–7	16.2	10.6	10.4	8.1	9.9	7.2	6.1
Residues 88–186
Helixes 4–6				4.0	5.0	4.3	4.1
Residues 99–164*
Helixes 3–7				5.8	8.1	6.3	8.6
Residues 88–186*

Alpha carbons positions are average over the last 20% of each trajectory.

^*Structural alignments performed changing the index number of alpha carbons of the x-ray crystal structure of lipid-free apoA-I (see Materials and Methods section).

Reduction methodology B was used to test convergence of MD simulations to the x-ray structure starting from four different pathways. This 2 × 2 table of particle production methodologies, S/R, S/C, C/R, and C/C (Fig. 2 A), was used to generate four particles containing 120 POPC molecules each. For all four particles, changes were observed in both lipid and apoA-I conformations as the particle size was decreased by sequential removal of POPC molecules followed by strikingly short MD simulations of 0.5 ns after each removal step (the last step of the C/C pathway required 4 ns simulation for convergence). In a very compelling result (Fig. 2 B), four steps of particle size reduction (totaling 2–7 ns) induced folding of the initial flat, circular double ring of apoA-I into an impressive approximation of the A and B chains from the 4 Å resolution tetrameric x-ray crystal structure of lipid-free apoA-I reported by Borhani et al. in 1997 (22). Compare the four views of the AB apoA-I dimer from the tetrameric x-ray structure in row 5 to comparable views of the four simulated structures in rows 1–4 (Fig. 2 B). To quantify the similarity between MD simulations and the x-ray crystal structure, different helical domains of apoA-I were chosen and their structural alignment was calculated and reported in Table 1. Only certain helixes were included in the RMSD results for two reasons: i), the lipid-free x-ray crystal structure is elongated relative to the simulated structures due to the presence of nonhelical extended regions in helixes 1 (residues 44–49) and 10 (residues 220–227) (22); and ii), both helix 10 domains (residues 220–241) are orientated at ∼60° to the plane defined by helixes 4–6 of apoA-I, suggesting that the lipid-associated structure would be different. Nevertheless, the central helixes fit relatively well considering that the simulations are dynamic and include lipid-protein interactions, whereas the crystal structure was obtained from high-salt solution in the absence of lipid (see Supplementary Material for more structural alignments).

Further, the average RMSDs for the alignments of the four different simulations of the 120:2 particles with each other (C/R, S/C, C/R, and C/C) are essentially identical to the average RMSD for the alignment of the four different particles with the 4 Å resolution x-ray crystal structure, 4.40 Å vs. 4.45 Å for helixes 4–6 and 7.20 Å vs. 7.83 Å for helixes 3–7, respectively. It is also interesting to note that RMSD values obtained by reindexing the x-ray crystal structure, as described in the Materials and Methods section, are lower for three of the simulated structures (S/R, S/C, and C/R), but somewhat higher for the C/C simulation as shown in Table 1 (see Table 1 of the Supplementary Material for more structural alignments). Given the resolution of the crystal structure, it is reasonable to consider structures with RMSDs within 8 Å of the apoA-I x-ray crystal structure as part of the conformational space that approximates the apoA-I structure. This indicates that the conformational space available to apoA-I to approximate the x-ray crystal structure is large (see Supplementary Material). This helps explain why only a few nanoseconds of MD simulation resulted in a dramatic conformational change in the apoA-I from a flat circle to the almost continuous nonplanar, twisted ellipsoidal, double amphipathic α-helical structure impressively resembling the x-ray crystal structure.

Analysis of the full set of particles produced by the S/R methodology

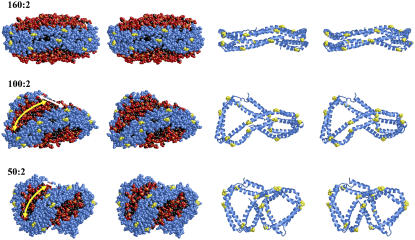
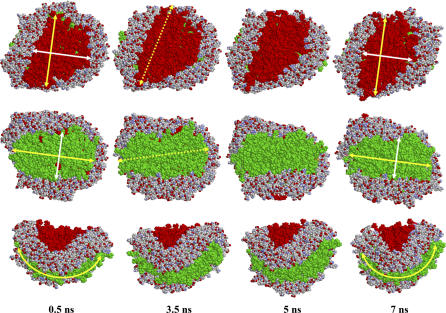
Of the 16 particles produced by reduction methodology A, the two particles containing 100 and 50 POPC were simulated for additional 5 and 7 ns, respectively, and their structures compared with that of the starting 160:2 particle in Fig. 4. Not only has the protein conformation changed dramatically in both the 100:2 and 50:2 particles from that of the starting particle, but so has the curvature of the lipid bilayer. The initially flat, circular POPC bilayer headgroup surfaces (Fig. 4, top row) become progressively more ellipsoidal and curved the smaller the particle. In one of the principal directions (those directions along which the curve of intersection between the surface and normal planes attains a maximum and a minimum) the surface narrows and the principal curvature tends to zero (white arrows in Fig. 4, middle and bottom rows), whereas in the other principal direction (necessarily perpendicular), the principal curvature (initially equal in magnitude and of opposite sign as the first one) increases in magnitude (yellow arrows in Fig. 4, middle and bottom rows). The three particles in Fig. 4 have the following dimensions: (top row) 160:2 particle, 104 × 104 × 43 Å; (middle row) 100:2 particle, 95 × 66 × 44 Å; and (bottom row) 50:2 particle, 81 × 50 × 50 Å.

FIGURE 4.

Relaxed eyed stereo images of the 160:2 (5 ns), 100:2 (7 ns), and 50:2 (5 ns) particles produced by the particle reduction method A. Two different views are shown as space filling and ribbons representations of each particle containing POPC/Δ40 apoA-I at molar ratios of 160:2 particle, which represents the starting 106 particle (R2-2); 100:2 particle, which has the approximate molar ratio of the 95 Å particle (R2-1); and 50:2 particle, which has the approximate molar ratio of the 78 Å particle (R2-0). Charged portions of the POPC headgroups are space filling in red (oxygen atoms) and orange (phosphorus atoms), and fatty acyl chains are space filling in black. The protein is in blue and prolines are space filling in yellow in both representations. The width of the surface in one principal direction (in which the principal curvature is nearly zero) is denoted by white arrows, whereas the other principal direction is indicated by yellow arrows.

Negative stain electron microscopy of the R2-2, R2-1 and R2-0 particles

Methods to experimentally reconstitute individual R2-2, R2-1, and R2-0 particles (L. Li, J. Chen, F. Gu, J. C. Patterson, A. Catte, and J. P. Segrest, unpublished results) were recently developed. Using these methods, each of the three particles was subjected to negative stain electron microscopy. The results are shown in Fig. 5. The R2-2 particles form discoidal particles that tend to stack with measured diameters of 89 Å and thicknesses of 30 Å; the center-to-center distances of the stacked disks, however, measure 43 Å, which is the thickness of the bilayer in our simulated 160:2 particle, suggesting these electron-microscopy measurements are an underestimation of the particle's true dimensions (Fig. 5, top panel). The R2-1 particles are similar in appearance to the R2-2 particles, except they do not stack; the majority have measured diameters of 75 Å and thicknesses of 31 Å (Fig. 5, second panel from top), although several have thicknesses of 43 Å (red arrows). The R2-0 particles are generally oval in appearance and do not stack; the majority have measured dimensions of 60 × 37 Å (Fig. 5, third panel from top), although several are spheroidal in appearance (red arrows), with diameters of ∼37 Å, suggesting that these particles are prolate ellipsoidal in shape. Assuming that direct measurement of edge-to-edge negative stain images underestimate size by 13 Å (see above), the dimensions of the negative stain particles can be corrected to: R2-2, 102 × 102 × 43 Å; R2-1, 88 × 56 × 43 Å; and R2-0, 73 × 50 × 50 Å. Therefore, R2-2, R2-1, and R2-0 particles seen by electron microscopy are similar in shape and proportionate dimensions to the 160:2, 100:2, and 50:2 structures generated by MD simulations (right-hand insets).

FIGURE 5.

Negative stain electron microscopy of experimentally reconstituted R2-2, R2-1, and R2-0 particles. Each reconstituted HDL particle is compared to its corresponding simulated particle in a right-hand inset. Black or white arrows denote representative images in each field. The red arrows in R2-1 denote particles with thicknesses of 43 Å; the red arrows in R2-0 denote particles that are spheroidal in appearance with diameters of 37 Å.

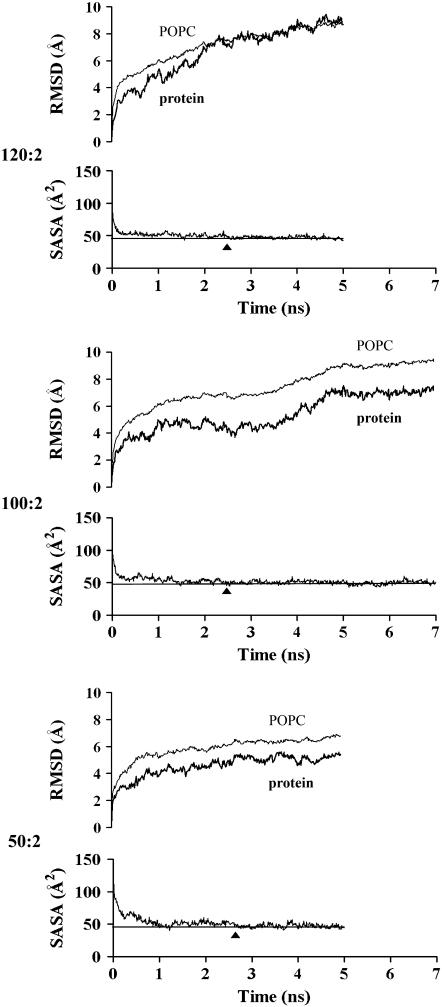
Changes in RMSD and SASA as a function of time of simulation

To measure the convergence of individual particles, RMSD for the protein and POPC components and SASA of the POPC acyl chains/POPC were plotted against time of simulation (Fig. 6). It was assumed that convergence of a given particle was independent of the convergence of intermediate particles. The results of Figs. 2 and 3 for the 120:2 particle clearly support this assumption; the four brief simulations each using different starting and removal conditions produced four protein conformations similar both to the x-ray crystal structure and to the 120:2 particle subjected to a 10-fold longer simulation time. Our longer simulation times thus focused upon the three particles of most interest, 120:2, 100:2, and 50:2, that were subjected to 5 ns, 7 ns, and 5 ns MD simulations, respectively.

FIGURE 6.

Changes in RMSD and SASA of the POPC acyl chains per POPC molecule with time of simulation for the 120:2 (5 ns), 100:2 (7 ns), and 50:2 (5 ns) particles produced by the particle reduction method A.

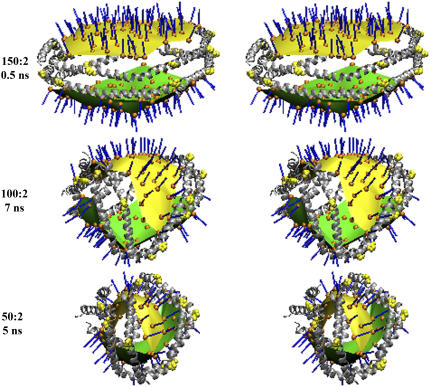
From Fig. 6, it is apparent that the RMSDs for the 120:2, 100:2, and 50:2 particles increase rapidly until 0.5–1 ns, at which point the rates of change decrease. In addition, the decrease in SASA of the POPC acyl chains/POPC is similar for all three particles, each particle reaching a limiting value of 47–50 Ų/POPC at ∼2.5 ns (solid triangles). The 100:2 particle took longer to converge than the 120:2 and 50:2 particles. The rapid increase in RMSD reached a plateau by 1 ns for all three particles but increased again at ∼3.5 ns for the 100:2 particle, reaching a second plateau at 5 ns. This additional complexity is believed due to slow relaxation of several acyl-chain interdigitations created between the two monolayers by random removal of POPC from the central region in the 100:2 particle. Because of this added complexity, the 100:2 particle was simulated for 7 ns.

Fig. 7 illustrates important structural changes in the 100:2 particle occurring during the 7 ns of MD simulation. Between 0.5 and 3.5 ns, there is closure of surface gaps between headgroups but little change in total headgroup area. Between 3.5 and 5 ns, there is a significant decrease in total headgroup area that results in narrowing of the headgroup surface along one of the principal directions (solid white arrows) and a corresponding decrease in radius of curvature along the other principal direction (solid yellow arrows). No significant structural changes occur in the 100:2 particle beyond 5 ns. The rather abrupt change in particle dimensions between 3.5 and 5 ns likely is due to relaxation of acyl chain interdigitation. No comparable changes in particle dimensions occur after 0.5 ns for either the 120:2 or the 50:2 particles (data not shown). The long axes of the two ellipsoidal headgroup surfaces (dashed yellow arrows on red versus green surfaces) are tilted at angles of ∼60° to one another. Since differential geometry dictates that two principal directions of curvature must be offset by 90°, the long axes of the opposite surfaces are close, but not identical, to the principle axes of curvature (dashed versus solid yellow arrows, respectively).

FIGURE 7.

Changes in 100:2 particle during 7 ns of MD simulation. Three different views of the 100:2 particle taken at four different time frames are shown. All structures are shown in space-filling representation; the protein is in CPK colors and the two different leaflets of the lipid bilayer are shown in red and green. Yellow and white arrows show how the two radii of curvature of the particle change during simulation. The dotted yellow arrows show the long axes of the two ellipsoidal headgroup surfaces.

Changes in SASA as a function of POPC/ApoA-I ratio

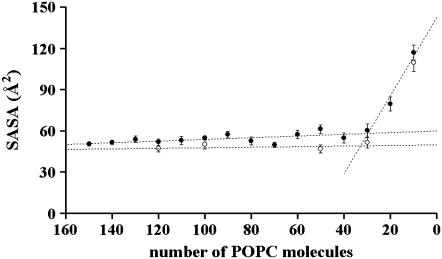
Fig. 8 is a plot of the mean SASA of POPC acyl chains/POPC molecule (34) over the last 20% of the simulation for each particle (150:2–10:2) produced by particle reduction methodology A. A linear least-squares fit for the points between 150:2 and 40:2 gives a straight line with essentially zero slope, indicating no measurable differences in the SASA of POPC acyl chains/POPC molecule between any of these particles. This conclusion is supported by plotting the mean SASA of POPC acyl chains/POPC molecule for the last 20% of the trajectory of the longer simulations of the 120:2, 100:2, 50:2, and 30:2 particles. Since the value for the 30:2 particle decreased with longer simulation, the linear least-squares fit for this plot also gives a straight line with zero slope and an average value of ∼49 Ų per POPC. These results are important, since they show that for even the smallest, most highly curved particles, such as 50:2 and 30:2, headgroup coverage of the solvent/acyl chain interface is indistinguishable from that of the larger, essentially flat discoidal particles.

FIGURE 8.

SASA of the POPC acyl chains per POPC molecule for the particles simulated by particle reduction method A and PME are reported as a function of the number of POPC molecules. The solid and open circles refer to model HDL particles subjected to short (0.5–1 ns) MD simulations and to long (3–7 ns) MD simulations, respectively. The reported values are averaged over the last 20% of the trajectory of the MD simulations. The error bars are standard deviations.

However, even after a total of 6 ns simulation involving a 1 ns temperature jump to 410 K followed by 2 ns annealing at 310 K, the average SASA per POPC for the 10:2 particle reached a constant minimum that remained elevated at ∼110 Ų per POPC. Thus it appears that there may be a fundamental increased exposure of acyl chains to the solvent in the 10:2, and probably the 20:2, particle(s), relative to the larger particles, perhaps due to the absence of residues 1–40 in the simulated particle.

The POPC monolayer interface in the 100:2 particle approximates a minimal surface

After 0.5 ns of simulation, the 100:2 particle formed saddle-shape surfaces, both at its headgroup surfaces (Fig. 7, bottom panel) and at the interfacial surface between the two monolayers (data not shown). After longer simulation times, one of the principal curvatures of the two headgroup surfaces became essentially flat (Fig. 7, bottom panel), but the saddle-shaped curvature of the monolayer interface remained (see Fig. 4, middle row). It is now generally recognized, based upon x-ray diffraction analysis by Luzzati and co-workers (35), that the monolayer interfacial region of inverted cubic lipid phases, called inverted bicontinuous cubic phases, approximate minimal surfaces (35,36). Mathematically, a minimal surface is one that has zero mean curvature at every point, i.e., every point is a saddle point with principal curvatures of opposite sign and equal magnitude.

Due to the equivalence, at physiological temperatures, of the cross-sectional areas of the headgroup and acyl tail regions of each molecule, a flat bilayer, a trivial minimal surface, is the preferred organization for lamellar-forming lipids. To say it another way, the lamellar POPC molecules seek to minimize their surface area through minimization of the absolute value of their surface mean curvature at each point. Any spontaneous curvature vanishes for symmetric lipid bilayers, but in general becomes finite for nonsymmetric monolayers (spheroidal micelles, inverted hexagonal phases), and thus plays an important role in determining the morphology of lipid phases (37). The different forces acting on the two monolayers of a symmetric bilayer tend to counterbalance, namely the electrostatic attractive and repulsive interactions between polar headgroups and the attractive hydrophobic interactions between acyl chains of lipid molecules, by reaching a minimum in the mean curvature of their monolayer interfacial region. Thus, lamellar-forming lipids can form saddle-shaped minimal surfaces. The interfacial surfaces between lipid monolayers in stoichiometric and thermal equilibrium approximate minimal surfaces due to the highly disordered state of the so-called chaotic zones where acyl methyl groups from each monolayer meet (35–37). The physical basis for this phenomenon is that within this chaotic, but symmetric, zone, equivalent positions on opposite sides of the interface must have equivalent pressures, driving the chaotic zone to an approximation of a minimal surface. We suggest that decreasing the POPC surface area while the protein boundary length is unchanged, as occurs in the transition from the 160:2 to the 100:2 particle, produces a saddle-shaped curvature of the POPC monolayer interface that resembles a patch of a minimal surface. An alternate mechanism to allow a decreased POPC surface area would be the formation of a hinged domain, a result not observed in our simulations.

Although in the literature there are a large number of publications about infinite periodic minimal surfaces, or IPMS, (37–40), other than the mathematically trivial minimal surface of a flat bilayer disk, nonperiodic minimal surfaces, such as Enneper's minimal surface (41–43), have not been reported for lipid phases. This is to be expected since nonperiodic geometry would exclude lipid phases with that geometry from ever having been observed in x-ray diffraction studies.

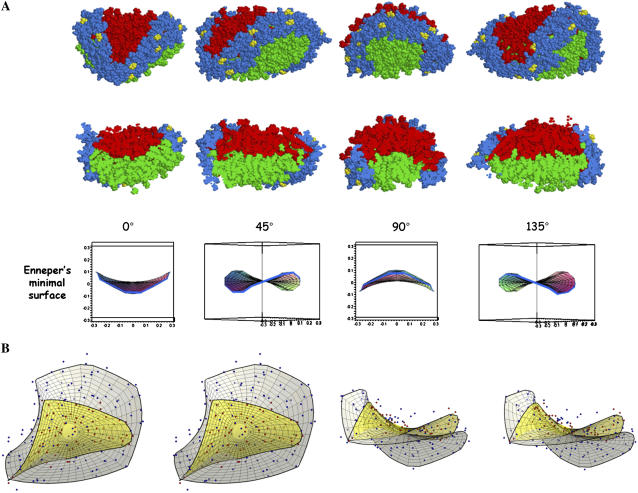
To test the postulated formation of an approximation of a minimal surface, the end methyl carbon atoms of both leaflets of the 100:2 particle were used to obtain an approximation of the monolayer interface (35). Fig. 9 illustrates both qualitative (A) and quantitative (B) fits of the monolayer interface to a minimal surface. Qualitatively, the apoA-I double belt undergoes substantial bending and twisting to conform to the edge of the distorted bilayer in the way that a wire frame with the appropriate shape will create a patch of a minimal surface from a soap film (44) (compare Fig. 9 A, top row, with Fig. 9 A, middle row). The saddle-shaped curvature of the monolayer interface of the 100:2 particle displayed in cross section at 45° rotational intervals in Fig. 9 A, middle row, and the corresponding topography of its double belt, Fig. 9 A, top row, correspond closely to the cross-section and edge topography of a patch of Enneper's minimal surface shown in Fig. 9 A, bottom row.

FIGURE 9.

Qualitative and quantitative fit of 100:2 particle (7 ns simulation) with Enneper's minimal surface. (A) Rotational fit of the 100:2 particle monolayer interface a patch of Enneper's minimal surface. Top row, side view of space-filling images of the complete particle rotated with a periodicity of 45°; middle row, side view of space-filling images of a cross section of the particle to show the alternating curvature of the lipid bilayer monolayer interface; and bottom row, side view of images of a patch of Enneper's minimal surface. From left to right, alternating curvatures with opposite signs with a period of 90° are clearly recognizable in the monolayer-monolayer interface. Also, the bounding curve for Enneper's minimal surface and the apoA-I protein belt undergo similar transformations. ApoA-I molecules are shown in blue; POPC molecules of the two leaflets are shown in red and green, respectively; and prolines are shown in yellow. (B) Relaxed eyed stereo images of mathematical fit of 100:2 particle monolayer interface. The 78 points data set (in red) and the 200 points data set (in blue) are shown together with the corresponding patches of Enneper's minimal surface in two views: top view and side view.

Table 2 shows R² values for fits of the monolayer interface defined by three criteria to three saddle-shaped families of surfaces, Enneper's minimal surface, and the catenoid, both representing minimal surfaces, and the hyperbolic paraboloid that approximates a minimal surface. From the table, one can see that the best fit is to the surface defined by the average position of the 78 acyl methyl carbon atoms within 4.5 Å of methyl carbons in the opposite leaflet, with an R² of 0.798. In every case, the Enneper's surface has only a slightly better R² value than either the catenoid or the hyperbolic paraboloid. The particular patch on the Enneper's surface producing the best fit for each set of points representing monolayer interfacial acyl methyl carbon atoms are essentially indistinguishable from the best fit patch on either of the other two surfaces: when the points were projected onto best-fitting Enneper's minimal surface and then fitted back to one of the other surfaces, R² values of 0.974 for the hyperbolic paraboloid to 0.998 for the catenoid were obtained. Therefore, it is likely that these particles fit other minimal surfaces possessing saddle shapes, including those formed by the cubic phase of lipids. Indeed, it is even possible these particles may represent a patch of the cubic phase, bound by protein.

TABLE 2.

Analysis of shape of chaotic zones in 100:2 particle

	No. of acyl methyl carbon atoms	Minimization of sum of square residues with perpendicular offsets (R2)
		Enneper	Catenoid	Hyperbolic paraboloid
Acyl methyl carbon atom trajectories*	2193	0.715	0.707	0.714
Average acyl methyl carbon atom positions†	200	0.644	0.633	0.642
Average acyl methyl carbon atom positions‡	78	0.798	0.767	0.789

Fits of monolayer interfacial chaotic zone to saddle-shaped surfaces.

^*Trajectory over full 7 ns of simulation of acyl methyl carbon atom trajectories within 0.2 Å of any atom on the opposite monolayer in the 100:2 particle.

^†Average position of acyl methyl carbon atoms over last 2 ns.

^‡Average position of acyl methyl carbon atoms over last 2 ns within 4.5 Å of opposite methyl carbons.

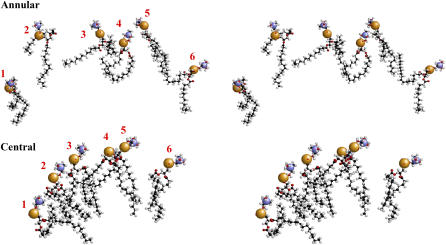
Fig. 9 B shows stereo views of the graphic plot of the fit to corresponding patches of Enneper's minimal surface of the point cloud represented by: i), the average position of the 78 acyl methyl carbon atoms with the least disorder relative to the opposite acyl methyl carbons, and ii), the point cloud of the average position of all 200 acyl methyl carbon atoms. Note that the set of 78 points cluster entirely at the center of the overall surface defined by all 200 points. Thus the fit is better in the center of the patch than on the periphery, consistent with the results of the order parameter calculations shown in Fig. 10 and discussed below, showing that the annular or perimeter POPC molecules are disordered compared to the central POPC molecules.

FIGURE 10.

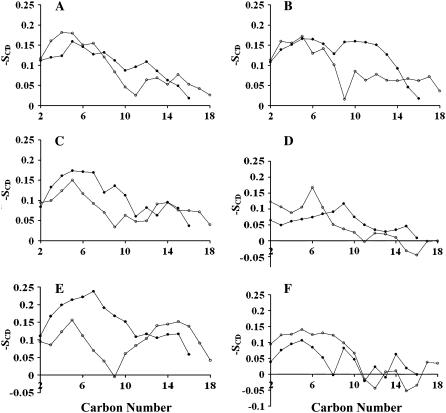
Deuterium order parameters for the simulated particles with POPC/Δ40 apoA-I molar ratios of (A) 150:2, (B) 120:2, (C) 100:2, (D) 50:2, (E) central lipids of 100:2, and (F) annular lipids of 100:2 averaged over the last 40% of each trajectory. The values for the S_CD are averages over both hydrogen atoms on each methylene carbon and are shown as solid circles for the sn-1 (palmitoyl) chain and as open circles for the sn-2 (oleoyl) chain.

Orientation of POPC molecules in model HDL particles

The order parameters of POPC molecules for four different model HDL particles are reported in Fig. 10. It is noteworthy that the order parameters profiles of the sn-1 (palmitoyl) and the sn-2 (oleoyl) chains observed for 150:2 (Fig. 10 A) are similar to those reported by Klon et al. (18) for different model HDL particles with 160 POPC and 2 Δ43 apoA-I molecules and are comparable to experimental results for flat POPC lipid bilayers. It is also worth noting that the oleoyl chain exhibits the characteristic minimum in the double bond region (45). The model HDL particle with 120 POPC molecules showed a less ordered sn-2 chain and a more ordered sn-1 chain (Fig. 10 B) compared to 150:2. The observed change in the orientation of POPC molecules might depend on the increased portion of the analyzed trajectory (2 ns for 120:2 vs. 200 ps for 150:2) but more likely arises from an increase in the population of annular POPC (operationally defined as POPC, whose phosphorous atom is within 6.8 Å of any protein atom). The order parameters of 100:2 and 50:2 particles (Fig. 10, C and D) had profiles progressively more disordered than the 150:2 and 120:2 particles. So, it was postulated that the dramatic decrease of order observed for the 50:2 particle for both sn-1 and sn-2 chains was related to a population of annular POPC approaching 100%. This hypothesis was confirmed by calculating the order parameters for central and annular lipids of 100:2 (Fig. 10, E and F). This difference in the order of the POPC molecules can be seen in Fig. 11 (standard deviations of the average order parameters were between 0.01 and 0.02), where six randomly selected annular and central lipids of the 100:2 particle are shown. Of the selected POPC, five of six of the annular POPC are distinctly more disordered than five of six of the central POPC.

FIGURE 11.

Relaxed eyed stereo images of six randomly selected annular and central POPC molecules from the model HDL particle with a POPC/Δ40 apoA-I molar ratio of 100:2 simulated for 7 ns. The phosphorous and the choline nitrogen atoms are shown in space-filling mode and the remainder of the POPC molecules in ball-and-stick mode. In the annular view, POPC 5 is ordered, and in the central view, POPC 1 is disordered.

Measurement of surface areas of model HDL particles

The average areas per POPC headgroup for the 120:2, 100:2, and 50:2 particles were calculated using the procedure and equations reported in the Materials and Methods section and were found to be 85.7, 90.3, and 107.4 Ų, respectively. The standard deviation of the mean bilayer surface area per lipid was 7 Ų. The triangulated surfaces used for the calculations are shown in Fig. 12. This figure also shows the normals determined for each phosphorous atom in the three models. Note that the radial divergence of the angles of the normals for the 100:2 and 50:2 particles suggests that their headgroup surfaces are becoming more spherical.

FIGURE 12.

Triangulated POPC surfaces of three different model HDL particles with POPC/Δ40 apoA-I molar ratios of 150:2 (0.5 ns), 100:2 (7 ns), and 50:2 (5 ns) calculated for the last frame of each trajectory. The normals employed by the script described in the Materials and Methods section to draw the lipid surface of each model HDL particle are shown as blue cylinders. All triangulated surfaces are shown in yellow and green for the two different leaflets. All structures have the protein in silver ribbons representation, and phosphorus atoms and prolines in orange and yellow space filling, respectively.

The area of the monolayer interface as defined by the end methyl carbon atoms (Table 2) was calculated for the 100:2 particle using the average positions of the deep hydrophobic residues at position 6 (referring to the sixth position within the tandem 11/3 α-helical motif in the lipid associating domain of apoA-I; see Segrest et al. (21)); this residue essentially defines the edge of the bilayer center. The value obtained by fitting these positions to the Enneper's surface patch corresponding to the average positions of the 200 end methyl carbons shown in Table 2 was 4427 Ų or 88.5 Ų/POPC. From the previous paragraph, the average headgroup surface area per POPC for the 100:2 particle is 90.3 Ų; thus the ratio of headgroup to end methyl group for the 100:2 particle is calculated to be 1.02, the ratio expected for a phospholipid that favors bilayer formation.

DISCUSSION

The results reported here provide detailed molecular models for the discrete particles, termed R2-1 and R2-0, produced by in vitro reconstitution of nascent HDL particles ((26) and L. Li, J. Chen, F. Gu, J. C. Patterson, A. Catte, and J. P. Segrest, unpublished results). These experimentally derived particles correspond in composition and size to the simulated particles with molar ratios of 100:2 and 50:2, respectively. Further, examination of R2-1 and R2-0 by negative stain electron microscopy shows particles that are similar in size and shape to the 100:2 and 50:2 particles, respectively, generated by our MD simulations.

It is important to note that the methodology for generating particles through the progressive removal of phospholipid from discoidal HDL is simply the reverse of the pathway of assembling larger HDL particles from lipid-free or lipid-poor apoA-I (according to the principle of microscopic reversibility). Moreover, apoA-I/lipid complexes with varying lipid concentrations have been observed in cellular environments when apoA-I is exposed to ABCA1 (46). This article shows that human skin fibroblasts whose ABCA1 was upregulated 10-fold when incubated with human apoA-I produce two forms of nascent HDL, peak III with a size of 80 Å and a phospholipid/apoA-I molar ratio of 50:2 (identical to our 50:2 or R2-0 particles) and peak II with a size of 110 Å and a phospholipid/apoA-I molar ratio of 190:2 (similar to our R2-2 particles). Consequently, these particles of varying size are likely to also occur during HDL assembly in the liver. Hence, these structures may hold biological insight into the structures present in the formation of HDL complexes.

Furthermore, it should be noted that there is precedent for the process of lipid transfer to premade apoA-I disks in the absence of enzymes like phospholipid transfer protein. Preformed DMPC disks made from either apoA-I or (Δ43)apoA-I take up DMPC from multilamellar vesicles coincubated with the disks and thus shift the distribution of stepwise heterogeneous particles toward larger particles: R2-1 converts to R2-2, R2-3 to R2-3, etc. (26). Also, it has been shown that lipid molecules (DMPC) can be exchanged between apoA-I disks (47). Moreover, apoA-I discoidal particles produced by cholate dialysis with POPC after short incubation times at room temperature form stepwise heterogeneous particles with much broader size distributions than disks produced under comparable conditions from DMPC. With increased time and/or temperature of incubation, the size distribution of the POPC disks narrows to band widths comparable to those formed by DMPC (L. Li, J. Chen, F. Gu, J. C. Patterson, A. Catte, and J. P. Segrest, unpublished results). This indicates that, under the appropriate conditions, the slower rate of exchange of POPC versus DMPC between disks kinetically traps a broader range of continuously heterogeneous particles when apoA-I is incubated with POPC than with DMPC. The biological process of HDL particle formation in reverse cholesterol transport is cyclical; the initial particle in the process, lipid-poor apoA-I, is regenerated after removal of cholesterol ester from spherical HDL after interaction with the transmembrane protein, SR-B1 (Fig. 1). During in vivo remodeling of HDL particles, phospholipid is removed or added to individual HDL particles through the action of phospholipid transfer protein (48).

The results reported here are particularly compelling for three reasons:

1. Our MD simulations give fundamentally new and, to our knowledge, unprecedented protein-lipid structures that are consistent with experimental particles imaged by electron microscopy. Since activation of the enzyme, LCAT, by apoA-I is necessary for esterification of the cholesterol molecules of HDL and conversion of discoidal to spheroidal (circulating) HDL (10,49), it is noteworthy that the three-dimensional shapes of the 100:2 and 50:2 particles shown in Fig. 12 approach a sphere, suggesting that the conformation of apoA-I in these two particles might approximate the conformation of apoA-I in spheroidal circulating HDL, raising the possibility that these particles are intermediates in the formation of cholesteryl ester containing HDL particles.

2. The apoA-I amphipathic α-helical double belt, independent of four different conditions of particle shrinkage, twists to conform to the minimal surface edge of the lipid bilayer by closely approximating the x-ray structure of lipid-free apoA-I.

3. The dramatic changes in the structure of both protein and lipid occur within a few nanoseconds of MD simulation time, a timescale that to our knowledge is unprecedented for such large, complex supramolecular assemblies containing 206,000–312,000 atoms, including explicit water molecules in the periodic boundary box.

Our MD simulations are in agreement with the experimental evidence that apoA-I is a unique lipid-scavenging protein capable of assembling a continuously expanding range of phospholipid molecules into stable particles. The calculations of order parameters for the simulated particles are particularly important in developing a detailed molecular model to explain the unique nature of the interactions of apoA-I with phospholipid and its role in HDL assembly. The plot of the order parameters for the 50:2 particle (Fig. 10 D) shows that essentially all of its POPC molecules are highly disorganized and thus unlike bulk bilayer lipid (compare annular versus central lipid in Fig. 11). Based upon the similarity of Fig. 10 D with F, it follows that all POPC in 50:2 and smaller, such as 30:2, are annular (i.e., are in contact with the protein). This family of particles (equivalent to the experimentally defined R2-0 particles) thus possesses a lipid pocket capable of binding a variable number of phospholipid molecules, ranging from a few to 50 or more. The source of this lipid pocket flexibility can be deduced from Fig. 4; variations in the width of the relatively flat lipid surface in one of the principal directions (white arrow in Fig. 4, bottom row) allows the lipid pocket to accommodate varying numbers of phospholipid molecules.

These new models for the shapes of the smaller HDL particles provide an alternative hypothesis to the hinged domain model that was previously put forth by this lab (13). The hinged domain hypothesis was postulated for purely discoidal particles, but there is no reason that the smaller HDL particles have to be discoidal. Although Davidson et al. (50) experimentally investigated the presence of the hinged domain of apoA-I, no such structure ever formed in the simulations presented here. It may be that various experimental conditions drive the formation of the hinged domain. Thus, on the basis of MD simulations alone, the hinged domain hypothesis cannot be ruled out.

The plot of the order parameters for 100:2 (Fig. 10, C, E, and F) suggests that it and stoichiometrically similar particles contain significant amounts of both bulk bilayer lipid and annular lipid. In 100:2, the two monolayers of bulk central bilayer lipid and annular lipid minimize their interfacial contact through formation of a saddle-shaped surface approximating a minimal surface (Fig. 10 and Table 1). The 100:2 family of particles, in which the bulk central lipid and annular lipid are in approximate equal molar concentrations, corresponds to the experimentally defined R2-1 particles.

Finally, as the stoichiometry approaches or exceeds 160:2, the particle is transformed into a flat discoidal bilayer structure corresponding to the experimentally defined R2-2 particles. This family of particles possesses a percentage of annular lipid that is significantly less than the percentage of bulk central lipid.

We thus propose that lipid-free apoA-I captures phospholipid, perhaps one molecule at a time, within its highly flexible lipid pocket to produce the R2-0 particle. Discoidal HDL assembly continues with the formation of R2-1, a particle composed of a minimal surface lipid structure containing elements of a lipid bilayer. Disk assembly then terminates with the formation of a planar bilayer disk beginning with R2-2. The energy required to bend the bilayer to form a nontrivial minimal surface for the R2-1 family of particles most likely comes from the transformation of the protein from a flat ring to a more stable conformation similar to the x-ray crystal structure of apoA-I (21).

Experimental techniques, such as cryoelectron microscopy, can be used to test features of the detailed molecular models for nascent HDL presented here. The mapping of cryoelectron microscopy images onto computational simulations of HDL may be one way to obtain atomic-resolution structural information of apoA-I and lipids in these supramolecular assemblies. Clearly, because of their detailed predictions of lipid-associated apoA-I structure, our models provide a molecular map for future research directed at molecular mechanisms of HDL structure and function, for example, the role of ABCA1 in this process of discoidal HDL assembly.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.