Macromolecular Size-and-Shape Distributions by Sedimentation Velocity Analytical Ultracentrifugation

Abstract

Sedimentation velocity analytical ultracentrifugation is an important tool in the characterization of macromolecules and nanoparticles in solution. The sedimentation coefficient distribution c(s) of Lamm equation solutions is based on the approximation of a single, weight-average frictional coefficient of all particles, determined from the experimental data, which scales the diffusion coefficient to the sedimentation coefficient consistent with the traditional s ∼ M^2/3 power law. It provides a high hydrodynamic resolution, where diffusional broadening of the sedimentation boundaries is deconvoluted from the sedimentation coefficient distribution. The approximation of a single weight-average frictional ratio is favored by several experimental factors, and usually gives good results for chemically not too dissimilar macromolecules, such as mixtures of folded proteins. In this communication, we examine an extension to a two-dimensional distribution of sedimentation coefficient and frictional ratio, c(s,f_r), which is representative of a more general set of size-and-shape distributions, including mass-Stokes radius distributions, c(M,R_S), and sedimentation coefficient-molar mass distributions c(s,M). We show that this can be used to determine average molar masses of macromolecules and characterize macromolecular distributions, without the approximation of any scaling relationship between hydrodynamic and thermodynamic parameters.

INTRODUCTION

Sedimentation velocity analytical ultracentrifugation (SV) has a long history for the characterization of synthetic polymers, biological macromolecules, and viral particles. Among current important applications are the study of proteins and their interactions (1–4), carbohydrates (5), and nanoparticles for drug delivery (6,7). One of the useful properties of SV is that the measurement takes place with molecules free in solution, and that the size distribution is a faithful representation of the ensemble of particles in solution. The hydrodynamic resolution is typically significantly higher than that of diffusion-based techniques, due to the mass dependent gravitational driving force of migration. Diffusional spreading of the sedimentation boundary makes both the hydrodynamic frictional coefficient and the molar mass experimentally accessible quantities. The coupled diffusion and sedimentation process is described by the Lamm equation (8), and significant progress in SV was stimulated in the last decade by the ability to efficiently solve this partial differential equation and model experimental data for noninteracting (9–17) and interacting (12,18–21) macromolecular mixtures.

In previous work, we have proposed the use of diffusion-deconvoluted sedimentation coefficient distributions c(s), computed by inversion of a Fredholm integral equation that has Lamm equation solutions as kernel (22–24). In this method, the diffusion coefficient is scaled according to the sedimentation coefficient with a hydrodynamic scaling law D(s) based on the approximation of a single, weight-average frictional ratio (f/f₀, which will be abbreviated in the following to f_r). Theoretical considerations, as well as many practical applications (25), show that this is a successful approximation when studying systems such as mixtures of folded proteins, small nucleic acids, or generally mixtures of chemically homogeneous macromolecules. We have shown recently, that when applied to heterogeneous interacting protein systems, the c(s) distributions are approximations of the asymptotic boundary predicted from Gilbert-Jenkins theory (26), which can be utilized for a robust boundary analysis of protein interactions to derive thermodynamic binding parameters, and hydrodynamic properties of the complex.

An old difficulty of SV has been that the sedimentation coefficient alone reports only indirectly on the species molar mass. The identification of sedimenting species can be an important problem in SV when applied to protein samples. For single species, discrete Lamm equation solutions, in combination with continuous segments, can be used to estimate molar masses (24). However, this approach is not possible for ensembles of macromolecules exhibiting microheterogeneity in the sedimentation coefficient. For multicomponent protein mixtures, we have recently developed a multisignal technique to exploit differences in the protein absorbance spectra to determine the composition and identity of the complexes formed (27). In conventional SV, frequently, the hydrodynamic separation has been combined with an analysis of the molar mass of the main species in solution by virtue of a transformation of c(s) to a molar mass distribution c(M) (28). The latter is based on the observation that the most abundant species will be represented well by the weight-average frictional ratio, such that a molar mass derived from the ratio of s and D(s), via the Svedberg equation, will be a good estimate of the species molar mass. This is an appropriate strategy when the sample is known to have similar frictional ratios, or when c(s) exhibits only a single major peak. The c(M) approach implies only the traditional assumption of a 2/3 power relationship between s and M (28), and is applied such that microheterogeneity in mass and sedimentation coefficient can both be accounted for. This is important, as it is well known that a molar mass analysis by SV of particle mixtures cannot be based on the interpretation of the time-dependent spread of the sedimentation boundary as if arising from a single, apparent diffusion coefficient, but requires consideration of the heterogeneity of the sedimentation properties of the mixture.

Nevertheless, although the scaling relationship based on a single frictional coefficient has proven powerful in practice, clearly many cases can be conceived where it would fail. This includes protein mixtures exhibiting more than one major peak in the c(M) distribution and dissimilar frictional ratio when molar mass values are of interest, or mixtures of chemically heterogeneous macromolecules. Therefore, the question arises how molar mass information can be reliably extracted from the SV patterns of such pauci-disperse or polydisperse mixtures.

In this work we examined a more general, two-dimensional size-and-shape distribution that is free of assumptions of scaling laws. We have found that such a distribution can be conveniently calculated as c(s,f_r), and be transformed to other equivalent size-and-shape distributions of Stokes radii, molar masses, and diffusion coefficients. As will be shown, although the boundary spread does not lend itself to a high resolution in f_r (and D or M), the additional degrees of freedom in this dimension are accompanied by surprisingly little loss of hydrodynamic resolution. This provides a tool to verify if the conventional approximation of a scale relationship in c(s) and c(M) is warranted by the data, and if not, to abandon it in the general analysis of the size-and-shape distribution c(s,f_r).

METHODS

A differential distribution of sedimentation coefficients and frictional ratios c(s,f_r) can be defined as

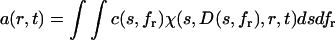(1)

with a(r,t) denoting the total signal as a function of distance from the center of rotation, r, and time, t, with χ(s,D,r,t) denoting the solution of the Lamm equation

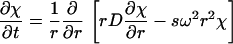(2)

(8), and with D(s,f_r) denoting the dependence of the diffusion coefficient from the sedimentation coefficient and frictional ratio

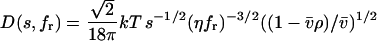(3)

(with Boltzmann constant k, absolute temperature T, macromolecular partial-specific volume 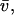solvent viscosity η, and solvent density ρ) (22). This scaling law is based on the Stokes-Einstein relationship and the Svedberg equation

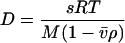(4)

(with molar mass M, and the gas constant R) (29). In this definition, c(s,f_r) is the loading signal of species with s-values between s and s + ds and with f_r-values between f_r and f_r + df_r. This is a two-dimensional extension of the conventional c(s) distribution, which in the standard form is defined as

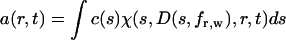(5)

(22). The conventional c(s) distribution is confined to a single frictional ratio, which is typically determined as a weight-average frictional ratio f_r,w of all sedimenting material from nonlinear optimization of this parameter (23,28). It is based on the assumption that the frictional ratios of the sedimenting species are not too dissimilar (in particular when studying chemically homogeneous macromolecules, such as folded proteins), that D is not a strong function of the molar mass, and that the influence of diffusion on the sedimentation profiles decreases at high rotor speeds, where the resolution of sedimentation coefficients is highest. As described previously (23), f_r,w is typically well defined by the experimental data, and this motivates the question if a different frictional ratio for each s-value, or, more generally, a two-dimensional distribution may be well defined by the data.

It is possible to transform the distribution c(s,f_r) to a molar mass distribution for each s-value, c(s,M)

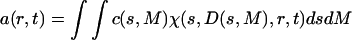(6)

by multiplication with a scaling factor dM/df_r. (This requires knowledge of the partial-specific volume for all molecules in the mixture; if this is unavailable or heterogeneous, only a buoyant molar mass can be calculated.) The distributions c(s,M) and c(s,f_r) are completely equivalent representations of the size-and-shape distribution of the sedimenting particles. We give preference to the c(s,f_r) distribution only for the computational convenience that it is better scaled to the information content of the sedimentation experiment, and the ease of parameterization honoring physical limitations of particle size and diffusion predicted by the Stokes-Einstein law. The size-and-shape distribution can be transformed easily also to related distributions of hydrodynamic parameters, because any pair of two of the hydrodynamic and thermodynamic quantities s, D, M, R_S, and f_r, except for D and R_S, determine all the others. (If no estimate of is possible, M reduces to a buoyant molar mass M_b, and f_r cannot be specified.)

The distribution c(s,f_r) is calculated on a discrete grid of s-values and f_r-values, as

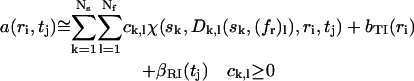(7)

with a least-squares fit to the experimental data a(r_i,t_j), and with consideration of the systematic time-invariant and radial-invariant noise components b_TI and β_RI, which are calculated algebraically as described in Dam and Schuck (28) and Schuck and Demeler (30). The consideration of the systematic noise components allows the direct boundary fit to be unbiased by the systematic offsets common in absorbance and interference optical systems. The algebraic solution of Eq. 7 was calculated with the same approach described earlier for the c(s) distribution (22), using an adaptation of the NNLS algorithm to ensure nonnegativity of the concentrations (22,31).

The Lamm equation solutions χ(s,D,r,t) were calculated with finite element solutions by Claverie (32), and at higher s-values, with the finite element solutions on a moving frame of reference (11), adaptively switched dependent on the value of sω². For covering very large s-values without requiring too high radial discretization, we have implemented the Lamm equation solutions with boundary conditions for permeable bottom described earlier (21).

The following criterion was used to determine if back-diffusion will be necessary: a sedimentation equilibrium distribution can be easily analytically calculated, based on mass conservation. The equilibrium profile is at all times the upper limit for concentrations at radial values past the hinge point. For large species, most of the material will be close to the bottom, and the concentration quickly decays exponentially with increasing distance from the bottom. It can be determined analytically at which distance from the bottom the concentration decreases below a threshold, which can be set, for example, at one-tenth of the experimental noise. If this point is outside of the radial observation window (or the radial range to be fitted, respectively), back-diffusion can be safely neglected, because any effect of back-diffusion will be undetectable. In this case, the experimentally observed sedimentation is well described by the Lamm equation with boundary conditions for a permeable bottom. This criterion was implemented in SEDFIT as an adaptive switch to simulate back-diffusion for small species, where it can be measured, and to exclude it for large species, where it is irrelevant. This also avoids the problem that for large species, which generate very high concentrations close to the bottom of the solution column, back-diffusion likely will proceed significantly different from the predictions by the ideal Lamm equation for dilute solutions.

The default radial discretization was ∼50 points/mm or higher. Much coarser grids, such as suggested in Cao and Demeler (17) are unable to describe a smooth boundary of large species. Because this stage of calculating Lamm equation solutions typically only takes ∼10% of the total computational time, a sacrifice of precision of the numerical Lamm equation solution is not warranted.

The numerical solution of Eq. 7 is combined with Tikhonov-Philips regularization (33), penalizing the fit with the integral over the square of the second derivative of c(s,f_r) both along the s- and the f_r-dimension. (Other regularization procedures are possible (34), such as maximum entropy regularization used usually in c(s) (22).) The penalty is scaled such that the resulting increase in the root-mean-square deviation (rmsd) of the fit just reaches a predetermined value signifying statistically still insignificant difference, based on the given number of experimental data points fitted. A one standard deviation confidence level was used unless otherwise noted. This procedure produces the most parsimonious distribution consistent with the experimental data, and is similar to the regularization strategy introduced by Provencher in the program CONTIN (35,36), and used subsequently in many other distributions, including c(s) and ls-g*(s) (37). Regularization is essential to stabilize the otherwise ill-posed Fredholm integral equation Eq. 1, and to prevent noise from being amplified in the inversion of Eq. 7, thus becoming the dominating feature of the distribution (34). At very low signal/noise ratio, it has the property of producing broad peaks, indicating low information content of the data.

Typically, the s-range was discretized in a square grid as s_k = s_min + (k − 1)Δs, and the f_r range as (f_r)_l = f_r,min + (l − 1)Δf_r. Limits are chosen such that all sedimenting material is covered, which can be ensured by verifying that the rmsd of the fit does not change when changing the distribution limits. Also, f_r values are chosen within the physical constraints on f_r (e.g., f_r > 1.0). For a sedimentation velocity experiment with 50,000 data points (for example, 50 scans of 10 mm columns with 0.001 cm radial increment), and a two-dimensional s-f_r grid with 1000 species (for example, 100 s-values and 10 f_r-values) the solution of Eq. 7 takes on the order of minutes on a PC with a 3 GHz processor. This enables the use of this approach for iterative analysis, for example, nonlinear regression of the meniscus, or manual exploration of the optimal discretization in the s and f_r dimensions.

The matrix c_k,l in Eq. 7 is identical to the distribution c(s,f_r) except for a normalization factor, which for a square grid is a constant factor ΔsΔf_r. For convenience (and in contrast to the implementation of c(s) in the program SEDFIT), this normalization factor is currently omitted. As a consequence, when determining the loading concentration of species in a certain area, the integration c(s,f_r)dsdf can be replaced with a summation over c_k,l(s_k,(f_r)_l). Omitting normalization factors permits a simple mapping of the distribution into a different plane, such as the s-M plane, with summation over grid points representing loading concentrations. However, a rectangular grid in s-f_r will become distorted in other planes if normalization factors are omitted, and the differential distributions will differ slightly from the mapped matrices c_k,l.

An average molar mass of a region of the distribution can be calculated via the weight average sedimentation coefficient divided by the weight average diffusion coefficient

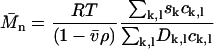(8a)

If taken along lines of constant s, this average corresponds to the number-average molar mass. It could be argued that, because the diffusional spread is the quantity directly fitted in the analysis besides the s-value, the SV experiment may determine best the number-average 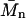(for species of identical s-value). Alternatively, a weight average molar mass can be calculated as

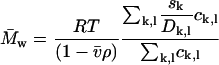(8b)

For single species and narrow peaks, the results are essentially identical, but for extended distributions, they assume different values.

Because the dimension of highest resolution is that of the sedimentation coefficients, it can be very useful to define a differential sedimentation coefficient distribution by integrating over the f_r dimension, abbreviated c(s,^*).

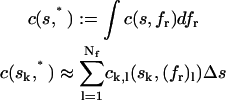(9)

This is an analog of the c(s) distribution, except for the absence of the assumption of the hydrodynamic scaling relationships. In the c(s,^*) distribution f_r can be different and even have many different values for each species. Displaying c(s,f_r) as c(s,^*) permits to neglect the f_r dimension if its resolution is too poor to be of use, or if it is not of interest.

To display the quality of the fit, we have previously introduced the residuals bitmap (28,38). It maps residual values to a pixel brightness value, linearly scaled between −0.05 and 0.05 from black to white (unless otherwise mentioned). Radial values determine the pixel columns, and the scan times determine the pixel rows. In this representation, systematic errors modeling the sedimentation boundary shape will generate diagonal patterns, while most systematic errors from instrumental imperfections will appear as horizontal and vertical features.

The algorithm described above is implemented in the software SEDFIT, and available for download from http://dbeps.ors.od.nih.gov, or www.analyticalultracentrifugation.com.

RESULTS

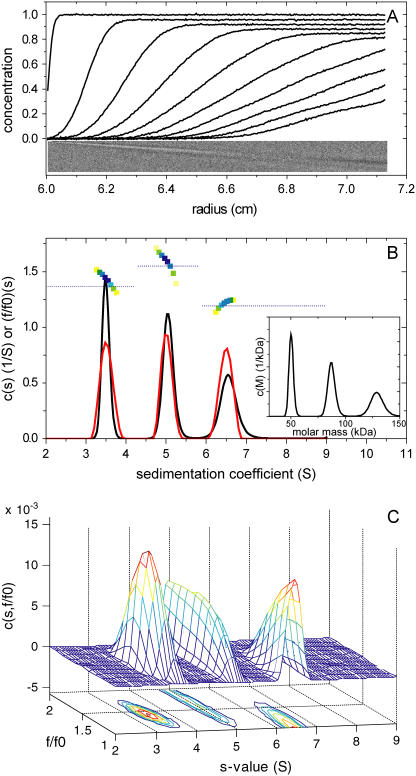
The properties of the c(s,f_r) distribution were examined theoretically, first, by simulating sedimentation velocity profiles for systems containing mixtures of species with dissimilar frictional ratio in significant amounts. In Fig. 1 A are shown the calculated signal profiles for a mixture with equal weight concentrations of a 50 kDa, 3.5 S species (f_r = 1.39), a 100 kDa, 5 S species (f_r = 1.55), and a 100 kDa, 6.5 S species (f_r = 1.19), at a total loading concentration of 1 and with a Gaussian noise of 0.005 (mimicking the typical signal/noise ratio of absorbance or interference optical detection).

FIGURE 1.

Application of c(s,f_r) analysis to a model system of large macromolecules. (A) Simulated signal profiles for a mixture of three species with 50 kDa, 3.5 S, 100 kDa, 5 S, and 100 kDa, 6.5 S, respectively, loaded at equal weight concentrations in a solution column from 6.0 to 7.2 cm, and sedimenting at a rotor speed of 50,000 rpm at 20°C. Traces were calculated in time intervals of 300 s, for a period of 15,000 s, and 0.005 Gaussian noise was added. For clarity, only every fifth scan is shown. (B) c(s) analysis with maximum entropy regularization with P = 0.7 (black line). The transformation of c(s) to c(M) is shown in the inset. The residuals bitmap of this fit is shown as inset to panel A, scaled to ±0.02 black to white. Shown in red in panel B is the c(s,^*) distribution derived from the c(s,f_r) distribution by summation over all f_r-values. The colored squares are the weight-average f_r-values for each s-value from c(s,f_r) distribution, with the color density indicating the signal at each s-value. The blue dotted horizontal lines are the weight-average frictional ratios for a conventional, but segmented c(s) model with one segment for each peak. (C) The calculated c(s,f_r) distribution is shown as two-dimensional distribution with grid lines representing the s and f_r grid of the analysis. Below this c(s,f_r) surface is shown a contour plot of the distribution projected into the s-f_r plane, where the magnitude of c(s,f_r) is indicated by contour lines at constant c(s,f_r) in equidistant intervals of c.

As shown in Fig. 1 B, the conventional c(s) distribution correctly displays the underlying s-values. It converges at an estimate for the weight-average frictional ratio of 1.40, which is close to the theoretically expected average value of 1.38. Interestingly, the best-fit rmsd is 0.0052, slightly above the noise of 0.0050, and a slight systematic diagonal trace can be discerned in the residual bitmap, indicative of a systematic small boundary misfit. This reflects the mismatch of the assumption in c(s) of a single average f_r with the design of this heterogeneous mixture. While such imperfections in the fit should be taken as an indication that the model assumed in the fit is not correctly reflecting the sedimentation process, the current deviation may be too small to be recognized as being relevant in practice. For this reason, as we have emphasized elsewhere (22–24,28), the transition from c(s) to a c(M) distribution is generally not a good transformation for distributions exhibiting multiple significant peaks. As can be expected in the present case, the c(M) distribution would result in erroneous estimates of the species masses, with peak values of 50, 87, and 129 kDa (inset in Fig. 1 B).

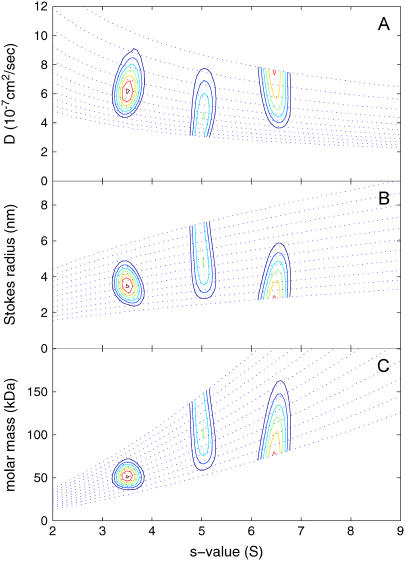
The c(s,f_r) distribution was calculated with an equidistant f_r-grid from 1.0 to 2.0 with 0.1 steps, a linear s-grid from 2 to 9 S with 100 s-values, and Tikhonov-Phillips regularization at one standard deviation (Fig. 1 C). The rmsd of the fit is 0.0050. The difference in the f_r-value of each species can be clearly discerned, even though the f_r dimension is fairly broad for the middle peak, and the 5 S and the 6.5 S peaks are bounded by the maximum and minimum f_r-values permitted, respectively. The lower bound reflects the physical constraints to frictional ratios larger than unity. The c(s,f_r) distribution is rescaled in Fig. 2 as c(s,D), c(s,R_S), and c(s,M) distributions. These are equivalent representations, because any of the four parameters s, M, D (or R_S), and f_r can be calculated if two parameters are known. The c(s,D) distribution represents orthogonally the two sources of information from the experimental data—unidirectional translation of the boundary midpoints (determining s) and bidirectional boundary spread (determining D). In each of the plots, the dotted lines indicate the lines of constant f_r, following the scaling law Eq. 3.

FIGURE 2.

Contour plots of the transformation of c(s,f_r) from Fig. 1 to a c(s,D) distribution (A), a c(s,R_S) distribution (B), and a c(s,M) distribution (C). The dotted lines indicate lines of constant f_r. The distributions are not normalized (see Methods section).

The resolution in s can be assessed via the “folded up” c(s,^*) distribution, which is plotted in Fig. 1 B as a red solid line. No loss of resolution in s is apparent here compared to the c(s) distribution. In contrast to the c(M) analysis (inset, Fig. 1 B), in c(s,f_r) the integration of the peaks leads to number-average molar mass values of 51.1, 99.1, and 99.1 kDa. The peak widths can be assessed as a second central moment of the peak molar mass distribution, resulting in values of 8, 25, and 24 kDa, respectively. The latter values do not correspond to error estimates of the average molar mass, but are simply a measure of the width of the distribution, which, similarly to the width of conventional c(s) curves, is a function of a combination of factors: the information content of the data, the regularization level, and finally the polydispersity of the material studied. Considering the limited information content of a single SV data set, the average molar masses obtained are in reasonable agreement with the values underlying the simulation. (It should be noted that it is a trivial exercise to get the correct molar mass values once the assumptions of a discrete model with three species is made. However, as outlined above, this transition is not possible unless the species are strictly uniform in buoyant mass and hydrodynamic shape, otherwise significant underestimation of the molar mass values can occur).

It is possible to envision a sedimentation coefficient distribution intermediate to the c(s,f_r) distribution, and the conventional c(s) distribution. This would be a distribution where f_r is a single-valued function of s. Such a function f_r(s) can be derived from the two-dimensional c(s,f_r) distribution by calculating the weight-average f_r obtained at each s-value. This is indicated in the square symbols in Fig. 1 B, with the color density indicating the signal from which each f_r-value is derived (obviously f_r(s) will be ill defined where c(s,^*) vanishes). This highlights the different f_r-values for each species, which are consistent with the values used for the simulation. For consistency, in the same plot is also indicated by dotted lines the results of a segmented conventional c(s) distribution, consisting of three segments, each covering one c(s) peak, with fitting different average f_r-values for each segment. The last analysis can be performed in SEDPHAT, for example, as a refinement following the observation of the peak structure in conventional c(s). This illustrates the connection between the different approaches, and the different assumptions made.

This example highlights the utility of c(s,f_r) for the analysis of mixtures of particles with dissimilar frictional ratio without any shape assumptions and scaling relationship of s and M. No loss of hydrodynamic resolution is apparent in this case, even though the information of a single SV run is not sufficient to reveal the details of the molar mass distribution much beyond the average mass for each peak.

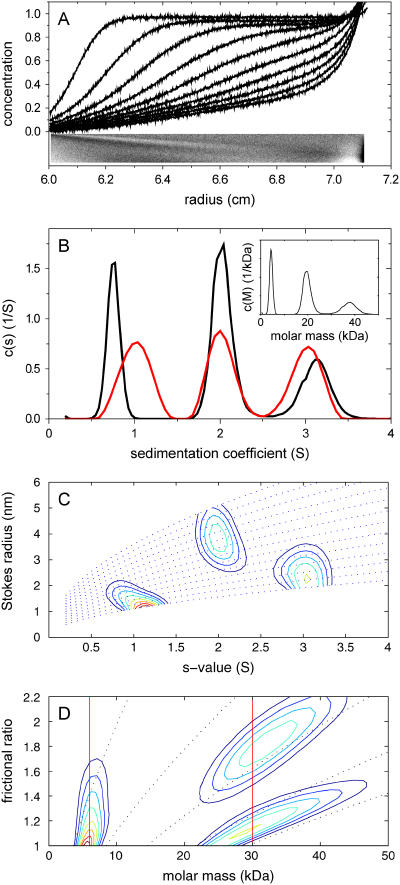
The question arises how well the c(s,f_r) distribution can resolve species under conditions where diffusion is predominant and the sedimentation boundaries of each species exhibit more substantial overlap. This was examined with a second, similarly designed model system, but with smaller molecules. Fig. 3 A shows the superimposed sedimentation profiles of a 6 kDa, 1 S species (f_r = 1.18), a 30 kDa, 2 S species (f_r = 1.73), and a 30 kDa, 3 S species (f_r = 1.15) at 50,000 rpm and at equimolar concentrations. The conventional c(s) converges to a weight-average frictional ratio of 1.29. With diffusion dominating the macromolecular redistribution, the violation of the assumption of constant f_r in the conventional c(s) has much more significant effects. First, the rmsd is 0.0069, significantly above the noise in the data, and with the residuals showing significant systematic deviations (inset in Fig. 3 A). Second, even though the presence of three species is clearly revealed, the s-values of the smallest and largest species are shifted to lower and higher s-values, respectively, to compensate for the overestimated diffusional spread of the middle species. This compensation can take place because the s-values of the two other species describe migration within the leading and trailing edge of the diffusion envelope of the middle species. (As shown in Schuck (24), this effect is much reduced at a higher rotor speed of 60,000 rpm.) As can be expected, the c(M) distribution fails (inset in Fig. 3 B). In contrast, the c(s,f_r) distribution achieves a significant improvement in the quality of fit (rmsd = 0.0050), and a more faithful representation of both the s-values and the molar mass values, with 6.0, 30.9, and 31.1 kDa (number averages from integration of the peaks). Contour maps of the distribution transformed to c(s,R_S) and c(M,f_r) are shown in Fig. 3, C and D. As in the first example, the distributions display dissimilar resolution in s and M. Also, as in the first example, the one-dimensional c(s,^*) distribution, shown in red in Fig. 3 B, does not appear to significantly suffer resolution compared to the conventional c(s) distribution.

FIGURE 3.

Application of c(s,f_r) analysis to a model system of small macromolecules. (A) Simulated signal profiles for a mixture of three species with 6 kDa, 1 S, 30 kDa, 2 S, and 30 kDa, 3 S, respectively, sedimenting at equal weight concentrations at a rotor speed of 50,000 rpm. Traces were calculated in time intervals of 600 s, for a period of 30,000 s, and 0.005 Gaussian noise was added. For clarity, only every fifth scan is shown. (B) c(s) analysis with maximum entropy regularization with P = 0.9, with the corresponding c(M) distribution shown in the inset. The residuals bitmap of this fit is shown as an inset to panel A, scaled to ±0.02 black to white. Shown in red is the one-dimensional c(s,^*) derived from the c(s,f_r) distribution by summation over all f_r-values for each s. (C and D) Calculated c(s,f_r) distribution, ranging from 0.2 to 4 S in 0.063 S steps, and from f_r = 1–2.2 in 0.1 steps. Shown are the transformations as c(s,R_S) and c(s,M), respectively. Also shown are lines of constant frictional ratio (dotted lines in C), and lines of constant s-value (dotted lines in D). The vertical red lines in panel D indicate the true molar mass values.

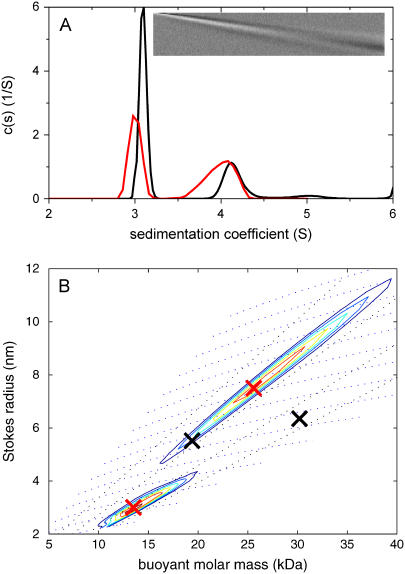
An assumption of the conventional scaling relationship underlying c(s) is the existence of an increasing mass with increasing s-value. This may not be fulfilled, for example, for mixtures of folded and unfolded macromolecules, or for mixtures of chemically dissimilar particles with different partial-specific volume. Fig. 4 shows the analysis of a mixture of two species, one with buoyant molar mass of 25.6 kDa and 3 S (corresponding, for example, to 160 kDa extended polymer with 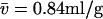), and one with buoyant molar mass 13.5 kDa and 4 S (corresponding, for example, to a folded protein of 50 kDa). If an impostor single-species fit is applied, a buoyant molar mass estimate of only 9.7 kDa is obtained (with rmsd = 0.0182 compared to 0.005 Gaussian noise), consistent with the well-known overestimation of diffusion if heterogeneity is unaccounted for. The c(s) analysis also does not lead to a satisfactory fit (rmsd = 0.0074 with systematic residuals, as shown in the inset in Fig. 4 A) but resolves the heterogeneity. However, examining the details, one can observe that the s-value of the faster sedimenting species appears slightly elevated (due to the overestimated diffusion of the smaller species), as well as traces of a third apparent species at 5 S. The transformation to c(M) leads to incorrect values. With the c(s,f_r) distribution, an excellent fit is found (rmsd = 0.0050), and the slower sedimenting species is correctly assigned the higher buoyant molar mass. It can be discerned that the peaks in c(s,^*) (red lines in Fig. 4 A) are slightly less sharp than in the c(s) distribution, which may indicate higher cross-correlation in the two-dimensional parameter space. Both buoyant molar masses and Stokes radii represent well the species underlying the simulation.

FIGURE 4.

Analysis of a theoretical mixture of two species with buoyant molar mass of 25.6 kDa and 3 S (corresponding, for example, to 160 kDa extended polymer with 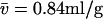), and with buoyant molar mass 13.5 kDa and 4 S (corresponding, for example, to a folded protein of 50 kDa). Sedimentation was simulated under the same conditions as in Figs. 1 and 3. (A) The c(s) distribution is shown as a black line, with the residuals bitmap from the c(s) analysis in the inset (rmsd = 0.0074). The red line is the c(s,^*) trace from the c(s,f_r) analysis, which is shown in panel B as a transformation to a parameter space of buoyant molar mass and Stokes radius. The dotted lines indicate directions of constant f_r and constant s. The red crosses are the parameters underlying the simulation, the black crosses are values resulting from integration of an impostor c(M) transformation of c(s).

The results from these theoretical studies suggest that it should be possible to apply the c(s,f_r) analysis in practice, with the expectation that the c(s,^*) trace should be comparable to c(s), perhaps at slightly reduced resolution. Even though it seems not possible to achieve a very high resolution along the f_r (or mass) dimension given current experimental signal/noise ratio from a single SV run, one could expect the average molar mass of the c(s,f_r) peaks to be a good estimate for species molar masses (see Fig. 2 C). The validity and robustness of this approach is examined in the following using experimental data.

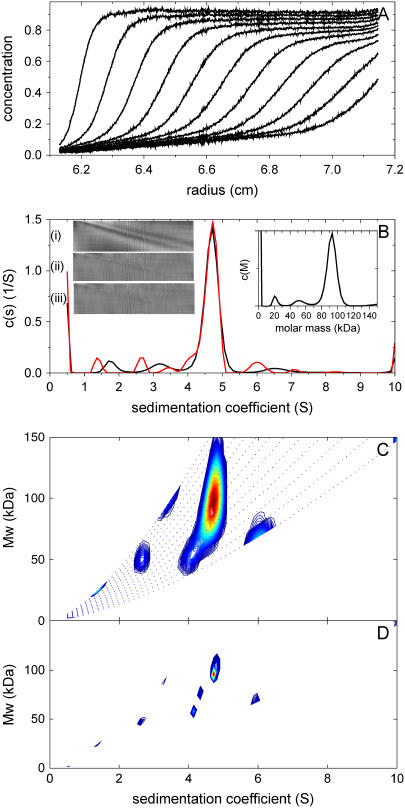
Fig. 5 A shows SV data from a study of the oligomeric state of an extracellular domain of an NK receptor with a monomer molar mass of ∼50.1 kDa, with ∼13% of the mass stemming from glycosylation. We have taken this data previously as an example to examine the utility of the estimation of molar mass by c(M) (28), and it may therefore serve as a first test case in this study. As described earlier, if the analysis is based on the assumption of the presence of a single sedimenting species, an apparent molar mass not far from the monomer mass is obtained. Because this is an underestimate due to unaccounted heterogeneity (most likely the unaccounted trace impurities) the precise value is somewhat dependent on the data selection and fitting limits, and with the presently chosen conditions a value of 60.1 kDa was obtained. The quality of the single-species fit is surprisingly good, with an rmsd of only 0.0087, but with significant systematic residuals that indicate the fit is a poor description of the boundary spread (inset (i) in Fig. 5 B). The c(s) distribution gives a much better fit (rmsd = 0.0042) and displays the presence of several contaminating species, but still a single major peak that permits the conversion to c(M), resulting in a molar mass of 90.8 kDa. The dimeric state was confirmed independently by sedimentation equilibrium. With the c(s,f_r) analysis (Fig. 5 C), a slight further improvement of the fit was found (rmsd = 0.0040). Integration of the main peak results in a weight-average molar mass average of 93 kDa. Interestingly, the distribution exhibits some details, including a bimodal peak structure, and a 2.7 S monomeric component. When c(s^,*) distribution is compared with the conventional c(s) distribution, it is consistent with regard to the main peak, but shows some deviations with regard to the location of the low level impurities.

FIGURE 5.

Analysis of experimental sedimentation velocity data from the study of the oligomeric state of a glycosylated NK receptor fragment. For experimental details, see Dam and Schuck (28). Panel A shows a representative subset of the raw data. Panel B shows c(s) analysis (black line) and transformation to c(M) (right inset). The left insets are residual bitmaps from (i) a single discrete species analysis, (ii) the c(s) analysis, and (iii) the c(s,f_r) analysis. The red line is the c(s,^*) trace of the c(s,f_r) distribution shown in panel C. Panel D shows the same analysis as in panel C, but without regularization.

Fig. 5 D shows the distribution calculated from the same data without regularization. All peaks, including the dimer peak, are much sharper, suggesting much more detailed results. Generally, distributions without regularization have the tendency of exhibiting many baseline-separated peaks, the number and precise location of which depends strongly on the noise in the data. In this case, for example, it can be discerned that the main peak is subdivided in three. However, their location (and existence) depends on the details of the discretization. In contrast, in the presence of regularization the distribution becomes independent on the detail of the discretization. Considering that the two distributions by design only differ insignificantly in their rmsd, it is clear that the apparent gain in detail in Fig. 5 D is not warranted by the data. When the regularization level is raised to two standard deviations, the main peak becomes more symmetrical, with otherwise very similar appearance (data not shown).

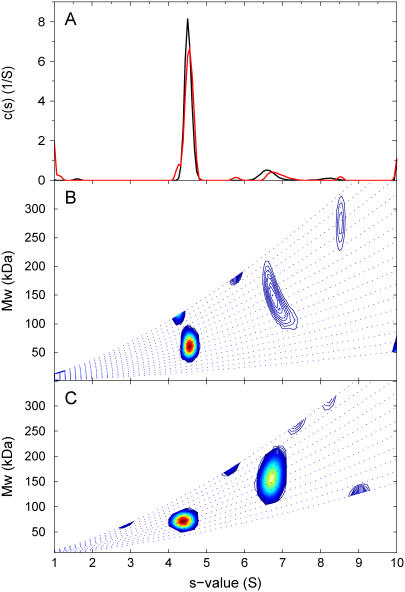
To explore further the response of c(s,f_r) distribution for species in lower relative abundance we have applied it to the analysis of a sample of bovine serum albumin, which shows the well-known series of oligomeric species. Fig. 6 A shows the c(s) distribution, with the monomer peak at 4.5 S and the dimer peak at ∼6.5 S, the latter amounting to ∼10% of the loaded material. The c(s,^*) trace is very similar, although a slightly different s-value for the dimer can be discerned. From integration of c(s,M) in Fig. 6 B, average apparent molar mass estimates of 61 kDa and 135 kDa for the monomer and dimer are obtained, reasonably consistent with the expectation of a 2:1 mass ratio. As a further example, Fig. 6 C shows the c(s,f_r) distribution of a mixture of bovine serum albumin and immunglobulin G.

FIGURE 6.

Analysis of SV data from a bovine serum albumin sample (commercial sample used without further purification) sedimenting at 55,000 rpm, 22°C. Panel A shows c(s) distribution (black) and c(s,^*) distribution (red) derived from the c(s,f_r) fit shown in panel B as c(s₁M). Integration of the c(s,f_r) peak results in an average apparent molar mass of 61 kDa (assuming a 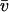value of 0.73 ml/g) for the monomer at ∼4.5 S, and 135 kDa for the dimer peak at ∼7 S, which amounts to ∼9% of the total sedimenting material. The dotted lines are lines of constant f_r. Panel C shows analysis of a mixture of a bovine serum albumin (taken from a different batch) with an IgG sample, sedimenting at 50,000 rpm, 20°C. Integration of the IgG peak leads to an average apparent molar mass of 154 kDa (assuming a 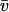value of 0.73 ml/g).

For some applications, it is of interest to quantify trace amounts of aggregates. For example, the minor species at ∼8.5 S from conventional c(s) analysis is ∼2.4% of the loading concentration, well above the limit for reliable detection in c(s) (24). In the c(s,f_r) and c(s,^*) analysis, the abundance of this species is estimated at 0.8%. To further study this topic, synthetic sedimentation profiles were simulated with BSA monomer at 99% and trimer at 1% of the total loading concentration, with a total signal of 1.0 and Gaussian noise of 0.005. In the c(s) analysis an estimated trimer fraction of 0.9% was recovered, and 0.7–0.9% in the c(s,f_r) and c(s,^*) analysis, dependent on discretization (data not shown). However, it was not possible to obtain good estimates of the molar mass of the trace species due to the low signal. Similarly, it is unclear if the less abundant species of Fig. 6 B, are assigned correct molar mass values (see Discussion).

Generally, it seems that c(s,f_r) is not as well suited to the interpretation of trace components as compared to c(s). This is probably due to the more ill-conditioned nature of the model of c(s,f_r), which can make the analysis also more susceptible to experimental imperfections, such as low-level convection, which might cause systematic errors in the data. At present, it is unclear, for example, if the five minor peaks in the distribution of Fig. 6 C reflect faithfully the trace populations of contaminating macromolecules. However, in noisy simulated data mimicking the same experiment with the monomeric BSA and IgG only, these minor peaks do not occur, and only the main peaks at the correct s-values appear (data not shown). This shows that the mathematical treatment of the data in this method does not generate such low level peaks as a result of amplification of random noise in the data. More reliable information about minor species from experimental data can be expected by comparison with the results of more experiments under the same or different conditions, and ultimately their global analysis (see Discussion).

Finally, we asked if the c(s,f_r) distribution can be applied to rapidly interacting systems. As a test case, we considered a system of small proteins (25 and 40 kDa) forming a 1:1 complex, where the concentration profiles are diffusionally broadened such that no distinct boundary can be discerned without deconvolution of diffusion. This system was used in a previous study (Fig. 5 in Dam and Schuck (26)), where we have shown that the conventional c(s) distributions can be regarded as approximations of the asymptotic boundaries from Gilbert-Jenkins theory, and that the s-values and amplitudes of the diffusion deconvoluted boundary components can be modeled well with isotherms derived from Gilbert-Jenkins theory.

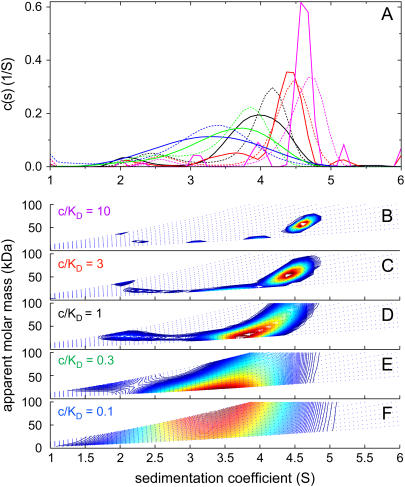
When the c(s,f_r) distribution was applied to the same data of equimolar mixtures at varying concentrations, although the overall position and concentration dependence of the undisturbed and the reaction boundary are consistent with c(s), they do not appear to reflect the asymptotic boundaries from Gilbert-Jenkins theory as well as the conventional c(s) distributions (Fig. 7). At very low concentrations and low signal/noise ratios, the c(s,f_r) distribution has a slightly lower resolution than c(s), which makes it more difficult to discern the undisturbed and the reaction boundary (Fig. 7, E and F). At very high concentrations and signal/noise ratio, the c(s,f_r) distribution shows several small peaks, which may be a result of over-parameterization of the fit, and greater susceptibility of c(s,f_r) to the approximations inherent to the application of a distribution of Lamm equation solutions to reaction boundaries (21) (Fig. 7 B).

FIGURE 7.

Application of c(s,f_r) to a reaction mixture with rapid kinetics on the timescale of sedimentation. Sedimentation velocity profiles were simulated for the interaction of a protein of 25 kDa, 2.5 S binding to a 40 kDa, 3.5 S species forming a 5 S complex with a equilibrium dissociation constant K_D = 3 μM, and a dissociation rate constant k_off = 0.01/s, studied at a rotor speed of 50,000 rpm. Interference optical detection was assumed, with conventional signal increments of 3.3 fringes/(mg/ml) and a noise level of 0.005 fringes. Concentrations were equimolar at 0.1-fold K_D (blue), 0.3-fold K_D (green), K_D (black), threefold K_D (red), and 10-fold K_D (magenta). c(s,f_r) distributions were calculated with s-values from 1 to 6 S and f_r-values from 0.8 to 2.0. Panel A shows c(s,^*) distributions (solid lines) and conventional c(s) distributions (dotted lines), both normalized to constant area. Panels B–F show c(s,f_r) distributions mapped into the c(s,M) plane, at the concentrations indicated.

Nevertheless, the overall weight-average s-values from c(s,f_r) are virtually identical to those of c(s) and the values calculated from the known parameters. This can be theoretically expected, because the weight-average s-values only depend on mass balance considerations and a faithful representation of the boundary shape, and not on the boundary model representing the true sedimentation process (42). As a consequence, the c(s,f_r) distribution can be used for determining s_w like any other differential sedimentation coefficient distributions. Interestingly, the apparent molar mass values in the undisturbed boundary are close to that of the smaller species, as expected for the equimolar mixtures (26). Further, the apparent molar mass values in the reaction boundary assume values in between those of the larger component and the complex (Fig. 7, B–D). This is consistent with the constant bath approximation for the sedimentation of reactive systems (21), which predicts that the diffusion coefficient in the reaction boundary will be between those of the larger component and the complex (see Eq. 6 in Dam et al. (21)), approaching that of the complex at higher concentrations.

DISCUSSION

We have described a new method to determine a two-dimensional size-and-shape distribution of macromolecular mixtures from the analysis of sedimentation velocity. The distribution was expressed conveniently as a differential sedimentation coefficient and frictional ratio distribution c(s,f_r), although it can be mapped into other parameters describing sedimentation and hydrodynamic friction, such as molar mass, diffusion coefficient, and Stokes radius. The distribution is based on a linear combination of Lamm equation solutions, such that the resolution in the dimension of sedimentation coefficients is deconvoluted from the effects of diffusion. It assumes “ultracentrifugal ideal” sedimentation (39), i.e., the absence of macromolecular interactions and constant sedimentation and diffusion coefficients for each species, which can be experimentally observed, for example, for proteins at not too high concentrations in the presence of sufficient supporting electrolyte.

Such distributions have been theoretically conceived by Gosting (40) and described by Fujita (39), but without practical approaches for their determination from experimental data. Modern computational tools that have enabled us to address this problem anew, including the possibility to calculate precise Lamm equation solutions, the systematic noise decomposition adapting the boundary analysis to the characteristic signal offsets in the optical systems, and modern regularization approaches for the stable inversion of Fredholm integral equations. As implemented in SEDFIT, the computational cost is not any more prohibitive, taking on the order of a few minutes on a laptop PC.

In particular, the regularization is an important technical point. It is well known that a simple inversion of Fredholm integral equations can magnify experimental noise, and lead to unwarranted detail in the distribution functions, as well as dependencies of the distribution on the details of the discretization. Regularization is the standard approach to address this problem (34). Following Occam's razor, the regularization process selects the most parsimonious distribution statistically consistent with the data on a predefined confidence level. For example, for data with poor signal/noise ratio, the distribution will display only very broad features, consistent with the information of the data, instead of series of artificial spikes. Changing this confidence level and observing the effects on the calculated distribution is a useful tool to display how well information on a given peak region is represented by the original experimental data (22). Regularization has been introduced into the dynamic light scattering analysis by Stephen Provencher with the program CONTIN (36), and it is widely used in other biophysical disciplines. Experience with regularization in SV analytical ultracentrifugation was gained in recent years from the application in the c(s) (22) and the ls-g^*(s) (37) distribution. Because many more grid points are necessary in the two-dimensional c(s,f_r) distribution as compared to the c(s) distribution, and because the additional dimension does not always seem to be well determined by the experimental data, we expect regularization to play an even more important role in c(s,f_r).

The c(s,f_r) approach provides a comparatively “model-free” (in a sense of not implying an explicit thermodynamic description of the system), yet diffusion-deconvoluted, sedimentation coefficient distribution. We envision it as a tool to examine the distribution of sedimenting macromolecules, either where the assumption of constant f_r in the conventional c(s) distribution is unclear, or where it is known not to hold, such as frequently encountered with chemically heterogeneous mixtures, with unfolded macromolecules, or other structures, for example, dendrimers. The examples in this study were designed to reveal the performance of c(s,f_r) in such cases. In principle, with appropriate adjustment of the distribution limits in s and f_r, the model should be large enough to accommodate any macromolecular mixture, unless interactions are present, e.g., in the form of hydrodynamic repulsive nonideal sedimentation, or attractive macromolecular interactions.

As many applications of conventional c(s) in the published literature have shown (25), the scaling relationship based on a weight-average frictional ratio is still an excellent approximation for obtaining a diffusion-deconvoluted, high-resolution sedimentation coefficient distribution in most cases when studying proteins or short nucleic acids and their interactions. Here, the c(s,f_r) distribution can be a tool where molar mass values of the species are of interest, and where possible impurities or the possible presence of microheterogeneity prohibits the substitution of a c(s,f_r) or c(s) peak with a discrete species in a hybrid discrete/continuous distribution (41). It can also be viewed as a starting point to examine the data, first, followed by judicious implementation of prior knowledge on the sample by switching to other models.

Although the resolution in M is not very high, when applied to samples exhibiting peaks originating from single species, the molar mass values determined from integration of the peaks were typically found within a few percent of that expected from mass spectroscopy, or within the typical uncertainties of the partial-specific volume. A prerequisite of this is that a good fit of the data is obtained. In our experience, the precision of M-values for species in lower abundance are particularly dependent on the quality of fit. In the examples tested so far, species that represent less than 5–10% of the sedimenting material did not reveal a reliable molar mass value in c(s,M). (This is different from the ability to detect the presence of sedimenting material in a certain interval of s-values, which has a much higher sensitivity.)

If the diffusion (or frictional ratio, or molar mass) information is not sufficient to produce well-defined peaks, this dimension can be “folded up” and a sedimentation coefficient distribution c(s,^*) is obtained, which is very similar to the conventional c(s) distribution, except for the absence of frictional ratio assumptions. It may seem computationally wasteful to first allow for the diffusion dimension in the c(s,f_r) fit, followed by disregarding this information in c(s,^*). But it eliminates the nonlinear regression of f_r,w in the conventional c(s) analysis. A comparison of c(s,^*) with c(s) with regard to the rmsd and the randomness of the residuals of the respective fits constitutes a criterion to judge whether the constant frictional ratio assumption in c(s) has to be rejected or not. In our experience, the c(s,^*) distribution displays surprisingly little degradation in hydrodynamic resolution compared to c(s). However, when applied to interacting systems, the c(s,^*) distribution did not seem to improve on the correspondence of c(s) with the asymptotic boundaries predicted from Gilbert-Jenkins theory (26). Interestingly, the apparent molar mass values obtained were found to be in a range expected from the constant bath theory, which predicts diffusion coefficients (and apparent molar masses) of the reaction boundary to be a weighted average between the larger species and the complex (21).

To improve the resolution of the size-and-shape distribution, we have embarked on the global analysis including sedimentation velocity experiments at different rotor speeds, sedimentation equilibrium, and dynamic light scattering (41). This raises additional computational problems of scaling the different data, and of possible variations in the loading concentrations in the different experiments, but has the promise of enhanced resolution of the diffusion domain, more reliable characterization of minor components, and self-consistent representation of results from different techniques. This will be reported in a forthcoming communication. Further, an extension to the global multisignal analysis for discriminating the size-and-shape distributions of components with different absorbance spectra seems possible (27).