Abstract
We provide a comprehensive thermodynamic description of lipid membrane dissolution by a charged detergent. To this end, we have studied the interactions between the anionic detergent sodium dodecyl sulfate (SDS) and the zwitterionic phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) in dilute aqueous solution (10 mM phosphate buffer, 154 mM NaCl, pH 7.4). Thermodynamic parameters of vesicle solubilization and reconstitution, membrane partitioning, and micelle formation were assessed by right-angle light scattering and isothermal titration calorimetry. Membrane translocation and dissolution proceed very slowly at 25°C but are considerably accelerated at 65°C. At this temperature, a simple SDS/POPC phase diagram (comprising vesicular, coexistence, and micellar ranges) and a complete set of partition coefficients and transfer enthalpies were obtained. Electrostatic repulsion effects at the membrane surface were implemented by combining Gouy-Chapman theory with a Langmuir adsorption isotherm to account for Na+ binding to membrane-incorporated DS−. This approach offered a quantitative understanding of solubilization and reconstitution processes, which were interpreted in terms of partition equilibria between and ideal mixing in all phases. More than any other property, the transbilayer flip-flop rate under given experimental conditions hence appears to dictate a detergent's suitability for thermodynamically controlled lipid membrane solubilization and reconstitution.
INTRODUCTION
Detergents are valuable tools for the permeabilization and solubilization of biological and model membranes (1) and for the purification and reconstitution of lipidic and proteinaceous membrane constituents (2). Solubilization and reconstitution of lipid vesicles are characterized by the appearance and disappearance of distinct surfactant aggregates (3–7), which, to a first approximation, can be regarded as pseudophases (8). In the initial stage of solubilization, a large excess of lipid ensures micelle disintegration and partitioning of detergent monomers between the aqueous phase and bilayers. Upon saturation of the mixed membranes with detergent, the appearance of first mixed micelles marks the beginning of the coexistence range. Further addition of detergent then shifts the equilibrium from bilayers to micelles without affecting the compositions of the two surfactant aggregates. Solubilization is completed when the last vesicles vanish, so that only micelles are left in the final range. Vesicle reconstitution proceeds in the opposite direction, that is, from mixed micelles to micelle/bilayer phase coexistence to mixed bilayer structures.
For systems comprising egg-yolk phosphatidylcholine and the nonionic detergent octylglucoside, a full set of transfer enthalpies between aqueous, micellar, and vesicular phases has been derived (9). If the critical micellar concentration (CMC) is low and the total surfactant concentration high enough, the fraction of monomeric detergent in solution becomes negligible (8). Then, both transfer enthalpies and partition coefficients are available, as is the case for mixtures composed of the nonionic detergent octa(ethylene oxide) dodecyl ether (C12EO8) and the zwitterionic lipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) (10–12). For many practical purposes, however, detergents with CMC values in the millimolar rather than micromolar concentration range are preferable because they can be rapidly and conveniently removed by dialysis, chromatography, or other methods (2).
Unfortunately, quantification of membrane solubilization by charged surfactants, which normally possess high CMC values, has thus far been limited to the determination of the critical detergent/lipid ratios at the phase boundaries (13–19). A more thorough thermodynamic analysis is not straightforward but, nonetheless, appears desirable for a number of reasons. First, theoretical considerations predict dramatic discrepancies between ideally and nonideally mixing surfactant systems when it comes to isolating so-called detergent-resistant membrane fractions (20). It therefore seems crucial to differentiate between purely electrostatic effects and those potentially arising from nonideal mixing. Second, it cannot be taken for granted that data obtained at low detergent/lipid ratios (19,21) may be extrapolated to higher detergent contents necessary for membrane solubilization. For instance, counterion binding is expected to modulate electrostatic effects at the membrane surface but, unlike ion adsorption in micellar systems (22), has not been investigated in great detail. Third, largely diverging surfactant flip-flop rates have been inferred to be responsible for different solubilization pathways, which, in turn, can give rise to selective or preferential interactions with certain lipids or membrane proteins (1,23).
Sodium dodecyl sulfate (SDS) is one of the most frequently used anionic detergents and has been studied extensively with respect to micellization (19,24,25), partitioning into monolayers (26) and bilayers ((19,21), M. Apel-Paz, G. F. Doncel, and T. K. Vanderlick, unpublished), membrane permeabilization (28), transmembrane movement ((21,23,29), M. Apel-Paz, G. F. Doncel, and T. K. Vanderlick, unpublished), and interactions with membrane proteins (1,23). Over a wide temperature range, binding of SDS to POPC membranes at low detergent/lipid ratios can be described by a surface partition equilibrium subject to electrostatic repulsion effects (19,21). At ambient temperature, SDS exhibits only weak membrane permeabilization (28) and very slow flip-flop ((19,21,23,29), M. Apel-Paz, G. F. Doncel, and T. K. Vanderlick, unpublished). These two concomitant phenomena have been blamed (M. Apel-Paz, G. F. Doncel, and T. K. Vanderlick, unpublished) for the poor microbicidal potency of SDS as compared with nonionic surfactants that both permeabilize and permeate lipid membranes under the same conditions (30). Moreover, the slow kinetics of transbilayer movement seems to obstruct a straightforward evaluation of solubilization and reconstitution experiments performed at room temperature (19,23). Indeed, raising the temperature beyond 50°C greatly accelerates SDS permeation (19,21), thereby enabling the construction of detergent/lipid phase diagrams (17,19). Despite this obvious correlation between SDS flip-flop and membrane dissolution, calorimetric experiments at elevated temperature (17) have unveiled a solubilization behavior that looks much more complex than that observed for C12EO8 (10–12) and many other nonionic bilayer-permeant detergents. Therefore, it has remained unclear whether the rate of membrane translocation is the only discriminating feature or whether there exist other fundamental peculiarities in the mode of action of ionic surfactants.
Here, we present a comprehensive thermodynamic characterization of SDS/POPC mixtures in dilute aqueous solution (10 mM phosphate buffer, 154 mM NaCl, pH 7.4). This system offers the great advantage that variation of temperature alone can be exploited to tune membrane permeability without leaving the liquid-crystalline phase range (21). Right-angle light scattering was employed to compare solubilization and reconstitution of large unilamellar vesicles (LUVs) under conditions leading to either half-sided binding (25°C) or fast transbilayer equilibration (65°C). Applying isothermal titration calorimetry (ITC), we found that membrane binding and solubilization at 65°C can be understood quantitatively on the basis of a simple partitioning model assuming ideal mixing in all (i.e., aqueous, micellar, and vesicular) phases. Discrepancies between ionic and nonionic detergents stemming from electrostatic effects can be fully accounted for by Gouy-Chapman theory if counterion binding is included adequately. Thus, the ability to undergo flip-flop on experimental timescales turns out to be the single most important prerequisite of a detergent for the solubilization and reconstitution of lipid membranes in thermodynamically rather than kinetically controlled processes.
MATERIALS AND METHODS
Materials
SDS was purchased from Sigma-Aldrich (Steinheim, Germany) and POPC from Avanti Polar Lipids (Alabaster, AL). All other chemicals were obtained from Merck (Darmstadt, Germany). All experiments were done in 10 mM phosphate buffer (154 mM NaCl, pH 7.4).
Vesicle preparation
POPC dissolved in chloroform at 20 mg/mL was dried in a rotary evaporator and subsequently under high vacuum overnight. The dry lipid films were suspended in buffer by vortex mixing for 5 min, yielding large multilamellar vesicles. LUVs were prepared by 35 extrusion steps through two stacked polycarbonate filters with a pore diameter of 100 nm using a LiposoFast extruder (Avestin, Ottawa, Canada). The vesicle size was narrowly distributed at around 100 nm, as checked by dynamic light scattering on an N4 Plus particle sizer (Beckman Coulter, Fullerton, CA) equipped with a 10-mW helium/neon laser with a wavelength of 632.8 nm at a scattering angle of 90°.
Right-angle light scattering
Light scattering intensities were taken at a wavelength of 632.8 nm and an angle of 90° in 1 cm × 1 cm polystyrene cuvettes (Sarstedt, Nümbrecht, Germany) on the N4 Plus instrument described in the preceding section. In solubilization assays, 10-, 20-, or 50-μL aliquots of a 25 or 50 mM SDS solution were titrated to 2.5 mL of a 0.1–2.5 mM POPC LUV suspension. In reconstitution experiments, 10-μL aliquots of a 10, 20, or 40 mM lipid vesicle suspension were injected into 1.25 mL of a 0–10 mM SDS solution. Intensity values were read 3 min after addition of detergent or lipid and stirring of the sample, which was sufficient to attain equilibrium at 65°C. By contrast, prohibitively long incubation times would have been required at 25°C, as the light scattering intensities did not remain constant even 24 h after injection (data not shown).
Isothermal titration calorimetry
High-sensitivity microcalorimetry (31) was performed on a VP-ITC (MicroCal, Northampton, MA) after vacuum degassing of the samples. For solubilization, 3- or 5-μL aliquots of 25, 50, or 100 mM SDS were injected to 0.1–5.0 mM POPC LUVs. For reconstitution, 3-μL aliquots of 20 or 40 mM lipid were titrated to 1.0–10 mM SDS. Before partitioning studies, POPC LUV suspensions were mixed with SDS solutions to yield final concentrations of 1.0 mM and 0.25–2.5 mM, respectively. After incubation for 1 h at 65°C, 10-μL aliquots of this mixture were injected into the calorimeter cell containing SDS at various concentrations.
The time spacings between the injections were chosen long enough to allow for complete reequilibration. Baseline subtraction and peak integration were accomplished using Origin 5.0 as described by the manufacturer (MicroCal Software, Northampton, MA). All reaction heats were normalized with respect to the molar amount of detergent or lipid injected. The first injection was always excluded from evaluation because it usually suffers from sample loss during the mounting of the syringe and the equilibration preceding the actual titration. Repetition of some representative experiments demonstrated high reproducibility.
Curve fitting
Nonlinear least-squares fitting was performed in an Excel (Microsoft, Redmond, WA) spreadsheet using the Solver (32) add-in (Frontline Systems, Incline Village, NV).
THEORY
Phase diagram
In solubilization experiments, the detergent (D) concentration, cD, is increased by titration, whereas the lipid (L) concentration, cL, slightly decreases as a consequence of dilution. In reconstitution experiments, cL is increased by titration, while cD slightly decreases. Breakpoints in light scattering assays (4–6) and inflection points in ITC measurements (8–12) yield two characteristic (cD, cL) pairs. In many cases, a simple phase diagram in dilute aqueous solution can then be obtained by plotting the critical cD values versus the corresponding cL values. The saturating (sat) detergent/lipid mole ratio,
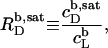 |
(1) |
provides the maximum detergent concentration, 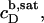 that can be incorporated into lipid bilayers (b) at a given lipid concentration, cL =
that can be incorporated into lipid bilayers (b) at a given lipid concentration, cL = 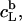 before the first mixed micelles appear.
before the first mixed micelles appear. 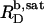 and the corresponding detergent concentration in the aqueous (aq) phase,
and the corresponding detergent concentration in the aqueous (aq) phase, 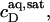 are obtained as, respectively, the slope and the ordinate intercept of a linear regression analysis according to
are obtained as, respectively, the slope and the ordinate intercept of a linear regression analysis according to
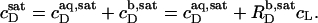 |
(2) |
Likewise, the solubilizing (sol) detergent/lipid mol ratio,
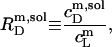 |
(3) |
specifies the minimum detergent concentration, 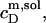 that is necessary to transfer all lipid,
that is necessary to transfer all lipid, 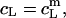 into micelles (m). Again,
into micelles (m). Again, 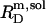 and
and 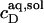 define a straight line according to
define a straight line according to
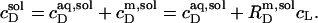 |
(4) |
Systematic deviations from the properties of ideal phases, such as intermicellar interactions or entropy changes associated with dispersing micelles, may account for 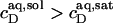 (33), an effect that is particularly pronounced for bile salts (13,14). Within the frame of the phase separation model (8), however, the transition between the two surfactant aggregates is ascribed to a coexistence of bilayers and micelles having fixed compositions of
(33), an effect that is particularly pronounced for bile salts (13,14). Within the frame of the phase separation model (8), however, the transition between the two surfactant aggregates is ascribed to a coexistence of bilayers and micelles having fixed compositions of 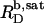 and
and 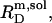 respectively. If this were to be strictly the case, the aqueous detergent concentration,
respectively. If this were to be strictly the case, the aqueous detergent concentration, 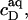 would also need to remain constant throughout the transition range. Then, the two phase boundaries should intersect the ordinate at the same point, denoted by
would also need to remain constant throughout the transition range. Then, the two phase boundaries should intersect the ordinate at the same point, denoted by 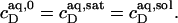 For SDS/POPC mixtures at 65°C, this is fulfilled to a good approximation (see Results). Note that
For SDS/POPC mixtures at 65°C, this is fulfilled to a good approximation (see Results). Note that 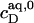 < CMC because the former refers to free detergent in equilibrium with lipid-saturated micelles, whereas the latter gives the aqueous detergent concentration in equilibrium with pure detergent micelles.
< CMC because the former refers to free detergent in equilibrium with lipid-saturated micelles, whereas the latter gives the aqueous detergent concentration in equilibrium with pure detergent micelles.
Partition coefficients
From the slopes of the regression lines in the phase diagram, the SDS mol fractions in coexisting bilayers and micelles are calculated as, respectively,
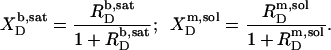 |
(5) |
The mol fraction partition coefficients of SDS and POPC between detergent-saturated bilayers and lipid-saturated micelles then read, respectively,
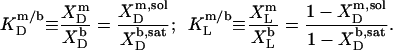 |
(6) |
With 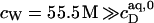 being the molar concentration of water (W) and
being the molar concentration of water (W) and 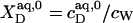 the SDS mol fraction in the bulk aqueous phase, the SDS partition coefficients between the latter and detergent-saturated bilayers or lipid-saturated micelles are, respectively,
the SDS mol fraction in the bulk aqueous phase, the SDS partition coefficients between the latter and detergent-saturated bilayers or lipid-saturated micelles are, respectively,
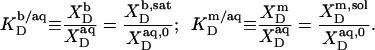 |
(7) |
It should be noted that partition coefficients as defined by Eq. 7 need not necessarily be constant but depend, in general, on the compositions of the phases and, in particular, on electrostatic repulsion or attraction effects at vesicular and micellar surfaces (see next section). 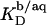 values at arbitrary cD and cL values are afforded by an ITC protocol introduced by Zhang and Rowe (34). This approach is more laborious than the more frequently used uptake experiment (10,13,14,19,21,35) but, in exchange, enables a model-free quantification of partition equilibria as a function of membrane composition. To this end, detergent/lipid mixtures at given
values at arbitrary cD and cL values are afforded by an ITC protocol introduced by Zhang and Rowe (34). This approach is more laborious than the more frequently used uptake experiment (10,13,14,19,21,35) but, in exchange, enables a model-free quantification of partition equilibria as a function of membrane composition. To this end, detergent/lipid mixtures at given 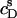 and
and 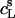 values are injected from the syringe (s) into the calorimeter cell containing only detergent at various concentrations, cD. The cD value for which the reaction heat, QL+D, equals the heat of vesicle dilution must also correspond to the free detergent concentration in the syringe,
values are injected from the syringe (s) into the calorimeter cell containing only detergent at various concentrations, cD. The cD value for which the reaction heat, QL+D, equals the heat of vesicle dilution must also correspond to the free detergent concentration in the syringe, 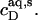 Writing the equilibrium concentrations of SDS in the syringe as
Writing the equilibrium concentrations of SDS in the syringe as 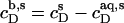 and
and 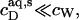 the partition coefficient between the bulk aqueous phase and lipid bilayers takes the form
the partition coefficient between the bulk aqueous phase and lipid bilayers takes the form
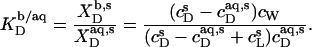 |
(8) |
Electrostatic effects
Membrane binding of SDS at detergent concentrations much below the critical saturating value is adequately described by a partition equilibrium between the interfacial (i) aqueous phase having a detergent mol fraction of 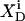 and bilayers characterized by
and bilayers characterized by 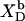 (19,21). The intrinsic mol fraction partition coefficient, as defined by
(19,21). The intrinsic mol fraction partition coefficient, as defined by
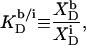 |
(9) |
is constant if mixing in both phases is ideal. 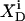 is related to the detergent mol fraction in the bulk aqueous phase,
is related to the detergent mol fraction in the bulk aqueous phase, 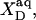 by a Boltzmann term,
by a Boltzmann term,
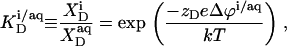 |
(10) |
where zD = −1 is the charge number of DS−, e the elementary charge, Δϕi/aq the electrostatic potential at the membrane surface with respect to the bulk aqueous phase, k the Boltzmann constant, and T the absolute temperature. Thus, partitioning between the bulk solution and the bilayer phase obeys
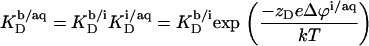 |
(11) |
Δϕi/aq is conveniently obtained from Gouy–Chapman theory (36–38), which relates it to the membrane surface charge density, σ, according to
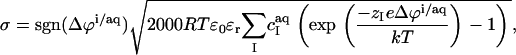 |
(12) |
with R being the universal gas constant, ɛ0 the permittivity of free space, and ɛr the dielectric constant of the medium, which, for an aqueous solution at 65°C, amounts to ɛr = 66 (39). The summation in Eq. 12 goes over the bulk aqueous concentrations, 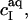 of all ionic species (I), including the detergent, the buffer (here, 10 mM phosphate) and its counterions (16 mM Na+), and the additional salt (154 mM NaCl). As above,
of all ionic species (I), including the detergent, the buffer (here, 10 mM phosphate) and its counterions (16 mM Na+), and the additional salt (154 mM NaCl). As above, 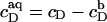 for SDS; the other bulk concentrations may be approximated by the corresponding total concentrations,
for SDS; the other bulk concentrations may be approximated by the corresponding total concentrations, 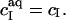 The Henderson-Hasselbach equation provides the fraction of protonated buffer as 1/(1 + 10pH − pKa), where pKa refers to the buffering group. pKa = 7.2 is the second pKa value of phosphate, implying that 3.9 mM of the buffer carries a charge of −e, while the remaining 6.1 mM has a charge of −2e.
The Henderson-Hasselbach equation provides the fraction of protonated buffer as 1/(1 + 10pH − pKa), where pKa refers to the buffering group. pKa = 7.2 is the second pKa value of phosphate, implying that 3.9 mM of the buffer carries a charge of −e, while the remaining 6.1 mM has a charge of −2e.
Neglecting counterion binding, a second, independent expression (40) for σ follows from its definition as
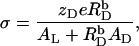 |
(13) |
where AL = 0.68 nm2 (41) and AD = 0.30 nm2 (19) denote the molecular surface area requirements of POPC and SDS, respectively. 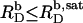 is the detergent/lipid mol ratio in the bilayer. Hence, Δϕi/aq is given implicitly by the equality of Eqs. 12 and 13 and can be calculated by standard iteration methods. Using Eqs. 11–13, we have recently derived (21) an intrinsic mole fraction partition coefficient of
is the detergent/lipid mol ratio in the bilayer. Hence, Δϕi/aq is given implicitly by the equality of Eqs. 12 and 13 and can be calculated by standard iteration methods. Using Eqs. 11–13, we have recently derived (21) an intrinsic mole fraction partition coefficient of 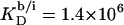 from ITC uptake and release experiments performed under the same conditions as those used here.
from ITC uptake and release experiments performed under the same conditions as those used here.
Counterion binding
The most obvious shortcoming of the approach outlined in the preceding section is the complete neglect of counterion binding. As in a micelle (22), the high surface charge density conferred upon a membrane by incorporation of DS− is partially neutralized by the binding of Na+ ions that are enriched near the bilayer surface. In analogy to the case of negatively charged lipids (40), the fraction of membrane-bound DS− neutralized by Na+, θ, can be envisaged to follow a Langmuir binding isotherm,
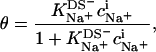 |
(14) |
where 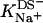 is the binding constant of Na+ to membrane-incorporated DS−. The interfacial Na+ concentration,
is the binding constant of Na+ to membrane-incorporated DS−. The interfacial Na+ concentration, 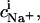 is related to the corresponding bulk value,
is related to the corresponding bulk value, 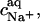 by
by
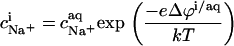 |
(15) |
Multiplication of Eq. 13 by (1 − θ) yields
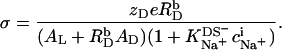 |
(16) |
Using Eq. 15, Δϕi/aq can now be calculated from the equality of Eqs. 12 and 16 rather than Eqs. 12 and 13. As no data on the affinity of Na+ to membrane-bound DS− seem to be available, 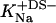 has to be included as a fitting parameter to find the best agreement between the experimental
has to be included as a fitting parameter to find the best agreement between the experimental 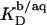 values obtained from Eq. 8 and their theoretical counterparts calculated from Eq. 11.
values obtained from Eq. 8 and their theoretical counterparts calculated from Eq. 11.
Interpretation of ITC solubilization and reconstitution experiments
In this section, we lay out the rationale underlying the quantitative interpretation of ITC solubilization and reconstitution experiments; the equations used for simulations are derived in detail in the following section.
Solubilization
In the bilayer range of ITC solubilization experiments, several elementary processes take place sequentially or simultaneously upon injection of SDS micelles to POPC LUVs. Throughout this range, all micelles disintegrate; however, whereas detergents with CMC values in the micromolar range are virtually completely taken up into the membrane at sufficiently high cL values (8,10), partitioning into the aqueous phase cannot be neglected in solubilization studies using SDS. This series of events is equivalent to complete demicellization 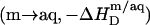 followed by partial transfer from the aqueous solution into the bilayer phase
followed by partial transfer from the aqueous solution into the bilayer phase 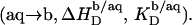 The second process has two consequences. On one hand, a negative surface charge is imparted upon the membrane, which repels free DS− ions. On the other hand, the bilayer phase becomes more abundant as compared with the aqueous phase, so that the equilibrium is shifted to membrane incorporation. At low detergent contents, the first effect dominates and gives rise to a drastic increase in and even a change in sign of the reaction heat,
The second process has two consequences. On one hand, a negative surface charge is imparted upon the membrane, which repels free DS− ions. On the other hand, the bilayer phase becomes more abundant as compared with the aqueous phase, so that the equilibrium is shifted to membrane incorporation. At low detergent contents, the first effect dominates and gives rise to a drastic increase in and even a change in sign of the reaction heat, 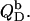 As the membrane becomes enriched in DS−, addition of further detergent entails only a modest enhancement of the surface charge density, and the two effects basically cancel each other out, such that
As the membrane becomes enriched in DS−, addition of further detergent entails only a modest enhancement of the surface charge density, and the two effects basically cancel each other out, such that 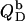 levels off.
levels off.
In the coexistence region, both SDS and POPC are shifted from detergent-saturated bilayers to lipid-saturated micelles. In addition, some of the free detergent from the syringe partitions into micelles upon injection because the aqueous detergent concentration in the syringe (CMC) is higher than that in the cell 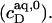 These events correspond to detergent transfer from bilayers to water
These events correspond to detergent transfer from bilayers to water 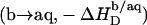 followed by micellization
followed by micellization 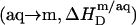 and concomitant lipid transfer from vesicles to micelles
and concomitant lipid transfer from vesicles to micelles 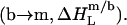 The extent to which these processes occur depends on the compositions of the phases involved, which are given by
The extent to which these processes occur depends on the compositions of the phases involved, which are given by 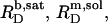 and
and 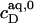 for membranes, micelles, and aqueous solution, respectively. As these values remain constant throughout the phase coexistence range, so does
for membranes, micelles, and aqueous solution, respectively. As these values remain constant throughout the phase coexistence range, so does 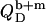 (10).
(10).
In the micellar range, finally, part of the pure detergent micelles from the syringe disintegrate upon injection to maintain the SDS partition equilibrium between the aqueous phase and mixed micelles 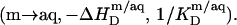 As the micellar detergent mol fraction and the aqueous SDS concentration in the sample cell approach unity and the CMC, respectively,
As the micellar detergent mol fraction and the aqueous SDS concentration in the sample cell approach unity and the CMC, respectively, 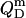 smoothly decreases in magnitude. This is not the case for detergents with much lower CMC values, for which nonzero reaction heats beyond completion of solubilization can be explained only by nonideal mixing in the micellar phase or a second-order micellar transition (10).
smoothly decreases in magnitude. This is not the case for detergents with much lower CMC values, for which nonzero reaction heats beyond completion of solubilization can be explained only by nonideal mixing in the micellar phase or a second-order micellar transition (10).
Reconstitution
In the micellar region of reconstitution experiments, all of the injected lipid is transferred to micelles 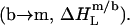 The ensuing decrease in the micellar detergent mole fraction entails redistribution of SDS from the aqueous phase into micelles
The ensuing decrease in the micellar detergent mole fraction entails redistribution of SDS from the aqueous phase into micelles 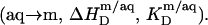 This effect is most pronounced at the beginning of the experiment, and
This effect is most pronounced at the beginning of the experiment, and 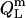 decreases in magnitude with consecutive injections. Here, the coexistence range corresponds to the transfer of detergent
decreases in magnitude with consecutive injections. Here, the coexistence range corresponds to the transfer of detergent 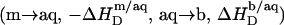 and lipid
and lipid 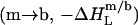 from micelles to vesicles. Again, constant compositions of all phases lead to constant
from micelles to vesicles. Again, constant compositions of all phases lead to constant 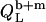 values. In the bilayer range, the titration eventually reduces to an uptake experiment (19,21), where injection of lipid vesicles causes detergent binding from the aqueous solution
values. In the bilayer range, the titration eventually reduces to an uptake experiment (19,21), where injection of lipid vesicles causes detergent binding from the aqueous solution 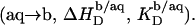
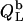 approaches zero as less and less free detergent is available in the calorimeter cell.
approaches zero as less and less free detergent is available in the calorimeter cell.
Simulation of ITC solubilization and reconstitution experiments
Bilayer range
The normalized heats measured upon injection of SDS or POPC to a bilayer vesicle suspension, 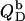 and
and 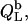 respectively, are given by an equation recently derived (21) for evaluating uptake experiments,
respectively, are given by an equation recently derived (21) for evaluating uptake experiments,
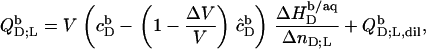 |
(17) |
where V stands for the volume of the calorimeter cell, ΔV for the injection volume, and QD,dil (QL,dil) for the heat of dilution normalized with respect to the molar amount of detergent (lipid) injected, ΔnD (ΔnL). 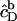 and
and 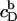 denote the equilibrium concentrations of membrane-bound SDS in the cell before and after injection, respectively. Ideal mixing in both phases yields (10,21)
denote the equilibrium concentrations of membrane-bound SDS in the cell before and after injection, respectively. Ideal mixing in both phases yields (10,21)
 |
(18) |
A corresponding equation holds for 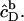
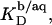 in turn, can be calculated from
in turn, can be calculated from 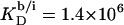 (21) with the aid of Eq. 11 using Eqs. 12 and 16.
(21) with the aid of Eq. 11 using Eqs. 12 and 16.
Micellar range
In analogy to Eq. 17, the heats upon detergent or lipid titration to a micellar solution, 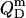 and
and 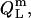 respectively, are
respectively, are
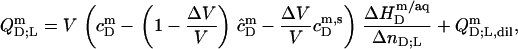 |
(19) |
where all parameters have definitions analogous to those introduced above. The additional term in Eq. 19 as compared with Eq. 17 accounts for the concentration of micellar SDS in the syringe, 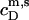 (see Eq. 3 in (21)). The latter is
(see Eq. 3 in (21)). The latter is 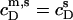 − CMC for solubilization but
− CMC for solubilization but 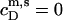 for reconstitution, where the syringe contains lipid vesicles rather than detergent micelles. Assuming ideal mixing also in the micellar phase gives
for reconstitution, where the syringe contains lipid vesicles rather than detergent micelles. Assuming ideal mixing also in the micellar phase gives
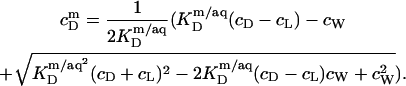 |
(20) |
A corresponding equation holds for 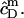 Owing to the highly curved, rough, and dynamic surfaces of micelles, the intrinsic partition coefficient of SDS between the interfacial aqueous and the micellar phases,
Owing to the highly curved, rough, and dynamic surfaces of micelles, the intrinsic partition coefficient of SDS between the interfacial aqueous and the micellar phases, 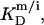 cannot be derived from electrostatic theory as easily as
cannot be derived from electrostatic theory as easily as 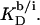 In the present case, however, the value of the apparent partition coefficient,
In the present case, however, the value of the apparent partition coefficient, 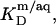 is virtually constant (see Results and Supplementary Material) and thus can be directly inserted into Eq. 20.
is virtually constant (see Results and Supplementary Material) and thus can be directly inserted into Eq. 20.
Coexistence range
In the coexistence range, we need to consider the partitioning of SDS between the aqueous phase, bilayers, and micelles as well as the transfer of lipid between the two surfactant aggregates. In analogy to Eqs. 17 and 19, the heats upon detergent or lipid injection, 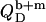 and
and 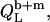 respectively, read
respectively, read
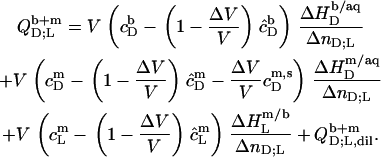 |
(21) |
Now, the equilibrium concentrations 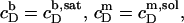 and
and 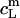 are readily obtained from the definitions of
are readily obtained from the definitions of 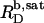 and
and 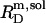 according to Eqs. 1 and 3, respectively, from two equations of mass balance,
according to Eqs. 1 and 3, respectively, from two equations of mass balance, 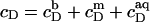 and
and 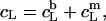 and from
and from 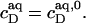 This yields
This yields
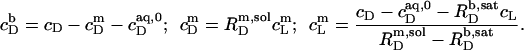 |
(22) |
Corresponding equations hold for 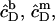 and
and 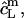 whereas
whereas 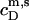 is again given by
is again given by 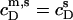 − CMC for solubilization or by
− CMC for solubilization or by 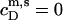 for reconstitution.
for reconstitution.
RESULTS
Light scattering
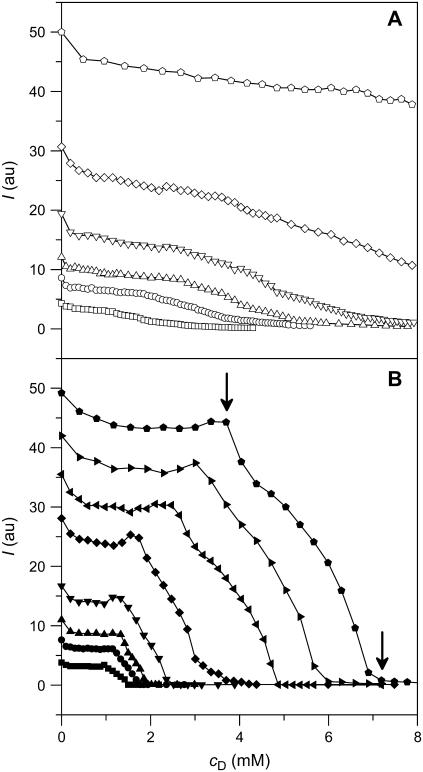
Solubilization of 100-nm-diameter POPC LUVs by SDS in aqueous solution (10 mM phosphate buffer, 154 mM NaCl, pH 7.4) was monitored by right-angle light scattering (19). Fig. 1 depicts the relative scattering intensities, I, of 0.1–2.5 mM lipid suspensions as a function of cD at 25°C (A) and 65°C (B). The I values taken 3 min after addition of detergent revealed a striking difference between these two temperatures. Although SDS titration at 25°C led to a continuous decrease in I, the curves depicted in Fig. 1 A are rather featureless. By contrast, three ranges could be distinguished at 65°C, as shown in Fig. 1 B: I varied only little with cD up to a first breakpoint (arrow), then decreased rapidly and nearly linearly, and finally almost vanished at a second breakpoint (arrow). Importantly, kinetic experiments (data not shown) revealed that I values taken at 65°C represented equilibrium situations, whereas an incubation time of 3 min after each detergent injection was too short to allow the mixture to attain equilibrium at 25°C. At the latter temperature, in fact, I continued to decrease for more than 24 h after the first injection (data not shown).
FIGURE 1.
Solubilization as monitored by right-angle light scattering at 25°C (A, open symbols) and 65°C (B, solid symbols). Scattering intensity at a wavelength of 632.8 nm, I, versus SDS concentration, cD. Initial POPC LUV concentrations in the cuvette were 0.1 mM (squares), 0.2 mM (circles), 0.3 mM (up-triangles), 0.5 mM (down-triangles), 1.0 mM (diamonds), 1.5 mM (left triangles), 2.0 mM (right triangles), and 2.5 mM (pentagons, breakpoints indicated by arrows). I was registered 3 min after addition of SDS, which was sufficient to attain equilibrium at 65°C but not at 25°C.
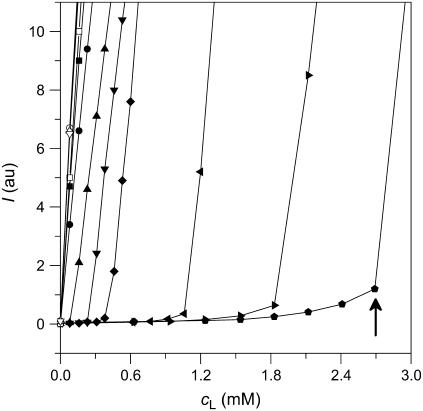
This behavior was confirmed by reverse titrations, that is, by injecting lipid vesicles into SDS solutions. Fig. 2 exemplifies some of these membrane reconstitution experiments in dependence on cL. At 25°C, addition of POPC LUVs caused a drastic and linear rise in I irrespective of the SDS content. At 65°C and cD > 1.0 mM, however, I remained virtually constant at first and started to increase dramatically only beyond a certain cL value (arrow). Again, I values were read 3 min after addition of lipid vesicles and represented equilibrium situations at 65°C but not at 25°C.
FIGURE 2.
Reconstitution as monitored by right-angle light scattering at 25°C (open symbols, near the ordinate) and 65°C (solid symbols). Scattering intensity at a wavelength of 632.8 nm, I, versus POPC concentration, cL. Initial SDS concentrations in the cuvette were 0 (squares), 1.0 mM (circles), 1.5 mM (up-triangles), 2.0 mM (down-triangles), 2.5 mM (diamonds), 5.0 mM (left triangles), 7.5 mM (right triangles), and 10 mM (pentagons, breakpoint indicated by arrow). I was registered 3 min after addition of POPC, which was sufficient to attain equilibrium at 65°C but not at 25°C.
ITC solubilization and reconstitution experiments
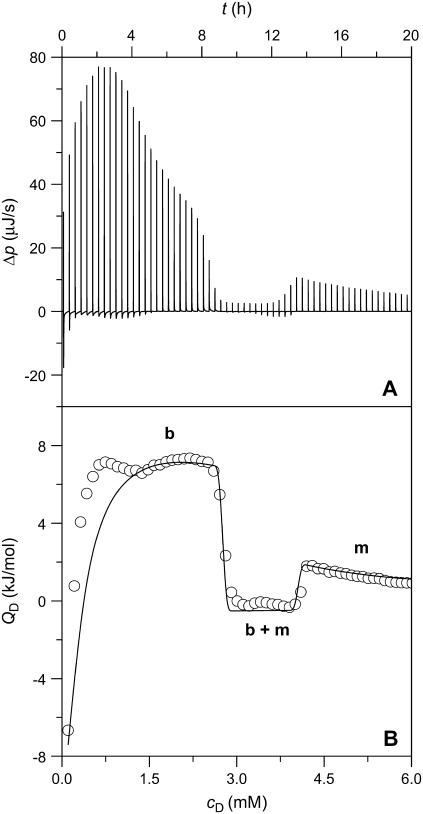
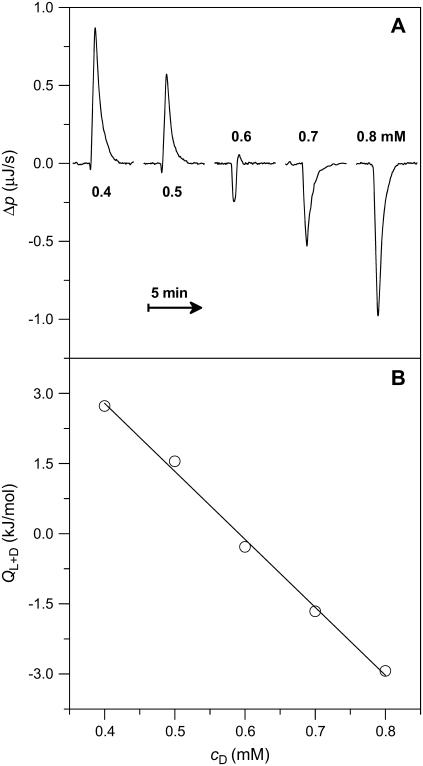
A more detailed characterization of membrane solubilization by SDS at elevated temperature was possible with ITC (8,10). Fig. 3 gives the differential heating power, Δp (A), and the integrated heats of reaction, QD (B, circles), obtained upon injecting 3-μL aliquots of 50 mM SDS into 1.0 mM POPC LUVs at 65°C. The Δp peak heights did not correlate with the integral QD values because of varying kinetics of several overlapping processes. This became particularly evident during the initial injections, which exhibited a complex behavior comprising a rapid endothermic process and a slower exothermic reaction. In this range, the QD values first increased and even changed sign but then approached a plateau, the height of which inversely correlated with cL in the calorimeter cell (data not shown). During the experiment exemplified in Fig. 3, QD dropped to slightly exothermic and roughly constant values at cD = 2.7 mM and resumed endothermic and smoothly decaying values only beyond cD = 4.1 mM.
FIGURE 3.
ITC solubilization experiment at 65°C. Three-microliter aliquots of 50 mM SDS were titrated to 1.0 mM POPC LUVs. Only 60 out of 100 injections are shown. (A) Differential heating power, Δp, versus time, t. (B) Normalized heats of reaction, QD, versus SDS concentration in the cell, cD. Experimental data (circles) and simulation (solid line) according to Eqs. 17–22. b, b + m, and m denote the ranges where, in addition to the aqueous phase, only bilayers, bilayers and micelles in coexistence, and only micelles are present, respectively.
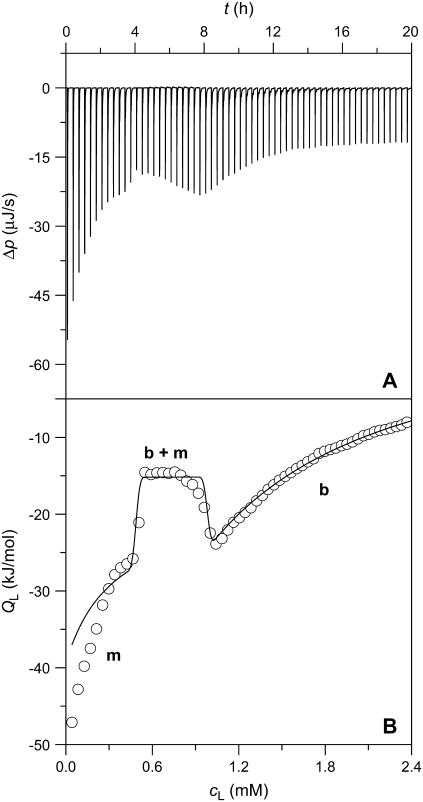
This was again corroborated in reconstitution experiments by injecting lipid vesicles into SDS solutions. Fig. 4 illustrates the raw data (A) and the QL values (B, circles) afforded by titrating a 3.0 mM SDS solution with 3-μL aliquots of 20 mM POPC LUVs at 65°C. Although QL was always exothermic, boundaries at cL = 0.5 mM and cL = 1.0 mM became apparent as the borders of a trough separating two regions of decaying magnitude. At the lowest cD value in the sample cell examined (cD = 1.0 mM), this trough disappeared, leaving only the last range corresponding to an uptake assay (data not shown; see (21)).
FIGURE 4.
ITC reconstitution experiment at 65°C. Three-microliter aliquots of 20 mM POPC LUVs were titrated to 3.0 mM SDS. Only 60 out of 100 injections are shown. (A) Differential heating power, Δp, versus time, t. (B) Normalized heats of reaction, QL, versus POPC concentration in the cell, cL. Experimental data (circles) and simulation (solid line) according to Eqs. 17–22. The values m, b + m, and b denote the ranges where, in addition to the aqueous phase, only micelles, bilayers and micelles in coexistence, and only bilayers are present, respectively.
Using ITC solubilization and reconstitution, the two critical cD (cL) values for a broad range of cL (cD) values in the calorimeter cell were thus obtained from the maxima and minima in the first derivative of QD (QL) with respect to cD (cL) (13,14,17). As the simulations (solid lines) in Figs. 3 B and 4 B are based on additional information derived from experiments described below, they will be discussed in the last Results section.
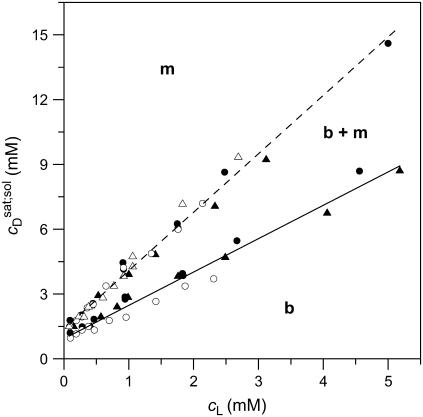
Phase diagram and partition coefficients
A simple phase diagram of dilute aqueous SDS/POPC systems at 65°C was obtained by plotting the critical cD values versus the corresponding cL values, as shown in Fig. 5. Linear regression according to Eq. 2 yields 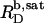 = 1.5 and
= 1.5 and 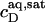 = 0.9 mM, implying that POPC LUVs can incorporate up to 1.5 SDS molecules per lipid before solubilization commences at a free detergent concentration of 0.9 mM. Analogously, Eq. 4 gives
= 0.9 mM, implying that POPC LUVs can incorporate up to 1.5 SDS molecules per lipid before solubilization commences at a free detergent concentration of 0.9 mM. Analogously, Eq. 4 gives 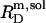 = 2.7 and
= 2.7 and 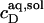 = 1.4 mM, suggesting that a micelle must contain at least 2.7 SDS molecules per POPC. Linear regression analysis under the constraint
= 1.4 mM, suggesting that a micelle must contain at least 2.7 SDS molecules per POPC. Linear regression analysis under the constraint 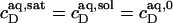 is virtually as good as that illustrated in Fig. 5, yielding
is virtually as good as that illustrated in Fig. 5, yielding 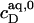 = 1.1 mM, whereas
= 1.1 mM, whereas 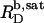 and
and 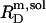 are hardly affected (data not shown). According to Eq. 5, the SDS mole fractions in coexisting bilayers and micelles amount to
are hardly affected (data not shown). According to Eq. 5, the SDS mole fractions in coexisting bilayers and micelles amount to 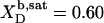 and
and 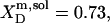 respectively. The mol fraction partition coefficients of SDS and POPC between detergent-saturated bilayers and lipid-saturated micelles are given by Eq. 6 as, respectively,
respectively. The mol fraction partition coefficients of SDS and POPC between detergent-saturated bilayers and lipid-saturated micelles are given by Eq. 6 as, respectively, 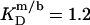 and
and 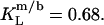 Equation 7 finally provides the partition coefficients of SDS between the bulk aqueous phase and bilayers or micelles as
Equation 7 finally provides the partition coefficients of SDS between the bulk aqueous phase and bilayers or micelles as 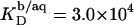 and
and 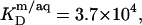 respectively.
respectively.
FIGURE 5.
Phase diagram of dilute aqueous SDS/POPC mixtures. Data were taken from solubilization (circles) and reconstitution (triangles) experiments conducted with light scattering (open symbols) and titration calorimetry (solid symbols). Linear regression analyses for the onset (solid line) and the completion (dashed line) of solubilization correspond to Eqs. 2 and 4, respectively, and separate the bilayer (b) and the micellar (m) areas from the transition range (b + m). Note that the aqueous phase is always present. cL and cD are the concentrations of POPC and SDS, respectively.
ITC membrane partitioning assay
The partition coefficient of SDS between the bulk aqueous phase and lipid bilayers was determined as a function of 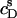 using a model-free ITC partitioning assay (34). In this kind of experiment, SDS/POPC mixtures at subsaturating detergent contents were injected into pure SDS solutions spanning a range of concentrations, cD. As an example, Fig. 6 A depicts a set of representative peaks resulting from five independent series of injections. The syringe always contained both SDS and POPC at concentrations of
using a model-free ITC partitioning assay (34). In this kind of experiment, SDS/POPC mixtures at subsaturating detergent contents were injected into pure SDS solutions spanning a range of concentrations, cD. As an example, Fig. 6 A depicts a set of representative peaks resulting from five independent series of injections. The syringe always contained both SDS and POPC at concentrations of 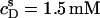 and
and 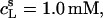 respectively, whereas the SDS solution in the calorimeter cell ranged in concentration from cD = 0.4 mM to cD = 0.8 mM. Endothermic peaks at cD < 0.6 mM indicated that the free detergent concentration in the syringe,
respectively, whereas the SDS solution in the calorimeter cell ranged in concentration from cD = 0.4 mM to cD = 0.8 mM. Endothermic peaks at cD < 0.6 mM indicated that the free detergent concentration in the syringe, 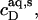 was higher than cD in the cell, thus leading to desorption from the membrane. At cD = 0.6 mM, the reaction heat almost disappeared, whereas cD > 0.6 mM gave rise to strong exothermic peaks because of additional binding of SDS to the membrane upon injection.
was higher than cD in the cell, thus leading to desorption from the membrane. At cD = 0.6 mM, the reaction heat almost disappeared, whereas cD > 0.6 mM gave rise to strong exothermic peaks because of additional binding of SDS to the membrane upon injection.
FIGURE 6.
ITC partitioning experiment at 65°C. 10-μL aliquots of a mixture consisting of 1.5 mM SDS and 1.0 mM POPC LUVs were injected to SDS at different concentrations. (A) Differential heating power, Δp, of the respective third peak of five independent titrations into the calorimeter cell containing SDS at the concentrations indicated in the panel. (B) Normalized heats of reaction, QL+D, versus SDS concentration in the cell, cD. Experimental data (circles) and linear regression analysis (solid line).
As can be seen from Fig. 6 B, the integrated reaction heats, QL+D (circles), unveiled a roughly linear decrease with cD. Linear regression analysis (solid line) returns a value of cD = 0.6 mM for the SDS concentration in the cell at which QL+D = −0.02 kJ/mol just equals the heat of vesicle dilution (21). Thus, this value of cD must correspond to the equilibrium concentration of free detergent in the syringe, 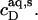 Inserting
Inserting 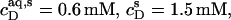 and
and 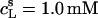 into Eq. 8 yields an apparent partition coefficient of
into Eq. 8 yields an apparent partition coefficient of 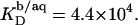
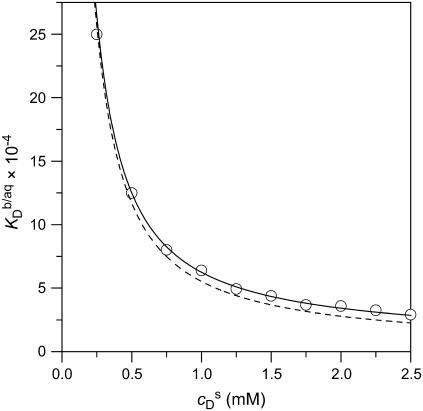
In Fig. 7, more 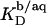 values thus determined for the partitioning of SDS into 1.0 mM POPC LUVs are plotted versus
values thus determined for the partitioning of SDS into 1.0 mM POPC LUVs are plotted versus 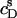 (circles). An increase in
(circles). An increase in 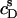 led to a steep drop in
led to a steep drop in 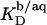 because of electrostatic repulsion of DS− ions from the membrane surface. According to Eq. 2 and the phase diagram in Fig. 5, the sample at the highest SDS concentration investigated
because of electrostatic repulsion of DS− ions from the membrane surface. According to Eq. 2 and the phase diagram in Fig. 5, the sample at the highest SDS concentration investigated 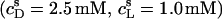 consisted of detergent-saturated vesicles. For this case, we determined an apparent partition coefficient of
consisted of detergent-saturated vesicles. For this case, we determined an apparent partition coefficient of 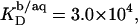 which equals the value determined from Eq. 7 for bilayers in the coexistence range (see preceding section). Table 1 provides an overview of all partition coefficients,
which equals the value determined from Eq. 7 for bilayers in the coexistence range (see preceding section). Table 1 provides an overview of all partition coefficients, 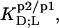 molar transfer enthalpies,
molar transfer enthalpies, 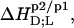 and other thermodynamic parameters derived from these.
and other thermodynamic parameters derived from these.
FIGURE 7.
Partition coefficient of SDS between the bulk aqueous phase and POPC bilayers, 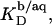 as a function of the total detergent concentration in the syringe,
as a function of the total detergent concentration in the syringe, 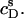 The concentration of POPC LUVs was
The concentration of POPC LUVs was 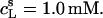 Experimental data as given by Eq. 8 (circles) and theoretical predictions according to Eq. 11 and
Experimental data as given by Eq. 8 (circles) and theoretical predictions according to Eq. 11 and 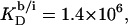 calculated either without considering counterion binding by using Eqs. 12 and 13 (dashed line) or upon including Na+ adsorption to DS− by using Eqs. 12 and 16 (solid line).
calculated either without considering counterion binding by using Eqs. 12 and 13 (dashed line) or upon including Na+ adsorption to DS− by using Eqs. 12 and 16 (solid line).
TABLE 1.
Thermodynamics of SDS and POPC partitioning between aqueous phase, micelles, and bilayers at 65°C
| Surfactant | p1 → p2 | 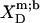 |
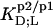 |
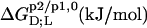 |
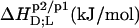 |
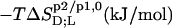 |
|---|---|---|---|---|---|---|
| 1 | 3.4 × 104* | −29.3 | −20.5* | −8.8 | ||
| SDS | aq → m | 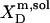 |
3.7 × 104† | −29.5 | ||
| aq → b | 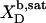 |
3.0 × 104†‡ | −29.0 | −31.8¶ | +2.8 | |
| b → m | 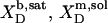 |
1.2† | −0.5 | +11.3*¶ | −11.8 | |
| POPC | b → m | 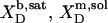 |
0.68† | +1.1 | −18.0† | +19.1 |
Partition coefficients, 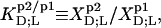 and molar transfer enthalpies,
and molar transfer enthalpies, 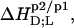 of SDS and POPC between phases p1 and p2, representing aqueous (aq) solution, micelles (m), and bilayers (b), were determined from demicellization, solubilization and reconstitution, partitioning, as well as uptake and release experiments. Standard molar Gibbs free energies,
of SDS and POPC between phases p1 and p2, representing aqueous (aq) solution, micelles (m), and bilayers (b), were determined from demicellization, solubilization and reconstitution, partitioning, as well as uptake and release experiments. Standard molar Gibbs free energies, 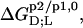 and entropic terms,
and entropic terms, 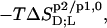 were calculated in analogy to, respectively, Eqs. S2 and S3 (see Supplementary Material). The compositions of the surfactant aggregates at which the
were calculated in analogy to, respectively, Eqs. S2 and S3 (see Supplementary Material). The compositions of the surfactant aggregates at which the 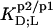 values were determined are specified in terms of their SDS mole fractions,
values were determined are specified in terms of their SDS mole fractions, 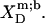
Demicellization.
Solubilization and reconstitution.
Partitioning.
Uptake and release.
The simulated 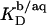 values (dashed line) included in Fig. 7 can be obtained from
values (dashed line) included in Fig. 7 can be obtained from 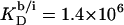 (21) with the aid of Eq. 11 by neglecting counterion binding, that is, by calculating Δϕi/aq from the equality of Eqs. 12 and 13. Although the experimentally determined values (circles) are reproduced fairly well, small but systematic deviations are apparent at high cD values. By contrast, accounting for Na+ adsorption to DS− by using
(21) with the aid of Eq. 11 by neglecting counterion binding, that is, by calculating Δϕi/aq from the equality of Eqs. 12 and 13. Although the experimentally determined values (circles) are reproduced fairly well, small but systematic deviations are apparent at high cD values. By contrast, accounting for Na+ adsorption to DS− by using 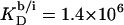 (21) and Eqs. 11, 12, and 16 allows for a much better fit (solid line) and suggests a binding constant of Na+ to membrane-incorporated DS− of
(21) and Eqs. 11, 12, and 16 allows for a much better fit (solid line) and suggests a binding constant of Na+ to membrane-incorporated DS− of 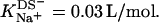 For the above example representing SDS-saturated vesicles (cD = 2.5 mM, cL = 1.0 mM), electrostatic effects at the membrane surface and counterion binding are characterized by σ = −162 mC/m2, Δϕi/aq = −113 mV,
For the above example representing SDS-saturated vesicles (cD = 2.5 mM, cL = 1.0 mM), electrostatic effects at the membrane surface and counterion binding are characterized by σ = −162 mC/m2, Δϕi/aq = −113 mV, 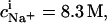 and θ = 20%, as calculated from Eqs. 12 and 14–16.
and θ = 20%, as calculated from Eqs. 12 and 14–16.
Simulation of ITC solubilization and reconstitution experiments
The simulations (solid lines) depicted in Figs. 3 B and 4 B are based on Eqs. 17–22. In the bilayer ranges, the 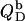 and
and 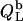 values were calculated from Eqs. 17 and 18 using
values were calculated from Eqs. 17 and 18 using 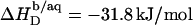 (21).
(21). 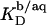 was again obtained from
was again obtained from 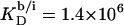 (21) with the aid of Eqs. 11, 12, and 16, thus taking into account counterion binding. For the solubilization experiment, we inserted
(21) with the aid of Eqs. 11, 12, and 16, thus taking into account counterion binding. For the solubilization experiment, we inserted 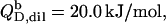 which equals the total heat of micelle disintegration and dilution determined from the initial injections in demicellization experiments (see Supplementary Material). For the reconstitution assay,
which equals the total heat of micelle disintegration and dilution determined from the initial injections in demicellization experiments (see Supplementary Material). For the reconstitution assay, 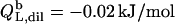 was taken as the negligible heat of vesicle dilution observed toward the end of uptake experiments (21).
was taken as the negligible heat of vesicle dilution observed toward the end of uptake experiments (21).
In the micellar ranges, the 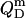 and
and 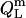 values were calculated from Eqs. 19 and 20 on the basis of
values were calculated from Eqs. 19 and 20 on the basis of 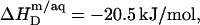 as provided by demicellization experiments (see Supplementary Material). Because the apparent partition coefficient between the bulk aqueous and the micellar phases,
as provided by demicellization experiments (see Supplementary Material). Because the apparent partition coefficient between the bulk aqueous and the micellar phases, 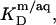 only slightly decreases from 3.7 × 104 to 3.4 × 104 when going from lipid-saturated to pure detergent micelles (see Table 1), we used a constant value of
only slightly decreases from 3.7 × 104 to 3.4 × 104 when going from lipid-saturated to pure detergent micelles (see Table 1), we used a constant value of 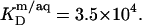 For the solubilization assay, demicellization (see Supplementary Material) also yielded
For the solubilization assay, demicellization (see Supplementary Material) also yielded 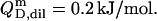 For the reconstitution experiment, the constant heat contribution was assumed to amount to
For the reconstitution experiment, the constant heat contribution was assumed to amount to 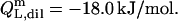 Neglecting the small heat of vesicle dilution
Neglecting the small heat of vesicle dilution 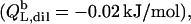 this value must correspond to the molar transfer enthalpy of POPC from bilayers into micelles, so that
this value must correspond to the molar transfer enthalpy of POPC from bilayers into micelles, so that 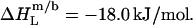 Note that this was the only quantity not determined independently and, during the entire simulation of calorimetric solubilization and reconstitution titrations, therefore constituted the only adjustable parameter.
Note that this was the only quantity not determined independently and, during the entire simulation of calorimetric solubilization and reconstitution titrations, therefore constituted the only adjustable parameter.
In the coexistence ranges, the 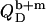 and
and 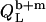 values were derived from Eqs. 21 and 22, again using enthalpy changes of
values were derived from Eqs. 21 and 22, again using enthalpy changes of 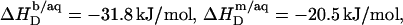 and
and 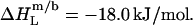
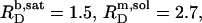 and
and 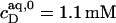 were derived from the phase diagram shown in Fig. 5. As above,
were derived from the phase diagram shown in Fig. 5. As above, 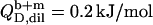 applied to the solubilization assay, whereas
applied to the solubilization assay, whereas 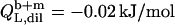 was used for simulation of the reconstitution experiment.
was used for simulation of the reconstitution experiment.
DISCUSSION
Phase diagram and partition coefficients
The anionic surfactant SDS undergoes rapid transbilayer flip-flop at 65°C (19,21) but not at 25°C ((19,21,23,29), M. Apel-Paz, G. F. Doncel, and T. K. Vanderlick, unpublished). As becomes obvious from inspection of Figs. 1 and 2, this has tremendous consequences for the solubilization of lipid membranes by SDS. At room temperature, the slow kinetics of vesicle dissolution largely precludes a thorough evaluation comparable to that described for nonionic detergents (4–6,8–12) because the detergent/lipid systems cannot reach their equilibrium states on experimental timescales. This calls for a cautious use of SDS and other nonpermeant detergents in biochemical procedures normally performed at low temperatures, such as dissolution of biological membrane samples, extraction of membrane constituents, and crystallization of membrane proteins. As seen in Fig. 5, however, a clearcut phase diagram of dilute aqueous SDS/POPC mixtures is obtained at 65°C, implying that the rate of detergent flip-flop is a crucial determinant of lipid bilayer solubilization and reconstitution.
A solubilizing SDS/POPC ratio of 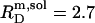 is in reasonable agreement with
is in reasonable agreement with 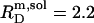 reported by Tan et al. (19) for similar conditions (56°C, 10 mM Tris, 100 mM NaCl, pH 7.4). A saturating ratio of
reported by Tan et al. (19) for similar conditions (56°C, 10 mM Tris, 100 mM NaCl, pH 7.4). A saturating ratio of 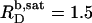 is also in line with the slope of
is also in line with the slope of 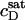 versus cL obtained by these authors from light scattering and ITC experiments at low cL values, whereas a much shallower slope of
versus cL obtained by these authors from light scattering and ITC experiments at low cL values, whereas a much shallower slope of 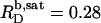 is implied by light scattering and NMR studies at considerably higher cL values (see Fig. 3 C in (19)). The low susceptibility of POPC membranes to SDS at 65°C in terms of high
is implied by light scattering and NMR studies at considerably higher cL values (see Fig. 3 C in (19)). The low susceptibility of POPC membranes to SDS at 65°C in terms of high 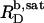 and
and 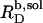 values can be explained by the small size of the sulfate headgroup as well as the high degree of acyl-chain disorder and the moderate extent of headgroup hydration expected at such a high temperature. For a homologous series of oligo(ethylene oxide) dodecyl ether (C12EOn) detergents and POPC (11), the saturating detergent/lipid mol ratio at 25°C has been found to augment from
values can be explained by the small size of the sulfate headgroup as well as the high degree of acyl-chain disorder and the moderate extent of headgroup hydration expected at such a high temperature. For a homologous series of oligo(ethylene oxide) dodecyl ether (C12EOn) detergents and POPC (11), the saturating detergent/lipid mol ratio at 25°C has been found to augment from 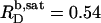 for n = 8 to
for n = 8 to 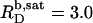 for n = 5. For C12EO8, in turn, this ratio increases from
for n = 5. For C12EO8, in turn, this ratio increases from 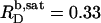 at 10°C to
at 10°C to 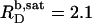 at 75°C. An SDS partition coefficient between bilayers and micelles of
at 75°C. An SDS partition coefficient between bilayers and micelles of 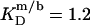 is also comparable to the corresponding values of nonionic detergents with small headgroups, as a decrease from
is also comparable to the corresponding values of nonionic detergents with small headgroups, as a decrease from 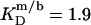 for C12EO8 to
for C12EO8 to 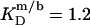 for C12EO5 is observed at 25°C (11).
for C12EO5 is observed at 25°C (11).
SDS solubilization of LUVs made up of the saturated lipid 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) at 60°C is characterized by 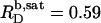 and
and 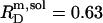 in pure water but by
in pure water but by 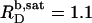 and
and 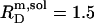 in the presence of 100 mM NaCl (17). A similar broadening of the coexistence range upon raising the ionic strength has been unveiled for bile salts (13,14). The remaining discrepancies between DMPC and POPC are due to systematic differences between saturated and unsaturated phospholipids. While the SDS and POPC partition coefficients amount to
in the presence of 100 mM NaCl (17). A similar broadening of the coexistence range upon raising the ionic strength has been unveiled for bile salts (13,14). The remaining discrepancies between DMPC and POPC are due to systematic differences between saturated and unsaturated phospholipids. While the SDS and POPC partition coefficients amount to 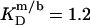 and
and 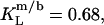 respectively, the corresponding values for SDS and DMPC in 100 mM NaCl at 60°C are
respectively, the corresponding values for SDS and DMPC in 100 mM NaCl at 60°C are 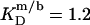 and
and 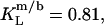 respectively (17). This indicates that the saturated lipid DMPC can more readily be transferred into the micellar state. This phenomenon has also been observed for bile salts and has been explained by the greater affinity of saturated, short-chain phospholipids to positively curved surfaces (13,14).
respectively (17). This indicates that the saturated lipid DMPC can more readily be transferred into the micellar state. This phenomenon has also been observed for bile salts and has been explained by the greater affinity of saturated, short-chain phospholipids to positively curved surfaces (13,14).
Electrostatics and counterion binding
SDS partition coefficients between the bulk aqueous phase and bilayers or micelles of, respectively, 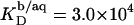 and
and 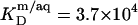 are 1–2 orders of magnitude below the corresponding values reported for the above-mentioned C12EOn series (11) because DS− ions, unlike nonionic detergents, are subject to electrostatic repulsion from the negatively charged vesicular and micellar surfaces (19). However, correcting for electrostatic effects yields a much higher value of
are 1–2 orders of magnitude below the corresponding values reported for the above-mentioned C12EOn series (11) because DS− ions, unlike nonionic detergents, are subject to electrostatic repulsion from the negatively charged vesicular and micellar surfaces (19). However, correcting for electrostatic effects yields a much higher value of 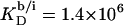 (21) for membrane adsorption of SDS from the interfacial aqueous phase. As for many nonionic surfactants, partitioning of SDS into POPC bilayers then follows a linear correlation between the detergent's hydrocarbon chain length and the standard molar Gibbs free energy of membrane binding,
(21) for membrane adsorption of SDS from the interfacial aqueous phase. As for many nonionic surfactants, partitioning of SDS into POPC bilayers then follows a linear correlation between the detergent's hydrocarbon chain length and the standard molar Gibbs free energy of membrane binding, 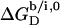 (19).
(19).
As becomes apparent from Fig. 7, implementing Na+ binding to membrane-incorporated DS− (solid line) allows for a much better reproduction of the experimental data (circles) at high cD values than does the simpler approach neglecting counterion adsorption (dashed line). At detergent contents in the membrane of 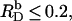 as used in our previous study (21), counterion binding amounts to θ < 3% and can thus be neglected. In fact, replacing Eq. 13 by Eq. 16 does not affect the evaluation of uptake and release experiments performed at
as used in our previous study (21), counterion binding amounts to θ < 3% and can thus be neglected. In fact, replacing Eq. 13 by Eq. 16 does not affect the evaluation of uptake and release experiments performed at 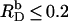 (data not shown, see (21)). In conclusion, a combination of a surface partition equilibrium with simple electrostatic theory is well suited for characterizing the interactions of SDS with POPC membranes even at very high detergent contents, provided that counterion binding is taken into account appropriately.
(data not shown, see (21)). In conclusion, a combination of a surface partition equilibrium with simple electrostatic theory is well suited for characterizing the interactions of SDS with POPC membranes even at very high detergent contents, provided that counterion binding is taken into account appropriately.
ITC solubilization and reconstitution experiments
The reasons for the lack of quantitative information about the solubilization of lipid membranes by charged detergents are threefold. First, the concentration of free detergent monomers usually cannot be neglected, such that, besides bilayers and micelles, an additional phase has to be taken into account. Second, partition equilibria are established between surfactant aggregates (vesicles, micelles) and the aqueous phase adjacent to their surfaces rather than the bulk solution. In comparison with the bulk detergent concentration, the interfacial concentrations can be lowered by several orders of magnitude as a consequence of electrostatic repulsion. Third, this is further complicated by the binding of counterions to the headgroups of membrane-incorporated detergent ions.
As demonstrated in this work, a wealth of data gathered from the SDS/POPC phase diagram (Fig. 5) as well as from partitioning (Fig. 7), demicellization (see Supplementary Material), and a combination of uptake and release (21) studies makes possible a quantitative treatment of ITC solubilization (Fig. 3) and reconstitution (Fig. 4) experiments. Clearly, the general hallmarks of the QD and QL values shown in Figs. 3 B and 4 B, respectively, are reproduced by a simple quantitative treatment assuming ideal mixing in all phases. The deviations at low cD values in the bilayer range of the solubilization experiment in Fig. 3 B were more pronounced at higher cL values but disappeared at cL ≤ 0.5 mM (data not shown), thus pointing to an endothermic process involving intervesicle contacts. As for nonionic detergents (10–12), systematic discrepancies such as those in the micellar range of the reconstitution experiment in Fig. 4 B might be accounted for by considering nonideal mixing or second-order transitions. However, in view of the approximations already inherent in the present model, any refinement necessitating additional free parameters seems of doubtful validity. Furthermore, the small size of the SDS headgroup and the low degree of hydration of both detergent and lipid headgroups at elevated temperature point to small, or even negligible, nonideality parameters (11). Finally, the fact that 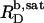 and
and 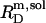 of SDS/POPC systems at 65°C can be identified with the breakpoints (arrows) in the light scattering studies shown in Figs. 1 and 2 argues against a noticeable population of large intermediate structures, such as wormlike micelles (10,42). The latter have been observed for many nonionic detergents and may severely obscure interpretation of light scattering data in terms of
of SDS/POPC systems at 65°C can be identified with the breakpoints (arrows) in the light scattering studies shown in Figs. 1 and 2 argues against a noticeable population of large intermediate structures, such as wormlike micelles (10,42). The latter have been observed for many nonionic detergents and may severely obscure interpretation of light scattering data in terms of 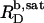 and
and 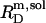 (42).
(42).
All other features of solubilization and reconstitution titrations performed over a wide range of cD and cL values are predicted very well by this model using the same set of parameters as above. Intriguingly, neglecting counterion binding by using Eq. 13 rather than Eq. 16 would lead to much poorer simulations in the bilayer ranges of both types of experiments (data not shown), thereby underlining the importance and the value of combining different calorimetric assays for quantifying membrane solubilization and reconstitution by a charged detergent.
According to Table 1, the molar transfer enthalpy of SDS from POPC bilayers into micelles is 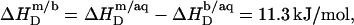 as determined by comparing uptake and release measurements (21) with demicellization data (see Supplementary Material). This is in conflict with exothermic
as determined by comparing uptake and release measurements (21) with demicellization data (see Supplementary Material). This is in conflict with exothermic 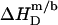 values reported for DMPC/SDS at 30 and 60°C (17). In that study, it was explicitly assumed that the endothermic plateau in the vesicular range of ITC solubilization experiments arises exclusively from the complete transfer of the injected detergent from micelles into bilayers. Hence, this approach neglects the SDS fraction in the aqueous phase and, in the framework of ideal mixing, predicts constant
values reported for DMPC/SDS at 30 and 60°C (17). In that study, it was explicitly assumed that the endothermic plateau in the vesicular range of ITC solubilization experiments arises exclusively from the complete transfer of the injected detergent from micelles into bilayers. Hence, this approach neglects the SDS fraction in the aqueous phase and, in the framework of ideal mixing, predicts constant 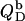 values, irrespective of the cL value in the sample cell. By contrast, Eqs. 17 and 18 imply a decrease in the height of the
values, irrespective of the cL value in the sample cell. By contrast, Eqs. 17 and 18 imply a decrease in the height of the 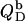 plateau with increasing cL, which is indeed borne out experimentally (data not shown, see Fig. 3 in (17)). Thus, all SDS and POPC transfer enthalpies between any two phases p1 and p2,
plateau with increasing cL, which is indeed borne out experimentally (data not shown, see Fig. 3 in (17)). Thus, all SDS and POPC transfer enthalpies between any two phases p1 and p2, 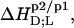 are opposite in sign to the corresponding quantities determined for systems containing nonionic detergents (9,10). As the standard molar Gibbs free energy changes,
are opposite in sign to the corresponding quantities determined for systems containing nonionic detergents (9,10). As the standard molar Gibbs free energy changes, 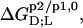 always have the same sign, a detergent or lipid transfer between two phases that is driven by an exothermic enthalpy change in the case of a nonionic detergent must be dominated by a gain in entropy in the case of an ionic surfactant and vice versa. Moreover, with the exception of
always have the same sign, a detergent or lipid transfer between two phases that is driven by an exothermic enthalpy change in the case of a nonionic detergent must be dominated by a gain in entropy in the case of an ionic surfactant and vice versa. Moreover, with the exception of 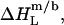 all
all 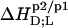 and
and 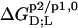 values listed in Table 1 are similar in magnitude to those published for C12EO8/POPC in water at 25°C (10).
values listed in Table 1 are similar in magnitude to those published for C12EO8/POPC in water at 25°C (10).
CONCLUSIONS
The present work provides a quantitative account of lipid membrane solubilization and reconstitution by a charged detergent. It also provides an experimental test of Gouy-Chapman theory and a new approach to monitoring counterion adsorption at the membrane surface.
Flip-flop of the anionic detergent SDS across POPC bilayers is very slow at room temperature, thus impeding a straightforward thermodynamic evaluation of membrane solubilization and reconstitution experiments. At elevated temperature, however, fast membrane translocation gives rise to a solubilizing behavior reminiscent of that observed for many nonionic detergents. The critical values at 65°C are 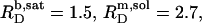 and
and 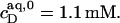 At this temperature, the mole fraction partition coefficient of SDS between the bulk aqueous phase and micelles amounts to
At this temperature, the mole fraction partition coefficient of SDS between the bulk aqueous phase and micelles amounts to 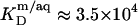 and varies only slightly with the composition of the micelles. The partition coefficient between the interfacial aqueous phase and POPC membranes is
and varies only slightly with the composition of the micelles. The partition coefficient between the interfacial aqueous phase and POPC membranes is 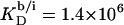 at 65°C, whereas the corresponding value referring to the bulk aqueous solution can be lowered down to
at 65°C, whereas the corresponding value referring to the bulk aqueous solution can be lowered down to 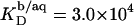 because of electrostatic repulsion. Gouy-Chapman theory can account for these effects; at high SDS concentrations, however, it is mandatory to include counterion binding as the Langmuir binding constant of Na+ to membrane-incorporated DS− amounts to
because of electrostatic repulsion. Gouy-Chapman theory can account for these effects; at high SDS concentrations, however, it is mandatory to include counterion binding as the Langmuir binding constant of Na+ to membrane-incorporated DS− amounts to 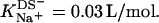 Finally, with the aid of the partition coefficients and transfer enthalpies determined in different ITC assays, the heats of solubilization and reconstitution can be understood quantitatively by assuming ideal mixing in all phases.
Finally, with the aid of the partition coefficients and transfer enthalpies determined in different ITC assays, the heats of solubilization and reconstitution can be understood quantitatively by assuming ideal mixing in all phases.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Prof. Joachim Seelig (Biocenter) for fruitful discussions and Heike Nikolenko, Katrin Guse, and Julian Heuberger (all FMP) for excellent technical assistance.
This work was supported by the European Commission with grant No. QLK3-CT-2002-01989 to S.K.
References
- 1.le Maire, M., P. Champeil, and J. V. Møller. 2000. Interaction of membrane proteins and lipids with solubilizing detergents. Biochim. Biophys. Acta. 1508:86–111. [DOI] [PubMed] [Google Scholar]
- 2.Ollivon, M., S. Lesieur, C. Grabielle-Madelmont, and M. Paternostre. 2000. Vesicle reconstitution from lipid-detergent mixed micelles. Biochim. Biophys. Acta. 1508:34–50. [DOI] [PubMed] [Google Scholar]
- 3.Lasch, J. 1995. Interaction of detergents with lipid vesicles. Biochim. Biophys. Acta. 1241:269–292. [DOI] [PubMed] [Google Scholar]
- 4.Lichtenberg, D., R. J. Robson, and E. A. Dennis. 1983. Solubilization of phospholipids by detergents—structural and kinetic aspects. Biochim. Biophys. Acta. 737:285–304. [DOI] [PubMed] [Google Scholar]
- 5.Lichtenberg, D. 1985. Characterization of the solubilization of lipid bilayers by surfactants. Biochim. Biophys. Acta. 821:470–478. [DOI] [PubMed] [Google Scholar]
- 6.Lichtenberg, D., E. Opatowski, and M. M. Kozlov. 2000. Phase boundaries in mixtures of membrane-forming amphiphiles and micelle-forming amphiphiles. Biochim. Biophys. Acta. 1508:1–19. [DOI] [PubMed] [Google Scholar]
- 7.Schurtenberger, P., N. Mazer, and W. Kanzig. 1985. Micelle-to-vesicle transition in aqueous solutions of bile salt and lecithin. J. Phys. Chem. 89:1042–1049. [Google Scholar]
- 8.Heerklotz, H., G. Lantzsch, H. Binder, G. Klose, and A. Blume. 1995. Application of isothermal titration calorimetry for detecting lipid membrane solubilization. Chem. Phys. Lett. 235:517–520. [Google Scholar]
- 9.Opatowski, E., D. Lichtenberg, and M. M. Kozlov. 1997. The heat of transfer of lipid and surfactant from vesicles into micelles in mixtures of phospholipid and surfactant. Biophys. J. 73:1458–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Heerklotz, H., G. Lantzsch, H. Binder, G. Klose, and A. Blume. 1996. Thermodynamic characterization of dilute aqueous lipid/detergent mixtures of POPC and C12EO8 by means of isothermal titration calorimetry. J. Phys. Chem. 100:6764–6774. [Google Scholar]
- 11.Heerklotz, H., H. Binder, G. Lantzsch, G. Klose, and A. Blume. 1997. Lipid/detergent interaction thermodynamics as a function of molecular shape. J. Phys. Chem. B. 101:639–645. [Google Scholar]
- 12.Heerklotz, H. H., H. Binder, and H. Schmiedel. 1998. Excess enthalpies of mixing in phospholipid-additive membranes. J. Phys. Chem. B. 102:5363–5368. [Google Scholar]
- 13.Hildebrand, A., R. Neubert, P. Garidel, and A. Blume. 2002. Bile salt induced solubilization of synthetic phosphatidylcholine vesicles studied by isothermal titration calorimetry. Langmuir. 18:2836–2847. [Google Scholar]
- 14.Hildebrand, A., K. Beyer, R. Neubert, P. Garidel, and A. Blume. 2003. Temperature dependence of the interaction of cholate and deoxycholate with fluid model membranes and their solubilization into mixed micelles. Colloids Surf. B. 32:335–351. [Google Scholar]
- 15.López, O., M. Cócera, R. Pons, N. Azemar, and A. de la Maza. 1998. Kinetic studies of liposome solubilization by sodium dodecyl sulfate based on a dynamic light scattering technique. Langmuir. 14:4671–4674. [Google Scholar]
- 16.López, O., M. Cócera, E. Wehrli, J. L. Parra, and A. de la Maza. 1999. Solubilization of liposomes by sodium dodecyl sulfate: new mechanism based on the direct formation of mixed micelles. Arch. Biochem. Biophys. 367:153–160. [DOI] [PubMed] [Google Scholar]
- 17.Majhi, P. R., and A. Blume. 2002. Temperature-induced micelle-vesicle transitions in DMPC-SDS and DMPC-DTAB mixtures studied by calorimetry and dynamic light scattering. J. Phys. Chem. B. 106:10753–10763. [Google Scholar]
- 18.Meister, A., and A. Blume. 2004. Solubilization of DMPC-d54 and DMPG-d54 vesicles with octylglucoside and sodium dodecyl sulfate studied by FT-IR spectroscopy. Phys. Chem. Chem. Phys. 6:1551–1556. [Google Scholar]
- 19.Tan, A., A. Ziegler, B. Steinbauer, and J. Seelig. 2002. Thermodynamics of sodium dodecyl sulfate partitioning into lipid membranes. Biophys. J. 83:1547–1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Keller, S., A. Tsamaloukas, and H. Heerklotz. 2005. A quantitative model describing the selective solubilization of membrane domains. J. Am. Chem. Soc. 127:11469–11476. [DOI] [PubMed] [Google Scholar]
- 21.Keller, S., H. Heerklotz, and A. Blume. 2006. Monitoring lipid membrane translocation of sodium dodecyl sulfate by isothermal titration calorimetry. J. Am. Chem. Soc. 128:1279–1286. [DOI] [PubMed] [Google Scholar]
- 22.Moroi, A. 1992. Micelles. Theoretical and Applied Aspects. Plenum Press, New York.
- 23.Kragh-Hansen, U., M. le Maire, and J. V. Møller. 1998. The mechanism of detergent solubilization of liposomes and protein-containing membranes. Biophys. J. 75:2932–2946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Majhi, P. R., and A. Blume. 2001. Thermodynamic characterization of temperature-induced micellization and demicellization of detergents studied by differential scanning calorimetry. Langmuir. 17:3844–3851. [Google Scholar]
- 25.Paula, S., W. Süs, J. Tuchtenhagen, and A. Blume. 1995. Thermodynamics of micelle formation as a function of temperature—a high-sensitivity titration calorimetry study. J. Phys. Chem. 99:11742–11751. [Google Scholar]
- 26.Meister, A., A. Kerth, and A. Blume. 2004. Interaction of sodium dodecyl sulfate with dimyristoyl-sn-glycero-3-phosphocholine monolayers studied by infrared reflection absorption spectroscopy. A new method for the determination of surface partition coefficients. J. Phys. Chem. B. 108:8371–8378. [Google Scholar]
- 27.Reference deleted in proof.
- 28.Apel-Paz, M., G. F. Doncel, and T. K. Vanderlick. 2003. Membrane perturbation by surfactant candidates for STD prevention. Langmuir. 19:591–597. [Google Scholar]
- 29.Cócera, M., O. López, J. Estelrich, J. L. Parra, and A. de la Maza. 1999. Transbilayer movement of sodium dodecyl sulfate in large unilamellar phospholipid vesicles. Langmuir. 15:6609–6612. [Google Scholar]
- 30.Fichorova, R. N., M. Bajpai, N. Chandra, J. G. Hsiu, M. Spangler, V. Ratnam, and G. F. Doncel. 2004. Interleukin (IL)-1, IL-6, and IL-8 predict mucosal toxicity of vaginal microbicidal contraceptives. Biol. Reprod. 71:761–769. [DOI] [PubMed] [Google Scholar]
- 31.Wiseman, T., S. Williston, J. F. Brandts, and L. N. Lin. 1989. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 179:131–137. [DOI] [PubMed] [Google Scholar]
- 32.Brown, A. M. 2001. A step-by-step guide to nonlinear regression analysis of experimental data using a Microsoft Excel spreadsheet. Comput. Methods Programs Biomed. 65:191–200. [DOI] [PubMed] [Google Scholar]
- 33.Roth, Y., E. Opatowski, D. Lichtenberg, and M. M. Kozlov. 2000. Phase behavior of dilute aqueous solutions of lipid-surfactant mixtures: effects of finite size of micelles. Langmuir. 16:2052–2061. [Google Scholar]
- 34.Zhang, F. L., and E. S. Rowe. 1992. Titration calorimetric and differential scanning calorimetric studies of the interactions of n-butanol with several phases of dipalmitoylphosphatidylcholine. Biochemistry. 31:2005–2011. [DOI] [PubMed] [Google Scholar]
- 35.Seelig, J., and P. Ganz. 1991. Nonclassical hydrophobic effect in membrane binding equilibria. Biochemistry. 30:9354–9359. [DOI] [PubMed] [Google Scholar]
- 36.Aveyard, R., and D. A. Haydon. 1973. An Introduction to the Principles of Surface Chemistry. Cambridge University Press, Cambridge, UK.
- 37.McLaughlin, S. 1977. Electrostatic potentials at membrane-solution interfaces. Curr. Top. Membr. Transport. 9:71–144. [Google Scholar]
- 38.McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
- 39.Lide, D. R. 2005. CRC Handbook of Chemistry and Physics, 86th Ed. CRC Press, Boca Raton, FL.
- 40.Beschiaschvili, G., and J. Seelig. 1990. Melittin binding to mixed phosphatidylglycerol/phosphatidylcholine membranes. Biochemistry. 29:52–58. [DOI] [PubMed] [Google Scholar]
- 41.Altenbach, C., and J. Seelig. 1984. Ca2+ binding to phosphatidylcholine bilayers as studied by deuterium magnetic resonance—evidence for the formation of a Ca2+ complex with two phospholipid molecules. Biochemistry. 23:3913–3920. [DOI] [PubMed] [Google Scholar]
- 42.Vinson, P. K., Y. Talmon, and A. Walter. 1989. Vesicle-micelle transition of phosphatidylcholine and octylglucoside elucidated by cryo-transmission electron microscopy. Biophys. J. 56:669–681. [DOI] [PMC free article] [PubMed] [Google Scholar]