Design of Minimally Strained Nucleic Acid Nanotubes

Abstract

A practical theoretical framework is presented for designing and classifying minimally strained nucleic acid nanotubes. The structures are based on the double crossover motif where each double-helical domain is connected to each of its neighbors via two or more Holliday-junctionlike reciprocal exchanges, such that each domain is parallel to the main tube axis. Modeling is based on a five-parameter characterization of the segmented double-helical structure. Once the constraint equations have been derived, the primary design problem for a minimally strained N-domain structure is reduced to solving three simultaneous equations in 2N+2 variables. Symmetry analysis and tube merging then allow for the design of a wide variety of tubes, which can be tailored to satisfy requirements such as specific inner and outer radii, or multiple lobed structures. The general form of the equations allows similar techniques to be applied to various nucleic acid helices: B-DNA, A-DNA, RNA, DNA-PNA, or others. Possible applications for such tubes include nanoscale scaffolding as well as custom-shaped enclosures for other nano-objects.

INTRODUCTION

DNA double-crossover (DX) molecules were first prepared in the early 1990s (1) to model recombination intermediates (2,3) in small systems. By using two immobile Holliday junctions (4) to connect them, a pair of DNA double helices could be fixed stably into a structure where the two helical domains have parallel axes. This paved the way for a large number of similar structures and devices: triple crossover (5), paranemic crossover (6,7), and juxtaposed crossover (8) molecules, as well as the B-Z device (9) and the PX/JX₂ device (8). Multiple versions of these motifs have been constructed with different sequences but otherwise similar appearance when modeled in a very simple system (10). Since they are only one double-helix in thickness, such structures can be represented effectively on a simple two-dimensional diagram for preliminary design. With the assembly of nucleic acid nanotubes in recent years (11–16), new, intrinsically three-dimensional structures are being formed, which are much more difficult to represent or design. It is important to point out that nucleic acid nanotubes are nonplanar two-dimensional DNA systems, capable, in principle, of scaffolding a variety of species in arrangements that utilize the third dimension. All the tubes built to date have taken advantage of symmetries to simplify their design process. As a result, they have all been designed to have the cross sections of regular polygons (insofar as they are rigid). There is no reason, however, why they must be so limited. Standard experimental methods of structural nucleic acid nanotechnology should allow for the controlled construction of a broad variety of tubes, including those with highly eccentric, or even concave cross sections. Unfortunately, even with the simple structural models used so successfully for the smaller motifs, the complex interplay of local and global geometries makes design and classification of these tubes highly challenging. The mathematical constraints associated with designing cyclical and periodic structures consisting of double helices and junctions were noted 20 years ago (17). The simple structural nature of DX molecules allows us to recast the constraints into a more convenient form for solving the particular problem of nanotube design. We focus primarily on the most stable, minimally strained structures. The rich array of possible tubes suggests numerous potential uses as molecular scaffolding, possibly with structurally specified catalytic features. Naturally, nucleic acid nanotubes share the virtues of other branched nucleic acid motifs, including sequence-directed cohesion and controllable movement.

THEORETICAL BASIS

For the convenience of the reader, a glossary of terms has been provided in an Appendix.

Strand exchanges

Fig. 1 shows the key features of our treatment. Fig. 1, a–e, illustrate the central role of positioning in the connection of double-helical domains. In Fig. 1, b and e, are two versions of a pair of double helices. Each duplex has its bases denoted by horizontal struts with the outer end of each nucleoside represented by a gray sphere. The red spheres mark the nucleoside end midpoints (NEMids). These NEMids are located approximately at the midpoints between consecutive C3′ atoms—not at the locations of the phosphates. The left pair of duplexes have cylinders drawn around them. The tangency line between the two cylinders is used as the reference point for angular measurements around each helix's axis. The backbones of the two duplexes are juxtaposed differently in Fig. 1, a and c, because of the 10.5-fold helicity of DNA. In Fig. 1 e, the two double helices are shown with the same base-stacking structure as in b, but with a different backbone shape. The helix that runs upward in the 3′ direction (called the up-helix) in the right duplex, and the down-helix in the left duplex, are joined via a strand exchange that forms a Holliday-like crossover. It is possible to produce this junction without disrupting the base structure, because the section of the backbone involved with the exchange is the phosphodiester linkage between two bases, as shown in Fig. 1 d. The two linkages in a Holliday junction always surround one NEMid on each of the helices involved, so the location of the junction always refers to the location of one of the NEMids, not the bases. It is important for clarity to distinguish between the helices, which are abstract shapes that remain in their respective helical domains, and strands, which represent actual molecules that may cross from one helix to another.

FIGURE 1.

Relating junctions to double-helix structure. Panels b and e show two nucleic acid double helices. The bases are represented by horizontal gray struts. The nucleoside end midpoints (NEMids) are represented by red spheres. The cones on the end of each strand indicate the 3′ end. (b) Two duplexes next to each other with cylinders drawn around them illustrating the line of tangency where the duplexes can interact with minimal strain. (a) Two NEMids are both on the line of tangency; at this point, the two duplexes can have a minimally strained strand exchange, as seen in panel e (enlarged view of exchange is in d). (c) Two duplexes touch at a point along their backbones where there are no NEMids and thus cannot form a minimally strained strand exchange. Note that in panel e, the down-helix of the left domain, and the up-helix of the right domain, have two strands in them. Here “up” is arbitrarily selected to be the positive Z-axis parallel to the tube axis. Panels f and g show a top and side view of the helical backbones of a double helix, with NEMids represented by spheres along each strand and cones representing the 3′ ends. Three of the basic parameters of the nucleic acid are H, the height of one full turn of a helix, Z_S, the rise along the Z-axis as one jumps from a NEMid on the down-helix (blue) up to a NEMid on the up-helix (yellow). The value θ_S is the (signed) angle between these two NEMids. Two other parameters of the nucleic acid are the characteristic angle, θ_C, the smallest angle made between two (green) NEMids on the same strand, and Z_C, the vertical rise associated with angle θ_C.

For the purposes of this article, a minimally strained Holliday junction is defined as one where the NEMids involved lie directly on the tangency line between the two domains (as they do in Fig. 1 a). It is yet to be determined whether such junctions are, in fact, minimally strained. Nevertheless, practical experience has shown that systems designed with these junctions as goals have proved stable. This is particularly the case for antiparallel junctions, where the strand exchange is between helices of opposite polarity (18), such as the one depicted in Fig. 1 e, where the strand exchange is from an up-helix to a down-helix. Parallel junctions, between two up- or two down-helices, have proved problematic in their formation (1). The backbones in Fig. 1 b are also juxtaposed lower down on the helices (Fig. 1 c), but no minimally strained exchange can form there, because, for this example with 10.5-fold DNA, the nucleosides, instead of the NEMids, are on the tangency line; this configuration would lead to strained exchanges. The geometry of minimally strained tubes thus depends entirely on the distribution of NEMids about the underlying duplex domains. Further, the analysis of strained tubes can be expressed in terms of the displacement of the junction NEMids from the tangency lines.

It is crucial to have a clear picture of the relationships between the elements we will be using. Each double helix is made up of exactly two helices, an up-helix and a down-helix. Along each of the helices in a duplex, midway between the outer ends of consecutive nucleosides, is a NEMid. If two duplexes are juxtaposed, it may be possible to form junctions between them. The junctions can only form where a NEMid from one helix in the first domain and a NEMid from one helix in the second domain are touching—which can only occur along the line of tangency. A junction is formed by a strand exchange between the two touching helices. After the junction is formed, the same four helices are still in the two duplexes; however, two of the strands move from a helix in one duplex to a helix in the other duplex. Of the two helices in a given duplex, a junction is said to be “on” the helix that actually has a NEMid involved in the junction, and the junction is said to be “at” that NEMid. Equivalently, the junction is also on one of the helices in the other duplex, at the other NEMid. So in Fig. 1 g we see two helices that make up a single duplex: the blue down-helix, and the yellow up-helix. In Fig. 1 a we see two helices, each with a NEMid sitting on the line of tangency, and in Fig. 1 d we see the resulting junction, on the down-helix of the left domain and the up-helix of the right domain, “at” the two NEMids. By moving the two cylinders in Fig. 1 b around each other, the molecular architect is free to join the two duplexes together at different places, but minimally strained junctions only form where NEMids can be arranged to overlap at the line of tangency. The set of structures that can be built thus depends on identifying where, on each of the two helices in a duplex, NEMids are available to form junctions.

Duplex parameters

The success of structural nucleic acid nanotechnology has depended, to a large extent, upon the well-known three-dimensional structure of the B-DNA double helix. For purposes of this work, the structures of the double helices will be assumed to be perfect fits to a set of five parameters. The first two parameters are integers: there are T turns every B bases (where T and B are relatively prime). The last three parameters (illustrated in Fig. 1, f and g), are real numbers: H is the height of one complete turn of a given helix projected onto its axis, Z_S is the distance projected along the helical axis between two NEMids on different helices of a duplex, and θ_S is the angle about the helix axis between those two NEMids. It also is useful to think in terms of three derived quantities shown in the illustrations: θ_C = 360°/B, called the characteristic angle, is the smallest angle made between any two NEMids on the same helix of DNA, and Z_C = H/B, called the characteristic rise, is the distance along the helical axis subtended by the helix as it rotates through angle θ_C. Finally, note the angle from one base to the next, θ_B = 360°T/B. For practical design of B-DNA structures in solution, we use a modified fiber data (MFD) model: T = 2, B = 21, H = 35.5 Å, Z_S ∼ 12.6 Å, θ_S ∼ 2.3°, θ_C = 17.1°, Z_C = 1.7 Å, θ_B = 34.3°, and the angle between Watson/Crick mates about the helix axis, roughly the minor groove angle, g ∼ 135°. See below for a discussion of this model and the derivation of these values.

Stable joints: double crossovers

The Holliday junction is structurally flexible (19), so more than one strand exchange is necessary to form a joint between two duplexes that is stable to within a few Ångstroms. The minimal strain for such a structure occurs when there are precisely an integral number of helical turns between consecutive crossovers. This happens when both the crossovers are on the same helix and there are an integral multiple of B bases between them, as is illustrated in Fig. 2 a. For practical purposes, this is the only type of minimally strained joint. It is theoretically possible for a nucleic acid with θ_S = 0 or equal major and minor grooves to have a minimally strained joint where consecutive strand exchanges occur on different helices of a given duplex domain, but we will not address that prospect here. Fig. 2 b is an example of a low (but not minimal) stress joint. The stress is apparent in the bottom view of the structure, it can be seen that the orange and magenta strand segments are longer than the blue and yellow segments.

FIGURE 2.

Minimally strained joints and angles. Panels a and b show side and bottom views of double crossover joints, with enlarged bottom view below. The bases are represented by horizontal struts, the NEMids are represented by red spheres, and the 3′ end of each strand is denoted by a cone. Panel a depicts a minimally strained double crossover joint. The crossover strands in the lower junction (blue, magenta), are perfectly aligned with (and therefore occlude in the bottom view) the crossover strands in the upper junction (orange, yellow). Panel b depicts a strained double crossover joint, where the crossover strands can be seen to be misaligned between the top and bottom junctions. (In a and b, the distance between the helical domains has been exaggerated for clarity.) Panels c and d show top and side views of the helical backbones of two three-domain complexes. The NEMids are denoted by brown spheres, and the bases are denoted by spheres of other colors. In panel c, domain 2 has no helix switch (s₂ = 0), so all the junctions are on the down-helix. In panel d, domain 2 has a helix switch, so the junctions on the left are on the down-helix, and the junctions on the right are on the up-helix (s₂ = +1). In both cases, the angles formed by the complexes are indicated on the top views. In general, the possible values for the angle are θ₂ = m₂θ_C–s₂θ_S.

Multiple domains and helix switches

Once two duplexes have been joined, one can attach another duplex to one of the first two, forming a three-domain structure like those depicted in Fig. 2, c and d. The value θ₂ is the angle about the axis of domain 2 between the tangency line of domains 1 and 2, and the tangency line of domains 2 and 3. The question arises: what are the possible values that the architect can assign to θ₂? If the duplex domains are not to overlap, then clearly 60° ≤ θ₂ ≤ 300°. In Fig. 2 c, all of the junctions in domain 2 occur on the down-helix (thus the blue strand can be seen to go from domain 1 to 2, and then through to domain 3). For such a system, the angles available are θ₂ = m₂θ_C, where m₂ is an integer. If, as shown in Fig. 2 d, the junctions between domains 1 and 2 occur on the down-helix of domain 2, and the junctions between domains 2 and 3 occur on the up-helix of domain 2, then domain 2 is said to have a helix switch, and θ₂ will be of the form m₂θ_C–s₂θ_S, where s₂ is called the helix switch number for domain 2. In this case, s₂ = +1, whereas s₂ would equal −1 if the junctions were on the opposite helices of domain 2. Thus, in general, possible values of θ₂ are m₂θ_C–s₂θ_S (where s₂ = 0 for the case of no helix switch in domain 2).

In principle, an arbitrarily large number of duplex domains can be joined in an analogous manner, with each domain having one of the specified angles. Some angles may be forbidden if the resulting structure is to be self-avoiding, although it is theoretically possible to avoid any overlap of different parts of the system by varying the lengths of the double-helical segments. To form a tube that is sealed cyclically, the last duplex incorporated into the structure must join two other domains where all three of the angles formed are acceptable. Designing a tube in such a way to satisfy this constraint is typically not trivial.

Validity of approximations

At this point, the stage has been set for the design of nanotubes, but before taking that step, we should discuss the validity of the approximations used in this analysis. There are two main approximations: 1), sequences of bases are treated as consisting of a set of perfectly average bases; and 2), junctions are not supposed to disrupt substantially the structure of the helices involved.

Although individual basepair steps are known to vary substantially in their structural parameters (20), practical experience has shown that the flexibility of DNA is generally sufficient to accommodate the difference in structure between an actual stretch of five or more basepairs and an ideal model of an equal number of perfectly average bases (provided known atypical sequences, such as A-tracts (21), are avoided). Naturally, shorter runs are less likely to be near average in structure, but if the need arises, sequences can be evaluated for their likely structure based on x-ray structure surveys, and the designs of sequences adjusted accordingly (20). Similar techniques can be used profitably to design chimerical nucleic acid structures, which may prove useful for creating a nanoscale nucleic acid analog of a liposome.

Little is known about the detailed structure of strand exchanges. One atypical structure crystallized by Ho et al. (22) shows some distortion of the helix, but no x-ray data for the DX structures have been published to date. Ligation studies on antiparallel DX molecules with two turns between crossovers found that the strand between the crossovers has approximately the same helicity as solution DNA (10.5 bases/turn) (23). Related work revealed that such molecules have a maximum bend of 8° per 10 nucleotides (23). Studies of DNA DX arrays have found that they are flattest when the average helicity of the DNA in the duplex is designed to be 10.5 bases/turn (24). Additionally, the formation of junction-rich triple crossover molecules and arrays designed on the assumption of 10.5 bases/turn implies that the crossovers cannot have a very large effect on the helical structure of the underlying helices. This statement holds for antiparallel crossovers. Ultimately, the strongest support for the approximations used in this article is the successful formation of the six-helix bundle, the design of which was based on the same approximations (11).

DESIGN METHODS

Before discussing the practical techniques used to design a nucleic acid nanotube, it is important to clarify exactly what qualities a successful nanotube must possess. In this context, there are two productive ways of examining a tube. The first perspective involves looking down the axis of the tube, where its polygonal cross section can be analyzed. The second perspective should come from a projection of the tube, akin to a Mercator projection of a globe, whereby the entire strand structure of the tube can be unrolled and laid flat for examination. Each of these perspectives yields a set of equations that any tube must satisfy.

Top view

Fig. 3 a shows a sample 10-domain nanotube viewed down the Z axis. Lines have been drawn from the central axis of each helical domain, through the tangency line to the axis of the neighboring domain. Together these lines form a polygon, each edge of which has the same length (approximately the diameter of the nucleic acid). Each helical domain can be seen to have a sector inside the tube and another sector outside the tube. The angle, θ_j, associated with domain number j, is the angle inside the tube. In general, θ_j = m_jθ_C–s_jθ_S. Let Θ be defined as the sum of the internal angles of the associated polygon with N edges,

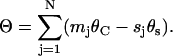(1)

FIGURE 3.

Two views of a 10-gon with angles designed for MFD B-DNA (θ_C = 360°/21). The angles are θ₁ = 6θ_C, θ₂ = 14θ_C, θ₃ = 6θ_C, θ₄ = 8θ_C, θ₅ = 8θ_C, θ₆ = 6θ_C, θ₇ = 14θ_C, θ₈ = 6θ_C, θ₉ = 8θ_C, and θ₁₀ = 8θ_C. (a) The top view of the tube, with lines drawn between the axes of each helical domain to illustrate the polygon associated with the tube. The helix graph shown in panel b shows the tube unrolled and laid flat with the outside of the tube facing the viewer. The NEMids are indicated by crosses or plusses in the odd helical domains, and boxes or diamonds in the even helical domains. Boxes or diamonds around crosses or plusses indicate minimal strain spots for strand exchange between the helices. The vertical lines on either side of each helical domain represent the tangency lines with the neighboring domains. The horizontal coordinates of each NEMid are calculated relative to the local tangency line. E.g., a NEMid that is one-third of the way around from one tangency to the next is graphed one-third of the way between the two lines. Arcs of helical domains 2 and 6 have been colored in panel a for comparison with their representation in panel b. Arcs inside the tube, such as the red and pink arcs, are represented by line segments with negative slopes in the helix graph. Arcs outside the tube are represented with positive slopes in the helix graph. The magnitudes of the slopes are proportional to the associated arc lengths. Only one helix in each domain has been color-coded, but both helices proceed around the domain in a like manner albeit with a different phase.

Equating this with the internal angle for plane polygons yields the polygonal closure equation,

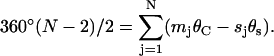(2)

Quasi-Mercator projection—helix graphs

Fig. 3 b shows a diagram, termed a helix graph, of the tube in Fig. 3 a. The diagram should be understood to represent what one would see if one sliced the tube between helical domains 1 and 10, unrolled the tube, and laid it out flat with the outside of the tube facing the viewer. For irregular structures, such as that shown in Fig. 3, this unrolling procedure is more complicated than simple cylindrical projection. The vertical coordinates of the NEMids are unchanged by this process. The horizontal coordinates are, of necessity, distorted as a result of the unrolling procedure. The vertical tangency lines are spaced regularly across the helix graph. Each NEMid in the three-dimensional structure is some fraction of the way about the duplex axis from one tangency line to the next. Each NEMid in the helix graph is placed between the two tangency lines at the same fraction of the way between them. The angular information in the three-dimensional structure is then contained in the slopes of the helix segments. Segments representing NEMids on the inside of the tube go up to the left in the helix graph, while those on the outside of the tube are represented going up to the right. The magnitude of the slope of each line is proportional to the angle subtended by the associated arc in the end view. This can be seen by comparing the colored regions in Fig. 3 a with the corresponding colored segments in Fig. 3 b. Domain 2 has a small, green arc outside the tube, and a large, red arc inside the tube. By contrast, domain 6 has a large, blue, outer arc and a small, pink, inner arc. Thus in Fig. 3 b domain 2 is divided into green segments with small positive slopes, and red segments with large negative slopes, while domain 6 has blue segments with large positive slopes, and pink segments with small negative slopes. This style of diagram shows exactly where NEMids fall on the tangency lines and are positioned to make minimally strained crossovers. NEMids in the odd domains are represented by plusses and crosses, and those in the even domains are represented by squares and diamonds, so squares or diamonds around plusses or crosses indicate that there are NEMids from each of the neighboring helical domains overlapping on each of the tangency lines in the diagram—which is required for a minimally strained tube to form.

Fig. 4 is a larger helix graph of the tube shown in Fig. 3. Another requirement for the formation of the tube is that one of the NEMids on the left edge of domain 1 (call it NEMid_1, shown as a red box with a black cross) must somehow have a mate on the right side of domain 10 (call it NEMid_2, a black box around a red square). Thus, there must be a path that starts at NEMid_1, moves through the helix graph by traversing along helices making helix switches where needed, and jumping from one domain to the next only where NEMids are overlapping, and that ends on a NEMid in domain 10 with the exact same x, y, and z coordinates as NEMid_1. There are many paths that could satisfy these requirements, but for purposes of mathematical analysis, one can, without loss of generality, focus on paths similar to the one shown in Fig. 4. The first part of the path, called an orbit (marked in green), goes as directly as possible around the inside of the tube from NEMid_1 to the far right side of domain 10 (its endpoint is marked by an orange triangle). Note that, for some structures, such a direct orbit may not be possible, but the equations below are generally applicable. See the Supplementary Material for detailed discussion. The second part of the path, called the ascent (marked in brown), runs straight up one helix an integer number of turns, C_Z, connecting the bottom of the orbit to NEMid_2.

FIGURE 4.

Orbit, ascent, and deriving the closure equations. A helix graph for the structure in Fig. 3. For the tube to seal shut, there must be a path from a NEMid on the left of domain 1 to a NEMid on the right of domain 10 that has the exact same coordinates in three-dimensional space. The red square with the cross on the left has a path leading from it to the boxed red square on the right. The green portion of the path, called the orbit, goes around the inside of the tube as directly as possible, ending at the right edge of the graph at the orange triangle. The brown portion of the path, called the ascent, goes from the orange triangle to the red box above. Together the orbit and ascent define a path from the left red NEMid to the right red NEMid. Analysis of this path leads to the key equations that must be satisfied to form a tube.

For NEMid_1 and NEMid_2 to have the same coordinates, there are three conditions that must be satisfied. First, the x and y coordinates of the lines in the three-dimensional model that are represented by the left and right edges of the helix graph must be the same. This is guaranteed for a closed polygon that satisfies the polygonal closure equation, Eq. 2. Second, the path from NEMid_1 to NEMid_2 must have zero net change in Z. This is guaranteed by the Z-closure equation,

(3)

which must have a solution for some integer, C_Z. Finally, the path that starts on NEMid_1 must be just the right length such that it ends exactly on a NEMid (not between NEMids). This is guaranteed by the phase-closure equation,

(4)

which must have a solution for integer C_φ. Any self-avoiding polygon with equal edge-lengths that satisfies all three closure equations (Eqs. 2–4) describes a viable minimally strained tube.

Designing a tube

The steps involved in designing a tube vary somewhat, depending on what the particular objectives are for the tube: should it have a particular number of helical domains, a certain symmetry, should it be well suited to forming devices, or should it have a particular size? As an example, we will design a tube from MFD B-DNA with 10 helical domains. The steps involved are:

1. Find a polygon that is made with the available angles, and check that the structure satisfies all the closure equations.

2. Draw the helix graph of the tube, specifying which junctions are parallel, and which are antiparallel.

3. Draw the strand graph of the tube, selecting where to put the junctions and the lengths of each helical domain.

4. Estimate the annealing pathway to determine where to nick the strands.

5. Generate base sequences for the system.

Finding a polygon

It can be difficult (or even impossible) to find a closed polygon with equal length edges made from the available angles. Matters are complicated because, if all junctions are antiparallel, then a helix switch in one domain affects which helix switches can occur in the domains that follow. It is always possible for a given domain to have no helix switch, i.e., s = 0, but if s_j = (–)1, then s_j+1 cannot equal (+)–1. Similarly if s_j = (–)1 and s_j+1 = 0, then s_j+2 cannot equal (–)1, etc. These requirements can be relaxed by the use of bowtie junctions (3′ to 3′ and 5′ to 5′ connectors) in strand synthesis (25,26). In general, it is easiest to look for structures where the sum of the helix switches is zero. Below, we will discuss strategies that take advantage of rotational symmetry or merging tubes to generate acceptable polygons. For small systems, however, exhaustive computer search is not prohibitive. We will work out this example using the structure shown in Figs. 3 and 4. A quick check confirms that the closure equations are all satisfied with C_Z = 4 and C_φ = 0.

Drawing the helix graph

It is essential for detailed design of the strand structure of the tube that an unrolled picture of it should be drawn such as the one used to derive the closure equations in Fig. 4. This is most easily handled with the use of a spreadsheet available from the authors. The internal angles of each domain must be entered. Then, as each duplex is added, it must be rotated on, and possibly translated along, its axis until its NEMids overlap the NEMids on the helical domain immediately to its left. This starts with domain 1, which must have NEMids on the left edge of the drawing. There are frequently decisions to be made here as to whether the desired junctions should be between helices of the same or opposite polarity (i.e., should the junctions be parallel or antiparallel). Antiparallel junctions are usually better behaved, but it may be possible to use parallel junctions as well. One could also allow for the use of bowtie junctions at this stage of design. It is important, whatever the polarity or the specific nature of the junctions, that the appropriate helix switches occur in the domains consistent with the angular requirements of the polygon being formed.

The strand graph: junction placement and length selection

The initial drawing of the tube should include at least 2B bases, and it may be convenient to draw 4B or more, which will generate 4T turns of DNA. The helices in the tube each have a period of B bases between repeats, and each pair of tangent helical domains needs to be connected by at least two junctions B bases apart. Thus, it may be necessary to have several helical repeats for the tube to hold together. It is ideal to have all the junctions as widely spaced as possible, so they do not destabilize each other and also so the average base model is a better approximation. Thus it is sometimes desirable not to put a junction somewhere even when two NEMids are juxtaposed. For example, in Fig. 5 a, there is no strand exchange of the orange and pink strands between domains 2 and 3, since that would put the resulting junction too close to the pink/blue junction near helical turn 8 between domains 3 and 4. As a practical matter, the assignment of junctions is conveniently handled by printing the helix graph in gray, and then using colored markers to draw the path of the strands through the structure. Once the junctions have been placed, one can determine what the minimum length of each helical domain needs to be. Ideally, there should be at least five or six bases between a junction and any disruption of the helix such as another junction or a nick. Sometimes additional concerns arise. For example, if the tubes are supposed to stack linearly, then each domain must be the same length, which must be an integral multiple of B bases long. Once all these determinations have been made, a strand graph like Fig. 5 a can be drawn, except that no considerations of nick placement have been made, so all the strands start out as continuous (thus, all the green strands, for example, would appear as one long strand at this stage of the design).

FIGURE 5.

Strand graphs and three-dimensional models. The same 10-gon as in Fig. 3. The strand graph (a) shows the strands overlaid in color onto the helix graph. (Strands that never change helices are gray.) Strand ends are indicated by red NEMids. The full three dimensional phosphate backbone model is shown at right (b), with the separation between domains slightly exaggerated to expose the strand crossings. Bases are indicated by spheres along the backbone, and the 3′ end of each strand is indicated by a cone. For orientation, note that the orange strand at the top of domains 1 and 2 in the strand graph is at the lower right of the three-dimensional model, and that the domain numbers run counter-clockwise when the model is viewed from this angle.

Annealing pathway estimation and nick placement

The strand graph allows one to consider clearly the practical question of where to place nicks in the strands forming the tube. Aside from issues of what strand lengths are convenient to synthesize, there are stability and kinetic issues that must be taken into account. Nicks should always be placed as far from junctions as possible, preferably at least six bases away so that the strand ends do not come loose and disrupt the junctions (27). Similarly nicks should not be placed too close together, to avoid the short space between the nicks being unstable at the desired temperature.

The primary concern in nick assignment is to avoid any kinetic traps in the annealing of the tube. Consider the case of trying to form a parallel DX molecule. The system illustrated in Fig. 6 a shows a target structure at the top, with a 10-base central region surrounded by two 11-base outer regions. As the four strands come together out of an annealing reaction, the 11-base regions stabilize before the 10-base regions as shown at the bottom. Unfortunately, there is no way for the blue and red strands to weave around each other since their ends are pinned to the pink and green strands. Such a kinetic trap might be avoided by the judicious placement of a nick in one of the strands as illustrated in Fig. 6 b.

FIGURE 6.

Kinetic considerations for annealing pathway estimation. At the top of panel a is a target structure with 11 base long outer arms and 10 base long inner segments. This structure does not form well because the ends of the strands, which are 11-bases-long, are pinned before the middle section can wind up appropriately as shown below. In panel b, a nick has been added to the final structure at the top. With this nick, the intermediate state (bottom) leaves the ends of the blue and green strands free to wind around their mates (middle) before they reach the target state (top).

Similar kinetic traps must be avoided in the formation of the much more complex tubes being designed here, which makes nick assignment a particularly delicate task. One supposes that the most stable—typically the longest—uninterrupted segments in the system will form first, and one attempts to avoid having any section hybridize after the ends of all the strands involved have already set. The easiest way to do this is to arrange the nicks in such a manner that hybridization progresses along each strand from the center of the strand outward, or else from one end to the other. Note that as long as one of the two strands at any point is free to wind up, the mating strand can have its ends pinned. For example, in Fig. 5 a, the light-gray strand in domain 5 hybridizes with the brown and green strands before the blue strands, but the blue-gray section could still form, since the blue strand has a strategically placed nick (shown as a red square with a black cross). Similar considerations must be made for every section of the tube, and nicks placed accordingly as shown in Fig. 5 a.

Sequence generation

Base sequences for the structure may be generated using sequence symmetry minimization techniques as discussed earlier (28). Particular care should be taken in regions where junctions occur close together, so that the sequences between junctions should be average sequences. Gorin et al. (20) have provided a useful survey of x-ray data indicating the relative twists of the various base sequences (essentially a table of the twists of all the possible NEMids, where a NEMid is characterized by the two bases that surround it). Naturally, if any nonstandard bases or other components are introduced into the sequence, they must be matched with the overall tube geometry.

DISCUSSION

With the framework established for how to design a nucleic acid tube, the natural question is: what tubes are possible to design? Analysis of this sort is best carried out in terms of

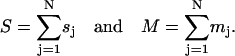(5)

With these substitutions, the three closure equations become

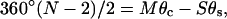(6)

(7)

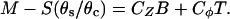(8)

We have not found any solutions for the nucleic acids we have checked except where S = 0. In this case, C_φ = 0, and all three of the equations can always be solved provided there is an integral solution to

(9)

(10)

Since all the variables involved are integers, the latter equation shows there are no solutions for odd N. This result is generally true for any S = 0 system, regardless of the structural parameters of the nucleic acid in question. Note, however, that this does not preclude the formation of strained tubes with odd numbers of helical domains (15,16).

Rotational symmetries

What tubes can be designed with R-fold rotational symmetry? If there are helix switches, then they must have the same rotational symmetry as the overall tube, but we will focus here on the case of no helix switches (s_j = 0 for all j). Clearly, R must divide N. Similarly, R must divide M (since M represents the total internal angle of the polygon). Equation 9 expresses the relationship between M and N. Note, however, that N and (N−2)/2 have at most a factor of 2 in common, so the only possible common divisors of M and N are 2B and its factors. Once a suitable N and M have been found for an R > 1, that information proves to be extremely useful in the design of tubes. See the Supplementary Material for a table of all possible rotational symmetries for MFD B-DNA tubes with N = 6 up to N = 42.

Consider, for example, the case of MFD B-DNA, where B = 21. If N = 12 = 3 × 4, then M = 105 = 3 × 35. Since both of these numbers are divisible by 3, a threefold symmetric polygon can be designed by selecting four angles that sum up to 35θ_C. For example, suppose θ₁ = 11θ_C, θ₂ = 9θ_C, θ₃ = 11θ_C, and θ₄ = 4θ_C. These angles define a segment shown in Fig. 7 a. Three copies of this segment can be combined to form the full threefold symmetric 12-gon shown in Fig. 7 b. The power of this technique comes from the fact that any set of four angles summing to 35θ_C will form a suitable polygon (providing the resulting structure is self-avoiding). This provides the molecular architect with tremendous flexibility in designing tubes to satisfy a broad variety of structural requirements. The inner and outer radii can be selected to within a fraction of a nanometer. The system can be bulged into two or more lobes like the 10-gon shown in Fig. 3 a. (Such structures might be useful for holding nano-objects close together but not touching.) This design strategy also greatly facilitates the development of nanotube-based mechanical devices to be discussed in a future article.

FIGURE 7.

Symmetric and merged tube examples for MFD B-DNA (θ_C = 360°/21, and θ_S ∼ 2.3°). (a) Four duplexes can be joined together with angles θ₁ = 11θ_C, θ₂ = 9θ_C, θ₃ = 11θ_C, and θ₄ = 4θ_C. (b) Three copies of the structure from a can be joined up to form a threefold symmetric 12-gon. (c) The six sevenfold symmetric 14-gons that may be formed. Each tube is characterized by two angles. From left to right, top to bottom we have: θ₁ = 4θ_C, θ₂ = 14θ_C; θ₁ = 5θ_C, θ₂ = 13θ_C; θ₁ = 6θ_C, θ₂ = 12θ_C; θ₁ = 7θ_C, θ₂ = 11θ_C; θ₁ = 8θ_C, θ₂ = 10θ_C and θ₁ = 9θ_C, θ₂ = 9θ_C. The inner diameters are 1.6, 2.1, 2.6, 3.0, 3.3, and 3.5 nm and the corresponding outer diameters are 5.0, 5.3, 5.5, 5.6, 5.6 and 5.5 nm (assuming the distance between helix axes is equal to the helix diameter). (d) A 14-gon formed by merging three 6-gons. (e) A blue 16-gon formed by merging the 12-gon from panel a and an 8-gon with angles designed for MFD B-DNA with angles θ₁ = 7θ_C − θ_S, θ₂ = 10θ_C, θ₃ = 4θ_C + θ_S, θ₄ = 11θ_C, θ₅ = 6θ_C − θ_S, θ₆ = 11θ_C, θ₇ = 4θ_C + θ_S, and θ₈ = 10θ_C. Two edges, shown in pink, are deleted from each of the two components.

Fig. 7 c shows the six possible minimal strain 14-gons with sevenfold symmetry that can be designed with MFD B-DNA. To form such a system, one must select two angles, which sum to 18θ_C. If one picks θ₁ = 9θ_C, θ₂ = 9θ_C, one gets a regular 14-gon. There are a series of other choices one could make, however: θ₁ = 4θ_C, θ₂ = 14θ_C; θ₁ = 5θ_C, θ₂ = 13θ_C; θ₁ = 6θ_C, θ₂ = 12θ_C; θ₁ = 7θ_C, θ₂ = 11θ_C; or θ₁ = 8θ_C, θ₂ = 10θ_C. Each of these choices is illustrated in Fig. 7 c. Each structure satisfies all the closure equations and is a viable tube. Supposing the helical domains have no space between them, the inner diameters vary from 1.6 to 3.5 nm and the outer diameters vary from 5.0 to 5.6 nm.

Tube merging

Once polygons have been found that satisfy the closure equations, they can be merged with one another to yield new polygons that also satisfy closure. Fig. 7 d shows a 14-gon that can be formed by merging three of the six tubes that have already been built. Note that one edge has been removed from each of the hexagons wherever two are merged. In this structure, however, the interior of the tube is divided up into different regions. It is possible to merge two tubes to generate one interior section as shown in Fig. 7 e. It shows a 16-gon formed by the merging of the 12-gon described above and the 8-gon described in the Supplementary Material. In many instances, it is possible to merge two tubes without deleting the common edges of the polygons. Thus the techniques described here can be used to design structures with multiply connected tubes—although the graphs of the two tubes must be carefully coordinated. Tilings of the plane are also theoretically possible.

Tube space

If we focus on tubes with no helix switches at all (s_j = 0 for all j), we can still generate tubes of virtually any size for virtually any nucleic acid. As mentioned earlier, we can only make tubes with even N. Which N can we actually make? Consider three cases: N = 4, N = 6, and N = 8.

Rhombus, N = 4

A rhombus always has twofold rotational symmetry about its center. Following the line of reasoning discussed for symmetric tubes, 4-gons can only be formed when there is a solution to

(11)

where M is divisible by 2. Naturally, to form a 4-gon, M must be greater than or equal to 4. Thus we find that it is possible to form a rhombus for every even B greater than or equal to 4. Further, by merging 4-gons, we can form 6-gons, 8-gons, 10-gons, etc. Thus for any even B greater than 3, there are minimally strained tubes for any even N.

Hexagons, N = 6

Hexagonal tubes with twofold rotational symmetry must satisfy

(12)

where M must be divisible by 2. This is obviously satisfied for any B. Since M must equal at least 6 to form a hexagon, we find that hexagonal tubes can be formed for any B greater than 2. Merging of 6-gons allows the formation of 10-gons, 14-gons, and in general 4I+2-gons, for positive integers, I. Note, however, that this does not include any 4I-gons.

Octagons, N = 8

Octagons must satisfy

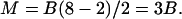(13)

The only symmetries available to an 8-gon are two-, four-, and eightfold, but those can only form for even B. What about odd B nucleic acids? Fig. 8 shows an octagon of a subclass called Σ-gons. They are so named because the left halves frequently resemble the shape of a Greek Σ. Note that each pair of like-colored lines in the figure is parallel. This is possible only if the three angles between the parallel lines sum to 360°. Thus θ₁ + θ₈ + θ₇ = 360° makes the red lines parallel. Similarly, the opposite angles on the edges of the square sum to 360°. Thus θ₄ + θ₈ = θ₂ + θ₆ = 360°. In fact, as long as these equations are satisfied, one is guaranteed to have a closed octagon. This gives one a method for generating octagons even for odd B systems. One can form a Σ-gon for any B greater than 3 except 7 (where there are no self-avoiding octagons of any sort, although there is a 12-gon). Merging of 6-gons and 8-gons then allows one to form any even N-gon for N > 5 for virtually all odd B systems.

FIGURE 8.

A sample Σ-gon for MFD B-DNA (θ_C = 360°/21). The like-colored edges are parallel to each other. θ₁ = 5θ_C, θ₂ = 11θ_C, θ₃ = 5θ_C, θ₄ = 10θ_C, θ₅ = 6θ_C, θ₆ = 10θ_C, θ₇ = 5θ_C, and θ₈ = 11θ_C.

Modified fiber data B-DNA tubes

To date, most of the experimental work in structural nucleic acid nanotechnology has been done on DNA in solution. As mentioned earlier, modified fiber data can be used to construct an effective model of this material. The fiber data are taken from the Arnott and Hukins x-ray study of B-DNA fibers (29). The 10-fold DNA they describe has a twist of 36° per nucleotide pair. Subsequent studies suggest, however, that B-DNA in solution more typically is ∼10.5-fold, with a twist of 34.3° per nucleotide pair (30,31). Our MFD model combines these two results. We take the fiber data model as our starting point. The NEMids between consecutive basepairs but on opposite helices are taken to have the same angle and rise between them as the C1′ atoms of the associated nucleotide pairs. The z coordinates of the C1′ atoms are retained, as are the angles between C1′ Watson-Crick mates; the twist between consecutive C1′ atoms along the helix backbone is decreased to 34.3° to accommodate the nonfiber data. As stated above, the resulting structure has H = 35.5 Å, Z_S ∼ 12.6 Å, θ_S ∼ 2.3°, Z_C = 1.7 Å, T = 2, and B = 21, which gives θ_C = 17.1°, θ_B = 34.3°, and g ∼ 135°. There are several noteworthy structures that can be formed with this nucleic acid system. Of particular interest are the accessible regular polygons. With S = 0, the tubes must satisfy

(14)

As shown in the earlier rotational symmetry analysis, the only R-fold symmetries possible are R = 42 and its factors, that is, R∈{1, 2, 3, 6, 7, 14, 21, 42}. For a regular polygon, N = R. However, N has the additional constraints that it must be even, and it must be greater than 4, so the values of N which yield N-fold symmetric polygons are N = 6, 14, or 42. These are the only three values of N that make minimally strained regular N-gons for MFD B-DNA.

Applications

Nucleic acid nanotubes have several promising features for application purposes. The 6-tubes have already been observed to form linear arrays some 500 tiles long, with apparent persistence length on the order of microns (11). This makes them promising for multiscale assemblies: micron-length struts addressable on the nanometer scale. Additionally, since the tubes can be engineered to have an assortment of different inner and outer surfaces, they have potential uses organizing and aligning nano-objects that may not be amenable to covalent attachment to nucleic acids. Similar strategies may make nucleic acid nanotubes promising frameworks for engineered catalysts or to bind and orient biological macromolecules at specific distances from each other. Similar techniques might be used to direct assembly of complex circuitry or nanomachinery.

CONCLUSION

We have determined which classes of minimally strained nucleic acid nanotubes can and cannot be formed, although we cannot exclude the formation of various strained species. We have provided a practical technique for identifying and designing those tubes that can be formed with low strain. We have limited ourselves primarily to two connected systems, although simple multiply connected systems are currently being explored experimentally. Many of the basic concepts applied here to the design of nanotubes can likely be applied profitably to the design of most nucleic acid nanostructures. The five parameters of a segmented double helix (together with an additional parameter for the radius of the double helix) provide a practical, comprehensive model of the secondary and tertiary structures. NEMids as the central locations for Holliday junctions also simplify the analysis of many complex nucleic acid structures. Careful annealing analysis is essential to avoid mishaps in the formation of any complicated structure. The simple annealing analysis presented here will need to be expanded to include kinetic and energetic considerations. Ultimately, the analysis will need to be automated to a level compatible with the sequence generation programs currently available. Future work will present design strategies for strained nucleic acid nanotubes, as well as for nanotube-based mechanical devices.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: GLOSSARY OF TERMS

Term	Glossary definition
Ascent	Used in the derivation of the Z and phase-closure equations. It is the part of a closed path around a tube that connects the two ends of the orbit. The ascent runs upward along a single helix and is always an integer number of helical turns.
B	There are T turns every B bases for a given nucleic acid, where T and B are relatively prime integers. (I.e., they have no common factors greater than 1.) For MFD B-DNA there are two turns every 21 bases.
g	The angle about the helix axis between the C1′ atoms of Watson/Crick mates. Approximately the minor groove angle. For MFD B-DNA, this is ∼135°.
H	H represents the height of one turn of the helix of a nucleic acid. For MFD B-DNA, H = 35.5 Å.
Helix	Half of a double helix, an abstract geometrical shape that stays within one duplex domain. A helix may be composed of several different strands.
Helix graph	A representation of the helices that make up a tube. Roughly what one would see if one unrolled the tube and pressed it flat with the outside of the tube facing the viewer.
Helix switch	When a duplex forms a junction with the domain to its left on its down-helix, and a junction with the domain to its right on its up-helix, it has a helix switch s = +1. If the left junction is on the up-helix, and the right junction is on the down-helix s = −1, and if the junctions to the left and right are on the same helix, there is no helix switch and s = 0.
Line of tangency	If two duplex domains are envisioned as a pair of parallel cylinders that touch each other. They touch along a line called the line of tangency. NEMids lying off the line of tangency cannot form minimally strained junctions.
m, M	The angle between two junctions on a double helix can be any integer multiple, m, of the characteristic angle θc. M is the sum of all the m-values for each angle around a tube.
Minimally strained	For purposes of this article a minimally strained structure is taken to be one where all the junctions are directly between NEMids on neighboring duplexes that lie along the line of tangency.
N	The number of duplex domains in a given tube.
NEMid	Nucleoside End Midpoint; the spot midway between the outer end of two stacked nucleosides. Minimally stressed immobile Holliday junctions only form directly between neighboring NEMids on different duplex domains.
Orbit	Used in the derivation of the Z and phase-closure equations. It is the simplest path that goes directly around the inside of a tube. The orbit can jump between helices in the same double helix, or jump from one duplex domain to another whenever two helices are tangent—even if there are no NEMids located at the point of tangency (see Supplementary Material) .
θB	The angle that one base makes about the helix axis. For MFD B-DNA, this is 34.3°.
θc	The characteristic angle. This is the smallest angle about the helix axis possible between two NEMids on the same helix.
θs	The angle about the helix axis between two NEMids on different helices of a double helix.
s, S	If a given duplex has junctions only on one of its two helices, then s = 0; otherwise, s = +/−1. S is the sum of all the s-values around a tube. (See Helix switch.)
Σ-gon	A structure in which each edge is parallel to another edge. Called an Σ-gon because of similarity to the Greek Σ.
Strand	A connected set of nucleotides that may cross through a junction from one helix to another.
Strand graph	A helix graph where the paths of the strands through the tube and possibly the nicks have been marked.
T	There are T turns every B bases for a given nucleic acid, where T and B are relatively prime integers. (I.e., they have no common factors greater than 1.) For MFD B-DNA, there are two turns every 21 bases.
Up/down helix	The helix that runs from the 5′ end at the bottom of a tube to the 3′ end at the top of the tube is the up-helix. The helix that runs from the 5′ end at the top of a tube to the 3′ end at the bottom is the down-helix.
Zc	The characteristic height. The height a helix climbs as it rotates through the characteristic angle, θc.
Zs	The vertical height between two NEMids on different helices of the same double helix. (See θs.)