Quantitative Microbial Risk Assessment Models for Consumption of Raw Vegetables Irrigated with Reclaimed Water

Abstract

Quantitative microbial risk assessment models for estimating the annual risk of enteric virus infection associated with consuming raw vegetables that have been overhead irrigated with nondisinfected secondary treated reclaimed water were constructed. We ran models for several different scenarios of crop type, viral concentration in effluent, and time since last irrigation event. The mean annual risk of infection was always less for cucumber than for broccoli, cabbage, or lettuce. Across the various crops, effluent qualities, and viral decay rates considered, the annual risk of infection ranged from 10⁻³ to 10⁻¹ when reclaimed-water irrigation ceased 1 day before harvest and from 10⁻⁹ to 10⁻³ when it ceased 2 weeks before harvest. Two previously published decay coefficients were used to describe the die-off of viruses in the environment. For all combinations of crop type and effluent quality, application of the more aggressive decay coefficient led to annual risks of infection that satisfied the commonly propounded benchmark of ≤10⁻⁴, i.e., one infection or less per 10,000 people per year, providing that 14 days had elapsed since irrigation with reclaimed water. Conversely, this benchmark was not attained for any combination of crop and water quality when this withholding period was 1 day. The lower decay rate conferred markedly less protection, with broccoli and cucumber being the only crops satisfying the 10⁻⁴ standard for all water qualities after a 14-day withholding period. Sensitivity analyses on the models revealed that in nearly all cases, variation in the amount of produce consumed had the most significant effect on the total uncertainty surrounding the estimate of annual infection risk. The models presented cover what would generally be considered to be worst-case scenarios: overhead irrigation and consumption of vegetables raw. Practices such as subsurface, furrow, or drip irrigation and postharvest washing/disinfection and food preparation could substantially lower risks and need to be considered in future models, particularly for developed nations where these extra risk reduction measures are more common.

Agricultural irrigation with wastewater is known to occur in many parts of the world, although the extent of the practice is a debatable point (39). A recent estimate is that worldwide 20 million ha of irrigated agriculture uses raw, treated, and/or partially diluted wastewater (11). One of the most economically feasible agricultural uses of reclaimed water is the irrigation of high-value horticultural crops, which typically have high returns per volume of water invested in (5). But this practice has been approached with trepidation, owing primarily to concerns about risks to human health via contamination of food with pathogenic microorganisms (14, 45). It has been impossible to either allay or justify such concerns through traditional hypothesis testing science: infection rates are so low that the sample sizes needed for adequate statistical power render such studies impracticable. A more pragmatic approach, which has been gaining favor in recent years, is the application of probabilistic models (16, 19). In the microbiological/human health context this methodology is referred to as quantitative microbial risk assessment (QMRA). It is a powerful tool for estimating order-of-magnitude risks associated with specific scenarios.

The risk of illness to consumers of vegetables irrigated with reclaimed water may be reduced to a negligibly small probability through the implementation of high-technology tertiary treatments and disinfection systems, such as activated carbon, reverse osmosis, membrane filtration, chlorination, ozonation, and UV irradiation (2). However, such systems are often prohibitively expensive, particularly in developing nations, where only about 10% of wastewater undergoes treatment of any kind (18). Even in affluent nations, treatment costs are a key consideration in scheme development (7, 34). An important first step in addressing the safety of horticultural reuse is to determine likely risks associated with a simple worst-case scenario: consumption of raw (uncooked and unpeeled) vegetables irrigated with nondisinfected secondary treated effluent. A sound understanding of such risks not only will be of significant value in managing low-technology reuse schemes but will form the basis of risk assessments for advanced reuse proposals.

QMRA models have been constructed for reclaimed-water irrigation of cucumber (41), lettuce (30, 31, 41), and food crops in general (1, 43, 49). Here, the first published QMRA models for enteric virus infection associated with the consumption of raw broccoli and cabbage irrigated with nondisinfected secondary effluent are presented. Necessary data on the volume of irrigation water captured by these crops were lacking. Consequently, a field experiment was conducted to address this gap. We also present improved models for cucumber and lettuce. This suite of models represent the first variety-specific QMRAs to accommodate for variability in consumption behavior. To maximize the value of the models for decision making, a wide range of plausible scenarios were simulated. The model variables having the greatest impact on the risk of infection were identified using sensitivity analysis.

MATERIALS AND METHODS

Enteric viruses were chosen as the specific microbial hazard to model, as they are known to be highly infective (13), are often found in high concentrations in secondary effluent (21), are relatively persistent in the environment (53), and are believed to be responsible for the majority of waterborne infections in developed countries such as the United States (23). The daily dose of enteric viruses, λ, taken as a result of consuming the product was calculated as λ = M_iM_bodyc_iwV_prode^(−kt), where M_body = human body mass (kg), M_i = daily consumption per capita per kg of body mass [g (kg ca day)⁻¹], c_iw = concentration of enteric viruses in the irrigation water (PFU ml⁻¹), V_prod = volume of irrigation water caught by product (ml g⁻¹), k = virus kinetic decay constant (day⁻¹), and t = time between last reclaimed-water irrigation event and harvest/consumption/storage (i.e., length of environmental exposure) (days). Viral decay postharvest is assumed to be negligible (4).

Daily consumption data were obtained from the most recent (1994 to 1996) Continuing Survey of Food Intakes by Individuals of the U.S. Department of Agriculture. This is the most comprehensive study on consumption behavior available. It represents the population of the United States and is weighted to account for age, socioeconomic, racial, and geographic demography. Published empirical cumulative probability functions (CDFs) fitted to the data (48) were used to describe the rates of consumption of broccoli, cabbage, lettuce, and cucumber. Cultivar distinctions are not made in this data set.

Body mass data were obtained from the Exposure Factors Handbook (47). As the model deals with risk to the population as a whole, the body mass distribution needed to be representative of all ages. Therefore, following the recommendation of the U.S. Environmental Protection Agency (48), a log-normal probability density function (PDF) that accounted for the age structure of the population was constructed.

The largest known available database on enteric virus concentrations in nondisinfected secondary effluent is derived from comprehensive monitoring of five sewage treatment plants in California (1). Tanaka et al. (43) fitted PDFs to counts from the four most intensively sampled plants: Orange Council Water District, trickling filter (OCSD TF); Orange County Water District, activated sludge (OCSD AS); Pomona, activated sludge (Pomona AS); and Monterey Regional Water Pollution Control Agency, activated sludge (MRWPCA AS). They found that the log-normal function was an adequate descriptor for each plant (parameter values are reported in Table 1). In the interest of accounting for variation in the quality of raw sewage and of treatment efficiencies, independent QMRA simulations based on each of these fitted models were run.

TABLE 1.

Distributions and fit parameters used in models

Model parameter and sample	Unit	Distribution and fit parameters
Virus concn in secondary effluent	Log PFU liter−1	Log normal (normal fitted to log data)
OCSD TF		μ = 0.15, σ = 0.63
OCSD AS		μ = −1.47, σ = 0.91
Pomona AS		μ = −3.81, σ = 2.06
MRWPCA		μ = 0.37, σ = 0.86
Vol of water on produce	ml g−1
Broccoli		Log logistic, α = 4.246, β = 1.583 × 10−2, λ = 1.085 × 10−3 (μ = 0.0185)
Savoy King/Grand Slam cabbage		Empirical CDF (μ = 0.0352)
Winter Head cabbage		Empirical CDF (μ = 0.0889)
Cucumber		Normal, μ = 0.0036, σ = 0.0012 (truncated at 0)
Lettuce		Normal, μ = 0.108, σ = 0.019 (truncated at 0)
Virus kinetic decay constant	Day−1	Normal, μ = 1.07, σ = 0.07 (truncated at 0), point estimate of 0.69
Consumption	g(kg day)−1	Empirical CDFs for all crop types, separate distributions for total and consumer-only populations
Body mass	kg	Log normal, μ = 61.429, σ = 13.362
Dose-response model	PI(λ)	β-Binomial, β = 0.167, α = 0.191

In determining the likely concentration of enteric viruses on the product, we adopted the previously used conservative approach whereby it is assumed that all pathogens in the irrigation water found on the plant attach to it (30, 41). For most crops, data on the volume of water captured during irrigation do not exist. An estimate for lettuce was determined in a laboratory study by Shuval et al. (41) where 12 lettuces were fully submersed in water. While this point estimate (0.018 ml g⁻¹) has been used in previous QMRAs (30, 41), it does not account for variation. We attempted to do this by assigning a normal probability density function to the parameter (μ = 0.108, σ = 0.019 ml g⁻¹). The PDF was truncated at zero to prevent simulating negative volumes of water. The original data of Shuval et al. were not available (but σ was), so the goodness of fit of the normal distribution could not be tested. Nonetheless, the normal distribution approximates many distributions well, and we felt that it was important to make at least some attempt to account for variation. Likewise, we used the data derived from an analogous study on 26 cucumbers by Shuval et al. to construct a zero-truncated normal PDF (μ = 0.0036, σ = 0.0012 ml g⁻¹). In the absence of other available data, we have followed the lead of others (30) in using the estimates of Shuval et al., but it must be acknowledged that such submersion experiments probably account for a worst-case scenario and may not be representative of spray irrigation. For broccoli and cabbage we conducted field trials to determine how much water they captured. These trials and associated analyses are described below. Fit parameters for all probability distributions were determined using maximum-likelihood estimation and are reported in Table 1.

Two different estimates of k of were used to characterize environmental inactivation of enteric viruses. First, the normally distributed k (μ = 1.07, σ = 0.07) derived by Petterson et al. (31, 32) from experiments on Bacteroides fragilis bacteriophage B40-8 on lettuce was used. This phage is believed to be more resistant to decay than most enteric viruses and is thus a conservative model organism. Second, following previous QMRA studies, we used a point estimate of 0.69 day⁻¹, which has been propounded as a generic environmental decay coefficient for viruses (1, 3).

The volumes of water caught by broccoli (Brassica oleracea var. capitata) and cabbage (B. oleracea var. italica) were determined from field experiments on separate commercial properties in the Boneo growing region on the outskirts of Melbourne, Victoria, Australia (38°24′S, 144°53′E). Both trials were conducted on 22 June 2005. One cultivar of broccoli, Grevillea, was investigated. For cabbage, which shows far greater intercultivar structural diversity than broccoli, three cultivars were examined: Grand Slam, Savoy King, and Winter Head. One hundred broccoli florets were harvested immediately after a scheduled irrigation event of 20 min. The length of the irrigation period represented the maximum irrigation duration that the grower used at that time of year. A longer schedule could not be used because of the risk of flooding and waterlogging, but the plants should have reached saturation well before 20 min. A 40- by 40-m portion of the crop was marked, and all samples were collected from within it. The crop was planted in beds that comprised two staggered rows, with plants in each row being spaced at 30-cm intervals. Standard fixed-set overhead sprinklers were positioned in every eighth row at 9.8-m intervals. A systematic sampling protocol was used, whereby one plant was harvested every 2 m in every fifth bed (five beds were sampled, and 20 plants were harvested from each). The side of the bed from which the samples were taken (i.e., the row) was alternated from one bed to the next. Broccoli samples were collected by carefully placing a plastic bag over the floret. The bag was gathered by hand at the base, just above the point where the stalk was to be cut. After being cut with a sharp knife, the floret was sealed in the bag.

Cabbages were also collected in plastic bags. However, owing to the large size of cabbages, the procedure was more time-consuming, so fewer samples could be collected (15 cabbages of each cultivar). The outer/wrapper leaves of cabbages are harvested for some markets and not others. In the interest of representing a worst-case scenario, we chose to collect these leaves, which tended to gather relatively large volumes of water. This also accommodated the scenario of cross-contamination of the head by contact with the outer leaves during harvest. The crops were irrigated for 30 min, and the arrangement of plants and sprinklers in beds was the same as described for broccoli, with the exception that plants were spaced at 56- to 61-cm intervals. Because far fewer samples were collected, a sampling protocol different from that for broccoli was used. For each cultivar, three rows were chosen at random and five plants, successively 2 m apart, were collected from each. The side of the bed sampled was alternated between rows.

All samples were transported to a laboratory, where they were weighed prior to and after being spun vigorously in a lettuce spinner (part CH-3250; Zyliss, Switzerland) to remove surface water. Cabbages were cut into small sections, and leaves were separated to ensure that no water was trapped. Likewise, broccoli florets were carefully dissected prior to being spun. The rip cord was pulled six times to ensure comprehensive removal of the surface water. Preliminary trials revealed that for all crop types two or three pulls were sufficient to remove the vast majority of the water.

Several PDFs were fitted to the broccoli data using BestFit software (Palisade Corporation, Newfield, New York), and the log-logistic function proved to be the most adequate model (test statistics: χ² = 6.040 [P = 0.812]; Anderson-Darling = 0.211; Kolmogorov-Smirnoff = 0.041). Prior to considering distributions for the cabbage data, we tested for a cultivar effect by using restricted maximum likelihood (28) in the statistical package GenStat (version 6.1; Lawes Agricultural Trust, IACR-Rothamsted). Restricted maximum likelihood is a more general procedure than analysis of variance (ANOVA) and reduces to ANOVA in simple balanced cases. The cabbage data were unbalanced because one cultivar was represented by one fewer sample than the other two due to accidental leakage from a bag. Differences between the cultivars were compared using a Wald statistic, which is analogous to the F statistic used to compare treatments in ANOVA. Bed was modeled as a random effect, which corresponds to a block effect in ANOVA. The data did not require transformation. A significant cultivar effect was found (P < 0.05), with post hoc least significant difference tests (at P = 0.05) indicating that Savoy King and Grand Slam were both significantly different from Winter Head but not from each other. We tried fitting several different distributions to the Savoy King/Grand Slam and Winter Head data, but all fits were inadequate. Thus, empirical CDFs were constructed instead, and these were sampled during simulations.

When modeling the dose-response relation, rotavirus was used to represent the enteric virus group. Rotaviruses are a subgroup of enteric viruses that are known to cause gastroenteritis. They are highly infectious and thus are commonly used to represent enteric viruses in QMRAs, with the clinical data of rotaviruses of Ward et al. (51) being used as the basis for most models (1, 3, 30, 35, 41, 43, 49). We used the β-binomial dose-response model (8) to describe the probability of infection given exposure to a dose [P_I(λ)]. The β-binomial is a modification of the β-Poisson dose-response model (10). The β-binomial model gives the variability for the probability of infection resulting from exposure to a particular dose (λ), as opposed to the β-Poisson model, which is concerned with a mean, Poisson-distributed dose. The former is more appropriate here as a specific dose is derived for each Monte Carlo iteration of the model. Furthermore, it is important to note that nearly all previous applications of the β-Poisson model to rotavirus data (see, e.g., references 12, 30, 36, 43, and 49) have actually used an approximation of the exact model. However, this approximation, proposed by Furumoto and Mickey (10), applies only when β is ≫1 and α is ≪β, and these assumptions were not met in these studies. This being said, for the rotavirus data of Ward et al., the two models differ most markedly at low doses (approximately <10⁻¹) and the difference is effectively negligible at higher doses (44). The β-binomial dose-response model is

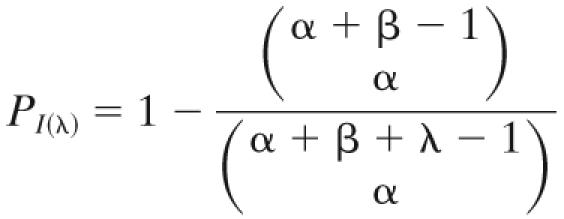where α and β are fit parameters used when fitting the exact β-Poisson model to dose-response data. The estimates for α and β (0.167 and 0.191, respectively) were obtained by Teunis and Havelaar (44) by using maximum-likelihood estimation to apply the exact β-Poisson model to the trial data of Ward et al. (51).

Monte Carlo simulations were run using @RISK version 4.5.2, professional edition (Palisade Corporation, Newfield, New York). Random variables were sampled 10,000 times using Latin hypercube sampling, whereby samples are selected in a stratified manner without replacement (20). Latin hypercube sampling is particularly useful for dealing with extremely low probabilities, as was the case here, and it represents extreme values more appropriately than traditional Monte Carlo sampling (50). The end point of the model is the annual probability of enteric virus infection, P_A(λ), which was calculated following Sakaji and Funamizu (38) as P_A(λ) = 1 − [1 − P_I(λ)]³⁶⁵. In the interest of conservativeness with respect to health protection, we chose to report the upper 95% confidence limit (UCL_0.95) of P_A(λ) (Tables 1 and 2).

TABLE 2.

Annual probabilities of enteric virus infection associated with consuming vegetables that have been spray irrigated with secondary effluent from four different treatment plants and where the viral kinetic decay constant (k) is assumed to be normally distributed (μ = 1.07, σ = 0.07 day⁻¹)

Crop	Time (days)b	PA(λ) (UCL0.95)a
		MRWPCA AS	OCSD AS	OCSD TF	Pomona AS
Broccoli	1	2.8 × 10−2	5.1 × 10−3	2.4 × 10−2	2.8 × 10−3
	7	8.0 × 10−4	4.9 × 10−5	4.1 × 10−4	8.7 × 10−5
	14	9.5 × 10−7	6.3 × 10−8	4.7 × 10−7	5.4 × 10−8
Cucumber	1	2.2 × 10−2	1.4 × 10−3	1.4 × 10−2	1.7 × 10−3
	7	3.4 × 10−4	3.0 × 10−6	1.5 × 10−4	1.9 × 10−4
	14	2.6 × 10−7	2.2 × 10−9	9.9 × 10−8	2.7 × 10−7
Savoy King /Grand Slam (cabbage)	1	5.3 × 10−2	8.5 × 10−3	4.1 × 10−2	4.0 × 10−3
	7	2.0 × 10−3	3.8 × 10−5	6.5 × 10−4	4.7 × 10−4
	14	2.6 × 10−6	2.7 × 10−8	5.3 × 10−7	3.6 × 10−6
Winter Head (cabbage)	1	7.4 × 10−2	1.5 × 10−2	6.1 × 10−2	5.9 × 10−3
	7	3.9 × 10−3	1.1 × 10−4	1.3 × 10−3	7.4 × 10−4
	14	6.7 × 10−6	9.1 × 10−8	1.1 × 10−6	5.8 × 10−6
Lettuce	1	1.8 × 10−1	3.3 × 10−2	1.5 × 10−1	1.3 × 10−2
	7	7.9 × 10−3	3.9 × 10−4	2.9 × 10−3	6.8 × 10−4
	14	1.1 × 10−5	2.3 × 10−7	2.2 × 10−6	6.9 × 10−5

^aEstimates were derived from 10,000 Latin hypercube iterations of the model.

^bDuration of environmental exposure.

Sensitivity analysis to determine the influence of variation in the random input variables on P_A(λ) was conducted using Spearman rank order correlation (performed in @RISK). This approach was chosen in preference to stepwise multivariate linear regression, which accounted for little of the variance for most variables, thus implying nonlinearity.

RESULTS

The mean annual risk of infection was less for cucumber than for the other vegetables for all combinations of time since irrigation and source effluent (Tables 2 and 3). The extent of the difference varied between scenarios but was typically in the range of 1 to 2 orders of magnitude. The levels of risk posed by broccoli, the cabbage cultivars, and lettuce were roughly similar across all scenarios, although they tended to be higher for lettuce (Tables 2 and 3). The choice of decay constant had a marked effect on the estimate of P_A(λ) when a 7- or 14-day withholding period was imposed. Typically, the 0.69 day⁻¹ value resulted in infection probabilities that were 1 order of magnitude higher than for Petterson et al.’s normally distributed k (31) at 7 days and 2 orders higher at 14 days. The lowest risks were consistently associated with the OCSD AS effluent. The MRWPCA AS effluent tended to give rise to the highest risks.

TABLE 3.

Annual probability of enteric virus infection associated with consuming vegetables that have been spray irrigated with secondary effluent from four different treatment plants and where the viral kinetic decay constant (k) is assumed to be 0.69 day⁻¹

Crop	Time (days)b	PA(λ) (UCL0.95)a
		MRWPCA AS	OCSD AS	OCSD TF	Pomona AS
Broccoli	1	3.1 × 10−2	6.3 × 10−3	2.8 × 10−2	3.3 × 10−3
	7	5.3 × 10−3	5.5 × 10−4	3.1 × 10−3	6.0 × 10−4
	14	8.5 × 10−5	6.4 × 10−6	3.9 × 10−5	1.2 × 10−5
Cucumber	1	2.7 × 10−2	1.9 × 10−3	1.8 × 10−2	2.0 × 10−3
	7	2.5 × 10−3	4.0 × 10−5	9.7 × 10−4	4.8 × 10−4
	14	3.8 × 10−5	3.2 × 10−7	1.9 × 10−5	1.8 × 10−5
Savoy King/Grand Slam (cabbage)	1	6.0 × 10−2	1.1 × 10−2	4.7 × 10−2	4.6 × 10−3
	7	9.5 × 10−3	5.6 × 10−4	4.8 × 10−3	1.1 × 10−3
	14	3.8 × 10−4	5.4 × 10−6	9.7 × 10−5	1.7 × 10−4
Winter Head (cabbage)	1	8.2 × 10−2	1.8 × 10−2	6.9 × 10−2	6.8 × 10−3
	7	1.7 × 10−2	1.2 × 10−3	9.4 × 10−3	1.5 × 10−3
	14	7.6 × 10−4	1.2 × 10−5	1.9 × 10−4	2.7 × 10−4
Lettuce	1	2.0 × 10−1	4.1 × 10−2	1.7 × 10−1	1.5 × 10−2
	7	4.1 × 10−2	2.9 × 10−3	2.3 × 10−2	2.8 × 10−3
	14	1.2 × 10−3	7.1 × 10−5	4.2 × 10−4	3.3 × 10−4

^aEstimates were derived from 10,000 Latin hypercube iterations of the model.

^bDuration of environmental exposure.

Sensitivity analyses were performed for all scenarios, and the results for the OCSD TF and Pomona AS are shown in Tables 4 and 5. These plants were used for illustration because effluent from the Pomona AS had the lowest mean concentration of enteric viruses and a substantially higher σ, and the OCSD TF effluent had relatively high concentrations of viruses, had the lowest σ, and represented the only trickling filter plant. Because sensitivity analysis is concerned only with random variables, it was restricted to the models based on the normally distributed k value. In both cases, variation in the rate of consumption of product had the most significant effect of any random variable on the variation in P_A(λ) (Tables 4 and 5). The influence of the variation in virus concentration on the annual risk of infection tended to decline over time for the OCSD TF effluent but increased for the Pomona AS effluent. The relative influences of the various parameters for the OCSD AS and MRWPCA scenarios were similar to those observed for OCSD TF and Pomona AS.

TABLE 4.

Sensitivity of the annual probability of infection [P_A(λ)] to variation in input random variables for models run using the OCSD TF effluent and a normally distributed k

Crop	Time (days)a	Spearman rank order correlation coefficient (rs) for variable
		Virus concn	Vol water	k value	Consumption
Broccoli	1	+0.307	+0.095	−0.031	+0.402
	7	+0.003	0.000	−0.018	+0.513
	14	+0.005	0.000	−0.022	+0.498
Cucumber	1	+0.047	+0.020	−0.013	+0.732
	7	+0.018	+0.012	−0.021	+0.729
	14	+0.018	+0.017	−0.040	+0.688
Savoy King/Grand Slam (cabbage)	1	+0.124	+0.050	−0.016	+0.707
	7	+0.023	+0.003	−0.020	+0.733
	14	+0.031	+0.008	−0.036	+0.702
Winter Head (cabbage)	1	+0.191	+0.034	−0.023	+0.677
	7	+0.023	+0.009	−0.020	+0.736
	14	+0.029	+0.001	−0.034	+0.710
Lettuce	1	+0.148	+0.015	−0.006	+0.807
	7	+0.071	+0.010	−0.024	+0.825
	14	+0.075	+0.010	−0.056	+0.798

^aDuration of environmental exposure.

TABLE 5.

Sensitivity of the annual probability of infection [P_A(λ)] to variation in input random variables for models run using the Pomona AS effluent and a normally distributed k

Crop	Time (days)a	Spearman rank order correlation coefficient (rs) for variable
		Virus concn	Vol water	k value	Consumption
Broccoli	1	+0.083	+0.008	−0.020	+0.482
	7	+0.052	+0.001	−0.019	+0.478
	14	+0.130	+0.015	−0.025	+0.378
Cucumber	1	+0.084	+0.013	−0.012	+0.703
	7	+0.134	+0.016	−0.024	+0.643
	14	+0.252	+0.021	−0.046	+0.444
Savoy King/Grand Slam (cabbage)	1	+0.085	+0.011	−0.009	+0.713
	7	+0.105	+0.014	−0.022	+0.674
	14	+0.233	+0.036	−0.053	+0.500
Winter Head (cabbage)	1	+0.092	+0.010	−0.012	+0.715
	7	+0.097	+0.012	−0.022	+0.683
	14	+0.211	+0.016	−0.056	+0.539
Lettuce	1	+0.215	+0.006	+0.002	+0.797
	7	+0.233	+0.008	−0.017	+0.757
	14	+0.344	+0.009	−0.060	+0.604

^aDuration of environmental exposure.

DISCUSSION

Despite increasing pressure to make more efficient use of water resources, irrigation of food crops with reclaimed water still remains a contentious issue, primarily because of risks to human health arising from infectious disease. The debate is complicated by the fact that reuse scenarios can vary substantially. In the reuse scenarios considered here, marked differences in risk were often observed. The fact that risks were typically lowest for cucumber appears to arise from the fact that of the vegetables considered, it retained the smallest volume of water on its surface and was consumed at the lowest rate. For the other vegetables, where risks were generally similar, there appeared to be a compensatory relationship between the volume of water retained on the plant's surface and the amount of food consumed. For example, the cabbage cultivars retained more water than broccoli but less cabbage is consumed, and the predicted annual probabilities of risk associated with these vegetables were similar.

When we applied the decay coefficient of Petterson et al. (31), the annual risk of infection for all combinations of crop type and effluent was below the benchmark of ≤10⁻⁴ (26, 46) as long as the last wastewater irrigation event was no less than 14 days ago, and this criterion was not achieved for any scenarios where only 1 day had elapsed since irrigation with wastewater. Risks were higher when the decay rate of k = 0.69 was used, and broccoli and cucumber were the only crops for which the benchmark of ≤10⁻⁴ was satisfied for all water qualities given a 14-day withholding period. These results highlight the potential usefulness of a wastewater abstinence period as a risk mitigation technique.

Only two parameters were allowed to vary between vegetable types in this model, namely, the volume of water retained on the plant's surface and the rate of consumption of the product. In reality, though, the viral die-off rate could also differ as a function of plant architecture. While viral decay studies on different crops have been conducted (9, 25), few k values have been derived (3, 31, 32). The results of our study and that of Petterson and Ashbolt (29) highlighted the potential significance of the choice of k parameter. Refinement of the parameter, including the development of crop type-specific values, is an area of research demanding attention.

QMRA models to date, including this one, have considered only contamination of the surface of the plant (30, 49). van Ginneken and Oron (49) justified this approach by pointing out that pathogen uptake by roots is trivial (22, 27, 37) and can be considered negligible compared to surface contamination. It may be possible, however, for pathogens to enter the harvested plant through its cut surface. Experiments on lettuce have shown that green fluorescent Escherichia coli was taken up into the lettuce tissue (52). The practice of adding water to cut surfaces to keep harvested lettuce looking fresher, which is commonplace in Australia, could allow more potential pathogens to penetrate cut surfaces. The risk of pathogen uptake via this route is likely to be exacerbated for products that are packed in waxed boxes, wherein water pools. Feeding damage by insects may also provide pathogens with a means of entry into the plant, and levels of damage have been observed to vary significantly between cultivars of the same variety (15). While the plant's surface is still likely to harbor the majority of pathogens, those inside the plant, or even those protected by tightly cupped leaves, would be protected from exposure to sunlight. Consequently, rates of inactivation via UV light and desiccation would differ. Petterson and Ashbolt (29) suggested that biphasic decay models that account for such persistent subpopulations may be more appropriate for horticultural QMRAs.

Conversely, risks can be reduced through postharvest practices such as washing and disinfection and through kitchen processes such as further washing, peeling, and cooking. While some studies on the efficacy of washing at removing bacteria have been conducted (6, 24), we have very little understanding of the effects on viruses and, perhaps more importantly, next to no information on the prevalence, frequency, or intensity of vegetable washing in most societies. On the other hand, it can be argued that ingestion of food should not be considered the sole route for infection: cross-contamination via surfaces (e.g., cutting boards) and from direct handling of contaminated produce could also poses a risk. Such household processes (both those that decrease risk and those that increase it) demand further study.

Like in all previous stochastic models for horticultural reuse, it was not possible to separate variability and uncertainty in this model. Variability is the natural variation in the phenomenon of interest. Uncertainty, on the other hand, represents our lack of knowledge about the phenomenon. Uncertainty can be minimized through improved sampling, whereas variability cannot. Total uncertainty, hitherto referred to as variation, is the combination of the two. The sensitivity analyses carried out in this study identified the total uncertainty in the amount of food consumed to be the most significant determinant of the annual risk of infection. It is conceivable that a reasonable proportion of the total uncertainty associated with the consumption data represents true uncertainty. This total uncertainty nonetheless had a marked impact on the total uncertainty about the estimate of risk. The sensitivity analyses suggested that the total uncertainty associated with k and V_prod generally had little influence on the total uncertainty of the risk estimate.

The influence of virus concentration, while not as significant as that of food consumption rate, was moderate, particularly for the Pomona AS effluent, which was characterized by high variation, as evidenced by the much larger standard deviation than for the other effluents (Table 1). Considering the sensitivity of tests for viruses, it is probably reasonable to assume that most of this total uncertainty could be attributed to variability. Nevertheless, analytical limitations warrant attention. For example, the tendency of some enteric viruses to clump together or around particulate matter (42), and subsequent breakup of such aggregates, could lead to substantial errors in measurement, i.e., high uncertainty. As noted by Yates and Gerba (53), dose-response studies are typically performed using monodispersed inocula. It is also interesting to note that for the OCSD TF effluent the influence of the virus concentration diminished as the length of environmental exposure increased, but the converse was observed for the Pomona AS effluent. This is because there was considerably more variability in the Pomona AS data, as evidenced by the higher standard deviation, and it highlights the importance that variability in pathogen concentrations has on the final estimate of risk.

It is difficult to compare the predictions of this model with those of previous QMRAs for horticultural reuse. Previous models either have used a different end point, such as the probability of infection per consumption of 100 g of product (30, 41); have been concerned with vegetables in general (1, 3, 43, 49); have exclusively considered tertiary treated and/or disinfected effluent (1); or were based on thermotolerant coliform bacteria, assuming a given ratio of enteric virus to thermotolerant coliforms (41). This is the first crop type-specific model that explicitly accounts for variation in consumption behavior. Perhaps the most appropriate comparisons to be made are with the models of Tanaka et al. (43) and van Ginneken and Oron (49). Tanaka et al. assumed that through consuming vegetables irrigated with reclaimed water, people would be exposed to an equivalent of 10 ml of secondary effluent. An environmental exposure time of 14 days and a k of 0.69 day⁻¹ were assumed. The UCL_0.95s of the annual probability of enteric virus infection, assuming consumption every day, for vegetables were estimated to be 3.3 × 10⁻³, 5.9 × 10⁻⁵, 8.3 × 10⁻⁴, and 2.3 × 10⁻⁴ for the MRWPCA, OCSD AS, OCSD TF, and Pomona AS effluents, respectively. Keeping in mind that the 10-ml daily consumption estimate is intended to represent intake of all vegetables, these estimates were within 1 order of magnitude of ours for broccoli, lettuce, and all cabbage cultivars, where we assumed a decay rate of 0.69 day⁻¹, but were 1 to 3 orders of magnitude less than our estimates derived from the normally distributed k of 1.07.

van Ginneken and Oron (49) estimated the UCL_0.95 of the annual probability of enteric virus infection for spray irrigation of vegetables, with a 15-day environmental exposure time, to be 10⁻². This is a substantially higher risk than that arrived at in our study or in that of Tanaka et al. (43). A notable feature of the model of van Ginneken and Oron is that the concentration of viruses was arrived at indirectly, by applying a secondary treatment to data for raw sewage. This appears to have led to the use of a secondary effluent that had substantially higher concentrations of enteric viruses than were used here. Presuming that this is largely responsible for the discrepancies between the models, it highlights the significance of the effluent's viral concentration on the level of risk. We attempted to account for this by using data from four treatment plants, but these were all from California. Treatment technologies aside, the microbiological characteristics of sewage are known to differ between populations (53). Likewise, consumption behavior could differ between populations. Therefore, the application of QMRAs demands diligence: the appropriateness of the model's derivation for the situation at hand needs to be considered.

The QMRA model presented here provides a useful starting point for managing risks associated with the spray irrigation of certain horticultural crops with secondary effluent. It can be built upon, refined, and adjusted to accommodate different scenarios. For example, tertiary treatment and/or disinfection of effluent could be added to the front end of the model. Another potentially significant future refinement could include the use of a burden-of-disease end point such as the disability-adjusted life year (33). The disability-adjusted life year metric was not used here because disease burden estimates have not yet been determined for broad groups such as the enteric viruses. While estimates for rotavirus are available (17), it is probably not reasonable to assume that these are representative of enteric viruses as a whole, considering the diverse symptoms of enteric virus infections. The model could also be used as a framework for developing QMRAs for other microbiological hazards. For example, helminths could be considered a more significant hazard in certain third-world populations where frequent exposure to viruses (e.g., hepatitis A virus and poliovirus) results in high levels of immunity (40).