Hierarchical structures induce long-range dynamical correlations in written texts

Abstract

Thoughts and ideas are multidimensional and often concurrent, yet they can be expressed surprisingly well sequentially by the translation into language. This reduction of dimensions occurs naturally but requires memory and necessitates the existence of correlations, e.g., in written text. However, correlations in word appearance decay quickly, while previous observations of long-range correlations using random walk approaches yield little insight on memory or on semantic context. Instead, we study combinations of words that a reader is exposed to within a “window of attention,” spanning about 100 words. We define a vector space of such word combinations by looking at words that co-occur within the window of attention, and analyze its structure. Singular value decomposition of the co-occurrence matrix identifies a basis whose vectors correspond to specific topics, or “concepts” that are relevant to the text. As the reader follows a text, the “vector of attention” traces out a trajectory of directions in this “concept space.” We find that memory of the direction is retained over long times, forming power-law correlations. The appearance of power laws hints at the existence of an underlying hierarchical network. Indeed, imposing a hierarchy similar to that defined by volumes, chapters, paragraphs, etc. succeeds in creating correlations in a surrogate random text that are identical to those of the original text. We conclude that hierarchical structures in text serve to create long-range correlations, and use the reader’s memory in reenacting some of the multidimensionality of the thoughts being expressed.

Language is a central link through which we interact with other people. As a channel of communication it is limited by our physical ability to speak only one word at a time. The question arises therefore how the complex products of our brain are transformed into the linear string of words that comprise speech or text. Since our mental processes are far from being one-dimensional, the use of memory is essential, as is the existence of some type of correlations in time.

Such questions have a long and intense history. Bolzano (1) already noted the need for specific organization in scientific texts, while Ingarden devotes his book (2) to understanding the process by which a text is understood and assimilated. Modern methods (3, 4) combine the work of linguists with those of computer scientists, physicists, physiologists, and researchers from many other fields to cover a wide range of texts, from the phoneme (5), going on to words (6–9, ‖ ) and grammar (10, 11), and all of the way to global text analysis (12) and the evolution of language (13, 14).

Recent interest has focused on applying methods of statistical physics to identify possible trends and correlations in text (15–18). In ref. 18, for example, the authors study the distribution of words across different works by the same authors, combining notions of information, entropy, and statistics to define a random walk on the text. Long-ranged correlations have been found in the writings of Shakespeare and Dickens, and a number of hypotheses as to their origin have been proposed. These include the overall existence of ideas and meaning (16, 17) or of some semantic hierarchy (18).

Here we aim at a middle ground both in methods of analysis and in ranges of text, based on geometric intuition developed in refs. 19 and 20. The framework we consider is a vector space W_all, which includes all of the words in the English (or any other) language. A base direction in this space is associated with each distinct word of the language. Given a text, the words in it define vectors that span a subspace W_text of W_all. If we consider the part of the text that is being read, there will be a “window of attention” that is currently at the focus of the reader. We can associate with this window a vector in W_text, defined as the normalized sum of the basis vectors of the words in the window, counted with multiplicity. Further insight on this vector and on W_text in general is obtained by measuring co-occurrence of words within the window of attention. We use a variant of latent semantic analysis [using singular value decomposition (SVD)] (21–23) to identify cohesive groups of words in W_text, and it turns out to be useful to think of these groups as describing “concepts.” We restrict our attention to the most important of these groups, whose corresponding vectors define specific word combinations in the text that form an (orthogonal) basis of a subspace W of W_text. Once we have constructed this basis of concepts, which depends on the text, we can view reading through the text as following a dynamic trajectory in W that sweeps through the different directions that represent the various topics and concepts as they develop in the text. We find long-ranged, power-law correlations in the time dependence of this “attention vector.” These would be barely discernible if we remain in the complete space W_text. Their origin is uncovered by considering the hierarchical structure (24) of the text. Hierarchy and structure bring us back and connect to the classic work of Bolzano and Ingarden, regarding the ways to make texts intelligible.

The Concept Space

We begin with the vector space W_all in which each word of the English language represents a base vector, but immediately restrict the discussion to the subspace W_text of the words in a specific text. We define on the set of words in the text {w} an arbitrary order, w₁, w₂, …, for example using their rank, which is the number of times m_i that word w_i appears in the text under consideration. We associate with w₁ the vector e₁ = (1, 0, 0, …), with w₂ the vector e₂ = (0, 1, 0, …), and in general the word w_i is represented by e_i, the vector which has a “1” at position i and all others “0”. Arbitrary directions in this vector space are therefore combinations of words. Among these combinations we are interested in those that represent certain topics, or concepts that are discussed in the text. We look for these word groups within a window of size a in the text, namely the words that have just been read. We suggestively term a as the “window of attention” and typically take it to be of size a = 200. The reader is aware of the words that appear within the window of attention, and these comprise at each point of the text a momentary “vector of attention.”

More precisely, assume we have fixed a and that there are A ≤ a words in the window that are not in the list of “stop words” (discussed below), and whose abundance passes a threshold for significance (also defined below). Given a specific window, we define its vector of attention V⃗ as the normalized sum over the vectors of those A words, with weights according to their number of appearance m_j(a) in the specific window. The number of appearances of word w_j in the specific window is less or equal to its abundance in the whole text, m_j(a) ≤ m_j. Words w_j that do not occur in the window have weight m_j(a) = 0. Thus, we can write

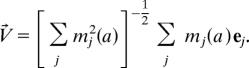We would like to project the vector V⃗ onto a smaller base related with the different concepts or themes that appear in the text. This projection onto a vector space with reduced dimensions will prove particularly useful when we measure long-ranged correlations. The starting point is the construction of a symmetric connectivity matrix M based on co-occurrence of words. This matrix has rows and columns indexed by words, and the entry M_ij counts how often word w_i occurs within a distance a/2 on either side of word w_j.

The connectivity matrix M will be normalized to take into account the abundance of words. We let L denote the number of words in the original text (before removal of stop words and threshold on significance). If the m_i occurrences of w_i were randomly distributed and not closer to each other than a (a reasonable assumption if a ≪ L), then the probability that any of the occurrences m_j of word w_j will randomly fall within a distance a/2 of any occurrence of w_i is given by

so that R is the connectivity matrix of the corresponding “random book,” with a the context window defined earlier. The normalized connectivity matrix is then

This normalization quantifies the extent to which the analyzed text deviates from a random book (with the same words) measured in units of its standard deviations. We continue the analysis by using N.

To improve the statistical significance, as well as to cut the matrix down to a manageable size, we only consider words that occur enough times in the book. We define a threshold value m_thr, which the number of occurrences m_i must exceed for word w_i to be included. m_thr is set by the random normalization R_ij and must therefore be proportional to $\sqrt{L/a}$. We found empirically that m_thr ≥ 0.4 $\sqrt{L/a}$ gave consistently good statistical significance.

Discarding words with lower m_i reduces the effect of single co-occurrences between rare words, where Eq. 1 would lead to unrealistically high N_ij (≳2). In the texts we considered, the values of the cut-off range from m_thr = 4 to 23 (see Table 1). Words that cross this threshold are “significant” and are indexed from i = 1 to d_thr.

Table 1.

Book parameters and results

Book	Length	mthr	dthr	P	dconv	Exponent
MT	22,375	4	377	17.6	25	0.45 (0.05)
HM	32,564	5	446	16.4	30	0.95 (0.07)
NK	62,190	8	762	20.6	60	0.80 (0.05)
TS	73,291	8	669	17.5	40	0.47 (0.04)
DC	77,728	8	816	20.5	80	0.45 (0.08)
IL	152,400	12	830	22.7	70	0.38 (0.04)
MD	213,682	14	1,177	20.2	70	0.44 (0.05)
QJ	402,870	20	1,293	19.6	75	0.36 (0.03)
WP	529,547	23	1,576	24.3	200	0.45 (0.05)
EI	30,715	5	474	26.4	50	0.85 (0.10)
RP	118,661	11	628	15.6	70	0.57 (0.05)
KT	197,802	14	704	27.9	50	0.30 (0.03)

m_thr is the threshold for the number of occurrences and d_thr is the number of words kept after thresholding. P is the percentage of the words in the book that pass the threshold, P = Σ_i=1^d_thr m_i/L. d_conv is the dimension at which a power law is being fit. The absolute values of the negative exponents of the fit are given in the last column, together with their error in parentheses.

Once we have reduced the size of the matrix N, we change the basis by performing a singular value decomposition. We can then project onto a smaller subspace by keeping only those d basis vectors with highest singular values. We will use the terminology of rectangular matrices, even in the case of square (symmetric) ones, as we are going to use later matrices with unequal numbers of rows and columns. We therefore use the terms singular vector rather than eigenvector and singular value rather than eigenvalue.

The idea behind this choice of principal directions is that the most important vectors in this decomposition (those with highest singular value) describe concepts. A connectivity matrix similar to the one we use has been introduced before (9, 25), based on adjacency of words rather than our looser requirement that words appear together within a wider window. This resulted in the ability to cluster words according to context and identify ambiguity in words.^‖ What we derive here may be viewed as a large-scale version of the assignation of meaning by co-occurrence, in comparison with the local result obtained previously.^‖ The vector space approach has already been used in ref. 22 for disambiguation of words.

Given d vectors from the SVD basis, every word can be projected onto a unique superposition of those basis vectors. Thus,

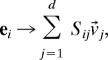where e_i is the vector of all zeros except at position i (representing the word w_i) while the v⃗_j are the first d vectors of the SVD of N.

Texts

We used 12 books (in their English version) for our analysis. Nine of them were novels: War and Peace by Tolstoi (WP), Don Quixote by Cervantes (QJ), The Iliad by Homer (IL), Moby-Dick: or, The Whale (MD) by Melville, David Crockett by Abbott (DC), The Adventures of Tom Sawyer by Twain (TS), Naked Lunch by Burroughs (NK), Hamlet by Shakespeare (HM), and The Metamorphosis by Kafka (MT). They span a variety of periods and styles and also have very different lengths (see Table 1).

In addition to the nine novels, we analyzed the scientific didactic book Relativity: The Special and the General Theory by Einstein (EI), and the philosophical treatises Critique of Pure Reason by Kant (KT) and The Republic by Plato (RP).

Each of the books was processed by eliminating punctuation and extracting the words. Each word was “stemmed” by querying wordnet 2.0 (26). The leading word for this query was retained, keeping the information on whether it was originally a noun, a verb, or an adjective. We have checked the effects of disregarding the information about the class of words and have not detected any significant changes.

All of the stop words, i.e., words that carry no significant meaning, were assigned a value of zero. The list of these words consists of determiners, pronouns, and the like. This standard list was supplemented with a list of broadly used words that are abundant in any text. In practice we rejected those words that occur significantly in an least 11 of the 12 texts we studied. Books were thus transformed into a list of stemmed words with which the connectivity matrix was defined, and to which the SVD process was applied.

Examples of concept vectors from the different books are illuminating (see Table 2). The first 10 words in the principal component with highest singular value in Moby-Dick immediately carry us into the frame of the story and introduce many of its protagonists. The next three principal components are somewhat similar, with the addition of familiar words such as white, shark, captain, and ship. By the fifth largest principal component a change of scene occurs as the story takes a detour indoors, and this is evidenced by the positive entries in the second column of Table 2.

Table 2.

Examples of the highest singular components for three books

MD(1)	MD(5)	EI(1)	EI(2)	TS(1)	TS(2)
whale	bed	surface	planet	spunk	ticket
ahab	room	euclidean	sun	wart	bible
starbuck	queequeg	rod	ellipse	nigger	verse
sperm	dat	continuum	mercury	huck	blue
boat	aye	geometry	orbital	tell	pupil
cry	door	universe	orbit	stump	yellow
aye	moby	curve	star	johnny	ten
stubb	dick	numbers	angle	reckon	spunk
sir	landlord	slab	arc	bet	thousand
leviathan	ahab	plane	newton	water	red

Given are component one and five of Moby-Dick (MD), one and two of Einstein (EI) and of Tom Sawyer (TS). The coefficients of the words in the singular component may be positive (plain text) or negative (italic), and their absolute values range from 0.1 to 0.37.

Similarly, the first 10 words of the principal component with highest singular value of Einstein’s book launch us immediately into the subject matter of special relativity, whereas its second component brings in the applications to astrophysics. It is perhaps amusing to recall the tales of Tom Sawyer by viewing the principal component with highest singular value. These deal with Tom’s various escapades, for example the instructions given in chapter 6 on how to cure warts by dunking the hand in a stump with spunk water at midnight, or the bible competition that Tom wins by procuring tickets through various trades and bargains.

The dominance of nouns in Table 2 is striking, because our analysis did not single out nouns from verbs and other classes of words. This reinforces the notion that nouns are generally better suited for “indexing” a text than other word classes. Adjectives and adverbs are typically very broad in their use and only in very specific cases (such as the importance of the ticket color in the history of Tom Sawyer) appear related with a single “theme.” Verbs generally have multiple meanings (according to wordnet the average polysemy of verbs is 2.3 compared with 1.2 for nouns). As a result, nouns provide the strongest elements in the co-occurrence matrix and are more directly related with the different “concepts.” The groups of words we identify as topics may be reminiscent of sets of synonyms defined in wordnet (synsets), but in fact they are more in the spirit of semantic fields.

We can conclude that the “concepts” we defined by using singular vectors do indeed capture much of the content of the text.

Dynamic Analysis

Having found a representative basis for each of the texts, our main interest is in the dynamics of reading through the text. What is new here in comparison with earlier statistical analysis (18) or linguistic research (27) is that the basic ingredient is not the byte (as in the statistical studies) or the word, but rather a contextual collection of words (our concept vector). In this way, our study links the word connectivity matrix to semantic meaning.

Basically, we again slide the “window of attention” of fixed size a = 200 along the text and observe how the corresponding vector V⃗ moves in the vector space spanned by the SVD. If this vector space were irrelevant to the text, then the trajectory defined in this space would probably be completely stochastic and would perform a random walk. If, on the contrary, the evolution of the text is reflected in this vector space, then the trajectory should trace out the concepts alluded to earlier in a systematic way, and some evidence of this will be observed.

Trajectories in this vector space can be connected to the process of reading of the text by replacing the notion of distance along the text with the time it takes to read it. Word distance is measured on the original text, with the stop and nonsignificant words included, and then replaced with the concept of time. We define the discretized time as t = l × δt, with l the distance into the text and δt the average time it takes a hypothetical reader to read a word.

At each time t we define in this way a vector of attention, V⃗(t) corresponding to the window [t/δt − a/2, t/δt + a/2]. We project the vector V⃗(t) onto the first d vectors (ordered by singular value) of the SVD basis, so that V⃗(t) leads to

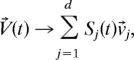with the SVD basis {v⃗_j} chosen as before. V⃗(t) is normalized after this projection.

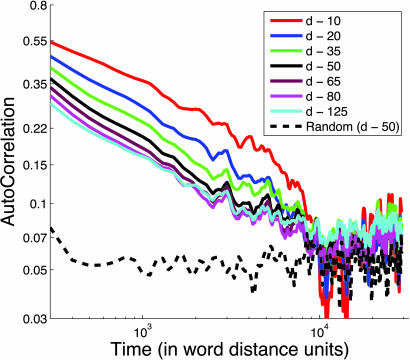
The moving unit vector V⃗(t) ∈ R^d is a dynamical system, and we proceed to study its autocorrelation function in time C(τ) = 〈V⃗(t)·V⃗(t + τ)〉_t, where 〈·〉_t is the time average. Fig. 1 shows the correlation function of the concept vector in time for Tom Sawyer given in a log–log scale. The different lines correspond to different values of d. At short distances the correlation is on the order of 0.5 (the maximal value attainable is 1) and remains higher than the noise level over a large range, on the order of >1,000 words. This range is much longer than what we found when measuring correlations among sentences, without using the concept vectors (data not shown).

Fig. 1.

Log–log plot of the autocorrelation function for The Adventures of Tom Sawyer using different numbers of singular components for building the dynamics. For comparison, the autocorrelation of a randomized version of the book is also shown.

The results one obtains depend on the dimension d taken for the projection. For low d/d_thr (d ≈ d_thr/100) the correlation function does not display a particular common behavior for all of the books. However, as d/d_thr approaches values of ≈0.1 the correlation function converges to a straight line in the log–log plot, indicating a power law. This convergence to a power-law behavior and the dimension necessary to produce it depend on the book. We did not find a clear correlation of the genre of the book with the value of its exponent.

The range over which the power-law behavior is evident depends both on the exponent and the natural noise in the system. The noise can be estimated by considering a randomized text. To do this we permute the words in the text, keeping the same probability distribution of words but changing their order (dashed line in Fig. 1). The average value of this correlation function is determined by the underlying distribution of words in the text.

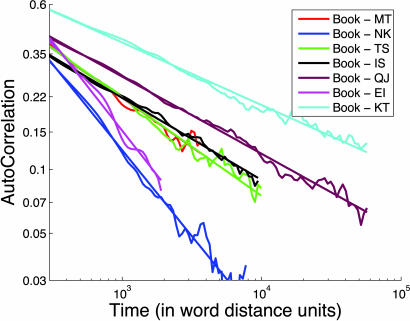
The results presented in Table 1 (see Fig. 2) are given for the lowest value d_conv of d at which the convergence to a power-law behavior is clearly discerned.

Fig. 2.

Autocorrelation functions and fits for seven of the books listed. The autocorrelation functions are truncated at the level where the noise sets in.

If d/d_thr is further increased to values close to unity, then the correlation function levels out and the slope is reduced by a factor of between 2 and 5. More importantly, the difference between the actual value of the autocorrelation functions for the real and random book at short distances (Δt ≈ 300 in word distance) is reduced by a factor of 5–10 when compared with d/d_thr ≈ 0.1. The SVD processing and the truncation to the main ideas is thus fundamental to uncover the high long-range correlations, which are less evident in the high dimensions of the full vector space spanned by all significant words.

The long-range correlations uncovered in this fashion are in line with previous measurements obtained by using the random walk approach of refs. 15, 17, and 18. However, the range over which we find correlations is much larger, and the quality of the power-law fit is accordingly significantly better.

Controls

The methods we have described above require a certain number of parameters, such as the threshold rank value m_thr of the matrix, or the size of the windows that are being moved along the text. We describe here some tests that were performed to check the robustness of the method when these parameters are changed, summarizing the most relevant findings.

1. The threshold m_thr must be chosen carefully. Choosing a lower value m_Lthr < m_thr increases the number of accepted words to d_Lthr. To keep the computation manageable while retaining the comparison to the case with m_thr, we performed the SVD on an asymmetric matrix with d_Lthr rows and d_thr columns. This also serves to omit additional entries in the matrix N that are large because of words w_j with few occurrences m_j. In effect we use the same number of basis vectors to describe more words. We furthermore used the same value of d_conv to measure the value of the power law. The results for this control are shown in Table 3 and should be compared with those of Table 1. In general, we find that the correlations remain but decay faster, as indicated by the higher values for the exponents.

2. A change in the size of the window of attention (the variable a) does not affect the results significantly as long as it is kept above ≈100 words. Below a = 100 the number of words becomes too small to create true correlations, and the correlation function measures only the noise created by the statistical distribution of the words in the text. Windows longer than a = 200 words preserve the correlation and the power law but lose information on the shorter distances.

3. We checked, to some extent, the language dependence of the method, by comparing Don Quixote in Spanish and English. Although languages can have quite different local syntactic rules, the long-term correlations practically do not depend on the language. This is perhaps related to the importance of nouns in creating the correlation function, and these are translated more or less one-to-one from one language to another.

Table 3.

Book parameters and results for rectangular connectivity matrices

Book	mLthr	mthr	dLthr	dthr	P	Exponent
MT	1	4	1,894	377	27.2	0.70 (0.05)
HM	1	5	3,599	446	30.8	1.40 (0.20)
NK	2	8	3,869	762	36.9	1.10 (0.10)
TS	2	8	2,983	669	27.9	0.75 (0.08)
DC	2	8	3,315	816	31.6	0.65 (0.10)
IL	3	12	2,637	830	29.0	0.48 (0.05)
MD	4	14	4,271	1,177	30.1	0.53 (0.05)
QJ	5	20	3,865	1,293	25.7	0.46 (0.03)
WP	6	23	4,448	1,576	30.4	0.60 (0.05)
EI	1	5	1,851	474	33.6	1.00 (0.20)
RP	3	11	2,142	628	22.1	0.67 (0.07)
KT	4	14	1,655	704	31.3	0.37 (0.03)

The values of d_conv are the same as in Table 1. The threshold value for the rows m_Lthr is smaller than that of the columns m_thr so accordingly the number of rows d_Lthr is bigger than the number of columns d_thr. P is as defined in Table 1. The dynamics change when more words are added, and thus the exponents (absolute values are shown) are more negative, that is, the correlations are weaker.

Hierarchy and the Origin of Scaling

The existence of power laws is often traced to hierarchical structures (24). We put forward the hypothesis that in our case these structures are parts of the texts (such as “volumes,” “parts,” “chapters” within parts, “sections” in chapters, “paragraphs” in sections, and so on). This is a hierarchy of K levels, each containing several parts. For example, a book may be in 3 volumes that each have about 10 chapters, each of which is divided in 8 or so sections, etc. For simplicity, we assume that each level contains the same number of parts H. Typical values are K = 4 and H ≈ 7. The important point is that the text has the structure of a tree.

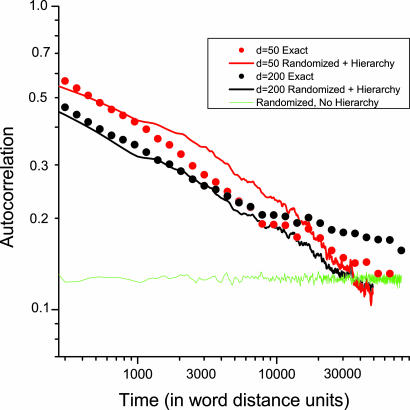
Since the power-law correlations appear in all of the books we considered, regardless and independent of their subject or underlying ideas, the possibility arises that a computer-generated book that implements this hierarchy could recreate these correlations. We now proceed to show that the power law we found earlier for the text is not changed if words are permuted in the text, provided that one respects as much as possible the structure of the book as a whole. On the other hand, it does change if these structures are not preserved. As shown in Fig. 1, if the randomized text includes only a permutation of the words, and the structure is not kept, then the randomized text has no long-ranged correlations.

We construct the hierarchical text by first preparing an empty template into which we will insert the words from the original book. The empty text is divided in H roughly equal parts, each subdivided again in H parts. This subdivision is repeated K times. We end up with the book divided in K levels and a total of H^K subdivisions at the smallest scale. K and H are chosen so that the lowest level (corresponding to “paragraph”) will have ≈100 words.

Into this empty hierarchical template we sequentially place each word, according to the following process. Assume the word w_i appears m_i times in the original text. We would like to find for it m_i positions at the lowest levels in the template. To define the probability at the lowest level, we begin at the highest level and progress downwards from there step by step.

Fix a parameter E > 1 (for concreteness take E = 5). We define recursively for each subdivision the probabilities for w_i to reside in it, starting at the top level, where each part has the initial weight J. One of the subdivisions at this level is randomly chosen, and the probability for w_i to reside there is enlarged by a factor of E, to a weight J·E. The next level inherits the probabilities introduced before, either J or J·E. Now, repeat the process at the second level by the choice of a random subdivision in each of the H subgroups. Depending on which subdivision has been chosen at each level, slots will have weight JE², JE, or J.

Going on in this fashion we fill all of the levels, so that the values of the probability at the lowest level of the hierarchy span the range of weights JE^k, with k ∈ {0, …, K}. We then normalize the probabilities to 1 by choosing J so that the sum of weights is 1. We may now distribute the m_i copies of word w_i randomly according the weights in the finest subdivision.

This procedure is repeated for all words and produces a hierarchical randomized text that preserves the word distribution and resembles the structural hierarchy of the book.

As seen in Fig. 3, performing this hierarchical randomization process on the book preserves the power-law behavior of correlations found in the original text. Since the simple randomization (no hierarchy) destroys the power law (see Figs. 1 and 3) we can conclude that the power laws of the original text do indeed originate in their hierarchical structure. We have verified that the results of this hierarchical randomization are reasonably robust to variations in the algorithm for building the hierarchical template and for filling it with the correct number of copies of each word.

Fig. 3.

Comparison of autocorrelation functions for the original book of Kant (dots), the randomly reorganized version (green), and the hierarchically reorganized version (lines) using E = 5.

Conclusions

Many questions remain to be addressed; for example, application of the dynamic approach to the transmission of complex ideas in spoken text, in which repetitions are known to be of importance, and comparison of the results to those of written text. It may also be of interest to characterize different types of text or of authors according to the correlation exponent. It remains to be seen whether the hierarchical organization we have identified in texts is related to a hierarchical organization in our thought processes.

Our approach enables the quantification and rigorous examination of issues that have been introduced long ago and discussed heuristically in the great classics of the field. Bolzano, in his Wissenschaftslehre (1), written in 1837, studies the theory of scientific writing and points out in great detail how such writing should proceed. In particular, in Vol III, he points out that, starting from “symbols” (he probably thinks of mathematics) one works one’s way to a fully structured text, containing paragraphs, sections, chapters, and so on. He clearly instructs the reader as to how to maintain the intelligibility of the text by the careful use of structure. Ingarden, in his Vom Erkennen des Literarischen Kunstwerkes (2) talks, from his philosopher’s point of view, about the activity of the brain that compresses parts of texts so that they may be more easily recalled. He also alludes to the importance of structural units in creating intelligible text. The entities he has in mind are “layers of understanding” (chapter 16, page 111: “. . . not every layer of an already read part of a text is kept in the same way in memory, . . . The reader keeps bigger and smaller text-connections—Satzzusammenhänge—in his living memory . . .”).

Our study allows the measurement of the degree to which the insights of authors like these can be understood. Therefore, it adds a piece to the puzzle of understanding the nature of language.

Abbreviation

SVD

singular value decomposition.