Counterions between charged polymers exhibit liquid-like organization and dynamics

Abstract

Current understanding of electrostatics in water is based on mean-field theories like the Poisson–Boltzmann formalism and its approximations, which are routinely used in colloid science and computational biology. This approach, however, breaks down for highly charged systems, which exhibit counterintuitive phenomena such as overcharging and like-charge attraction. Models of counterion correlations have been proposed as possible explanations, but no experimental comparisons are available. Here, collective dynamics of counterions that mediate like-charge attraction between F-actin filaments have been directly observed in aqueous solution using high-resolution inelastic x-ray scattering down to molecular length-scales. We find a previously undescribed acoustic-like phonon mode associated with correlated counterions. The excitation spectra at high wave-vector Q reveal unexpected dynamics due to ions interacting with their “cages” of nearest neighbors. We examine this behavior in the context of intrinsic charge density variations on F-actin. The measured speed of sound and collective relaxation rates in this liquid agree surprisingly well with simple model calculations.

Electrostatic interactions between charged surfaces in water are dominated by counterion behavior. Current understanding is based on mean-field theories like the Poisson–Boltzmann formalism, which is routinely used in colloid science and computational biology (1). In systems with strong electrostatic interactions, such as DNA packaging in bacteria (2, 3), artificial gene delivery systems (4), cytoskeletal organization (5), electrophoresis for macromolecular separations (6), and transport within ion channels (7), such theories break down, and counterion correlations or dynamics become important (8–15). Models of dynamic van der Waals-like correlations of long-wavelength ion fluctuations (16) have been suggested, as well as models from low-temperature physics such as counterion Wigner lattices (12, 17) as an extreme limit, but no experimental comparisons at sufficient spatial resolution are available. Likewise, no direct measurements of ion dynamics in these strongly charged systems exist. Both are crucial elements for comparisons between theory and experiment. Moreover, real polyelectrolytes exhibit chemical heterogeneity that results in spatial charge modulations on the polyelectrolyte surface. Such charge modulations can potentially strongly influence the behavior of counterions.

In this work, we directly measure spatial and temporal correlations and collective dynamics of counterions that mediate binding between charged F-actin polymers in aqueous solution using high-resolution inelastic x-ray scattering (IXS). IXS is a recently developed technique capable of measuring elementary excitations at molecular length-scales with millielectronvolt (meV; 1 eV = = 1.602 × 10⁻¹⁹ J) energy resolution (18–20), which is ≈6 orders-of-magnitude higher than that in typical synchrotron diffraction experiments. Surprisingly, we find that the counterions exhibit an acoustic-like phonon mode that suggests the existence of a correlated phase. This system exhibits unexpected dynamics due to ions interacting with their “cages” of nearest neighbors at large wave vectors, which allow us to experimentally access interion correlations. An examination of the spatial charge heterogeneity on the surface of F-actin suggests that the ions are hierarchically organized: they modulate their density according to charge density variations of the F-actin surface. High-density counterion domains are observed, with a density comparable with that of highest local charge densities on F-actin. At small length scales within the domains, counterions exhibit liquid-like correlations and dynamics. The measured speed of sound and collective relaxation rates in the liquid-like domains agree well with simple model calculations.

Results and Discussion

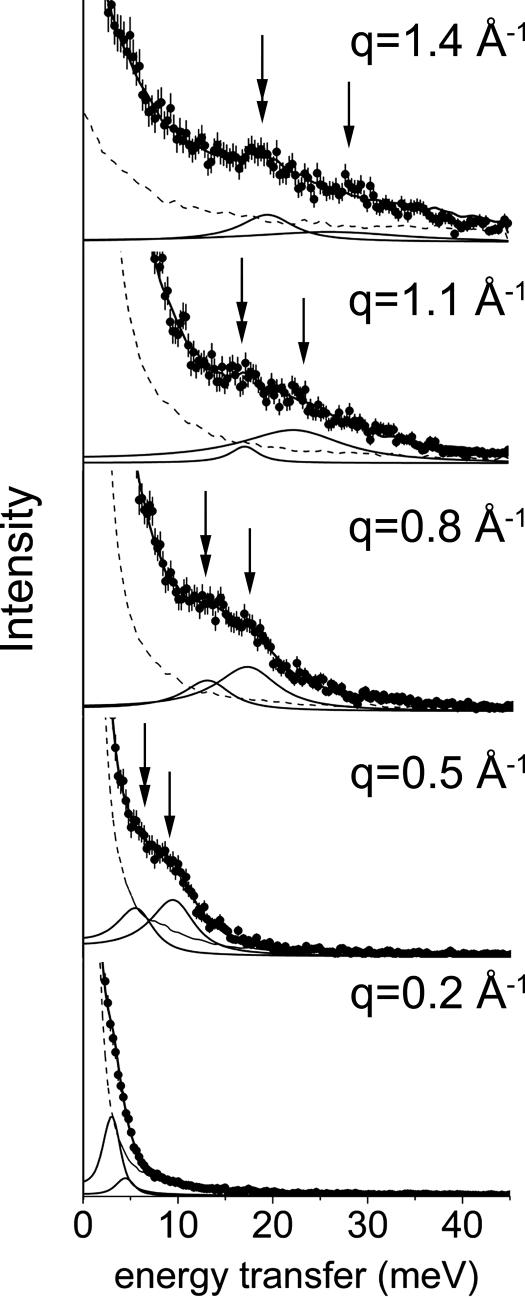
IXS spectra of BaCl₂-condensed bundles of close-packed F-actin are shown in Fig. 1. As expected, the signal levels are weak but are much larger than the statistical counting errors indicated by the error bars, which are shown on all of the data points. (Some of the data points have error bars that are comparable in size with the symbols.) Because of the high degree of monochromatization, the incident beam is only ≈10–100 times more intense than a typical rotating-anode laboratory x-ray source and is therefore orders-of-magnitude less intense than that in a typical synchrotron x-ray diffraction experiment. Although we limited count times to <10 h for each sample to avoid radiation damage, the spectra clearly indicate features with well defined dispersion behavior. Because the samples consist of F-actin bundles surrounded by aqueous buffer, a significant part of the IXS signal comes from water. At low energy transfers, we observe an excitation similar to the transverse-like mode of pure water and the well known fast-sound mode of water with sound velocity c = 3,280 ± 40 m/s (21), as expected.

Fig. 1.

IXS spectra of F-actin bundles reveal an acoustic phonon mode from correlated counterions. Arrows indicate the high-frequency water mode (right) and previously undescribed acoustic counterion mode (left). The dashed line is the resolution function. Solid lines below the data are the fitted damped harmonic oscillator functions, and the solid line through the data is the total fit. Error bars (some comparable with symbol size) indicate the counting error.

In addition to the signal from water, we observe a previously undescribed acoustic-like mode (sound velocity c = 2,450 ± 90 m/s), which exhibits a linear dispersion down to molecular length scales (≈4 Å) (Figs. 1 and 2). Both the aqueous acoustic mode and the previously undescribed mode are required to satisfactorily fit the data (except the lowest q-point, which can be fit almost as well with a single broadened peak). To elucidate the physical origin of this mode, three types of reference samples were measured: F-actin only, salt buffer only, and a low-salt buffer containing dispersed rather than bundled F-actin. To check that the new mode is not from actin, we “condensed” actin without using divalent ions. For the case of reference sample with F-actin only, an osmotically concentrated gel (50 mg/ml) of F-actin with no added salt was measured to see whether there was any significant contribution from internal modes of the protein itself in the present range of q and ω. As shown in Fig. 3, instead of two modes, only a single acoustic mode is observed with c = 3,050 ± 50 m/s, which is quite different from that of the new acoustic mode but is close to that for the high-frequency sound mode of the buffer solution. To check that the new mode is not from water or the salt solution, reference samples of salt buffers also were measured. The spectra of salt solutions without F-actin (35 mM BaCl₂ buffer and 25 mM MgCl₂ buffer) are also very similar to the spectra of pure water (c = 3,050 ± 120 and 3,080 ± 40 m/s, respectively), and the previously undescribed mode disappears.

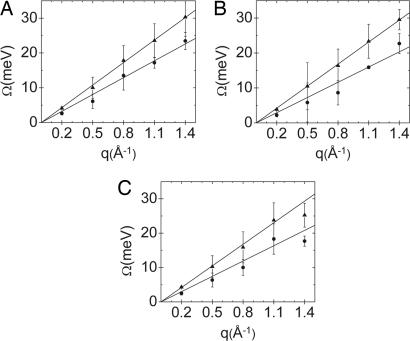
Fig. 2.

Fitted dispersion relations for F-actin bundles with 35 mM Ba²⁺ (A), 35 mM Sr²⁺ (B), and35 mM Mg²⁺ (C) are shown. The slopes give sound velocities of 3,280 ± 40 (A), 3,190 ± 20 (B), and 3,180 ± 70 m/s (C) for the aqueous mode and 2,450 ± 89 (A), 2,210 ± 150 (B), and 2,260 ± 180 (C) m/s for the previously undescribed acoustic counterion mode.

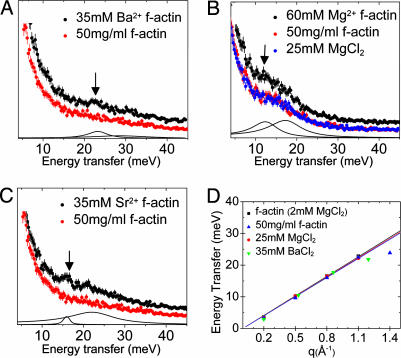
Fig. 3.

Direct comparison between the new excitation mode in ion-bundled actin and the water modes in reference samples. (Spectra have been vertically displaced for clarity.) (A–C) Arrows indicate the new acoustic phonon mode at 23 meV and q = 1.4 Å⁻¹ from 35 mM Ba²⁺ bundled F-actin (A); 14 meV and q = 0.8 Å⁻¹ from 60 mM MgCl₂ bundled F-actin (B); and 16 meV and q = 1.1 Å⁻¹ from 35 mM Sr²⁺ bundled F-actin (C). None of the reference spectra contain these new features; they exhibit only water-like behavior. (D) The disappearance of these features also can be seen in the four reference dispersion relations from two synchrotrons, which also demonstrate the robustness of the fits.

In all of these reference measurements, the spectra were very similar to that of water, suggesting that the previously undescribed acoustic mode is not associated with ions in solution or internal modes of F-actin, but rather with the ions linking F-actin into bundles. It is likely that these ions interact with water, and the observed excitation is a composite mode with ions and water molecules coorganized with it. Moreover, the sound velocity c associated with the ion mode increases with ion number density. Samples at 25, 35, and 60 mM global [Mg²⁺] exhibited the previously undescribed mode with associated sound velocities of 2,000 ± 140, 2,260 ± 180, and 2,450 ± 150 m/s, respectively. We observed similar dispersion behavior with Mg²⁺, Sr²⁺, and Ba²⁺(see Fig. 2), as expected for an ion mode. Representative F-actin bundle spectra showing both modes for the three different ion species are shown together with reference spectra. The dispersion behavior and peak widths of the reference spectra measured at the European Synchrotron Radiation Facility and the Advanced Photon Source show excellent agreement with one another and with published values, using a free fitting procedure that does not constrain them to do so. This result further demonstrates the reproducibility of these weak signals.

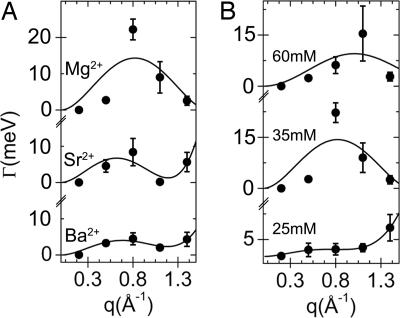
The observation of an acoustic phonon mode suggests the existence of a condensed phase (such as a liquid rather than a gas.) This hypothesis is confirmed in the behavior of the Brillouin linewidth Γ(q). In this experiment, we measured data over a q-range that corresponds to length scales from a little less than the actin monomer size down to ion sizes. The evolution of Γ(q) of the ion mode contains information on ion dynamics at these small length scales. Brillouin linewidths of the water modes increase with q throughout the q-range measured (see Fig. 1) and are always underdamped (2Γ(q) < cq), consistent with previous work (21). Behavior of the ion mode is complex and shows nonmonotonic behavior, as can be seen in the data for three different ion densities (25, 35, and 60 mM MgCl₂; Fig. 4B). We believe that this result is due to the “caging” dynamics of ions interacting strongly with their first shell of neighbors, in analogy to behavior in dense atomic fluids and colloidal suspensions, where intermediate and large q collective density fluctuations relax at a rate (22, 23)

Here, D₀ is a self-diffusion constant, and S(q) is the fluid structure factor, which at high densities is strongly peaked at the q_p = 2π/d, where d is the effective particle diameter. For one-component liquids and particle suspensions, the location of the S(q) peak q_p is primarily controlled not by the particle concentration but rather by the effective hard sphere diameter. For charged fluids, the latter reflects the combined influence of the bare ion diameter, Coulomb repulsion, and a hydration shell. In a dense one-component fluid, this d = 2π/q_p is a good approximation of the mean interparticle spacing (24). The curves superimposed onto the data are fits of Eq. 1 (Fig. 4). To avoid the assumptions associated with a particular liquid model, we chose a simple parameterized Lorentzian S(q), which fits the salient data features surprisingly well. The best-fit full-width at half-maximum (FWHM) of S(q) is ≈0.5 Å⁻¹, consistent with that expected from the nearest-neighbor “shell” of a dense liquid of spherical particles of diameter ≈4 Å, a typical hydrated ion size (22–24). Estimating an effective ion diameter as d = 2π/q_p, where q_p is the S(q) peak position extracted from a fit to Eq. 1, we find d = 6.0, 3.8, and 3.2 Å for the 25, 35, and 60 mM MgCl₂ samples, respectively. This result indicates that as the global ion concentration increases, the ion density in this correlated liquid increases, and/or the effective ion size decreases.** Ba ions have a larger radius and a higher condensation threshold, so a lower condensed ion density at the polymer surface is expected at the same global concentration. With SrCl₂ and BaCl₂ at 35 mM, we find d = 5.2 and 5.1 Å (Fig. 4), which is, as expected, larger than that for MgCl₂ at 35 mM and is also consistent with the proposed picture. It is interesting that these trends persist despite the complicating presence of water.

Fig. 4.

Measured Brillouin linewidths reveal “ion-caging” dynamics. (A) The linewidth Γ(q) for condensed ionic liquids between charged polymers at [35 mM] Ba²⁺, Sr²⁺, and Mg²⁺ (from bottom to top) can be fit surprisingly well with Γ(q) = D_0q²/S(q) using a simple Lorentzian structure factor S(q). (B) Γ(q) for Mg²⁺ ions between charged polymers at increasing global ion concentrations (25, 35, and 60 mM from bottom to top) indicate an increase in the condensed number density within the ionic liquid, and hence a decrease in the interion spacing, estimated from the fitted S(q).

The dynamics of counterions play a crucial role in our understanding of electrodynamic phenomena in complex fluids, such as electrophoresis for macromolecular separation technologies. However, experimental measurements of key physical parameters are difficult (6). These IXS measurements allow us to estimate the self-diffusion constant D₀ of the condensed counterions that mediate the attraction between highly charged F-actin polyelectrolyte filaments. Applying Eq. 1 to the data it describes best, we find that D₀ is 4.7 × 10⁻⁹, 5.0 × 10⁻⁹, and 4.9 × 10⁻⁹ m²/s for 25 mM Mg, 35 mM Sr, and 35 mM Ba, respectively, which are values typical of dense simple liquids. We can estimate the “residence time” t₀ of a counterion as the time it takes to diffuse a distance equal to d. From this range of D₀ values, we get a t₀ of order 1 × 10⁻¹¹ s.

It is important to emphasize that this liquid-like organization of counterions occurs in bundled F-actin, but not dispersed F-actin, as indicated by the reference spectra on dispersed F-actin in low divalent salt buffers, in which the characteristic counterion liquid mode is not observed. Having stated that, in the bundled F-actin phase, it is likely that the observed dense counterion liquid coexists with a gas of counterions in the aqueous solution, which is expected to have an IXS signature similar to the reference spectra of salt solutions in isolation (and, by implication, similar to that of water).

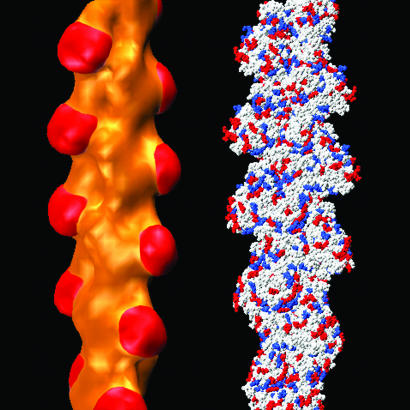
The surface of F-actin is net negatively charged. However, it has a heterogeneous topography as well as a heterogeneous distribution of charges. For example, each actin monomer is composed of amino acids that have a large number of positive as well as negative charges. This heterogeneity is illustrated in Fig. 5, where the distribution of positive and negative charges on the F-actin surface is shown. The charge density of F-actin can be roughly estimated by assuming that it is a cylinder with a diameter of 75 Å. It can be seen that although the average charge density of the actin cylinder is approximately −1 e/590 Ų, the actual local surface charge can deviate significantly. By using the simplified abstraction of a uniformly distributed layer of compensating divalent cations to neutralize a schematic actin cylinder, we estimated the intercation spacing to be ≈34 Å, which would correspond to a dilute counterion fluid. In contrast, the experimentally derived S(q) have the form corresponding to a dense liquid, with effective diameters for Mg ranging from 6.0 to 3.2 Å. We believe this result is not a discrepancy, but rather is due to imperfections of the simple, spatially homogeneous schematic model. Given that overall charge neutrality has to be maintained in the F-actin bundle, the low global ion concentration combined with the experimentally derived S(q), both in the large S(q) peak positions q_p and the sharp S(q) peak widths, imply that the divalent ions on F-actin must have a heterogeneous distribution with dense local domains. This hypothesis seems likely given the highly heterogeneous distribution of charge depicted in Fig. 5, which has regions of high local charge. For example, subdomain 1 of the actin monomer has an average charge density that is ≈4 times higher than the monomer average value and has local densities that are even higher. The observed local counterion separations are approximately in the right range to compensate regions of high local charge on F-actin. Interestingly, an examination of Fig. 5 shows that most of the positive and negative amino acids on actin are clustered near one another, forming a weakly charged surface over most of the filament. The charge distribution of subdomain 1 of the actin monomer contrasts sharply to that of the rest of the monomer. Subdomain 1 has a large number of uncompensated negative amino acids in close proximity (red) and is strongly anionic. In fact, the net charge on subdomain 1 is −10. (By comparison, the average charge on the entire monomer is −11.) This observation of heterogeneity is qualitatively consistent with the general picture of a counterion density wave along F-actin, as inferred from previous small-angle x-ray scattering measurements (25), in which the counterion distribution is influenced by charge density variations on F-actin. Moreover, because the experimentally deduced effective counterion diameters are moderately (≈20–50%) smaller than the hydrated ion size inferred from diffusion experiments in dilute solutions (26), it suggests that ions on these highly charged surfaces are partially dehydrated. The largest deviations from the simple caging model occur at the highest ion densities, where the fits do not fully reproduce the sharpness of Γ(q) (Fig. 4, top traces). This density range is also the limit where water-restructuring effects are expected to exert the most influence.

Fig. 5.

The charge distribution on the surface of F-actin is highly heterogeneous, leading to local surface charge densities much larger than the average charge density. Shown on the right is a high-resolution representation of F-actin. Negatively charged residues are colored red, positively charged residues are blue, and all other residues are white. Shown on the left is a low-resolution density map of F-actin to better show topographic variations. The periodic protrusions (red) on the filament are the highly charged subdomain 1s. This heterogeneous charge density can significantly modulate the counterion distribution.

It is well known that molecules with anionic functional groups can be linked together by cations to form “salt bridges” (27). The results here indicate if a polymer has many charged groups, then instead of forming an array of salt bridges, counterions can locally form a dynamic, correlated liquid “patch” instead. This finding also may be related to the heterogeneous charge distribution of the F-actin surface. With such a complicated surface charge distribution (Fig. 5) and dynamic protonation/deprotonation events, it may not be possible to form a set of stable, static, salt bridges between adjacent F-actin filaments. The composite counterion/heterogeneous polyelectrolyte system is extremely complex, and it is not possible at present to simultaneous describe all aspects of it rigorously in a single, unified model. Nevertheless, we will engage these experimental results using a number of simple theoretical estimates.

We can further test the proposed physical picture of liquid-like behavior within the local counterion patches in a different way. The linewidth has been computed based on a minimalist theoretical model of the condensed ions as a Newtonian fluid of hard spheres of effective diameter d, mass m, and volume fraction φ. The self-diffusion constant in Eq. 1 is accurately given by the classic Boltzmann–Enskog result (23), D₀ = D_B/g(d), where D_B = (d/16φ)$\sqrt{\pi k_{\mathrm{B}}T/m}$, and g(d) is the radial distribution function at contact that quantifies the binary collision rate. Based on the known hard sphere g(d) and S(q) (23, 24), the linewidth computed using Eq. 1 attains a local maximum, Γ_max, only if φ > 0.2 and at a reduced wavevector qd ∼ 3.5. Our experiments find the local maximum also at a nearly constant q ∼ 0.8 ± 0.15 Å⁻¹, which implies d ∼ 4–6 Å, consistent with our estimates above as well as the interpretation of a dense counterion fluid with partial ion dehydration. As the effective volume fraction increases from 0.2 to ≈0.45, the calculated shape of Γ(q) evolves from a plateau-like to an oscillatory form in qualitative accord with experiment (see data for Mg in Fig. 4, bottom to top). Moreover, the model suggests the observed increase of the linewidth for the Ba–Sr–Mg series is a dynamic effect associated with decreasing ionic mass, because Γ_max varies as 1/m^1/2. By using d = 5 Å, we find Γ_max ∼ 20, 10, and 8 meV for Mg, Sr, and Ba, respectively (Fig. 4A), in remarkable accord with the observed peak values of Γ(q). For this effective hard-sphere model, the sound velocity for small q is given by $\sqrt{k_{\mathrm{B}}T/\mathrm{mS(}0)}$, where S(0) is the dimensionless compressibility (23, 24). For Mg ions, sound velocities in the observed range of 1,800–2,500 m/s are obtained for 0.4 < φ < 0.5, which are the same φ values deduced from the linewidths Γ(q) for the 35- and 60-mM data. The interpretation is therefore self-consistent.

The effective hard-sphere model above approximates Coulomb repulsion by means of an effective diameter and will not likely capture details of electrostatic interactions between the counterions accurately. Models based on the Debye–Hückel approximation cannot be used to treat these strongly charged systems because they cannot generate correlations. However, we construct a model that implicitly accounts for counterion correlations by using our experimentally measured interion spacings characteristic of a dense correlated liquid and then estimate the effect of electrostatic interactions at the Debye–Hückel level. In this simplified approach, the limit of elongated counterion domains along the F-actin axis is assumed, and a 1D model in which the ions interact through repulsive electrostatic forces at the Debye–Hückel level is used. Placing ions of mass m in a 1D array with an interion spacing d, the dispersion relation for an acoustic phonon is given by ω(q) = cq, where the sound velocity is c = {(k_BT/m)(4z²ℓ_B/d)ln(π/κb)]^1/2, where ℓ_B = e²/k_BT is the Bjerrum length, z is the ion valence, κ⁻¹ is the Debye length, and b is a microscopic cutoff length. By using the measured values of the interion spacing at room temperature and an optimized cut-off length of b = 4.3 Å, this estimate yields 2,033, 2,446, and 2,474 m/s for 25, 35, and 60 mM Mg²⁺, respectively, which agree with our measured values to within ≈10%. By comparison, the sound velocity of a counterion gas can be estimated by (k_BT/m)^1/2, which is at least 1 order of magnitude less.

Our expressions for the acoustic sound velocity in both limits vary as the inverse square root of mass but are independent of the solvent viscosity. This observation makes sense because both calculations are based on a short time (or high frequency) view of a liquid where it can be treated as an effective solid, and hence acoustic waves are not damped. Because dissipative or viscous processes that can damp acoustic waves require a finite time to develop, they do not enter these estimates. A note to this effect has been added to the text.

Interestingly, although the linewidth data show an ion mass dependence that agrees with theoretical estimates, the sound velocity data show a significantly weaker dependence than expected for Sr and Ba, despite the good agreement with Mg. The magnitude of sound velocities, however, is dominated by the bulk modulus or compressibility (24). Moreover, it is controlled to a first approximation by the total density (water + ions), which is expected to be nearly constant in the present context. In contrast, the linewidth Γ(q) probes instead the mass-dependent dissipative transport processes associated with structural relaxation of caged ions (23).

Corrections are likely needed to fully describe the physics of this complex system. Because the net negatively charged actin surface actually contains charges of both signs, the surface counterion distribution will be modulated, and coions also will likely contribute. However, because Cl⁻ is the coion for all of the salts we used, the fact that the counterion mass (Mg, Sr, and Ba) scaling by the simple model works well seems to imply that the number of participating coions is much smaller than the number of counterions, which makes it difficult for coions to “screen” counterions by surrounding them. A rigorous treatment of coions requires additional experiments and theoretical development. Putting these experimental results in the context of the F-actin surface charge distribution (Fig. 5), it would be interesting to examine theoretically and computationally the influence of the positive- and negative-charged patches of different sizes on counterion and coion behavior. For example, how big and how densely charged must a surface patch be before it is wetted by condensed counterions or coions, and what kind of correlations exist between them? We speculate that most of the condensed counterions are organized near subdomain 1 of the actin monomer, where anionic residues are strongly clustered, whereas the condensed counterion and coion population is small on the rest of the actin surface, where the net charge is weak (even though the numbers of mingled positive and negative charges are large). Nonelectrostatic effects also will likely be important. For example, individual ions are expected have complex interactions with water, especially at high densities. Nevertheless, agreement between the experiment with simple theoretical estimates is striking, which provides strong support for the existence of counterion correlations between condensed polyelectrolytes.

Materials and Methods

Monomeric G-actin [molecular weight (MW) 43,000] was prepared from a lyophilized powder of rabbit skeletal muscle purchased from Cytoskeleton (Denver). The nonpolymerizing G-actin solution contained a 5 mM Tris buffer (pH 8.0), with 0.2 mM CaCl₂, 0.5 mM ATP, 0.2 mM DTT, and 0.01% NaN₃. G-actin (2 mg/ml) was polymerized into F-actin (linear charge density λ_A ∼ −1 e/2.5 Å at pH 7) with the addition of salt (100 mM KCl). Human plasma gelsolin (Cytoskeleton) was used to control the F-actin length. The filaments were then treated with phalloidin (MW 789.2) to prevent actin depolymerization. F-actin gels were ultracentrifuged at 100,000 × g to pellet the filaments. After the removal of the supernatant buffer solution, the F-actin was resuspended to a final concentration of 10 mg/ml using Millipore H₂O (18.2 MΩ). Aqueous solutions of 10 mg/ml F-actin were condensed into close-packed bundles by the addition of divalent salts (Mg²⁺, Sr²⁺, and Ba²⁺) and sealed in 4-mm-diameter amorphous quartz x-ray capillaries (Charles Supper Co., Natick, MA). Measurements on empty capillaries indicate that their contribution to the IXS spectra is negligible.

These experiments were performed at ID-28 at the European Synchrotron Radiation Facility and at 3-ID at the Advanced Photon Source. IXS spectra were collected at an x-ray energy of 21.747 keV using the Si(11,11,11) reflection with an instrumental energy resolution of ≈1.5 meV and a q-resolution of 0.3 Å⁻¹. Collected spectra were normalized to the incident beam intensity. The measured IXS spectra were fitted by convoluting the experimentally determined resolution function R(q, ω) for each analyzer to a model function F(q, ω)

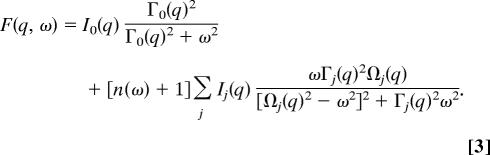The Lorentzian term in Eq. 3 contains the intensity, I₀(q), and width, Γ₀(q) of the central line, and n(ω) denotes the Bose factor. The expression in the sum is the damped harmonic oscillator (DHO) function, with the intensity, I_j(q), the energy, Ω_j(q), and the width, Γ_j(q), of the jth fitted inelastic peak. We used the DHO functions to facilitate the comparison between our measurements and previous IXS work done on liquid water, a crucial point of reference for analyzing our data (21, 28).

Abbreviation

IXS

inelastic x-ray scattering.