Abstract
Strong, short-ranged positional correlations involving counterions can induce a net attractive force between negatively charged strands of DNA and lead to the formation of ion pairs in dilute ionic solutions. However, the long range of the Coulomb interactions impedes the development of a simple local picture. We address this general problem by mapping the properties of a nonuniform system with Coulomb interactions onto those of a simpler system with short-ranged intermolecular interactions in an effective external field that accounts for the averaged effects of appropriately chosen long-ranged and slowly varying components of the Coulomb interactions. The remaining short-ranged components combine with the other molecular core interactions and strongly affect pair correlations in dense or strongly coupled systems. We show that pair correlation functions in the effective short-ranged system closely resemble those in the uniform primitive model of ionic solutions and illustrate the formation of ion pairs and clusters at low densities. The theory accurately describes detailed features of the effective attraction between two equally charged walls at strong coupling and intermediate separations of the walls. Analytical results for the minimal coupling strength needed to get any attraction and for the separation at which the attractive force is a maximum are presented.
Keywords: effective short-ranged model, ion pairing, mean field theory, Poission–Boltzmann
Strong Coulomb interactions in crowded, nonuniform environments have important experimental consequences in a wide variety of biophysical applications ranging from DNA packaging in viruses to transport in ion channels (1–4). These interactions present major challenges to theory and computer simulations not only because of their characteristic long range but also because they can be very strong at short distances. Here, we present a local molecular field (LMF) theory (5) that averages over particular long-ranged and slowly varying components of the Coulomb interactions (6) while still maintaining an accurate description of the short-ranged components. Our model provides a general and physically suggestive theory for strongly coupled Coulomb systems and reduces exactly to the classical Poisson–Boltzmann (PB) approximation for dilute, weakly coupled systems.
We consider a general starting point where a molecule of species i, described by a rigid body frame with center at ri, interacts with an external field, φfi(ri), that comes from fixed charged solutes, or walls, or particular fixed molecules of a mobile species, as illustrated below. The subscript f indicates the source of the field, which we treat as a special fixed species f. The interaction between a pair of molecules of species i and j is assumed to have the general form wij(rij) = ws,ij(rij) + wq,ij(rij), where rij ≡ rj − ri. The ws,ij(rij) denote general (repulsive core and other), short-ranged intermolecular interactions. There are angular coordinates expressing orientations of the body frames that we do not denote explicitly. The wq,ij(rij) arises from Coulomb interactions between rigid charge distributions qi(r − ri) in the body frame of each molecule, so that
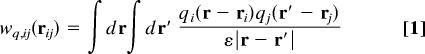 |
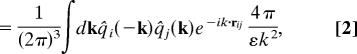 |
where the caret denotes a Fourier transform and we assume that there is a uniform dielectric constant ε everywhere.
To generate uniformly slowly varying components u1,ij of the full wq,ij ≡ wq0,ij + u1,ij that are well suited for LMF averaging, we limit the magnitude of wave vectors making significant contributions to the integration in Eq. 2. To that end, we introduce a Gaussian function parameterized by an important length scale σ that provides a smooth cutoff in k-space and write
The first term on the right has all of the characteristic long-ranged Coulomb divergences as k → 0 but decays very rapidly to zero for kσ ≳ 2. The desired slowly varying components arise when only this term is used in Eq. 2 with an appropriate choice of σ. For localized charge distributions q̂i(k), we expand in a Taylor series about k = 0 and take the lowest order multipole moment (7). This simplified expression defines the u1,ij we consider and thus prescribes a σ-dependent separation of the full intermolecular potentials wij(rij) = ws,ij(rij) + wq,ij(rij) = ws,ij(rij) + wq0,ij(rij) + u1,ij(rij) ≡ u0,ij(rij) + u1,ij(rij) into short- and long-ranged parts.
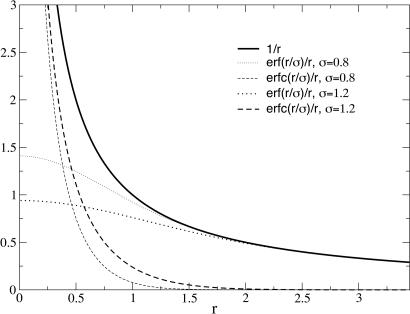
In r-space, Eq. 3 becomes 1/r = erf(r/σ)/r +erfc(r/σ)/r. Here, erf and erfc are the usual error and complementary error functions. The erf(r/σ)/r term is the electrostatic potential from a normalized Gaussian charge distribution with width σ. As shown in Fig. 1, this electrostatic potential remains smooth and slowly varying on the scale of σ while decaying as 1/r at large r. This use of a Gaussian charge distribution is related to the Ewald sum method, which considers periodic images of ion configurations with embedded screening and compensating Gaussian charge distributions. However, our focus is on the separation of the potential itself and not the effects of periodic boundary conditions, and our choice of σ is usually much smaller than that used in Ewald sum methods, which typically is proportional to the width of the simulation cell (8).
Fig. 1.
Separation of the 1/r potential into a slowly varying piece erf(r/σ)/r and the short-ranged remainder erfc(r/σ)/r. Two relevant σ values are shown; a bigger σ generates a more slowly varying long-ranged component.
The short-ranged components u0,ij(rij) define the intermolecular interactions in the special short-ranged “mimic system.” The mimic interactions are composed of the short-ranged parts of the Coulomb interactions wq0,ij ≡ wq,ij − u1,ij and the other short-ranged core interactions ws,ij:
As suggested by Fig. 1, σ sets the range of wq0,ij and thus determines an effective Coulomb core size (6). The external potential from fixed charged solutes or walls φfi(ri) ≡ φ0,fi(ri) + φ1,fi(ri) can similarly be separated into short- and long-ranged parts, as illustrated below.
It is straightforward to arrive at explicit results for u1,ij(r) and φ1,fi(ri). Here, we consider localized charge distributions with a net charge q̄i ≡ ∫drqi(r) or a net dipole moment pi ≡ ∫drrqi(r). If both molecules carry a net charge, we find u1,ij(r) = q̄iq̄jerf(r/σ)/εr. The associated Coulomb core component is wq0,ij = q̄iq̄jerfc(r/σ)/εr. Thus, the results of Fig. 1, scaled by q̄iq̄j/ε, give examples of possible u1,ij and wq0,ij for ionic solution models (6). For a monopole and a dipole, we find u1,ij(r) = q̄i(pj·∇)[erf(r/σ)/εr], and for dipoles we find u1,ij(r) = −(pi·∇)(pj·∇)[erf(r/σ)/εr]. The latter will lead to dipolar mimic systems with short-ranged angular-dependent interactions.
Local Molecular Field Approximation
LMF theory introduces renormalized effective fields φR,fi(ri) that induce nonuniform singlet densities in the mimic system (denoted by the subscript R) that are supposed to equal those induced by φfi(ri) in the full system of interest:
This equation defines a general mapping relating structure in the mimic and full systems. Thermodynamic properties can be determined by integration of these structural relations.
We represent the effective field φR,fi(ri) ≡ φ0,fi(ri) + φR1,fi(ri) as the sum of the known short-ranged part φ0,fi(ri) of the external field in the full system and a renormalized “perturbation component” φR1,fi(ri) that accounts for the averaged effects of the slowly varying interactions, u1,ij. As discussed in detail in refs. 5 and 6, by considering the balance of forces in the full and mimic systems when Eq. 5 holds and by making some physically motivated approximations, we find that φR1,fi is determined up to a constant by the local molecular field equations:
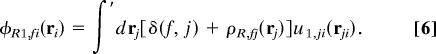 |
Here, the prime on the integral indicates an implicit summation over all species j and an integration over the angles of the body frames. Long-ranged interactions from the fixed species f are accounted for by the δ(f, j) term, which denotes products of δ-functions describing the fixed location and orientation of f.
Note that the average over the slowly varying u1,ji(rji) in Eq. 6 is weighted by ρR,fj(rj), the singlet density for species j (in the effective field of fixed species f but with no explicit reference to species i). This neglect of pair correlations between molecules at rj and ri characterizes a mean field approximation (2), which would in most contexts represent a major source of error. However, a general feature illustrated by Fig. 1 is that, as σ increases, u1,ji becomes progressively more slowly varying at short distances. Thus, we can ensure that all of the u1,ji will slowly vary over the length scales of relevant local pair correlations in the system by choosing σ larger than some state-dependent minimum value σmin. This choice permits a consistent and controlled use of the mean field approximation in computing the average, and we anticipate very accurate results from the LMF theory for any σ ≥ σmin if we properly describe the resulting density in the mimic system (6).
At strong coupling, we argue that σmin should be on the order of a characteristic nearest-neighbor spacing ā. The strong, short-ranged parts of the Coulomb interactions on the scale of ā and below directly affect pair correlations between nearest-neighbor molecules. These correlations will be consistently described in the mimic system if we choose σ = σmin on the order of ā so that there are essentially nearest-neighbor interactions between the effective Coulomb cores, and the averaged effects of the u1,ji from the furthest neighbors are slowly varying on this scale. We illustrate below the utility of these ideas for simple models of ionic solutions at strong coupling.
Size-Asymmetric Primitive Model
A model of great current interest is the size-asymmetric primitive model (SAPM) of ionic solutions, a fluid of oppositely charged hard spheres of different sizes in a uniform dielectric continuum. The different hard sphere diameters crudely account for the different core sizes of real cations and anions, and there is an interesting and not well understood dependence of the critical temperature and critical density in this model as the size or charge ratio is varied (9). We consider in particular the uniform equimolar system studied with Monte Carlo (MC) simulations by Weis and Levesque (WL) (10), with symmetric unit charges e0 = q̄1 = −q̄2 and a diameter ratio d1/d2 = 0.4. Thus, ws,ij(r) = ∞ for r ≤ dij ≡ (di + dj)/2 and is zero otherwise, and wq,ij(r) = q̄iq̄j/εr.
WL characterize the states by two dimensionless parameters: a reduced density ρ* ≡ (N1 + N2)d23V and an effective coupling strength Γ* ≡ lB/d2 (called q*2 in the notation of WL). Here, lB ≡ βe02/ε is the Bjerrum length, the distance at which the interaction energy between two unit charges e0 equals kBT and β ≡ (kBT)−1. The simulations of WL indicate that the critical point occurs at ρ* = 0.195 and Γ* = 15.15. We report results here for two strong coupling states with very different properties: a high-density subcritical liquid state with ρ* = 1.4 and Γ* = 16 and a low-density supercritical vapor state with ρ* = 0.04 and Γ* = 9.
The competition between the Coulomb interactions and the packing arrangements of the embedded hard cores in the SAPM produces elaborate local structures in these strong coupling states as exhibited in the pair correlation functions gij(r), proportional to the density response to an external field φij(r) = wij(r) arising from a fixed ion of type i at the origin. Thus, in LMF theory, even uniform fluid correlation functions are described from a nonuniform point of view. These characteristic features can be very accurately reproduced in the mimic system by using the strong coupling approximation (SCA). The SCA replaces φR,ij(r) by the known strong short-ranged component φ0,ij(r) = u0,ij(r) of the field from fixed ion i. This field corresponds to fixing a mimic particle at the origin, or equivalently, approximating the gij(r) in the uniform ionic system by the g0,ij(r) in the uniform mimic system (6).
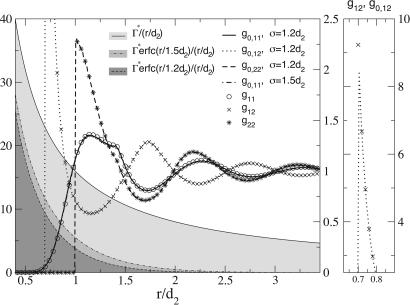
In Fig. 2, we compare correlation functions determined by WL for the high-density state, with ρ* = 1.4 and Γ* = 16, to MC simulations we carried out in the uniform mimic system by using the SCA, with a “molecular-sized” choice of σ = 1.2d2. Simulations of the long-ranged system required careful and costly treatment of periodic boundary conditions using the Ewald sum method, which was not needed for the short-ranged mimic system. Despite the very different range and magnitude of the mimic system interactions, all of the pair correlation functions are strikingly similar to those of the full SAPM. These functions are very different from the profiles of the associated hard sphere mixture with the charges set equal to zero, indicating the crucial importance of including the strong short-ranged parts of the Coulomb interactions wq0,ij in defining the mimic interactions in Eq. 4. Equally good results are found for larger values of σ, as illustrated in Fig. 2, but the good agreement fails for much smaller σ, indicating that σmin is ≈1.2d2 for this state.
Fig. 2.
Dimensionless potentials and pair correlation functions for the SAPM at high density and strong coupling, with d1 = 0.4 and d2 = 1.0, ρ* = 1.4, and Γ* = 16. (Left) The potentials use the left vertical axis. Both the full potential between positive ions (light gray shading) and the mimic interactions for two different values of σ (darker gray shading) are shown. The various pair correlation functions use the right vertical axis. Results for g0,11 using two different values of σ are shown; the differences are barely visible on the scale of the graph. (Right) The high first peak of the cation–anion correlation function.
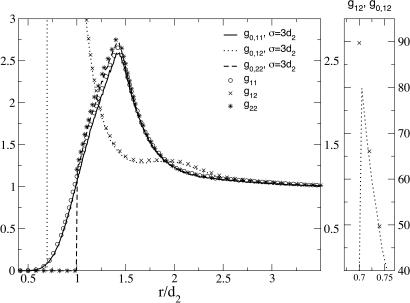
Qualitatively different structures are seen in the low-density vapor state, with ρ* = 0.04 and Γ* = 9, as illustrated in Fig. 3. The simulations of WL show that oppositely charged ions pair together with a typical spacing close to the minimum permitted by the hard core diameters, along with some transient formation of longer chain-like structures. The correlation functions between like-charged pairs exhibit pronounced peaks of essentially the same magnitude at a separation of r = 1.4d2 = d1 + d2. These results indicate the existence of small clusters of ion pairs, with the same peak position and amplitude for both “+−+” or “−+−” configurations at the minimum distance permitted by a linear arrangement of the embedded hard cores. These peaks also illustrate how counterions can induce an effective attraction between like charged objects, as discussed in detail in Charged Walls with Point Counterions. Very good agreement between full and mimic system correlation functions is achieved with a choice of σmin = 3.0d2, consistent with the larger average spacing between dilute ion pairs.
Fig. 3.
Pair correlation functions for the SAPM in the low-density ion pairing regime, with ρ* = 0.04 and Γ* = 9, using the same conventions as in Fig. 2.
The clustering of the ions has probably presented the most severe challenges to theories of ionic systems. It is particularly crucial for the study of critical phenomena and vapor–liquid coexistence (9). The PB approximation and the frequently used hypernetted chain integral equation fail to predict ion clustering; indeed, the hypernetted chain equation has no solution in most of the ion pairing regime (10). In contrast, the mimic system as described by the simple SCA already builds in the most important local features of ion aggregation. This very good agreement strongly suggests that the LMF theory can accurately represent the Coulomb cores that contribute to local correlation functions in more realistic models of ionic systems. Any remaining errors can be attributed mainly to deficiencies in the description of the other short-ranged core interactions, thus permitting the efficient development of more accurate models.
Charged Walls with Point Counterions
The suspension and self-assembly of highly charged polyelectrolytes (macroions) in the presence of mobile counterions (microions) is of great interest in biological systems (1). These systems usually involve charge and size asymmetries much greater than that of the SAPM and are often studied by fixing a certain macroion configuration and computing the microion distribution and resulting forces on the macroions. We discuss here the simplest such model system (11) consisting of uniformly charged infinite hard walls with neutralizing point counterions (and no co-ions) in a uniform dielectric environment. This model is simple enough that exact results in certain limits are known (12), but it still illustrates many fundamental issues that arise from the interplay between long- and short-ranged forces in an explicitly nonuniform environment. It is clear from Size-Asymmetric Primitive Model that the LMF theory can deal with more realistic models for the walls and counterions.
One Charged Wall.
We first consider the case of a single hard wall with a uniform negative charge density qw at the z = 0 plane, where we take the zero of electric potential energy. Without loss of generality we can assume that the counterions have a (unit) charge e0 and express the wall charge density qw ≡ −e0/lw2 in terms of the length lw of the side of a square enclosing that amount of charge. The potential energy φ1w(z) of a counterion at a distance z from the wall is 2πe02z/(εlw2). The Gouy–Chapman length lG is defined as the distance at which this potential equals kBT, i.e., lG ≡ kBTεlw2/(2πe02) = lw2/(2πlB). lG characterizes the effective strength of the attractive wall–counterion interaction, and most counterions will be found near the wall in an effective slit whose width is proportional to lG. Dimensionless combinations of thermodynamic variables in this simple system depend only on a single control parameter ξ ≡ lB/lG = lw2/(2πlG2) (13).
As ξ increases (e.g., by decreasing T at a fixed wall and counterion charge), counterions are driven increasingly close to the wall by the decreasing lG. At strong coupling with ξ ≫ 1 or lG ≪ lw, most counterions are next to the wall and form a (“strongly correlated”) two dimensional (2D) liquid layer (14, 15) with average lateral spacing ā ≃ a2D ≡ lw fixed by local neutrality. There are indeed strong lateral correlations between the counterions in the 2D layer: the coupling strength Γa2D ≡ lB/a2D = ξ1/2/(2π)1/2 ≫ 1 for large ξ. As discussed above, we then expect the effective Coulomb core size σmin to be on the order of a2D = lw. However, because of these repulsive cores, particles cannot stack perpendicular to the wall and still remain near the narrow slit. Thus, the density outside the slit is very low, and there are only weak correlations normal to the wall.
In the opposite weak coupling limit, with ξ ≪ 1 or lG ≫ lw, counterions can take advantage of the larger effective volume of the slit and adopt a more diffuse 3D packing to reduce their repulsive interactions. Crudely assuming all counterions are found within lG of the wall and using a simple cubic lattice to estimate the characteristic counterion spacing in this volume, we now have ā ≃ a3D ≡ (lw2lG)1/3 = lw/(2πξ)1/6. There is weak coupling between the counterions, with Γa3D ≡ lB/a3D = ξ2/3/(2π)1/2 ≪ 1, and here it is natural to take σmin ≃ lB = lw(ξ/2π)1/2 as an estimate for the effective Coulomb core size (6). The crossover to strong coupling with essentially 2D packing and σmin ≃ a2D = lw occurs for ξ on the order of unity, and the 2D packing indeed provides a larger average spacing at large ξ.
Quantitative results take an especially simple form (13) if we introduce a dimensionless rescaled density n(z/lG) ≡ lGlw2ρ(z) that incorporates the anticipated (ξ-dependent) scaling of the profile with lG. Local neutrality requires that ∫0∞dz̃n(z̃) = 1, where z̃ ≡ z/lG. Lengths scaled by lG will generally be indicated by a tilde. Moreover, because of the impulsive δ-function force at a hard wall, there is an exact relation between the pressure and the contact density. This relation yields the well known contact theorem, which implies n(0) = 1 for the contact value of the rescaled density at a single charged hard wall (11).
Exact results (12) for n(z̃) are known in the limit ξ → 0 from a rigorous weak coupling expansion, which gives results agreeing with the PB approximation, nPB(z̃) = 1/(z̃ + 1)2. A different strong coupling expansion gives exact results as ξ → ∞: nSC(z̃) = e−z̃. However, attempts to connect these limits by analyzing higher-order terms in each expansion have had only limited success (13). We now show that the LMF theory provides a simple, accurate, and unified approach for general ξ.
LMF Equation for One Charged Wall.
We can take advantage of planar symmetry and integrate exactly over the lateral degrees of freedom in the long-ranged parts u1,ji(rji) of the counterion–counterion and wall–counterion interactions in Eq. 6. The resulting LMF equation can be written in dimensionless form for z̃1, z̃2 ≥ 0 as
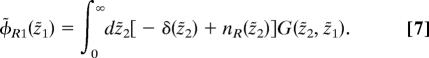 |
Here, φ̃R1(z̃1) ≡ βφR1(z̃1lG), and G(z̃2, z̃1) ≡ −|z̃1 − z̃2|erf(|z̃1 − z̃2|/σ̃) − π−1/2σ̃e−[(z̃1 − z̃2)/σ̃]2 + |z̃2|erf(|z̃2|/σ̃) + π−¿σ̃e−[z̃2/σ̃]2 is the Green’s function associated with a normalized planar Gaussian charge distribution centered at z̃2, with the zero of potential energy at z̃1 = 0.
The −δ(z̃2) term in Eq. 7 accounts for the long-ranged component φ̃1(z̃1) = −G(0, z̃1) of the dimensionless attractive potential φ̃1w(z̃1) = z̃1 between a counterion at z̃1 and the negatively charged wall at z̃2 = 0. The remaining short-ranged part [φ̃0(z̃1) = z̃1 − φ̃1(z̃1)] of the wall potential is
The effective field is then φ̃R(z̃1) = σ̃0(z̃1) + φ̃R1(z̃1), with φ̃R1 given by Eq. 7 for z̃1 ≥ 0 and infinity otherwise.
mPB Approximation.
To solve Eq. 7 self-consistently, we must accurately determine the density nR(z̃) induced by φ̃R(z̃). At weak coupling, neighboring ions interact weakly and the density response to the effective field is proportional to the ideal gas Boltzmann factor exp[−φ̃R(z̃)]. By using this approximation in Eq. 7, we have a closed equation, which we refer to as the mimic PB (mPB) equation. Moreover, we can show (7) for all ξ that a self-consistent solution of the mPB equation will exactly satisfy both neutrality and the contact theorem. The contact theorem implies that the density response takes the simple form nR(z̃) = exp[−φ̃R(z̃)] with our choice of the zero of energy.
Remarkably, however, the mPB approximation also gives accurate results at strong coupling with ξ ≫ 1, where there is an essentially 2D arrangement of the mimic particles in an effective narrow slit. Correlations normal to the wall are very weak, and the Boltzmann factor again can accurately describe the density response to the z-dependent field φ̃R(z̃), as can be verified by more formal arguments (13, 16).
These limits motivate our use of the mPB approximation with nR(z̃) = exp[−φ̃R(z̃)] for all ξ in Eq. 7. The mPB approximation is least justified at intermediate values of ξ, and it breaks down if σ is chosen much larger than σmin so that there would be strong direct interactions between further neighbors in the mimic system. Thus, we provide a smooth interpolation between the known limiting values of σmin in the weak and strong coupling regimes by choosing σ = σ1w ≡ C min(lB, lw), and fix C = 0.60 by finding the best fit to simulations (13) at a moderately strong coupling state with ξ = 40. In this example, it is numerically more convenient to differentiate the resulting mPB equation and solve for the effective force, which vanishes far from the wall, and then get the effective field by integration (J. Rodgers, C. Kaur, Y.-G.C., and J.D.W., unpublished data). An iterative solution is straightforward, and no other simulation data are required.
Results for One Charged Wall.
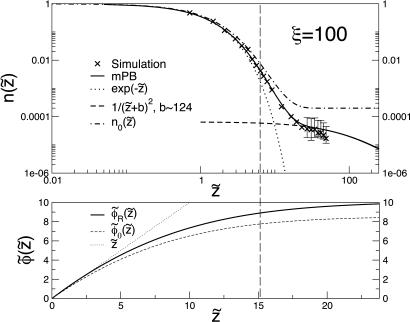
Fig. 4 gives results for nR(z̃) at strong coupling, with ξ = 100. There is excellent agreement between the results of the mPB theory and MC simulations of the long-ranged system carried out by Moreira and Netz (13). The log–log plot emphasizes that nR(z̃) has two characteristic regions. Near the wall, there is an initial exponential decay arising mainly from particles in the 2D layer, which continues until approximately z̃ ≃ σ̃min/2, where the density is very low and there is a crossover to algebraic decay as in the PB solution but with a much larger effective lG. A natural physical interpretation is that the small fraction of counterions outside the 2D layer adopt a diffuse PB-like profile generated by an effective wall whose charge density has been greatly reduced by the charge of the tightly bound counterions. This idea has been suggested before (15), but LMF theory provides a unified description of both limiting regions and the crossover region.
Fig. 4.
Densities and potentials for one charged wall. (Upper) Rescaled counterion density near one planar charged wall calculated by the full mPB theory and by the SCA compared with computer simulation data in ref. 13. (Note the log scales.) The limiting exponential profile provides a good fit only near the wall. We can show analytically (7) that there is a crossover to an algebraic tail of the form 1/(z̃ + b)2 in the mPB theory for z̃ ≃ σ̃1w, as seen in the graph. (Lower) The full dimensionless wall potential z̃ compared with φ̃R(z̃) and φ̃0(z̃) from the mPB theory. (Note the linear scales.) The vertical dashed line in both graphs indicates the value of σ̃1w.
The density near the wall is very accurately described by the even simpler SCA, where φ̃R(z̃) is approximated by φ̃0(z̃). The resulting density n0(z̃) ≡ exp[−φ̃0(z̃)] can be written down immediately from Eq. 8. As shown in Fig. 4, both φ̃0(z̃)] and φ̃R(z̃) closely resemble the full potential z̃1 near the wall for z̃1 ≲ σ̃min/2. But n0(z̃) cannot describe the PB-like region at large z̃ as does the full mPB theory, and it does not obey the neutrality condition. This example highlights both the strengths and weaknesses of the SCA. When properly used to describe only short-ranged correlations at strong coupling, very accurate results can be found.
Two Charged Walls.
We now briefly consider two equally charged hard walls forming a real slit with width d, with neutralizing point counterions in between. At strong coupling and intermediate widths, the counterions can induce an effective attractive force between the walls. Such effective attraction between like charged objects may have important experimental consequences, and it has generated a great deal of theoretical interest (1–4).
Ref. 11 gives an exact expression for the dimensionless (osmotic) pressure P̃ ≡ βlGlw2P arising from neutralizing point counterions confined between charged hard walls at z = 0 and z = d:
Thus, if the rescaled contact density n(0) is less than (greater than) 1, there is an effective attractive (repulsive) force on the walls. As d → ∞, we recover the one-wall results discussed earlier, where P = 0 and n(0) = 1.
Because the total force on a counterion from equally charged walls exactly cancels for all z and all d, we now have φ̃2w(z̃) = 0 for 0 ≤ z̃ ≤ d̃. As in the one-wall case, it is useful to divide φ̃2w into a short-ranged part,
given by a sum of short-ranged, single-wall terms (indicated by the superscript 1w) defined in Eq. 8, and the remainder. We take the zero of energy on the left wall at z̃ = 0. The effective field φ̃R(z̃) = φ̃02w(z̃; d̃) + φ̃R1(z̃) is determined from the two-wall LMF equation. This equation closely resembles Eq. 7, except that the integration is from 0 to d̃ and there is an additional −δ(d̃ − z̃2) term in the integrand, accounting for interactions with the second wall at z = d. Again we use the mPB approximation nR(z̃) = A exp[−φ̃R(z̃)] and fix the constant A (which equals the contact density with our choice of the zero of energy) by using the neutrality condition ∫0d̃ dz̃nR(z̃) = 2. The pressure is then given by Eq. 9.
The resulting two-wall mPB equation reduces exactly to an integrated form of the PB equation if σ = 0. The latter has an analytic solution and predicts a repulsive force for all d and ξ (2, 13). The mPB theory also predicts a weak repulsive force at strong coupling for sufficiently large d, arising from weak repulsions between counterions in the dilute PB-like tails of the one-wall profiles discussed above. In contrast, at strong coupling and sufficiently small d, core repulsions make it unfavorable for particles in the narrow slit to stack perpendicular to the walls, and counterions will be forced into a single 2D layer with characteristic lateral spacing ã ≃ lw/ fixed by neutrality. To interpolate between this limit and weak coupling, we choose σ = σ2w ≡ C min(lB, lw/) and take the same value of C = 0.60 that we used for the one-wall theory. Because σ̃min = Cξ at small ξ, the PB approximation is consistent only as ξ → 0. The mPB theory naturally introduces a crucial new length scale σmin that allows for a change in the functional form of nR(z̃) as ξ increases.
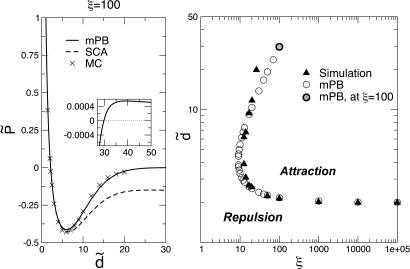
Fig. 5 compares numerical results of mPB theory (J. Rodgers, C. Kaur, Y.-G.C., and J.D.W., unpublished data) to simulation data (13) for strong coupling states. The left graph shows that, for ξ = 100, there is very good agreement between the mPB theory and computer simulations for all widths at which simulations can be performed. As shown in Fig. 5 Left Inset, the mPB theory predicts that, at still larger widths, there is a weak repulsive force between the walls. This reentrant behavior is illustrated more generally in Fig. 5 Right, which also shows that a minimal coupling strength of ξ ≥ ξc ≃ 12 is needed to get any attraction (13).
Fig. 5.
Effective interaction between two equally charged walls. (Left) Dimensionless pressure at strong coupling between two equally charged hard walls as a function of width d̃ from ref. 13 compared with predictions from the full mPB theory and the SCA. (Inset) The mPB theory predicts a weak repulsive force at larger widths. (Right) Regions with repulsive or attractive force between two charged walls as a function of width and coupling strength as determined by MC simulations and the mPB theory.
Fig. 5 Left also shows results from the analytic SCA, where n(z̃) is approximated by n0(z̃) ≡ A0 exp[−φ̃02w(z̃; d̃)], with A0 similarly determined by neutrality. At strong coupling and large d, φ̃02w(z̃; d̃) has a deep attractive well near each wall essentially identical to that found near a single wall. However, at small enough d, the wells from the individual φ̃01w terms in Eq. 10 begin to overlap, and their depth decreases. As d → 0, φ̃02w(z̃; d̃) vanishes for all z̃ in the slit. The SCA fails at large widths, just as it did far from the wall in the one-wall case, and the reentrant behavior is completely missed. However, the SCA is very accurate at smaller widths, and it gives a good description of the location and magnitude of the maximum attractive force.
The formation of the single 2D layer at sufficiently small widths d̃ < σ̃2w plays a key role in producing a strong attractive force. Because of the absence of correlations normal to the walls, the density profile will be relatively constant across the slit. We can use the SCA to describe several features analytically in this regime. The minimum pressure P̃* should occur near the largest width d̃* ≡ 2z̃*m for which the single 2D layer remains stable, defined by σ̃02w(z̃*m; d̃*) = 1. At larger widths, there will be higher contact densities as separate 2D layers at each wall begin to form, and the nearly constant profiles at smaller widths will have higher contact densities by normalization. Expanding φ̃02w(z̃; d̃) in a Taylor series, we have φ̃02w(z̃; d̃) = 2z̃(d̃ − z̃)/(π1/2σ̃2w) to lowest order; higher order terms are negligible for d̃ ≪ σ̃2w. This expansion implies d̃* = (2π1/2σ̃2w)1/2 ≃ 1.94ξ1/4 using our expression for σ̃2w. Similarly evaluating A0, the minimum pressure is P̃* ≃ 3.717/d̃* − 1. When P̃* = 0, there can be no attractive forces, which determines the minimal coupling strength ξc ≃ 13.48 and associated critical spacing d̃*c ≃ 3.717 needed to get any attraction. Finally, for ξ ≫ ξc and d̃ = 2, we see φ̃02w(z̃; d̃) ≪ 1; therefore, the constant profile n0(z̃) = 2/d̃ is very accurate. Eq. 9 then implies that, at very strong coupling, the transition from strong repulsive forces to strong attractive forces occurs near d̃ = 2, as shown in refs. 12 and 13. All these predictions are in very good agreement with numerical solutions of the mPB theory (and with simulations of the full and mimic systems, where available) for all strong coupling states, as illustrated in Fig. 5.
Discussion
In strong coupling regimes the short-ranged parts of the Coulomb interactions efficiently compete with the other short-ranged molecular core interactions and strongly influence pair correlations between neighboring molecules. In LMF theory, the choice of σmin determines the strength and range of these important Coulomb core interactions. These core interactions play a key role in inducing an effective attraction between like-charged objects at strong coupling, as illustrated in Fig. 3 for the correlation functions between like-charged ions in the SAPM and in Fig. 5 for the osmotic pressure on two like-charged walls. In both cases, strong, short-ranged forces mainly involving single counterions or a single counterion layer can mediate a strong effective attraction. Such phenomena have traditionally been interpreted as illustrating the “breakdown of mean field theory” and the need for new and more sophisticated approaches. But LMF theory using the simple SCA, in which only the short-ranged parts of the Coulomb interactions are taken into account, provides very accurate results at small and moderate separations. At weak coupling and for long-wavelength correlations, the averaged effects of the long-ranged interactions as determined by the LMF equation are needed as well (6).
LMF theory provides a general conceptual framework that connects and clarifies previous work on systems with both short- and long-ranged interactions. It has been used to describe liquid–vapor interfaces and wetting and drying transitions for simple fluids (5) and hydrophobic interactions in water (17). LMF theory suggests simplified simulation models for general Coulomb systems based on the mimic system that do not require special treatment of periodic boundary conditions. The short-ranged intermolecular interactions in the Coulomb mimic system are reminiscent of the truncated interactions used in reaction field methods (18), but it was not very clear in those approaches how to choose an appropriate cutoff and how to treat nonuniform environments. The determination of σmin and the effective field in LMF theory provides a way to deal with both problems. We believe that the LMF picture will prove useful not only in formal theory but also for qualitative reasoning and in detailed simulations of biophysical systems.
Acknowledgments
We thank Michael Fisher, Charanbir Kaur, and Jocelyn Rodgers for many helpful remarks and J. J. Weis for sending us simulation data for the SAPM correlation functions. This work was supported by National Science Foundation Grants CHE01-11104 and CHE05-17818.
Abbreviations
- LMF
local molecular field
- PB
Poisson–Boltzmann
- SAPM
size-asymmetric primitive model
- WL
Weis and Levesque
- MC
Monte Carlo
- SCA
strong coupling approximation
- mPB
mimic PB.
Footnotes
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Gelbart W. M., Bruinsma R. F., Pincus P. A., Parsegian V. A. Phys. Today. 2000;53:38–44. [Google Scholar]
- 2.Levin Y. Rep. Prog. Phys. 2002;65:1577–1632. [Google Scholar]
- 3.Grosberg A. Y., Nguyen T. T., Shklovskii B. I. Rev. Mod. Phys. 2002;74:329–345. [Google Scholar]
- 4.Boroudjerdi H., Kim Y.-W., Naji A., Netz R. R., Schlagberger X., Serr A. Phys. Rep. 2005;416:129–199. [Google Scholar]
- 5.Weeks J. D. Annu. Rev. Phys. Chem. 2002;53:533–562. doi: 10.1146/annurev.physchem.53.100201.133929. [DOI] [PubMed] [Google Scholar]
- 6.Chen Y.-G., Kaur C., Weeks J. D. J. Phys. Chem. B. 2004;108:19874–19884. [Google Scholar]
- 7.Chen Y.-G. Ph.D. thesis. College Park: Univ. of Maryland; 2004. [Google Scholar]
- 8.Frenkel D., Smit B. Understanding Molecular Simulations. San Diego: Academic; 2002. [Google Scholar]
- 9.Kim Y. C., Fisher M. E., Panagiotopoulos A. Z. Phys. Rev. Lett. 2005;95:195703. doi: 10.1103/PhysRevLett.95.195703. [DOI] [PubMed] [Google Scholar]
- 10.Weis J. J., Levesque D. Chem. Phys. Lett. 2001;336:523–528. [Google Scholar]
- 11.Wennerstrom H., Jonsson B., Linse P. J. Chem. Phys. 1982;76:4665–4670. [Google Scholar]
- 12.Moreira A. G., Netz R. R. Europhys. Lett. 2000;52:705–711. [Google Scholar]
- 13.Moreira A. G., Netz R. R. Eur. Phys. J. E. 2002;8:33–58. doi: 10.1140/epje/i2001-10091-9. [DOI] [PubMed] [Google Scholar]
- 14.Rouzina I., Bloomfield V. A. J. Phys. Chem. 1996;100:9977–9989. [Google Scholar]
- 15.Shklovskii B. I. Phys. Rev. E. 1999;60:5802–5811. doi: 10.1103/physreve.60.5802. [DOI] [PubMed] [Google Scholar]
- 16.Chen Y.-G., Weeks J. D. J. Phys. Chem. B. 2005;109:6892–6901. doi: 10.1021/jp0446884. [DOI] [PubMed] [Google Scholar]
- 17.Lum K., Chandler D., Weeks J. D. J. Phys. Chem. B. 1999;103:4570–4577. [Google Scholar]
- 18.Hummer G., Soumpasis D. M., Neumann M. J. Phys.: Condens. Matter. 1994;6:A141–144. [Google Scholar]