Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations

Abstract

By representing the high-resolution crystal structures of a number of enzymes using the elastic network model, it has been shown that only a few low-frequency normal modes are needed to describe the large-scale domain movements that are triggered by ligand binding. Here we explore a link between the nearly invariant nature of the modes that describe functional dynamics at the mesoscopic level and the large evolutionary sequence variations at the residue level. By using a structural perturbation method (SPM), which probes the residue-specific response to perturbations (or mutations), we identify a sparse network of strongly conserved residues that transmit allosteric signals in three structurally unrelated biological nanomachines, namely, DNA polymerase, myosin motor, and the Escherichia coli chaperonin. Based on the response of every mode to perturbations, which are generated by interchanging specific sequence pairs in a multiple sequence alignment, we show that the functionally relevant low-frequency modes are most robust to sequence variations. Our work shows that robustness of dynamical modes at the mesoscopic level is encoded in the structure through a sparse network of residues that transmit allosteric signals.

A common theme in the function of many biological nanomachines is that they undergo large-scale domain movements in response to binding of ligands or other biomolecules. DNA polymerases are well studied examples in which such large conformational changes have been described using crystal structures and biophysical studies (1, 2). The global structure of polymerases is described by using the hand metaphor (3). The first step in the function involves the binding of the duplex DNA to the unliganded polymerases, which triggers the closing of the thumb domain around the DNA. Subsequent binding of dNTP to the binary complex results in the rotation of the fingers from the open conformation to the closed state. Similarly, large-scale conformational changes, induced by ATP binding and hydrolysis, are involved in the directed movements of myosins on actin filaments (4). In another class of nanomachines, binding of ATP to the equatorial domain of the Escherichia coli chaperonin GroEL results in a downward movement of the intermediate domain, which results in the locking of the ATP-binding sites (5). Upon binding of GroES, the apical domain swings upward and simultaneously twists, thus doubling the volume of the cavity as compared with the unliganded state. Such large-scale conformational changes are linked to the function of GroEL (6).

To obtain insights into these universally prevalent motions, normal modes analysis (NMA) of the elastic network model (ENM) representations of large protein complexes have been used to describe ligand-induced conformational changes. A number of studies on vastly different enzymes have shown that the domain movements are dominated by one or a few normal modes (7–17). To understand how the allosteric transitions are executed with high fidelity, it is important to explore the relationship between the global dynamics at the macromolecular level and the amino acid variations at the microscopic level.

In the context of ENM, we introduce a previously undescribed method to assess the robustness of all of the normal modes to the variations in model parameters (force constants). Such variations naturally arise from differences in sequences in homologous proteins. We propose that evolution should preferentially conserve strongly those contacts that are critical to the functional dynamics, while leaving those functionally unimportant contacts susceptible to unconstrained mutations. Therefore, we hypothesize that the functionally relevant normal modes computed from the NMA of the ENM are robust to the sequence variations.

Recently, we showed, using the structural perturbation method (SPM), that in a number of polymerases a sparse network of physically connected residues that transmit allosteric signals through the functionally relevant modes are also strongly conserved (18). In this work, we establish, by probing the variations in the response of all of the normal modes to changes in the interactions that are expressed in forms of perturbations involving contacts, that the low-frequency modes are robust to large sequence variations across a given family. Applications to three biological nanomachines, namely, DNA polymerase, myosin II, and the E. coli chaperonin to sequence variations. Moreover, other subdominant modes show that robustness of the dynamically relevant modes is not only an indicator of the functional relevance but also may be encoded in the structures of biological nanomachines.

Results

To test our hypothesis, we consider the conformational changes in DNA polymerase, myosin II, and the E. coli chaperonin GroEL. The open/closed transitions in polymerases are well described by just one normal mode (8). Similarly, only one or two modes account for the large conformational changes in myosin II upon ATP binding (13). The ligand-induced changes in the structure of GroEL analyzed by ENM (19) also showed the dominance of only the low-frequency modes. We first evaluated the relevance of each normal mode to the observed functional conformational changes. Then, we quantitatively assessed the robustness of each mode to sequence variations using two complementary methods (contact-based and δω-based; see Methods). The final step involved cross-examining the above plots of relevance-vs.-mode and robustness-vs.-mode to assess possible correlations between them.

Thermus aquaticus (Taq) DNA Polymerase I.

The transition from the open form [Protein Data Bank (PDB) ID code 2KTQ) to the closed form (PDB ID code 3KTQ) results in the closing of the finger-palm crevice (20). The large conformational change can be deconvoluted into two rotations successively affecting different parts of the fingers domain. First, a 6° rigid-body rotation of helices N, O, O1, and O2 results in a partial closing of the crevice (see figure 4 of ref. 20 for definition of secondary structures). This motion is amplified by a second rotation of 40°, affecting only the N and O helices.

Fig. 4.

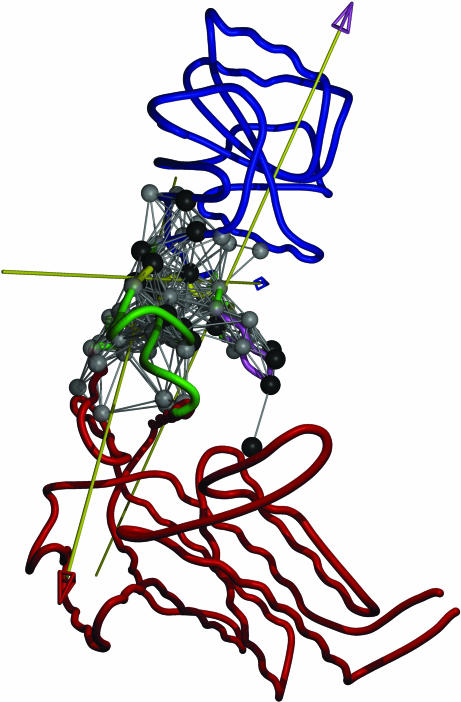
Dynamical domain partitions for conformational changes described by the most robust modes, 1 (a) and 2 (b), of Dictyostelium myosin. For the meaning of the relative domain motions given by the arrows, see the legend to Fig. 1. The hot-spot residues of modes 1 and 2 are shown in space-filled circles colored in gray. Residues in black have the same meaning as in Fig. 2 (for residue numbers, see Table 3, which is published as supporting information on the PNAS web site).

Higher modes are involved in the open/closed transition.

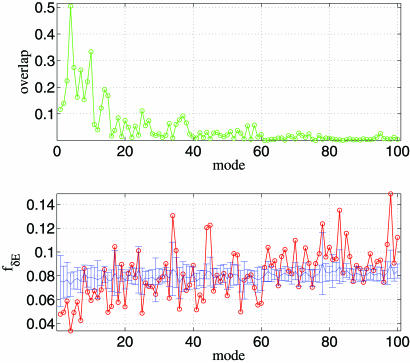
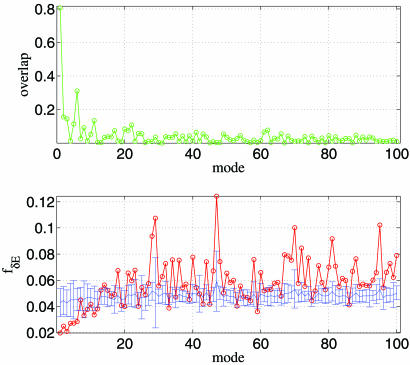
The NMA for the open-form structure 2KTQ yields a number of low-frequency normal modes that describe the observed conformational changes. The open/closed transition is dominated by mode 4 (overlap = 0.50; see ref. 8) that involves the fingers domain bending toward the active site. Several subdominant modes (modes 5, 7, and 10; see Fig. 1Upper) also supplement mode 4 in describing the fine details of the observed structural changes (see below). As the mode number increases, the overlap value decreases rapidly (Fig. 1 Upper).

Fig. 1.

ENM and sequence analysis for Taq DNA polymerase’s open/closed transition (2KTQ → 3KTQ). (Upper) Overlap between each mode and the observed conformational changes for the lowest 100 modes. (Lower) The mode-dependent robustness (f_δΕ) computed by the contact-based SPM for the lowest 100 modes, where the red curve (with circles) is for the original MSA and the blue curve (with error bars) represents the average (and standard deviation) of f_δΕ distribution computed for 100 randomly permuted MSA.

Dominant modes are most robust to sequence variations.

We used contact-based SPM (see Methods) to calculate f_δE for the 100 lowest modes. The relevance of a mode to the open/closed transition increases as f_δE decreases. The values of f_δE for the various modes show that the global minimum occurs for mode 4. There are other subdominant modes (modes 7 and 10) that also have relatively low f_δE values (Fig. 1). The minimum in f_δE together with negative Z score (Z = −3.98) for mode 4 establishes it to be the most dominant in the open/closed transition as well as the most robust to sequence variations. There is a weak trend of increasing f_δE as mode number increases that also is accompanied by decaying statistical significance (Z score less negative). This finding is consistent with the observation that the lowest modes are more functionally relevant than higher modes (see Table 1).

Table 1.

Dominant modes in domain movements and their robustness to sequence variations

Proteins	PDB pairs*	Mode†	Overlap‡	δω-based analysis§		Contact-based analysis¶
				fδE′‖	z-score**	fδE‖	Z score**
TaqDNA pol I	2KTQ → 3KTQ	4	0.50	0.0811	−5.210	0.0338	−3.979
Dictyostelium myosin II	1VON → 1MMA	1	0.56	0.0414	−3.460	0.0161	−2.597
		2	0.39	0.0453	−2.954	0.0125	−2.667
E. coli GroEL	1AON_A → 1GRL	1	0.81	0.0485	−3.315	0.0198	−2.159

*The two structures represent the beginning and end states in the allosteric transitions.

^†Dominant mode(s) in the specific transition.

^‡Overlap describes the extent to which the mode describes the domain movements. A value close to unity implies that a single mode suffices to represent a given allosteric transition. A value >0.5 is highly significant.

^§δω-based SPM to probe robustness of modes to perturbations (see Supporting Text).

^¶SPM in which contact energy is varied to probe robustness of modes to perturbations (see Methods).

^‖A dimensionless score (f_δE or f_δE′) to assess the robustness of a mode (see Eq. 9).

**Statistical significance of f_δE or f_δE′ (see Eq. 11).

To ensure that our results do not depend on the exact implementation of the SPM, we also used a variation of the method introduced in ref. 18. The dependence of f_δE′ on the mode number also exhibits a minimum for mode 4 (see Fig. 7 and Supporting Text, which are published as supporting information on the PNAS web site). The associated Z score is large and negative (Z = −5.21). Just as in Fig. 1 Upper, we also find modes 7 and 10 to be robust, which make subdominant but significant contribution to the open/closed transition.

The two independent methods reveal a significant correlation between mode relevance and its robustness. Both pinpoint mode 4 as the most robust mode to sequence variations. The contact-based SPM confirms that specific contacts are “conserved,” which implies that for functional reasons only those mutations that preserve the contacts are tolerated. This finding is in accord with a number of experiments that have probed the fidelity of DNA polymerases to specific mutations (see below and Supporting Text). The strong conservation and robustness of the dominant and a few subdominant modes may be a requirement for the high-fidelity replication function of DNA polymerase I.

Dynamical domain partition on each mode reveals the specific structures involved in the open/closed transition.

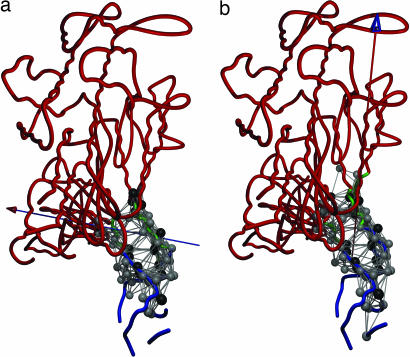
For mode 4 (Fig. 2a), the fingers domain is comprised of three smaller dynamical domains. The top one (T, in yellow) includes the O1/O2 helices, the middle one (M, in cyan) sits in between, and the bottom one (B, in purple) is at the interface with the palm domain (in blue). The O, N helices are in the hinge/bending region (green). Therefore, the movement of the fingers domain consists of three coupled hinge motions. The first corresponds to twisting of T relative to the M, the second represents twisting of B relative to T, and the third describes the bending of B relative to the palm domain (see three arrows in Fig. 2a). The hinge/bending residues (green) are distributed across the fingers domain, which is in accordance with the finding of an extensive network of eight clusters of dynamically important residues (18). Besides the fingers motions that open/close the cleft, mode 4 also describes a hinge motion of the thumb domain (red), which may, however, be locked by DNA binding.

Fig. 2.

Dynamical domain partitions, performed by using dyndom, for conformational changes described by the most robust modes, 4 (a), 7 (b), and 10 (c), of Taq DNA polymerase. The hinge regions are colored in green. The rotation axis for each pairwise interdomain motion is shown as an axis with an arrowhead; the color of the axis stem is set to be the same as the domain fixed for the structural alignment, whereas the color of the arrowhead is set to be the color of the moving domain. The hot-spot residues are shown in space-filled circles colored in gray. Residues in black have been experimentally identified to affect function (for residue numbers, see Table 2, which is published as supporting information on the PNAS web site).

For mode 7 (Fig. 2b), the top half of the fingers (including the N/O/O1/O2 helices; T, colored in yellow) forms a dynamical domain, whereas the bottom half is fused with the palm (blue) as one dynamical domain. Although mode 7 describes a bending motion of T, the bending region is smaller and more localized than in mode 4, which is consistent with its accessory role in the open/closed transition. In mode 10 (Fig. 2c), a localized twisting of O1 and O2 helices (red) is seen. This mode has the second-highest overlap with the measured conformational changes. This finding supports the importance of internal flexibility of fingers in the open/closed transition.

Therefore, a detailed examination of the above robust modes suggests that they involve different hinge motions of the fingers domain, although they share some bending regions. Although the contributions from the subdominant modes to the open/closed transition are smaller than mode 4, they are still functionally important. Several modes are needed to describe it with accuracy. The importance of the subdominant modes is further supported by the observed strong robustness to evolutionary sequence variations.

Dictyostelium Myosin II.

Myosin II belongs to a family of motor proteins that are involved in the transport of cargo by coordinating ATP hydrolysis and movement along actin filaments. The enzyme senses and responds to the binding of actin and the presence or absence of a γ-phosphate and transmitting this information along a pathway of increasingly larger conformational changes that ultimately results in a force-generating event (21). The available crystal structures and cryo-EM results of myosins capture their conformations in several structural states, namely, transition, near-rigor, detached (22), and rigor-like states (23–25). The transition state mimics the prepower-stroke state compatible with ATP hydrolysis before binding to actin. The near-rigor state is believed to be a weak-binding state that occurs shortly after detaching from actin. The detached state is structurally similar to the near-rigor state with unwound SH1 helix and unconstrained converter/lever arm (22). The newly solved crystal structures of rigor-like state (23, 24) resemble the strong-binding state that occurs at the end of a power stroke.

Two low-frequency modes dominate the ligand-induced conformational changes.

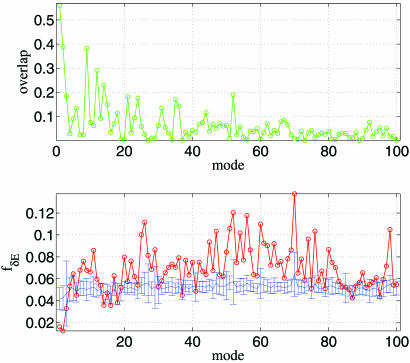
We study the conformational changes from the transition state (PDB ID code 1VOM) to the near-rigor state (PDB ID code 1MMA). The NMA for the transition-state structure (PDB ID code 1VOM) yields a spectrum of low-frequency normal modes. The transition (1VOM → 1MMA) is dominated by mode 1 (overlap = 0.558), which describes a swinging motion of the converter relative to the rest of the structure. We also found several subdominant modes (such as mode 2 with overlap = 0.388; see Fig. 3Upper). As the mode number increases, the overlap value decreases, although there are a few minor peaks (Fig. 3).

Fig. 3.

ENM and sequence analysis for Dictyostelium myosin (1VOM → 1MMA). The legend for the two graphs is the same as that for Fig. 1.

Modes 1 and 2 are most robust to sequence variations.

The plot of contact-based robustness f_δE (Fig. 3 Lower) shows two minima at modes 2 and 1. The value of f_δE of modes 1 and 2 are both statistically significant (Z = −2.60 for mode 1 and −2.67 for mode 2). However, for mode numbers ≥ 3, the computed measure of robustness loses statistical significance (Z > −1). This finding shows that the lowest two modes are statistically robust (the only two modes with Z < −2 among the lowest 10 modes). The plot of δω-based robustness f_δE′ (see Fig. 8, which is published as supporting information on the PNAS web site) also has two minima at modes 1 and 2. It has similar peaks and dips as the contact-based f_δE. Thus, both methods show that only the dominant modes in the conformational changes are invariant to sequence variations.

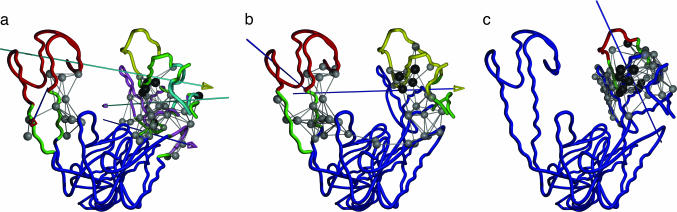
The domain partition for modes 1 and 2 (Fig. 4) reveals two dynamical domains. One is the converter (blue), and the other is the rest of the motor domain (red). Mode 1 describes a closure motion of the converter, whereas mode 2 describes a twisting motion. The hot-spot residues of modes 1 and 2 (Fig. 4) are mostly distributed over the relay helix, SH1 helix, and the converter. They partially overlap with the bending region (green) identified by dyndom (26). These hinge residues are critical in mediating signals that ultimately lead to force generation. Preservation of the function requires that these residues be highly conserved.

E. coli GroEL Chaperonin.

Chaperonins are multisubunit protein assemblies comprising of two rings that are stacked back-to-back. In the ATP-hydrolyzed state [PDB ID code 1AON (5)], asymmetric intermediates of GroEL are formed with the cochaperonin GroES and nucleotides bound only to one of the seven-subunit rings (the cis ring). The structure of the GroEL–GroES–(ADP)₇ complex reveals large en bloc movements of the cis ring’s intermediate and apical domains. Elevation and twist of the apical domains double the volume of the central cavity that results in the burial of the hydrophobic peptide-binding residues at the interface between GroEL subunits and GroES. The large-scale domain movement results in a predominantly hydrophilic cavity that is conducive to protein folding (6).

A single mode dominates the ligand-induced conformational changes.

We focus on the conformational change for a single subunit from the ADP+GROES state to the apo state (1AON_A → 1GRL). The NMA for the ADP+GROES state structure (PDB ID code 1AON_A) yields a spectrum of low-frequency normal modes. The conformational change in the transition 1AON_A → 1GRL is dominated by mode 1 (overlap = 0.806) that describes multiple hinge motions of the apical, intermediate, and equatorial domains (19). As the mode number increases, the overlap value decays rapidly, although there are occasional minor peaks (Fig. 5Upper).

Fig. 5.

ENM and sequence analysis for E. coli GroEL (1AON_A → 1GRL). See the legend to Fig. 1 for a description.

Low-frequency modes are robust to sequence variations.

The measure of contact-based robustness f_δE (Fig. 5 Lower) has a global minimum at mode 1. The minimum value of f_δE for mode 1 is statistically significant (Z = −2.16). There are several other modes (modes 2 and 3) with fairly low f_δE. Almost all of the modes above 10 have statistically insignificant robustness (Z > −1). We found similar results in the plot of δω-based robustness f_δE′ as a function of mode (see Fig. 9, which is published as supporting information on the PNAS web site). There is a global minimum at mode 1 (Z = −3.32). Most of the modes lack statistically significant robustness except for a few among the lowest 10. Therefore, the results from the above two assessments of robustness support our hypothesis that functionally relevant modes are most robust to sequence variations.

Based on the dynamical domain partition for mode 1 (Fig. 6), four domains are found. Three of them correspond to the apical (A, blue), intermediate (I, yellow), and equatorial domain (E, red), respectively, and the fourth (purple) corresponds to a loop at the interface between A and I. For mode 1, the hot-spot residues (Fig. 6) are clustered around domain I and the A–I and E–I interfaces where many functionally important and highly conserved residues are distributed.

Fig. 6.

Dynamical domain partitions for conformational changes described by the most robust mode 1 of E. coli GroEL. The description of the arrows indicating the relative motions of domains is the same as that given in the legend to Fig. 2. The hot-spot residues are shown in space-filled circles colored in gray. Residues in black have the same meaning as in Fig. 2 (for residue numbers, see Table 4, which is published as supporting information on the PNAS web site).

Identification of Network of Residues (“Wiring Diagram”) That Transmit Allosteric Signals.

The SPM also can be used to identify the network of distantly connected residues that cooperatively orchestrate the large-scale domain movements. By assessing the degree of response to site-specific perturbations, the importance of a given residue in facilitating allosteric transitions can be gauged. By using the SPM, which can be implemented by the contact-based analysis or the δω-based method (see Supporting Text), we have identified the mechanically “hot” residues for the three nanomachines (see Figs. 2, 4, and 6).

Taq DNA polymerase I.

For the TaqDNA polymerase I several residues that span the fingers/palm domains are involved in the three modes that are required in the domain movements. Among the hot-spot residues, I614 (27) and F667 (28) were shown to be critical for fidelity of DNA replication (see Supporting Text for detailed comparisons with experiments). The network of allostery transmitting residues are explicitly shown in Fig. 2.

Dictyostelium myosin II.

Many of the residues identified by SPM have been shown to be functionally relevant in myosin II. The amino acid sequence similarity between Dictyostelium myosin II and human β-cardiac myosin have facilitated the study of the structural consequences of those hypertrophic cardiomyopathy (HCM) mutations in human β-cardiac myosin heavy chain (see the mutation database at www.angis.org.au/Databases/Heart). Five HCM mutations are mapped to residues E492, F506, R695, A699, and F745 in Dictyostelium myosin II (see Supporting Text for details). The residues, which have been found to be relevant for myosin allostery, form a sparse network (Fig. 4).

E. coli GroEL chaperonin.

Our analysis correctly identifies Y360 and D361 as being functionally relevant. Mutant Y360E has reduced ATPase activity, whereas D361K lacks the ability to bind to the cochaperonin GroES (29). Supporting Text contains comparisons between the predictions of the SPM and experiments. The wiring diagram for allostery is shown in Fig. 6.

Discussion and Conclusion

The ability to transmit signals over long distances so that specific function can be carried out is the hallmark of allostery. In this work, we have established a precise connection between functionally relevant motions that describe allosteric transitions in three structurally unrelated biological nanomachines and their invariance to large sequence changes. The nature of these modes is encoded at the structural level and is evolutionarily conserved.

We also used the SPM to identify a network of residues in DNA polymerase, myosin motor, and the E. coli chaperonin that are responsible for allostery. Remarkably, not only do we find that residues in this network are strongly conserved but also that the network is sparsely connected (30, 31).

Methods

Multiple Sequence Alignment (MSA).

We used psi-blast (www.ncbi.nlm.nih.gov/blast) to obtain homologous sequences (search nr database with E cutoff = 10, j = 1). Subsequently, we used clustalw (www.ebi.ac.uk/clustalw) to align the sequences. We retained only sequences with >30% sequence identity to the query sequence. To ensure the generality of the results, we also performed psi-blast against other protein databases (such as SwissProt).

ENM.

By using the C^α atomic coordinates of a protein’s native structure, we built an ENM (32, 33) using a harmonic potential to account for pairwise interactions between all of the C^α atoms that are within a cutoff distance (R_C = 10 Å). The energy in the elastic network representation is

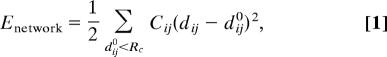where C_ij is the force constant for contact (i, j), which is taken to be a constant C for all contacts; d_ij is the distance between the C_α atoms i and j; and d_ij⁰ is the corresponding distance as given in the crystal structure. For the Hamiltonian in Eq. 1, we performed NMA. The eigenvectors of the lowest-frequency normal modes were used to compute the overlaps (generalized cosines) with the conformational changes between two states with known structures (13). Our calculations were unaffected when R_C was varied in the range 10 Å ≤ R_C ≤ 15 Å.

Assessing the Dynamical Importance of a Spatial Contact.

The dynamical importance of a specific contact (i, j) for a mode M was assessed by using the elastic energy

in the contact (i, j) if the ENM was displaced along the direction given by the eigenvector of mode M (18). The perturbation energy E_ij^M is related to δω_i^M (18) by

The residues with high δω_i^M (top 10% by ranking) are dynamically critical (18) to the ENM motion of mode M and are the “hot-spot residues.”

SPM.

The basic premise of SPM is that the response of the modes of the ENM to local perturbations can be used to discern the network of functionally relevant residues. The local perturbation in the force constant (δC_ij) for contact (i, j) was modeled by using the MSA of homologous sequences. The contact-dependent changes in the spring constant were taken into account by using a statistical interaction term between residues i and j that explicitly depends on their local environment. By using evolutionary information in the sequences, we used a probability-based modeling to compute δC_ij.

For two residue pairs λ₁ = (R_iα, R_jα) and λ₂ = (R_iβ, R_jβ) that form the contact (i, j), where α, β are indices for any two homologous sequences in the MSA, we define the residue-pair similarity score using

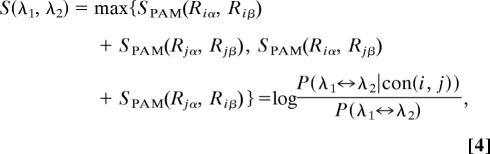where P(λ₁ ↔ λ₂|con(i, j)) is the conditional probability of occurrence of residues pair substitution λ₁ ↔ λ₂ provided contact (i, j) is conserved. By “conserved” we mean that the context-dependent statistical interaction is maintained upon λ₁ ↔ λ₂ substitution. Here we allowed the swapping of residues between (i, j) (see the second term in Eq. 4), because that should not alter the physical pairwise interaction between them. We use the PAM250 substitution matrix to evaluate residue similarity. We assume that the commonly observed residue substitutions in homologous proteins preserve residue–residue contact interactions within the protein native structure.

The variation of the statistical interaction for contact (i, j) due to the residue pair substitution λ₁ ↔ λ₂ was taken to be proportional to the probability of not conserving the contact (i, j) if the substitution λ₁ ↔ λ₂ was allowed

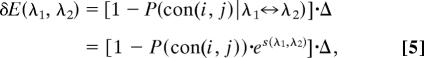where Δ is a constant that yields the maximal variation of interaction.

For two randomly generated pairs (λ₁, λ₂) (for each pair λ₁ or λ₂, both residues are randomly chosen from all 20 types of amino acids), we computed the average S_rand = 〈S(λ₁, λ₂)〉_rand and set

By using Eq. 5 and Bayes theorem, we get

Here we set P_rand = 0.5. The variation of the force constant for contact (i, j) is

where the average is over all (λ₁, λ₂) for the given pair (i, j) from the MSA at column i and j.

The robustness of a mode to sequence variations was assessed by using the fractional variation of the distortional energy E

If f_δE is small, then the specific mode is robust to sequence variations. For the contact-based analysis

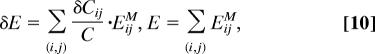where δC_ij is computed in Eq. 8 and E_ij^M is defined in Eq. 2.

Statistical Significance of the Mode Robustness.

To evaluate the statistical significance of the mode robustness, we calculated the distribution of f_δE for randomly generated sequence–structure alignments. We performed 100 random permutations of the one-to-one mapping between the positions (columns), the MSA, and the positions (nodes) in the ENM. This procedure eliminates all correlations encoded in the original mapping of the protein structure. For each mode, we compute f_δE for every random permutation and obtain a distribution of f_δE, from which we can compute both its average 〈f_δE〉_rand and standard deviation σ_rand. The Z score for f_δE is

which is used to quantitatively assess the statistical significance of f_δE. The more negative Z is, the more statistically significant is f_δE. A mode is robust if f_δE is small and if Z is as negative as possible.

Dynamical Domains Partition.

To visualize the collective conformational changes described by each low-frequency normal mode (see Figs. 2, 4, and 6), we used the dynamical domains partition analysis based on analyzing the interdomain conformational changes described by the eigenvector of each mode. This analysis was performed by a computational tool called dyndom (26).

Abbreviations

ENM

elastic network model

MSA

multiple sequence alignment

NMA

normal modes analysis

PDB

Protein Data Bank

SPM

structural perturbation method

Taq

Thermus aquaticus.