Abstract
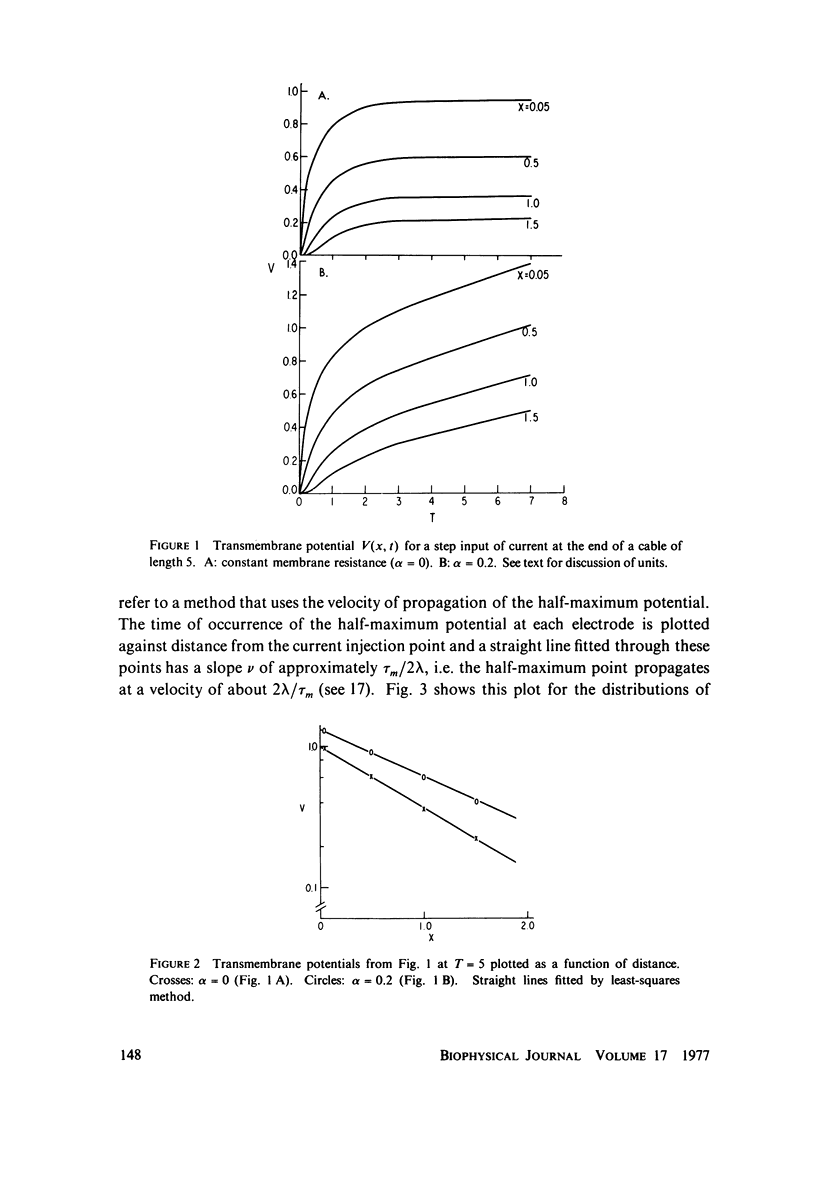
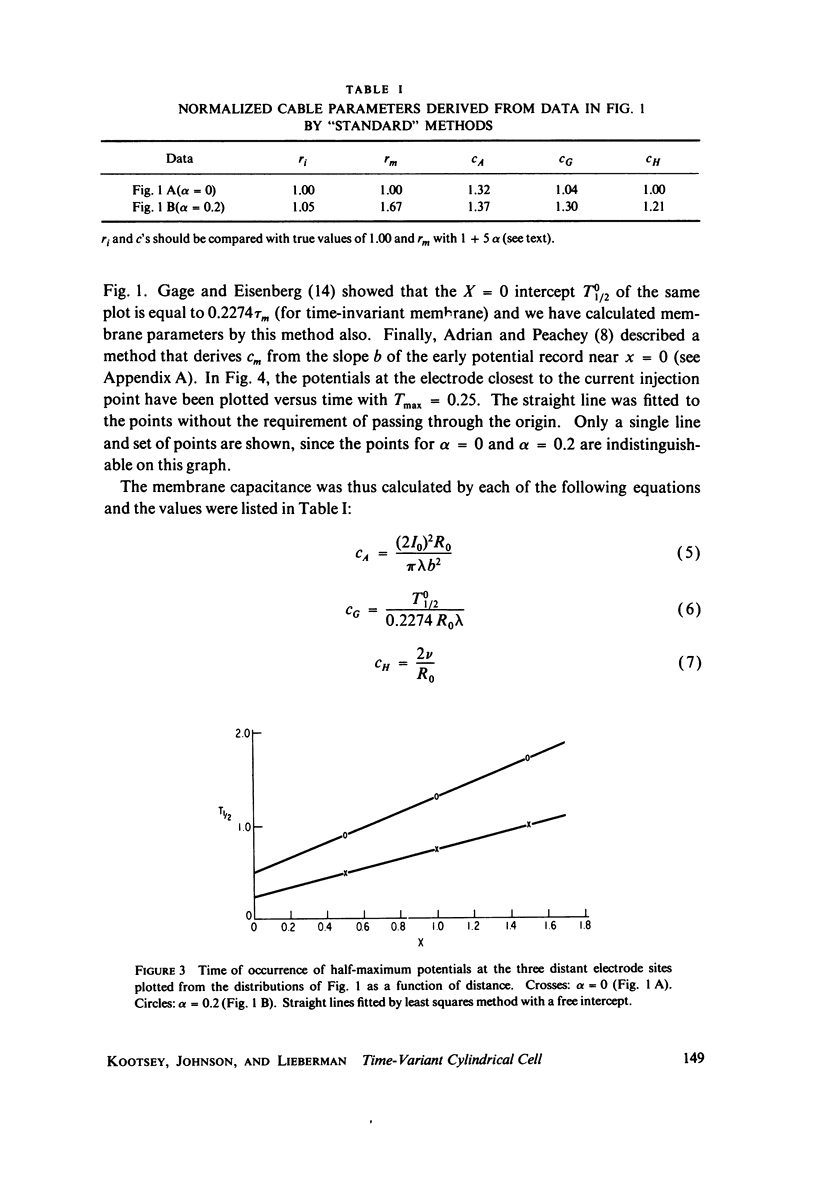
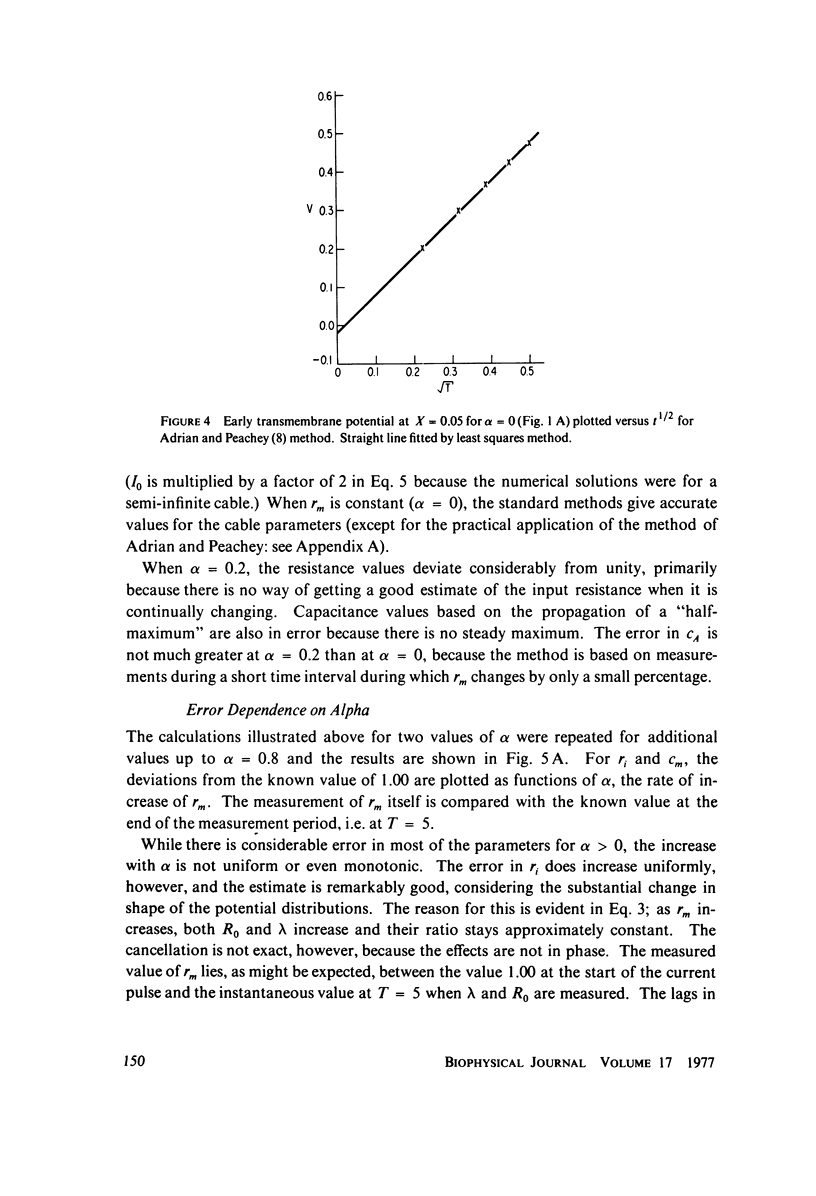
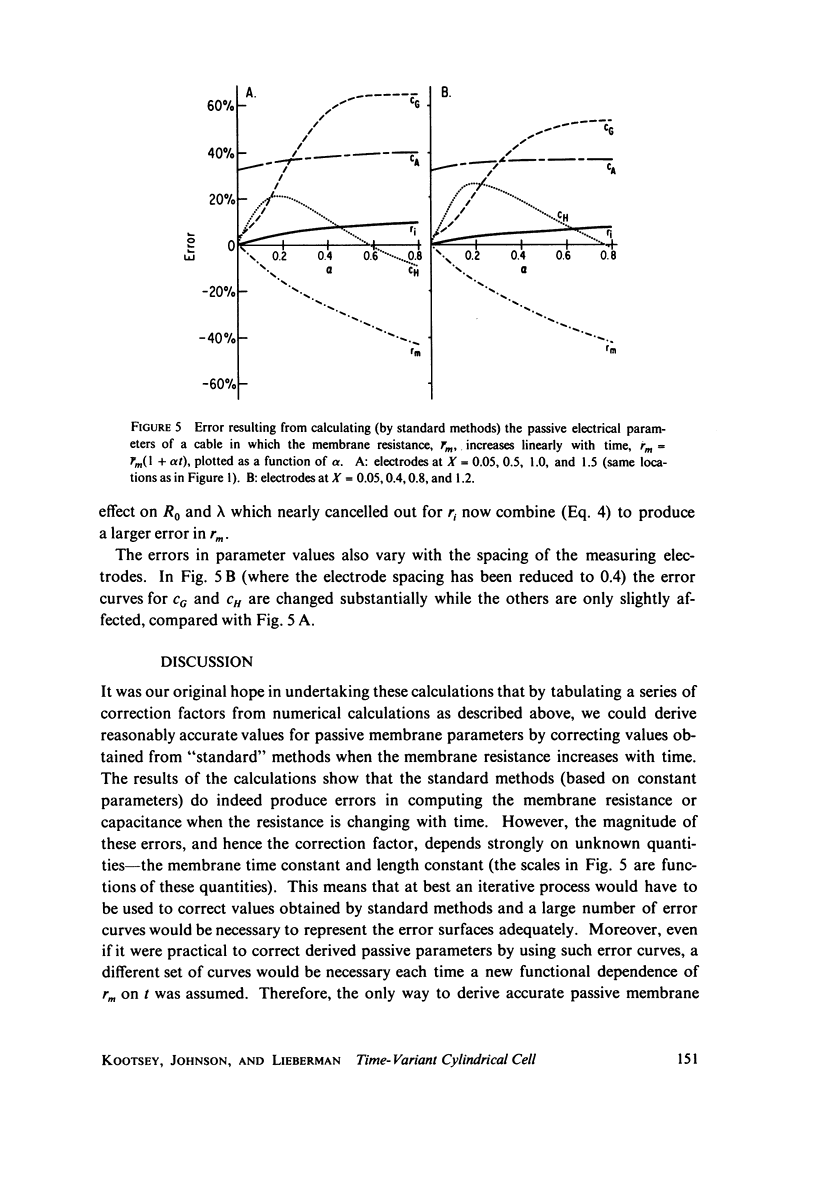
The passive electrical properties of a cable can be measured by injecting a step of current at a point and fitting the resulting potentials at several positions along the cable with analytic solutions of the cable equation. An error analysis is presented for this method (which is based on constant membrane resistance) when the membrane resistance is not constant, but increases linearly with time. The increase of rm produces a "creep" in the membrane potential at long times, as observed in cardiac, skeletal, and smooth muscle. The partial differential equation describing the time-varying cable was solved numberically for a step of current and these "data" were fit by standard constant-resistance methods. Comparing the resulting parameter values with the known true values, we suggest that a correction of the standard methods is not satisfactory for resistance changes of the kind observed; instead, the cable equation must be solved again for the particular form of rm(t). The practical implementation of a method by Adrian and Peachey for measuring the membrane capacitance and an approximate method for estimating the rate-of-change of membrane resistance are discussed in appendices.
Full text
PDF




Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Adrian R. H., Peachey L. D. The membrane capacity of frog twitch and slow muscle fibres. J Physiol. 1965 Nov;181(2):324–336. doi: 10.1113/jphysiol.1965.sp007764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonke F. I. Electronic spread in the sinoatrial node of the rabbit heart. Pflugers Arch. 1973 Mar 5;339(1):17–23. doi: 10.1007/BF00586978. [DOI] [PubMed] [Google Scholar]
- Bonke F. I. Passive electrical properties of atrial fibers of the rabbit heart. Pflugers Arch. 1973 Mar 5;339(1):1–15. doi: 10.1007/BF00586977. [DOI] [PubMed] [Google Scholar]
- CORABOEUF E., WEIDMANN S. Temperature effects on the electrical activity of Purkinje fibres. Helv Physiol Pharmacol Acta. 1954;12(1):32–41. [PubMed] [Google Scholar]
- FALK G., FATT P. LINEAR ELECTRICAL PROPERTIES OF STRIATED MUSCLE FIBRES OBSERVED WITH INTRACELLULAR ELECTRODES. Proc R Soc Lond B Biol Sci. 1964 Apr 14;160:69–123. doi: 10.1098/rspb.1964.0030. [DOI] [PubMed] [Google Scholar]
- Gage P. W., Eisenberg R. S. Capacitance of the surface and transverse tubular membrane of frog sartorius muscle fibers. J Gen Physiol. 1969 Mar;53(3):265–278. doi: 10.1085/jgp.53.3.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman M., Sawanobori T., Kootsey J. M., Johnson E. A. A synthetic strand of cardiac muscle: its passive electrical properties. J Gen Physiol. 1975 Apr;65(4):527–550. doi: 10.1085/jgp.65.4.527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakamoto Y., Goto M. A study of the membrane constants in the dog myocardium. Jpn J Physiol. 1970 Feb 15;20(1):30–41. doi: 10.2170/jjphysiol.20.30. [DOI] [PubMed] [Google Scholar]
- Sevcik C., Narahashi T. Electrical properties and excitation-contraction coupling in skeletal muscle treated with ethylene glycol. J Gen Physiol. 1972 Aug;60(2):221–236. doi: 10.1085/jgp.60.2.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomita T. Electrical responses of smooth muscle to external stimulation in hypertonic solution. J Physiol. 1966 Mar;183(2):450–468. doi: 10.1113/jphysiol.1966.sp007876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WEIDMANN S. The electrical constants of Purkinje fibres. J Physiol. 1952 Nov;118(3):348–360. doi: 10.1113/jphysiol.1952.sp004799. [DOI] [PMC free article] [PubMed] [Google Scholar]


