Quantitative Assessment of Coronary Artery Plaque Vulnerability by High-Resolution Magnetic Resonance Imaging and Computational Biomechanics: A Pilot Study ex Vivo

Abstract

The risk of atherosclerotic plaque disruption is thought to be closely related to plaque composition and rupture triggers such as external mechanical forces. The purpose of this study was to integrate MR imaging and computational techniques for the quantification of plaque vulnerability with morphologic data and biomechanical stress/strain distributions that were all based on high-resolution MR images of coronary artery plaque specimens ex vivo. Twenty-two coronary artery plaque specimens were selectively collected from 10 cadavers. Multislice T₂-weighted spin echo images were acquired with a resolution of 100 × 100 μm². Histopathological images were used as the gold standard for the identification of plaque components and vulnerability. Plaque components were classified on MR images, and the stress/strain components were calculated with a two-dimensional computational model with fluid–structure interactions. As expected, vulnerable plaques appeared to result from a large lipid pool, a thin fibrous cap, and some critical stress/strain conditions. An empiric vulnerability marker was derived and was closely related to the vulnerability score that was determined through pathologic examination. Noninvasive quantification of the MR contrast and mechanical properties of plaque may provide a comprehensive biomarker for the assessment of vulnerability of atherosclerotic plaques.

Acute coronary syndrome accounts for over 1 million deaths in the United States (1). Plaque rupture/erosion and fissures are the primary causes of acute coronary syndrome and may occur without any warning. This acute process that culminates with plaque rupture is complicated and the precise mechanism remains hypothetical. Largely derived from the observations of autopsy tissues by Davis and Thomas (2), the widely held concept of the general characteristics of a ruptured plaque is the formation of a large, soft, lipid-rich necrotic core (LRNC). This core occupies approximately 40% of the plaque area and is covered by a thin fibrous cap (<65 μm), which is densely infiltrated by inflammation cells such as macrophages (3). Rupture of this thin cap and then the subsequent thrombus formation are thought to be the most important mechanisms underlying acute syndromes. However, rupture of plaque depends not only on its cap thickness, but also on biomechanical factors such as hemodynamic shear stress, transient compression, external compression, and bent plaque edges due to the propagating pulse wave (4,5).

Our hypothesis is that comprehensive characterization of plaque geometry, components, and critical stress/strain distribution would greatly enhance the capability to assess the vulnerability of atherosclerotic lesions. Many imaging modalities have been applied to determine the characterization of plaques, including ultrafast CT (6), positron emission tomography (7), and MRI (8,9). However, only elastographic intravascular ultrasound, an invasive imaging modality, can provide information simultaneously about both plaque components and strain distribution (10). Compared with other imaging methods, MRI has the greatest potential for noninvasive and comprehensive assessments of atherosclerotic plaques, not only on luminal stenosis and plaque burden, but also on differentiation of plaque components such as the LRNC, the fibrous cap, intraplaque thrombosis, and calcification (Ca) (11,12). Although sophisticated computational models have already been built from MR image data to calculate shear stress in the carotid artery (13–15), comprehensive evaluation of plaque components and mechanical features by MRI remains virtually undocumented in the relatively small coronary arteries.

Although there were several biomechanical studies performed on the histologic images of ex vivo coronary artery specimens, these images were often distorted in geometry during the process of specimen preparation. Because biomechanical computation relies on the geometry of the plaque and vessel, the distortion may alter the final results. The aim of this study was to initialize and integrate MRI contrasts and computational methods to assess both plaque components and stress/strain distributions. The study was performed ex vivo on coronary artery specimens before histologic imaging, and findings were compared with the vulnerability of the plaques, as defined through pathologic examination. Furthermore, the plaque vulnerability was quantified empirically on the basis of the observations in one group of specimens, and its effectiveness was determined with a different group of plaque specimens.

METHODS

Coronary Artery Specimens

Twenty-two coronary artery specimens were selectively collected from 10 cadavers (6 males, 64 ± 16 years old). Five subjects died of coronary artery disease (CAD) (59 ± 22 years old), and 5 others died of other causes (non-CAD) (69 ± 8 years old). The criterion for selection of these specimens was the relatively large size of atherosclerotic plaques by visual inspection. All specimens were fixed in a 10% buffered formalin solution, placed in a polyethylene tube, and stored at 4°C within 12 h after removal from the heart. MRI was performed within 24 h at room temperature.

MRI

All imaging procedures were performed on a 3-T Siemens Allegra clinical system (Siemens Medical Solutions, Malvern, PA, USA). A single-loop volume coil (Nova Medical, Inc, Wilmington, MA, USA) with a diameter of 3.5 cm was used as a transmitter and receiver. Three-dimensional gradient-echo images with a slice thickness of 0.5 mm were first obtained to define the orientation of the coronary artery vessel axis. Six data sets of multislice two-dimensional spin echo images were acquired perpendicular to the vessel axis with a resolution of 100 × 100 μm². These data sets differed in echo time (TE) values (20, 30, 40, 50, 60, and 70 ms) but used the same pulse repetition time (TR) of 1000 ms. This TR is similar to the same parameter used in the in vivo studies (12,16). Other imaging parameters were as follows: signal average number = 4, field of view = 25 × 19 mm², matrix = 256 × 192, and slice thickness = 1 mm.

Histology

After MR scanning, the specimens were submitted to a histology laboratory for physical slicing and mounting. For the distance between MRI slices to be approximated, transverse sections with 10-μm thickness were cut 1 mm apart. These paraffin-embedded sections were dyed in hematoxylin– eosin (H&E) and elastic van Gieson (EVG) stains. The calcified areas of the specimens were decalcified with ethylenediamine tetraacetic acid extraction before the stains were used. This preparation of tissue made it possible to section the tissue for microscopic analysis and reduction of artifacts in the histologic slides. MR images and histologic images were matched on the basis of the distance between each slice and one edge of the vessel along the vessel axis. With the use of landmarks such as lumen shape and calcification locations, the photographs of the histologic slides were then sized and rotated with Adobe Photoshop 6.0 (Adobe Systems, Inc., San Jose, CA, USA) to approximately match the size and orientation of MR images.

An experienced pathologist (JES) examined the matched histologic images (matched with slice specificity to maximize correlation between MR images and histologic images) to determine major plaque components: Ca, the LRNC, and fibrous tissue (FT), including medium. The areas of major plaque components were also traced and digitized on the photomicrographs of histologic images with homemade software. In addition, pathologic evaluation of diseased vessels included a qualitative analysis of structural features known to correlate with vulnerability to plaque rupture. Overall plaque vulnerability was graded with a composite score on a scale of 0 to 4 (Table 1). This scale mainly pertains to plaques with lipids and calcification for the purpose of biomechanical analysis. Also in Table 1 is a list of the American Heart Association’s classifications of atherosclerotic lesions (types I–IV) that approximately corresponded to the scale. Both classifications in two columns are not exactly equal. For instance, large lipid core and thin cap thickness in the score of 4 are not defined in type IV, since our focus in this study was on the plaque with lipid and calcification. The pathologic finding was regarded as the gold standard for comparison with MR and biomechanical results.

Table 1.

Vulnerability Scores and Their Coordinating AHA Classifications

Score	Definition	Specification	AHA classification (included)
0	Very stable	Normal or slight intimal thickening	I (enough atherogenic lipoprotein, adaptive artery intimal thickening)
1	Stable	Moderate intimal thickening with the involvement of some, but minimal extracellular lipid (<10%); little or no calcification and inflammation	II (fatty streak), III (preatheroma)
2	Slightly unstable	Small core of extracellular lipid (<30% of plaque size); Ca may be present but thick fibrous cap (>200 μm); little or no inflammation at plaque shoulders	IV, Vb, and Vc
3	Moderately unstable	Moderate size (30–40% of plaque size) of lipid core, moderately thin fibrous cap (65–200 μm); moderate intraplaque hemorrhage; moderate inflammation at plaque shoulders	Va
4	Highly unstable	Large lipid core (>40%); thin fibrous cap (<65 μm); thrombus, intraplaque hemorrhage, or surface defect; extensive inflammation at plaque shoulders; evidence of previous plaque rupture	VI

MR Image Segmentation

Segmentation software was developed in our laboratory to identify major plaque components in MR plaque images with different T₂-weighted MR images that matched histologic images by visual inspection. The software was written in MATLAB 6.5.1 release 132 (The MathWorks, Natick, MA, USA). The choice of these three image contrasts was based on our observations and other reported results (8,17). First, a few boundary points were identified manually on a T₂-weighted image to represent the vertices of a polygon, which were connected in a piecewise linear fashion. Designating the points inside the polygon “1” and those outside “0” created a mask by which all images were cropped. The classification of plaque components was performed with a K-means algorithm. For the use of this algorithm, a feature vector was first defined as x = [x₁(i,j),x₂(i,j), … x_N(i,j)]. The symbols x₁,… x_N were the intensities of images at location (i,j), and N refers to different image contrasts available (N = 3 in this study). After K-initial cluster centers were manually selected, the cluster memberships were updated with a hard decision distance metric, followed by updating cluster centers. This procedure was repeated until a minimal change of the following objective function was achieved,

$$J(x,c)=\sum _{i=1}^p\sum _{j=1}^K\left|\right| x_i-c_j |{|}^2,$$ [1]

where p is the image size, K is the number of tissue classes, x is the feature vector at the ith pixel, and c is the jth class cluster center (18). An optional postprocessing step was also used to refine clustering results with morphologic filtering. This procedure consisted of two steps: (1) smoothing contours and eliminating small islands and sharp peaks and (2) fusing narrow breaks and removing small holes (19).

All clusters were assigned different colors for visual comparison with histopathological images. Vessel lumen and major plaque components (medium, LRNC, FT, and Ca) were consistently identified on computed images (>5 pixels in diameter). Usually, FT showed hyperintensity on T₂-weighted images, the LRNC’s signal intensity was slightly hypointense, and Ca had the lowest signal intensity. If the apparent shape and location of clusters differed from histologic images, the initial clusters were adjusted until a match was found. Finally, the area of each cluster was obtained automatically.

Biomechanical Analysis

Computational models with fluid–structure interactions for blood flow in arteries have been well developed by Tang et al. (20). These models quantify pressure and stenosis severity conditions under which critical flow conditions and artery compression may occur in a stenotic artery. Mechanical analysis based on MR images of carotid arteries with plaques has been reported in detail recently by Tang et al. (21). Briefly, after the classification of plaque components with different colors, images were digitized and smoothed before they were used in the numerical computation. The software package VTK (Kitware, Clifton Park, NY, USA) (22) was used to read MRI data to find regions for different components, which were based on the MRI segmentations. Relatively large-size structures were selected for numerical simulation. Materials for the artery wall and the various plaque components were assumed to be hyperelastic, isotropic, incompressible, and homogeneous. Moreover, blood flow was assumed to be laminar, Newtonian, viscous, and incompressible. The Navier–Stokes equation and the arbitrary Lagrangian–Eulerian formulation were used as the governing equations in our mechanical computations (23). The modified Mooney–Rivlin model was used to describe the nonlinear material properties of the vessel wall. The input pulsating blood pressure conditions were set with 90 and 150 mm Hg as the diastolic and systolic pressures, respectively. Incremental steps were taken so that the artery was pressurized gradually to specified conditions (plaque shape and locations). The strain energy function for the modified Mooney–Rivlin model is given by (24)

$$W=c_1(I_1-3)+c_2(I_2-3)+D_1[exp(D_2(I_1-3))-1],$$ [2]

where I₁ and I₂ are the first and second strain invariants and c_i and D_i are material constants chosen to match experimental measurements.

Material properties in this study were chosen from other literature, including Beattie et al. (25), Huang et al. (26), and our prior study (27). The coupled fluid and structure model was solved with the commercial finite-element package ADINA (ADINA R & D, Inc., Watertown, MA, USA), and stress/strain within the plaques was given. Nonlinear incremental iterative procedures were used to handle fluid–structure interactions. The governing finite element equations for both solid and fluid models were solved with either the Newton–Raphson iteration method or a sparse solver, depending on the total size of problem. Proper mesh was chosen to fit the shapes of each component, the vessel, and the fluid domain. Finer mesh was used for the thin plaque cap and components with sharp angles to get better resolution and handle high stress concentration behaviors. We defined stress as the symbol τ and strain as σ. All components of the stress/strain tensors were examined to find maximum stretch and compression conditions. These included τ_xx/σ_xx, τ_xy/σ_xy, τ_yy/σ_yy, and τ_P1 (the so-called maximum principal stress). Figure 1 shows the vectors of these parameters. Figure 2 shows the schematic diagram of procedures in the mechanical analysis.

FIG. 1.

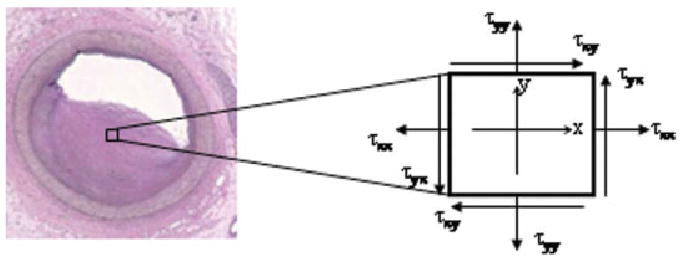
Definition of stress vectors in 1 pixel. Similar definition applies for the strain vectors. The stresses of τ_xy and τ_yx are often called shear stresses, and τ_xx and τ_yy are called normal stresses.

FIG. 2.

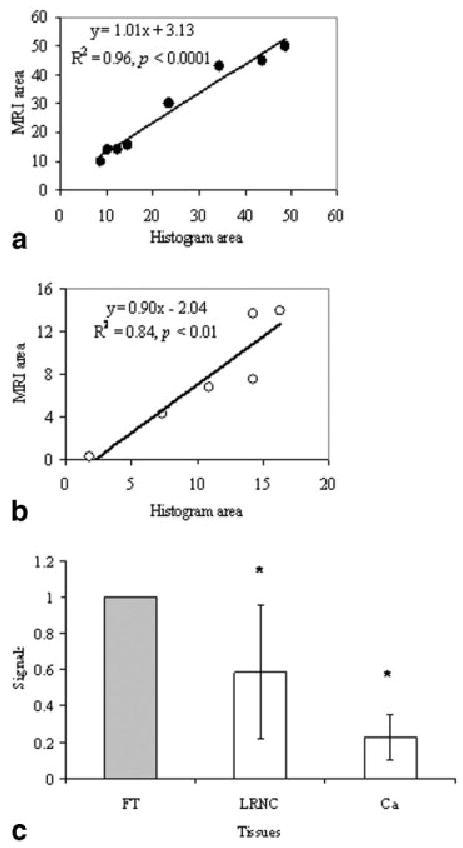
Correlations of areas of plaque tissue components measured on MR images and histopathological images (a) (LRNC) and (b) (Ca). The normalized contrasts of plaque tissue components on MR images are shown in (c).

Image Analysis and Quantification of Plaque Vulnerability

One MR image slice presenting the maximum plaque area was selected from each specimen. The areas of the LRNC and Ca components were correlated with the areas measured on histopathological images. These areas were then normalized to the total plaque areas on respective images. The stenosis of the plaque, the ratio of LRNC area to the entire plaque area (LAR), and the fibrous cap thickness (defined as the minimal distance from the edge of the LRNC to the lumen and labeled LcH [lipid-cap thickness] in millimeters) were obtained from classified color images of selected slices. In addition, averaged signal intensity of the LRNC and calcification were normalized to the averaged signal intensity of fibrous tissue to account for the difference in the transmission and receiver gains of inter-scans. The MR morphologic and mechanical data were compared with repeated-measure methods of analysis of variance.

To exam the feasibility of quantification of plaque vulnerability, we divided the selected 22 slices into two groups. The first group consisted of 14 slices; 2 slices had scores of 0 and 3 and 3 slices had scores of 1, 2, and 4. This group served as the learning set used to explore the relationship between the vulnerability scores and the morphologic and mechanical parameters. An empiric vulnerability biomarker was proposed on the basis of this relationship. The remaining 8 slices formed a test group and were used to examine the effectiveness of this biomarker. This second group had 4 slices with a vulnerability score of 1, 2 slices with a score of 3, and 1 slice with scores of 2 and 4.

RESULTS

There were no ruptured plaques in any cadavers. The pathologic examination revealed that all plaques were primarily composed of fibrocalcific and necrotic tissues. The correlation and linearity were excellent between areas segmented on MR images and histopathological images (Fig. 2a and b). The R² was 0.96 and 0.84 for the LRNC and Ca plaque components, respectively, whereas the slope values were 1.01 and 0.9. These values indicated good correlations and unity of areas segmented with MR and pathologic images. Figure 2c shows the comparison of tissue contrast relative to the fibrous tissue and shows a large variation in LRNC contrast but a consistent low signal in calcification. Both tissues can be well differentiated from fibrous tissue (P < 0.02). The two slices with a vulnerability score of 0 show no lipid deposit. No correlation was found between vulnerability scores and CAD/non-CAD category. In morphologic data sets measured by MRI, the lipid area showed strong trends with the vulnerability score determined by pathohistology: a larger lipid area led to more vulnerable status (P < 0.05). Plaque vulnerability scores also strongly depended on the thickness of fibrous cap (LcH) (i.e., a thinner fibrous cap was likely to result in much more vulnerable plaques).

Different tensor components of stress and strain showed different distribution patterns in the same plaque. Maximum stress and strain components were often located adjacent to the lipid pools close to the lumens or at the shoulders of the plaques but not necessarily in the same spots (Fig. 3). Compared with the location of the maximum values of τ_P1, the location of the maximum values of τ_xx and σ_xx showed the same location in 14 (64%) of 22 cases, followed by approximately 12 (54%) of 22 in the maps of τ_yy and σ_yy and 6 (27%) of 22 in τ_xy and σ_xy. These results may be explained partially by different material properties. For instance, a lipid pool is soft, which often results in high strain and low stress values.

FIG. 3.

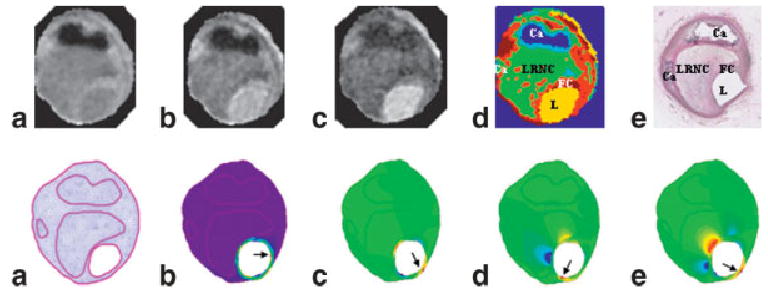
Illustration of the procedure for the creation of biomechanical maps using MR images of coronary atherosclerotic plaque specimens. Top: a– c are MR images obtained with TE of 20, 40, and 70 ms; d: a segmented color map that can be compared with the histologic image (e). Bottom: a mesh map (a) can be created based on the MR segmented image; biomechanical maps are shown in the following order: τ_P1 (b), τ_xy (c), σ_xx (d), and σ_xy (e). The arrows point to the pixels with maximum values. Notice that maximum values are often located close to the thinnest cap or shoulder of the plaque. The locations of these maximum pixels are also different in these maps.

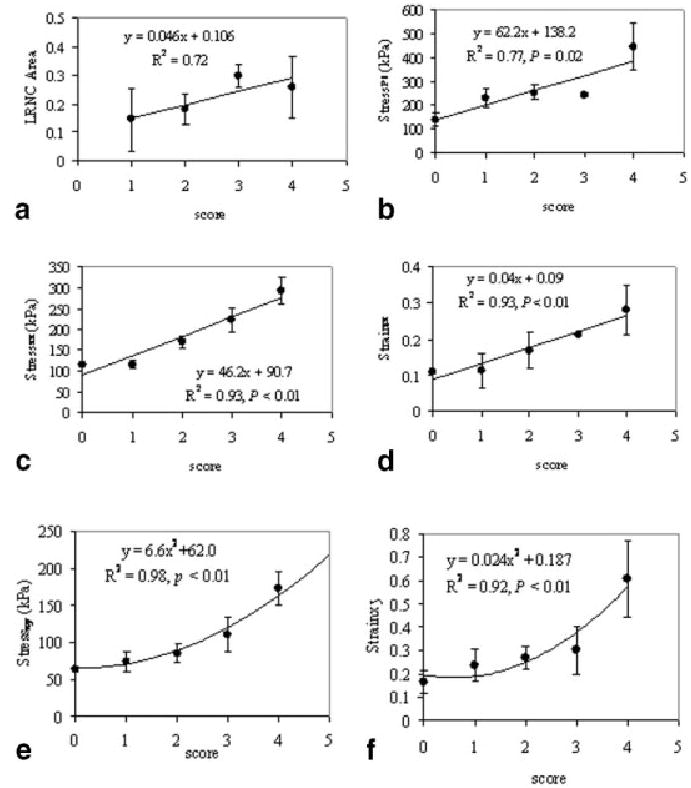
The data calculated at a systolic blood pressure of 150 mm Hg provided more and clearer patterns than at a diastolic blood pressure of 90 mm Hg in all mechanical data sets. However, the differences in all stress/strain values with the two pressures show no significant correlations with the vulnerability scores. Figure 4 shows the morphologic data averages of maximum τ_P1, τ_xx, σ_xx, τ_xy, and σ_xy as a function of the vulnerability scores, with an input systolic blood pressure of 150 mm Hg for Group 1 specimens. All mechanical data sets and lipid areas showed highly positive correlations with the vulnerability scores, whereas the fibrous cap thickness was inversely related to the scores (not shown in Fig. 4). Figure 5 shows two examples of plaque with scores of 1 (top row) and 3 (bottom row).

FIG. 4.

The correlations of biomechanical and morphologic parameters of plaques with their vulnerability scores in Group 1 specimens. The parameters are self-explained in the y-axis of these plots. The fitting curves are empiric regressions to the data.

FIG. 5.

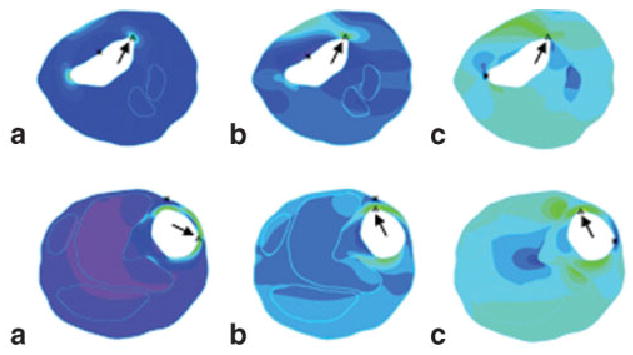
The examples of τ_P1 (a), τ_xx (b), and σ_xx (c) maps computed with the fluid–structure interaction model from two plaque specimens, plaque A (top) and plaque B (bottom). The vulnerability scores are 1 and 3, respectively. The color scales of these maps varied and thus are not provided here. The arrows point to the maximum value of each tensor component. The asterisks indicate the minimum values.

On the basis of the statistical results from Group 1 data sets, regardless of the location of these maximum values of stress and strain, an empiric formula to connect a biomechanical marker (BM) to the plaque vulnerability was proposed,

$$BM=\frac{LAR\cdot {\tau }_{P1}\cdot {\tau }_{xx}\cdot {\sigma }_{xx}\cdot \sqrt{{\tau }_{xy}\cdot {\sigma }_{xy}}}{\sqrt{LcH}},$$ [3]

where stress data use a unit of kilopascal and BM thus has a unit of kilopascal^5/2/mm^1/2. Because plaque geometry directly affects the computational results of stress and strain, we selected multiplications of different components rather than summations in Eq. [3]. All stress and strain data in this formula are maximum values from the calculated stress/strain maps. For calculation of the SD of BM, error propagation was derived, and the SD of BM at each vulnerability score was obtained from the standard deviations of parameters in Eq. [3]. For a systolic blood pressure of 150 mm Hg, the average BM values, standard deviations, and the range that correlated with the vulnerability score are shown in Table 2. This data range could be scaled down or up, depending on the input of blood pressures.

Table 2.

Correlation of Defined Biomechanical Marker (BM) Range at a Systolic Blood Pressure of 150 mm Hg and Pathological Vulnerability Scores

Vulnerability score	Average BM (kPa5/2/mm1/2)	SD	Defined BM range
0 (no lipid)	0	0	0
1	2509	2670	1–5200
2	12651	7820	5201–21000
3	31194	10050	21001–42000
4	205727	155606	>42001

With Eq. [3], the remaining eight data sets were examined for comparison with the pathologic score. Six (75%) of eight plaques were correctly scored. One plaque with less than 5% of extracellular lipid was given a pathologic score of 1, but mechanical calculation neglected this small lipid area. Another plaque received a BM score of 4 with a pathologic score of 3. If all data sets were scored on the basis of the BM, then 86% (19/22) of the total data sets were identified with a score equal to the pathologic score. The third missed set was scored as 3 instead of 4.

DISCUSSION

Vulnerable plaque in the cardiovascular system can be characterized as plaque that has intrinsic morphologic and functional markers that result in acute coronary syndrome. Consequently, plaque vulnerability should be assessed in multiple dimensions. More comprehensive characteristics of coronary artery atherosclerotic plaques, which were determined through high-solution ex vivo MR images, are presented here in terms of plaque components, size, and stress/strain distributions. Because plaque disruption is a complicated process, this report only focuses on the most common model described by Davies and Thomas (2). Indeed, vulnerable plaques are associated with a large lipid pool, a thin fibrous cap, and certain critical stress/strain conditions with intraluminal blood pressure. In this study, we have examined two blood pressure conditions that simulate the pulsatile pressures at diastole and systole. Although similar correlations were observed between vulnerability scores and stress/strain values under both pressure conditions, it is the systolic blood pressure that presented stronger correlations given a small number of samples. Thus, this data set became the focus of our study. On the other hand, cyclic expansion and compression of the heart can lead to constant bending of the coronary arteries, which would aggregate plaque disruption because of the loss of elasticity of atherosclerotic arteries. Such characteristics should be reflected in the differences between the same stress or strain parameters with two blood pressures. However, these differences in our study show neither clear patterns nor significant correlations with the vulnerability scores. These differences may be explained by the small number of samples (n = 10), choice of blood pressures, and/or systemic errors associated with our modeling. Vigorous future research is necessary to investigate the effects of varying parameters on our computational modeling and MR methods.

The segmentation algorithm was designed to identify relatively large plaque components because small structures (<5% of total vessel area) have little impact on the outcome of mechanical calculations (21). These major plaque components included Ca, FT, and the LRNC in this study. All selected MR plaque images were successfully segmented with three MR contrast weightings. These images were assessed by the match between MR segmented maps and corresponding pathologic images in terms of size, shape, and location of each plaque component. In general, a multicontrast imaging method (e.g., T₁, T₂, proton density, gradient-echo) (8) is applied for the identification of different plaque components. Different TR and TE values are formed to create these contrast weightings, in which a relatively long TR (> 3 T₁ of the tissue) was applied for T₂-weighted imaging. For the in vivo study, the TR was frequently limited to a 1 or 2 RR interval (12,16) (i.e., approximately 1000 to 2000 ms for the acquisition of proton-density and T₂-weighted images) because of the limitation of acquisition time for coronary artery plaque imaging. For this reason, we have selected a relatively short TR and varied TE to yield different contrast weighting. These contrasts more or less involve T₂ weighting with progressive increased TE, although some T₁-weighting signals due to this short TR were involved. A similar data acquisition and segmentation method was already reported by Morrisett et al. (28). Using a 3-T MR system, Raynaud et al. (29) showed well-differentiated T₂ contrast between lipid core and collagenous cap and other FT. This result is in agreement with observations from studies performed with 1.5-T MR systems (17,30). We have also found a correlation in the LRNC area between MR images and histologic images (R²) = 0.9). The detailed comparison between MR and histologic findings will be summarized in another report. Although using more contrast weightings may improve the accuracy of segmentation, it appears that segmented images with three different T₂ weightings matched histograms well with regard to the large plaque components in our study. Our future work will focus on using more and/or different combinations of contrast weightings, as well as different algorithms, for the examination of the accuracy of human or computer-assisted segmentation in comparison with histograms on a pixel-by-pixel basis (31). Another major plaque component, intraplaque hemorrhage, was not seen in our nonruptured plaques. Therefore, the time-of-flight data set was not used in our segmentation (32,33), although it was available (data not shown).

The critical stress/strain points were often located on the shoulders of the lumen surface of the eccentric plaques, where inflammatory cells such as macrophages and T lymphocytes accumulate. This observation was consistent with other findings in the literature with other imaging methods. In an early study involving coronary artery specimens (34), plaque rupture sites were often located close to the region where the maximum circumferential stress occurred and exceeded 2250 mm Hg (300 kPa). Our finding also pinpoints the high sensitivity of both circumferential stress and strain (Fig. 3e and f) to the vulnerability or the likelihood of plaque rupture. In addition, the maximum principal stress and normal stress/ strain are also linearly dependent on vulnerability scores. The former has been used by others (26) to address the biomechanical stability of plaques. It is worth noting that both stress and strain components are four-element tensors. The mechanism of plaque rupture is complicated and involves both biologic and mechanical processes. A single serologic marker is unlikely to identify rupture-prone plaques. It is for this reason that we have analyzed all components of the mechanical properties, plaque geometry, and MRI contrast related to the plaque components such as T₂ values. Although the T₂ contrast has been used to segment the plaque components in MRI (17,28,35), its correlation with vulnerability is not significant in our study with a limited number of samples (data not shown). Whether other MR contrast (e.g., diffusion and T₁) is associated with plaque vulnerability remains unclear. Nevertheless, MRI has shown the ability to classify plaque components and thus provides an image base for mechanical modeling, not only in the in vitro studies, but also possibly in the in vivo studies.

The vulnerability scores were largely derived from the morphologic classification scores proposed by the American Heart Association. Certain consideration was given to the mechanical forces on the plaques, particularly on the shoulder of the plaques and the quantity of presented macrophage cells. This pathologic determination of plaque vulnerability may not always correctly predict the plaque rupture, but has largely reflected the characteristics of ruptured plaques and thus was considered the gold standard. In this preliminary study, we have connected this gold standard of plaque rupture with the features of plaque biomechanics and morphology on the basis of MR ex vivo images and modeling. The underlying mechanism with this connection is not clear at this time, but our finding has supported the common belief that a large lipid pool, a thin cap, or both may lead to a vulnerable plaque. A large-scale study of symptomatic patients with follow-up or consecutive monitoring of plaque progression in animal models may be the solution to find the true mechanism responsible for plaque rupture. This is beyond the scope of our current study, but will certainly be a focus of our future work.

The proposed BM is an empiric index, and its value depends on the input blood pressure. An initial idea was that BM should be calculated with the stress and strain values at the same location. However, maximum values of the stress and strain components are not always in the same locations, but most of them correlated highly with plaque vulnerability. It is for this reason that we combined these characteristics of plaque vulnerability into a single marker. It is evident that by no means can BM tell where the precursor plaque is likely to rupture, but BM may provide a quantitative clue as to which plaque is likely to be the culprit lesion. In addition, analysis of test data reveals that BM appears to offer more accurate assessment of plaque vulnerability than any single parameter. Figure 4 shows that in plaque A, the maximum values for τ_P1 = 339 kPa, τ_xx = 205 kPa, and σ_xx = 0.205. However, because the LAR is approximately 0.034 and the LcH is 0.54, plaque A has a low BM value of 1828 (score = 1). The relatively large τ_P1 value was caused by the irregular shape of the plaque geometry. In contrast, the τ_P1 value (215 kPa) of plaque B is much lower than that of plaque A, whereas the maximum values of τ_xx and σ_xx are comparable with those of plaque A. However, the LAR (0.34) and the LcH (0.28) of plaque B differ significantly from those of plaque A; plaque B has a larger BM of 26434 (BM score = 3). Again, the applicability of this BM is limited and is affected by factors such as input blood pressure and image resolution. In addition, the role of each biomechanical and morphologic parameter in the BM is not yet determined. A substantially large amount of data is needed for this evaluation.

Study Limitations

Certain limitations are presented in our study. First, in vitro results with fixed tissue may not have the same morphologic features and mechanical behaviors (effect of autolysis) as in vivo results. Because our mechanical calculations were based on the geometry of in vitro plaques, the mechanical results may not accurately represent the stress/strain conditions in vivo. Furthermore, image contrast generated from formalin-fixed plaques may be different from the contrast in fresh plaque tissue. Dalager-Pedersen et al. (35) reported that T₂ values of three components—fibrous cap, medium, and adventitia—increased approximately 7 to 9% from fresh specimens to formalin-fixed specimens, whereas the T₂ value of the lipid core decreased slightly (4%). Therefore, the contrast between lipid core and surrounding fibrous tissue would only slightly increase from fresh plaque specimens to formalin-fixed specimens. Second, material properties were obtained from data in other literature, which represent only averaged values over different ages and intercardiac cycles. A large scale of work is needed for determination of the elastic properties of each plaque component including subject-specific and/or local mechanical data in the targeted plaques and arteries. Third, image resolution is merely 100 μm, which does allow identification of cap thickness less than 65 μm. Therefore, thin cap thickness less than 100 μm was often overestimated to 100 to 200 μm. Thus, the derived BM score ranges apply only to images with this spatial resolution. Finally, inflammation is an important risk factor affecting plaque vulnerability, but it was not considered in our computational modeling because of a lack of information about the material property of inflamed tissue. Substantial work with different MR contrasts and mechanical testing is needed for the segmentation of inflamed tissue.

In conclusion, we have shown the feasibility of integrating MR imaging and computational modeling to assess plaque vulnerability. Results of this ex vivo study may provide a basis for the quantification of plaque vulnerability assessment from a mechanical point of view. This study is our motivation to perform more analysis on a larger number of specimens to define effective quantitative biomarkers to noninvasively assess the vulnerability of atherosclerotic plaques in vivo. Future work will be focused on tasks such as performing more accurate segmentation of plaque components and obtaining subject-specific material properties and semiautomatic quantification of plaque features. A comprehensive evaluation of plaque components with both MRI contrasts and biomechanical forces by modeling could significantly advance our understanding of plaque progression and rupture and may further help the planning and monitoring of therapeutic treatment such as lipid-altering therapy.

Table 3.

Quantitative Measurements of Test Data Set

Pathological score	LcH (mm)	LAR (%)	τP1 (kPa)	τxx (kPa)	τxy (kPa)	σxx	σxy	BM (kPa5/2/mm1/2)	BM score
1	0.54	0.034	339	205	48	0.21	0.15	1828	1
1	1.32	0.076	129	95	67	0.08	0.17	233	1
1	0.16	0.17	168	85	73	0.08	0.33	2298	1
1	—	0	216	212	65	0.21	0.21	0	0
2	0.17	0.24	200	160	85	0.15	0.38	15977	2
3	0.283	0.34	216	209	85	0.20	0.23	26434	3
3	0.13	0.29	262	261	71	0.25	0.31	67606	4
4	0.2	0.38	289	179	111	0.17	0.36	46366	4