Structural analysis of hyperperiodic DNA from Caenorhabditis elegans

Abstract

Several bioinformatics studies have identified an unexpected but remarkably prevalent ∼10 bp periodicity of AA/TT dinucleotides (hyperperiodicity) in certain regions of the Caenorhabditis elegans genome. Although the relevant C.elegans DNA segments share certain sequence characteristics with bent DNAs from other sources (e.g. trypanosome mitochondria), the nematode sequences exhibit a much more extensive and defined hyperperiodicity. Given the presence of hyperperiodic structures in a number of critical C.elegans genes, the physical characteristics of hyperperiodic DNA are of considerable interest. In this work, we demonstrate that several hyperperiodic DNA segments from C.elegans exhibit structural anomalies using high-resolution atomic force microscopy (AFM) and gel electrophoresis. Our quantitative analysis of AFM images reveals that hyperperiodic DNA adopts a significantly smaller mean square end-to-end distance, hence a more compact coil structure, compared with non-periodic DNA of similar length. While molecules remain capable of adopting both bent and straight (rod-like) configurations, indicating that their flexibility is still retained, examination of the local curvatures along the DNA contour length reveals that the decreased mean square end-to-end distance can be attributed to the presence of long-scale intrinsic bending in hyperperiodic DNA. Such bending is not detected in non-periodic DNA. Similar studies of shorter, nucleosome-length DNAs that survived micrococcal nuclease digestion show that sequence hyperperiodicity in short segments can likewise induce strong intrinsic bending. It appears, therefore, that regions of the C.elegans genome display a significant correlation between DNA sequence and unusual mechanical properties.

INTRODUCTION

DNA structures are frequently modeled as flexible, isotropic rods both in solution and in their ability to contribute to native biological structures such as chromatin (1). Despite the utility of such models, it has been clear for some time that the sequence of a DNA molecule can contribute very specifically to its 3D structure, both in vitro (2,3) and in vivo (4). Particularly striking in their non-linear structure, certain sequences can introduce a stereo-specific bend in DNA. The most prominent sequence contributing to these structural anomalies are strings of three, four or more consecutive A or T residues (A-tracts) (5,6), although other nucleotide segments can also induce structural anomalies (7). A-tract bending has been investigated using X-ray crystallography, gel electrophoresis, electric birefringence, circular dichroism and NMR [for reviews see (8,9)]. DNA curvature of non-genomic DNA has also been investigated with electron microscopy (10,11) and atomic force microscopy (AFM) (12–14).

Many of the unusual DNA sequences that have been the subject of biophysical and modeling studies have involved relatively short (10–80 bases) bent regions either examined in isolation (15) or examined in the context of a longer fragment (13). This type of DNA structure is common in many genome sequences and in numerous cases has been associated with biological function, either in facilitating a specific protein interaction at the site of the bend as in the case of nucleosomes (16) or in facilitating a long-range interaction of two sites in the genome that otherwise might not be capable of interacting (17).

Recently, it has become clear that certain eukaryotic genomes include sequences with a more extended anomalous character in which groups of A_n/T_n residues are present in a periodic and highly non-random manner over a range of several hundred nucleotides (18,19). In the Caenorhabditis elegans genome, a remarkable periodicity of ∼10 bp AA/TT dinucleotides has been described elsewhere (20–24). One proposed role for such sequences has been to limit the capability of nucleosomes to slide into the kind of ordered arrays needed for heterochromatin formation (19). Although such long DNAs can be readily modeled using the extensive data available for shorter bent segments, it is by no means clear that such models continue to provide an accurate approximation as the length of the Periodic A_n/T_n Cluster (PATC) increases. At extremes of possibility, it could be imagined that such DNAs would form complex coils and knots in solution or, alternatively, might behave as relatively straight segments perhaps with unusual microscopic flexibility properties.

In order to understand the genesis and role for extended PATCs in eukaryotic genomes, we first need to define their physical properties. Genomes for C.elegans and other nematode species have been shown to exhibit an unusual high frequency of extended PATCs (20,23,24), particularly in regions of the genome that are transcribed in germline tissues. The C.elegans genome has the additional advantage that it is among the most extensively characterized both in structure and function, since the sequence is known and individual genetic studies, genome expression and phenotype analysis have been done.

In this work, we have used gel electrophoresis and AFM to carry out an extensive analysis of several extended PATCs from the genome of the nematode C.elegans. We find that the hyperperiodic DNA shows a significant and readily discernible degree of bending compared with non-periodic DNAs, adopting correlated angles over long distances, and that increased flexibility alone cannot explain the mechanical properties of this DNA.

MATERIALS AND METHODS

AFM constructs

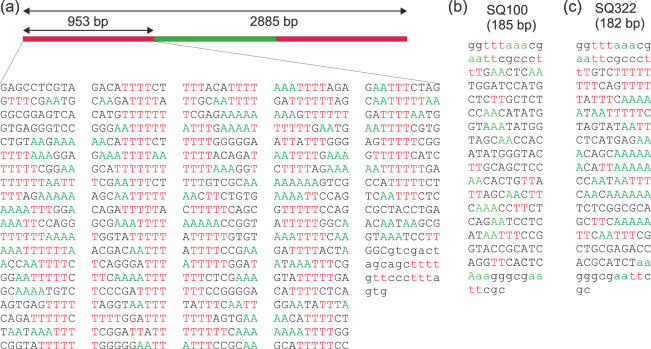
For AFM imaging, we fabricated a pseudo-palindrome construct of 2885 bp using a method similar to that described in Ref. (14). This construct contained two segments of 923 bp of hyperperiodic Ω4 fragments from C.elegans in an inverse orientation each located at the ends of the construct (for description of the fragments of C.elegans used, see Results). We refer to this construct as the periodic palindrome construct (PPC). Our AFM analysis focused on the first 953 bp at both ends, which included the hyperperiodic sequences. We analyzed a fragment of DNA slightly longer than the pure hyperperiodic fragment because the very ends were not considered in the analysis. The extra non-periodic 979 bp, located in the middle part of the construct, was chosen to be non-palindromic, although it was also part of the C.elegans genome. In doing so, we avoided the synthesis of a real palindromic construct, which could generate two independent double-stranded DNA molecules of length equal to half of the original one. The scheme of the PPC, including the sequence of one of the hyperperiodic DNA fragments (capital letters), is shown in Figure 1a. PPC fabrication and long-term stability was verified using gel electrophoresis.

Figure 1.

Sequences of DNA used in the AFM experiments. (a) Schematic representation of the PPC (2885) and sequence of the region analyzed (953 bp) that contains the hyperperiodic fragment Ω4 from C.elegans (923 bp). In the PPC the hyperperiodic region is located at both ends of the molecule, hence tracing of the molecule is independent of the particular end chosen as a starting point. Capital case letters denote the hyperperiodic fragment Ω4 from C.elegans. (b) Sequence of SQ100 fragment (185 bp, non-periodic) that contains the fragment Ω7 and (c) sequence of SQ322 (182 bp, hyperperiodic) that contains the fragment Ω6 from C.elegans. Two or more consecutive As or Ts were colored in green and red, respectively. The sequences were plotted in columns of 10 bases to highlight ∼10 bp periodicities. Capital letters in (a) denote the hyperperiodic fragment Ω4 from C.elegans and in (b and c) denote the Ω7 and Ω6 fragments, respectively.

We also analyzed two short DNAs, which contained fragments Ω6 and Ω7 (for description of these fragments see Results). Fragments Ω7 and Ω6 were amplified by cloning into the pCR4Blunt-TOPO vector (Promega), yielding two short DNAs (SQ100 and SQ322) that were analyzed with gel electrophoresis and AFM. SQ100 (185 bp) contained the non-periodic fragment Ω7 (Figure 1b) and SQ322 (182 bp) contained the hyperperiodic fragment Ω6 (Figure 1c). Capital letters in Figure 1b and c denote the Ω7 and Ω6 sequence components. Sequences are specified excluding the single-stranded overhangs.

All sequences in Figure 1 are displayed in a 10 bp arrangement to facilitate visualization of same-residue coincidence every helical turn. To assist this, two or more consecutive Ts are colored in red and two or more consecutive As in green. The sequences in Figure 1a and c, corresponding to the hyperperiodic fragment in the PPC and the SQ322 construct fragment, respectively, demonstrate a propensity for an AA/TT to be present every 10 bp. In contrast, the degree of periodicity in SQ100 (Figure 1b) is negligible.

Gel electrophoresis

Both 1D and 2D electrophoresis techniques were used to identify anomalous migration behavior of fragments of DNA from C.elegans. 2D gels were cast in 4% NuSieve agarose gels using 1× TAE Buffer in the absence of ethidium bromide. For DNA samples run with an internal standard, it was important to avoid overloading of DNA and consequent smearing of the first dimension during electrophoresis; this was achieved by constructing single-tooth combs that were relatively wide (2.5–5 mm) rather than the narrower combs used in other 2D gel systems. The first ‘vertical’ direction in all 2D gels was run at 53 V for ∼3 h in a cold room at ∼4°C. At this voltage, heating by the electrophoretic current was observed to be minimal. Each gel was then soaked for ∼2 h in 1× TAE Buffer with ethidium bromide (0.3 µg/ml) at room temperature. Next, the second dimension (horizontal direction in the 2D gels) was run with the gel box at room temperature at 80 V for 2 h. Temperatures are somewhat raised by the higher voltage of the second dimension electrophoresis, and were estimated to be ∼37°C.

Similar analysis using 1D electrophoresis was carried out by running two separate gels on each sample. One gel was cast with 0.3 µg/ml ethidium bromide present and run at 60 V for 6 h at room temperature, while the other was cast with no intercalator present and run at 30 V for 15 h in a cold room at ∼4°C and then stained with ethidium bromide (2.0 µg/ml) in 1× TAE for 1 h. Although the two gel systems are comparable in resolution, the paired 1D gels offer the ability to analyze greater numbers of samples, while the 2D gels allow more sensitive detection of modest electrophoretic anomalies.

Sample preparation and AFM imaging

DNA samples for AFM imaging were prepared by depositing 5 ng of DNA, diluted in 6 µl of 10 mM Tris–HCl (pH 8.0) and then supplemented with 15 mM MgCl₂, onto freshly cleaved mica. After 60 s, the mica was washed with MilliQ-filtered water and blown dry in a gentle stream of nitrogen gas. Samples were imaged at 1.95 nm per pixel resolution in air at room temperature and humidity using tapping mode. We used an AFM from Nanotec (Nanotec Electrónica, Madrid, Spain) and also a Nanoscope IIIa (Digital Instruments, Santa Barbara, CA). We utilized tapping mode SuperSharpSilicon tips, type SSS-NCH-8 (Nanosensors, Neuchâtel, Switzerland). Image processing, including plane subtraction and flattening, was done using WSxM freeware (www.nanotec.es). Traces were obtained using the tracing routine described in (P.A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Phillips, J. Widom, C. Dekker and P.C. Nelson, manuscript submitted).

Calculation of periodicity value and predictions of curvature

Calculations of predicted radius of curvature for DNA segments and of overall periodicity used several available algorithms (5,7,19) (see also Supplementary Data). Source code for local analysis and display of these parameters is available on request.

RESULTS

Periodic DNA segments from C.elegans

We chose a number of hyperperiodic DNA fragments from C.elegans for analysis based on the relevance of the proteins that they encode and on the periodicity value provided by the PATC algorithm described in Ref. (19). This algorithm is by no means unique and we note that many different algorithms identify a strongly periodic character to C.elegans DNA (data not shown) and could have been used to select specific fragments. For reference, the PATC algorithm returns a numerical score with greater numbers indicating more highly periodic character. A score of >95 is reached at <10⁻⁶ frequency in a random sequence with base composition equivalent to C.elegans. There is no segment in the entire unique genomes of Drosophila melanogaster (euchromatin) or Schizosaccharomyces pombe (two genomes with comparable AT content to C.elegans) with a periodicity score >200. Of the natural bent DNAs that have been analyzed previously on a biophysical level, only the mitochondrial DNA of Crithidia shows a substantial signal in the PATC assay (a score of 235 maintained over a distance of 175 bp). Supplementary Figure S2 shows the periodicity values as a function of sequence for the DNAs used in this work.

Fragment Ω4 is a 932 bp segment comprising the fourth intron of C.elegans gene F54C4.1 on chromosome III. The F54C4.1 gene is essential, encodes mitochondrial ribosomal protein L40, and is likely expressed in both somatic and germline tissue of the animal. The intron 4 fragment Ω4 was chosen from among the many hyperperiodic segments in the C.elegans genome based on its localization in a well-defined essential gene. Informatic analysis of fragment Ω4 using the PATC algorithm (19) or standard bending algorithms (5,7) indicated a degree of periodicity that is characteristic of a subset of germline-expressed C.elegans genes but which has not been seen outside of nematode DNA. Using the PATC algorithm, an average score of 433 for the Ω4 fragment was observed. This magnitude of score has never been observed in random DNA or in the genomes of non-nematode species. Of sequences in the Ω4 fragment 89.7% have PATC scores above 95 (the cutoff for 10⁻⁶ occurrence in random DNA).

Several other fragments have also been analyzed in this work. Fragment Ω6 is a strongly periodic 147 bp segment comprising the third intron of C.elegans gene ZK792.7 on chromosome IV. The gene is predicted to encode a protein with metallophosphoesterase activity. The periodicity value of Ω6 is 122 with 76.9% of the sequences with PATC scores above 95. Fragment Ω6 was originally isolated among a set of random clones of Microccocal nuclease treated C.elegans lysates, consistent with the possibility that this fragment represents a single nucleosome core (25). We stress, however, that no further in vivo analysis has been carried out on this segment of the chromosome.

As controls, we have examined the behavior of several DNAs which had no unusual periodic character. These include lambda DNA, pUC plasmid backbones and Ω7, a distinct C.elegans genome fragment. Fragment Ω7 was 150 bp and was also derived from Micrococcal nuclease digestion of C.elegans lysates, but did not show distinct periodicity. Ω7 is an exonic fragment from gene Y38F1A.3. Table 1 summarizes the DNAs employed in this study including the origin of the DNA, the periodicity value and the derived AFM construct.

Table 1.

Relevant DNAs used in this study

DNA (size)	Gene in C.elegans	Periodicity value Ave, (Frac>95 cutoff)	AFM sample (size)
Fragment Ω4 (932 bp)	F54C4.1	433, (89.7%)	PPC (2885 bp)
Fragment Ω6 (147 bp)	ZK792.7	122, (76.9%)	SQ322 (182 bp)
Fragment Ω7 (150 bp)	Y38F1A.3	0.93, (0%)	SQ100 (185 bp)
Control Pgem-3Z (2743 bp)	—	3.21, (0%)	Control (2743 bp)

Periodicity values were calculated using the algorithm described in Ref. (19).

From the periodicities above one would expect unusually bent DNA structures for the fragments Ω4 and Ω6, but not for Ω7. We tested this prediction by gel electrophoresis, which exactly confirmed the expectations (Figure 2). Each of the hyperperiodic fragments (Ω4 and Ω6) was retarded compared to size markers, with retardation relieved at higher temperatures and with the addition of an intercalating agent (ethidium bromide) during electrophoresis. In contrast, the non-periodic fragment Ω7 did not show any retardation. Interestingly, our observations were made using agarose gel electrophoresis, which has not been seen to distinguish DNA structures in previous studies (3). Similar migration anomalies were observed in other two different hyperperiodic fragments from C.elegans (data not shown).

Figure 2.

Migration of hyperperiodic and control DNA in agarose gels. (a) Two-dimensional 4% NuSieve agarose gel electrophoresis of lambda DNA fragments (cut with NciI and PvuII) and (b) lambda fragments plus Ω4 fragments cut with the same restriction enzymes. Gels were run first at 4°C in the absence of intercalator (Ethidium Bromide, vertical) and then at 37°C in the presence of intercalator in the perpendicular direction (horizontal). The hyperperiodic Ω4 fragments (indicated by arrows) migrated more slowly than one would expect on the basis of its length. Similar anomalies were observed when using 2% agarose gels (data not shown). Gel electrophoresis on fragments SQ100 (185 bp, non-periodic, lane 3) and SQ322 (182 bp, hyperperiodic, lane 4) run at 37°C with EtBr (c) and at 4°C without EtBr (d). Lanes 1, 2, 5 and 6 correspond to 100 and 25 bp DNA ladders. At low temperature, the hyperperiodic fragment migrates more slowly than expected.

Single-molecule AFM imaging

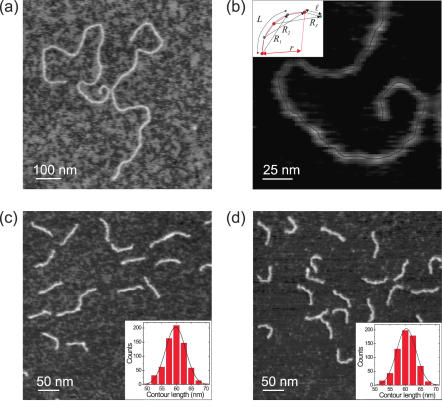
After the electrophoresis experiments indicated the presence of unusual DNA structures, we analyzed our samples with quantitative AFM analysis. The different DNA samples were imaged at high resolution and traced using a custom-written tracing routine. Typically, measured DNA profiles displayed a width of 4–7 nm at half height. We imaged the PPC (2885 bp), the control DNA (2743 bp) and the short C.elegans fragments (182 and 185 bp). Figure 3a shows an image of the PPC, where two DNA molecules are visible. The average measured contour length L₀ was 1032 ± 27 nm, yielding a rise per bp of 0.36 ± 0.01 nm. To illustrate the analysis, we plotted in Figure 3b an example of a single trace. The tracing routine accurately generates XY pairs separated by ℓ = 2.5 nm that follow the contour of the molecule. We found this length to be the lowest meaningful length that faithfully followed the contour given the pixel size of the images, 1.95 nm, and the high resolution obtained by using ultra-sharp tips. A magnification of the trace illustrates the three quantities deduced that are important for the analysis that follows (Figure 3b, inset). These are the contour length spacing L (in the example, L equals 3 × 2.5 = 7.5 nm), and the end-to-end distance R. Clearly, a given contour length spacing L can be associated with several values of R (three of them are plotted in the inset). The inset also shows the definition of curvature, C. The curvature of a 10 nm long segment is defined as the inverse of the radius r of the circle that encompasses three points separated by 5 nm (showing in red in the inset in Figure 3b).

Figure 3.

High-resolution AFM images of DNA samples. (a) Two representative DNA molecules of the PPC adsorbed on a mica surface. (b) Illustration of the data analysis and tracing of the DNA molecules. A segmented line made of points separated by ℓ = 2.5 nm follows the contour of the molecule. The important parameters we employ are the contour length spacing L, the end-to-end distance R and the curvature C defined as the inverse of the curvature radius r that embraces three contour points, C = 1/r. In the inset in (b), these parameters are shown together with an example of three values of R for the same contour length spacing L, in this case L = 3 × ℓ = 7.5 nm. We also show an example for the calculation of r for three points separated by L = 2 × ℓ = 5 nm (red arc). (c) AFM image of sample SQ100 and histogram of contour lengths L₀ [inset in (c)]. (d) AFM image of sample SQ322 and histogram of contour lengths L₀ [inset in (d)].

High-resolution AFM images of the short DNA samples, SQ100 and SQ322, are shown in Figure 3c and d. Figure 3c corresponds to the non-periodic sequence and Figure 3d to the hyperperiodic one. By eye, one can already notice that Figure 3d displays more bent molecules. This was confirmed in the subsequent numerical and analytical analysis (see below). Insets represent histograms of contour lengths for each sample. They show that our tracing routine precisely deduces the contour length with a standard deviation of 3 nm. For samples SQ100 and SQ322, 692 and 653 molecules were analyzed, respectively.

Single molecule AFM-based quantitative analysis of hyperperiodic C.elegans DNA

A quantitative analysis of the traces of hyperperiodic DNA showed systematic deviations from the worm-like-chain (WLC) model consistent with extra bending induced by sequence periodicity. As described by Rivetti et al. (26) DNA equilibrates on a mica surface when adsorption is promoted by divalent ions such as Mg²⁺. The behavior of DNA molecules under these conditions can be predicted by the WLC model (26). The WLC describes a mean trajectory of the polymer on the mica with the following equation:

$$〈R_{s,s+L}^2〉=4P\left(L+2P\left(e^{-L/\left(2P\right)}-1\right)\right),$$ 1

where P is the persistence length of the polymer, L is the contour length spacing and $〈R_{s,s+L}^2〉$ is the mean-squared separation between points along the chains located at distances s and s+L from the end of the molecule. The average is computed over s and over all observed contours. The averaging is done up to the upper limit in the contour length of the molecule L₀ (for the PPC, L₀ equals 325 nm) minus the contour length spacing L analyzed, thus 0 < s < L₀ − L.

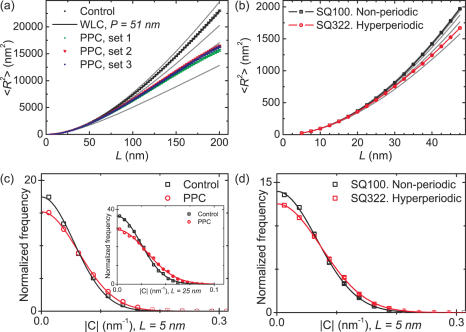
Using this analysis, the control DNA and the non-periodic short fragment SQ100 displayed exactly the behavior predicted by the WLC model; the hyperperiodic DNA, however, did not. Figure 4a shows $〈R_{s,s+L}^2〉$ versus L for the Control and PPC samples. We calculated $〈R_{s,s+L}^2〉$ up to a contour length spacing of L = 200 nm. This is because the length of the segment studied in the PPC was 325 nm, necessarily restricting one to values of L < L₀ to obtain a statistically reliable calculation for all L. For consistency, we also used an upper limit for L of 200 nm for the control DNA. A fit using Equation 1 was done for the control DNA (Figure 4a, black line). The fit yielded a value for the persistence length of 51 nm, in agreement with published results (26,27). These data were consistent with the hypothesis that our sample preparation yields contours that reflect equilibrium 2D chain conformations. We repeated the same type of analysis on the PPC, tracing 325 nm (953 bp) from both ends. The use of a palindrome construct is very convenient because it avoids ambiguity in the sequence analyzed: the traced fragments always included the hyperperiodic Fragment Ω4 from C.elegans independently of which end was selected. In this way, 190 fragments coming from three sets of experiments done on different days, mica surfaces and preparations were traced and analyzed. Remarkably, the same analysis done on the PPC showed significantly smaller $〈R_{s,s+L}^2〉$ than predicted by the WLC model (Figure 4a), which is indicative of extra bending. To guide the eye we included plots of Equation 1 using P = 20, 30, 40, 50 and 60 nm (solid lines in Figure 4a). The PPC data curves mostly overlaid the curve of P = 30 nm. It should be noted, though, that the WLC model does not necessarily hold for intrinsically curved DNA.

Figure 4.

Analysis of unusual character in hyperperiodic DNA from C.elegans using AFM. (a and b) Plots of <R²> versus contour length spacing L of the ends of the PPC, control DNA, SQ100 and SQ322 samples. Different sets of data in (a) correspond to different experiments, mica surfaces and sample preparations. In total, 190 PPC fragments were studied. The control DNA follows the prediction given by the worm-like-chain model with a persistence length of 51 nm. The hyperperiodic DNA regions from the C.elegans genome clearly show a very different behavior, characterized by lower <R²>. To guide the eye, predictions from WLC with different values for the persistence length are included (solid grey). The five curves included are for P = 20, 30, 40, 50 and 60 nm. The slope of the curves increases as P increases. Bending of the DNA, is evidenced by lower <R²> than predicted by WLC. (c) Normalized histograms of absolute curvature |C| for the PPC and the control DNA sample for L = 5 nm and for L = 25 nm [inset in (c)]. (d) Normalized absolute curvature |C| histograms for SQ100 and SQ322 for L = 5 nm. Distributions were fit to a Gaussian function centered at zero. The hyperperiodic DNA consistently showed larger standard deviations, independently of the spacing L [inset in (c)]. Bins and associated errors (square root of number of points in the bin) were normalized by the area of the histogram. We note that occasionally one cannot distinguish the error bars because they are smaller than the points.

We conducted a similar analysis using samples SQ100 and SQ322. In this case due to the shorter length of the molecules we plotted $〈R_{s,s+L}^2〉$ up to a contour length spacing of L = 47.5 nm (Figure 4b). This required tracing many more molecules to have comparable statistics with those for the PPC sample. We traced 692 and 653 molecules for SQ100 and SQ322, respectively. The analysis showed that SQ322 contours had smaller mean squared end-to-end distances than those of non-periodic SQ100 (Figure 4b). To stress the significance of the result, we included in Figure 4b plots of Equation 1 with P = 20, 30, 40, 50 and 60 nm to guide the eye. Whereas SQ100 data lay as expected between the curves of P = 50 and 60 nm, SQ322 data overlaid the curve of P = 25 nm.

Summarizing the results from these different DNA samples (Figure 4a and b), we find consistently that hyperperiodic DNA results in a shorter $〈R_{s,s+L}^2〉$ than predicted by the WLC at the two length scales studied: hundreds of bp and tens of bp. This can be most easily explained by increased bending of the DNA. Furthermore, the plot for $〈R_{s,s+L}^2〉$ deviates from the WLC at lower persistence length. This suggests that the increase in bending is not due to an increase in random bending/flexibility, which would exhibit WLC behavior, but rather due to non-random bending.

The presence of increased bending in hyperperiodic C.elegans DNA compared to non-periodic DNA was further supported by examining distributions of absolute curvatures ∣C∣. We calculated curvatures from traces at a fixed spacing L (see inset in Figure 3b as an example, for L = 5 nm). To do this, we fitted a circle to three points separated by L along the contour of the DNA. The curvature (C) at this spacing is defined as the inverse of the radius of that circle and its value was assigned to the middle point of the three contour points. Hence to calculate C_i at a given position i, for a given L, we used DNA stretches of 2 × L nm. Then we moved to the next point i + ℓ along the contour, which is ℓ = 2.5 nm (7 bp) apart from the previous, and we obtained a new value of C_i+ℓ. We arbitrarily assigned positive curvature if by progressing along the DNA the contour turned to the right, and we assigned negative curvature if it turned to the left. As expected, we found Gaussian distributions of C centered at zero for all type of molecules studied, proving no preferential curvature orientations due to adsorption (data not shown).

Absolute curvatures ∣C∣ distributions were calculated at different values of L. Figure 4c shows absolute curvature distributions for the PPC and the control non-periodic DNA for L = 5 nm. We analyzed 100 control DNA molecules, which yielded ∼12 000 curvature values, and 190 PPC molecules, which yielded ∼24 000 curvature values. Figure 4d shows similar absolute curvature distributions for the short DNA fragments studied, SQ100 (non-periodic) and SQ322 (highly-periodic). We analyzed 613 SQ100 and 567 SQ322 molecules, each yielding ∼12 000 curvature values. Distributions were normalized to have an area of one, and error bars denote normalized square root of number of points in the bin. All absolute curvature distributions were fit with a Gaussian function centered at curvature zero. From these fits we extracted the standard deviation σ_C. The values σ_C of the Control, PPC, SQ100 and SQ322 samples from curvature histograms calculated using a spacing of L = 5 and 25 nm are quoted in Table 2 (the latter only for long DNAs). Systematically, we found that DNA with hyperperiodic sequences had larger σ_C than non-periodic DNA. This was found to be independent of the spacing L used to calculate curvatures up to 50 nm. The inset in Figure 4c proves this by showing ∣C∣ distributions for PPC and control samples calculated at a larger spacing of L = 25 nm. Spacings larger than 50 nm, the persistence length of the DNA, did not generate statistically significant curvature distributions.

Table 2.

Standard deviation σ_C of curvature distributions and standard deviation σ_<C>molecule and intrinsic curvature <C>_0,molecule of mean curvature distributions

	Control	PPC	SQ100	SQ322
σC,L=5 nm(nm−1)	0.0547 ± 0.0007	0.0618 ± 0.0005	0.0667 ± 0.0004	0.0737 ± 0.0004
σC, L=25 nm (nm−1)	0.0241 ± 0.0003	0.0298 ± 0.0003	—	—
σ<C>molecule, L=5 nm (nm−1)	0.0077 ± 0.0003	0.0072 ± 0.0008	0.0163 ± 0.0005	0.024 ± 0.002
<C>0,molecule, L=5 nm (nm−1)	0	±0.010 ± 0.001	0	±0.010 ± 0.002
σ<C>molecule, L=25 nm (nm−1)	0.007 ± 0.001	0.008 ± 0.001	—	—
<C>0,molecule, L=25 nm (nm−1)	0	±0.013 ± 0.001	—	—

Values correspond to Gaussian fits to distributions shown in Figures 4c, 4d, 5b and 5c. The segment length was 5 and 25 nm, where indicated. Distributions for the short DNAs were not calculated at L = 25 nm.

Intrinsic curvature in hyperperiodic C.elegans DNA

In principle, a broad ∣C∣ distribution could result from either increased flexibility or intrinsic curvature (Supplementary Data). In order to determine which of the two phenomena dominates in our hyperperiodic DNA, we performed two calculations: (i) we calculated the distance over which the handedness of the curvature persists, and (ii) we calculated an average curvature per single imaged AFM molecule and considered its absolute value ∣<C>_molecule∣.

One way to measure the persistence of handedness is to plot a correlation function CC_L,D of the form:

$$C{C}_{L,D}=\frac{{\sum }_s^{L_0-D}{C}_{L,s}{C}_{L,s+D}}{{\sum }_s^{L_0-D}\left|C_{L,s}\right|\left|C_{L,s+D}\right|},$$ 2

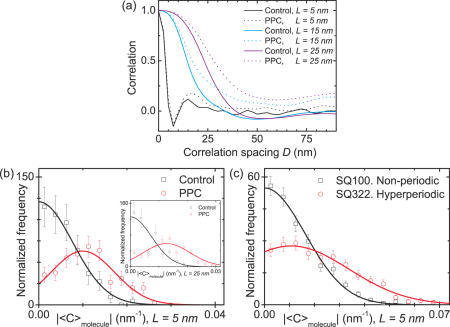
where C_L,s is the curvature calculated at spacing L at position s and L₀ is the total contour length of the molecule. C_L,s can therefore be positive or negative as defined above. The function CC_L,D involves addition over all the molecules considered in this study, 100 for the control DNA and 190 for the PPC. To examine the persistence of handedness, renormalization was included to compare the two datasets. For a given spacing L, CC_L,D is a function that depends on the correlation spacing D. Figure 5a shows a plot of CC_L,D for L = 5, 15 and 25 nm for the PPC (dashed lines) and the control DNA (solid lines). Systematically, a significantly larger correlation distance was found for the hyperperiodic DNA than for the non-periodic DNA. As expected, at large correlation spacing D, the correlation function approached zero for non-periodic DNA, showing that the ‘memory’ of handedness is lost very quickly. Interestingly, for hyperperiodic DNA the correlation function approaches a non-zero value, for large D. Qualitatively similar correlation functions were predicted from theoretical calculations for chains with long-range correlations (28). Therefore, these data are strongly indicative of the presence of an intrinsic bend rather than increased flexibility.

Figure 5.

Measurement of the intrinsic curvature in hyperperiodic C.elegans DNA. (a) Curvature correlation function (Equation 2 in the main text) for PPC and Control DNA calculated for curvatures measured at contour length separations of L = 5, 15 and 25 nm. A long-range persistence of handedness in hyperperiodic DNA is evident from the graph, indicating the presence of intrinsic bending. (b) Normalized histograms of absolute mean curvatures per molecule |<C>_molecule| for the PPC and the control DNA sample for L = 5 nm and for L = 25 nm [inset in (b)]. (c) |<C>_molecule| histograms for SQ100 and SQ322 for L = 5 nm. Hyperperiodic DNA showed a preferred mean curvature per molecule of ∼0.01 nm⁻¹ at L = 5 nm, consistent with the presence of intrinsic bending. Bins and associated errors (square root of number of points in the bin) were normalized by the area of the histogram.

A complementary approach to the correlation distance consisted of calculating an average curvature per molecule and taking its absolute value ∣<C>_molecule∣. The distributions of absolute curvature per molecule are shown in Figure 5b and c. The statistics in these experiments is poorer (resulting in larger error bars) than in the ∣C∣ distributions (shown in Figure 4c and d), as per definition the total number of values for the histogram equals the number of molecules imaged. Figure 5b shows ∣<C>_molecule∣ distributions for the PPC and the non-periodic control DNA, and Figure 5c shows ∣<C>_molecule∣ for the SQ100 and SQ322 fragments. Distributions were calculated using a spacing of L = 5 nm to calculate the curvature values, except the inset in Figure 5b, which used L = 25 nm. The distributions were fit with Gaussian functions. As expected, the distributions for both non-periodic DNA molecules had a maximum at curvature zero. However, the distributions for the two hyperperiodic DNA samples displayed an offset, ∣<C>_{0,molecule L=5 nm}∣ of ∼0.01 nm⁻¹. This implies that a given molecule has the tendency to bend either more towards the right than towards the left or vice versa. This observation can only be explained by the presence of an intrinsic curvature, as the distributions for the ‘random’ control DNAs had a maximum at around zero. We note that the effect is more pronounced for the long DNA samples, as here more curvature values contribute to the mean curvature, which can directly be seen from the width of the distributions σ_<C>molecule (Table 2). Similar conclusions can be drawn from the analysis done at L = 25 nm (inset in Figure 5b), showing that the detection of an intrinsic bend is independent of the spacing L used.

DISCUSSION

We report anomalous gel migration of several fragments of the nematode C.elegans genome with unusual periodicity of AA/TT dinucleotides. AFM allowed detailed characterization of the bending of these DNA structures showing that PATCs generate intrinsic bending. Despite the presence of an intrinsic bend, the AFM images also showed that hyperperiodic DNA can still adopt a wide range of bending configurations (Figure 3d), suggesting that flexibility is retained.

In order to be able to extract quantitative information related to bending of DNA, we first verified that our DNA contours reflect 2D equilibrium states and that the average behavior can be accurately described by the WLC model. For this, we used as a control the plasmid pGem-3Z, which had no unusual periodic character. We observed that the average trajectory of adsorbed control DNA molecules fulfilled several criteria: (i) the distribution of curvatures was Gaussian (Figure 4c, black squares), and (ii) the mean square end-to-end distance followed Equation 1 with the accepted value for the persistence length (Figure 4a, black squares). Thus, we conclude that the WLC describes accurately the average trajectory of our molecules and that these trajectories reflect equilibrium states of the molecules on the mica surface. The fact that the control DNA molecules are equilibrated on the surface is crucial for allowing us to extend the same analysis to DNAs with hyperperiodic sequences. Plots of mean squared end-to-end distances of hyperperiodic DNA samples, PPC (Figure 4a, colored symbols) and SQ322 (Figure 4b, red circles), showed that AA/TT periodicity induces extra bending in the DNA structure. This was demonstrated by significant deviations of the hyperperiodic DNA from the predictions of the WLC model using a persistence length of 50 nm.

Subsequent analysis to determine the source of this deviation took into account distributions of absolute values of curvatures ∣C∣. As a check for the validity of this analysis, we found that curvature distributions had a maximum at zero, showing equal probability for the observation of positive and negative curvatures. The value σ_C (Table 2) obtained from Gaussian fits to the ∣C∣ distributions indicated how often large curvatures were present in the trace or the degree of bendability. Figure 4c and d showed that hyperperiodic DNA (PPC and SQ322) accommodates high curvatures more readily than non-periodic DNA (Control and SQ100). However, it is not possible from the value of σ_C alone to attribute the increased presence of high curvatures to increased flexibility or to the presence of intrinsic bends: indeed either intrinsic curvature or unusual flexibility will widen the C distribution (Supplementary Data). Nevertheless, it is accurate to say that if the DNA does not have an intrinsic bend, then the value of σ_C directly reflects the degree of flexibility.

One characteristic feature of the C.elegans hyperperiodic sequences analyzed in this work is the distance over which substantial periodicity is maintained. In the AFM images, this corresponds to what appears to be a considerable distance over which the handedness of the curvature persists (Figure 3a). We quantified the distance D over which handedness was correlated using Equation 2. These correlation plots were computed for the PPC and the Control DNA (Figure 5a). It was observed that at a given distance D the probability of finding a curvature with the same sign was significantly higher in the hyperperiodic DNA than in non-periodic DNA. The curvature correlation increased with larger values of L. This indicates that AA/TT periodicity induces a long-scale effect in the structure of DNA and provides a strong argument for bending as opposed to flexibility, since flexibility would definitely not increase the correlation distance. In principle, the process of adsorption itself could cause switching of handedness as the DNA might flip over at certain points, leading to an underestimation of the correlation distance D, compared to the 3D structure in solution.

A complementary approach to analyze the presence or absence of long-scale correlated intrinsic bends consists of calculating the mean curvatures per molecule (Figure 5b and c). This analysis showed a maximum at zero for the non-periodic DNA samples (control and SQ100), in agreement with purely random bending. A clear peak, however, was found for both of the hyperperiodic DNA samples (PPC and SQ322), suggesting the presence of a large-scale intrinsic bend with an average curvature of ∼0.01 nm⁻¹ (at L = 5 nm). It should be noted that we underestimate the bending of the DNA, because it is not clear how the bent regions absorb to the mica, resulting in a mixture of regions with positive and negative curvature. The absence of intrinsic bending for the non-periodic SQ100 DNA suggests that its widened curvature distribution (Figure 4d) could be due to an increase in flexibility compared to the non-periodic Control (Figure 4c). For hyperperiodic DNA, however, it was not possible to address flexibility, as flexibility is convoluted by intrinsic bending in the curvature distributions. However, the variety of shapes displayed in the AFM images (Figure 3d) indicated that hyperperiodic DNA seems to be flexible enough to adopt straight and strongly bent conformations.

DNA sequences from numerous organisms have been shown to contain regions with periodic character corresponding to the helical repeat of 10–10.5 bp. Despite a number of cases in which structural roles have been assigned to relatively short periodic regions (17), the functions of extended periodic regions in DNA are unknown. Of the numerous ‘model’ genomes that have been subject to intensive analysis, C.elegans has (at least by some measures) the strongest periodicity signal (19,24). Given that 1–2% of the base pairs in the C.elegans genome appear constrained by their contribution to periodic character (19), it seems likely that these sequences have substantial roles in the evolution and/or function of the genome. One role that has been considered by virtually every investigator who has studied these sequences has been to constrain or otherwise influence nucleosome positioning. Despite these proposals, it remains a possibility that other extended surfaces in the nucleus are implicated in the observed long-range sequence relationships.

In summary, we analyzed molecules with a greater degree and extent of periodicity than any previously analyzed DNA. We used gel electrophoresis and AFM to investigate the effect of long PATCs in the structure of the genome of the nematode C.elegans. Gel electrophoresis showed that hyperperiodic DNA migrates more slowly than non-periodic DNA. We quantified trajectories of equilibrated molecules on a mica surface obtained with high-resolution AFM, and proved that the PATCs exhibit large-scale intrinsic bending. This explained the anomalous gel migration. Finally, we studied two nucleosome-length DNA fragments that survived vigorous Micrococcal nuclease digestion in situ, and likewise found the presence of an intrinsic bend for the fragment containing hyperperiodic sequences. The fragment without intrinsic bending exhibited increased flexibility. This is consistent with the idea that bendability of the DNA might be a relevant factor in promoting binding to nucleosomes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.