A Note on Permutation Tests in Multistage Association Scans

To the Editor:

There is currently a great deal of interest in performing whole-genome scans for association between genetic markers—mainly SNPs—and biological or clinical end points.¹ Often, the most cost-effective strategy for these studies is a staged design in which a subset of the full sample is genotyped for all SNPs, and only those SNPs that show a trend of association are genotyped in the remainder of the sample.²

For calculating the significance of a genome scan, permutation tests have been suggested to adjust for multiple testing while preserving the correlation structure among linked markers.³ In the staged design, however, permutation may result in a marker being selected for the second stage that had not been selected in the original analysis. Such a marker will not have been genotyped in the full sample, and data will not be available to complete the analysis of the permuted data. Recently, Lin⁴ proposed a Monte Carlo method for assessing significance in two-stage association scans. The method is sound but is limited to analysis based on efficient score functions and does not use permutation. Other investigators have reported methods to address this problem.⁵

I wish to draw attention to a property of genome scans that permits a simple permutation procedure for staged designs, which is that the sample sizes are large enough for the null distributions to be asymptotically stable. Although this observation is trivial, its utility might have escaped some readers, because of the origins of permutation testing in small-sample inference. It means that any large subset of the data can be used to simulate the null distribution. In particular, we can simulate a staged design with just the first-stage subjects, by using a subset of the first stage as the simulated first stage, selecting markers on the basis of that subset, and using the remainder of the first stage as the simulated second stage. This ensures that full genotype data are always available and will generate approximately the same null distribution as exists for the full sample.

More precisely, consider a two-stage scan of a set of markers, M, in a set of subjects, S. In the first stage, all markers in M are genotyped in a subset of subjects, S₁⊂S. An algorithm, A(M;S₁), selects a subset of markers, M₁, on the basis of the data for S₁, which are then genotyped in the remaining subjects S₂=S∖S₁. Next, perform a permutation test by using just the first-stage subjects as follows. Choose a simulated first-stage subsample, S^*₁⊂S₁, and a second-stage subsample, S^*₂=S₁∖S^*₁. After each permutation, select markers M^*₁=A(M;S^*₁). Compute statistics for markers M^*₁ in subjects S₁, and compare them with the statistics of the original data for markers M₁ in subjects S. Assume that (i) there exists an asymptotic joint null distribution of test statistics on M and (ii) subjects are exchangeable between S₁ and S₂. Then, for sufficiently large 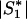, , 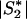and 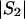, the permutation test will sample from the same null distribution (up to an arbitrary accuracy) as holds for the two-stage analysis of the full sample S.

For illustration and to confirm that the sample sizes proposed for genomewide scans are sufficiently large, a simulation was performed using 1,000 cases and 1,000 controls, which is a smaller sample than current estimates for well-powered scans.⁶ Chromosomes were drawn from the phased CEU (CEPH subjects from Utah) data of chromosome 1, released in phase 1 of the International HapMap Project.⁷ Parental chromosomes were drawn independently and grouped in pairs, and gametes were constructed using the supplied recombination maps, under the assumption of the Kosambi function with no interference between adjacent SNPs. Chromosomes of children were assigned from the constructed gametes according to Mendelian transmission and random union of gametes and were randomly assigned to the case or control group. In each replicate, 50% of subjects were used in the first stage, with the 10% most-significant markers considered in the second stage.² The significance of individual SNPs was calculated by the trend test,⁸ and empirical distributions of the maximum trend statistic were generated from 1,000 replicates.

It is sufficient to show that the two-stage analysis of the first 500 cases and controls yields the same distribution as the analysis of all 1,000. The distributions were compared by the two-sample Kolmogorov-Smirnov test and also by the Kuiper test, which is more sensitive in the tail. No significant difference was found, implying that the null distribution is indeed stable at this sample size.

The main assumption of this approach is that subjects are exchangeable between stages, meaning that the null distribution is independent of the allocation of subjects to stages. This is true when the sample population is homogeneous but not when there are systematic differences between subpopulations. In particular, different patterns of linkage disequilibrium will invalidate this approach, as will population stratification in which differences in both allele frequency and trait distribution create a relationship between the null distribution and the specific subjects analyzed. When the sample consists of known proportions of different populations, the approach can be used if the proportions in the original data are preserved in the permutation test. Also, the large-sample assumption implies that only common variation is included; this is true for Hapmap SNPs, but, if rare variation is included, the permutation test will be less accurate. Nevertheless, for most well-designed scans of common variation, this approach is a practical and easily implemented solution for permutation testing in staged designs.