Diplotype Trend Regression Analysis of the ADH Gene Cluster and the ALDH2 Gene: Multiple Significant Associations with Alcohol Dependence

Abstract

The set of alcohol-metabolizing enzymes has considerable genetic and functional complexity. The relationships between some alcohol dehydrogenase (ADH) and aldehyde dehydrogenase (ALDH) genes and alcohol dependence (AD) have long been studied in many populations, but not comprehensively. In the present study, we genotyped 16 markers within the ADH gene cluster (including the ADH1A, ADH1B, ADH1C, ADH5, ADH6, and ADH7 genes), 4 markers within the ALDH2 gene, and 38 unlinked ancestry-informative markers in a case-control sample of 801 individuals. Associations between markers and disease were analyzed by a Hardy-Weinberg equilibrium (HWE) test, a conventional case-control comparison, a structured association analysis, and a novel diplotype trend regression (DTR) analysis. Finally, the disease alleles were fine mapped by a Hardy-Weinberg disequilibrium (HWD) measure (J). All markers were found to be in HWE in controls, but some markers showed HWD in cases. Genotypes of many markers were associated with AD. DTR analysis showed that ADH5 genotypes and diplotypes of ADH1A, ADH1B, ADH7, and ALDH2 were associated with AD in European Americans and/or African Americans. The risk-influencing alleles were fine mapped from among the markers studied and were found to coincide with some well-known functional variants. We demonstrated that DTR was more powerful than many other conventional association methods. We also found that several ADH genes and the ALDH2 gene were susceptibility loci for AD, and the associations were best explained by several independent risk genes.

Several linkage studies, including the Collaborative Study on the Genetics of Alcoholism,^1–4 a study by investigators at the National Institute on Alcohol Abuse and Alcoholism,⁵ and a study involving Mission Indians,⁶ have provided evidence supporting the localization of a risk locus or loci for alcohol dependence (AD [MIM 103780]) to a region harboring the alcohol dehydrogenase (ADH) gene cluster at chromosome 4q21-25 (reviewed by Luo et al.⁷). One or more risk alleles at the ADH gene cluster may directly predispose to AD. To identify these risk alleles, association studies using linkage disequilibrium (LD) mapping methods are most commonly used, which include case-only association designs,⁷ case-control association designs, and family-based association designs.

Both case-only designs (using a Hardy-Weinberg disequilibrium [HWD] test) and case-control designs can be valid association and fine-mapping methods. However, both designs are vulnerable to population stratification that could result in spurious findings. We therefore used a structured association (SA) method based on a case-control design, a novel method developed by Pritchard et al.,⁸ to exclude population stratification and admixture effects on associations. This method and related methods have been applied in several previous studies.^e.g.,9–12 However, this method also has its limitations: (1) it does not take gene-gene interactions into account, and (2) it cannot accurately analyze haplotype data when some individuals have uncertain haplotype pairs (which are always observed when statistical inference is used to reconstruct haplotypes). The present study aims to extend this SA approach and to overcome its limitations by developing a novel method, which we call “diplotype trend regression” (DTR) analysis, a method similar to haplotype trend regression,¹³ that extends our previous application.¹¹

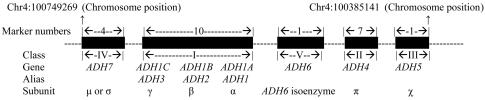
Certain ADH variants are among the best-known AD-vulnerability genes (table 1). This set of genes with partially redundant function may have created a situation relatively tolerant of functional variation in individual genes. Seven ADH genes at the ADH gene cluster are located so close together within an ∼364-kb region (fig. 1) that the LD between them cannot be neglected. Different markers within the same ADH gene could also, of course, be in strong LD. Furthermore, the expression products of different ADH genes—that is, the ADH isoenzymes—have similar amino acid sequences, structures, and properties, co-contributing to liver or stomach ADH activity, with only minor differences in preferred substrates.^37–41 Therefore, theoretically, there may be interactions among different ADH genes that cause epistasis. For example, ADH1B (MIM 103720) and ADH1C (MIM 103730) have long been considered to be independent genes influencing risk of alcohol dependence, but Chen et al.²⁹ and Osier et al.¹⁴ claimed that, on the basis of stratification analysis or regression analysis, the contribution to risk of alcoholism represented by ADH1C^∧SNP17 (Ile/Val) might actually be attributable to LD with ADH1B^∧SNP16 (Arg/His). Additionally, there may be strong physiological interactions between ADH genes and aldehyde dehydrogenase (ALDH) genes, because they appear to have the potential to exert multiplicative effects during the metabolism of alcohol: the ADHs convert alcohol to acetaldehyde, and then the ALDHs quickly convert acetaldehyde into acetate. Acetate is then oxidized via the tricarboxylic acid cycle to yield CO₂ and H₂O.

Table 1.

Positive Associations between the ADH and ALDH Genes and AD in Different Populations

Gene or Allele	Positive Finding	Population(s)	Reference(s)
SNP16*Arg (ADH2*1) allele	Increases risk for AD	Japanese, Chinese	6, 14–26
SNP16*His (ADH2*2) or SNP14*Cys (ADH2*3) allele	Protects against AD	Taiwan Atayal natives, Chinese, Europeans, Jews, AAs	6, 14–26
SNP17*Ile (ADH3*1) allele	Protects against AD	Chinese, Europeans	16, 20, 21, 23, 27, 28
SNP17*Val (ADH3*2) allele	Increases risk for AD	Chinese, Mexican Americans, American Indians	16, 20, 21, 23, 27, 28
ALDH2*1 allele	Increases risk for AD	Chinese, Japanese	20, 29–32
ALDH2*2 allele	Protects against AD	East Asians, Asian Americans	20, 29–32
ADH5 gene	Two markers related to AD	…	33
ADH4 gene	Several variants associated with AD	EAs, Brazilians	34, 35
ADH7 gene	Epistatic role in protecting against AD	Asians (majority)	36

Figure 1.

ADH gene cluster

Detection of gene-gene interactions among different ADH and ALDH genes is important for two main reasons. (1) Identifying an interaction will increase our understanding of the mechanisms through which the genes act to control expression of the trait; ignoring a true gene-gene interaction in an analysis can, erroneously, make the main effects of the genes appear nonsignificant.⁴² (2) Failing to model a gene-gene interaction in an analysis can lead to incorrect conclusions with respect to determination of the mode of inheritance and estimation of the magnitude of genetic effects.^43,44 Thus, these marker-marker or gene-gene interactions should not be neglected. When gene-gene interactions are detected, we evaluate the strength of these interactions and study the effect of each gene by controlling for the interaction effects on the trait. One common analytic method to study gene-gene interaction effects is called “stratification analysis” (discussed by Luo et al.¹¹). However, stratification analysis, through subsetting the sample, reduces statistical power for the identification of interactions. Another common analytic method to study gene-gene interaction effects is regression analysis, which directly models all the variables in a single analysis, thereby increasing the statistical power.^11,45–48 DTR is one such regression model (see the “Material and Methods” section).

Because a multilocus haplotype incorporates the LD information from single markers and also might reflect additional information from unknown neighboring markers, it has the potential to provide more information in association analysis than any single marker. But inevitably, unambiguous haplotype pairs will often be unavailable if statistical inference is used to reconstruct haplotypes. In the analysis, if we use the most likely pair (i.e., the “best pair”) of haplotypes (“reduced mode”)—which has the highest probability among all the inferred uncertain haplotype pairs in each individual—so that we can use an existing analytic method such as SA (which requires that each individual’s haplotype be identified), the bias may become significant, including LD overestimation and biased estimates of haplotype effects. If we use all possible haplotype pairs inferred (“full mode”), which may have different probabilities in one individual, the bias will be maximally reduced, and the results will therefore be a better approximation of the truth. We are not aware of any previously existing analytic method that can use this “full mode” of haplotype pairs.

Disease is a natural-selection factor; this can be reflected in HWD at a disease locus, or in markers in LD with the disease locus. One may observe HWD at a locus when an association exists between that locus and disease.⁷ Under HWD, alleles at a locus are not independent of each other, and this may invalidate allelewise analysis of that locus.^7,49 A multilocus haplotype is actually the subset of every single-locus allele; both allele and haplotype reflect the features of chromosomes in the population. Thus, under HWD, haplotypewise analysis may also be invalid. In this situation, genotypewise analysis may be the only way to draw fully valid conclusions. A diplotype (i.e., a haplotype pair) is the subset of every single-locus genotype; both genotype and diplotype represent the types of chromosome pairs in each individual. Therefore, under HWD, diplotypewise analysis may be a valid and maximally informative method. We also note that, under a recessive mode of inheritance, genotypewise and diplotypewise analyses should be considerably more powerful than allelewise and haplotypewise analyses.^7,12 DTR is a diplotypewise analytic method (see the “Material and Methods” section).

In summary, in the present study, we used a DTR method that controls for any population stratification and admixture effects, allows for unknown haplotype phase, takes marker-marker and gene-gene interactions into account, obviates the need for Hardy-Weinberg equilibrium (HWE), and avoids multiple testing due to consideration of multiple populations, multiple markers, and multiple genes.

Many studies have shown positive associations between the ADH1B, ADH1C, ADH5 (MIM 103710), ADH4 (MIM 103740), ADH7 (MIM 600086), and ALDH2 (MIM 100650) loci and AD within specific populations or have shown consistent positive findings across different populations (e.g., see table 1). For the present study, we investigated associations between AD and all ADH genes (except ADH4, which we studied previously and reported elsewhere^7,12) and ALDH2 in European Americans (EAs) and African Americans (AAs), the two most common distinct populations in the United States, and tested the population specificity of any detected associations, using DTR.

Material and Methods

Subjects

A total of 801 unrelated subjects were included in this study, as described elsewhere.¹¹ This sample includes two different populations (651 EAs and 150 AAs; the populations were classified by statistical determination of ancestry proportions, as discussed below), comprising 365 healthy controls (317 EAs and 48 AAs) and 436 cases (334 EAs and 102 AAs) and including both females (n=324) and males (n=477). The cases met lifetime DSM-IIIR or DSM-IV criteria^50,51 for AD. The control subjects were screened to exclude major axis I mental disorders, including substance-use disorders, psychotic disorders (including schizophrenia or schizophrenia-like disorders), mood disorders, and major anxiety disorders. Males constituted 75.9% of the cases and 40.0% of the controls. The average ages were 28.1±9.1 years for controls and 40.3±9.2 years for cases. The subjects were recruited at the University of Connecticut Health Center or at the VA Connecticut Healthcare System, West Haven Campus. All subjects gave informed consent before participating in the study, which was approved by the institutional review board at each institution.

Marker Selection

The present study aimed to create a basis for a future fine-mapping study with denser sets of markers at each potential risk gene. These markers were selected because (1) they were available from and validated by Applied Biosystems (ABI) or were studied in a prior publication (e.g., four ALDH2 markers were selected from the study by Peterson et al.⁵²) or (2) they had previously been reported to be associated with AD. After validation by PCR and allele-frequency evaluation in our sample, one ADH5 marker (located in a haplotype block that covers 80% of the full length of ADH5 [according to the ^ABI SNP and haplotype database]), one ADH6 (MIM 103735) marker (located in a haplotype block that covers 100% of the full length of ADH6), three ADH1A (MIM 103700) markers, four ADH1B markers, three ADH1C markers, four ADH7 markers, and four ALDH2 markers were ultimately included (table 2). Seven ADH4 markers were studied previously.^7,12 Although the results with respect to phenotype have been reported elsewhere, these data were included in this study for LD analysis. All the rs numbers for these markers were available from the SNP database (dbSNP).

Table 2.

Information and Genotyping Methods for ADH and ALDH2 Gene Markers

Marker	Alias	rs Number	Chromosome	Position	Distancea (bp)	Substitution	Amino Acid	Location	Genotyping Technique
ADH5∧SNP1	…	rs1154400	4	100468404	0	C/T	…	Exon 1	Assays-on-Demand
ADH4∧SNP2	…	rs6532795	4	100500615	32,211	T/C	…	3′	Assays-on-Demand
ADH4∧SNP3	…	rs1042364	4	100503968	3,353	G/A	Gly/Arg	Exon 10	Assays-on-Demand
ADH4∧SNP4	…	rs1126671	4	100506808	2,840	G/A	Val/Ile	Exon 8	Assays-by-Design
ADH4∧SNP5	…	rs1126670	4	100511127	4,319	T/G	Pro/Pro	Exon 7	Assays-on-Demand
ADH4∧SNP6	…	rs7694646	4	100518126	6,999	A/T	…	Intron 5	Assays-on-Demand
ADH4∧SNP7	A−75C	rs1800759	4	100523903	5,777	A/C	…	Promoter	Assays-on-Demand
ADH4∧SNP8	…	rs1984362	4	100529367	5,464	C/T	…	5′	Assays-on-Demand
ADH6∧SNP9	…	rs13104485	4	100599217	69,850	A/T	…	3′	Assays-on-Demand
ADH1A∧SNP10	…	rs6837311	4	100653667	54,450	A/T	…	5′	Assays-on-Demand
ADH1A∧SNP11	…	rs975833	4	100660133	6,466	C/G	…	Intron 7	Assays-on-Demand
ADH1A∧SNP12	…	rs1229966	4	100671827	11,694	A/G	…	3′	Assays-on-Demand
ADH1B∧SNP13	…	rs1042026	4	100686860	15,033	C/T	…	Exon 11	Assays-on-Demand
ADH1B∧SNP14	ADH2*1/3	rs2066702	4	100687411	551	C/T	Arg/Cys	Exon 10	PCR-RFLPb
ADH1B∧SNP15	C96T	rs2066701	4	100696807	9,396	C/T	…	Intron 3	PCR-RFLPc
ADH1B∧SNP16	ADH2*1/2	rs1229984	4	100697713	906	G/A	Arg/His	Exon 4	PCR-RFLPd
ADH1C∧SNP17	ADH3*1/2	rs698	4	100719183	21,470	A/G	Ile/Val	Exon 9	PCR-RFLPe
ADH1C∧SNP18	…	rs1693482	4	100722359	3,176	A/G	Gln/Arg	Exon 7	Assays-by-Design
ADH1C∧SNP19	…	rs1693427	4	100725221	2,862	C/T	…	Intron 4	Assays-on-Demand
ADH7∧SNP20	…	rs284786	4	100792371	67,150	A/T	…	Exon 11	Assays-on-Demand
ADH7∧SNP21	…	rs971074	4	100800255	7,884	C/T	Arg/Arg	Exon 7	Assays-on-Demand
ADH7∧SNP22	…	rs1573496	4	100808063	7,808	C/G	Ala/Gly	Exon 4	Assays-by-Design
ADH7∧SNP23	…	rs1154470	4	100814731	6,668	A/G	…	Intron 2	Assays-on-Demand
ALDH2∧SNP24	G−355A	rs886205	12	110667147	…f	G/A	…	5′	PCR-RFLPg
ALDH2∧SNP25	T348C	rs440	12	110691434	24,287	T/C	…	Intron 6	PCR-RFLPg
ALDH2∧SNP26	T483C	rs11613351	12	110691512	78	T/C	…	Intron 6	PCR-RFLPg
ALDH2∧SNP27	G69A	rs4646777	12	110692756	1,244	G/A	…	Intron 8	PCR-RFLPg

^aMap distance between markers.

^bPrimers: AGCTGGGATCACAGACAGATTT and GGCATCTCTATTGCCTCAAAAC; restriction endonuclease: AlwNI.

^cPrimers and restriction endonuclease are the same as those used by Osier et al.¹⁴

^dPrimers: AATCTTTTCTGAATCTGAACAG and TTGCCACTAACCACGTGGTCATCTGcG; restriction endonuclease: HhaI.

^ePrimers: ACCTCTTTCCAGAGCGAAGCAG and CTTTAAGAGTAAAGATCTGTCC; restriction endonuclease: SspI.

^fLocated at different chromosomes.

^gPrimers and restriction endonuclease are the same as those used by Peterson et al.⁵²

Thirty-eight ancestry-informative markers (AIMs) unlinked to the ADH and ALDH genes, including 37 STRs and one Duffy antigen gene (FY) marker (rs2814778), were genotyped to detect the population structure of our sample. These marker sets were employed in many previous studies,^9–12 and their characteristics have been described elsewhere⁵³ in a report that included many of the subjects in the present study.

Genotyping

By TaqMan technique

Genomic DNA was extracted from peripheral blood by standard methods. Most SNPs were genotyped with a fluorogenic 5′-nuclease assay method: the TaqMan technique.⁵⁴ PCR conditions were described elsewhere.⁷ All genotyping was performed in duplicate, and results were compared to ensure validity of the data. Mismatched genotypes, which constituted <0.5% of the total number of duplicate genotypes performed, were discarded.

By PCR-RFLP technique

Three ADH1B markers, one ADH1C marker, four ALDH2 markers, and one FY marker were genotyped by PCR-RFLP. The FY marker (rs2814778), highly informative for the ethnic ancestry of the subject, was genotyped by a PCR-RFLP technique as described elsewhere.⁵⁵ Approximately 8% of genotypes on each plate cohort were genotyped again for quality control, with complete concordance.

By fluorescence capillary electrophoresis technique

The 37 STR markers were genotyped by a fluorescence capillary electrophoresis technique with the ABI PRISM 3100 semiautomated capillary fluorescence sequencer, as described elsewhere.⁵³

Statistical Analysis

LD analysis

Pairwise LD between any two ADH or ALDH2 gene markers was analyzed separately by population (EAs and AAs). The D′ value for each LD pair was calculated and visualized using the program Haploview⁵⁶ (fig. 2).

Figure 2.

LD analysis for ADH and ALDH2 markers in EAs and AAs. a, ADH genes in EAs. b, ADH genes in AAs. c, ALDH2 gene in EAs or AAs.

HWE test

HWE was tested within populations and separately in cases and controls, by use of an exact test of goodness of fit that is implemented in the program PowerMarker, version 3.0; P values are shown in table 3. Deviation from HWE expectations (i.e., HWD) in cases can indicate a valid disease-gene association.

Table 3.

P Values for HWE Tests in Cases^[Note]

	P
Marker	EAs	AAs
ADH5∧SNP1	.037	.058
ADH1B∧SNP16	.0001	>.10
ADH1C∧SNP17	>.10	.012
ADH1C∧SNP18	.055	.035
ADH1C∧SNP19	.061	.056
ADH7∧SNP22	>.10	.016
ADH7∧SNP23	>.10	.091

Note.— Markers with P>.10 in all phenotype groups are not listed.

Genotype frequency analysis

Allele and genotype frequencies of the ADH and ALDH2 markers among EAs and AAs are shown in table 4. Genotype-phenotype associations were tested using exact tests (2 df) in the program PowerMarker; P values are listed in table 5.

Table 4.

Genotype and Allele Frequencies in EAs and AAs^[Note]

		EAs				AAs
		With AD		Controls		With AD		Controls
Marker	Genotype or Allele	n	Frequency	n	Frequency	n	Frequency	n	Frequency
ADH5∧SNP1	TT	153	.475	136	.459	46	.455	20	.417
ADH5∧SNP1	TC	127	.394	135	.456	50	.495	24	.500
ADH5∧SNP1	CC	42	.130	25	.084	5	.050	4	.083
ADH5∧SNP1	T	433	.672	407	.688	142	.703	64	.667
ADH5∧SNP1	C	211	.328	185	.313	60	.297	32	.333
ADH6∧SNP9	TT	94	.296	83	.278	73	.730	35	.729
ADH6∧SNP9	AT	156	.491	140	.468	24	.240	13	.271
ADH6∧SNP9	AA	68	.214	76	.254	3	.030	0	.000
ADH6∧SNP9	T	344	.541	306	.512	170	.850	83	.865
ADH6∧SNP9	A	292	.459	292	.488	30	.150	13	.135
ADH1A∧SNP10	TT	126	.387	106	.353	80	.808	37	.787
ADH1A∧SNP10	AT	152	.466	142	.473	19	.192	10	.213
ADH1A∧SNP10	AA	48	.147	52	.173	0	.000	0	.000
ADH1A∧SNP10	T	404	.620	354	.590	179	.904	84	.894
ADH1A∧SNP10	A	248	.380	246	.410	19	.096	10	.106
ADH1A∧SNP11	GG	198	.623	169	.569	59	.596	21	.438
ADH1A∧SNP11	CG	105	.330	108	.364	36	.364	26	.542
ADH1A∧SNP11	CC	15	.047	20	.067	4	.040	1	.021
ADH1A∧SNP11	G	501	.788	446	.751	154	.778	68	.708
ADH1A∧SNP11	C	135	.212	148	.249	44	.222	28	.292
ADH1A∧SNP12	AA	136	.421	123	.423	13	.134	3	.063
ADH1A∧SNP12	AG	141	.437	127	.436	44	.454	24	.500
ADH1A∧SNP12	GG	46	.142	41	.141	40	.412	21	.438
ADH1A∧SNP12	A	413	.639	373	.641	70	.361	30	.313
ADH1A∧SNP12	G	233	.361	209	.359	124	.639	66	.688
ADH1B∧SNP13	TT	174	.537	154	.520	83	.847	43	.915
ADH1B∧SNP13	TC	119	.367	115	.389	14	.143	4	.085
ADH1B∧SNP13	CC	31	.096	27	.091	1	.010	0	.000
ADH1B∧SNP13	T	467	.721	423	.715	180	.918	90	.957
ADH1B∧SNP13	C	181	.279	169	.285	16	.082	4	.043
ADH1B∧SNP14	CC	316	1.000	280	1.000	70	.745	24	.511
ADH1B∧SNP14	TC	0	.000	0	.000	22	.234	22	.468
ADH1B∧SNP14	TT	0	.000	0	.000	2	.021	1	.021
ADH1B∧SNP14	C	632	1.000	560	1.000	162	.862	70	.745
ADH1B∧SNP14	T	0	.000	0	.000	26	.138	24	.255
ADH1B∧SNP15	CC	131	.524	116	.487	78	.839	43	.915
ADH1B∧SNP15	TC	101	.404	101	.424	14	.151	4	.085
ADH1B∧SNP15	TT	18	.072	21	.088	1	.011	0	.000
ADH1B∧SNP15	C	363	.726	333	.700	170	.914	90	.957
ADH1B∧SNP15	T	137	.274	143	.300	16	.086	4	.043
ADH1B∧SNP16	GG	218	.956	215	.888	83	.988	41	.953
ADH1B∧SNP16	AG	8	.035	27	.112	1	.012	2	.047
ADH1B∧SNP16	AA	2	.009	0	.000	0	.000	0	.000
ADH1B∧SNP16	G	444	.974	457	.944	167	.994	84	.977
ADH1B∧SNP16	A	12	.026	27	.056	1	.006	2	.023
ADH1C∧SNP17	AA	108	.359	105	.376	57	.626	35	.761
ADH1C∧SNP17	AG	134	.445	126	.452	34	.374	10	.217
ADH1C∧SNP17	GG	59	.196	48	.172	0	.000	1	.022
ADH1C∧SNP17	A	350	.581	336	.602	148	.813	80	.870
ADH1C∧SNP17	G	252	.419	222	.398	34	.187	12	.130
ADH1C∧SNP18	GG	123	.381	113	.382	64	.640	38	.792
ADH1C∧SNP18	AG	139	.430	130	.439	36	.360	9	.188
ADH1C∧SNP18	AA	61	.189	53	.179	0	.000	1	.021
ADH1C∧SNP18	G	385	.596	356	.601	164	.820	85	.885
ADH1C∧SNP18	A	261	.404	236	.399	36	.180	11	.115
ADH1C∧SNP19	TT	115	.365	111	.370	62	.674	38	.792
ADH1C∧SNP19	TC	138	.438	132	.440	30	.326	9	.188
ADH1C∧SNP19	CC	62	.197	57	.190	0	.000	1	.021
ADH1C∧SNP19	T	368	.584	354	.590	154	.837	85	.885
ADH1C∧SNP19	C	262	.416	246	.410	30	.163	11	.115
ADH7∧SNP20	TT	166	.519	147	.497	26	.260	9	.188
ADH7∧SNP20	AT	127	.397	116	.392	56	.560	22	.458
ADH7∧SNP20	AA	27	.084	33	.111	18	.180	17	.354
ADH7∧SNP20	T	459	.717	410	.693	108	.540	40	.417
ADH7∧SNP20	A	181	.283	182	.307	92	.460	56	.583
ADH7∧SNP21	CC	241	.746	225	.771	61	.610	24	.511
ADH7∧SNP21	TC	75	.232	62	.212	35	.350	20	.426
ADH7∧SNP21	TT	7	.022	5	.017	4	.040	3	.064
ADH7∧SNP21	C	557	.862	512	.877	157	.785	68	.723
ADH7∧SNP21	T	89	.138	72	.123	43	.215	26	.277
ADH7∧SNP22	GG	249	.764	242	.796	96	.970	44	.936
ADH7∧SNP22	CG	70	.215	56	.184	3	.030	3	.064
ADH7∧SNP22	CC	7	.021	6	.020	0	.000	0	.000
ADH7∧SNP22	G	568	.871	540	.888	195	.985	91	.968
ADH7∧SNP22	C	84	.129	68	.112	3	.015	3	.032
ADH7∧SNP23	GG	133	.430	133	.455	65	.707	36	.750
ADH7∧SNP23	AG	138	.447	118	.404	27	.293	11	.229
ADH7∧SNP23	AA	38	.123	41	.140	0	.000	1	.021
ADH7∧SNP23	G	404	.654	384	.658	157	.853	83	.865
ADH7∧SNP23	A	214	.346	200	.342	27	.147	13	.135
ALDH2∧SNP24	AA	213	.705	129	.686	11	.118	5	.114
ALDH2∧SNP24	AG	83	.275	52	.277	42	.452	22	.500
ALDH2∧SNP24	GG	6	.020	7	.037	40	.430	17	.386
ALDH2∧SNP24	A	509	.843	310	.824	64	.344	32	.364
ALDH2∧SNP24	G	95	.157	66	.176	122	.656	56	.636
ALDH2∧SNP25	TT	173	.671	123	.715	62	.689	25	.581
ALDH2∧SNP25	TC	80	.310	42	.244	27	.300	17	.395
ALDH2∧SNP25	CC	5	.019	7	.041	1	.011	1	.023
ALDH2∧SNP25	T	426	.826	288	.837	151	.839	67	.779
ALDH2∧SNP25	C	90	.174	56	.163	29	.161	19	.221
ALDH2∧SNP26	TT	178	.685	117	.718	61	.678	26	.591
ALDH2∧SNP26	TC	77	.296	39	.239	28	.311	16	.364
ALDH2∧SNP26	CC	5	.019	7	.043	1	.011	2	.045
ALDH2∧SNP26	T	433	.833	273	.837	150	.833	68	.773
ALDH2∧SNP26	C	87	.167	53	.163	30	.167	20	.227
ALDH2∧SNP27	GG	146	.658	117	.701	57	.663	26	.619
ALDH2∧SNP27	AG	71	.320	44	.263	28	.326	16	.381
ALDH2∧SNP27	AA	5	.023	6	.036	1	.012	0	.000
ALDH2∧SNP27	G	363	.818	278	.832	142	.826	68	.810
ALDH2∧SNP27	A	81	.182	56	.168	30	.174	16	.190

Note.— n = number of individuals (for genotypes) or number of chromosomes (for alleles).

Table 5.

P Values of Comparisons for Genotype Frequency Distributions between Cases and Controls in EAs and AAs^[Note]

	P Beforea		P Afterb
Marker	EAs	AAs	EAs	AAs
ADH1A∧SNP11	>.10	>.10	>.10	.075
ADH1B∧SNP14	NA	.012	NA	.004
ADH1B∧SNP16	.001	>.10	.007	>.10
ADH1C∧SNP17	>.10	.040	>.10	>.10
ADH1C∧SNP18	>.10	.025	>.10	.056
ADH1C∧SNP19	>.10	.068	>.10	>.10
ADH7∧SNP20	>.10	.068	>.10	.068

Note.— Markers with P>.10 in all phenotype groups are not listed. NA = not applicable.

^a“Before” refers to conventional case-control comparison before admixture effects are controlled for.

^b“After” refers to case-control comparison after admixture effects are controlled for (SA analysis).

Fine mapping the risk alleles

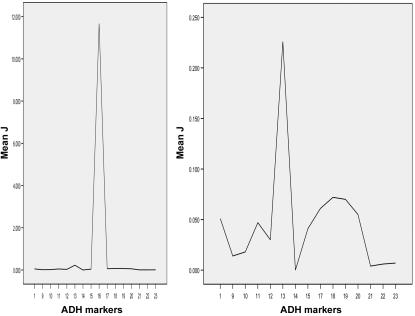
HWD of a marker in cases sometimes indicates a valid gene-phenotype association, especially when the marker is in HWE in controls.^7,11 Thus, HWD measures can be used for fine mapping a risk locus—ideally, in the situation where markers are in HWD in cases but in HWE in controls, as was often the case in the present study (table 3) and in the study by Luo et al.⁷ Many measures of HWD in case-only samples have been advanced for this purpose, including F, F^′, J, and J^′.^57,58 Among these, J is the preferred disequilibrium measure for fine mapping, because it is a direct decreasing function of the recombination fraction between the disease and the marker loci and does not depend on allele frequencies of the disease and marker loci. J can be derived from the genotype frequency data but not from the allele frequency data.^7,58 If there are several peak J values in the ADH gene cluster, this might suggest that there are several risk alleles for disease within that cluster (fig. 3). Therefore, among the many HWD measures, this statistic is best suited for fine mapping in the present application.

Figure 3.

Fine mapping the risk alleles at the ADH gene cluster in EA cases on the basis of J values. The X-axis represents the marker names; the Y-axis represents the J values. Marker numbers (which do not include markers mapped to the ADH4 gene) correspond to the order presented in table 2. The marker ADH1B^∧SNP16 (i.e., ADH2*Arg/His, with the highest J value) is included in the left figure but excluded in the right figure (to enlarge the scale of the Y-axis).

Population structure analysis

The two most common genetically distinguishable populations in the United States—EAs and AAs—have their origins in ancestral populations that migrated from multiple geographic locations in Europe and Africa, respectively. Both populations have admixture histories in recent generations in the United States, although the admixture rate for EAs is much lower than that for AAs. As reported elsewhere,^59,60 AAs are admixed primarily with EAs, and some EA individuals have (usually small) proportions of African ancestry. Thus, both of these populations were treated as potentially admixed populations in the present study.

Even when the statistical analysis is conducted separately for EAs and AAs, population stratification could still have an effect on the analysis, because admixture within these two populations could still produce spurious LD block size, confuse HWD tests, or cause spurious associations. Pritchard et al.⁸ and Falush et al.⁶¹ developed a software program, STRUCTURE, based on a model-based clustering method, that can infer ancestry proportions of an admixed sample to detect its underlying population structure by use of information from unlinked AIMs. For this purpose, we selected 38 AIMs, including 37 STR markers and 1 FY marker. The suitability of these AIMs for detecting the presence of population structure, their adequacy for providing information for assigning all individuals into different genetic ancestral populations, and the feasibility of validly analyzing them with the program STRUCTURE have already been demonstrated by many previous studies.^9–12,53 These 38 AIMs are unlinked to each other and to the ADH and ALDH2 genes. All AIMs were in HWE, and there was no LD among these AIMs, nor was there association between the AIMs and any phenotype. These AIMs are appropriate for detection of population structure without significant bias. More details of the features of this set of AIMs are provided elsewhere.^12,53

To estimate the ancestry proportions of the subjects more accurately, all subjects were studied together as a single “admixed” sample. Parameter settings for running STRUCTURE are reported elsewhere.¹²

SA analysis

In admixed populations, each individual may have ancestries from different populations, and the ancestry proportions may vary among individuals, which can cause spurious findings in association analysis. By stratifying the admixed population to nonadmixed subpopulations and then performing the association analysis within these subpopulations, spurious findings can be avoided; or, by conditioning the association analysis on the ancestry proportions of each subject, the admixture effects can be accounted for statistically and thereby eliminated. Conversely, correction of the spurious associations—for example, elimination of the associations between the 38 unlinked AIMs and any phenotypes—also indicates that the admixed populations have been successfully structured or that the admixture effects have been successfully controlled. This can be achieved by an SA analysis performed using the program STRAT.⁶² (Parameter settings for running STRAT are described elsewhere.¹²) It should be noted that the association analysis was limited to the genotypewise level, not the allelewise level, because of HWD existing among the ADH and ALDH2 markers. This SA method is also not suitable for the unphased diplotype data.

Haplotype reconstruction

The expectation-maximization (EM) algorithm, as employed by many programs that reconstruct estimated haplotypes, assumes HWE. But, in our study, the genotype frequency distributions of many markers were in HWD in the cases (table 3), which violates the assumption of the EM algorithm. This may increase the error of EM estimates, especially when the HWD is attributable to an excess of the expected heterozygote frequency over that observed.⁶³ The Bayesian approach and the partition-ligation algorithm that the program PHASE is based on have been claimed to be more accurate in reconstructing haplotypes than the EM algorithm and are valid even under HWD.^64–66 Consequently, we applied PHASE to reconstruct haplotypes and to estimate the diplotype (haplotype pair) probabilities for each subject in the present study. Parameter settings for running PHASE are presented elsewhere.¹² Haplotypes were reconstructed for “genetic” EAs (European ancestry proportion >0.5) and AAs (African ancestry proportion >0.5) rather than self-reported EAs and AAs. In the present study, all analyses conducted separately by population were performed using “genetic” EAs and AAs rather than self-reported EAs and AAs.

Alleles at the ADH gene markers that map to the cluster on chromosome 4, especially those within the same haplotype block (e.g., alleles at ADH6, ADH1A, and ADH1B) (fig. 2), can be “put” in the same haplotype, but we constructed haplotypes only within single genes because we wanted to differentiate haplotype effects among different genes. (Alternatively, interactions between different genes were considered via the regression methods described below.)

Gene-gene interaction analysis

Pairwise LD analysis between markers can direct us to the observation of marker-marker correlation. However, single markers usually cannot fully reflect the information for an entire gene. Haplotype-haplotype or diplotype-diplotype interactions might be more representative of gene-gene interaction. Haplotypes or diplotypes themselves incorporate the marker-marker LD information. A multilocus haplotype or diplotype is actually the subset of an allele or a genotype of a single marker, so haplotype or diplotype analysis is actually equivalent to stratification analysis of every single marker,⁶⁷ with the correlations among single markers already incorporated. Thus, the use of haplotype or diplotype data obviates the analysis of marker-marker interaction effects. Haplotypes or diplotypes are mutually exclusive in structure (i.e., no two haplotypes can be located on the same chromosome), and interactions among them may reflect their joint effects on the trait. To study correlations among diplotypes at different genes, a Pearson correlation analysis can be performed between any two diplotypes (a similar procedure was used by Dong et al.⁶⁸). Correlation analysis on single markers can be used as a valid LD measure.⁶⁹ Strong correlation between two intergene diplotypes suggests that these two diplotypes may have additive, or multiplicative, effects on the trait. Strong correlation between two within-gene diplotypes suggests that these two diplotypes may have similar effects on trait. Any two diplotypes within the same gene that are highly correlated can be combined as a single variable in the DTR model (if the variance inflation factor is >10),⁷⁰ or the interactions between them should be considered if they are not combined as a single variable in DTR. Only the interactions between those diplotypes having correlations with r>0.9 and P<.01 were considered in DTR.

Determined by statistical inference but not molecular experimentation, the inferred haplotype probability in each individual is usually not equal to 1.0; uncertainty remains. Thus, most individuals have several possible diplotypes even within one gene, which can be described as follows (“full mode”): the individual has a% of diplotype A (i.e., the probability is a% that A is the correct diplotype), b% of diplotype B, and [100-(a+b)]% of diplotype C (if there are three possible diplotypes). Supposing this individual’s true diplotype is A, we can look at it as a special case of the “full mode”—that is, the individual has 100% of diplotype A, 0% of diplotype B, and 0% of diplotype C. Thus, this method of analysis fits for any certain or uncertain diplotype data.

DTR analysis

A backward stepwise logistic regression analysis implemented in SPSS, version 13.0, was used to test associations between genes and diseases within “genetic” EAs and AAs (see the regression model elsewhere^11,12). Backward regression variable selection was applied. In the regression model, phenotypes served as the dependent variables, and the covariates included ancestry proportion, age, sex, genotype probabilities at ADH5 and ADH6 (we only genotyped one SNP at each of these two genes), diplotype probabilities at other genes, and interactions among genotypes or diplotypes. Age and sex were included because they were highly asymmetrically distributed between cases and controls and therefore could potentially confound the association analysis. Ancestry proportions were included in the model to control for population stratification and admixture effects. Genotype and diplotype probabilities were included, but allele and haplotype probabilities were excluded because of HWD.⁷ Genotypes at ADH5 and ADH6 and diplotypes at other genes can be entered into a single DTR model, because genotypes can be taken as supersets of diplotypes.

In the regression model, phenotype and sex are categorical variables, whereas ancestry proportion, age, genotype probability, and diplotype probability are continuous variables. The use of continuous variables, such as proportions and probabilities, preserves more information than does the use of categorical variables, such as population categories, genotype categories, and diplotype categories. We named this regression analysis that uses diplotype probability as the predictor variable “diplotype trend regression” (DTR) analysis, analogous to haplotype trend regression.¹³

(As an alternative to this DTR analysis, an even more complete analysis of “full mode” would involve the use of a true complete mixture model,^71,72 in which the probabilities of various diplotypes for each person are considered in the analysis. This was beyond the scope of the present study.)

Results

ADH markers were located in several haplotype blocks, whereas ALDH2 markers were in one haplotype block (fig. 2). Twenty-three ADH markers span 346,327 bp, covering 95% of the full length of the ADH gene cluster (364,128 bp) on chromosome 4, with an average intermarker distance of 15 kb (table 2). LD between ADH markers differs substantially between EAs and AAs (fig. 2a and 2b). Pairwise LD analysis showed that three ADH1C markers belong to one haplotype block (D^′>0.9) in both EAs and AAs. The seven ADH4 markers also belong to one haplotype block in both EAs and AAs (as described by Luo et al.⁷). The sets of markers at ADH6, ADH1A, and ADH1B belong to one haplotype block in EAs, and three markers at ADH7 belong to another haplotype block in EAs, but these markers do not define any haplotype blocks in AAs. (Markers were in much weaker LD in AAs than in EAs, possibly because AAs are an older population in which recombination may have had more time to reduce haplotype block size.) In both EAs and AAs, there were no significant differences in LD between cases and controls for these markers (data not shown).

Four ALDH2 markers, spanning 25,609 bp of the gene on chromosome 12, cover 60% of the full length of ALDH2 (table 2). LD analysis showed that these four markers were in one haplotype block in both EAs and AAs (fig. 2). Two markers, T348C and T483C, are in complete LD (D^′=1). In both EAs and AAs, there were no significant differences in LD between cases and controls for these markers (data not shown).

The genotype frequency distributions of all markers were in HWE in both EA and AA controls, but some markers were in HWD in either EA or AA cases (table 3). In EAs, all ADH and ALDH markers were in HWE in controls. However, many ADH markers were nominally in significant (P<.03), modest (.03⩽P⩽.05), or suggestive (.05<P<.09) HWD in cases (table 3), including ADH5^∧SNP1, ADH1B^∧SNP16 (Arg/His), ADH1C^∧SNP18 (Gln/Arg), and ADH1C^∧SNP19. Seven ADH4 markers were also in significant HWD in cases, as reported elsewhere.⁷ After correction for multiple testing by use of SNPSpD (an effective Bonferroni-type correction that takes marker correlation into account),⁷³ ADH1B^∧SNP16 remained in significant HWD (P=.0001).

In AAs, all ADH and ALDH markers were in HWE in controls (except ADH1A^∧SNP11 [P=.044], which we presume is because of its rare genotype frequency and the small sample size). However, many ADH markers were nominally in significant (P<.03), modest (.03⩽P⩽.05), or suggestive (.05<P<.09) HWD in cases (table 3), including ADH5^∧SNP1, ADH1C^∧SNP17 (Ile/Val), ADH1C^∧SNP18 (Gln/Arg), ADH1C^∧SNP19, and ADH7^∧SNP22 (Ala/Gly). After correction by SNPSpD, no markers remained in significant HWD.

Genotypes of some ADH markers were associated with AD (table 5). In EAs, the genotypes of ADH1B^∧SNP16 were nominally associated with AD. (Genotypes of seven ADH4 markers were also significantly associated with AD, as reported elsewhere.⁷) After correction by SNPSpD, ADH1B^∧SNP16 remained significantly associated with AD (P=.0013).

In AAs, the genotypes of many markers were nominally significantly (P<.03), modestly (.03⩽P⩽.05), or suggestively (.05<P<.09) associated with AD, including ADH1B^∧SNP14 (Arg/Cys), ADH1C^∧SNP17, ADH1C^∧SNP18, ADH1C^∧SNP19, and ADH7^∧SNP20. After multiple-comparison correction by SNPSpD, no association remained significant.

There are several peak J values among markers within the ADH gene cluster and the ALDH2 gene for AD in EAs and AAs (fig. 3). In both EAs (fig. 3) and AAs (not shown), there are several peak J values among the ADH markers that might indicate proximity of the risk alleles. The highest J peak in the ADH gene cluster is at a functional variant, ADH1B^∧SNP16 (Arg/His) (|J|=11.667 in EAs and 1.000 in AAs). Other J peaks are at the following markers (grouped by gene): (1) ADH5^∧SNP1 (|J|=0.051 in EAs and 0.439 in AAs), (2) ADH1A^∧SNP10 (|J|=1.000 in AAs) and ADH1A^∧SNP11 (6.5 kb to SNP10) (|J|=0.047 in EAs), (3) ADH1B^∧SNP13 (|J|=0.226 in EAs) and ADH1B^∧SNP14 (551 bp to ADH1B^∧SNP13) (|J|=0.112 in AAs), (4) ADH1C^∧SNP17 (|J|=0.053 in AAs) and ADH1C^∧SNP18 (3.2 kb to SNP17) (|J|=0.072 in EAs), and (5) ADH7^∧SNP20 (|J|=0.055 in EAs) and ADH7^∧SNP22 (Ala→Gly) (|J|=1.000 in AAs).

Peak J values among the ALDH2 markers were at SNP24 (|J|=0.197 in EAs) and SNP27 (|J| = 0.618 in AAs). We note that every gene had at least one marker with a J peak.

Two ancestries were detected in our sample. The genotypes of some ADH markers were associated with AD after admixture effects were controlled for. These results are almost completely consistent with, although less statistically significant than, those from the aforementioned case-control genotypewise analysis (table 5).

All subjects were assigned to two ancestral populations, Europeans and Africans; therefore, each subject has two complementary ancestry proportions. According to the ancestry proportions, the mixed sample can be separated into two distinct subpopulations: “genetic” EAs (European ancestry proportion >0.5) and “genetic” AAs (African ancestry proportion >0.5). The concordances between the “genetic” status and the self-reported ethnicity are 100% for EAs and 99.1% for AAs. Among the “genetic” EA subjects, the admixture degree is 1.7%; among the “genetic” AA subjects, the admixture degree is 4.0% (more details given elsewhere¹²). These two groups are quite distinct, not only in their asymmetric ancestry proportions, but also in the greatly different results from LD analysis, HWE tests, and case-control association analysis.

SA analysis based on this structured sample showed that, in “genetic” EAs, genotypes of ADH1B^∧SNP16 were significantly associated with AD (P=.007). In “genetic” AAs, genotypes of many markers were nominally significantly (P<.03), modestly (.03⩽P⩽.05), or suggestively (.05<P<.09) associated with AD, including ADH1A^∧SNP11, ADH1B^∧SNP14, ADH1C^∧SNP18 (Gln/Arg), and ADH7^∧SNP20. After correction by SNPSpD, no association remained significant (table 5).

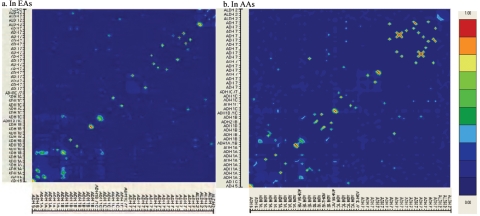
There were correlations between different diplotypes, mainly within genes (fig. 4). Within each population, the results from correlation analyses in cases and controls were similar. However, the correlations were quite different between populations. In EAs, there were significant diplotype-diplotype correlations within the ADH1B, ADH1C, ADH7, and ALDH2 genes (r>0.9; P<.01) but weak correlations between genes. In AAs, there were significant diplotype-diplotype correlations within the ADH1A, ADH1B, ADH1C, and ADH7 genes (r>0.9; P<.01). There were also diplotype-diplotype correlations between ADH1B and ADH7 in AA cases.

Figure 4.

Pairwise correlations between different genotypes (at the ADH5 and ADH6 genes), diplotypes (at other genes) in EAs (a) and AAs (b). The gene names corresponding to the genotypes and diplotypes are shown on the axes, but the detailed names of genotypes and diplotypes are not shown (the names of parts of the risk genotypes and diplotypes can be found in table 6). The colored scale denotes the correlation coefficient (r). This figure was generated using the program GOLD.⁷⁴

DTR analysis demonstrated that several genes studied were risk genes for AD (table 6). In both EAs and AAs, the genotypes of ADH5^∧SNP1 and some diplotypes at the ADH1A, ADH1B, ADH7, and ALDH2 genes were associated with AD. Some of these risk diplotypes exerted consistent effects on phenotype across EAs and AAs. For example, the diplotype TCCG/CCTG at the ADH1B gene protected against disease in both populations (β<0). Some of the risk genotypes or diplotypes exerted opposite effects on phenotype in EAs and AAs. For example, genotype C/C of ADH5^∧SNP1 and all of the diplotypes at ADH1A increased risk for disease in EAs (β>0) but protected against disease in AAs (β<0). Some of the risk diplotypes exerted effects on phenotype in EAs only. For example, the diplotype CCTG/CCTG at ADH1B and the diplotype ACGG/TCGA at ADH7 increased risk for disease in EAs (β>0). The diplotype-diplotype interaction effects occurred mainly in EAs. For example, the diplotype ATTG/ATTG and the diplotype ATTG/GCCA at ALDH2 have interaction effects on phenotype in EAs. Some of the risk diplotypes exerted effects on phenotype in AAs only—for example, the diplotypes TCCG/TCCG and TTCG/TCCG at ADH1B and the diplotype TTGG/TCGG at ADH7 protected against disease (β<0) in AAs, whereas the diplotype TCGG/TCGG at ADH7 increased risk for disease in AAs (β>0). Table 6 lists only those variables that remained in the last step of the DTR equations.

Table 6.

DTR Analysis in EAs and AAs^[Note]

Population and Variable	f	P	β
EAs:
European ancestry	…	.0678	−
Male	…	1.7 × 10−7	+
Age	…	8.7 × 10−29	+
ADH5:
C/C	…	.0124	+
ADH1A:
AGA/TGA	.203	.0109	+
AGA/TCG	.181	.0108	+
AGA/AGA	.164	.0110	+
TCG/TGA	.109	.0108	+
AGA/TGG	.088	.0109	+
TGA/TGA	.060	.0109	+
TCG/TGG	.060	.0110	+
TGA/TGG	.057	.0108	+
TCG/TCG	.055	.0112	+
ADH1B:
TCCG/CCTG	.366	.0071	−
CCTG/CCTG	.075	.0945	+
TCCA/TCCG	.058	.0005	−
ADH7:
ACGG/TCGA	.036	.0590	+
ALDH2:
ATTG/ATTG × ATTG/GCCAa	…	4.6 × 10−9	−
AAs:
Male	…	.0012	+
Age	…	.0035	+
ADH5:
T/T	…	.0042	+
ADH5:
C/T	…	.0073	+
ADH1A:
TCG/TCG	.083	.0083	−
TGA/TGA	.059	.0451	−
ADH1B:
TCCG/TCCG	.425	.0106	−
TTCG/TCCG	.270	.0089	−
TCCG/CCTG	.113	.0100	−
ADH7:
ACGG/TCGG	.216	.0259	+
ACGG/ACGG	.124	.0425	−
TCGG/TCGG	.108	.0381	+
TTGG/TCGG	.057	.0265	−
ALDH2:
GTTG/GCCA	.197	.0306	+

Note.— f = diplotype frequency in cases and controls for EAs and AAs; β = regression coefficient. Only the signs (not the values) of β are shown. Positive (+) values of β reflect increased risk of the disorder when the diplotype is present; negative (−) values reflect a protective effect of the diplotype.

^a“×” indicates interaction between diplotypes.

Discussion

Two main issues in this study warrant discussion: (1) the implications of the results in terms of the gene-phenotype relationships and (2) the properties and advantages of the DTR method. Some ADH and ALDH genes have been shown by other studies to be important risk factors for AD, mainly in Asians (table 1), but we show that they are also important in EAs and AAs, and we are the first to show that other ADH and ALDH genes are important for risk of AD in these two populations. In the present study, we found, using DTR, associations between AD and the ADH5, ADH1A, ADH1B, ADH7, and ALDH2 genes, findings that are consistent with the roles of ADH and ALDH isoenzymes in the metabolism of alcohol. We expected to find evidence of association between ADH loci and AD, but the association was surprisingly comprehensive.

These associations constitute an important part of the genetic risk for AD. This is reflected both in the overall attributable risk for this set of genes, each of which has an independent contribution to disease, and in the fact that this genomic region has consistently been identified as one that harbors AD risk-affecting loci in linkage studies.

DTR is a powerful method, and, in using it, we detected associations that were not seen using many other association methods, such as the HWD test, case-control comparison, and SA. Several features make DTR more powerful than other conventional association methods. First, DTR allows use of a case-control sample, which is easier than a family sample to collect and to expand to reach sufficient statistical power. Second, cases and controls, and even different populations, can be combined in a single DTR model, thereby increasing sample size and statistical power. Third, an unmatched case-control design has been demonstrated to be more powerful than a matched case-control design or a family-based association design in detecting gene-gene interactions, especially when the disease prevalence is moderate (such as with AD).⁷⁵ Fourth, different variables, including different genotypes and diplotypes from different genes, can be entered into a single DTR model, which avoids the multiple testing that leads to loss of information. Fifth, DTR allows analysis even in the presence of deviation from HWE. Sixth, DTR allows diplotype phase to be uncertain (in the present study, the maximal proportion of individuals with unambiguous diplotypes [i.e., probability = 1] in a single gene was only 37%; the proportion of individuals with unambiguous diplotypes across all the genes studied was only 15%). Seventh, DTR can control for population stratification and admixture effects on association analysis (assuming, of course, that ancestry coefficients are available), and it allows for the control of other potential confounders of association analysis, such as age and sex. Eighth, DTR takes into account gene-gene interactions, an approach that has been demonstrated to be more powerful than single-locus analysis (despite correction for multiple comparisons).⁷⁶ Finally, DTR is able to account for LD effects and, additionally, cis-acting functional effects. There is reason to believe that, in some cases, cis-acting elements are mediating phenotypic expression (e.g., there are variants in the promoter of a gene that influence the way other variants impact that gene’s function, so that it is necessary to know, from a functional standpoint, what specific variants are on each chromosome). These may be detected by using diplotype-based (or haplotype-based) analytic approaches but not by using other methods that employ multilocus genotype data. On the basis of these considerations, findings obtained through application of DTR have a high likelihood of being valid.

In our sample, the genotypes of all markers were in HWE in controls, but some were in HWD in cases, indicating the existence of associations between genes and disease.^{7,57,58,77–81} Comparing the results of these HWD tests with the case-control comparisons, we found two things. First, the results from these methods are largely consistent, which supports the notion that the HWD test can be a valid association method, equivalent to a case-control approach. Second, more markers were found to be associated with phenotypes by the HWD test than by case-control comparison, and P values generally were lower by the HWD test than by case-control comparison. Some P values greater than but close to .05 in the case-control study were <.05 by the HWD test; thus, the HWD test sometimes appears to be more powerful than a case-control approach, which supports the conclusions of Nielsen et al.⁷⁷ and Luo et al.⁷ This may reflect a recessive mode of inheritance.

Case-only studies and case-control studies are potentially vulnerable to population stratification, so all association analyses were performed separately for EAs and AAs. To control for admixture effects, SA was applied via the program STRAT, which gave results similar to those obtained using a case-control comparison, indicating that admixture effects were not strong in our sample. We noted that many associations from the HWD test, case-control comparison, and SA method became nonsignificant after correction for multiple tests, which indicates that these association methods often led to information loss. However, this information is preserved using DTR, which does not require adjustment of significance level for multiple tests.

Under HWD, alleles and haplotypes are not independent of one another. The effects of disease-predisposing alleles and haplotypes may be “masked” by other non–disease-predisposing alleles and haplotypes (i.e., epistatic interactions).⁸² This may be particularly true for recessive diseases, in which the non–disease-associated allele obscures an effect of the disease-associated allele. Therefore, allelewise and haplotypewise analyses might lose power or otherwise be invalid.^7,49 Since some of our markers were in HWD, exploratory allelewise and haplotypewise analyses were performed and showed fewer and less significant positive results than genotypewise and diplotypewise analyses for our sample (authors' unpublished data), which is consistent with conclusions from our other studies^7,11,12 about the relative power of these methods in an HWD situation. Genotypewise and diplotypewise analyses may be valid even under HWD, and therefore they served as the primary analyses in the present study.

The HWD test, case-control comparison, and SA analyses cannot correct for interaction effects between markers and between genes. Diplotypes incorporate the LD information from different markers, and the interactions between diplotypes can be considered in the DTR model. A diplotype is more representative of gene background than is a single genotype, and diplotype-diplotype interactions from different genes are more representative of gene-gene interactions than are marker-marker interactions. Therefore, DTR works well with respect to the evaluation of gene-gene interactions.

Under HWD, the EM algorithm is not suitable for reconstructing diplotypes. However, in the DTR model, we used the diplotype probabilities predicted by the program PHASE that waived the HWE assumption. When the PHASE approach to haplotype reconstruction is used, DTR is thus also independent of the HWE assumption.

In summary, our findings by DTR analysis include the following points. (1) In EAs and/or AAs, the genotypes of ADH5^∧SNP1 and the diplotypes at the ADH1A, ADH1B, ADH7, and ALDH2 genes are associated with AD. Some associations are universal across both populations. Some associations have opposite effects in different populations (suggesting that the actual risk-influencing variant is in a different phase in the two populations, or, alternatively, that there are differing epistatic effects). Some associations are population specific—that is, some associations appear only in EAs or in AAs (table 6). (2) Most associations from DTR analysis are much more significant than those from other association methods. DTR detected strong associations between ALDH2 and disease that were not observed at all by use of other association methods—including a multilocus genotype data analysis with a regression method (the results of which were similar to the single-locus genotype frequency analysis in table 5; data not shown), which may reflect a cis-acting functional effect in this gene. (3) The correlations between the genes are weak. But within the genes, diplotype-diplotype correlations are strong, which include those within ADH1A in AAs, ALDH2 in EAs, and ADH1B, ADH1C, and ADH7 in both populations (data not shown). Considering these correlations by DTR, only a significant interaction effect between two diplotypes within ALDH2 was detected in EAs (table 6). Additionally, we found that ADH1C diplotypes were significantly associated with drug dependence, one of the disorders most commonly comorbid with AD (authors' unpublished data).

Markers can be dependent on one another (i.e., correlated) without being in complete LD, or their dependence may not be statistically significant, so that the effects of markers on traits can be decomposed into main effects and interaction effects. If an interaction effect is strong, one marker can “mask” the main effect of another marker.⁸² The interaction effect depends on the correlation between markers and is related to the trait of interest. Correlation between markers per se (such as LD) depends on the physical distance between markers, the allele frequencies of markers, population history, and the nature of the traits, including the definition of phenotypes (e.g., mutation-related disease), sample size, and ethnicity. Several of these factors—notably, allele frequencies and population history—also vary between populations. Therefore, the interaction effects of markers are affected by many factors. Such effects may also be population-specific. In the present study, ADH1B^∧SNP16 (Arg/His) was associated with AD in EAs (P=.001), and ADH1C^∧SNP17 (Ile/Val) was associated with AD in AAs (P=.040) (table 5). Our EA sample size was relatively large, and the correlation between ADH1B^∧SNP16 and ADH1C^∧SNP17 was weak (D^′=0.758; r²=0.019; P=.463>.05). In our AA sample, the correlation between these two markers was also weak (D^′=0.900; r²=0.004; P=.231>.05; here, we interpret the high D′ as being reflective of the different allele frequencies for the two markers). Thus, the interaction effect of these two markers was weak, but the main effect was strong in both populations (by use of regression analysis). Even with this interaction effect taken into account via stratification analysis, as per Osier et al.,¹⁴ the main effects of these two markers did not change significantly (data not shown), and the effect of ADH1B^∧Arg/His and that of ADH1C^∧Ile/Val did not modify each other significantly in our samples. These findings are not consistent with those reported by Osier et al.,¹⁴ who claimed that the contribution of ADH1C^∧Ile/Val to risk for AD was actually attributable to LD with ADH1B^∧Arg/His in the Taiwanese Chinese population. This inconsistency may result from the population specificity of the interaction effects; in other words, this effect could be weak in EAs and AAs but strong in Taiwanese Chinese.¹⁴ However, the conclusion by Osier et al.¹⁴ may simply be incorrect, given the following points. (1) Their sample size (n=135) was small. Such a sample size might result in type I error in analysis of interaction effects. (2) The use of a stratification analytic method, and not a regression method, to consider the marker-marker interaction effects could reduce power, because dividing the sample (i.e., into nine subgroups based on three genotypes for each marker) further reduces the sample size. Moreover, this should have occasioned correction for multiple comparisons. (3) The reported D′ of 0.77 between the ADH1B^∧Arg/His and ADH1C^∧Ile/Val variants¹⁴ does not constitute strong enough disequilibrium for the markers to be in the same haplotype block (as defined by Gabriel et al.⁸³); markers should usually show higher LD to exert interaction effects on traits through that mechanism. Increasing the sample size may help to clarify whether this D′ value was accurate and whether such LD can result in as strong an interaction effect in Taiwanese Chinese as that reported by Osier et al.¹⁴ (4) Finally, two markers represent only two points or two haplotype blocks in genes; a marker-marker interaction effect is not sufficient to represent a gene-gene interaction effect (that is, additional markers at these two loci might not have any interaction effects at all). It may therefore have been excessive to state that the ADH1C gene exerted its effect via the ADH1B gene in all populations, especially because the authors tested only two markers in a small sample of a specific population. Our design overcomes these particular limitations, and we were able to demonstrate that these two genes exert independent main effects on phenotype—at least in EA and AA populations.

The multiplicity of gene effects that we observed (several ADH genes and the ALDH2 gene were associated with AD) confirms that these disorders are multigenic—minor effects from different genes produced additive effects on risk for AD. This is consistent with the roles of different ADH and ALDH isoenzymes in contributing to alcohol metabolism (although different isoenzymes have minor differences in the preferred substrates). Although the activity of ADH1 enzyme (α subunit) is weak in adults, the ADH1A gene still has effects on risk for AD.

Replacing multilocus diplotypes with single-locus genotypes in the DTR model can be done to fine map the risk locus (data not shown). One advantage of DTR as a fine-mapping method is that it allows for marker-marker interactions, so that the confounding effects of these interactions can be accounted for. However, DTR fine mapping is limited by the fact that it does not control for the influence of the allele frequency of markers.¹² The best approach for fine mapping would be to combine DTR with HWD measures—that is, use DTR to screen potential susceptibility genes and then use an HWD measure, such as the J value, to fine map the risk alleles within those genes. In the present study, the results from fine mapping with a J value (fig. 3) are basically consistent with those from HWD tests (table 3) and case-control comparisons (table 5).

We noted that every gene had at least one marker with a J peak. This suggests that, despite the fact that LD is sometimes present between markers at different genes, association signals are actually originating within the genes that show J peaks, which is consistent with the DTR results. Interestingly, we localized some risk alleles close to well-known functional variants, such as ADH1B^∧SNP16 (Arg/His; previously called “ADH2*1/2”), ADH1B^∧SNP14 (Arg/Cys; previously called “ADH2*1/3”), ADH1C^∧SNP17 (Ile/Val; previously called “ADH3*1/2”), and ADH7^∧SNP22 (Ala→Gly), which is consistent with findings from the existing literature (listed in table 1) and supports the validity of our findings. Among these peaks, the J value at ADH1B^∧SNP16 for AD in EAs is extremely high (11.667) and is consistent with the significance levels from HWD tests and case-control comparisons, suggesting either that this marker is extremely close to the disease locus at the ADH1B gene or that the marker might be the disease locus itself. In future studies aimed at fine mapping the risk alleles, a denser set of markers at each risk gene will be required. This is a necessary next step in understanding the complex association between the genes encoding multiple alcohol-metabolizing enzymes and AD in a variety of populations.