Abstract
Nonparametric linkage strategies often involve estimation of identity by descent (IBD) with the use of affected sibling pairs. Methods for IBD estimation are well established and have been successful for mapping complex traits. However, the majority of linkage approaches involving IBD have focused on statistical testing, rather than on the effect estimates themselves. Through a bootstrap procedure developed for linkage-scan data sets, we provide standard errors for the estimated mean IBD that are broadly applicable. Applications that benefit from the availability of standard errors include effect-size estimates and confidence intervals; meta-analyses, including tests for heterogeneity; and discordant-sibling-pair evaluation. We demonstrate the use of estimated mean IBD and its standard errors in the National Institute of Mental Health Human Genetics Initiative linkage samples for bipolar disorder and Alzheimer disease. Mean IBD and its standard errors are valuable tools for the further assessment and evaluation of linkage-scan samples involving complex disease.
A popular strategy for NPL analysis involves the estimation of allele sharing among affected relative pairs. Variations of affected-relative-pair strategies are implemented in some of the more popular linkage analysis software packages, including GENEHUNTER,1 GENEHUNTER-PLUS,2 ALLEGRO,3 MERLIN,4 and SAGE. Irrespective of the explicit analytic approach, the majority of these strategies estimate the probability of sharing zero, one, or two alleles identical by descent (IBD).
A seminal paper in the 1970s by Haseman and Elston5 introduced the Haseman-Elston method, which brought the use of IBD estimation to the forefront of NPL analysis for quantitative traits. For methods designed explicitly for binary traits, IBD estimation in affectedsibling-pair (ASP) samples has typically been at the core of such approaches. Existing approaches to IBD-based methods include comparing the observed sharing of zero, one, and two alleles IBD (p0, p1, and p2) with the expectation under the null hypothesis of no linkage (0.25, 0.50, and 0.25), in which the primary intent is to construct a test statistic that provides evidence either for or against linkage. Under fully informative conditions (i.e., IBD is known with certainty for each ASP), a variety of test statistics have been proposed that manipulate the degree of excess allele sharing observed among ASPs.6 Alternatively, under more-realistic scenarios where IBD cannot be observed exactly, likelihood-based methods were developed to compare the likelihood of sharing zero, one, or two alleles IBD with the likelihood of that under the null hypothesis of no linkage.7
The majority of NPL methodologies using IBD of ASPs have focused on constructing test statistics rather than on the IBD estimates themselves. We focus here on obtaining valid SEs and CIs for estimated mean IBD (IBDm), which can be used for assessing heterogeneity, combining across studies, and evaluating sharing patterns for different sibling-pair configurations. To provide easily computed SEs that are applicable in any sample design, we use a bootstrap procedure. The use of the bootstrap to obtain SEs is a standard, albeit possibly computationally intensive, statistical approach.8 Our implementation avoids repeating the Lander-Green algorithm on each bootstrap sample, resulting in a simple and computationally feasible method.
Methods
The probability of sharing i alleles IBD (pi) is estimated via maximum likelihood (ML), with the use of the approach described by Risch7 combined with the Lander-Green algorithm for using all family members and all marker data to extract full information about IBD. Our proposed use of IBDm for linkage studies requires a valid estimate of the variance of IBDm, without the assumption that the null hypothesis is true. We define IBDm (π) in the following way:
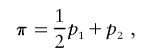 |
where p1 is the probability of sharing one allele IBD and p2 is the probability of sharing two alleles IBD. Most of the linkage analysis software packages use the expectation-maximization (EM) algorithm to provide likelihood estimates of IBDm that are constrained to fit the triangle constraints,9 such that IBDm must be ⩾0.5. For the present analysis, we chose to calculate the unconstrained estimates, since the constraints are not always appropriate. For example, it has been shown that constraining IBD estimates in the presence of heterogeneity may reduce the power to detect linkage.10 In addition, combining estimates over studies is more meaningful with the unconstrained estimates, since values of IBDm are allowed to converge at their maxima, irrespective of whether they fit into Holmans’s triangle.
To calculate the unconstrained estimates of IBD, we use a custom-written program (written in SAS, available from the corresponding author upon request) that inputs the pairwise IBD estimates generated from either GENEHUNTER (“dump ibd”) or MERLIN (“–ibd”). Conceptually, these estimates can be thought of as the probability of sharing zero, one, or two alleles IBD per sibling pair under the null hypothesis of no linkage and as conditional on all of the observed marker information in the family. We then use the EM algorithm to maximize the estimates of IBD over all pairs (p0, p1, and p2),7 and we calculate 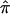 without the use of constraints. The pairwise IBD estimates are used to calculate starting values for the EM algorithm and to compute the expectations in the expectation step. They also play a key role in the bootstrap calculations, as discussed below, because they are, effectively, a summary of all the relevant IBD information in each family. For more details on the use of the pairwise IBD estimates, see appendix A.
without the use of constraints. The pairwise IBD estimates are used to calculate starting values for the EM algorithm and to compute the expectations in the expectation step. They also play a key role in the bootstrap calculations, as discussed below, because they are, effectively, a summary of all the relevant IBD information in each family. For more details on the use of the pairwise IBD estimates, see appendix A.
A simple approach to estimate the variance of 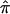 is to assume (1) that IBD can be observed directly for each pair of siblings and (2) that sibling pairs are independent. Then, the sample forms a trinomial distribution,11 and the variance of
is to assume (1) that IBD can be observed directly for each pair of siblings and (2) that sibling pairs are independent. Then, the sample forms a trinomial distribution,11 and the variance of 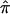 is easily calculated as
is easily calculated as
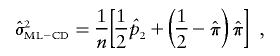 |
where n is the number of sibling pairs. Under the assumption of complete IBD information and independent pairs, this is also the appropriate ML variance. Hence, we refer to this as the “complete data ML” (ML-CD) formula, since it reflects the appropriate ML large sample SEs if IBD is observed correctly and if pairs are independent.
When IBD is not observed directly, we can use the incomplete data ML (ML-ID) approach outlined in Risch,7 coupled with the asymptotic variance estimation discussed in Meilijson,12 to derive a closed-form expression for the variance of the ML estimate based on the empirical information matrix, again with the assumption of independent pairs. Details of the ML-ID variance (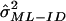 ) are available in appendix A.
) are available in appendix A.
Alternatively, estimation of the variance of 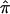 can be conducted through a bootstrap procedure, following Efron and Gong.8 The proposed bootstrap procedure for calculating the variance of
can be conducted through a bootstrap procedure, following Efron and Gong.8 The proposed bootstrap procedure for calculating the variance of 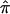 uses the same pair-specific unconstrained IBD estimates as are used above, as well as the unconstrained
uses the same pair-specific unconstrained IBD estimates as are used above, as well as the unconstrained 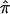 . In the context of linkage samples, we propose the following bootstrap strategy:
. In the context of linkage samples, we propose the following bootstrap strategy:
-
1.
Sample, with replacement, n families from all families, to obtain a bootstrap sample. In this step, we actually sample the pairwise IBD estimates, not the raw data for each family. Thus, the Lander-Green algorithm is not repeated for each bootstrap sample. If all founders have genotype data, or if estimates of allele frequencies that do not depend on the sample are used for the Lander-Green algorithm, then the pairwise IBD estimates for a family depend only on the data from that family and provide all the information needed from the family to calculate the ML estimates. When founder genotype data are missing and the sample is used to estimate allele frequencies, there may be a slight dependence of the pairwise IBD values on the composition of the sample, which introduces additional variability that can be controlled by redoing the Lander-Green algorithm separately for each bootstrap sample.
-
2.
Using all sibling pairs in the bootstrap sample, obtain the unconstrained
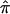 as outlined above.
as outlined above. -
3.
Repeat steps 1 and 2 for B replicates, where B is the number of bootstrap replications.
-
4.
Calculate the variance, using the bootstrap formula (eq. [1]).
Note that the bootstrap procedure can be performed on either ASPs or discordant sibling pairs (DSP) from the same bootstrap samples. Specifically, if 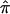 *b denotes the estimate of
*b denotes the estimate of 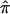 (for either ASPs or DSPs) from the bth bootstrap replicate, the bootstrap variance estimate is
(for either ASPs or DSPs) from the bth bootstrap replicate, the bootstrap variance estimate is
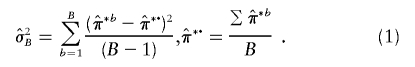 |
Further, the covariance between the 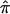 for ASPs and that for DSPs can be obtained from the sample covariance from the bootstrap samples, as an extension of equation (1).
for ASPs and that for DSPs can be obtained from the sample covariance from the bootstrap samples, as an extension of equation (1).
The advantage of the ML-CD formula is that it is easy to calculate. However, the complete-data formula makes strong assumptions about the estimation procedure. It assumes (1) that IBD is observed directly (i.e., that there is no missing information) and (2) that pairs are independent. In the context of missing parental information, as well as multipoint strategies of estimating IBD at chromosomal positions between genotyped markers, these assumptions may result in an underestimation of the variance. In addition, since some families in linkage studies have more than one sibling pair, the assumption of independence is not valid unless information is discarded. An alternative to the complete-data approach is ML-ID. An advantage of ML-ID over ML-CD is that ML-ID does not assume that IBD is observed directly and, thus, allows for the uncertainty in the estimation procedure. Nonetheless, ML estimation of the allele sharing, as currently implemented in standard packages, is based on a likelihood that assumes independent pairs. Thus, ML-ID is subject to some of the same issues as those found with the ML-CD formula. In contrast, use of the bootstrap circumvents both the assumptions of no missing data and of independent pairs. Finally, we note that neither ML variance formula is appropriate if the triangle constraints are used, but the bootstrap approach easily adapts to this setting by constraining the estimates in each bootstrap sample.
Application
Here, we characterize and demonstrate the application of the bootstrap variance, using the three waves of the National Institute of Mental Health (NIMH) Bipolar Disorder (BP) Human Genetics Initiative linkage analysis data sets. We also show the application to the NIMH Alzheimer’s Disease (AD) Human Genetics Initiative linkage samples. All data sets are available via the NIMH Human Genetics Initiative Web site. Applications presented here include effect-size estimates and CIs for 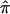 , a traditional meta-analytic approach, and an exploratory assessment of the
, a traditional meta-analytic approach, and an exploratory assessment of the 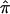 difference between ASPs and DSPs.
difference between ASPs and DSPs.
NIMH BP Data Sets
Details relevant to ascertainment, assessment, diagnosis, genotyping, and linkage findings from each of the NIMH BP Human Genetics Initiative samples can be found in each primary reference,13,14 respectively (see also the NIMH Human Genetics Initiative Web site). For the purposes of this analysis, we chose to focus on sibling pairs diagnosed using the DSM-IIIR (wave 1) or the DSM-IV (waves 3 and 4) criteria of bipolar disorder I (BPI). Siblings who have diagnoses of other affective disorders (i.e., bipolar disorder II or recurrent unipolar depression) were coded as “unknown” for both ASP and DSP analysis. Therefore, we define ASPs as sibling pairs in which both siblings have a BPI diagnosis, and we define DSPs as sibling pairs in which one sibling has a BPI diagnosis and the other sibling has no known affective disorder diagnosis. The numbers of ASPs and DSPs are provided in table 1. The number of ASPs varies across data sets, and wave 4 has the largest number of ASPs (338). Similarly, the number of DSPs ranges from 213 in wave 3 to 20 in wave 1. Collection of blood and family history information for the NIMH BP data sets was done with informed consent and was approved by the institutional review boards.
Table 1.
Description of the NIMH Genetics Initiative Linkage Samples
| Data Seta | No. of Families |
No. of Individuals |
No. of ASPs |
No. of DSPs |
| NIMH BP wave 113 | 95 | 525 | 95 | 20 |
| NIMH BP wave 314 | 220 | 982 | 255 | 213 |
| NIMH BP wave 4 | 274 | 1,053 | 338 | 193 |
| NIMH AD15 | 437 | 1,439 | 151 | 255 |
All data sets were obtained through the NIMH Human Genetics Initiative Web site, and all were of mixed ethnicity.
NIMH AD Data Set
Details relevant to ascertainment, assessment, diagnosis, genotyping, and linkage findings from the NIMH AD Human Genetics Initiative sample can be found in the primary reference.15 The total sample for the present analyses comprises 1,439 individuals from 437 families, including 994 affected individuals, 411 unaffected, and 34 with phenotype unknown. We define ASPs as sibling pairs in which both siblings have a diagnosis of AD (age at onset between 50 and 70 years). We define DSPs as sibling pairs in which one sibling has AD (age at onset between 50 and 70 years) and the other sibling has no known psychiatric diagnosis. All other diagnoses (and ages at onset) are coded as “unknown.” The number of ASPs in this sample is 151, and the number of DSPs is 255 (table 1). Collection of blood and family history information for the NIMH AD data set was done with informed consent and was approved by the institutional review boards.
SE Estimates of IBDm
We compare the bootstrap approach with the ML-ID and ML-CD approaches, using both independent ASP samples and full ASP samples of the NIMH BP wave 3 data as well as the NIMH AD data set. We used the linkage region on chromosome 6 reported elsewhere for the NIMH BP wave 3 data14 and the established linkage region on chromosome 19 (apolipoprotein-E [APOE] gene region) for the NIMH AD data set.15 Each data set is broken down in two different ways. First, one randomly selected ASP is used per family. Second, the entire sample of available ASPs is used. The SE is then calculated for each data subset.
Traditional Meta-Analysis and Heterogeneity Assessment
Following a traditional meta-analytic approach, we used estimates of 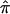 sharing and the proposed bootstrap variance to quantify heterogeneity among the three NIMH BP data sets at particular regions along the genome. Using the unconstrained estimates of sharing zero, one, or two alleles IBD (p0, p1, and p2) for ASPs, we calculated the
sharing and the proposed bootstrap variance to quantify heterogeneity among the three NIMH BP data sets at particular regions along the genome. Using the unconstrained estimates of sharing zero, one, or two alleles IBD (p0, p1, and p2) for ASPs, we calculated the 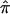 separately for each study. Note that using the unconstrained probabilities means that the estimated
separately for each study. Note that using the unconstrained probabilities means that the estimated 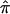 for a study can be <0.5, whereas using the constraints forces it to be at least 0.5. To derive the variance of the
for a study can be <0.5, whereas using the constraints forces it to be at least 0.5. To derive the variance of the 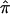 , we used the proposed bootstrap procedure. The Q-statistic was used to provide a formal test of heterogeneity.16 Then, continuing along the traditional meta-analytic path, we pooled the study-specific estimates of
, we used the proposed bootstrap procedure. The Q-statistic was used to provide a formal test of heterogeneity.16 Then, continuing along the traditional meta-analytic path, we pooled the study-specific estimates of 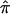 , using a random-effects model16 that allows for the incorporation of between-study heterogeneity and, therefore, provides a more realistic summary measure of IBDm (
, using a random-effects model16 that allows for the incorporation of between-study heterogeneity and, therefore, provides a more realistic summary measure of IBDm (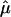 ), as well as more accurate CIs. Gu et al.11 provides a detailed description of this general approach in the context of ASP linkage samples. Further, we provide more information on this approach in appendix B.
), as well as more accurate CIs. Gu et al.11 provides a detailed description of this general approach in the context of ASP linkage samples. Further, we provide more information on this approach in appendix B.
IBDm Difference Between ASPs and DSPs
There is mounting evidence that unselected sibling pairs tend to share more than half of their alleles IBD.17 This introduces potential biases for linkage studies that employ ASP methodology, since they assume uniform 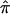 =0.5 across the genome, under the null hypothesis. One strategy to assess whether this potential bias exists is to estimate IBD and its variance with the use of DSPs at a suspected region of linkage. If DSPs tend to share alleles IBD at or near the expectation under the null hypothesis of no linkage (
=0.5 across the genome, under the null hypothesis. One strategy to assess whether this potential bias exists is to estimate IBD and its variance with the use of DSPs at a suspected region of linkage. If DSPs tend to share alleles IBD at or near the expectation under the null hypothesis of no linkage ( 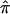 =0.5), then it follows that excess allele sharing detected in the ASPs is related to affection status rather than to distorted transmissions. To explore the difference between ASPs and DSPs, with respect to
=0.5), then it follows that excess allele sharing detected in the ASPs is related to affection status rather than to distorted transmissions. To explore the difference between ASPs and DSPs, with respect to 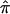 , we used the NIMH AD data set to qualitatively compare the allele sharing between ASP and DSP near the region that harbors the APOE gene on chromosome 19q, as well as the region on chromosome 12 that harbors the alpha-2-macroglobulin gene (A2M). The APOE region is an established linkage region to AD. The A2M gene has been reported to be strongly associated with AD in this sample.18 Further, the A2M region on chromosome 12 has shown modest linkage to AD in other AD data sets; however, no strong linkage evidence has been established in the NIMH AD sample.15
, we used the NIMH AD data set to qualitatively compare the allele sharing between ASP and DSP near the region that harbors the APOE gene on chromosome 19q, as well as the region on chromosome 12 that harbors the alpha-2-macroglobulin gene (A2M). The APOE region is an established linkage region to AD. The A2M gene has been reported to be strongly associated with AD in this sample.18 Further, the A2M region on chromosome 12 has shown modest linkage to AD in other AD data sets; however, no strong linkage evidence has been established in the NIMH AD sample.15
Results
SE Estimates of IBDm
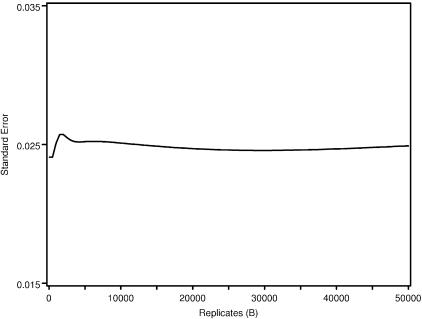
Figure 1 is a plot of the SE as a function of the number of bootstrapped replicates (B=50,000) among all ASPs in the NIMH BP wave 3 data on chromosome 6, at ∼120 cM. This region of chromosome 6 in the NIMH BP wave 3 sample has been implicated elsewhere as being linked to BP.14 As can be seen in the plot, estimates of SE stabilize at or near 5,000 replicates. On the basis of the results of this plot, we adopted the B=5,000 replicate strategy for all variance calculations via the bootstrap.
Figure 1.
The SE of 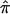 as a function of the number of bootstrapped replicates, for the NIMH BP wave 3 data set on chromosome 6, at ∼120 cM.
as a function of the number of bootstrapped replicates, for the NIMH BP wave 3 data set on chromosome 6, at ∼120 cM.
Table 2 displays the SEs of 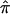 , as calculated using the ML-CD, ML-ID, and bootstrap strategies for both the NIMH BP wave 3 data (chromosome 6, 110 cM) and the NIMH AD data set (chromosome 19, 60 cM). The
, as calculated using the ML-CD, ML-ID, and bootstrap strategies for both the NIMH BP wave 3 data (chromosome 6, 110 cM) and the NIMH AD data set (chromosome 19, 60 cM). The 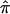 s are essentially the same for both the independent and nonindependent ASP subsets, in both the BP and AD data. This is in line with the expectation that the presence of nonindependence has little impact on an effect-size estimate such as
s are essentially the same for both the independent and nonindependent ASP subsets, in both the BP and AD data. This is in line with the expectation that the presence of nonindependence has little impact on an effect-size estimate such as 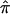 . The SE for the independent ASP sample was higher than that for the full ASP sample, which is likely a reflection of the smaller sample size attributable to the independent ASP subset. The ML-CD approach generates substantially smaller SEs for both the independent ASP samples and the full samples, which is consistent with the fact that the ML-CD approach assumes complete information. In contrast, there is little difference between the bootstrap and the ML-ID variance estimates, either for the independent ASP samples or for the full samples. When the independent ASP subset is used, the ML-ID is close to that of the bootstrap variance, since the assumption of independence is valid for this particular sample. We also bootstrapped the raw data to generate new pairwise IBD estimates, using the smallest data set (NIMH wave 1), and found the results to be the same (data not shown).
. The SE for the independent ASP sample was higher than that for the full ASP sample, which is likely a reflection of the smaller sample size attributable to the independent ASP subset. The ML-CD approach generates substantially smaller SEs for both the independent ASP samples and the full samples, which is consistent with the fact that the ML-CD approach assumes complete information. In contrast, there is little difference between the bootstrap and the ML-ID variance estimates, either for the independent ASP samples or for the full samples. When the independent ASP subset is used, the ML-ID is close to that of the bootstrap variance, since the assumption of independence is valid for this particular sample. We also bootstrapped the raw data to generate new pairwise IBD estimates, using the smallest data set (NIMH wave 1), and found the results to be the same (data not shown).
Table 2.
The ML-CD, ML-ID, and Bootstrap SEs
| Data Seta | Chromosome | Position (cM) |
No. of Pedigreesb |
No. of ASPs |
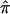 |
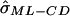 |
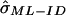 |
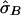 c c
|
| BP one | 6 | 110 | 182 | 182 | .5929 | .02530 | .02965 | .02915 |
| BP full | 6 | 110 | 182 | 255 | .5980 | .02062 | .02419 | .02429 |
| AD one | 19 | 60 | 89 | 89 | .7030 | .03696 | .04393 | .04483 |
| AD full | 19 | 60 | 89 | 151 | .6775 | .02735 | .03353 | .03661 |
BP = NIMH BP wave 3; AD = NIMH AD sample. One = one randomly selected ASP per family; full = all ASPs.
For the NIMH BP wave 3 data set, only families with at least one sibling pair with BPI are included. For the NIMH AD data set, only families with at least one sibling pair with AD onset between 50 and 70 years of age are included.
Bootstrap based on 5,000 replicates.
Traditional Meta-Analysis Application
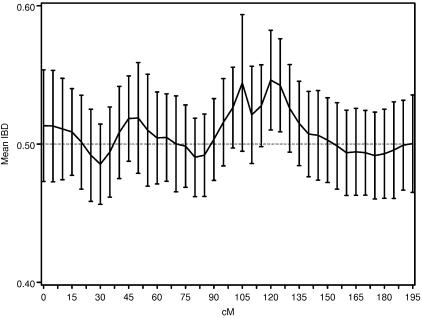
The results of the more traditional meta-analytic strategy of combining IBDm estimates across data sets, while allowing for possible between-study heterogeneity, support the previous reports of linkage to BP in this region.14 In the chromosomal regions that were reported to generate the linkage signals, there was little evidence of heterogeneity among data sets, as tested via the Q-statistic (table 3). However, modest evidence of heterogeneity is found in the 105–110-cM region, with P values of .01 and .02. The summary IBDm estimates (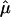 ) for chromosome 6 are shown in figure 2. The error bars reflect the 95% CIs, and regions where the CIs cross the null (
) for chromosome 6 are shown in figure 2. The error bars reflect the 95% CIs, and regions where the CIs cross the null (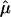 =0.50) provide no evidence overall of excess allele sharing among ASPs. Regions where the lower bound of the 95% CI is >0.50 provide evidence for excess allele sharing in the combined sample. In the 120–125-cM region, the 95% CIs do not include 0.50, and, thus, evidence for excess allele sharing exists at those regions. Note that these CIs are not adjusted for genomewide comparisons.
=0.50) provide no evidence overall of excess allele sharing among ASPs. Regions where the lower bound of the 95% CI is >0.50 provide evidence for excess allele sharing in the combined sample. In the 120–125-cM region, the 95% CIs do not include 0.50, and, thus, evidence for excess allele sharing exists at those regions. Note that these CIs are not adjusted for genomewide comparisons.
Table 3.
Test for Heterogeneity among NIMH BP Data Sets on Chromosome 6
| Position (cM) |
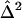 a a
|
Q | P Value |
| 100 | 0 | 2.2 | .54 |
| 105 | .0025 | 8.4 | .01 |
| 110 | .0024 | 7.1 | .02 |
| 115 | 0 | 2.9 | .40 |
| 120 | 0 | 2.7 | .45 |
| 125 | 0 | 2.6 | .43 |
| 130 | 0 | 2.8 | .45 |
| 135 | 0 | 2.5 | .33 |
| 140 | 0 | 3.2 | .21 |
Between-study variance.
Figure 2.
Random effects summary IBDm (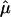 ) and 95% CIs across chromosome 6, for the three waves of the NIMH BP data.
) and 95% CIs across chromosome 6, for the three waves of the NIMH BP data.
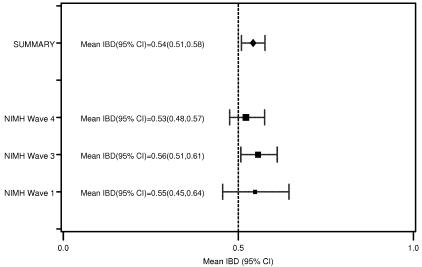
With regard to the 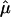 plot in figure 2, we identified the location that displayed the most significant allele sharing for chromosome 6 and provided a forest plot of the
plot in figure 2, we identified the location that displayed the most significant allele sharing for chromosome 6 and provided a forest plot of the 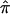 and 95% CIs for each of the component data sets, as well as the
and 95% CIs for each of the component data sets, as well as the 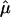 estimate and 95% CI (fig. 3). We selected the 120-cM position for chromosome 6. The effect estimates and 95% CIs for each of the three NIMH BP data sets are shown in figure 3. The only data set that shows statistically significant allele sharing (CIs that do not include 0.50) at this position is wave 3 (
estimate and 95% CI (fig. 3). We selected the 120-cM position for chromosome 6. The effect estimates and 95% CIs for each of the three NIMH BP data sets are shown in figure 3. The only data set that shows statistically significant allele sharing (CIs that do not include 0.50) at this position is wave 3 (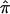 =0.56, 95% CI 0.51–0.61). As expected, the variance of
=0.56, 95% CI 0.51–0.61). As expected, the variance of 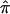 varied as a function of sample size, with the smallest variance corresponding to the largest data set (wave 4) and the largest variance corresponding to the smallest data set (wave 1). As seen in figure 3, the combined estimate of
varied as a function of sample size, with the smallest variance corresponding to the largest data set (wave 4) and the largest variance corresponding to the smallest data set (wave 1). As seen in figure 3, the combined estimate of 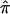 , which is the random effects summary estimate using each component data set IBDm estimate
, which is the random effects summary estimate using each component data set IBDm estimate 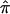 and variance, suggests an excess in allele sharing at the chromosomal position for the studies combined. As noted above, we were not able to detect significant heterogeneity among the three waves of BP data at this chromosomal position (table 3). We note that the results presented here have been replicated in a larger data set of 11 studies.19
and variance, suggests an excess in allele sharing at the chromosomal position for the studies combined. As noted above, we were not able to detect significant heterogeneity among the three waves of BP data at this chromosomal position (table 3). We note that the results presented here have been replicated in a larger data set of 11 studies.19
Figure 3.
The 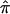 and 95% CIs for the NIMH BP component data sets, as well as the random effects
and 95% CIs for the NIMH BP component data sets, as well as the random effects 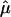 on chromosome 6, at ∼120 cM.
on chromosome 6, at ∼120 cM.
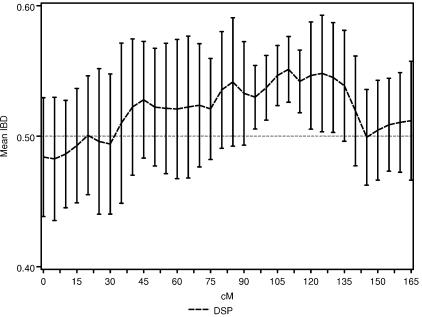
DSP Analysis Application
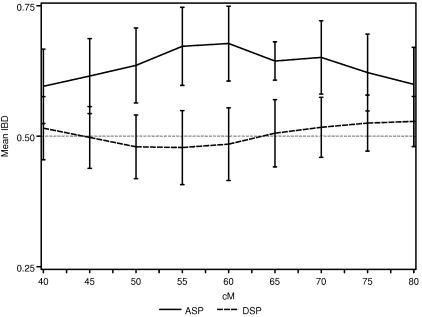
Figure 4 is a graphical representation of the DSP analysis, overlaid with the results from the ASP analysis for the NIMH AD data. Here, we have focused on a broad region of proposed linkage (40–80 cM) on chromosome 19 containing the APOE gene, and we plot the 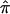 and SE from both the ASP and DSP analyses. As is evident in figure 4, the
and SE from both the ASP and DSP analyses. As is evident in figure 4, the 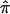 across this region in the ASPs shows excess sharing, whereas the DSPs show allele sharing below the null expectation (0.50). If the linkage signal from this region were a result of distorted transmission unrelated to affection status (i.e., AD), then we would expect to see similar ASP and DSP results. As is evident in figure 4, this is not the case, and, therefore, we confirm that the excess allele sharing in this region is largely attributable to affection status as expected, given that APOE resides there.
across this region in the ASPs shows excess sharing, whereas the DSPs show allele sharing below the null expectation (0.50). If the linkage signal from this region were a result of distorted transmission unrelated to affection status (i.e., AD), then we would expect to see similar ASP and DSP results. As is evident in figure 4, this is not the case, and, therefore, we confirm that the excess allele sharing in this region is largely attributable to affection status as expected, given that APOE resides there.
Figure 4.
The 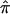 and SEs in the established AD linkage region on chromosome 19, for ASP (solid line) and DSP (dotted line) analysis from the NIMH AD data set.
and SEs in the established AD linkage region on chromosome 19, for ASP (solid line) and DSP (dotted line) analysis from the NIMH AD data set.
Figure 5 shows chromosome 12 for the DSP analysis only. On this chromosome, we see the DSPs display excess allele sharing in the 100–125-cM region. In fact, the majority of the estimated allele sharing across chromosome 12 for DSPs is above the null. This is not the case with the ASP analysis (data not shown), since there was no evidence of excess sharing anywhere on chromosome 12. Reasons for excess sharing among DSPs include transmission distortion, as well as genotyping or data-coding errors. The peak excess sharing among DSPs occurred at 95–130 cM, which does not include the approximate location of the A2M gene (20–25 cM) that was found to be associated with AD.18 However, the same was true for ASPs, since no excess sharing was observed at this location (data not shown).
Figure 5.
The 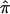 and SEs across chromosome 12, including the region that harbors the A2M gene, for the DSP analysis from the NIMH AD data set.
and SEs across chromosome 12, including the region that harbors the A2M gene, for the DSP analysis from the NIMH AD data set.
Discussion
Here, we present the application of 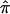 and a valid variance estimate of
and a valid variance estimate of 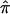 , using sibling pairs from the NIMH Human Genetics Initiative linkage samples. The proposed bootstrap procedure provides a realistic estimate of the variance, since the assumptions of missingness and nonindependence are accounted for. The proposed variance estimate may be applied to a variety of situations to explore the data in more detail, as well as to assess heterogeneity and to synthesize data over several data sets. We have chosen to implement the bootstrap in the setting where we do not use the triangle constraints and where each pair of siblings is weighted equally, regardless of the number of siblings in a family. However, the approach extends easily to accommodate the use of constraints as well as the use of weights, depending on family size.
, using sibling pairs from the NIMH Human Genetics Initiative linkage samples. The proposed bootstrap procedure provides a realistic estimate of the variance, since the assumptions of missingness and nonindependence are accounted for. The proposed variance estimate may be applied to a variety of situations to explore the data in more detail, as well as to assess heterogeneity and to synthesize data over several data sets. We have chosen to implement the bootstrap in the setting where we do not use the triangle constraints and where each pair of siblings is weighted equally, regardless of the number of siblings in a family. However, the approach extends easily to accommodate the use of constraints as well as the use of weights, depending on family size.
A conceptually intuitive approach to data analysis involves effect estimates and CIs, as opposed to summary statistics and/or P values exclusively. Toward that end, we demonstrated the ability to construct 95% CIs of 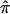 for each of the three data sets included in this analysis. Not only do
for each of the three data sets included in this analysis. Not only do 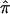 measures give the direction and relative strength of allele sharing in the data, but the 95% CIs are also an accurate reflection of the true variation within each data set. Thus, collectively, this strategy can give investigators a sense of what is contributing to the linkage signals from nonparametric methodology.
measures give the direction and relative strength of allele sharing in the data, but the 95% CIs are also an accurate reflection of the true variation within each data set. Thus, collectively, this strategy can give investigators a sense of what is contributing to the linkage signals from nonparametric methodology.
Using a more traditional meta-analytic approach to synthesize data, we also showed how 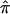 and the variance of
and the variance of 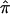 from different data sets could be combined to generate a summary IBDm measure (
from different data sets could be combined to generate a summary IBDm measure (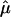 ). This strategy using ASP linkage samples has been proposed elsewhere,11 and we build upon this strategy to include unconstrained estimates of
). This strategy using ASP linkage samples has been proposed elsewhere,11 and we build upon this strategy to include unconstrained estimates of 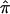 as well as the more realistic bootstrap variance. One of the more useful aspects of this approach is the ability to test for heterogeneity across studies. This is particularly important in the context of large-scale meta-analyses of original, raw linkage sample data. Often, it is unclear whether ignoring between-study heterogeneity is appropriate when pooling data. Using the traditional meta-analytic approach presents the opportunity for estimating the between-study heterogeneity and, therefore, offers an indication of whether pooling independent data sets is appropriate. Furthermore, it opens the door for exploring the source of the heterogeneity among the data sets. In addition, through the random effects model, it is possible to present a summary IBDm and CIs that incorporate both the within- and between-study heterogeneity.
as well as the more realistic bootstrap variance. One of the more useful aspects of this approach is the ability to test for heterogeneity across studies. This is particularly important in the context of large-scale meta-analyses of original, raw linkage sample data. Often, it is unclear whether ignoring between-study heterogeneity is appropriate when pooling data. Using the traditional meta-analytic approach presents the opportunity for estimating the between-study heterogeneity and, therefore, offers an indication of whether pooling independent data sets is appropriate. Furthermore, it opens the door for exploring the source of the heterogeneity among the data sets. In addition, through the random effects model, it is possible to present a summary IBDm and CIs that incorporate both the within- and between-study heterogeneity.
Performing a linkage analysis on ASPs exclusively is analogous to performing a case-control study without controls.17 The assumption underlying ASP methods of analysis is that, in regions of no linkage, siblings will share, on average, about half of their alleles IBD. There is now growing evidence that this assumption may not hold in all situations, even in apparently outbred populations.20,21 Estimating 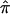 and the bootstrap variance among DSPs allows one to test this assumption directly in and around regions of suspected linkage. Observation of null or even less-than-expected allele sharing in the DSPs within a region of suspected linkage provides evidence in favor of the linkage signal resulting from affection status and not from distorted transmission.
and the bootstrap variance among DSPs allows one to test this assumption directly in and around regions of suspected linkage. Observation of null or even less-than-expected allele sharing in the DSPs within a region of suspected linkage provides evidence in favor of the linkage signal resulting from affection status and not from distorted transmission.
The proposed strategy is not without limitations. It requires access to the output of the Lander-Green algorithm, which limits its use in the context of meta-analysis, since other strategies may be able to use published results if estimates of sharing zero, one, and two alleles IBD are available. Furthermore, often there are not enough DSPs for analysis, since expensive linkage study designs typically maximize the number of affected relative pairs in the interest of optimizing the sample size for nonparametric strategies. To make the method computationally feasible even with large samples, we also proposed bypassing the Lander-Green algorithm for each bootstrap sample, which means that a small downward bias may be introduced in the SEs if the sample is used to estimate founder allele frequencies. This bias is generally ignored in all linkage studies, and redoing the Lander-Green algorithm for every bootstrap sample made no difference with the data sets used in this application.
To summarize, we propose a bootstrap procedure to estimate the variance of 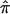 that provides an accurate reflection of the variation in an ASP linkage data set. Application of this procedure affords a more refined and often more intuitive view of the data and can be used to synthesize data, as well as to aid in the identification of heterogeneity among independent data sets.
that provides an accurate reflection of the variation in an ASP linkage data set. Application of this procedure affords a more refined and often more intuitive view of the data and can be used to synthesize data, as well as to aid in the identification of heterogeneity among independent data sets.
Acknowledgments
M.B.M. and N.M.L. were supported by NIMH grant MH063445. M.B.M. was additionally supported by NIMH grant T32-MH017119. Data and biomaterials from the three NIMH BP studies were collected in four projects that participated in the NIMH BP Genetics Initiative. From 1991 to 1998, the principal investigators and coinvestigators were, from Indiana University in Indianapolis (U01 MH46282), John Nurnberger, Marvin Miller, Howard Edenberg, Tatiana Foroud, and Elizabeth Bowman; from Washington University in St. Louis (U01 MH46280), Theodore Reich, Allison Goate, and John Rice; from Johns Hopkins University in Baltimore (U01 MH46274), J. Raymond DePaulo Jr., Sylvia Simpson, and Colin Stine; and, from the NIMH Intramural Research Program, Clinical Neurogenetics Branch, in Bethesda, Elliot Gershon, Diane Kazuba, and Elizabeth Maxwell. Data and biomaterials were collected as part of 10 projects that participated in the NIMH BP Genetics Initiative. From 1999 to 2003, the principal investigators and coinvestigators were, from Indiana University (R01 MH59545), John Nurnberger, Marvin J. Miller, Elizabeth S. Bowman, N. Leela Rau, P. Ryan Moe, Nalini Samavedy, Rif El-Mallakh (at the University of Louisville), Husseini Manji (at Wayne State University), Debra A. Glitz (at Wayne State University), Eric T. Meyer, Carrie Smiley, Tatiana Foroud, Leah Flury, Danielle M. Dick, and Howard Edenberg; from Washington University (R01 MH059534), John Rice, Theodore Reich, Allison Goate, and Laura Bierut; from Johns Hopkins University (R01 MH59533), Melvin McInnis, J. Raymond DePaulo Jr., Dean F. MacKinnon, Francis M. Mondimore, James B. Potash, Peter P. Zandi, Dimitrios Avramopoulos, and Jennifer Payne; from the University of Pennsylvania in Philadelphia (R01 MH59553), Wade Berrettini; from the University of California at Irvine (R01 MH60068), William Byerley and Mark Vawter; from the University of Iowa in Iowa City (R01 MH059548), William Coryell and Raymond Crowe; from the University of Chicago (R01 MH59535), Elliot Gershon, Judith Badner, Francis McMahon, Chunyu Liu, Alan Sanders, Maria Caserta, Steven Dinwiddie, Tu Nguyen, and Donna Harakal; from the University of California at San Diego (R01 MH59567), John Kelsoe and Rebecca McKinney; from Rush University in Chicago (R01 MH059556), William Scheftner, Howard M. Kravitz, Diana Marta, Annette Vaughn-Brown, and Laurie Bederow; and, from the NIMH Intramural Research Program (1Z01MH002810-01), Francis J. McMahon, Layla Kassem, Sevilla Detera-Wadleigh, Lisa Austin, and Dennis L. Murphy. Genotyping services were provided in part by the Center for Inherited Disease Research (CIDR). CIDR is fully funded through a federal contract from the National Institutes of Health to Johns Hopkins University (N01-HG-65403). Data and biomaterials were collected in three projects that participated in the NIMH AD Genetics Initiative. From 1991 to 1998, the principal investigators and coinvestigators were, from Massachusetts General Hospital in Boston, Marilyn S. Albert and Deborah Blacker; from Johns Hopkins University, Susan S. Bassett, Gary A. Chase, and Marshal F. Folstein; and, from the University of Alabama in Birmingham, Rodney C. P. Go and Lindy E. Harrell.
Appendix A
Here, we give details on the calculations of the ML estimate of  and the variance of
and the variance of 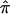 when there are n independent sibling pairs.
when there are n independent sibling pairs.
Since 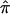 is a simple linear function of
is a simple linear function of 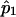 and
and 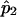 , it suffices to compute their variance-covariance matrix. Following Meilijson,12 we can estimate this variance-covariance matrix by using the empirical variance of the scores of the likelihood matrix evaluated at the ML estimates of pi. In this case, the result is particularly simple:
, it suffices to compute their variance-covariance matrix. Following Meilijson,12 we can estimate this variance-covariance matrix by using the empirical variance of the scores of the likelihood matrix evaluated at the ML estimates of pi. In this case, the result is particularly simple:
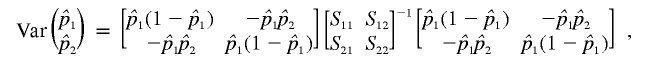 |
where
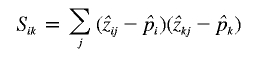 |
for i,k=1,2, and 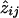 can be calculated from the pairwise IBD probabilities available from the Lander-Green algorithm.
can be calculated from the pairwise IBD probabilities available from the Lander-Green algorithm.
Formally, 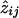 is defined as P(jth pair shares i alleles ∣ observed marker data on the jth pair, pi), where pi is the probability of sharing i alleles in the overall population. With the use of Bayes's rule,
is defined as P(jth pair shares i alleles ∣ observed marker data on the jth pair, pi), where pi is the probability of sharing i alleles in the overall population. With the use of Bayes's rule,
 |
and wij=P(observed marker data on the jth pair ∣ jth pair shares i alleles).
Note that, if we set pis equal to their null values of 0.25, 0.50, and 0.25, then the resulting zij in equation (A1) yields the pairwise IBD probabilities.7 That is, if αi denotes the null values, the pairwise values—say, aij—are defined as
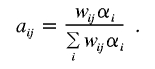 |
The wijs are not given by the Lander-Green algorithm, but the aijs are, and it is easy to see that we can compute 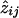 from equation (A1). Using the ML estimates for pi and for wij, substitute aij/αi.
from equation (A1). Using the ML estimates for pi and for wij, substitute aij/αi.
Note that, at the ML estimate,
 |
and this is the basis for using the EM algorithm to estimate the pis.7 Starting with the pairwise IBD probabilities, one obtains an initial estimate of pi with equation (A2). That is, substitute aij for 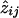 , and call the result p(1)i. Given p(1)i, estimate z(1)ij with equation (A1), with aij/αi replacing wij. Use the z(1)ijs to get p(2)i, etc., from equation (A2), and continue cycling between equations (A1) and (A2) until no change is observed. Thus, at the last iteration of the EM, the
, and call the result p(1)i. Given p(1)i, estimate z(1)ij with equation (A1), with aij/αi replacing wij. Use the z(1)ijs to get p(2)i, etc., from equation (A2), and continue cycling between equations (A1) and (A2) until no change is observed. Thus, at the last iteration of the EM, the 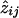 s are already computed.
s are already computed.
Appendix B
Here, we give details on the calculation of the random effects summary IBDm estimate 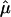 and the Q-test of homogeneity.
and the Q-test of homogeneity.
Suppose we have k independent sibling-pair linkage samples. The estimate of 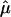 is given by
is given by
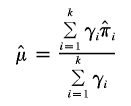 |
and
where 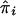 and
and 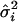 are the IBDm and the within-study variance for the ith study, respectively.
are the IBDm and the within-study variance for the ith study, respectively.
The between-study variance, 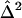 , is given by
, is given by
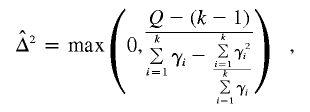 |
where
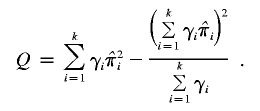 |
It can be shown under H0 that Q ∼ χ2k-1. Therefore, the P value can be computed as P(χ2k-1>Q).
Web Resources
URLs for data presented herein are as follows:
- NIMH Human Genetics Initiative Web site, http://nimhgenetics.org/
- SAGE: Statistical Analysis for Genetic Epidemiology, http://darwin.cwru.edu/sage/
References
- 1.Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- 2.Kong A, Cox NJ (1997) Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61:1179–1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gudbjartsson DF, Jonasson K, Frigge ML, Kong A (2000) Allegro, a new computer program for multipoint linkage analysis. Nat Genet 25:12–13 10.1038/75514 [DOI] [PubMed] [Google Scholar]
- 4.Abecasis GR, Cherny SS, Cookson WO, Cardon LR (2002) MERLIN—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30:97–101 10.1038/ng786 [DOI] [PubMed] [Google Scholar]
- 5.Haseman JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 10.1007/BF01066731 [DOI] [PubMed] [Google Scholar]
- 6.Blackwelder WC, Elston RC (1985) A comparison of sib-pair linkage tests for disease susceptibility loci. Genet Epidemiol 2:85–97 10.1002/gepi.1370020109 [DOI] [PubMed] [Google Scholar]
- 7.Risch N (1990) Linkage strategies for genetically complex traits. III. The effect of marker polymorphism on analysis of affected relative pairs. Am J Hum Genet 46:242–253 [PMC free article] [PubMed] [Google Scholar]
- 8.Efron B, Gong G (1983) A leisurely look at the bootstrap, the jackknife and cross-validation. Am Stat 37:36–48 10.2307/2685844 [DOI] [Google Scholar]
- 9.Holmans P (1993) Asymptotic properties of affected-sib-pair linkage analysis. Am J Hum Genet 52:362–374 [PMC free article] [PubMed] [Google Scholar]
- 10.Dizier MH, Quesneville H, Prum B, Selinger-Leneman H, Clerget-Darupoux F (2000) The triangle test statistic (TTS): a test of genetic homogeneity using departure from the triangle constraints in IBD distribution among affected sib-pairs. Ann Hum Genet 64:433–442 10.1046/j.1469-1809.2000.6450433.x [DOI] [PubMed] [Google Scholar]
- 11.Gu C, Province M, Todorov A, Rao DC (1998) Meta-analysis methodology for combining non-parametric sibpair linkage results: genetic homogeneity and identical markers. Genet Epidemiol 15:609–626 [DOI] [PubMed] [Google Scholar]
- 12.Meilijson I (1989) A fast improvement to the EM algorithm on its own terms. J R Stat Soc B 51:127–138 [Google Scholar]
- 13.Nurnberger JI, DePaulo JR Jr, Gershon ES, Reich T, Blehar MC, Edenberg HC, Foroud T, et al, for the NIMH Genetics Initiative Bipolar Disease Group (1997) Genomic survey of bipolar illness in the NIMH genetics initiative pedigrees: a preliminary report. Am J Med Genet 74:227–2379184304 [DOI] [Google Scholar]
- 14.Dick DM, Foroud T, Flury L, Bowman ES, Miller MJ, Rau NL, Moe PR, et al (2003) Genomewide linkage analyses of bipolar disorder: a new sample of 250 pedigrees from the National Institute of Mental Health Genetics Initiative. Am J Hum Genet 73:107–114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Blacker D, Bertram L, Saunders AJ, Moscarillo TJ, Albert MS, Wiener H, Perry RT, Collins JS, Harrell LE, Go RC, Mahoney A, Beaty T, Fallin MD, Avramopoulos D, Chase GA, Folstein MF, McInnis MG, Bassett SS, Doheny KJ, Pugh EW, Tanzi RE, for the NIMH Genetics Initiative Alzheimer’s Disease Study Group (2003) Results of a high-resolution genome screen of 437 Alzheimer’s disease families. Hum Mol Genet 12:23–32 10.1093/hmg/ddg007 [DOI] [PubMed] [Google Scholar]
- 16.Laird NM, Mosteller F (1990) Some statistical methods for combining experimental results. Int J Technol Assess Health Care 6:5–30 [DOI] [PubMed] [Google Scholar]
- 17.Elston RC, Song D, Iyengar K (2005) Mathematical assumptions versus biological reality: myths in affected sib pair linkage analysis. Am J Hum Genet 76:152–156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Saunders AJ, Bertram L, Mullin K, Sampson AJ, Latifzai K, Basu S, Jones J, Kinney D, MacKenzie-Ingano L, Yu S, Albert MS, Moscarillo TJ, Go RC, Bassett SS, Daly MJ, Laird NM, Wang X, Velicelebi G, Wagner SL, Becker DK, Tanzi RE, Blacker D (2003) Genetic association of Alzheimer’s disease with multiple polymorphisms in alpha-2-macroglobulin. Hum Mol Genet 12:2765–2776 10.1093/hmg/ddg310 [DOI] [PubMed] [Google Scholar]
- 19.McQueen MB, Devlin B, Faraone SV, Nimgaonkar NL, Sklar P, Smoller JW, Abou Jamra R, et al (2005) Combined analysis from eleven linkage studies of bipolar disorder provides strong evidence for susceptibility loci on chromosomes 6q and 8q. Am J Hum Genet 77:582–595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leutenegger AL, Genin E, Thompson EA, Clerget-Darpoux F (2002) Impact of parental relationship in maximum lod score affected sib-pair method. Genet Epidemiol 23:413–425 10.1002/gepi.10190 [DOI] [PubMed] [Google Scholar]
- 21.Zoller S, Wen Z, Hanchard NA, Herbert MA, Ober C, Pritchard JK (2004) Evidence for extensive transmission distortion in the human genome. Am J Hum Genet 74:62–72 [DOI] [PMC free article] [PubMed] [Google Scholar]