Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2005 Jun 23;567(Pt 2):665–671. doi: 10.1113/jphysiol.2005.089516

Colour helps to solve the binocular matching problem

HEM den Ouden 1,2, R van Ee 1, EHF de Haan 3
PMCID: PMC1474183  PMID: 15975983

Abstract

The spatial differences between the two retinal images, called binocular disparities, can be used to recover the three-dimensional (3D) aspects of a scene. The computation of disparity depends upon the correct identification of corresponding features in the two images. Understanding what image features are used by the brain to solve this binocular matching problem is an important issue in research on stereoscopic vision. The role of colour in binocular vision is controversial and it has been argued that colour is ineffective in achieving binocular vision. In the current experiment subjects were required to indicate the amount of perceived depth. The stimulus consisted of an array of fronto-parallel bars uniformly distributed in a constant sized volume. We studied the perceived depth in those 3D stimuli by manipulating both colour (monochrome, trichrome) and luminance (congruent, incongruent). Our results demonstrate that the amount of perceived depth was influenced by colour, indicating that the visual system uses colour to achieve binocular matching. Physiological data have revealed cortical cells in macaque V2 that are tuned both to binocular disparity and to colour. We suggest that one of the functional roles of these cells may be to help solve the binocular matching problem.

There is considerable interest in the possible contribution of colour information to binocular depth perception (stereopsis). Isoluminant stimuli have been the principal means of investigation to study colour processing. The underlying rationale to use stimuli defined by colour variations only was that, when luminance information is absent, the colour system can be studied in isolation.

Thirty years ago, Julesz (1971) used a random-dot stereogram in which the corresponding dots had polarity-reversed luminance. Subjects were unable to binocularly fuse the retinal images but the colour information aided fusion. Lu & Fender (1972) in a classical study reported that ‘colour differences alone do not give rise to the percept of depth’. Nevertheless, stereopsis from isoluminant stimuli was reported in later experiments (Comerford, 1974; de Weert & Sadza, 1983; Grinberg & Williams, 1985). There are, however, methodological problems with the isoluminance procedure. First, the point of isoluminance may vary depending on the location on the retina as a result of the varying density of the different types of cones. Second, chromatic aberrations may provide luminance information in supposedly isoluminant stimuli (Livingstone & Hubel, 1987). Thus, Livingstone and Hubel concluded that depth disappears at isoluminance and proposed that colour is processed by the parvocellular processing stream, whereas depth, motion and orientation are processed by the magnocellular stream. The information of one processing stream is not available to the other until very late in visual processing (Livingstone & Hubel, 1987).

More recently, it has become clear that there is extensive cross-communication between the parvo- and the magnocellular system (Stuart et al. 1992; Gegenfurtner & Hawken, 1996; Gegenfurtner et al. 1997). In addition, in a number of more recent, better-controlled studies sustained depth perception at isoluminance was reported (Tyler & Cavanagh, 1991; Scharff & Geisler, 1992; Simmons & Kingdom, 1997; Kingdom et al. 1999; Kingdom & Simmons, 2000). Even when colour information alone may not be able to induce depth perception, it might still contribute to stereopsis when luminance variations or other cues are present. A colour-contingent depth after-effect has been reported, supporting the existence of colour-dependent depth mechanisms (Domini et al. 2000), and Kingdom and Simmons proposed independent chromatic and achromatic stereopsis mechanisms (Simmons & Kingdom, 1997; Kingdom et al. 1999; Kingdom & Simmons, 2000; Simmons & Kingdom, 2002). However, in the most recent work on this issue, Krauskopf & Forte (2002) reported that disparity discrimination deteriorated in stimuli with an added chromatic component compared to monochrome stimuli, suggesting that colour information does not enhance stereoscopic depth perception.

Despite these mixed results, it remains a valid hypothesis that colour information could improve the identification of binocular disparities to recover the original three-dimensional scene from the two-dimensional retinal images (Jordan & Bovik, 1992). The computation of these disparities, and thus the volumetric aspects of the scene, depends critically on the correct matching of the corresponding features in the two images. Indeed when observers view ambiguous stereograms of vertical bars in which a bar in one eye could be matched to several bars in the other eye, both colour and luminance cues can aid disparity-based depth perception at a threshold level (Jordan et al. 1990). These results imply that colour can be used in simple binocular matching problems. In complex images with many potential matches it is known that the brain uses information such as orientation and motion for binocular matching (van Ee & Anderson, 2001). The presence of cortical neurones in the macaque area V2 that are tuned for both colour and binocular disparity (Ts'o et al. 2001) suggest that colour may also be one of the primitives that the brain uses to solve the matching problem.

Here, we examined the role of colour in binocular matching of complex images. Our protocol allows for volumetric (suprathreshold) measurements rather than forced-choice (threshold) responses that have been used previously. We designed a stimulus in which colour (monochrome/trichrome) and luminance (congruent/incongruent) could be manipulated. This stimulus was an array of fronto-parallel bars that were uniformly distributed inside a volume (cf. van Ee & Anderson, 2001). Observers judged the magnitude of the perceived depth of the volume subtended by the bars in terms of the perceived depth-to-width ratio of the volume (Fig. 1). These stimuli ranged in complexity from a few bars, in which few false matches are possible, to many bars entailing many potential matches. The rationale of using this stimulus for studying binocular matching is as follows. When two arbitrary, uncorrelated images are projected to the two eyes, very little volumetric depth is experienced and the perceived depth ‘shrinks’ towards the zero-disparity horopter. If a stimulus feature plays a role in binocular matching, the amount of perceived depth in complex stereoscopic displays will be greater when this feature is present than when it is absent. If colour contributes to binocular matching, it should reduce the number of false matches. As a result, the magnitude of perceived depth will be greater in colour than in monochrome stimuli (Fig. 2). Apart from colour, we also manipulated luminance. Luminance, a known primitive to solve the binocular matching problem, was used to validate our protocol. Luminance was either congruent, i.e. corresponding bars had the same luminance levels, or incongruent.

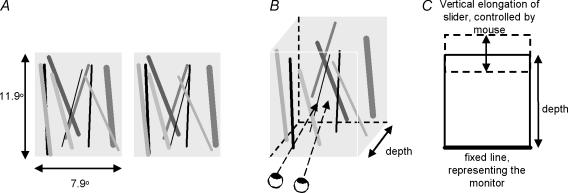
Figure 1. Stimuli and experimental procedure.

Figure 1

Open in a new tab

A 2D stimulus presented to each eye (A), in which the disparities between the images determine depth of the perceived 3D stimulus (B), upon which observers had to indicate the observed depth-to-width ratio using a vertical slider that could be manipulated with the computer mouse (C).

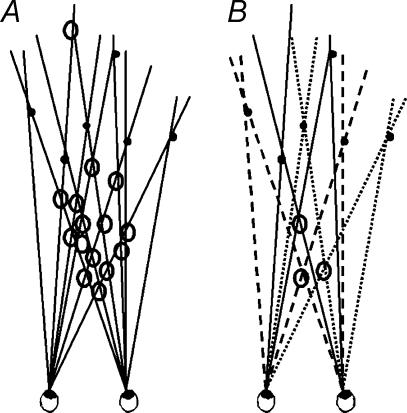
Figure 2. Top view of the geometry of the binocular matching problem.

Figure 2

Open in a new tab

The intersections of the visual lines indicate possible matches. The filled discs indicate the correct matches, the open discs are the false matches. A represents the possible matches in a monochrome stimulus. B shows how introduction of a stimulus feature such as colour (different lines) reduces the number of possible matches.

Method

Apparatus

Observers viewed stereograms on a LaCie electron 22 blue IV monitor of 38.7 × 28.2 deg at a constant viewing distance of 60 cm. The resolution was 1600 × 1200 pixels at a refresh rate of 85 Hz. The half-images of the stereogram were presented side by side on the monitor. The half-image of one eye was made invisible to the other eye by using a mirror set-up and a black septum, reducing the width of each eye's visual field to 19.1 deg (for more details see van Ee et al. 2001). The room was completely darkened. The head was stabilized with a chin and forehead rest.

Participants

Nine observers participated, all of whom were tested for normal colour and stereo vision prior to the experiment. All observers wore their corrective glasses, and were naïve with respect to the purpose of the experiment except for observer R.E. The experiment conformed to the standards set by the Declaration of Helsinki and the procedures had been approved by the Helmholtz Institute. Informed consent was obtained prior to the experiment.

Stimuli

The stimuli were stereograms of bright fronto-parallel bars of 5.6 arcmin width on a black background. These bars had disparities that evoked a percept of a three-dimensional volume of bars. Observers matched the perceived depth-to-width ratio evoked by the stimulus with the aspect ratio of the outline rectangle. This task is identical to the task used in previous studies (van Ee & Anderson, 2001; van Ee & Richards, 2002; van Ee, 2003). The bars were equally divided in depth and surrounded by a white rectangle at zero depth to facilitate correct eye posture. The far end of the volume had a relative disparity of 40.7 arcmin, which is consistent with a depth of 80 mm. The volume always receded in depth behind the monitor (uncrossed disparity). The stimuli had a constant height of 23.9 deg and a constant width of 15.8 deg. The length of the bars was varied randomly, between 100% and 80% of the volume's height. The orientation of the bars was random, varying from vertical to 10 deg. The number of bars (6, 24, 42, 72 and 96), their luminance, and colour properties varied across trials in a 2 × 2 factorial design: luminance was either congruent (bar A in the left eye had the same luminance level as bar A in the right eye), or incongruent (the luminance level in one eye did not predict the luminance level in the other eye). Note that the bar contrast polarity for congruent and incongruent luminance conditions is always the same (bright bars on a black background). Furthermore, the stimuli were either monochrome, in which all bars were green, or trichrome, in which the bars were red, blue or green, these being the phosphors of the CRT. Colour was always congruent. Stimuli were presented for 4 s and automatically appeared after a fixation cross disappeared. Each observer participated in 140 trials (5 numbers of bars, 2 × 2 colour luminance−1, 7 trial repetitions). All trials were counterbalanced and presented in pseudorandom order.

For the trichrome stimuli, four shades of each of the three colours were used. As a result each bar had one of three different colours and one of 12 (4 × 3) different luminance levels. To create monochrome stimuli that were equal to the trichrome stimuli with respect to luminance information, a near-isoluminant shade of green, corresponding to each shade of red or blue in the trichrome stimuli, was used. Thus each bar in the monochrome stimuli was green and had one of 12 different luminance levels. In other words, compared to the monochrome stimuli, the trichrome stimuli differed with respect to colour information, but were equal with respect to luminance information. The following luminance levels were used for the trichrome stimuli (cd m−2): green: max 51.78, min 19.56; red: max 22.34, min 9.07; blue: max 16.92, min 5.52. The difference between the shades of red and blue used in the trichrome stimuli, and the matched shades of green in the monochrome stimuli ranged between 0.34 and 0.17 cd m−2 for red/green and between 0.10 and 0.29 cd m−2 for blue/green. Luminance levels were measured using a photometer (LightScan, Cambridge Research Systems (Rochester, UK) OP200-E; photo cell: UDT Instruments (Baltimore, MD, USA) model 265).

Results

Multilevel analysis

A linear mixed-effect model, or multilevel, analysis was employed to test the influence of complexity, colour and luminance on observed depth. In a linear mixed-effects model, responses from a subject are thought to be the sum (linear) of so-called fixed and random effects. If an effect, such as a colour, affects the population mean, it is fixed. If an effect is associated with a sampling procedure (e.g. subject effect), it is random. Though the fixed effect is most important, it is necessary to model the random effects as well. The linear mixed-effect models solve these problems by estimating fixed and random effects in one model. This statistical procedure allows us to evaluate all the data of all subjects in one analysis (for more information on linear mixed-effects models see Goldstein et al. 1994; Langford et al. 1999; McCulloch & Searle, 2001; Hox, 2002). Observer-specific (random) effects are taken into account at the level of the individual observers; the effects of interest (colour, luminance information and complexity) were investigated at the level of the distinct responses. Five models of increasing complexity were fitted to the data. Each model is an elaboration of a simpler model, investigating the effect of a subsequent factor of interest on the fit of the model. The acceptance of a more complex model and the rejection of the simpler model was based on a comparison of the 2-log likelihoods of the models, using maximum likelihood estimates. Model 1, the reference model, did not contain any parameters of interest and assumes that all variance is error variance around the mean. Model 2 is based on the assumption that all variance is error variance around an individual mean. The models 3 and 4 have been subdivided to separately test the influence of each of the three fixed factors of interest: complexity, colour and luminance. Model 3 includes overall effects, and model 4 includes individual variation within these overall effects. Model 5, finally, investigates possible interactions of the main effects.

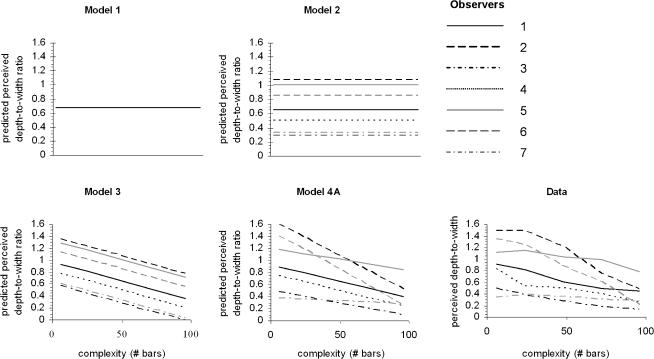
To illustrate the mixed-effect modelling process and to demonstrate the increasing fit to the data, the predicted values of the subsequent models are presented in Fig. 3 for the factor complexity (models 1, 2, 3 and 4A), and compared to the raw data. Similar graphs could be created for the factors colour and luminance. In Table 1 the fit of each model is compared to the simpler model. The result of model 2 shows that variation between subjects is significant (P < 0.001). The results of model 3 show that all independent variables modulate the observed depth (complexity (3A), P < 0.001, colour (3B), P < 0.001, luminance (3C), P < 0.05), and from model 4 it becomes clear that perceived depth was more affected by the complexity for some observers than for others (complexity (4A): P < 0.001). This latter effect was not significant for colour or luminance information (colour (4B): P = 0.326, luminance (4C): P = 1). Model 5 did not increase the fit to the data. This means that there is no interaction between any of the independent variables colour, luminance and complexity. In conclusion, model (4A) that fits the data best, includes a random effect at the level of observers, a fixed effect for complexity, colour and luminance, and a random observer-dependent effect of complexity.

Figure 3. The statistical linear mixed effect models and their fit to the perceived depths.

Figure 3

Open in a new tab

In model 1, the null hypothesis, all variance is assumed to be error variance around the mean, not modulated by any of the factors; therefore there is no parameter on the x-axis. In model 2, the separate observers are allowed different means, but all individual variance is still assumed to be error variance around the individual means. In model 3 an effect of complexity is shown; as the stimuli become more complex, less depth is perceived. This effect is assumed to be the same size in all individuals. In model 4A it is assumed that the effect of complexity is modulated differently in each observer. Each subsequent model has a better fit to the data (last graph) compared to the previous model.

Table 1.

The fit of the statistical linear mixed effect models to the data

Model Fixed Random 2-log- likelihood Number of parameters Increase in parameters 2-log- likelihood P value
m1 M – 11187.543 2 — — —
m2 m1 P 10683.365 3 1 504.178 0.000
m3 A m2+ S 2 10253.007 4 1 430.358 0.000
 B m2+ C 2 10667.032 4 1 16.333 0.000
 C m2+ L 2 10679.104 4 1 4.261 0.039
m2+ S + C + L 2 10236.427 6 3 446.938 0.000
m4 A m3 3+ S(P) 10010.734 7 1 225.693 0.000
 B m3 3+ C(P) 10235.461 7 1 0.966 0.326
 C m3 3+ L(P) 10236.427 7 1 0 1
m5 A m4A+ L × C 4A 10008.639 8 1 2.095 0.148
 B m4A+ S × C 4A 10010.683 8 1 0.051 0.821
 C m4A+ L × S 4A 10008.666 8 1 2.068 0.150
Open in a new tab

Each model includes one extra factor with respect to the previous model, and the effect of this factor on the fit is established by comparing it to the fit of a simpler model that does not include this factor of interest. For each model the 2-log-likelihood, the modelled factors and the total number of parameters are presented, as well as the difference in number of parameters and difference in 2-log-likelihood compared to the simpler model. The P values represent the significance of the present model compared to the simpler model. The abbreviations used are: M = mean, P = persons, S = complexity (number of bars), C = colour, L = luminance.

Increased depth in trichrome stimuli

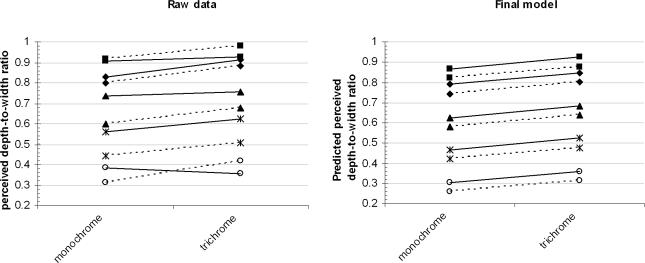
Model 4A shows that all the manipulated variables affected the perceived depth, but does not show the direction of this effect. Figure 4 depicts the raw data as well as the values predicted. Perceived depth ranged from approximately 50 to 150 mm, whereas the actual depth from disparity in all stimuli was 80 mm. Perceived depth increased for the trichrome compared to the monochrome stimuli (F1,966= 13.024, P < 0.001). Moreover, perceived depth increased for stimuli with congruent luminance compared to incongruent luminance stimuli (F1,966= 8.771, P < 0.01). Finally, when the complexity of the stimulus, i.e. the number of bars in the stimulus, increased, less depth was perceived (F1,7= 16.922, P < 0.01). Debriefing after the experiment showed that none of our observers had become aware of the difference between the congruent and incongruent luminance stimuli, neither for the trichrome nor for the monochrome stimuli.

Figure 4. The perceived depths (A) and predicted perceived depths (B) for the 20 different conditions for the two different colour information categories (monochrome versus trichrome).

Figure 4

Open in a new tab

The five different number of bars are represented by different symbols; 6(▪), 24(♦), 48(▴), 72(*) and 96 (○). The two luminance conditions (congruent and incongruent) are represented by dotted or continuous lines. A shows effects of complexity (F1,7= 16.992, P < 0.01), colour (trichrome > monochrome, F1,966= 13.024, P < 0.001) and luminance (congruent > incongruent, F1,966= 8.771, P < 0.01) on the perceived depth.

Discussion

We investigated whether colour is one of the primitives used by the visual system to establish binocular matching of complex images to recover depth information by manipulating complexity of the stimuli, as well as the colour (monochrome versus trichrome) and luminance (congruent versus incongruent) of the stimulus elements. Using a multilevel analysis, we found that perceived depth was greater for the trichrome stimuli than the monochrome stimuli, independent of luminance information. Effects of colour information as well as luminance information showed independent linear summation. Our task involved a metric depth estimate at supra-threshold depths rather than a forced-choice depth detection protocol as used in previous studies. Thus, our experiment was designed specifically to gauge the contribution of colour information to binocular matching in the presence of luminance variations, rather than at depth detection per se. Our results demonstrate that chromatic features help to solve the binocular matching problem in complex images and are consistent with the hypothesis of independent contributions of colour and luminance information. Perceived depth was reduced in stimuli with incongruent luminance information compared to congruent stimuli, even when the observers did not notice a difference between the congruent and incongruent stimuli.

Physiological models of stereopsis and binocular matching are largely based on cortical neurones that can compute disparity (e.g. Cumming & DeAngelis, 2001). In a recent study, Ts'o et al. (2001) reported the existence of single neurones in V2 of macaques that are sensitive to both colour and disparity. This supports the notion that the primate visual system multiplexes disparity and colour as early as V2. Although there is no direct evidence that these cells exist in humans as well, the macaque visual system is generally considered a good model for both human stereopsis and colour vision. These results are in accordance with previously reported observations that colour information is being used to resolve ambiguous stimuli at threshold (Jordan et al. 1990).

In sum, this study shows that colour information may be used to solve the stereo matching problem and modulates the perception of depth. This observation does not support the notion put forward by Livingstone & Hubel (1987), who proposed separate processing of colour and luminance information. In their view, only the latter processing route is involved in depth perception. Our data are in agreement with the study of Krauskopf & Forte (2002) in that colour information modulates the perception of depth. However, in contrast to their findings, we observed an increase in perceived depth. Future research is needed to define the different conditions that increase or reduce depth perception. Our work suggests that one of the functional roles of the cells that multiplex colour and disparity (V2) may be to help solve the binocular matching problem.

Acknowledgments

We are grateful to P. Schiphorst for developing stimulus generation software and to Drs O. Laudy for his support with the statistical analysis. We would like to thank the reviewers for their thoughtful and constructive comments. RVE was supported by a grant of the Netherlands Organization for Scientific Research.

References

  1. Comerford JP. Stereopsis with chromatic contours. Vision Res. 1974;14:975–982. doi: 10.1016/0042-6989(74)90166-7. [DOI] [PubMed] [Google Scholar]
  2. Cumming BG, DeAngelis GC. The physiology of stereopsis. Annu Rev Neurosci. 2001;24:203–238. doi: 10.1146/annurev.neuro.24.1.203. [DOI] [PubMed] [Google Scholar]
  3. de Weert CMM, Sadza KJ. New data concerning the contribution of colour differences to stereopsis. In: Mollon JD, Sharpe LT, editors. In Colour Vision: Physiology and psychophysics. London: Academic Press; 1983. pp. 553–562. [Google Scholar]
  4. Domini F, Blaser E, Cicerone CM. Color-specific depth mechanisms revealed by a color-contingent depth aftereffect. Vision Res. 2000;40:359–364. doi: 10.1016/s0042-6989(99)00181-9. [DOI] [PubMed] [Google Scholar]
  5. Gegenfurtner KR, Hawken MJ. Interaction of motion and color in the visual pathways. Trends Neurosci. 1996;19:394–401. doi: 10.1016/S0166-2236(96)10036-9. [DOI] [PubMed] [Google Scholar]
  6. Gegenfurtner KR, Kiper DC, Levitt JB. Functional properties of neurons in macaque area v3. J Neurophysiol. 1997;77:1906–1923. doi: 10.1152/jn.1997.77.4.1906. [DOI] [PubMed] [Google Scholar]
  7. Goldstein H, Healy M, Rasbash J. Multilevel models with applications to repeated measures data. Statistics Med. 1994;13:1643–1655. doi: 10.1002/sim.4780131605. [DOI] [PubMed] [Google Scholar]
  8. Grinberg DL, Williams DR. Stereopsis with chromatic signals from the blue-sensitive mechanism. Vision Res. 1985;25:531–537. doi: 10.1016/0042-6989(85)90156-7. [DOI] [PubMed] [Google Scholar]
  9. Hox J. Multilevel Analysis: Techniques and Applications. Mahwah, NJ, USA: Lawrence Erlbaum Associates; 2002. [Google Scholar]
  10. Jordan JR, Bovik AC. Using chromatic information in dense stereo correspondence. Pattern Recognition. 1992;25:367–383. [Google Scholar]
  11. Jordan JR, Geisler WS, Bovik AC. Color as a source of information in the stereo correspondence process. Vision Res. 1990;30:1955–1970. doi: 10.1016/0042-6989(90)90015-d. [DOI] [PubMed] [Google Scholar]
  12. Julesz B. Foundations of Cyclopean Perception. Chicago, USA: University Chicago Press; 1971. [Google Scholar]
  13. Kingdom FAA, Simmons DR. The relationship between colour vision and stereoscopic depth perception. J Soc for 3D Broadcasting Imaging. 2000;1:10–19. [Google Scholar]
  14. Kingdom FA, Simmons DR, Rainville S. On the apparent collapse of stereopsis in random-dot-stereograms at isoluminance. Vision Res. 1999;39:2127–2141. doi: 10.1016/s0042-6989(98)00257-0. [DOI] [PubMed] [Google Scholar]
  15. Krauskopf J, Forte JD. Influence of chromaticity on vernier and stereo acuity. J Vis. 2002;2:645–652. doi: 10.1167/2.9.6. [DOI] [PubMed] [Google Scholar]
  16. Langford IH, Marris C, McDonald AL, Goldstein H, Rasbash J, O'Riordan T. Simultaneous analysis of individual and aggregate responses in psychometric data using multilevel modelling. Risk Anal. 1999;19:669–677. doi: 10.1023/a:1007037720715. [DOI] [PubMed] [Google Scholar]
  17. Livingstone MS, Hubel DH. Psychophysical evidence for separate channels for the perception of form, color, movement, and depth. J Neurosci. 1987;7:3416–3468. doi: 10.1523/JNEUROSCI.07-11-03416.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lu C, Fender DH. The interaction of color and luminance in stereoscopic vision. Invest Ophthalmol. 1972;11:482–490. [PubMed] [Google Scholar]
  19. McCulloch CE, Searle SR. Generalized, Linear and Mixed Models. New York: Wiley; 2001. [Google Scholar]
  20. Scharff LV, Geisler WS. Stereopsis at isoluminance in the absence of chromatic aberrations. J Opt Soc Am. 1992;9:868–876. doi: 10.1364/josaa.9.000868. [DOI] [PubMed] [Google Scholar]
  21. Simmons DR, Kingdom FA. On the independence of chromatic and achromatic stereopsis mechanisms. Vision Res. 1997;37:1271–1280. doi: 10.1016/s0042-6989(96)00273-8. [DOI] [PubMed] [Google Scholar]
  22. Simmons DR, Kingom FA. Interactions between chromatic- and luminance-contrast-sensitive stereopsis mechanisms. Vision Res. 2002;42:1535–1545. doi: 10.1016/s0042-6989(02)00080-9. [DOI] [PubMed] [Google Scholar]
  23. Stuart GW, Edwards M, Cook ML. Colour inputs to random-dot stereopsis. Perception. 1992;21:717–729. doi: 10.1068/p210717. [DOI] [PubMed] [Google Scholar]
  24. Ts'o DY, Roe AW, Gilbert CD. A hierarchy of the functional organization for color, form and disparity in primate visual area v2. Vision Res. 2001;41:1333–1349. doi: 10.1016/s0042-6989(01)00076-1. [DOI] [PubMed] [Google Scholar]
  25. Tyler CW, Cavanagh P. Purely chromatic perception of motion in depth: Two eyes as sensitive as one. Percept Psychophys. 1991;49:53–61. doi: 10.3758/bf03211616. [DOI] [PubMed] [Google Scholar]
  26. van Ee R. Correlation between stereoanomaly and perceived depth when disparity and motion interact in binocular matching. Perception. 2003;32:67–84. doi: 10.1068/p3459. [DOI] [PubMed] [Google Scholar]
  27. van Ee R, Anderson BL. Motion direction, speed and orientation in binocular matching. Nature. 2001;410:690–694. doi: 10.1038/35070569. [DOI] [PubMed] [Google Scholar]
  28. van Ee R, Anderson BL, Farid H. Occlusion junctions do not improve stereoacuity. Spatial Vision. 2001;15:45–59. doi: 10.1163/15685680152692006. [DOI] [PubMed] [Google Scholar]
  29. van Ee R, Richards W. A planar and a volume tric test for stereoanomaly. Perception. 2002;31:51–64. doi: 10.1068/p3303. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES