Neuropeptide and calcium-binding protein gene expression profiles predict neuronal anatomical type in the juvenile rat

Abstract

Neocortical neurones can be classified according to several independent criteria: morphological, physiological, and molecular expression (neuropeptides (NPs) and/or calcium-binding proteins (CaBPs)). While it has been suggested that particular NPs and CaBPs characterize certain anatomical subtypes of neurones, there is also considerable overlap in their expression, and little is known about simultaneous expression of multiple NPs and CaBPs in morphologically characterized neocortical neurones. Here we determined the gene expression profiles of calbindin (CB), parvalbumin (PV), calretinin (CR), neuropeptide Y (NPY), vasoactive intestinal peptide (VIP), somatostatin (SOM) and cholecystokinin (CCK) in 268 morphologically identified neurones located in layers 2–6 in the juvenile rat somatosensory neocortex. We used patch-clamp electrodes to label neurones with biocytin and harvest the cytoplasm to perform single-cell RT-multiplex PCR. Quality threshold clustering, an unsupervised algorithm that clustered neurones according to their entire profile of expressed genes, revealed seven distinct clusters. Surprisingly, each cluster preferentially contained one anatomical class. Artificial neural networks using softmax regression predicted anatomical types at nearly optimal statistical levels. Classification tree-splitting (CART), a simple binary neuropeptide decision tree algorithm, revealed the manner in which expression of the multiple mRNAs relates to different anatomical classes. Pruning the CART tree revealed the key predictors of anatomical class (in order of importance: SOM, PV, VIP, and NPY). We reveal here, for the first time, a strong relationship between specific combinations of NP and CaBP gene expressions and the anatomical class of neocortical neurones.

The neocortex is a highly complex structure composed of a vast number of neurones displaying a variety of different electrical, morphological and biochemical properties. Classification according to these different properties is essential to understand the specific contribution of each cell type in neocortical computation. Morphology is particularly important in defining function because the shape of the dendritic arbor determines from which parts of the microcircuit (layers and columns) the neurone receives information, and the shape of the axonal arbor determines the sphere of influence of the neurone. Neocortical neurones are classified into two broad morphological categories: pyramidal cells (PCs) (∼80% of the neurones in the neocortex) and interneurones (INs) (whose axonal arborization is typically restricted to the neocortex and does not usually project into the white matter (Peters, 1984; White, 1989; Somogyi et al. 1998)). While PCs are relatively homogeneous in their morphology, INs differ markedly in their morphologies (Peters, 1984). Most types of interneurones may display various soma shapes and dendritic morphologies, but each type characteristically displays unique features in its axonal structure. Details of the axonal arborization (White, 1989), as well as the preferential placement of synapses onto different target-cell domains (Somogyi, 1989; Somogyi et al. 1998), have therefore provided the foundation for classifying interneurones into: interneurones that preferentially target somata and proximal dendrites (large basket cells (LBCs), small basket cells (SBCs), nest basket cells (NBCs)); interneurones that preferentially target dendrites (double bouquet cells (DBCs), bipolar cells (BPCs), neurogliaform cells (NGFCs), bitufted cells (BTCs)); interneurones that preferentially target dendrites and dendritic tufts (Martinotti cells (MCs) and Cajal–Retzius cells (CRCs)) and interneurones that preferentially target axons (chandelier cells (ChCs)) (Marin-Padilla, 1969; Somogyi, 1977; Fairen & Valverde, 1980; for review see Fairen et al. 1984; DeFelipe, 1997; Somogyi et al. 1998; DeFelipe, 2002; Toledo-Rodriguez et al. 2002; Markram et al. 2004).

Biochemical markers can expose different types of interneurones and may also indicate the potential function of different INs in the microcircuit. For example, calcium-binding proteins (CaBPs) may differ in their Ca²⁺-buffering properties and therefore also in their influence on intracellular Ca²⁺ dynamics. Neuropeptides (NPs) are cotransmitters that modulate the active state of the surrounding neurones, and their mode of action is much slower and more widely spread than the classical neurotransmitters such as GABA and glutamate. One may therefore expect some relationship between the expression of NPs and CaBP and the different anatomical classes of interneurones.

The most commonly studied CaBPs are calbindin (CB), parvalbumin (PV), and calretinin (CR), and the most commonly studied NPs are neuropeptide Y (NPY), vasoactive intestinal peptide (VIP), somatostatin (SOM), and cholecystokinin (CCK) (Cauli et al. 1997; DeFelipe, 1997; Kawaguchi & Kubota, 1997; Wang et al. 2002). The expression of these proteins has been studied at the mRNA level using in situ hybridization and single-cell RT-PCR, and at the protein level using immunohistochemistry. While these proteins can be detected throughout the neocortex (Hendry et al. 1984; Baimbridge et al. 1992; DeFelipe, 1993), single neurones specifically (co)express only subsets of CaBPs and NPs (Demeulemeester et al. 1991; DeFelipe, 1997; Gonchar & Burkhalter, 1997; Kawaguchi & Kubota, 1997; Hof et al. 1999; Markram et al. 2004). Numerous attempts have been made to classify neurones according to their expression of CaBP and NP, and its correlation with neuronal anatomical types. Nevertheless, the considerable overlap in expression in different anatomical types of neurones has resulted in only very rough separation of neuronal types, and in many cases has introduced considerable confusion and serious errors in analysis. For example, even the commonly accepted rule that PV expression typifies basket cells (or ‘fast-spiking’ cells) turns out to be correct only about half the time (Wang et al. 2002).

One possible solution to this apparently intractable problem is to study the simultaneous coexpression patterns of multiple CaBPs and NPs in a large number of morphologically characterized single neurones, using statistical tools. A few studies attempted to characterize the expression of two or more CaBPs or NPs in morphologically characterized neurones (Kawaguchi & Kubota, 1998; Porter et al. 1998) using immunohistochemistry, but this remains a low-throughput technique that permits simultaneous study of at most four proteins (meaningful correlation analyses would require tremendous numbers of morphologically identified cells).

To address this problem, we performed single-cell multiplex RT-PCR on 268 neurones, which were intracellularly stained to reveal their anatomical class, and from which we determined the expression profile of seven key genes (those encoding CB, PV, CR, NPY, VIP SOM, and CCK) and the house-keeping gene, GAPDH (encoding glyceraldehyde-3-phosphate dehydrogenase). Using a combination of classical correlation analysis, clustering, regression, and decision tree analyses, we found that while the expression of no single gene can isolate any one anatomical class, profiles of expression can predict anatomical type with a high degree of accuracy. These results suggest a strong link between the expression of specific combinations of NPs and CaBPs and the anatomical class of neurones.

Methods

All experimental procedures were carried out according to the Swiss federation guidelines for animal experiments. Wistar rats (13–16 days old) were rapidly decapitated and neocortical slices (sagittal; 300 mm thick) were sectioned on a vibratome (DSK, Microslicer, Japan) filled with iced extracellular solution (mm): 125 NaCl, 2.5 KCl, 25 glucose, 25 NaHCO₃, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Neurones were identified using IR-DIC microscopy as previously described (Stuart et al. 1993). Somatic whole-cell recordings (pipette resistance-3 mΩ) were employed for labelling the neurones and harvesting their cytoplasmic contents. Pipettes were filled with RNAse-free intracellular solution, containing (mm) 100 potassium gluconate, 20 KCl, 4 ATP-Mg, 10 phosphocreatine, 0.3 GTP, 10 Hepes (pH 7.3, 310 mosmol l⁻¹, adjusted with sucrose) and 0.5% biocytin (Sigma). The intracellular solution was prepared under RNAase free conditions: water was autoclaved; glassware and pH meter were cleaned with NaOH (10 N) and chemicals were opened from the first time using gloves and RNAase-free tools. After preparation, the intracellular solution was tested for RNAase contamination. Neurones were filled with biocytin by diffusion during 30–90 min recordings.

Histology and reconstruction

After recording, slices were fixed 0.1 m phosphate buffer (PB, pH 7.4) containing 2% paraformaldehyde, 1% glutaraldehyde and 0.3% saturated picric acid. Endogenous peroxidases were blocked with 3% H₂O₂-PB. Thereafter slices were incubated in biotinylated horseradish peroxidase conjugated to avidin according to the manufacturer's protocol (ABC-Elite, Vector Laboratories, Petersborough, UK) 2% A, 2% B and 1% Triton X100, developed with diaminobenzidine (DAB, 0.14%) under visual control, until all processes of the cells appeared clearly visible, and mounted in aqueous mounting medium (IMMCO Diagnostics, Inc). 3D neurone models were reconstructed from selected neurones using the Neurolucida system (MicroBrightField Inc., USA) and a bright-field light microscope (Olympus, Duesseldorf, Germany). After the staining procedure, there was ∼25% shrinkage of the slice thickness and ∼10% anisotropic shrinkage along the x and y axes. Only shrinkage of thickness was corrected.

Subjective criteria for anatomical type classification

Stained neurones were classified according to the following criteria for subjective anatomical type classification (for review see Fairen et al. 1984; DeFelipe 1997, 2002; Somogyi et al. 1998; Toledo-Rodriguez et al. 2002; Markram et al. 2004). PC: pyramidal shaped somata; apical dendrite (vertically orientated dendrite emerging from the apex of somata, usually reaching layer 1 and forming a terminal tuft); several horizontally radiating basal dendrites; spiny dendrites; axon emerging from the bottom of the somata, descending towards the white matter. Basket cells: preferentially target the somata and proximal dendrites of pyramidal neurones and interneurones. There are three subclasses of basket cells: LBC (the classic basket cells), NBC and SBC. LBC: multipolar or bitufted dendrites, sparse cluster of axonal collateral; long-range horizontal axonal collaterals; small side axonal branches; some vertically long axonal collaterals; low bouton density. NBC: multipolar, simple dendritic arbor with few short and infrequently branching dendrites; sparse to dense local axonal cluster; infrequent, long axonal branches; low bouton density. SBC: multipolar or bitufted dendrites; dense local axonal cluster; frequent, short, and curvy axonal branches; high bouton density; occasional a few far-reaching axonal collaterals. BPC: small ovoid or spindle somata; bipolar dendrites, narrow long dendritic tree; sometimes dendritic tuft in layer 1; axon emerges from a primary dendrite; simple, narrow axonal plexus; low bouton density. DBC: preferentially located in supragranular layers; ovoid or spindle shaped somata; bitufted or multipolar dendrites; narrow columnar axonal bundle- ‘horsetail like’(mainly descending); high bouton density. BTC: bitufted dendrites; long, vertically orientated axonal collaterals, mostly intracolumnar; axon mainly branch in a bifurcating manner; low bouton density. MC: long horizontal axonal collaterals or fan-like ramification in layer 1; spiny-like axons; bitufted or multipolar dendrites; sparsely to medium spiny dendrites.

Single-cell RT-multiplex-PCR

At the end of the recording, cell cytoplasm was aspirated into the recording pipette under visual control, by applying gentle negative pressure. Only cells in which the seal was intact throughout the recording, and whose nucleus was not harvested, were further processed. The electrode was then withdrawn from the cell to form an outside-out patch that prevented contamination as the pipette was removed. The tip of the pipette was broken and the contents of the pipette expelled into a test tube by applying positive pressure. mRNA was reverse transcribed using an oligo-dT primer (25 ng μl⁻¹) and 100 U MMLV reverse transcriptase (Gibco, BRL) in a final volume of 20 μl. After 50 min incubation at 42°C, the cDNA was frozen and stored at −20°C before further processing.

Multiplex PCR was carried out as described in Cauli et al. (1997) and Wang et al. (2002). Briefly the first amplification round consisted of 10 min hot start at 95°C followed by 25 cycles (94°C for 40 s, 56°C for 40 s and 72°C for 1 min). The first PCR mix contained RT product, 100 nm of each of the primers, 200 μm of each dNTP (Promega), 1 m Betaine (Sigma) and 5 U HotStarTaq DNA Polymerase (Qiagen, Hilden, Germany) in a final volume of 100 μl. A second round of PCR consisted of 40 cycles (94°C for 40 s, 56°C for 40 s and 72°C for 1 min) was performed. In this case, each gene was individually amplified in a separate test tube containing: 1 μm of its specific primers, 2 μl of the first PCR product (template), 200 μm of each dNTP, 1 m Betaine and 1 U of TaqZol DNA Polymerase (Tal-Ron Ltd, Israel), in a final volume of 20 μl. The products of the second PCR were analysed in 1.5% agarose gels using ethidium bromide. Primers for CB, PV, CR, NPY, VIP, SOM and CCK amplification are described in Cauli et al. (1997) and for GADPH in Aranda-Abreu et al. (1999). For each PCR amplification, controls for contaminating artifacts were performed using sterile water instead of cDNA. A control for non-specific harvesting of surrounding tissue components was randomly employed by advancing pipettes into the slice and retrieving without seal formation and suction. Both types of controls gave negative results throughout the study. Amplification of genomic DNA was avoided by the intron-overspanning location of many of the primers, and by never harvesting the cell nucleus. For 31 neurones where CB expression was found in a negative control, we designated its expression as ‘missing’; we then imputed these values according to a random-number generator with the same overall probability of expression as found in the non-missing subset of cells. Although this introduced increased variance into CB-specific correlations, its mean correlations were unaffected; importantly, we were then able to retain predictive power attributable to the other CaBPs and NPs accurately measured in these 31 cells.

Statistical analysis

Exploratory correlations

We performed Pearson correlation among pairs of genes coexpressed across all cells, and among pairs of cells based on their expression profiles of the seven genes. For each cell, the detected expression of a gene was coded as ONE (there was a band at the right molecular weight in the agarose gel) and the absence as ZERO (there was no band in the agarose gel). For correlations among pairs of genes, we performed the 28 pairwise correlations without respect to cell identity or anatomical type, and tested these correlations for statistical significance using the Bonferroni adjustment for multiple comparisons. For correlations among pairs of cells, we computed only the correlations, but did not attempt to evaluate for statistical significance because of the large number of correlations (over 30 000). For the latter, nearest-neighbour pairwise clustering (using Pearson correlation as the distance measure) was performed using the method of Ward (1963).

Bayes-optimal classification

Among the 286 cells studied, there were replicate gene profiles with conflicting anatomical class assignments. Assuming the sample is representative of future data to be collected, the most fair way to assign a ‘true’ class is to label it by the most prevalent cell population among the replicates. Bayes-optimal accuracy less than 100% thereby reflects potential limitations in the discriminating information, not necessarily the classifier. For example, addition of genes to the analysed set could potentially allow the classification techniques to demonstrate higher absolute accuracies. Thus, to fairly compare the statistical performance of different classifiers, it is the percentage of Bayes-optimal that provides a ‘level playing field’. This is also very important from the neuroscience perspective, because further research using gene-profile methods (e.g. developing rapid gene-testing tools for bench usage), and application of the given classifier, is more likely to be pursued if there is the potential for high accuracy (e.g. as reported below, of 85% Bayes-optimal rather than 57% raw accuracy using the classification tree approach).

Unsupervised classification

The quality threshold clustering (QTC) coexpression algorithm (as proposed by Heyer et al. (1999) and distributed in The Institute for Genomics Research Multi-experiment Viewer (Saeed et al. 2003)) was developed specifically for aggregating gene expression patterns; unlike most clustering algorithms, QTC does not require the user to specify in advance the number of clusters to be considered. In brief, the QTC algorithm attempts to grow clusters starting from a randomly selected first cell, iteratively adding the next most correlated cell (based on its gene profile). When the QTC score of similarity (the ‘diameter parameter’) is exceeded, a new cluster is created; the process is repeated until the largest remaining candidate cluster has fewer than the user-specified number of cells (grouped as ‘unclassified’). Every cell is considered as a starting candidate for the QTC procedure to determine the final number of clusters and cell assignment to each cluster. We tested the stability of QTC by varying the diameter setting. Diameters of 0.7 or greater led to three or fewer clusters which could therefore not be used to discriminate among cell types, and values from 0.2 to 0.4 led to a large numbers (> 15) of clusters as the algorithm attempted to make pure single- and pairwise-gene groups. A diameter of 0.5 (7 clusters and a shorter ‘unassigned’ list) provided robust results. Next we labelled each cluster using the following rule: name a given cluster according to the predominant anatomical type contained within each cluster, then apply a winner-take-all rule for evaluating the accuracy of the unsupervised classification.

Supervised classification

We used artificial neural network (ANN) regression (which optimizes the weights multiplying binary indicators of the presence or absence of neuropeptide expression) and the CART classification tree algorithm (which recursively splits data according to the values of the gene expression profiles).

ANN regression

For the ANN regression approach, we used the NevProp artificial neural network (Goodman & Harrell, 1998) with softmax logistic output units (Hastie et al. 2001) (which forces probabilities to add up to one using maximum likelihood optimization). The ANN modelling procedure is described in detail in Burke et al. (1996). In brief, the ANN consisted of three main layers. The first layer, an input layer, corresponded to the independent variables (gene expression profiles). The third layer, the output layer, corresponded to the dependent variable probabilities (anatomical class). An intermediate, ‘hidden’, layer was connected in all possible combinations to the input and output layers, to allow for the combined influence of multiple gene coexpression on the output class (analogous to testing all possible interactions in a linear regression model, but without introducing many extra degrees of freedom). Connections among all layers were initialized randomly. The log-likelihood statistic was used in a backpropagation algorithm to adjust the strengths of the connections among the network nodes, so as to minimize the discrepancy between actual and predicted class membership. To prevent overfitting, the training data were cycled through the algorithm until the residual log-likelihood error reached that expected by preliminary cross-validation (regularization). In order to estimate out-of-sample performance and variance, we compared an ANN model without non-linear interactive hidden units (i.e. a multiple dependent-variable logistic regression model) to a model with 10 hidden units, using 10-fold cross-validation of the entire model-building procedure.

Decision trees

For the decision trees, we used the CART (Breiman et al. 1993) software package provided in Matlab (Natick, MA, USA). CART considers all possible neuropeptides as candidates to initially split the dataset, selecting splits that maximize its accuracy rules. After each split, further splits among subgroup branches are then considered. CART forms terminal subgroups (nodes) when further splitting does not improve performance. Each node is labelled according to the predominant anatomical class and the accuracy computed, assuming all cells assigned to that node belonged to the labelled class.

CART decision tree pruning and validation

Because fully branched trees could overfit the data and be less interpretable upon direct inspection, we also enabled the internal CART tree-pruning subalgorithm, which uses an internal 10-fold cross-validation rule. We found no substantial differences among the final pruned tree structures in the course of generating and testing 300 such pruned trees. However, because even pruned trees could overfit the data, we estimated optimistic generalization bias using 200 bootstrapped samples, and repeating the entire modelling process for each sample (Efron & Tibshirani, 1991). Furthermore, in order to assess the sensitivity of our CART findings to a lower prevalence of Matinotti cells (as suggested elsewhere (Markram et al. 2004)), we generated synthetic datasets wherein half MCs were randomly removed, and repeated the modelling and cross-validation described above.

Results

The objective of this study was to explore the relationship between gene expression profiles (CaBPs and NPs) and anatomical class. For this purpose, we patched 268 layer 2–6 neocortical neurones (P13–16) and loaded the neurones with biocytin for subsequent staining and morphological identification. We then extracted the cytoplasm and performed single-cell RT-PCR to measure the coexpression of three CaBPs (CB, PV and CR) the four NPs (NPY, VIP, SOM and CCK) and the house-keeping gene encoding for GAPDH (used as a positive control for the harvesting procedure). Neurones were anatomically verified according to their axonal morphology (see Methods; Fig. 1A): pyramidal (PC; n = 41), large basket (LBC; n = 65), nest basket (NBC; n = 37), small basket (SBC; n = 13), Martinotti (MC; n = 67), bitufted (BTC; n = 23), bipolar (BPC; n = 11), and double-bouquet cells (DBC; n = 11). We performed the following sequence of analyses on the data: (1) exploratory correlation analysis (2) unsupervised clustering, and (3) supervised discriminative modelling using regression and decision-tree methods. The reliability of the supervised methods was assessed by cross-validation and bootstrap re-sampling.

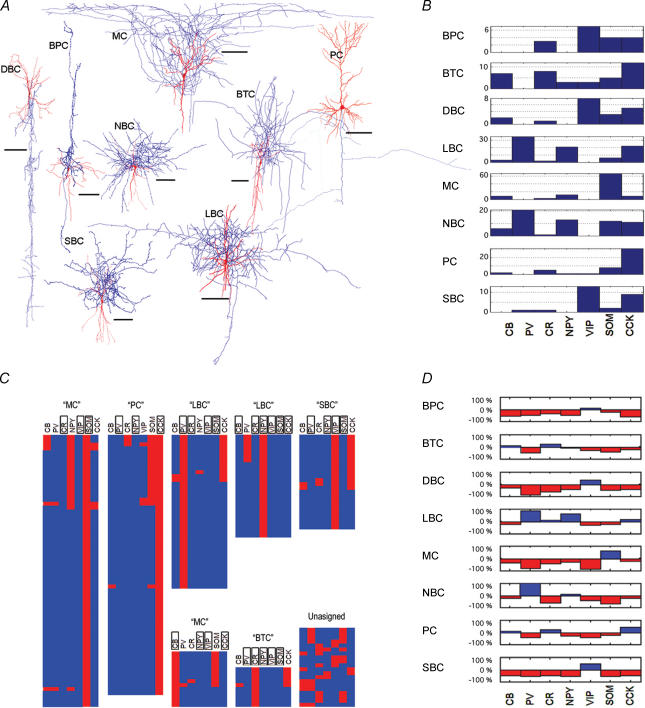
Figure 1. Gene expression and anatomical classification: prevalance, QTC clustering and supervised ANN classification.

A, representative examples of 3D histological reconstruction of neurone classes reported in this study. Soma and dendrites, red; axons, blue. Interneurones were classified according to their axonal arborizations (see Methods and for review see Fairen et al. 1984; DeFelipe 1997, 2002; Somogyi et al. 1998; Toledo-Rodriguez et al. 2002; Markram et al. 2004). Scale varies by cell class in order to represent detail; respective scale bars are all 100 μm. B, number of neurones expressing the three CaBPs (CB, PV, CR) and the four NPs (NPY, VIP, SOM, and CCK) by the eight studied anatomical types (BPC, BTC, DBC, LBC, MC, NBC, PC, and SBC). C, quality threshold clustering (QTC) algorithm, developed for expression analysis by Heyer et al. (1999) aggregates cells with similar expression patterns into non-overlapping, iteratively determined number of clusters, with a jacknifed quality score criterion defined by the cluster diameter (0.5) and the minimum number of cells per cluster (10). Cells not assignable to any QT clusters are grouped as ‘unclassified’. For each cluster the genes that are not expressed for all the cells in the same cluster have been framed, showing specific expression patterns for different cell types. D, anatomical type-specific profiles of regression weights derived from the linear artificial neural network. A positive weight (blue) indicates that expression of the corresponding neuropetide favours a given morphological classification; a negative weight (red) indicates a lower likelihood.

Gene expression in different anatomical types

Each of the tree CaBPs and four NPs investigated was expressed with a different frequency by each of the studied anatomical types (Fig. 1B). From the CaBPs, PV was found expressed in the basket cell family, with a higher prevalence in LBCs and NBCs. CR, although found in all the anatomical types, had a higher prevalence in BTCs and BPCs. CB was found expressed in all the anatomical types except BPC, with a higher prevalence in BTCs. For the NPs, NPY was never expressed in SBCs, DBCs or BPCs, while its highest prevalence was in LBCs and NBCs. VIP was mainly expressed in BPCs, DBCs and SBCs, and never found expressed in NBCs, LBCs, or MCs. SOM was expressed in all the anatomical types with a significantly higher prevalence in MCs. CCK was expressed in all the anatomical types, with highest prevalence in PCs and lowest in MCs.

Remarkably, there were two cases where a single gene was expressed in 100% of the cells from a specific anatomical class; SOM was expressed in all 67 MCs, and VIP was expressed in all 13 SBCs. While expression of SOM and VIP is obligatory for these neuronal types, respectively, they can also be expressed in other neurones. Since the frequency of expression of any one of these genes is therefore not correlated with the expression of any one anatomical class, we examined whether different types of neurones displayed different profiles of frequency of expression. While each anatomical class displays a different pattern in the expression frequency for the eight genes, this was not sufficiently different to separate unambiguously the anatomical type. Indeed, the expression frequency patterns of several anatomical types were similar: LBCs and NBCs, BPCs and DBCs, SBCs and DBCs, BTCs and PCs. Since expression frequency is a measure that is strongly influenced by detection errors, we applied more advanced statistical methods to explore the correlations between gene expression and anatomical classification.

Exploratory correlations

Pearson correlation analysis of gene coexpression (without regard to cell identity or anatomical class) revealed only weak pair-wise mRNA coexpression (−0.29 to 0.11), with most values near zero (Table 1), indicating that the coexpression of CaBPs and NPs is highly promiscuous and that many combinations of genes can be expressed (39 of the 127 possible combinations were expressed). This promiscuity demonstrates that there are no perfect inclusion principles for the expression any of these genes (i.e. relative independence), and explains the considerable difficulty encountered by researchers when trying to differentiate specific anatomical classes according to the expression of only one CaBP or NP. We did however, find three anticorrelations that were statistically significant after Bonferroni correction (SOM and PV, −0.29, P < 0.00001; SOM and CCK, −0.28, P = 0.0001; and NPY and CCK, −0.26, P = 0.0033), indicating that indeed there is some tendency, albeit not very high, for exclusion in the coexpression of some of these genes.

Table 1.

Pearson correlation matrix 28 pairwise correlation coefficients among seven coexpressed genes (the information about cell anatomical class was not used)

	CB	PV	CR	NPY	VIP	SOM	CCK
CB	1.00000	—	—	—	—	—	—
PV	0.04464	1.00000	—	—	—	—	—
CR	0.01367	−0.16301	1.00000	—	—	—	—
NPY	−0.03462	−0.01485	−0.08311	1.00000	—	—	—
VIP	−0.09678	−0.16327	0.08601	−0.17635	1.00000	—	—
SOM	0.05910	−0.29338	−0.04221	0.02029	−0.15921	1.00000	—
CCK	−0.07993	−0.16696	0.02085	−0.26024	0.11122	−0.28386	1.00000

These findings further demonstrate that neocortical neurones cannot be separated based on only one gene. We next performed correlations of gene profiles across cells, again without respect to anatomical type, in order to discern any natural multivariate clustering. The lack of such clustering mitigates against a meaningful association of multigene expression with any property (e.g. anatomical type). The presence of clustering, however, supports further multivariate, parametric modelling to test the predictive relationships for specific properties. Indeed, Pearson correlation of gene profiles across cells, followed by nearest-neighbour Ward clustering (see Supplemental Fig. 1) revealed at least four prominent cell clusters. These clusters were still overlapping to some extent, but they did show a correspondence with anatomical classes (as indicated by bar codes on the figure), revealing, for the first time, a hint of the complex relationship between expression patterns of NPs and CaBPs and anatomical type of neocortical neurones.

Unsupervised clustering and discrimination

We next wanted to know whether the structure among the patterns of expression of NPs and CaBPs described above would provide a basis for classification of anatomical classes. For this purpose, we clustered the neurones according to their coexpression patterns using QTC. QTC grouped the neurones into seven distinct coexpression clusters (Fig. 1C). Each cluster was made up of a population of neurones with a distinct pattern of expression, where the expression for at least three of the seven genes was identical for all the cells in a cluster (see rectangles in Fig. 1C).

Examining each cluster independently, a dominant anatomical type plurality was observed (with the exception of the smallest cluster; see Table 2 and legend). There were two pairs of redundant cluster–class associations (MC, LBC) when labelled according to the winner-take-all anatomical type rule; thus the seven QTC-determined clusters reduce to five effective predictive categories, with an overall empirical QTC classification accuracy of 53.0% (79.8% of Bayes-optimal, a classification algorithm that gives the maximal possible accuracy by considering all possible combinations of class assignment given the distribution of the anatomical classes in the dataset) (Duda et al. 2000). For most of the anatomical classes, this accuracy was statistically significant and much better than blindly assigning all cells to a class: MCs (85.1% correct versus 25.0% expected), SBCs (84.6% correct versus 4.9% expected), PCs (70.7% correct versus 15.3% expected), LBCs (63.1% correct versus 24.2% expected) and BTCs (17.4% correct versus 8.6% expected). Three anatomical classes did not constitute the majority of neurones in any cluster. This was probably due to: (a) low sample number (BPCs and DBCs), or (b), as in the case of NBCs, coclustering with another member of the basket cell family (LBC).

Table 2.

Empirical cluster assignment to dominant anatomical type

n cells	Cluster A 69	Cluster B 66	Cluster C 39	Cluster D 26	Cluster E 24	Cluster F 14	Cluster G 10	Unassigned 20
BPC	0.029	0.045	0	0	0.167	0	0.100	0.050
BTC	0.029	0.106	0	0.038	0.125	0.286	0.400	0.100
DBC	0.014	0.015	0	0	0.208	0	0	0.200
LBC	0.043	0.197	0.641	0.615	0	0	0.100	0.350
MC	0.725	0.121	0	0	0	0.500	0	0.100
NBC	0.101	0.061	0.359	0.308	0	0.071	0	0.150
PC	0.058	0.439	0	0.038	0.042	0.143	0.400	0
SBC	0	0.015	0	0	0.458	0	0	0.050

Seven distinct clusters suggested by QTC clusters A to G are represented in the supplementary Fig. 1. Bold indicates predominant cell anatomical type for each cluster. Cluster G has two values 0.400, but since chance expected accuracy for BTCs is much smaller than for PCs this cell type got priority for the assignment.

Regression-based prediction

In order to gain further insight into the possible mechanisms and significance of these correlations we performed regression-based prediction. Non-linear ANNs with 10 hidden units easily overfit the data with an accuracy of 65.3% (Supplemental Table S1, Fig. 2A), which is very close to the Bayes-optimal rate of 66.4% (see Methods and Supplemental Table S2). This indicates that the model had sufficient flexibility to find non-linear interactions if they were present. However, 10-fold cross-validation of the non-linear network model showed a drop in the accuracy to 54.5%. This did not differ substantially from the cross-validated accuracy (55.2%) for the linear logistic regression model (i.e. no hidden units; Table 3, Supplemental Table S3, Fig. 2B). This is consistent with the high degree of apparent promiscuity found in the coexpression of pairs of genes.

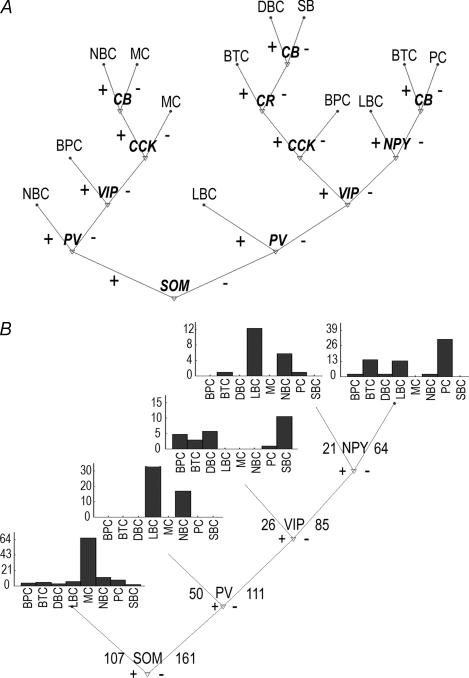
Figure 2. CART decision tree classification.

A, fully grown CART decision tree. Interpretation of the tree: at each bifurcation the gene expression of specific marker is considered: + branch is taken if the gene is expressed and – otherwise; terminal nodes are designated with corresponding anatomical types and root is the starting point. Evaluation of the observed cell, example: if SOM is expressed take the left branch, next if the PV is expressed take the left branch again and the observed cell would be classified as NBC. B, CART binary decision tree for laboratory application, pruned by 300 cross-validated data-splits. At each bifurcation the number of cells going into next splitting/terminal node is shown. Class probability for each cell type in each terminal node is represented on the graph placed by adequate terminal node (scale is given in percentages).

Table 3.

Non-linear 10-hidden unit and linear (in parenthesis) logistic regression softmax artificial neural network

Cell type	Classification accuracy for the full data set	Accuracy by 10-fold cross-validation	Standard deviation
BPC	0.18 (0)	0.1 (0.19)	0.17 (0.24)
BTC	0.48 (0.39)	0.21 (0.27)	0.14 (0.14)
DBC	0.36 (0.18)	0.16 (0.16)	0.2 (0.23)
LBC	0.69 (0.68)	0.63 (0.66)	0.16 (0.1)
MC	1 (0.97)	0.9 (0.91)	0.1 (0.09)
NBC	0.22 (0.22)	0.18 (0.16)	0.13 (0.07)
PC	0.61 (0.68)	0.58 (0.61)	0.22 (0.18)
SBC	1 (0.69)	0.47 (0.25)	0.32 (0.32)
Total	0.653 (0.616)	0.545 (0.552)

Accuracies of non-linear (and linear) artificial neural network for full data set (very close to the optimal) and for test data set after 10-fold cross-validation (less than optimal but close to the linear model) show that linear regression is well suited for modelling of anatomical categories.

Comparing the results of linear and non-linear regression modelling for each anatomical class, the only apparent change was a decrease in SBC accuracy and an increase in BPC accuracy in the linear model. These differences, however, fall within single standard deviations of their means (Table 3). Both regression models predicted better than chance for all anatomical categories, although this improvement was only significant at the P < 0.05 level (i.e. out-of-sample mean prediction greater than 1.96 times chance expected value) for LBCs (66% correct versus 24% expected), MCs (91% correct versus 25% expected) and PCs (61% correct versus 15% expected). The fact that the linear and non-linear ANN models performed similarly, indicated that simpler linear models are sufficient to derive predictive weights for the expression of each gene.

The weight vectors for the linear model are shown in profile in Fig. 1D. Each weight reflects the relative influence that each gene has (in the context of the rest of the genes and anatomical types studied) upon the probability of that profile belonging to a certain anatomical class. In general, the majority of weights were negative (if the gene is expressed, there are fewer probabilities that the cell will belong to that anatomical type) and a few were positive. For instance, the expression of PV will highly favour the likelihood of LBC or NBC class (normalized weights >50% maximal among classes), and strongly decrease the likelihood of MC or DBC class (normalized weights <50% maximal among classes). Likewise the expression of SOM will highly support the classification as MC, and the expression of VIP will highly increase the likelihood of SBC, DBC or BPC class and decrease the likelihood of MC class.

CART decision trees

The regression models used above give a simultaneous weighting of the predictors but do not provide a hierarchical structure in the coexpression patterns (which genes have a higher predictive power). For this purpose, we generated a CART decision tree for anatomical class prediction from gene expression patterns. The full CART decision tree shows the distribution profiles for the winning and losing neurones in each terminal node, based on the expression or lack of expression of a given gene at a time (see Fig. 2A). The accuracy of the fully bifurcated tree was 56.7% (85.4% of Bayes-optimal) when adjusted for optimistic bias using 300 bootstrap models (bias estimate was stable at 0.001 beyond 200 bootstraps; Table 4). However, the tree has many asymmetric branches making it difficult to understand which bifurcations are critical for the classification. We therefore pruned the full tree using rules that leave only branches supported by cross-validation of the data (Breiman et al. 1993). The pruned tree had a more interpretable structure (Fig. 2B) with only a modest reduction in bootstrap bias-adjusted accuracy to 54.0% (81.3% of Bayes-optimal; Table 4, parenthesis). This pruned tree shows the following decision sequence: declare cells positive for SOM as ‘MC’, then those positive for PV as ‘LBCs’, then those positive for VIP as ‘SBCs’, and finally those positive for NPY again as ‘LBCs’; the default negative for all four neuropeptides indicates a ‘PC’ classification (Fig. 2B). By comparing this pruned skeleton with the distal branching of the full tree (Fig. 2A and B), some insight into the potential importance of CB, CCK, and CR in decision making can be found.

Table 4.

CART classification accuracy using full and pruned (in parenthesis) trees by cross-validation, with bootstrapped adjustment for optimistic bias

Cell type	Tree	Chance expected	Bootstrapped trees (n = 300)		Complete data through bootstrapped trees		Adjusted tree
	Accuracy	Accuracy	Accuracy	Standard error	Accuracy	Optimistic bias	Accuracy
BPC	0.545 (0)	0.041 (0.041)	0.365 (0.224)	0.028 (0.024)	0.259 (0.155)	0.106 (0.069)	0.439 (0)
BTC	0.261 (0)	0.086 (0.086)	0.365 (0.217)	0.028 (0.024)	0.273 (0.159)	0.092 (0.058)	0.169 (0)
DBC	0.091 (0)	0.041 (0.041)	0.349 (0.181)	0.028 (0.022)	0.224 (0.111)	0.125 (0.07)	0 (0)
LBC	0.708 (0.708)	0.242 (0.242)	0.689 (0.695)	0.027 (0.027)	0.664 (0.681)	0.025 (0.014)	0.683 (0.694)
MC	0.985 (1)	0.25 (0.25)	0.98 (0.994)	0.008 (0.004)	0.956 (0.986)	0.024 (0.008)	0.961 (0.992)
NBC	0.162 (0)	0.138 (0.138)	0.259 (0.154)	0.025 (0.021)	0.2 (0.11)	0.059 (0.044)	0.103 (0)
PC	0.707 (0.756)	0.153 (0.153)	0.731 (0.725)	0.026 (0.026)	0.684 (0.694)	0.047 (0.031)	0.66 (0.725)
SBC	0.538 (0.846)	0.049 (0.049)	0.734 (0.744)	0.026 (0.025)	0.646 (0.692)	0.088 (0.052)	0.45 (0.794)
All types	0.623 (0.578)	1 (1)	0.663 (0.629)	0.027 (0.028)	0.607 (0.591)	0.056 (0.038)	0.567 (0.54)

Classification accuracy based on distribution of the different anatomical types in terminal nodes of the tree. Note that after pruning some of the numerous branches of the full tree, the pruned tree shows zero accuracy for certain anatomical types but keeps good overall accuracy.

Our dataset contained a percentage of MCs that is twice the real prevalence in somatosensory cortex (due to an overlapping study in which we specifically selected MCs for recording). To test if the model was sensitive to the ‘artificial’ high number of MCs, we created 10 datasets, each with only a random half of the original 67 Martinotti cells (mimicking the real prevalence, Supplemental Fig. 2). For all 10 models, the pruned trees were identical, and the only discrepancy with the complete-data pruned model of Fig. 2B was that the sequence of the initial two bifurcations was reversed (PV then SOM), reflecting the new relatively higher prevalence of the PV-expressing LBC subpopulation. All distal bifurcations were unaffected, and the overall model accuracy was not significantly changed. This result demonstrates a slight independence of the model from the relative prevalence of the different cell types.

ANN versus CART

Comparing accuracies among anatomical classes for the linear ANN (Table 3, first column, parenthetic values) and pruned CART (Table 4, first column) suggests that the two algorithms predict similarly for high-prevalence anatomical types (e.g. LBC, MC, PC), but were discrepant for the other categories. The two methods agreed about class assignment for 83% of all cells (Cohen's kappa of agreement, 0.778, P = 0.028).

Discussion

We describe here a multidisciplinary study that explores the relationship between profiles of NP and CaBP gene expression and anatomical class. In this study we found extreme promiscuity of coexpression of genes encoding NPs and CaBPs, indicating that the expression mechanism in neocortical neurones allows for many combinations of these particular genes. We further found that the expression of combinations of expressed genes is highly correlated to anatomical type, revealing a tight global control on the expression of sets of NPs and CaBPs in different neurones. Overall, the statistical analysis indicated that the expression profile of just these seven mRNAs provides over 85% of the Bayes-optimal classification accuracy, and the number of gene expression profiles for each anatomical class is limited. Nevertheless, perfect mapping onto anatomical types is not possible because there is still some variability in the expression patterns, although this promiscuity is considerably lower than for single genes. This apparent promiscuity of sets of genes expressed could be due to: methodological limitations, the low number of studied genes, or because the specific combinations of expressed genes correspond to physiological variants inside the anatomical classes.

Promiscuous coexpression

In this study, gene coexpression analysis revealed the lack of strong correlations between the expression of any pair of these key NPs and CaBPs. While this finding is bound to be influenced by false negatives to some extent, the contribution is likely to be minor since: (a) neurones included in the study expressed at least one NP or CaBP (b) the copy number of these NPs' and CaBPs' mRNAs in the cell is relatively high, and (c) for some anatomical types one NP was ubiquitously expressed in all cells. For example, SOM was detected in 100% of 67 MC, and VIP was detected in 100% of 13 SBCs. The promiscuity in coexpression was also indicated by the lack of improvement in prediction of anatomical class when using regression methods that can exploit non-linear interactions between genes. These results therefore provide direct evidence that neocortical neurones can express many combinations of these key genes, and that no single NP or CaBP can be used to unambiguously identify an anatomical type.

Coexpression exclusions

While all the studied NPs and CaBPs are expressed in neocortical neurones, we found a significant tendency for exclusion in the coexpression of: SOM with PV; SOM with CCK; and NPY with CCK. These restrictions at the mRNA level are consistent with the exclusions found at the protein level. For example, Kawaguchi, Kubota and colleagues reported that PV, SOM and CCK immunohistochemical staining distinguished three non-overlapping groups of neurones (Kawaguchi & Kubota, 1997). Demeulemeester and colleagues showed that SOM, CCK and NPY do not coexpress, while coexpression of SOM with PV is rare but possible (Demeulemeester et al. 1991). Coexpression of the genes encoding SOM and PV was also shown at the mRNA level (Cauli et al. 1997; Wang et al. 2002).

Combinations and clusters of gene expression profiles

Previous studies have shown that specific anatomical types express certain NPs and CaBPs. For example, some of the neurones expressing SOM are MCs or NBCs (Wahle, 1993; Kawaguchi & Shindou, 1998; Wang et al. 2002), some of the neurones expressing PV are LBCs or NBCs (Kawaguchi & Kubota, 1998; Wang et al. 2002), some of the neurones expressing VIP are SBCs, BPCs or DBCs (Cauli et al. 1997; Kawaguchi & Kubota, 1998; Wang et al. 2002), and some of the neurones expressing CCK are LBCs or MCs (Kawaguchi & Kubota, 1998; Kawaguchi & Shindou, 1998; for review see Kawaguchi & Kubota, 1997; Markram et al. 2004). This promiscuity of expression shows that no NP or CaBP can perfectly separate any one of the anatomical classes.

While this finding may seem to suggest that the expression of each gene is independently controlled, QTC analysis revealed that neocortical neurones expressed only 39 of the 127 possible combinations (gathered in seven clusters). Therefore almost 70% of the possible combinations are not found in neocortical neurones. Moreover, the cells in a cluster were identical for the expression of three to six of the seven genes. It is not likely that further sampling would reveal additional combinations or clusters since the dataset was already large and the mRNA detection highly reliable (see above). Moreover, QTC does not assume a priori how many clusters to form or how many cells each cluster should contain, and validates the clusters by bootstrap.

In six of the seven coexpression clusters, a single anatomical subtype dominated significantly over the other eight. Such a result was unexpected since the QTC is an unsupervised clustering method that does not use any morphological information to assign the neurones to each cluster. QTC assigns neurones into non-overlapping clusters according to the similarity of their gene expression profiles. The fact that clustering by gene expression separates anatomical classes, demonstrates the tight correlation between patterns of coexpression and anatomical class. This correlation is however not perfect; this may be due to methodological limitations, low sample number or the need to study the coexpression of additional genes. Additionally, specific coexpression patterns could be related to physiological variants inside each anatomical class.

Frequency of expression versus predictive weights

The predominance of a specific anatomical class in each of the coexpression clusters revealed a correlation between expression profiles and anatomical type. Based on this correlation, it is now possible to derive the weights for each gene in the prediction of anatomical class. Each weight describes the relative influence of that gene (in the context of the rest of the genes and anatomical classes studied) on the probability that the specific profile belongs to a certain anatomical class. It is important to point out that these weights differ from prevalence (frequency of expression) in that prevalence is independent of the other genes or anatomical types. Indeed, when comparing prevalence with weights, a high prevalence does not imply a high weight. Indeed, the fewer anatomical classes that express a particular gene, the higher its prediction power. For example, the prevalence of CCK is relatively high in most of the anatomical types, but its predictive weight is low. In SBCs CCK has a high prevalence but a low weight because CCK expression will also ‘drive’ the prediction to the rest of the cell types expressing CCK. Conversely, VIP is the major predictor for SBCs, as it is expressed less promiscuously.

In the case of PCs, CCK has a high prevalence and high weight. This is due to the fact that the frequency of expression for the other genes in PCs is very low (while the rest of the anatomical classes express other genes in addition to CCK). Nevertheless, while PCs express CCK mRNA, CCK protein has not been found in PCs. This could be due to low levels of the CCK protein or to the fact that the translation of CCK mRNA to protein is constitutively blocked and only permitted under specific circumstances. In this case, as the mRNA is already present, there would be a minimal delay for PCs to produce and release CCK.

The interneurone diversification tree

The regression models described above provide the relative influence of each gene in the context of the rest of the genes and anatomical types, but do not provide a hierarchical structure in the coexpression patterns or select a parsimonious subset of genes. Such a deduced hierarchy may provide insight into potential mechanisms of neuronal diversification. Indeed, a CART decision tree, for anatomical class prediction from gene expression patterns, reveals the genes involved at key bifurcations of morphological diversification. The non-pruned CART tree (not bootstrapped) predicted all anatomical classes using all seven genes. The pruned CART tree (after cross-validation using bootstrap) revealed four genes that lie at key bifurcations of neocortical neuronal diversification (SOM, PV, VIP and NPY). Reduction in the number of MCs to half only resulted in a priority shift of the two first bifurcations (PV versus SOM), and did not affect more distal branches. This finding therefore reveals the robust association between bifurcations in expression with morphological segregation.

Although ANN and CART demonstrated similar overall accuracies, we found that for the lower-prevalence anatomical classes (especially BPC, DBC, and SBC), the methods frequently assigned cells differentially. This is not unexpected, because the mathematics of optimization reflect the intended inference to be gained from each model. The ANN uses a maximum likelihood algorithm to return a single set of weights (i.e. it operates in weight-space), reflecting a trade-off in overall likelihood of misclassification. As described above, this provided a continuous, comparative measure of the influence of each predictor gene controlling for the influence of the others. On the other hand, CART applies a trial-and-error approach to iteratively split predictor data in a binary fashion (i.e. operating in ‘data-space’), in such a way as to maximize classification accuracy at terminal (anatomical type) nodes; this is advantageous when, as we found, a hierarchical decision process can promote understanding of the influence and relationships of predictors, or when resources are constrained, so that a limited sequence of measurements may be desired in practice.

Functional significance

Here we demonstrate the statistical significance of the relationship of three independent aspects of neocortical neurones: anatomical class (dependent on extracellular signalling molecules, membrane receptors and cytoplasmic cytoskeletal proteins); intracellular calcium buffering (via CaBPs); and modulation of neighbouring cells (via NP expression). Clustering by gene expression separates anatomical classes and therefore demonstrates the tight correlation between patterns of coexpression and anatomical type. This clearly suggests a coordination between the neurone's morphological spread (which part of the neocortex it innervates and which subdomains of the targeted neurones are innervated) and the nature of the neurotransmission (NP expression) as well as its internal biochemical activity and Ca²⁺ dynamics (CaBP expression). Moreover, as NPs may also be released from all parts of the neurone (Zhu et al. 1986; see also Thureson-Klein & Klein, 1990) the release of particular NPs on specific locations of the microcircuit (determined by the neurone's arborization) could fine-tune the unique influence of that particular neurone.

Supplemental material

The online version of this paper can be accessed at: 10.1113/jphysiol.2005.089250

http://jp.physoc.org/cgi/content/full/jphysiol.2005.089250/DC1 and contains supplemental material consisting of three tables and two figures.

Supplemental Figure 1. Neurones were compared for similarity of gene expression patterns (blue end of spectrum indicates greater similarity); neurones were subsequently sorted according to similarity of mRNA expression (unsupervised, nearest neighbour reshuffling (Ward, 1963) of pairwise-correlated gene profiles), which suggests four overlapping cell clusters

Supplemental Figure 2. CART binary decision tree, pruned by 300 cross-validated data-splits, for data sets constructed by randomly erasing 33 of the 67 starting Martinotti cells

Supplemental Table S1. Accuracy of unsupervised QTC cluster assignment

Supplemental Table S2. Bayes-optimal confusion matrix

Supplemental Table S3. True and predicted morphology

This material can also be found as part of the full-text HTML version available from http://www.blackwell-synergy.com