Integration of K⁺ and Cl^– currents regulate steady-state and dynamic membrane potentials in cultured rat microglia

Abstract

The role of ion channels and membrane potential (V_m) in non-excitable cells has recently come under increased scrutiny. Microglia, the brain's resident immune cells, express voltage-gated Kv1.3 channels, a Kir2.1-like inward rectifier, a swelling-activated Cl^– current and several other channels. We previously showed that Kv1.3 and Cl^– currents are needed for microglial cell proliferation and that Kv1.3 is important for the respiratory burst. Although their mechanisms of action are unknown, one general role for these channels is to maintain a negative V_m. An impediment to measuring V_m in non-excitable cells is that many have a very high electrical resistance, which makes them extremely susceptible to leak-induced depolarization. Using non-invasive V_m-sensitive dyes, we show for the first time that the membrane resistance of microglial cells is several gigaohms; much higher than the seal resistance during patch-clamp recordings. Surprisingly, we observed that small current injections can evoke large V_m oscillations in some microglial cells, and that injection of sinusoidal currents of varying frequency exposes a strong intrinsic electrical resonance in the 5- to 20-Hz frequency range in all microglial cells tested. Using a dynamic current clamp that we developed to actively compensate for the damage done by the patch-clamp electrode, we found that the V_m oscillations and resonance were more prevalent and larger. Both types of electrical behaviour required Kv1.3 channels, as they were eliminated by the Kv1.3 blocker, agitoxin-2. To further determine how the ion currents integrate in these cells, voltage-clamp recordings from microglial cells displaying these behaviours were used to analyse the biophysical properties of the Kv1.3, Kir and Cl^– currents. A mathematical model that incorporated only these three currents reproduced the observed V_m oscillations and electrical resonance. Thus, the electrical behaviour of this ‘non-excitable’ cell type is much more complex than previously suspected, and might reflect a more common oversight in high resistance cells.

Microglia are immune cells that reside in the central nervous system (CNS). They respond to essentially all insults (damage or disease) by undergoing complex changes, collectively called ‘activation’. As several functions of activated microglia can be harmful to bystander cells, understanding their mechanisms of activation will be important for developing therapies to regulate CNS inflammation. In this study, we test a strategy that uses potent and specific blockers of the voltage-gated K⁺ channel, Kv1.3 (Kotecha & Schlichter, 1999; Khanna et al. 2001; Schlichter & Khanna, 2002). Kv1.3, which is widely expressed in immune cells, plays a clear role in activation of human natural killer cells and T lymphocytes (Schlichter et al. 1986; Cahalan et al. 2001). Indeed, Kv1.3 appears to be a promising target for autoimmune diseases that involve T-cell activation (Beeton et al. 2001; Chandy et al. 2004). In T cells, one mechanistic role for Kv1.3 channels is to maintain a negative membrane potential (V_m), which promotes calcium influx (Krasznai et al. 1995; Cahalan et al. 2001; Chandy et al. 2004; Robbins et al. 2005). The same might be true for other immune cells. Numerous ion currents have been identified in microglia, including several K⁺ channels, a Cl⁻ current, ionotropic purinergic receptors, an H⁺ current and the cation channel, TRPM7 (see Eder, 1998; Eder & Decoursey, 2001; Schlichter & Khanna, 2002 for reviews; Cayabyab & Schlichter, 2002; Jiang et al. 2003). Little is known about how ion channels affect microglial cell functions and how V_m is controlled. In whole-cell recordings from cultured microglial cells, the predominant currents are Kv1.3 and a Kir2.1-like inward rectifier (Norenberg et al. 1994a; Visentin et al. 1995; Schlichter et al. 1996; Schilling et al. 2000). However, in comparing freshly isolated with cultured microglia, we showed that activity of Kv1.3, Kv1.5 and Cl⁻ channels promotes microglia proliferation (Schlichter et al. 1996; Kotecha & Schlichter, 1999) and have recently found that microglial Kv1.3 channel activity increases their ability to kill neurones (Fordyce et al. 2005). In addition, Kv1.3 and Ca²⁺-activated K⁺ channels regulate the respiratory burst of microglia (Colton et al. 1994; Spranger et al. 1998; Khanna et al. 2001), and Cl⁻ channels are involved in nitric oxide production (Pyo et al. 1997) and shape changes (Eder et al. 1997).

Why are so many channels expressed in ‘non-excitable’ microglia, and how do the channels integrate to contribute to the cells' functions? One proposed role for the inward rectifier current is to maintain a negative membrane potential (V_m) (Chung et al. 1999), which drives calcium entry when purinergic receptors are activated (Franchini et al. 2004). Clearly, elucidating the integrated roles of ion channels in microglial functions will require accurate measurements of V_m. Previous V_m measurements, which employed whole-cell recordings in the current-clamp mode have yielded diverse values: (i) bimodal distributions at −35 and −70 mV (Norenberg et al. 1994a), −61 and −29 mV, and −52 and −23 mV in brain slices (Boucsein et al. 2003); (ii) a relatively depolarized potential at −32 mV in unstimulated cells but bimodal values at about −70 and −44 mV after activation by lipopolysaccharide (Chung et al. 1999); or (iii) spontaneous jumps between about −35 and −74 mV (Norenberg et al. 1994a). Whole-cell recording itself can affect V_m by artificially altering intracellular ion concentrations and diluting channel regulatory molecules, which can affect the current prevalence, amplitudes and properties. For patch-clamp recordings to accurately measure V_m, the membrane resistance must be substantially lower than the seal resistance. Obvious signs of a leak artifact include more negative V_m values in recordings that have higher resistances, and a relatively linear current–voltage relation under current clamp. Conversely, if the leak allows Ca²⁺ entry, activation of Ca²⁺-activated K⁺ (KCa) channels (Eder, 1998; Khanna et al. 2001) could hyperpolarize V_m. Attempts to overcome leak artifacts include the historical use of sharp electrodes to report the V_m value at the instant of impalement, before the cells depolarize (Schlichter, 1983; Ince et al. 1983). More recently, the cell-attached configuration in voltage-clamp (Verheugen & Vijverberg, 1995) or current-clamp mode (Mason et al. 2005) has been used to non-invasively measure V_m; however, the latter measurements require relatively low membrane resistances. V_m values for microglial cells have not been verified using non-invasive methods.

Using a combination of fluorescent dyes, current-clamp and voltage-clamp recordings and mathematical modelling, we show: (i) several biophysical features of the Kv1.3, Kir2.1 and swelling-sensitive Cl⁻ currents in cultured rat microglia; (ii) that microglia have very high resistances in the physiological V_m range; (iii) that V_m measurements and current–voltage relations are easily compromised by leak around the electrode; (iv) that the Cl⁻ current contributes to V_m in intact cells; and (v) that these three currents cause strongly non-linear current–voltage relations and are capable of promoting V_m oscillations and sharp frequency selection.

Methods

Cells

Microglia were isolated from brain explants of 2-to 3-day-old Wistar rats as previously described (Cayabyab et al. 2000; Khanna et al. 2001). Rat pups were killed by cervical dislocation in accordance with guidelines from the Canadian Institutes of Health Research and the University Health Network. Neopallial brain tissue was digested by agitation in minimal essential medium (MEM; Gibco Invitrogen, Burlington, Ontario, Canada) containing 2.5% trypsin and 100 U DNase I (Pharmacia, Baie d'Urfe, Quebec, Canada) for 30 min at room temperature (21–23°C), and then triturated and digested for a further 30 min until no tissue clumps were visible. This mixture was pelleted, resuspended and seeded into flasks with MEM containing 10% fetal bovine serum (FBS; Gibco BRL) and 100 μm gentamycin (Gibco BRL). After 2 days, cellular debris, non-adherent cells and supernatant were removed and fresh medium was added to the flask. The mixed cultures were allowed to grow for 10 days and then shaken overnight on an orbital shaker at 8–10 Hz in a standard tissue culture incubator. The non-adherent microglia were harvested, suspended in culture medium containing 2% FBS, plated on coverslips for 2 h, and then washed with culture medium. For experiments using flow cytometry and voltage-sensitive dyes, microglia were used immediately after shaking. After plating, some cell batches were treated with 5 ng ml⁻¹ lipopolysaccharide (LPS; Sigma-Aldrich, Oakville, Ontario, Canada) for 12–16 h.

Patch-clamp electrophysiology

Microglia on coverslips were mounted in a perfusion chamber (Model RC-25, Warner Instruments, Hamden, CT, USA) and the tissue culture medium was replaced with an extracellular (bath) solution containing (mm): NaCl 125, KCl 5, MgCl₂ 1, CaCl₂ 1, glucose 5 and Hepes 10; pH adjusted to 7.4 with NaOH. Approximately 20 mm sucrose was added to adjust the osmolarity to 280–300 mosmol l⁻¹, measured with a freezing-point depression osmometer (Advanced Instruments, Norwood, MA, USA). When desired, a large swelling-activated Cl⁻ current was elicited with a hypo-osmotic solution made by diluting the bath solution with distilled water to 60% of the normal osmolarity. The Cl⁻ current remained activated for several minutes after the bath solution was replaced by a solution containing isotonic N-methyl-d-glucamine (NMDG) chloride, which was useful for isolating the Cl⁻ current while maintaining the normal Cl⁻ gradient. The intracellular (pipette) solution contained (mm): potassium aspartate 100, KCl 40, MgCl₂ 1, CaCl₂ 1, EGTA 10, Hepes 10, MgATP 2; pH adjusted to 7.2 with KOH, osmolarity 280–300 mosmol l⁻¹. Where indicated in the Results, 1 nm agitoxin-2 was added to the bath solution to block the Kv1.3 current.

Pipettes with resistances of 4–6 MΩ were pulled from borosilicate glass (WPI, Sarasota, FL, USA). A multiclamp 700A patch-clamp amplifier (Axon Instruments Molecular Devices, Sunnyvale, CA, USA) was used in either the current-clamp or voltage-clamp mode (filtered at 5 kHz), and recordings were compensated on-line for capacitance and series resistance. Data were digitized and acquired using a Digidata 1322 board with pCLAMP version 9.0 (Molecular Devices) and were analysed (see below) using Origin version 7.0 (OriginLabs, Northampton, MA, USA). Liquid–liquid junction potentials (e.g. between the NaCl bath and KCl/potassium aspartate pipette solution) were calculated with the utility in pCLAMP, confirmed by measuring the values using a 3-m KCl electrode (Barry & Lynch, 1991), and subtracted before data analysis.

Dynamic current clamp

Dynamic current clamp allows injection of a current whose amplitude is a function of the measured membrane potential (V_m) (Sharp et al. 1993). This method was used to compensate for leak through the electrode seal, as follows. We wrote a simple program in BASIC, running in DOS, and used a Tekmar Labmaster digitizer to rapidly (> 10 kHz) change the amplitude of the injected current as a linear (ohmic) function of V_m whenever it changed. Thus, the electrode leak was compensated for by injecting an opposing current of equal magnitude. The seal resistance was estimated by assuming that all of the current at the Nernst potential for K⁺ (E_K) was due to an ohmic leak around the seal; a reasonable assumption when the swelling-activated Cl⁻ current has not been induced. Further validation of this assumption comes from non-invasive measurements wherein the mean membrane resistance of microglia was shown to be ∼8 GΩ between the resting potential and ∼0 mV (see Figs 4D and 5C).

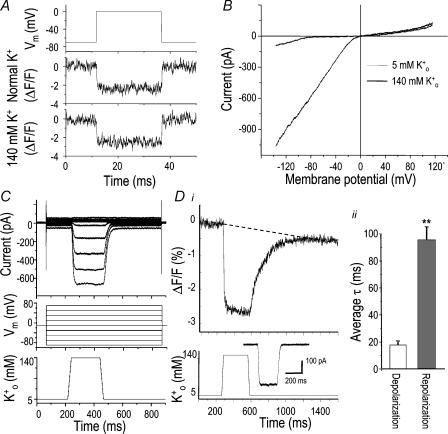
Figure 4. A voltage-sensitive dye, di-8-ANEPPS, reveals the high membrane resistance of microglia.

A, verification of the response speed of di-8-ANEPPS using the whole-cell voltage clamp. A 25-ms long voltage step from −70 to 0 mV (top trace) was applied while measuring di-8-ANEPPS fluorescence of the same cell in normal bath solution (5 mm K⁺_o; middle trace) or with 140 mm K⁺_o (bottom trace). Dye traces are an average of 30 such steps. B, dependence of inward rectifier current (Kir) on extracellular K⁺ concentration. Currents in normal solution (5 mm K⁺_o; smaller amplitude) or 140 mm K⁺_o were recorded in response to voltage ramps from +120 to −140 mV from a holding potential of −10 mV. C, Kir currents were used to test the rate of change of the external solution. The lower panel indicates when the position of the pipette superfusing the cell was switched from 5 to 140 mm K⁺ solution for 250 ms. The top panel shows that elevating external K⁺ produced larger inward Kir currents during voltage-clamp steps (middle traces) between −90 and +70 (in 20-mV increments) from a holding potential of −10 mV. The time course of each change in current was fitted to a mono-exponential, and used to calculate the average time constant (τ) for the solution change. Di, a representative recording of di-8-ANEPPS fluorescence from a single microglial cell. Cell depolarization in response to a 250-ms long exposure to 140 mm K⁺ solution reduced the fluorescence intensity (measured as photodiode current; upper trace). Note the slower fluorescence response to repolarization when the solution was switched back to 5 mm K⁺. The dashed line indicates the drift in signal over the 25 averaged traces. Lower panel, the position of the superfusing pipette controlling the external K⁺ concentration, with an inset showing the time course of the resulting change in Kir current (at −50 mV) on the same time scale (lower panel). Dii, for each cell, the time constants (τ) of depolarization and repolarization, calculated from mono-exponential curve fits, are shown for depolarization (17.7 ± 2.1 ms) and repolarization (95.4 ± 9.0 ms). Values are mean ±s.e.m. for 22 cells (**P < 0.0001, Student's t test).

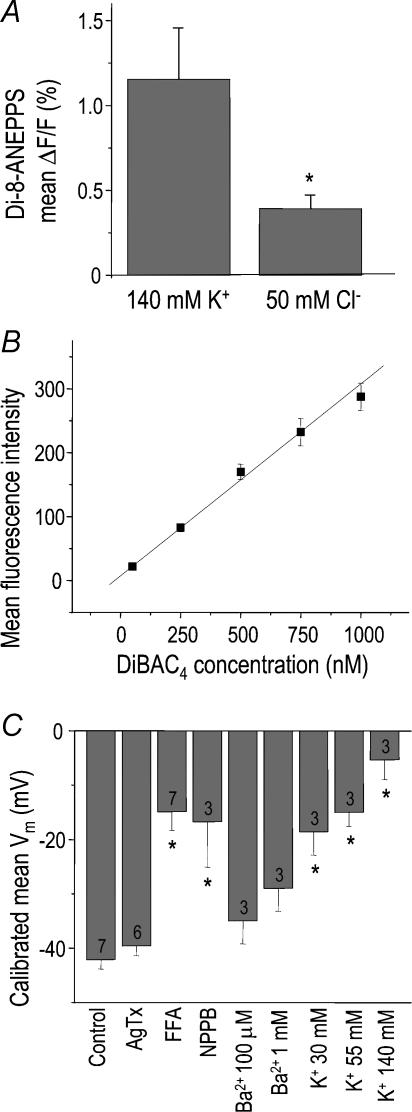
Figure 5. Non-invasive dye measurements of membrane potential in microglia.

A, initial evidence that a chloride conductance contributes to the membrane potential (V_m). The fast dye, Di-8-ANEPPS, was used in combination with fast solution changes as in Fig. 3. For each of five cells, the mean change in fluorescence (±s.e.m.) in response to 25 switches in the bath solution was divided by the total fluorescence (*P < 0.05; Student's t test). B, calibration of the more sensitive voltage-dependent dye, DiBAC₄, using flow cytometry on microglia. First, the membrane potential of all cell batches was set to 0 mV using 1 μm gramicidin, and then varying concentrations of DiBAC₄ were applied to the cells for ∼20 min before monitoring cell fluorescence with a flow cytometer (see Methods). This representative experiment shows the linear relationship between intracellular dye concentration and mean fluorescence intensity, from which the actual V_m was calculated. C, effects of ion-channel blockers and K⁺ concentrations on the mean membrane potential (V_m) of microglia. V_m values were determined using DiBAC₄ (see Methods and B). Values are mean ±s.e.m. for the number of separate cell batches indicated on each bar (*P < 0.05; ANOVA with Bonferroni correction for multiple comparisons). Bath solutions contained normal saline with 5 mm K⁺ and 134 mm Cl⁻ (control) and normal saline to which compounds were added (10 nm agitoxin-2, 150 μm flufenamic acid, 100 μm NPPB, 100 μm or 1 mm BaCl₂) or saline in which the K⁺ concentration was raised to 30, 55 or 140 mm in exchange for Na⁺.

Electrical resonance measurements

A sinusoidal current waveform was applied to each microglial cell under current clamp using the ‘stimulus file’ feature of pCLAMP. To continually vary the frequency, we used a modified ‘zap’ function whose frequency decreased (forward) or increased (reverse) according to a hyperbolic function (Hutcheon et al. 1996; Hutcheon & Yarom, 2000). This produced a sufficient number of low frequency oscillations to allow analysis of slow responses. When desired, the sinusoidal current stimulus was combined with an offset current (see Results). Impedance plots were created by dividing the fast-Fourier transform (FFT) of the output (mV Hz⁻¹) by the FFT of the input (pA Hz⁻¹) (Hutcheon et al. 1996) using pCLAMP, and then fitting the curves to an equation describing the impedance of a resistance/inductance/capacitance (RLC) circuit where all three components are in parallel, as follows:

(A)

where:

(B)

In this equation, Z is impedance, F_n is the frequency where Z peaks and represents the natural (or resonant) frequency of the circuit and L is the inductance. Q, the quality factor, which is an indication of the strength of the resonance, is the proportion of the energy stored by inductance versus that dissipated by resistance. Bandwidth (BW =F_n/Q) indicates the resonance sharpness, and is the range of frequencies within which the impedance power is 50% or more of the maximum. Both strength and sharpness are indicators of a cell's ability to respond selectively to specific frequency ranges (i.e. cells with higher Q and smaller bandwidth will respond strongly to a smaller range of frequencies). As seen from these equations, in an ideal RLC circuit with all components in parallel, Q will decrease by the addition of a parallel resistance (seal resistance) and bandwidth will increase. In contrast, the resonant frequency should be unaffected, as F_n= (√[1/(LC)])/2π is independent of R.

Voltage-sensitive dye measurements of membrane potential

Two fluorescent voltage-sensitive dyes were used to monitor the membrane potential (V_m). To measure absolute V_m values, we used the slow, monovalent anionic voltage-sensitive dye, DiBAC₄ (Molecular Probes, Invitrogen, Ontario, Canada) as previously described (Krasznai et al. 1995). DiBAC₄ equilibrates across the cell membrane (i.e. reaches a Nernstian distribution) according to the membrane potential. A standard curve was created relating the intracellular DiBAC₄ concentration to the measured fluorescence, as follows. Separate aliquots of freshly shaken, non-adherent microglia were treated with various concentrations of DiBAC₄ (0–1000 nm) for 20 min together with 1 μm gramicidin to fully depolarize the cells and the fluorescence was measured using the FL1 emission filter on a FACScan flow cytometer (Becton Dickinson, Ontario, Canada). Then, the fluorescence of test microglial samples exposed for the same time (20 min) was measured using 500 nm DiBAC₄ without gramicidin. Interpolation of the mean cell fluorescence onto the calibration curve yielded an apparent internal dye concentration, which was then used to calculate the Nernst potential for DiBAC₄ (i.e. V_m).

For measuring fast membrane potential changes, the cells were labelled with 10 μm di-8-ANEPPS and 0.05% Pluronic F-127 at room temperature for 10 min (Bullen & Saggau, 1999) and then washed in Hepes-buffered bath solution (see ‘Patch-clamp electrophysiology’). Di-8-ANEPPS is an electrochromic dye that partitions into the membrane and undergoes fast shifts in excitation and emission spectra when V_m changes (Loew, 1982). Di-8-ANEPPS fluorescence was monitored with an inverted microscope (Diaphot TMD, Nikon, Canada) using a 530-nm (530BP10) excitation filter, a 550-nm dichroic mirror (550DCLP) and a 590-nm emission filter (590ALP), all from Omega Optical (Brattleboro, VT, USA). For each experiment, light emitted from a field containing a single microglial cell was detected with a cooled Avalanche photodiode connected to a Photomax 200 amplifier (Dagan, Minneapolis, MN, USA) filtered at 2 kHz. To rapidly change extracellular solutions, a piezoelectric actuator (EXFO Burleigh, Quebec, Canada) controlled the position of a theta-glass perfusion pipette (pulled to ∼300 μm in diameter) positioned near the cell but outside the partially occluded field of the 100 × objective. To ensure that pipette movement did not affect the signal, some recordings from each cell were made near the isosbestic wavelength for di-8-ANEPPS using a 490-nm excitation filter (490DF20, Omega Optical).

Curve fitting, mathematical modelling and simulations

Curve fitting (see Results) was done using the non-linear least-squares reduction and Simplex method in Origin version 6.1 or 7.0. For simulations of membrane potential changes, the differential equations were entered into XPPAUT for Windows (WinPP) (Ermentrout, http://www.math.pitt.edu/~bard/xpp/xpp.html) and solved quantitatively. We used the RK4 method, which produced accurate simulations for a time step of 0.05 ms, and we confirmed that either longer (0.1 ms) or shorter (0.01 ms) time steps produced the same results. In order to add a sinusoidal current to the simulation, we used the same sine function that was used for the experimental stimulus file.

Reagents

DiBAC₄ and Di-8-ANEPPS were obtained from Molecular Probes, through Invitrogen. Agitoxin-2 (AgTx-2) was obtained from Alomone Laboratories (Jerusalem, Israel). Flufenamic acid, 5-nitro-2-(3-phenylpropylamino)benzoic acid (NPPB), adenosine 5′-triphosphate, magnesium salt (MgATP) and other salts were obtained from Sigma-Aldrich (Oakville, Ontario, Canada).

Results

Measuring the currents to incorporate into a mathematical model

First, we used voltage-clamp analysis to determine the amplitude, voltage-dependence and kinetic properties of the currents in microglial cells, and incorporated these parameters into a mathematical model that describes their contribution to the membrane potential (V_m).

Kv1.3 current

The kinetics of native Kv1.3 currents (Fig. 1A) have previously been described in detail for microglia (Norenberg et al. 1994a) and T lymphocytes (Cahalan et al. 1985; Decoursey, 1990; Pahapill & Schlichter, 1992; Panyi et al. 1995). For the present analysis, we used a model for Kv1.3 (Marom & Levitan, 1994) in which gating is described by six states: four closed states that undergo sequential voltage-dependent transitions to an open state, and an inactivated state that is accessible only from the open state. This model was used to show that inactivation is state-dependent, not voltage-dependent, and then the state model was reproduced using the standard Hodgkin–Huxley formalism (Marom & Abbott, 1994). Before curve fitting the Kv1.3 currents in microglial cells, we subtracted a small linear leak current by assuming that all current at the K⁺ equilibrium potential was leak. Justification for omitting Cl⁻ current in this calculation is presented below.

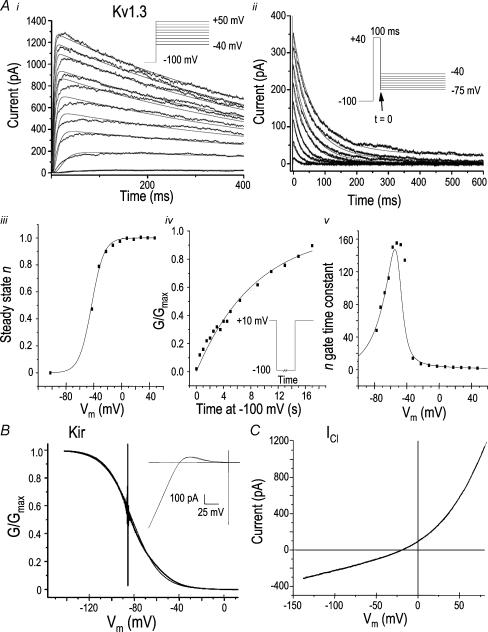
Figure 1. Measuring the current parameters used in the mathematical model.

A, representative voltage-clamp recordings of the Kv1.3 current. Outward Kv1.3 currents elicited by voltage-clamp steps between −40 and +50 mV, from a holding potential of −100 mV. The smooth curves are n⁴j fits of eqns (6)–(9) (see Results) used to calculate time constants of opening and inactivation. The maximal conductance in this LPS-treated cell was 9.72 nS, calculated at +50 mV (i). Tail currents were elicited by voltage-clamp steps between −40 and −75 mV (in 5-mV increments) after a 100-ms pulse to +40 mV. The smooth curves are fits to eqns (6)–(9) and were used to calculate the time constant for channel closing (ii). Steady-state values of n (the activation gate) were obtained from the curve fits shown in i and fitted to a Boltzmann equation, yielding a slope of 8.2 mV and a voltage for half-maximal activation (V_1/2) of −41.9 mV (iii). Time course of recovery from inactivation at −100 mV. V_m was held at +10 mV for 45 s to fully inactivate the Kv1.3 current, and then stepped for varying times to −100 mV to allow recovery from inactivation. The conductance was normalized to the maximal value after 18-s recovery time, and the time course was fitted with a mono-exponential function, yielding a time constant (τ) of 8.7 s (iv). Time constants for opening and closing as a function of voltage were obtained from the curve fits in i and iv. The smooth curve was fitted to the values calculated from the inverse of the sum of α and β curves (see eqns (10) and (11)). The parameters obtained for the rate constants, α and β, were: A_a, 0.00567; A_b, 41.5; A_c, 3.17; B_a, 0.0117; B_b, 68.6; B_c, 19.0 (v). B, voltage-clamp analysis of the inward rectifier (Kir) current. From a holding potential of 0 mV (chosen to inactivate the Kv1.3 current), 700-ms long voltage ramps were applied between 0 and 140 mV. To reduce the noise, 30 current–voltage traces were averaged. Then, the conductance was normalized to the maximal value at −140 mV, and the curve was fitted to a Boltzmann equation, yielding a slope of 12.4 mV and V_1/2 of −81.7 mV. Inset, a representative example of the observed Kir current, overlaid with a trace of the calculated current (eqns (12) and (13)). C, swelling-activated Cl⁻ current. A voltage-clamp ramp was applied between −140 and +75 mV after the swelling-activated chloride current was induced with hypotonic (60%, 200 mosmol l⁻¹) bath solution (see Methods). To eliminate Kir, the bath solution lacked potassium, and the holding potential was 0 mV to inactivate the Kv1.3 current. The current–voltage relation was very well fitted by a polynomial equation (smooth curve): I= (6.4)(10⁻⁷)(V_m⁴) + (3.3)(10⁻⁴)(V_m³) + (0.0553)(V_m²) + (6.061)(V_m) + 94.6 pA.

Kv1.3 currents were fitted from the first point after the end of the capacitance transient using the following equations.

(1)

(2)

(3)

(4)

(5)

n is the probability of each of the four gates being in the activated conformation; j is the probability that the state-dependent inactivation gate is open; and dj/dt depends on n⁴j (probability of each channel being open). For greater accuracy, activation and inactivation were fitted simultaneously at each voltage (Fig. 1Ai) using a constant-voltage solution to the previous equations, as follows:

(6)

(7)

(8)

(9)

The variable, x_j, was used to describe state-dependent inactivation, which changes with time during the voltage pulse. The initial condition was achieved by holding V_m at −100 mV to remove all inactivation (i.e. set j∼1). Then, the current inactivation was fitted during a step to +50 mV (time constant τ= 1/α_j). β_j, the inverse of the time constant of recovery from inactivation was calculated as follows (Fig. 1Aiv). V_m was held at +50 mV (to set j∼0) then stepped for variable durations to −100 mV to allow recovery from inactivation, and finally stepped back to +50 mV to determine the extent of recovery. For all curve fits, the maximal conductance (g_max) was determined by fitting the time course of the current at +50 mV (Fig. 1Ai), and then used to normalize the curve (Fig. 1Aiii). This simple method yielded the same results as calculating g_max from the measured peak current, because activation was much faster than inactivation.

From the curve fits to currents elicited by voltage steps between −40 and +50 mV, τ_n, and n_∞ were estimated after fixing g_max, α_i and β_i to the values obtained above (Fig. 1Ai). Similarly, tail currents at −50 mV and below (Fig. 1Aii) were fitted using an initial value of n = 1, because the maximal number of n gates is expected to accumulate in the open conformation during a 10-ms pulse to +50 mV. Initial values for j (j₀) were calculated by solving eqns (6)–(9) at +40 mV and t= 100 ms, then the closing time constants were obtained from curve fits that included the continuing inactivation. The closing time constant for n gates is equivalent to a mono-exponential decay with a time constant of 4/τ_n.

The n_∞ values obtained from fitting the activation curves (Fig. 1Ai) were fitted to a standard Boltzmann equation with a fixed minimum of 0 and maximum of 1 (Fig. 1Aiii). These values, combined with the τ_n values, were used to construct curves describing α_n and β_n as follows (see Fig. 1Av).

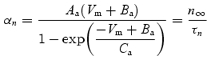(10)

(11)

The curve fits for activation, inactivation and closing obtained from the n⁴j model accurately described the voltage-clamp traces (Fig. 1Ai and ii), except for small deviations near the threshold for activation of the Kv1.3 current, where the kinetics of the rising phase were closer to mono-exponential. However, we determined that this small deviation did not affect the simulations. That is, when opening was modelled as one fast transition instead of four (i.e. nj, instead of n⁴j), the results (including V_m oscillations) were very similar. Steady-state inactivation–voltage relations were examined on many cells (not shown, but see Kotecha & Schlichter, 1999) but because inactivation was modelled as a voltage-independent process, this information was not required for parameter estimation. Nevertheless, the voltage-independent parameters, αj and βj, were estimated as described above and both inactivation and recovery from inactivation were included in the model and in all simulations. We found that inactivation played very little role in any of the simulations. This is not surprising, because the rate and extent of inactivation depend on the proportion of channels activated, which is small for the durations and voltages used in the simulations. Although one paper reported more complicated kinetics for recovery from inactivation (Levy & Deutsch, 1996), the differences were small and we found that the simulated V_m oscillations were not sensitive to this parameter.

Inward rectifier (Kir) current

The inward rectifier (Kir) current (Fig. 1B) is very similar to the cloned Kir2.1 channel, and Kir2.1 transcripts have been detected in microglia (Schilling et al. 2000). Although the Kir current is strongly inwardly rectifying, a small outward component is seen above E_K. We approximated Kir ‘activation’ as time independent, which is justified because Kir2.1 is gated on a millisecond time scale by voltage-dependent relief of block by cations, including Mg²⁺, spermine and spermidine (Matsuda et al. 1987; Xie et al. 2002). Ionic block of Kir channels has been exploited in cell functional studies wherein Ba²⁺ (or less commonly, Cs⁺) is added to the bath solution (Schlichter et al. 1996; Franchini et al. 2004); however, high concentrations are needed to reduce outward current because the block is strongly voltage dependent. Our simulations did not extend more negative than E_K (−85 mV), thus the slow voltage-dependent block by external Na⁺ at very negative potentials was not an issue. As no time-dependent changes were observed during voltage steps, when recording Kir current during voltage ramps its conductance−voltage relation was well described by a Boltzmann equation:

(12)

(13)

Since steady-state inactivation of the Kv1.3 current in microglia is complete at 0 mV (tested on same cells, data not shown; and Kotecha & Schlichter, 1999); a holding voltage of 0 mV was used to isolate the Kir current. Currents evoked by 20 consecutive voltage ramps between +40 and −160 mV were averaged before calculating the conductance in order to eliminate the exaggerated calculation errors near E_K caused by current noise. An overlay of the recorded current (Fig. 1B, inset) and that calculated from eqns (12) and (13) shows excellent agreement.

Swelling-activated chloride current

Under the whole-cell recording conditions used in the present study, the Cl⁻ current (Fig. 1C) was very small and extremely difficult to distinguish from the leak. Thus, in order to determine its current–voltage relations and kinetics we used a hypotonic solution to exploit its swelling-induced activation (Schlichter et al. 1996). For these measurements, Kir current was eliminated at all physiologically relevant voltages by using a K⁺-free bath solution, and Kv1.3 was inactivated using a holding potential of 0 mV. The observed reversal potential of the Cl⁻ current was about −20 mV, as expected from the chloride gradient (40 mm Cl⁻ and 100 mm aspartate in the pipette; 134 mm Cl⁻ in the bath). As previously observed (Schlichter et al. 1996), the Cl⁻ current was neither voltage activated nor time dependent during voltage-clamp steps (not shown); thus, the current–voltage relationship was fitted to a polynomial (see legend, Fig. 1C).

Current-clamp recordings

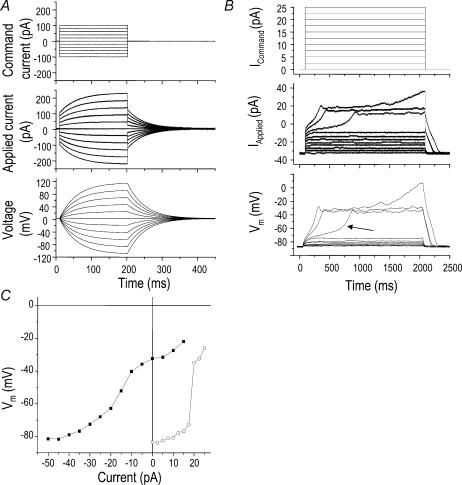
First, we attempted to use whole-cell, current-clamp recordings to measure the resting membrane potential (V_m) and the V_m responses to current injections. Our measured V_m values (from −5 to −85 mV, n > 40) were highly variable, as were the responses to current injection; however, small current injections often evoked large V_m changes, indicating a high resistance. The membrane resistance, calculated by dividing the holding current at E_K by the driving force (85 mV) for the leak, was ∼2.5 GΩ for the cell in Fig. 2A, with a mean of 2.1 ± 0.5 GΩ recorded in six microglia. This value was not significantly different from the seal resistance (R_seal) measured in the cell-attached configuration in the same six cells (3.2 ± 0.8 GΩ). Consequently, the V_m of microglia, as in other high-resistance cells (Ince et al. 1983) including some neurones (Tyzio et al. 2003; Pun & Kleene, 2004; Wang et al. 2003), will be susceptible to electrode-induced leak even when the seal resistance is in the gigaohm range. For example, with an electrode-induced leak as small as 10 pA, the true membrane potential of the cell in Fig. 2A would have been nearly −80 mV (Fig. 2Aii), rather than the recorded value of −64 mV (Fig. 2Ai). There would be 10 pA of leak current in the −60 to −80 mV range if R_seal was 6–8 GΩ: a realistic value (see below). Using a −10-pA holding current to maintain a more negative V_m had no effect on the largely leak-dominated voltage–current relationship (Fig. 2Aii).

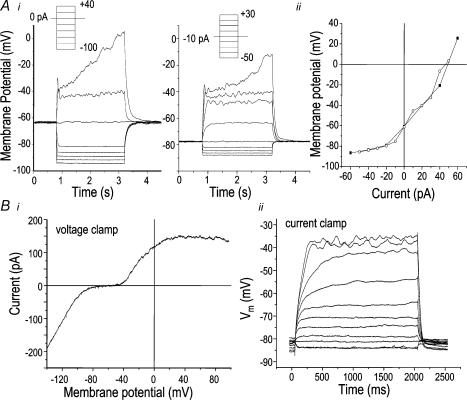
Figure 2. Non-linear relationship between current and voltage in microglia reveals high-resistance regions.

A, representative current-clamp recordings of membrane potential (V_m) from a microglial cell that had small Kv1.3 and inward rectifier (Kir) currents (see text). The uncorrected resting potential was −64 mV and V_m changes were evoked by steps of current (see inset) superimposed on a holding current of 0 pA (left) or −10 pA (right) (i). Voltage–current relations from the recordings in i, with a holding current of 0 pA (▪) or −10 pA (○). V_m values were measured at the 1000 ms time point and plotted against the injected current (ii). B, relationship between voltage- and current-clamp recordings in a representative untreated microglial cell that was also used for comparison in Fig. 3B. Under voltage-clamp, a voltage ramp from −120 to +80 mV was applied from a holding potential of −80 mV. This cell had relatively little Kir (inward current below −80 mV) and Kv1.3 (outward current above −40 mV). Note the extremely small current between −80 and −40 mV, indicating a total resistance of about 2.6 GΩ(i). (ii) Conventional current clamp. The traces are V_m responses to steps of injected current between −50 and +15 pA (in 5-pA increments), with a holding current of −40 pA, chosen to set the initial V_m to the Nernst potential for K⁺ (E_K; about −85 mV).

In order to understand how the Kv1.3, Kir and Cl⁻ currents and inherently high membrane resistance of microglia affect current-clamp recordings of V_m, we made voltage-clamp and current-clamp recordings on some of the same cells. Figure 2B shows an untreated microglial cell which had small K⁺ currents. In response to a voltage ramp stimulus, the current–voltage relation was highly non-linear, with an extremely high membrane resistance between about −80 and −40 mV (∼2.6 GΩ) where most Kv1.3 and Kir channels would be closed. Based on the observed high resistance in the region −80 to −40 mV, the Cl⁻ current must be very small, and this was verified by applying a Cl⁻ channel blocker. That is, at −85 mV, 150 μm flufenamic acid caused a non-significant change in holding current, from −40 ± 4.8 pA, which corresponds with a membrane resistance of 2.0 ± 0.4 GΩ (n = 6), to −34 ± 5.5 pA, which corresponds to 2.5 ± 0.8 GΩ. The flufenamic acid-sensitive current ranged from +18 to −1 pA, which was not significantly different from zero (i.e. when calculated for each cell and averaged; P= 0.1, one-sample t test). As the Cl⁻ current does not show voltage-dependent gating and its whole-cell current is nearly linear at negative potentials (Fig. 1C), it is easily mistaken for, or masked by, the electrode-induced leak. For the cell in Fig. 2Bii, small current injections produced large, nearly mono-exponential V_m excursions. Thus, opening of only a few channels would cause a substantial change in this V_m range. In contrast, at non-physiologically negative V_m values the membrane resistance was low and nearly constant (i.e. ∼130 MΩ below −80 mV in this cell), as expected when the Kir conductance is high (see Fig. 1C). Above −40 mV, the resistance progressively decreased due to Kv1.3 channel opening, thus the evoked V_m deflections were reduced. In Fig. 2Ai, note the dramatic time-dependent depolarization when V_m reached about −35 mV, consistent with time-dependent Kv1.3 inactivation (Fig. 1A) and a consequent increase in resistance with time. As expected, the current–voltage relation (Fig. 2Aii) was not changed when the initial V_m was set to −80 mV by a −10 pA holding current.

Dynamic current clamp to compensate for electrode damage

To reduce the error caused by electrode damage, we employed a dynamic current clamp, which counteracts the leak by electronically adding an equal and opposite parallel resistance to that of the R_seal (see Methods). The simple assumptions were that the electrode-induced leak conductance was ohmic (i.e. constant with voltage), reversed at 0 mV and carried almost all of the current at E_K. We recognize that dynamically compensating for leak through the patch-clamp seal may not be exact, as R_seal must be estimated and the assumption that the current at E_K is due to leak is accurate only if the net ionic current is zero at E_K. As shown in the previous section, these assumptions were well met under normal (non-swelling) recording conditions (i.e. there was very little current at E_K).

To demonstrate the ability to subtract a parallel resistance (e.g. R_seal) we used a model cell (PATCH-1 U, Axon Instruments) with an effective resistance (R_m) of 500 MΩ and a membrane capacitance (C_m) of 33 pF. We chose to subtract a parallel R_seal value of 1 GΩ with the dynamic current clamp. The resulting R_m should be 1 GΩ (i.e. = 1/(1/500 MΩ− 1/1000 MΩ)). As shown in Fig. 3A, an instantaneous step in command current elicited an instantaneous increase in applied current, followed by a time-dependent change in applied current as V_m changed. At the end of the command current step, the instantaneous decrease in applied current was followed by a time-dependent decrease that mirrored the change in V_m. Note that increasing the R_m increases the time constant for charging V_m because τ=R_mC_m (data not shown).

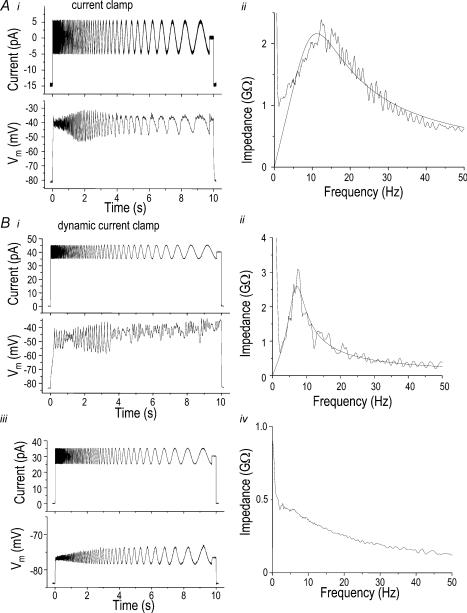
Figure 3. Seal resistance compensation using dynamic current clamp.

A, use of a model cell (Patch-1 U, Axon Instruments; C_m, 33 pF; R_m, 500 MΩ) to demonstrate parallel resistance compensation using dynamic current clamp (for details, see Methods). While compensating for a 1-GΩ seal resistance (R_seal), current steps from −100 to +100 pA were applied in 20-pA increments (upper traces). Middle traces show the actual applied current (I_APP) injected as a consequence of the resistance compensation (I_APP=I_CMD−V_m/R_seal, where I_CMD is the command current and R_seal is 1 GΩ). The bottom panel shows the V_m response of the model cell. B, recording from a microglial cell (same cell as in Fig. 2B) to show how dynamic current clamp can explain the existence of two quasi-stable resting potentials. The compensation current set the initial V_m to −85 mV (as in Fig. 2B), at which the seal resistance was calculated to be ∼2.5 GΩ. Current steps from 0 to 25 pA were applied in 2.5-pA increments (top traces). The actual applied current (I_APP, middle traces) is a function of both the command current (I_CMD) and the cell V_m (lower traces) as in A. C, current–voltage relations from the recordings using conventional current clamp (from Fig. 2B, ▪) and dynamic current clamp (from B, ○) on the same cell. V_m values were measured at 1000 ms.

A comparison of conventional (Fig. 2Bii) and dynamic current clamp (Fig. 3B bottom traces) in the same cell shows dramatic effects of compensating for the leak through the 2.2-GΩ seal resistance. The initial V_m was similar (about −87 mV, which is close to E_K) and small current steps produced small V_m changes that were nearly exponential with time. However, when V_m reached about −62 mV, there was a dramatic depolarization to about −35 mV (approximately E_Cl) and a clear inflection point. It is important this threshold effect was never seen with a model circuit (Fig. 3A), but was sometimes observed in microglia under conventional current clamp. A sharp depolarization is expected as Kir channels close, and has been observed in other cells with Kir currents (Gallin & Livengood, 1981; Goodman & Art, 1996b). Above the all-or-nothing depolarization, V_m entered another low-resistance range, dominated by Kv1.3. This behaviour might account for the commonly observed bimodal resting V_m values at about −35 and −70 mV (Norenberg et al. 1994a; Chung et al. 1999; Boucsein et al. 2003) and occasional spontaneous jumps between these values (Norenberg et al. 1994a).

Again, these V_m responses and the resulting current–voltage relations (Fig. 3C) are consistent with the underlying currents. At very negative V_m values both current-clamp methods show a relatively low R_m due to open Kir channels. In contrast, at V_m values between −70 and −40 mV, there was a dramatically higher R_m (steeper slope) under dynamic current-clamp conditions. Above about −40 mV, both methods revealed a lower R_m region due to open Kv1.3 channels. Concomitantly, in response to current steps (Fig. 3C), the V_m changes above −40 mV reflect a decrease in R_m as the Kv1.3 channels open, then an increase in R_m as they inactivate with time. Of most importance, although a normal seal resistance was obtained in this cell (∼2.2 GΩ), the current–voltage relation under standard current clamp was linearized by the seal resistance, and this masked the dynamic response seen in Fig. 3B.

Non-invasive measurements of membrane resistance

To more accurately measure the resistance of microglia, we devised a non-invasive method using a single photodiode and the extremely fast voltage-sensitive dye, di-8-ANEPPS (Loew, 1982). To demonstrate the properties of di-8-ANEPPS, Fig. 4A shows the fluorescence response of a single microglial cell to a voltage clamp step (whole-cell configuration) from −70 to 0 mV in normal bath solution (5 mm K⁺, middle trace) or 140 mm K⁺ (bottom trace). Clearly, in both solutions, the dye response is faster than the filtering frequency used (2 kHz). This approach exploited a rapid switch in external K⁺ concentration, which changed the driving force and caused a large (nearly instantaneous) increase in the inward Kir current at negative V_m values (Fig. 4B). Further validation in a microglial cell (Fig. 4C) is illustrated by measuring the di-8-ANEPPS voltage dependence and response time when the perfusion solution was changed with a fast piezoelectric device (see Methods) while monitoring the Kir current. Voltage-clamp steps of 800-ms duration were applied while rapidly switching the bath solution between 5 and 140 mm K⁺-containing saline. From the change in membrane current, we found that the time constant (τ) of solution exchange was 13.1 ± 2.3 ms when the bath was switched to 140 mm K⁺ and 19.8 ± 1.9 ms when it was switched to 5 mm K⁺ (n = 4 cells). As shown in Fig. 4A, the dye response is much faster than these values.

Finally, the di-8-ANEPPS responses were recorded from 22 individual microglial cells (e.g. Fig. 4Di), and the values of τ were calculated from mono-exponential curve fits (Fig. 4Dii). Notably, τ was 17.7 ± 2.1 ms during depolarization (with 140 mm K⁺), which is significantly faster than the 95.4 ± 9.0 ms value measured during repolarization (with 5 mm K⁺). For five of these cells, the fluorescence response of each intact cell was measured, then a whole-cell recording was immediately established and C_m was measured and used to calculate membrane resistance (R_m=τ/C_m). The value (8.8 ± 1.4 GΩ) during repolarization was almost identical to the 7.7 GΩ calculated from 25 additional whole-cell recordings of C_m (12.4 ± 1.5 pF) and the mean time constant obtained from the non-invasive di-8-ANEPPS measurements above (τ= 95.4 ms). It was not possible to calculate the membrane resistance during the depolarization phase (Fig. 4Di) because the observed response was nearly as fast as the kinetics of solution exchange (Fig. 4C). Nevertheless, the faster rate of change indicates a much lower resistance during depolarization. This difference is consistent with the position of each steady-state membrane potential on the current–voltage relation (e.g. Fig. 4B). That is, at the beginning of the depolarization caused by 140 mm K⁺, R_m is expected to be low because of the large Kir conductance, and hence the resulting time constant will be shorter. Conversely, after V_m is depolarized and the Kir conductance is very low (R_m high), the time constant for repolarization by low external K⁺ concentration will be longer.

Non-invasive measurements of membrane potential

Next, we used voltage-sensitive dyes to ascertain the contribution to the resting membrane potential (V_m) of the three ionic currents we had recorded: Kv1.3, Kir and Cl⁻. To assess whether the Cl⁻ conductance contributes (Fig. 5A) we used di-8-ANEPPS (as in Fig. 4) and fast changes in the external Cl⁻ concentration (from 134 to 50 mm) which changes E_Cl to about 0 mV. The result was compared with switching external K⁺ from 5 to 140 mm, which changes E_K to about 0 mV. Either condition is expected to depolarize the cells if the ion is significantly permeant. Switching to high external K⁺ concentration significantly decreased the fluorescence signal, indicating depolarization, and lowering external Cl⁻ concentration from 150 to 50 mm caused a smaller, yet significant depolarization. Although the fast dye, di-8-ANEPPS, was useful for avoiding intracellular ion changes that can occur with longer-term changes in extracellular ions, it was not useful for obtaining absolute V_m values, because it has a very low V_m sensitivity (< 5% change per 100 mV) and we observed a continuous drift in signal intensity (see dashed line in Fig. 4Di) which made calibration very difficult.

To obtain steady-state V_m values, we used DiBAC₄, which trades off a high V_m sensitivity with slow response kinetics. An advantage is that it can be calibrated and used with flow cytometry (Krasznai et al. 1995) to report V_m values in a large number of cells individually. Figure 5B shows the dye calibration procedure for a representative batch of microglia exposed to normal external ion concentrations. V_m was first set to 0 mV using the ionophore, gramicidin, and then the cells were exposed to a range of external DiBAC₄ concentrations, which were allowed to equilibrate across the membrane according to a Nernstian distribution. After using flow cytometry to measure the fluorescence intensity of 5000 cells at each DiBAC₄ concentration, the average cellular fluorescence was plotted to create a standard curve. For experiments, the linear standard curve was used with the fluorescence measurements from microglia without gramicidin (Fig. 5C). In control bath solution, the mean V_m was −42 ± 2 mV (i.e. near the activation threshold of Kv1.3 current). Thus, we predicted that the Kv1.3 current would be very small, and concordantly, we observed that the potent Kv1.3 blocker, agitoxin-2 (Garcia et al. 1997) had almost no effect on V_m (P= 0.34). Previous patch-clamp studies have reported resting V_m values of −54 mV (Kettenmann et al. 1990) or two stable states at about −35 and −70 mV for untreated microglia (Norenberg et al. 1994a; Chung et al. 1999; Boucsein et al. 2003), and about −48 mV for lipopolysaccharide-stimulated microglia (Chung et al. 1998).

At first surprisingly, as it has been generally assumed that Kir is responsible for the negative resting V_m of microglia (Franchini et al. 2004), we found that even a very high concentration (1 mm) of the Kir blocker, Ba²⁺, did not significantly affect the V_m. However, while inward Kir current in microglia is very sensitive to block by external Ba²⁺ (Schlichter et al. 1996; Franchini et al. 2004), the voltage dependence of block means that much higher Ba²⁺ concentrations are needed to block outward Kir current. A further important result (Fig. 5C) refutes the common assumption that raising external K⁺ will depolarize V_m to the new E_K value. This will not happen if other ion conductances are significant. We observed (Fig. 5C) that V_m did not reach E_K when external K⁺ was elevated (i.e. to 30 mm (E_K−39 versusV_m−19 mV), 55 mm (E_K−23 versusV_m−15 mV) or 140 mm (E_K 0 versusV_m−5.3 mV)). This finding is consistent with the lack of effect of agitoxin-2 and Ba²⁺. Instead, we found that both Cl⁻ channel blockers caused substantial depolarizations: to −14 ± 3 mV (NPPB) or −17 ± 8 mV (flufenamic acid), thus Cl⁻ channels contribute to the resting potential. Despite this, it is not surprising that isolating the Cl⁻ current was difficult in whole-cell recordings under non-swelling conditions. That is, a very small Cl⁻ current could account for this contribution to V_m when it is in the high-resistance region around −42 mV (for example, it is 6 pA when R_m is ∼8 GΩ). Moreover, the Cl⁻ current could be larger in intact cells if it is regulated by second messenger pathways that are compromised by whole-cell recording.

Electrical resonance in microglia

The two K⁺ currents we recorded in microglia, Kv1.3 and Kir, are very similar to those in low-frequency cochlear hair cells, where they are responsible for electrical resonance (Crawford & Fettiplace, 1981; Goodman & Art, 1996a); that is, the ability to discriminate input frequency. Thus, we tested for resonance in microglia by applying sinusoidal currents of continuously varying frequency and recording the V_m response under whole-cell current clamp. For the cell shown in Fig. 6Ai, a holding current of (−15 pA) was applied to maintain the initial V_m near the Nernst potential for K⁺ (−85 mV). Then, with a 0-pA offset, the V_m returned to about −42 mV; the same value observed from non-invasive dye measurements (Fig. 5C). From this V_m, a sinusoidal stimulus (± 5 pA) was injected and the V_m response was used to quantify the electrical resonance. Note that immediately after the depolarizing current step the V_m oscillations were heavily damped. Then, as the frequency decreased to between 10 and 15 Hz, larger oscillations occurred in phase with the stimulus. At lower frequencies the in-phase V_m oscillations were smaller. To quantify this resonance effect, impedance plots were constructed (see Methods) by dividing the FFT of the output signal (V_m) by the FFT of the input signal (injected current) for each experiment. Impedance was plotted as a function of the frequency and fitted with an equation describing an RLC circuit with all components in parallel (see Methods, eqn (A)). Under conventional current clamp, the values from this curve fit were: resonant frequency, 11.2 Hz; peak impedance, 2.07 GΩ; quality factor, 0.76 (Fig. 6Aii). These values were the same whether the applied current frequency increased or decreased during the stimulus (not shown).

Figure 6. Microglia display electrical resonance that requires Kv1.3 current.

Left-hand panels, a sine wave current of decreasing frequency (upper traces in each panel) was injected into the same LPS-treated microglial cell under conventional current clamp (A) or dynamic current clamp (B), and the resulting membrane potential (V_m) responses (lower traces in each panel) were monitored. Ai, from a holding current of −15 pA, the offset was switched to 0 pA and a sine wave of amplitude ± 5 pA was injected. Aii, the right panel for each experiment shows an impedance plot, fitted to eqn (A) (see Methods) to obtain resonant frequency, peak impedance, bandwidth and quality factor. B, electrical resonance is enhanced by using the dynamic current clamp to compensate for the leak resistance. i, from a holding current of 0 pA (V_m−83 mV), the offset current was switched to +40 pA, and a sine wave of amplitude ± 5 pA was injected (as in A). ii, the corresponding impedance plot and fitted function (smooth curve; eqn (A); see Methods) display a narrower peak at a lower frequency and have higher peak impedance than with conventional current clamp (A). iii, hyperpolarization can eliminate the resonance. From the same holding current (0 pA; V_m, −84 mV), a smaller offset current was applied (+30 pA), along with the same sine wave (± 5 pA) as in A. iv, the lack of a peak in the corresponding impedance plot indicates there is no resonance.

Many factors can influence the electrical resonance properties of a cell. These include C_m and the time constants of channel opening and closing, which are often a function of voltage. As in previous reports on Kv1.3 (Cahalan et al. 1985; Marom & Levitan, 1994), we found that the kinetics of activation and closing of Kv1.3 channels in microglia have a very steep voltage dependence with relatively slow closing kinetics, and the slowest closing time constants occur between −40 and −60 mV. It is important to note that for every cell tested, the resonant frequency and even the occurrence of resonance was affected by varying the mean V_m (i.e. varying the offset current). Electrical resonance was only observed in a microglial cell if the V_m was between −50 and −35 mV, and within this range, the resonant frequency increased with depolarization (five cells tested; not shown).

The high R_m of microglia makes the leak conductance a particularly powerful variable that should alter the quality and maximal impedance. The measured resonant frequency (F_n) should not be affected by the leak conductance because the cell acts like a parallel R_mLC_m circuit, where F_n= (√[1/LC])/2π. We next used the dynamic current clamp (see Methods and Fig. 3) to assess the effects of compensating for the leak conductance (Fig. 6Bi). While applying the dynamic current clamp, the holding current was stepped to +40 pA to set the initial V_m to about −46 mV, and then a sinusoidal stimulus of ± 5 pA amplitude was applied, as before. The V_m response (Fig. 6Bi) was more complicated than under conventional current clamp (compare Fig. 6Ai). That is, immediately after the depolarizing current step, the endogenous oscillations were damped because they were out of phase with the command current oscillations. Then, for stimulation frequencies between about 6 and 8 Hz, there were large V_m responses in phase with the stimulation. At lower frequencies, the V_m responses were smaller and again, were out of phase. Thus, with dynamic current clamp, phase synchrony occurred over a much narrower frequency range (compare Fig. 6Aii with Fig. 6Bii). It is expected that compensating for R_seal will increase the total R_m and peak impedance, as well as the quality factor value (i.e. Q=R/(2πF_nL); see Methods, eqn (B)), while decreasing the bandwidth. Accordingly, in Fig. 6Bii, when the V_m responses under dynamic current clamp were fitted to the all-parallel RLC impedance function (Methods, eqn (A)), the maximal impedance increased (from 2.2 to ∼3 GΩ), the frequency tuning sharpened (bandwidth decreased from 14.7 to 5.0 Hz), and the quality factor increased (from 0.76 to 1.4). The resonant frequency was lower in this example under dynamic current clamp (7.2 Hz), exactly as we expected from the hyperpolarized V_m and our observation that resonant frequency decreases with hyperpolarization. In principle, if R_seal is overcompensated under dynamic current clamp, the bandwidth and maximal impedance would decrease and the quality factor would increase; however, as illustrated below (see Fig. 8), the inaccuracies are much smaller than if leak compensation is omitted. As for conventional current clamp, resonance only occurred under dynamic current clamp when the mean V_m was in a permissive range. For instance, Fig. 6Biii shows that for the same sinusoidal stimulus as in Fig. 6A (or larger amplitude stimuli, not shown), no resonance peak was observed in the impedance plot (Fig. 6Biv) when a ‘subthreshold’ holding current (+ 30 pA) was applied to set the mean V_m to −77 mV.

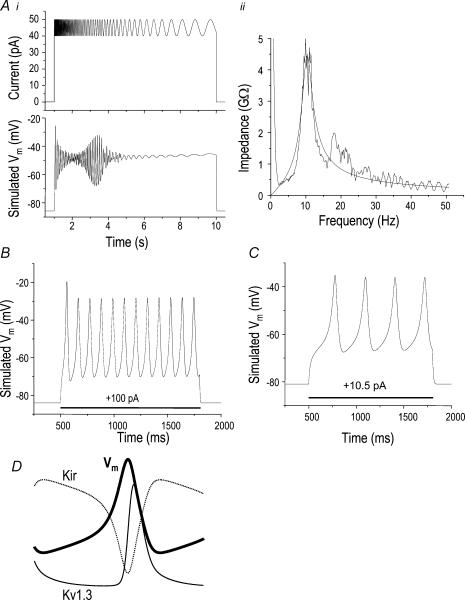
Figure 8. The quantitative model recapitulates the dynamic membrane potential responses.

A, electrical resonance is recapitulated by the quantitative properties of Kv1.3 and Kir currents in microglia. i, simulated current injection of +45 pA and a superimposed sine wave (amplitude, ± 5 pA) of decreasing frequency (see Methods; upper trace). The calculated V_m response based on the actual conductances and kinetics of the Kv1.3 and Kir currents in the microglial cell shown in Fig. 6 (lower trace). ii, impedance plot of the data, calculated by dividing the FFT_output by the FFT_input and fitting to eqn (A) (see Methods). B, calculated membrane potential (V_m) response to a simulated current injection of +100 pA for a microglial cell with relatively large Kv1.3 and Kir currents, and a modest Cl⁻ current. These simulations used actual parameters from the cells shown in Figs 1 and 6A, determined as described in the text. The maximal conductances were 9.72 nS for Kv1.3, 22.3 nS for Kir and 0.5 nS for Cl⁻, and the membrane capacitance was 22.5 pF. C, calculated V_m response to a simulated current injection (+10.5 pA) for a microglial cell with small Kv1.3 and Kir conductances. Values used for this simulation, obtained from the cell shown in Fig. 2B were maximal conductances of 1.5 nS for Kv1.3, 3.6 nS for Kir, 0.25 nS for I_Cl and a membrane capacitance of 10 pF. D, the time course of Kv1.3 current (thin trace), Kir current (dotted trace) and membrane potential during a single V_m oscillation (thick trace). The values were calculated from the simulation in B.

Membrane potential oscillations in microglia

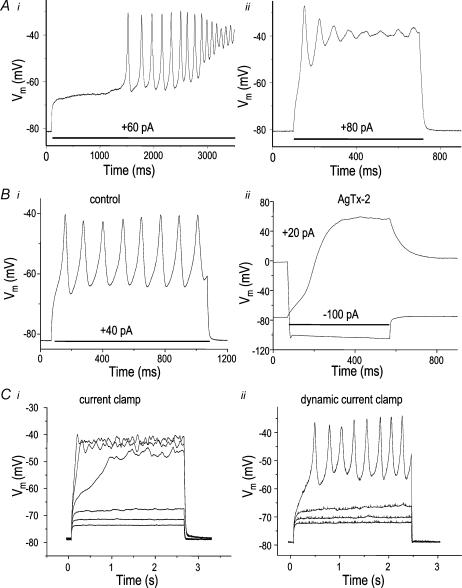
To our surprise, when current pulses were injected to examine current–voltage relations and membrane resistance (as in Fig. 2), occasionally V_m oscillations were seen that were damped (Fig. 7A) or nearly stable (Fig. 7Bi and Cii). The oscillatory response appeared to require a very negative initial V_m and a permissive range of injected current as larger current stimuli caused faster damping (e.g. Fig. 7Aii), and some cells displayed only damped oscillations. In cells that displayed V_m oscillations, the recording mode was subsequently switched to voltage clamp and the ion currents were quantified. Under conventional current clamp, large, stable oscillations were elicited only in cells that had large Kv1.3 and Kir currents. Kv1.3 was necessary as the blocker, agitoxin-2, stopped the oscillations that could be repeatedly evoked by current injection before adding blocker. Figure 7B shows an example wherein stable V_m oscillations (Fig. 7Bi) were prevented after AgTx-2 was applied (Fig. 7Bii) and could no longer be evoked by a wide variety of depolarizing current injections. Instead, even a small depolarizing current evoked a dramatic depolarization, with an inflection point and all-or-nothing response at about −45 mV in this cell. At the end of the stimulus, the cell re-polarized only when a large hyperpolarizing current was injected, after which V_m remained very negative because the large Kir current was activated. Thus, Kv1.3 was necessary for the V_m oscillations and repolarization after depolarizing events, while Kir could maintain a very negative membrane potential. As the permissive voltage range falls within the high resistance range, oscillations and resonance will be easily shunted by the electrode-induced leak. This is a plausible explanation for the infrequency of observing spontaneous oscillations in patch-clamp recordings.

Figure 7. Microglia can produce V_m oscillations that require Kv1.3 current.

A, conventional current-clamp recordings from an LPS-treated microglial cell that had large Kv1.3 and Kir currents, and an apparent resting potential of −82 mV i, V_m oscillations were elicited when a +60-pA current was injected for the duration of the recording. ii, injecting a larger current (+80 pA) elicited oscillations that were rapidly damped during the current injection (shown by the bar). B, under conventional current clamp, V_m oscillations are prevented by the Kv1.3-channel blocker, agitoxin-2. i, quasi-stable V_m oscillations were elicited by a depolarizing current (indicated by bar). ii after adding 1 nm agitoxin-2 to the bath, no V_m oscillations were elicited by depolarizing currents (+20 pA shown). Injection of −100 pA produced a rapid hyperpolarization of V_m. C, the dynamic current clamp can expose V_m oscillations in response to current injections. i, a conventional current clamp recording with a holding current of −40 pA, chosen to set the initial V_m to −85 mV. Currents were injected between −5 pA and +20 pA, in 5-pA steps. Note the inflection point at about −60 mV. ii, a dynamic current-clamp recording, wherein compensation for the seal resistance set the initial V_m to −85 mV. Depolarizing current steps from +50 to +65 pA in 5-pA increments show quasi-stable V_m oscillations and an inflection point at about −58 mV.

Although spontaneous V_m oscillations were seen in only three cells under conventional current clamp, they were seen in three formerly non-oscillating cells when recording was switched to dynamic current clamp. Of importance, these V_m oscillations even occurred in cells with smaller Kv1.3 and Kir conductances, such as the cell shown in Fig. 7C, which nevertheless displayed a very negative initial V_m (about −78 mV). In this cell, under standard current clamp (Fig. 7Ci), the V_m responses to a series of depolarizing current steps showed an inflection at about −60 mV but, at most, only very small damped oscillations. In contrast, under dynamic current clamp (Fig. 7Cii), which did not change the initial V_m, this cell displayed stable V_m oscillations in response to sufficient depolarizing current. The V_m responses of cells with small K⁺ conductances are more likely to be short-circuited by the electrode-induced leak.

The quantitative model predicts electrical resonance

For all simulations, the cell was modelled as a single compartment and a uniform distribution of each channel type was assumed. Changes in membrane potential (V_m) with time were calculated from ionic and injected currents by numerically solving the conservation of current equation, as follows.

(14)

C_m is the capacitance of the cell and I_App simulates the injected current. I_seal was used in selected simulations to mimic damage caused by the patch electrode. It is a simple ohmic current of the form: I_seal=V_m/R_seal, where R_seal is the seal resistance. I_Kv and I_ir were defined above (eqns (1)–(5) and (10)–(13)). First, the parameters obtained from the cell shown in Fig. 6 were used to test the hypothesis that the two prevalent K⁺ channels in microglia can cause the observed electrical resonance. The maximal conductance parameters for the simulation in Fig. 8A were Kv1.3: gKv_max, 9.4 nS; Kir: gKir_max, 7.3 nS. At the highest frequencies, the V_m response to the sinusoidal current stimulus (Fig. 8Ai) showed damped oscillations, and the maximal changes in V_m occurred over a narrow band of frequencies centred around 10 Hz. To quantify the electrical resonance, an impedance plot (Fig. 8Aii) was constructed by dividing the FFT of the output voltage by the FFT of the input current (see Methods) (Hutcheon et al. 1996). When fitted to a function describing impedance of an RLC circuit with all components in parallel (see Methods, eqn (A)), this plot yielded the following values: resonant frequency, 10.36 Hz; peak impedance, 4.45 GΩ; quality factor, 3.69. Moreover, with the parameters from the cell shown in Fig. 1, the simulations (not shown) showed that injecting sinusoidal currents of varying frequency yielded similar results to those in Fig. 8A.

These simulations omitted the small Cl⁻ current; thus, they mimic the slight overcompensation of R_seal previously described. In principle, this overcompensation would decrease the bandwidth, increase the quality factor and decrease the maximal impedance. However, as the following calculation shows, the inaccuracy is much smaller than if R_seal compensation is omitted. In Fig. 8A, a 2.1-GΩR_seal was compensated for, but if it was ignored, Q would decrease from 3.69 to 2.50; bandwidth would increase from 2.81 to 4.47 Hz; and maximal impedance would decrease from 4.45 to 1.77 GΩ. In contrast, if a Cl⁻ conductance of 0.07 nS was overcompensated for, Q would decrease from 3.69 to 3.52; bandwidth would increase from 2.81 to 2.96 Hz; and maximal impedance would decrease from 4.45 to 3.55 GΩ. Clearly, the consequences of not compensating for R_seal are much more serious than overcompensating by ignoring the Cl⁻ current.

The model predicts V_m oscillations produced by Kv1.3, Kir and Cl^– currents

Values of current kinetics and maximal conductances were obtained from the cell in Fig. 1 and from the same cell whose current-clamp recordings are shown in Fig. 7A, and then incorporated into the mathematical model (Fig. 8B). Assuming that I_Cl accounted for all the current at E_K, a conservative estimate of 0.5 nS was obtained for gCl: an overestimate because seal leak also contributes. In principle, overcompensating R_seal would favour voltage oscillations; however, the same general features of the V_m oscillations were obtained for gCl values between 0 and 2.5 nS (not shown). Most importantly, voltage oscillations were observed using conventional current clamp and entirely accounted for mathematically by known ion currents in microglia.

This model also predicts that dynamic V_m changes will occur in cells whose input resistance is too high for accurate current-clamp recordings; that is, in microglial cells with small K⁺ currents. For the untreated cell in Fig. 2B, the currents were too small to obtain accurate kinetic parameters; nevertheless, they appeared to be Kv1.3 (i.e. voltage-gated, AgTx-2-sensitive) and Kir (inwardly rectifying, Ba²⁺-sensitive). Thus, to simulate the behaviour of this cell, we used its actual values of g_max, obtained under voltage clamp, and substituted the same kinetics and voltage dependence as observed for the cell shown in Fig. 1. Based on the simulation for this high-resistance cell (Fig. 8C) we predict that microglia with small K⁺ currents will produce V_m oscillations within a similar membrane potential range but with a longer period and requiring much less depolarizing current injection.

One benefit of a mathematical model is that each contributing variable can be analysed individually. To illustrate the basic mechanism underlying the V_m oscillations, Fig. 8D shows an overlay of the calculated contribution of each K⁺ current to the membrane potential changes during a single oscillation. This simulation can be interpreted in light of the kinetics and voltage dependence we measured for the microglial currents. When the Kir current decreases because of a small depolarization, the Cl⁻ and injected currents dominate and further depolarize the cell. This depolarization activates Kv1.3 channels and increases the K⁺ conductance, which then dominates and begins to repolarize the cell. When V_m reaches a sufficiently negative value, Kir is re-activated and Kv1.3 channels close, thus restoring the initial conditions. The current-clamp observations in Fig. 7 are completely consistent with this interpretation; that is, the Kv1.3 blocker, AgTx-2, prevented repolarization (Fig. 7Bii) but did not affect depolarization. The cell depolarized to 0 mV because of Kir channel closing, and then V_m remained at ∼0 mV because the endogenous inward current (e.g. leak or Cl⁻) was still present and unopposed by K⁺ conductances. Injection of a large hyperpolarizing current then restored V_m to a stable negative value at which Kir was active and sufficiently large to overcome the endogenous depolarizing current.

Discussion

Despite numerous papers describing individual currents in microglia, none have addressed how the multiple channel types integrate to affect V_m. To address this question we used cultured rat brain microglia and several approaches: non-invasive V_m-sensitive dyes, conventional- and dynamic-current clamp, and mathematical simulations.

The only K⁺ currents we observed closely resembled Kv1.3 and Kir2.1, and their amplitudes and prevalence were quite variable. Such variability has been previously noted but the reasons are not well understood. We found increases in Kv1.3 transcript and current levels after LPS treatment without a change in protein expression (Fordyce et al. 2005). During microglial culturing and entry into the mitotic cycle, Kv1.3 protein increased at the cell surface (Kotecha & Schlichter, 1999). Substantial Kv currents have been reported in unstimulated microglial cells and some pro-inflammatory stimuli (e.g. lipopolysaccharide, interferon-γ) have been reported to increase the current (Illes et al. 1996; Visentin & Levi, 1997). Astrocyte-derived factors, such as granulocyte-macrophage colony-stimulating factor (GM-CSF) (Eder et al. 1995; Fischer et al. 1995) and transforming growth factor β (TGF-β) (Schilling et al. 2000), which are thought to promote a more resting state, have also been reported to increase the Kv current.

Our initial goal was to measure the membrane potential (V_m) and determine the contributions of each channel to V_m. Like many studies on numerous cell types, we used the conventional current-clamp configuration; however, concerns were raised when the current–voltage relationships were nearly linear over a wide V_m range. A key finding is that this linearity results from the input resistance of cultured rat microglia near the resting potential being much higher than the seal resistance, either before or after breaking into the whole-cell configuration. A more accurate, non-invasive measurement of R_m was obtained using the kinetics of V_m changes recorded with the fast voltage-sensitive dye, di-8-ANEPPS. We also devised a dynamic current-clamp circuit to actively compensate for the leak conductance which, as expected from the high R_m values, improved the recording accuracy. Consistently, the current–voltage relations, dynamic current clamp and V_m-sensitive dye measurements all show that R_m in microglia is very high, particularly in the resting V_m range. It is important that current-clamp measurements of V_m from high-resistance cells are interpreted cautiously; whereas the dye-based and dynamic current-clamp methods should be broadly applicable to many high-resistance cells, both excitable and non-excitable. Moreover, attempting to measure the true membrane resistance by blocking ionic currents with pharmacological agents (Pun & Kleene, 2004) is problematic for microglia and many other high-resistance cells, because the available channel blockers often are low potency, not very specific and block can be strongly voltage dependent (e.g. block of outward Kir current by Ba²⁺).

Our results provide the first evidence that a Cl⁻ current contributes to V_m in microglia. That is, voltage-sensitive dye measurements from intact microglia showed V_m responses to changes in external Cl⁻ concentration and to Cl⁻ channel blockers. In whole-cell recordings we observed one Cl⁻ current; the same swelling-sensitive current we previously described (Schlichter et al. 1996). Compared with the Kv1.3 and Kir currents, less is known about this Cl⁻ current, and other than cell swelling, factors that regulate its prevalence or amplitude have not been reported. Nevertheless, some roles have been ascribed to this current. We previously showed that several drugs that block the Cl⁻ current inhibit proliferation of rat microglia (Schlichter et al. 1996), and similar drugs reduced the development of cell extensions (‘ramification’) in cultured murine microglia (Eder et al. 1998).

Microglia, like other immune cells are considered to be non-excitable; that is, lacking regenerative action potentials. Thus, an intriguing result is that all cultured rat microglial cells examined displayed electrical resonance and a few produced large V_m oscillations. By combining voltage- and current-clamp measurements with mathematical modelling, we showed that a combination of Kv1.3, Kir and Cl⁻ currents can account for both behaviours. Although both K⁺ currents were necessary, their amplitudes did not critically affect the existence of electrical resonance; however, the V_m oscillations were more pronounced when both K⁺ currents were large. Of most importance, resonance and V_m oscillations occurred with either the conventional or dynamic current clamp, but only when V_m was in a physiologically relevant, permissive range. That is, impedance–frequency plots showed sharp frequency selection in the 5- to 20-Hz range. This ability of cultured rat microglial cells to discriminate input frequency occurred only when V_m was in the −20 to −50 mV range, which is in both the high resistance region and in the resting V_m range. Thus, the model predicts that both oscillations and resonance require a small inward current but will be inhibited if the inward current is too large. From the present study, the most likely inward current is the Cl⁻ current, as it is active over the full V_m range and contributes to the resting V_m. The model also shows that frequency selection in microglia results from elimination of lower frequency signals by the action of Kv1.3 current and that the signal is amplified by the Kir current. Electrical resonance has been observed in other cell types, most notably low frequency hair cells (Goodman & Art, 1996a) and some neurones (Hutcheon et al. 1994; Hu et al. 2002). Resonance was attributed to two currents: one with relatively slow kinetics that opposes V_m changes, with amplification by a second current with fast kinetics that favours V_m changes (Hutcheon & Yarom, 2000). For microglia and low-frequency hair cells, these appear to be a Kv and Kir current, respectively (Goodman & Art, 1996a). Kir has very fast ion-dependent gating and a negative slope conductance over the physiological V_m range, thus favouring voltage changes (Goodman & Art, 1996b). In neurones, other currents appear to fill these roles (Hutcheon et al. 1994; Hu et al. 2002).

The excellent agreement between the observed and simulated V_m oscillations in microglia demonstrates the roles of the same Kv1.3, Kir and Cl⁻ currents. During an individual event, outward Kir current was essential for establishing a rather negative initial V_m. Then, as inward current depolarized the cell, Kir current decreased, allowing the depolarizing current to dominate, leading to further depolarization. This positive feedback is expected from the negative slope of the current–voltage relationship, and has been described for Kir currents in other cells (Fuchs et al. 1988; Goodman & Art, 1996b). Then, depolarization activated the Kv1.3 current (faster near the peak V_m), which produced the hyperpolarizing phase of the V_m oscillation, whose duration was controlled by the slow closing time constant of Kv1.3 in this V_m range. Finally, Kv1.3 channels closed faster with further hyperpolarization and the inward Cl⁻ current could initiate the next V_m oscillation. It is interesting that similar V_m oscillations (between −30 and −60 mV) in outer cochlear hair cells are also driven by Kv and Kir currents, where they are used for low-frequency tuning (Goodman & Art, 1996a).

It is important to note that the whole-cell recordings necessarily restrict the types of active channels; thus, under other circumstances, additional inward and outward currents might contribute to V_m. For instance, Ca²⁺–calmodulin-dependent K⁺ currents (SK or IK currents) can be activated by a rise in cytoplasmic Ca²⁺ concentration (Khanna et al. 1999) and inward currents might be provided by store-operated or Ca²⁺-release activated Ca²⁺ (CRAC) channels (Toescu et al. 1998; Fanger et al. 2001), ionotropic purinergic receptors (Norenberg et al. 1994b), TRPM7 channels (Jiang et al. 2003) or even electrogenic pumps (Schrenzel et al. 1998) or exchangers (Nagano et al. 2004). Whether activation of a different set of inward and outward currents will result in steady-state or dynamic V_m changes will depend on their relative conductances and biophysical properties. In the future, it will be worthwhile to use a similar approach wherein the active currents and resulting V_m behaviours are measured and combined in a mathematical model for microglia responding to different stimuli and in ex vivo brain slices.

The physiological role of electrical resonance and V_m oscillations in microglia is not known. However, if Ca²⁺ influx is through CRAC channels like those in lymphocytes, then V_m oscillations should be more effective in promoting Ca²⁺ influx (Lewis, 2001). Although CRAC-channel gating is not voltage dependent, hyperpolarization promotes Ca²⁺ influx, and there is negative feedback because elevated cytoplasmic Ca²⁺ inactivates the channels. V_m oscillations might also promote Ca²⁺ influx through the Ca²⁺-entry mode of the Na⁺–Ca²⁺ exchanger, particularly if Na⁺ microdomains form (Arnon et al. 2000). If the depolarizing current in microglia involves Na⁺ entry (e.g. through non-selective channels or purinergic receptors) and Na⁺ microdomains form during the hyperpolarized period of each V_m oscillation, they may facilitate Ca²⁺ entry during the depolarized period when the Na⁺–Ca²⁺ exchanger reverses. A role for electrical resonance in frequency tuning is an obvious possibility for reptilian cochlear hair cells (Fuchs et al. 1988; Goodman & Art, 1996a), and for microglia, there are several intriguing possibilities. Given the very high membrane impedance of microglial cells at the resonant frequency, even small fluctuations in current (e.g. channel noise) at this frequency might evoke V_m oscillations. Microglia might also receive frequency information from neighbouring cells, as they interact intimately with T lymphocytes during antigen presentation through immunological synapses, and with neurones and glial cells. It is interesting that when T cells interact with antigen-presenting cells, oscillations in intracellular Ca²⁺ levels at a similar frequency (∼10 Hz) have been observed (M. Davis, personal communication). Moreover, information from rhythmically firing neurones might be communicated by electrotonic coupling, or by direct coupling though gap junctions. Microglia constitutively express ionotropic purinergic receptors whose activity can depolarize these cells (Norenberg et al. 1994b), thus microglia might be designed to detect rhythmic release of ATP from neurones or glia (Burnstock, 2004).